Тепловое излучение. (Тема 33)

1. ТЕМА XXXIII. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ

2. 1. ОПРЕДЕЛЕНИЯ

Излучение телами электромагнитных
волн (свечение тел) может происходить
за счет различных видов энергии.
Самым распространенным является
тепловое излучение,
при котором излучение
электромагнитных волн происходит
за счет внутренней энергии тел.
Все остальные виды свечения,
возбуждаемые за счет любого вида
энергии, кроме внутренней (тепловой),
объединяются под общим термином
«люминесценция»:
хемилюминесценция,
электролюминесценция,
катодолюминесценция,
фотолюминесценция.

3. 2. РАВНОВЕСНОСТЬ ТЕПЛОВОГО ИЗЛУЧЕНИЯ (I)

Тепловое излучение имеет место при любой температуре, однако чем
меньше температура, тем меньше интенсивность теплового излучения;
при низких температурах происходит практически
лишь длинноволновое (инфракрасное) излучение.
Окружим излучающее в вакууме тело оболочкой
с идеально отражающей поверхностью.
Излучение тела отражается оболочкой , падает на
тело, поглощается им (частично или полностью), а
затем опять переизлучается телом.
То есть происходит непрерывный обмен энергией
между телом и излучением, заполняющим полость.
Если распределение энергии между телом и излучением не изменяется с
течением времени (сколько энергии излучается телом в единицу времени,
столько же и поглощается) для каждой длины волны, то состояние
системы тело-излучение будет называться равновесным.
Единственным видом излучения, которое может находиться в равновесии
с излучающими телами, является тепловое излучение.

4. 2. РАВНОВЕСНОСТЬ ТЕПЛОВОГО ИЗЛУЧЕНИЯ (II)

Cпособность теплового излучения находиться в
равновесии с излучающими телами обусловлена
тем, что его интенсивность возрастает с ростом
температуры и уменьшается при ее уменьшении.
Допустим, равновесие между излучением и телом
нарушено: тело излучает больше, чем поглощает.
Тогда внутренняя энергия тела будет убывать,
а вместе с ней и температура.
Уменьшение температуры, в свою очередь, обусловит
уменьшение излучаемой телом энергии.
Температура тела будет понижаться пока количество излучаемой телом
энергии не станет равным количеству поглощаемой энергии.
Если равновесие нарушится в другую сторону,
т.е. количество излучаемой энергии окажется меньше, чем поглощаемой,
температура тела станет возрастать до тех пор,
пока равновесие снова не восстановится.

5. 3. ЭНЕРГЕТИЧЕСКАЯ СВЕТИМОСТЬ И ИСПУСКАТЕЛЬНАЯ СПОСОБНОСТЬ (I)

Тепловое излучение можно характеризовать потоком
энергии, то есть энергией излучаемой телом по всем
направлениям в единицу времени (мощность).
Поток энергии, испускаемый единицей поверхности
излучаемого тела по всем направлениям
(в пределах телесного угла 2 ),
называется энергетической светимостью тела.
dW
Дж
Вт
R
; R 1 2 1 2 .
м с
м
dSdt
Энергетическая
светимость является функцией температуры.
Излучение состоит из волн различных частот .
При малом интервале излучаемых частот d
поток, излучаемый в этом интервале частот dR ,
пропорционален ширине этого интервала, т.е.
r
dR r d ; r 1 Дж м2 .
Величина
называется испускательной способностью тела.

6. 3. ЭНЕРГЕТИЧЕСКАЯ СВЕТИМОСТЬ И ИСПУСКАТЕЛЬНАЯ СПОСОБНОСТЬ (II)

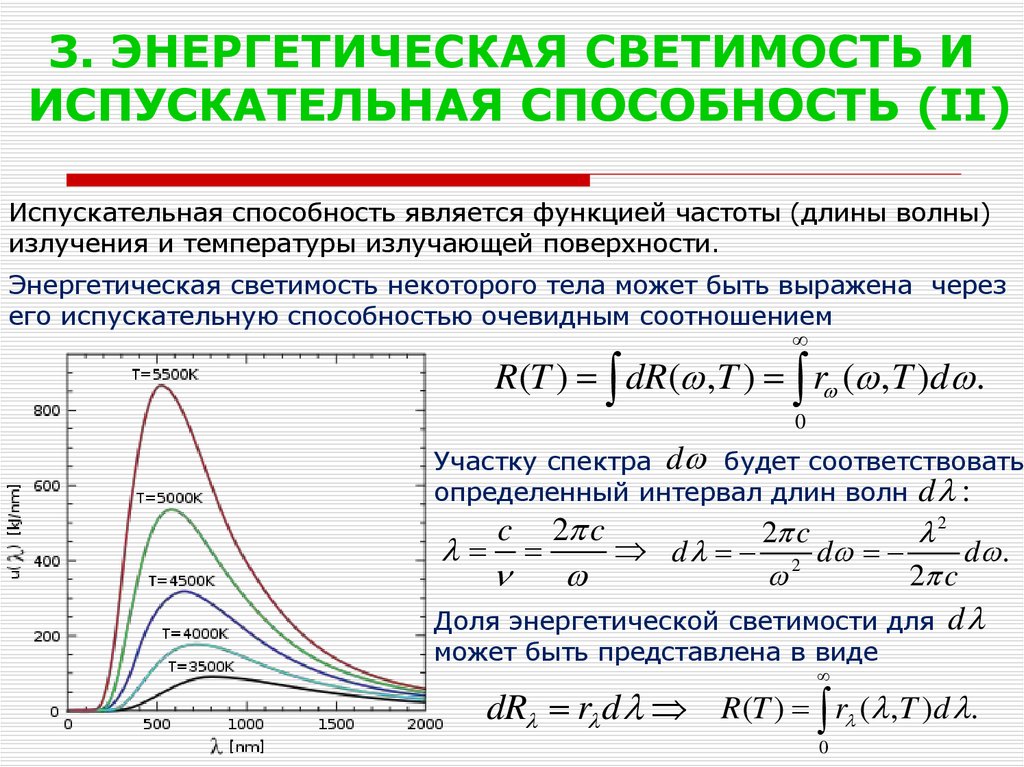
Испускательная способность является функцией частоты (длины волны)
излучения и температуры излучающей поверхности.
Энергетическая светимость некоторого тела может быть выражена через
его испускательную способностью очевидным соотношением
R(T ) dR( , T ) r ( , T )d .
0
Участку спектра d будет соответствовать
определенный интервал длин волн d :
2 c
2
d 2 d
d .
2 c
Доля энергетической светимости для d
c
2 c
может быть представлена в виде
dR r d R(T ) r ( , T )d .
0

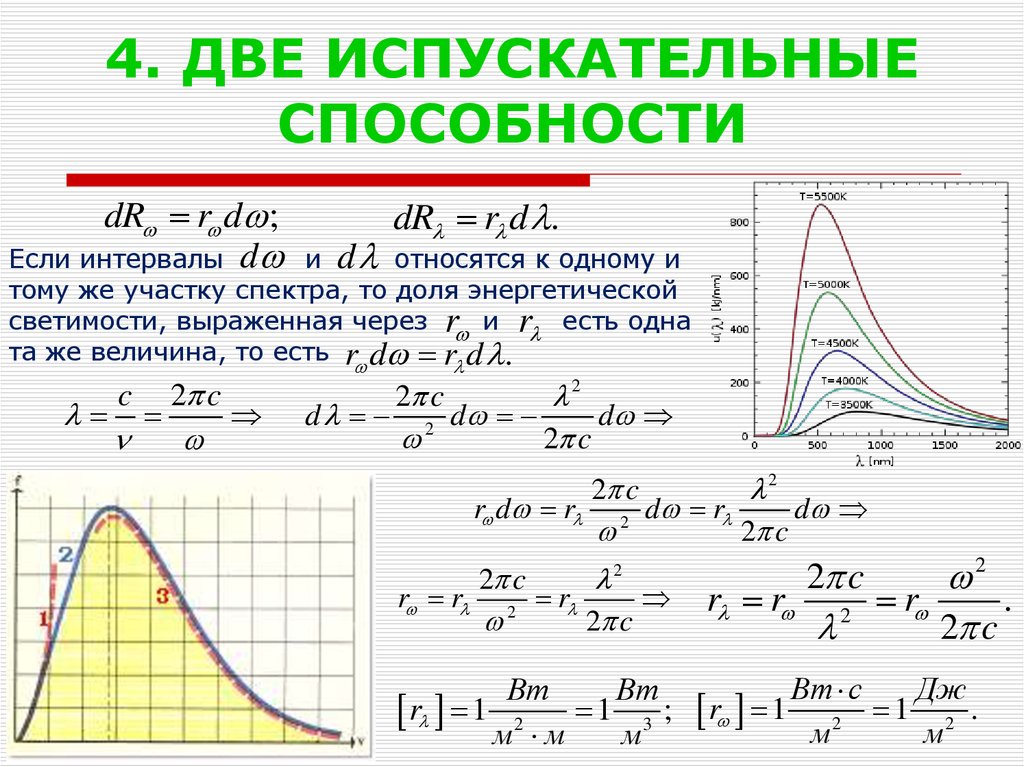
7. 4. ДВЕ ИСПУСКАТЕЛЬНЫЕ СПОСОБНОСТИ

dR r d ;
Если интервалы d
dR r d .
и d относятся к одному и
тому же участку спектра, то доля энергетической
светимости, выраженная через r и r есть одна
та же величина, то есть r d r d .
c
2 c
2 c
2
d 2 d
d
2 c
2 c
2
r d r 2 d r
d
2 c
2 c
2
r r 2 r
2 c
Вт
Вт
r 1 2 1 3 ;
м м
м
r r
2 c
2
2
r
.
2 c
Вт c
Дж
r 1 2 1 2 .
м
м

8. 5. ПОГЛОЩАТЕЛЬНАЯ СПОСОБНОСТЬ ТЕЛА

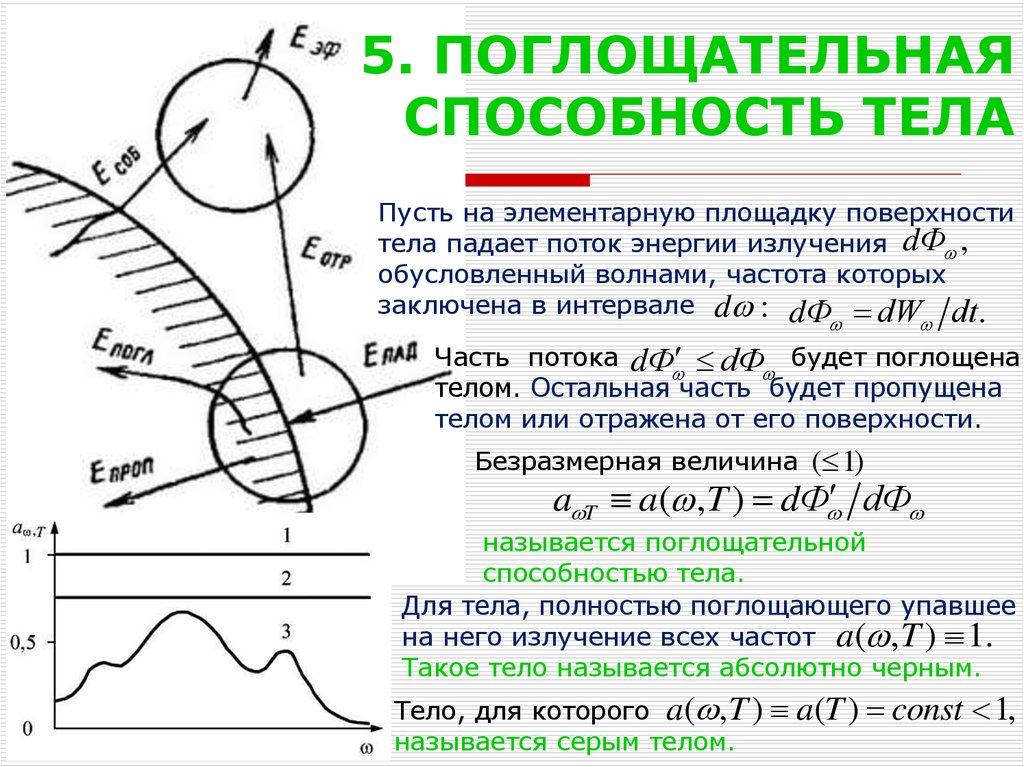
Пусть на элементарную площадку поверхности
тела падает поток энергии излучения dФ ,
обусловленный волнами, частота которых
заключена в интервале d : dФ dW dt.
Часть потока dФ dФ будет поглощена
телом. Остальная часть будет пропущена
телом или отражена от его поверхности.
Безразмерная величина ( 1)
a T a( ,T ) dФ dФ
называется поглощательной
способностью тела.
Для тела, полностью поглощающего упавшее
на него излучение всех частот a( , T ) 1.
Такое тело называется абсолютно черным.
Тело, для которого a( , T ) a(T ) const
называется серым телом.
1,

9. 6. ЗАКОН КИРХГОФА

Пусть внутри замкнутой эвакуированной оболочки, поддерживаемой при
постоянной температуре, помещены несколько тел. Опыт показывает,
что такая система через некоторое время придет в состояние теплового
равновесия – все тела примут одну и ту же
температуру равную температуру оболочки.
Поскольку температура (а следовательно, и
энергия) в состоянии теплового равновесия у
тел не меняется, то тело, испускающее больше
энергии, должно и больше поглощать, то есть
излучательная и поглощательная способности
тела должны быть связаны между собой.
Кирхгоф установил закон согласно которому,
отношение испускательной и поглощательной способностей не зависит от
природы тела, оно является для всех тел одной и той же (универсальной)
функцией частоты и температуры тела:
r
r ( , T )
Не следует путать испускание лучей
с их отражением поверхностью тела.
T
a T
a ( , T )
f ( , T ).

10. 7. УНИВЕРСАЛЬНАЯ ФУНКЦИЯ КИРХГОФА

Для абсолютно черного тела a( , T )
Тогда из закона Кирхгофа следует:
1.
r T
r *T
f ( , T )
f ( , T )
a T
1
f ( , T ) r .
*
T
Универсальная функция Кирхгофа есть
испускательная способность абсолютно
черного тела.
При теоретических исследованиях для характеристики спектрального
состава равновесного теплового излучения используют функцию f ( , T ).
В экспериментальных работах удобнее пользоваться функцией
Обе функции связаны между собой так же как T и T
r
2 c
2
f ( , T ) 2 ( , T )
( , T ).
2 c
f ( ,T ) 1
r :
Дж
;
2
м
( , T ).
Вт
( ,T ) 1 3 .
м

11. 8. ИЗЛУЧЕНИЕ АБСОЛЮТНО ЧЕРНОГО ТЕЛА

Абсолютно черных тел в природе не
существует – это модель.
Однако можно создать устройство сколь
угодно близкое к нему по своим свойствам.
Такое устройство представляет собой почти
замкнутую полость с малым отверстием.
Излучение, проникшее внутрь полости через
отверстие, многократно отражается от стенок
полости и почти полностью поглощается ими.
Согласно закону Кирхгофа
испускательная способность
такого устройства близка к
универсальной функции
Кирхгофа при температуре
стенок полости.
Если поддерживать температуру стенок полости, то из
отверстия выходит излучение абсолютно черного тела,
соответствующее температуре стенок полости.

12. 9. РАВНОВЕСНАЯ ПЛОТНОСТЬ ЭНЕРГИИ ИЗЛУЧЕНИЯ (I)

Представим себе эвакуированную полость,
стенки которой поддерживаются при
постоянной температуре T .
Излучение внутри полости будет находиться в
равновесии с веществом (стенками полости).
В равновесном состоянии энергия излучения
будет распределена в объеме полости с
определенной плотностью u u (T ) dW dV .
Спектральное распределение энергии можно охарактеризовать функцией
u ( , T ), определяемой условием du u ( , T )d ,
du доля плотности энергии, приходящаяся на интервал частот d .
Полная объемная плотность энергии u (T )
связана со спектральной объемной плотностью энергии
очевидным интегральным соотношением
u ( , T )
u (T ) du (T ) u ( , T )d .
0

13. 9. РАВНОВЕСНАЯ ПЛОТНОСТЬ ЭНЕРГИИ ИЗЛУЧЕНИЯ (II)

Из термодинамических соображений следует, что равновесная плотность
энергии излучения u(T) зависит только от температуры
и не зависит от свойств стенок полости.
Рассмотрим две полости, стенки которых
изготовлены из разных материалов и в
начале имеют одинаковую температуру.
Предположим, что равновесная плотность
энергии в обеих полостях различна.
Для определенности пусть u A (T ) uB (T ).
Тогда поток энергии из полости А в полость B будет больше встречного.
В результате стенки полости B станут поглощать больше энергии,
чем излучать, и температура их начнет повышаться.
Напротив, стенки полости А станут поглощать меньше, чем излучать,
и их температура будет уменьшаться – они охлаждаются.
Однако два тела с первоначально одинаковой температурой не могут в
результате только теплообмена приобрести различные температуры – это
запрещено вторым началом термодинамики, поэтому u A (T ) uB (T ).

14. 9. РАВНОВЕСНАЯ ПЛОТНОСТЬ ЭНЕРГИИ ИЗЛУЧЕНИЯ (III)

Полученный результат u A (T ) uB (T )
означает независимость плотности
равновесного теплового излучения от
природы излучающих поверхностей.
Вывод о равенстве u A (T ) и uB (T )
распространяется на каждый компонент
спектра излучения u A ( , T ) uB ( , T ).
Поясним полученный результат следующим образом.
Абсолютно черные стенки поглощают падающий поток
Ф полностью и излучают такой же поток.
э
Стенки с поглощательной способностью a T
поглотят долю упавшего потока энергии a T Фэ
а отразят долю (1 a T )Фэ .
И излучат поток, равный поглощенному, т. е. a Ф
T
э
.
В итоге произвольные стенки полости вернут в
излучение такой же поток, как и абсолютно черные.

15. 10. ПЛОТНОСТЬ ПОТОКА ЭНЕРГИИ (I)

Рассмотрим эвакуированную полость с абсолютно
черными стенками при постоянной температуре.
В случае равновесия через каждую точку внутри
полости будет проходить в любом направлении
поток излучения одинаковой плотности (изотропия).
Если бы излучение распространялось только в
одном направлении, то плотность потока энергии
dW
u (T ) dV u (T ) dScdt
j0
cu (T ).
dt dS
dt dS
dt dS
Для каждой точки внутри полости плотность потока энергии cu (T )
равномерно распределена в пределах полного телесного угла 4 страд.
Следовательно, в пределах элементарного телесного угла d
будет течь поток энергии, плотность которого будет
cu (T )
dj
d ,
4
d
dS r sin d rd
sin d d .
2
2
r
r

16. 10. ПЛОТНОСТЬ ПОТОКА ЭНЕРГИИ (II)

Возьмем на поверхности полости
элементарную площадку S .
Эта площадка посылает в пределах
телесного угла d sin d d
в направлении, образующем с
нормалью угол , поток энергии
dФэ dj Scos
cu (T )
cu (T )
d S cos
S cos sin d d .
4
4
По всем направлениям, заключенным в пределах телесного угла
площадка S
излучает в полупространство поток энергии Фэ :
cu (T )
Фэ dФэ
S
4
2
0
2
2
c
cos sin d d u (T ) S .
4
0
Поток энергии, испускаемый элементарной площадкой можно выразить
через энергетическую светимость:
Фэ R S
*
c
R S u (T ) S
4
*
c
c
R u (T ) f ( , T ) u ( , T ).
4
4
*

17. 11. ЗАКОНЫ СТЕФАНА-БОЛЬЦМАНА, ВИНА

11. ЗАКОНЫ СТЕФАНАБОЛЬЦМАНА, ВИНА
Австрийские физики Йозеф Стефан
(в 1879 г. экспериментально) и Людвиг Больцман
(в 1884 г. теоретически на основе термодинамики)
получили выражение для
энергетической светимости R* f ( , T ) d T 4 .
абсолютно черного тела:
0
Экспериментальную константу 5,67 10 8 Вт ( м 2 К 4 ),
называют постоянной Стефана – Больцмана.
Немецкий физик Вильгельм Вин (в 1893 г. связав термодинамику и
электромагнетизм ) показал, что универсальная функция Кирхгофа
(спектральное распределение плотности потока
3
энергии излучения абсолютно черного тела)
f ( , T ) F .
должна быть пропорциональна кубу частоты
T
Анализируя это соотношение Вин пришел к выводу, что длина волны m ,
на которую приходится максимум излучения абсолютно черного тела
обратно пропорциональна температуре тела (закон смещения Вина):
T m b,
b 2,90 10 3 м К
– постоянная смещения Вина.

18. 12. ЧИСЛО МОД КОЛЕБАНИЙ. ОДНОМЕРНЫЙ СЛУЧАЙ (I)

x
Уравнения волн имеют вид
Пусть вдоль оси
бегут во
встречных направлениях две
плоские волны, возникающие
в результате отражения от
стенок, расположенных в
точках x 0 и
x a.
1 A cos( t kx), 2 A cos( t kx ).
На границах наблюдаются либо узлы стоячей волны
(закрепленная на концах струна) ,
либо пучности стоячей волны (закрепленный в середине стержень)
0.
Произведем сложение колебаний для случая пучностей ( 0) :
1 2 A cos( t kx) A cos( t kx) 2 A cos(kx) cos( t ).
При x=0 очевидно наблюдается пучность.
Чтобы пучность наблюдалась и на второй границе, необходимо наложить
ограничение на волновое число, а именно должно выполнятся условие
ka n
(n 1,2,3,...)
k
a
n.

19. 12. ЧИСЛО МОД КОЛЕБАНИЙ. ОДНОМЕРНЫЙ СЛУЧАЙ (II)

В одномерном пространстве стоячие волны, возможны, если модуль
волнового вектора (волновое число) удовлетворят условию
k
Пусть существуют две волны:
k
n , и
a
Nk ,
Разность чисел n nn дает число стоячих волн
модули волновых векторов которых лежат в пределах k
N k n n
a
k
a
k
Nk
a
(k k )
a
k
k
a
a
n .
k k :
dN k
a
dk .
Модуль волнового вектора связан с частотой волны и ее скоростью
k
2
V
d
dk
V
a d
dN
V
a
dN
d .
V
Мы получили число стоячих dN (число мод колебаний),
частоты которых лежат в элементарном интервале от до
d .
n.

20. 13. ЧИСЛО МОД КОЛЕБАНИЙ. ДВУМЕРНЫЙ СЛУЧАЙ (I)

Пусть в пределах прямоугольной области
со сторонами a (вдоль оси x)
и b (вдоль оси y) возбуждена волна (1),
бегущая в направлении вектора k1.
После отражения от правой границы возникает
бегущая волна (2) с волновым вектором k2 .
Отражение волны (2) от верхней границы
приведет к возникновению волны (3)
с волновым вектором k3 .
Наконец, отражение волны (3) от левой границы
приведет к появлению волны (4) с волновым вектором k4 .
Другие волны не возникают. Отражение волны (1) от верхней границы
даст волну (4), отражение волны (2) от левой границы даст волну (1),
отражение волны (3) от нижней границы даст волну (2),
волны (4) от нижней и правой границ области даст волны (1) и (3).
Итак, произвольная плоская волна в двумерной области
вызовет появление еще трех за счет отражений.

21. 13. ЧИСЛО МОД КОЛЕБАНИЙ. ДВУМЕРНЫЙ СЛУЧАЙ (II)

y
и
Если проекции вектора k1 на оси
обозначить через k x и k y ,
то проекции всех четырех векторов для волн,
появляющихся при отражении, будут равны
(номер волны указан в скобках):
x
(1)
(3)
kx , k y ;
k x , k y ;
(2)
(4)
k x , k y ;
k x , k y .
Уравнения бегущих волн для случая пучностей на границах
(фаза волны не меняется при отражении) имеют вид
1 A cos( t k x x k y y );
3 A cos( t k x x k y y );
2 A cos( t k x x k y y );
4 A cos( t k x x k y y ).
Сложив попарно эти уравнения, получим
12 1 2 2 A cos(k x x)cos( t k y y ); 34 3 4 2 A cos(k x x)cos( t k y y ).

22. 13. ЧИСЛО МОД КОЛЕБАНИЙ. ДВУМЕРНЫЙ СЛУЧАЙ (III)

Cовокупность четырех волн в двумерной
области удалось уменьшить до двух:
12 2 A cos(k x x)cos( t k y y );
34 2 A cos(k x x)cos( t k y y ).
Волна 12 бежит вдоль оси y ,
а ей навстречу волна 34 .
Амплитуда обеих волн меняется вдоль
по гармоническому закону.
оси
Сумма этих волн дает двумерную стоячую волну:
x
12 34 2 A cos(k x x)[cos( t k y y ) cos( t k y y )]
1 2 3 4 4 A cos(k x x)cos(k y y )cos( t ).
Из этого уравнения следует, что амплитуда максимальна в точке (0,0).
Чтобы она была максимальна и в остальных вершинах: (a,0), (0, b), (a, b)
необходимо выполнение условий: k x a n1; k y b n2 .

23. 13. ЧИСЛО МОД КОЛЕБАНИЙ. ДВУМЕРНЫЙ СЛУЧАЙ (IV)

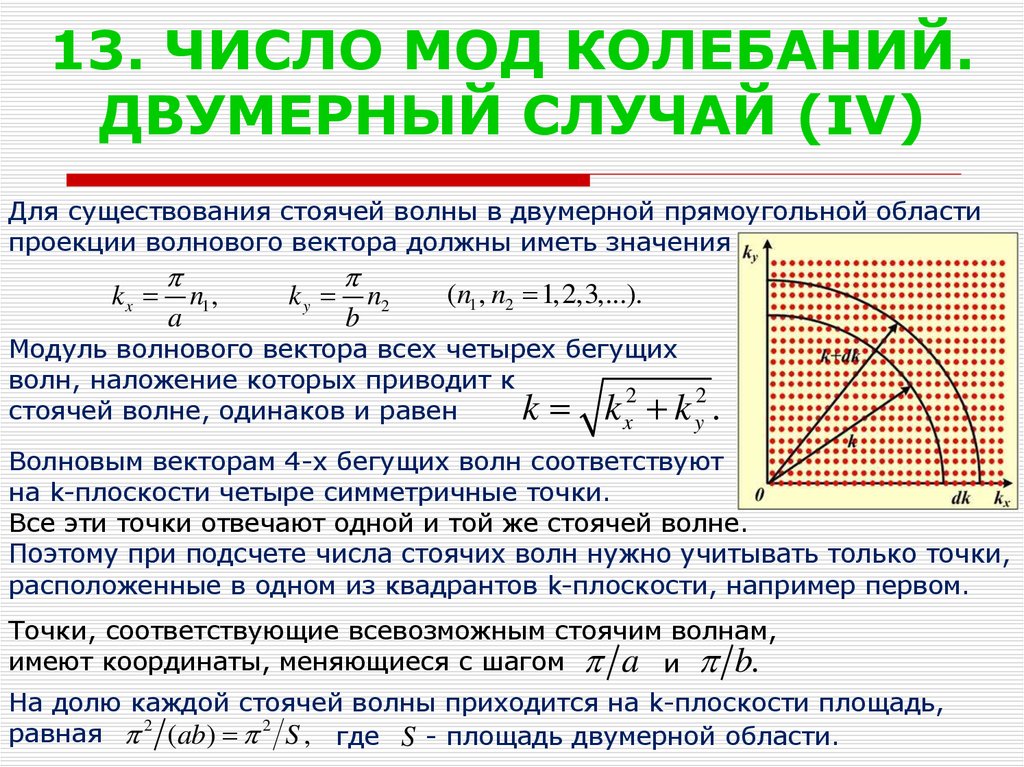
Для существования стоячей волны в двумерной прямоугольной области
проекции волнового вектора должны иметь значения
kx
a
n1 ,
ky
b
n2
(n1 , n2 1,2,3,...).
Модуль волнового вектора всех четырех бегущих
волн, наложение которых приводит к
k k x2 k y2 .
стоячей волне, одинаков и равен
Волновым векторам 4-х бегущих волн соответствуют
на k-плоскости четыре симметричные точки.
Все эти точки отвечают одной и той же стоячей волне.
Поэтому при подсчете числа стоячих волн нужно учитывать только точки,
расположенные в одном из квадрантов k-плоскости, например первом.
Точки, соответствующие всевозможным стоячим волнам,
имеют координаты, меняющиеся с шагом a и b.
На долю каждой стоячей волны приходится на k-плоскости площадь,
равная 2 (ab) 2 S , где S - площадь двумерной области.

24. 13. ЧИСЛО МОД КОЛЕБАНИЙ. ДВУМЕРНЫЙ СЛУЧАЙ (V)

Фазовая площадь для каждой стоячей волны
на k-плоскости Sk 2 (ab) 2 S .
Тогда, плотность точек на k-плоскости
k 1 Sk S 2 .
Число стоячих волн dN k ,
у которых модуль волнового вектора лежит
в пределах от k до k dk ,
равно числу точек, попадающих в область,
заключенную между четвертями окружностей
радиусов k и k dk . То есть
1
S k
S
dN k k 2 kdk 2
dk
kdk .
4
2
2
d
S d
S
k ; dk
dN
d ,
2
V
V
2 V V
2 V
где, dN – число стоячих волн в интервале частот от до d .

25. 14. ЧИСЛО МОД КОЛЕБАНИЙ. ТРЕХМЕРНЫЙ СЛУЧАЙ (I)

Cтоячая волна, возникающая в пределах прямоугольной области
с параллельными координатным осям сторонами a, b, c
образуется наложением восьми бегущих волн.
Проекции волновых векторов бегущих волн равны:
(1)
(2)
(3)
(4)
kx , k y , kz ;
k x , k y , k z ;
(5)
k x , k y , k z ;
k x , k y , k z ;
(7)
(6)
(8)
k x , k y , k z ;
k x , k y , k z ;
k x ,
kx ,
k y , k z ;
k y , k z .
1 Acos( t k x x k y y k z z ),
2 Acos( t k x x k y y k z z ),... 8 Acos( t k x x k y y k z z ).
Уравнения бегущих волн имеют вид:
Складывая эти уравнения попарно, и, вынося общие множители, получим
1 2 ... 8 8 A cos(k x x)cos(k y y)cos(k z z )cos( t ).

26. 14. ЧИСЛО МОД КОЛЕБАНИЙ. ТРЕХМЕРНЫЙ СЛУЧАЙ (II)

Из уравнения для стоячей волны
8 A cos(k x x)cos(k y y )cos(k z z )cos( t )
следует, что, для того чтобы амплитуда стоячей
волны имела одинаковые значения во всех восьми
вершинах области, в которой возбуждена эта
стоячая волна, необходимо выполнение условий
kx
n1 , k n , k n
y
2
z
3
a
b
c
(n1 , n2 , n3 1,2,...).
В k-пространстве каждой стоячей волне отвечает точка в первом октанте.
3
3
На долю каждой точки приходится фазовый объем Vk (abc) V0 .
Тогда, плотность точек в k-пространстве будет равна
k 1 Vk V0 3 .
Число стоячих волн, у которых модуль волнового вектора лежит
в пределах от k до k dk , равно количеству точек,
попадающих во внутрь 1 8 шарового слоя
радиусом k и толщиной dk :
1
V0 1 2
2
V0 2
dN k k 4 k dk 3 k dk 2 k dk .
8
2
2

27. 14. ЧИСЛО МОД КОЛЕБАНИЙ. ТРЕХМЕРНЫЙ СЛУЧАЙ (III)

1
V0 1 2
V0 2
2
dN k k 4 k dk 3 k dk 2 k dk ;
8
2
2
2
d
V0 2 d
k
; dk
dN 2 2
.
V
V
2 V V
Выражение для dN пропорционально
объему V0 полости, в которой возбуждена
стоячая волна. Удобно перейти к числу
стоячих волн в единице объема полости.
Это позволяет абстрагироваться от
dN
dn
.
геометрической формы полости:
V0
Вдоль заданного направления могут распространяться две волны одной
частоты, но различающиеся направлением поляризации.
2
2
Чтобы это учесть необходимо выражение
d
d
для объемной плотности колебательных мод
dn 2 3 2 3 .
стоячих волн в полости умножить на два.
V
c

28. 15. ФОРМУЛА РЭЛЕЯ-ДЖИНСА (I)

Джон Уильям Стретт
(Лорд Рэлей)
английский физик
1842 – 1919
Джеймс Хопвуд Джинс
английский физик и астроном
1877 - 1946

29. 15. ФОРМУЛА РЭЛЕЯ-ДЖИНСА (II)

Рэлей и Джинс в 1900 г. сделали попытку определить равновесную
плотность излучения абсолютно черного тела, исходя из теоремы о
равнораспределении энергии по степеням свободы.
Они предположили, что на каждую колебательную моду приходится
в среднем энергия kT , равная двум половинкам kT – одна
половинка на электрическую, а другая – на магнитную энергию волны.
Равновесное излучение в полости представляет собой систему стоячих
волн, для которых объемная спектральная плотность
2 d
dn 2 3 .
колебательных мод определяется выражением
Тогда, объемная плотность энергии, приходящаяся
на элементарный интервал частот d , будет равна:
c
2
u ( , T ) 2 3 kT ;
u ( , T )d dn kT 2 3 d
c
c
2
2
c
c
f ( , T ) u ( , T ) f ( , T ) r * ( , T )
kT 2 2 kT .
2 3
4
4 c
4 c
2

30. 16. УЛЬТРАФИОЛЕТОВАЯ КАТАСТРОФА

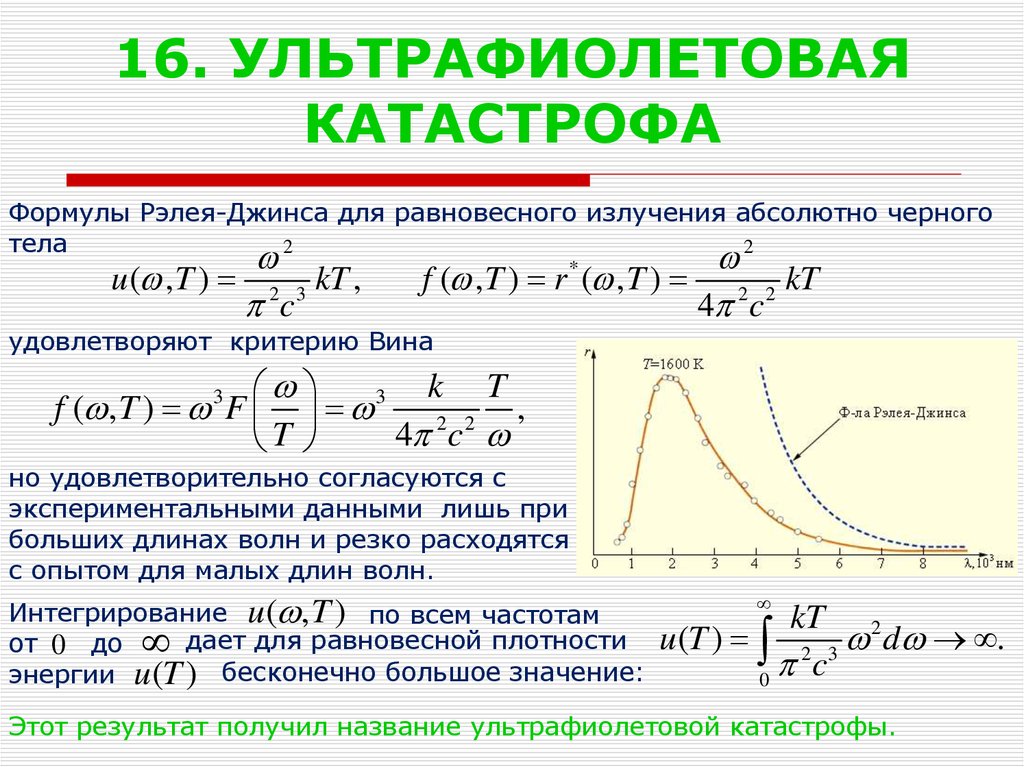
Формулы Рэлея-Джинса для равновесного излучения абсолютно черного
тела
2
2
u ( , T ) 2 3 kT ,
c
f ( , T ) r ( , T ) 2 2 kT
4 c
*
удовлетворяют критерию Вина
k T
3
f ( , T ) F
,
2 2
4 c
T
3
но удовлетворительно согласуются с
экспериментальными данными лишь при
больших длинах волн и резко расходятся
с опытом для малых длин волн.
Интегрирование u ( , T ) по всем частотам
от 0 до дает для равновесной плотности
энергии u (T ) бесконечно большое значение:
kT 2
d .
2 3
c
0
u (T )
Этот результат получил название ультрафиолетовой катастрофы.

31. 17. ФОРМУЛА ПЛАНКА (I)

С классической точки зрения вывод формулы
Рэлея-Джинса является безупречным.
Поэтому расхождение этой формулы с опытом
указывает на существование каких-то основных
закономерностей, несовместимых с классическими
представлениями.
Макс Планк
немецкий физик
1858 - 1947
В 1900 г. Планку удалось найти вид
функции u ( , T ), соответствующий
опытным данным.
Для этого ему пришлось сделать
предложение чуждое классической
физике – допустить, что тепловое
излучение происходит в виде квантов,
энергия которых пропорциональна
частоте излучения: h , где
h
;
2
h 6,626 10 34 Дж с.

32. 17. ФОРМУЛА ПЛАНКА (II)

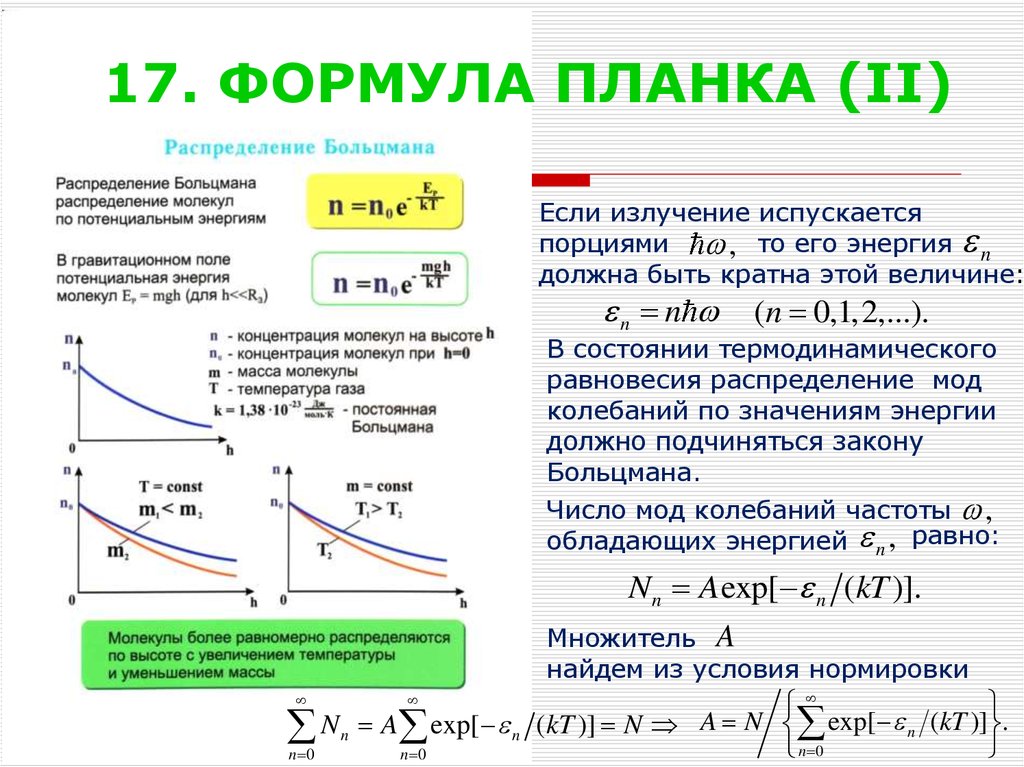
Если излучение испускается
порциями , то его энергия n
должна быть кратна этой величине:
n n (n 0,1,2,...).
В состоянии термодинамического
равновесия распределение мод
колебаний по значениям энергии
должно подчиняться закону
Больцмана.
Число мод колебаний частоты ,
обладающих энергией n , равно:
Nn A exp[ n (kT )].
Множитель A
N
n 0
n
A exp[ n
n 0
найдем из условия нормировки
(kT )] N A N exp[ n (kT )] .
n 0

33. 17. ФОРМУЛА ПЛАНКА (III)

Число мод колебаний частоты ,
обладающих энергией n , равно:
Nn A exp[ n (kT )].
Нормировочный множитель A :
A
N
n
exp
kT
n 0
Nn
N exp[ n (kT )]
.
n
exp
kT
n 0
Вероятность того, что энергия моды
колебаний частоты равна n :
exp n
N
kT
Pn n
.
N
n
exp
kT
n 0
Зная вероятности различных значений
энергии колебаний заданной частоты,
можно найти среднее значение энергии
для данной колебательной моды, а именно
Pn n .
n 0

34. 17. ФОРМУЛА ПЛАНКА (IV)

Cреднее значение энергии колебательной моды стоячей волны с данной
частотой определим зная вероятность всех возможных энергий:
Pn n ; n
n 0
n
n
n
exp
exp
Nn
kT
kT
.
n
0
n , Pn
N
n
n
exp
exp
kT
kT
n 0
n 0
Чтобы произвести вычисления, введем обозначение x
и допустим, что x может изменяться непрерывно. Тогда,
(kT )
n exp( nx)
n 0
exp( nx)
n 0
d
ln exp( nx).
dx n 0
Под знаком логарифма стоит сумма
членов бесконечной убывающей геометрической прогрессии
с первым членом b1 1, и знаменателем прогрессии q exp( x).

35. 17. ФОРМУЛА ПЛАНКА (V)

d
ln exp( nx).
dx n 0
Cумма N первых членов убывающей геометрической прогрессии равна
1 qN
SN
b1
1 q
S
1 exp( )
1
1
.
1 exp( x)
1 exp( x)
и продифференцируем
d
exp( x)
ln[1 exp( x)]
;
Подставим найденную сумму в формулу для
d
1
ln
dx 1 exp( x)
x
При
kT
1 exp( x)
dx
.
exp( kT ) 1
0 exp( kT ) 1 kT .
При этих условиях
Таким образом, если бы энергия могла принимать
непрерывный ряд значений, то kT .
exp( x) 1
1 kT 1
kT .

36. 17. ФОРМУЛА ПЛАНКА (VI)

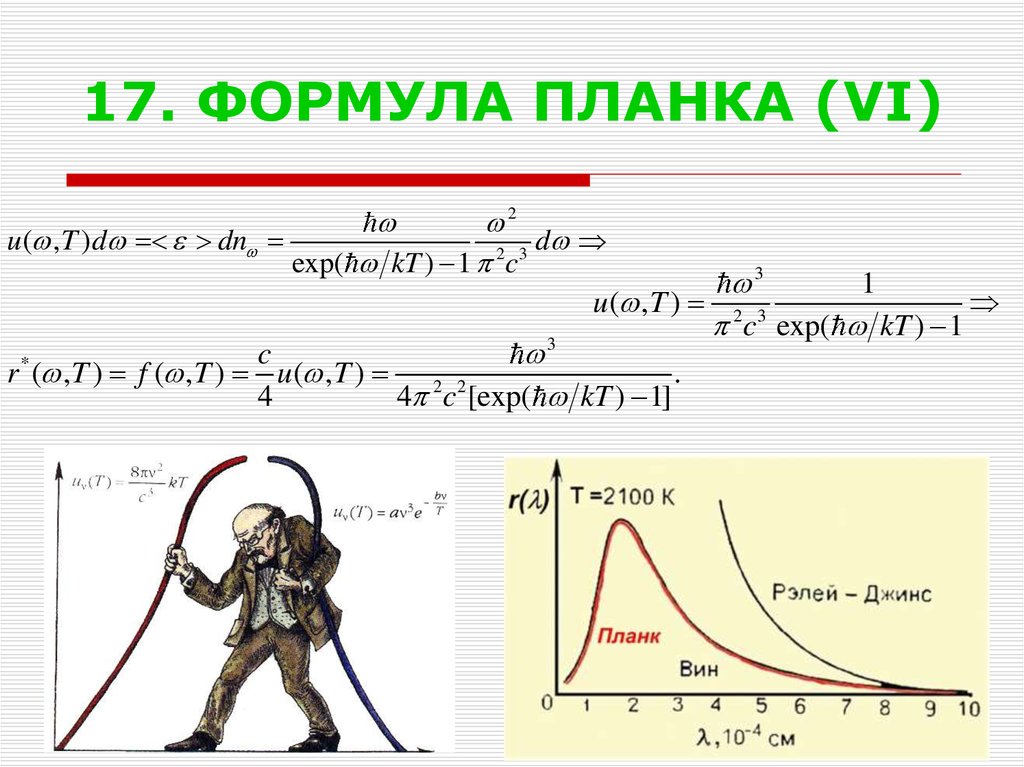
2
u ( , T )d dn
d
2 3
exp( kT ) 1 c
3
1
u ( , T ) 2 3
c exp( kT ) 1
3
c
*
r ( , T ) f ( , T ) u ( , T ) 2 2
.
4
4 c [exp( kT ) 1]