Части графа. Операции над частями графа

1. Дискретная математика

Части графа.
Операции над
частями графа.

2. Часть графа

Пусть G =(V, E) – н-граф.
Частью (подграфом) графа G
называется граф Н =(V', E' ),
где V' V, E' E ,
причем все ребра множества E'
входят в граф Н вместе со
своими концами.

3. Суграф

Подграф Н =(V', E' ), называется
суграфом, если V' = V.
Суграф называется
покрывающим, если каждая
вершина инцидентна хотя бы
одному ребру графа G.

4. Подграф, порожденным множеством вершин

Подграф Н = (V', E' ), называется
подграфом, порожденным
множеством вершин А V,
если V' = А, E' состоит из ребер
множества Е, соединяющих
вершины множества А.

5. Звездный граф

Подграф Н = (V', E' ), называется
звездным графом вершины
v V
если V' составляют вершина v и
все смежные ей вершины,
E' состоит из ребер множества
Е, инцидентных вершине v.

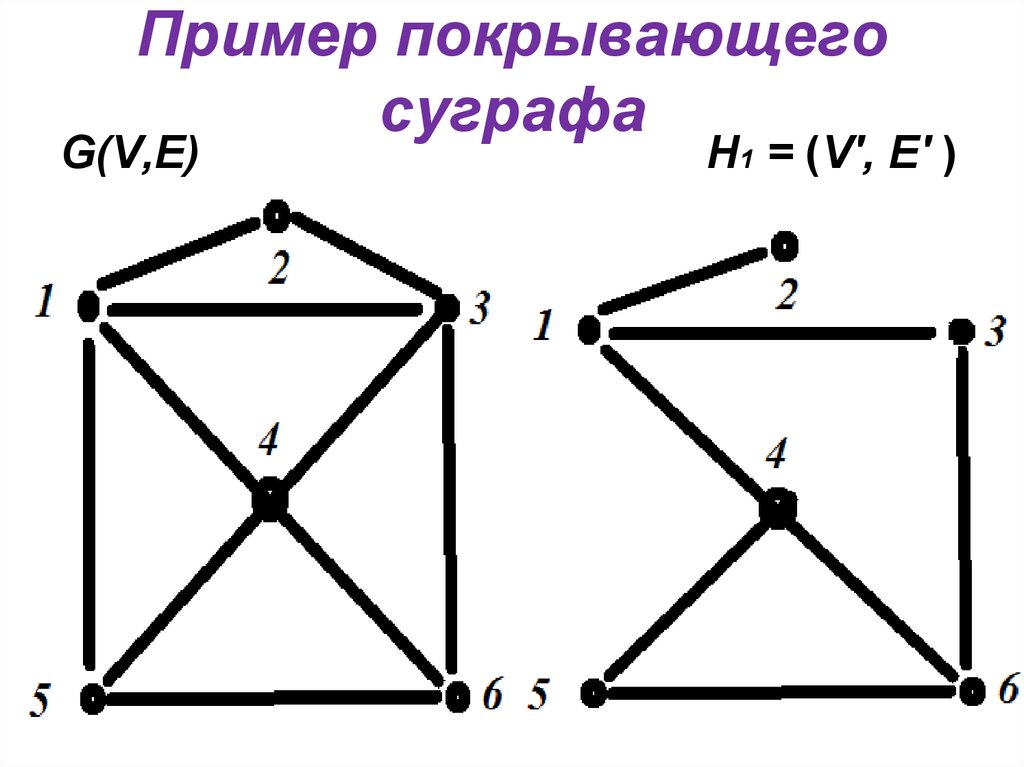
6. Пример покрывающего суграфа

G(V,E)
Н1 = (V', E' )

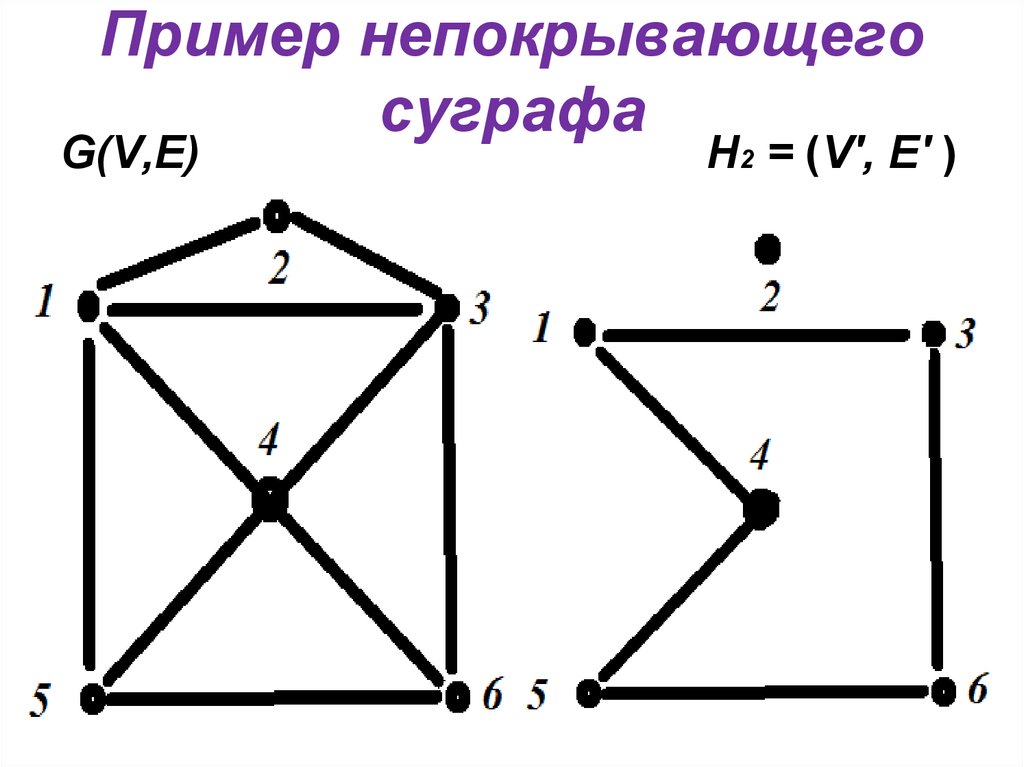
7. Пример непокрывающего суграфа

G(V,E)
Н2 = (V', E' )

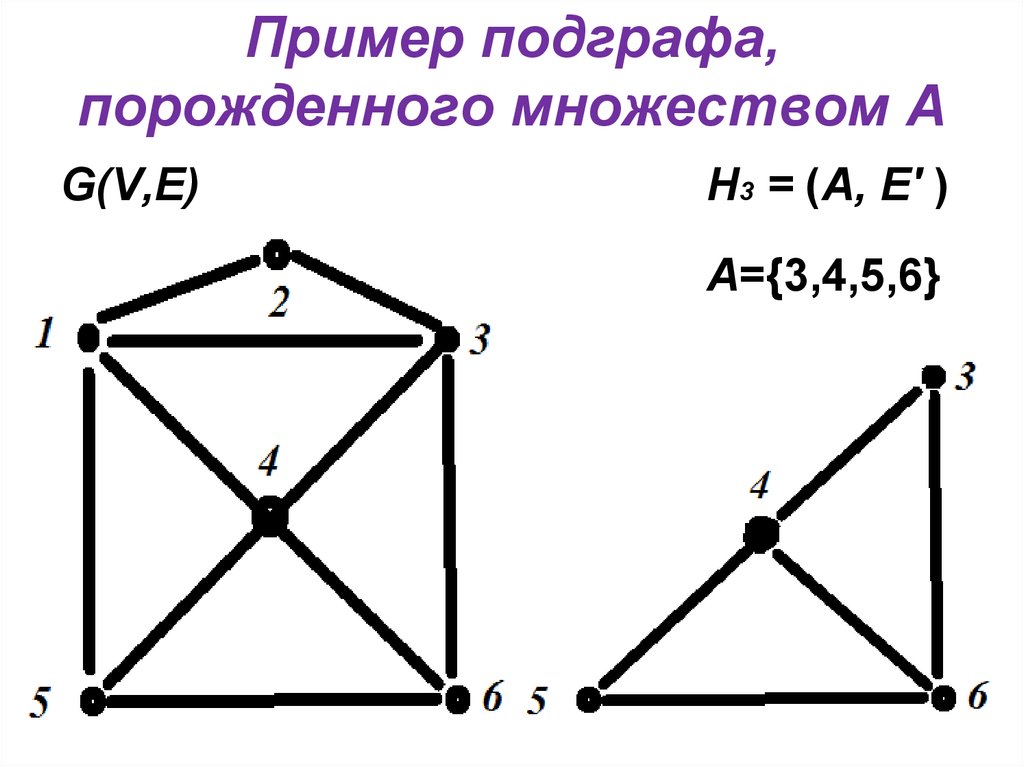
8. Пример подграфа, порожденного множеством А

G(V,E)
Н3 = (А, E' )
А={3,4,5,6}

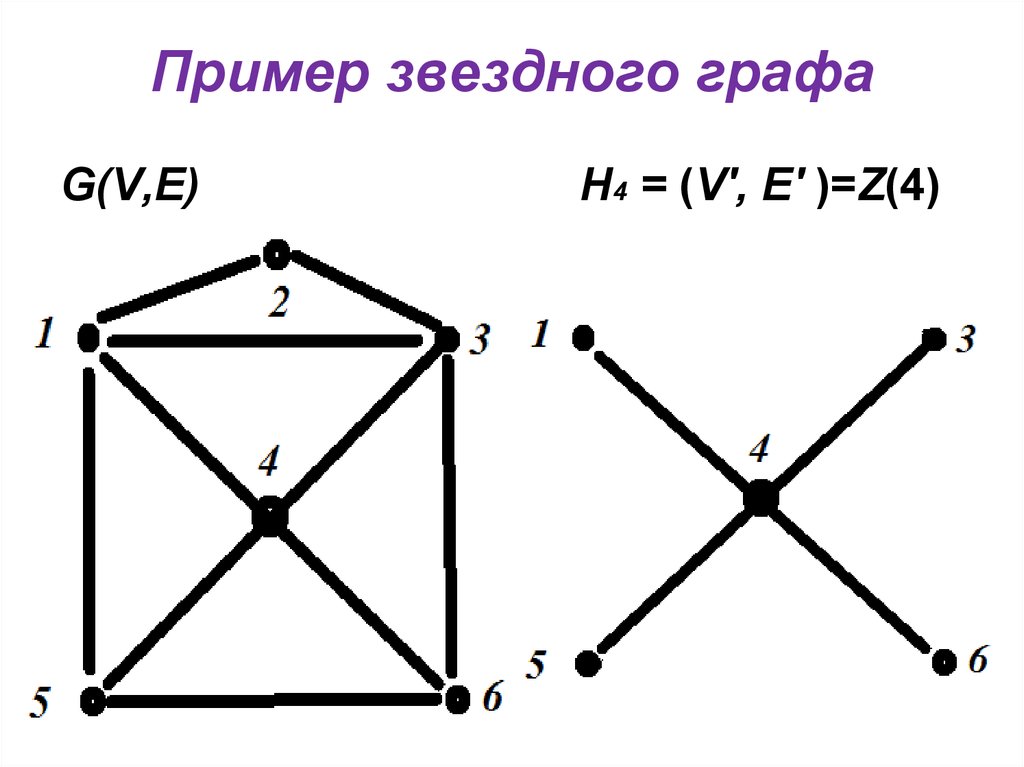
9. Пример звездного графа

G(V,E)
Н4 = (V', E' )=Z(4)

10. Операции над частями графа

Суммой подграфов
Н1 = (V1, E1 ) и Н2 = (V2, E2 )
называется граф Н = (V, E ),
такой что
V V1 V 2 , E E 1 E 2 .
Обозначается: H H1 H 2 .

11. Операции над частями графа

Пересечением подграфов
Н1 = (V1, E1 ) и Н2 = (V2, E2 )
называется граф D= (V, E ),
такой что
V V1 V 2 , E E 1 E 2 .
Обозначается: D H1 H 2 .

12. Операции над частями графа

Сумма подграфов
Н1 = (V1, E1 ) и Н2 = (V2, E2 )
называется прямой по ребрам,
если у них нет общих ребер:
E 1 E 2 Ø.

13. Операции над частями графа

Сумма подграфов
Н1 = (V1, E1 ) и Н2 = (V2, E2 )
называется прямой по вершинам,
если у них нет общих вершин:
V1 V 2 Ø.

14. Операции над частями графа

Дополнением подграфа
Н = (V1, E1 ) до графа G = (V, E )
называется подграф H V 2 , E 2 ,
где множество его ребер:
E 2 E E1,

15. Операции над частями графа

а множество вершин V2 состоит из
всех вершин множества V,
инцидентных ребрам из Е2 и
всех изолированных вершин, не
попавших в множество V1.

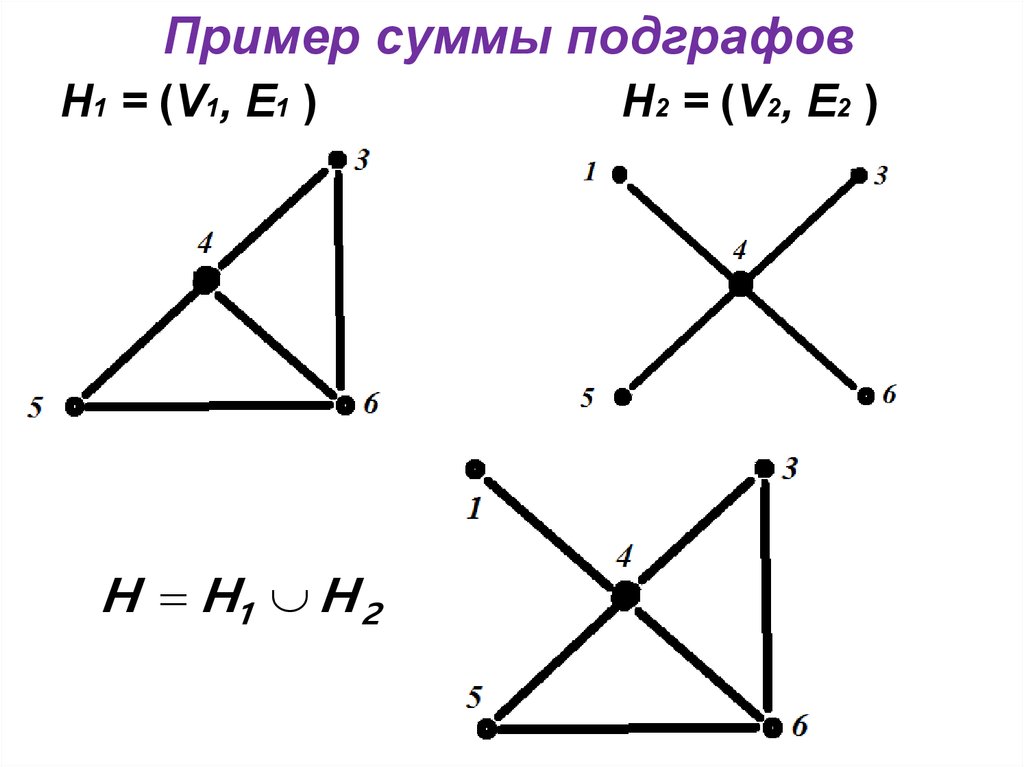
16. Пример суммы подграфов

Н1 = (V1, E1 )
H H1 H 2
Н2 = (V2, E2 )

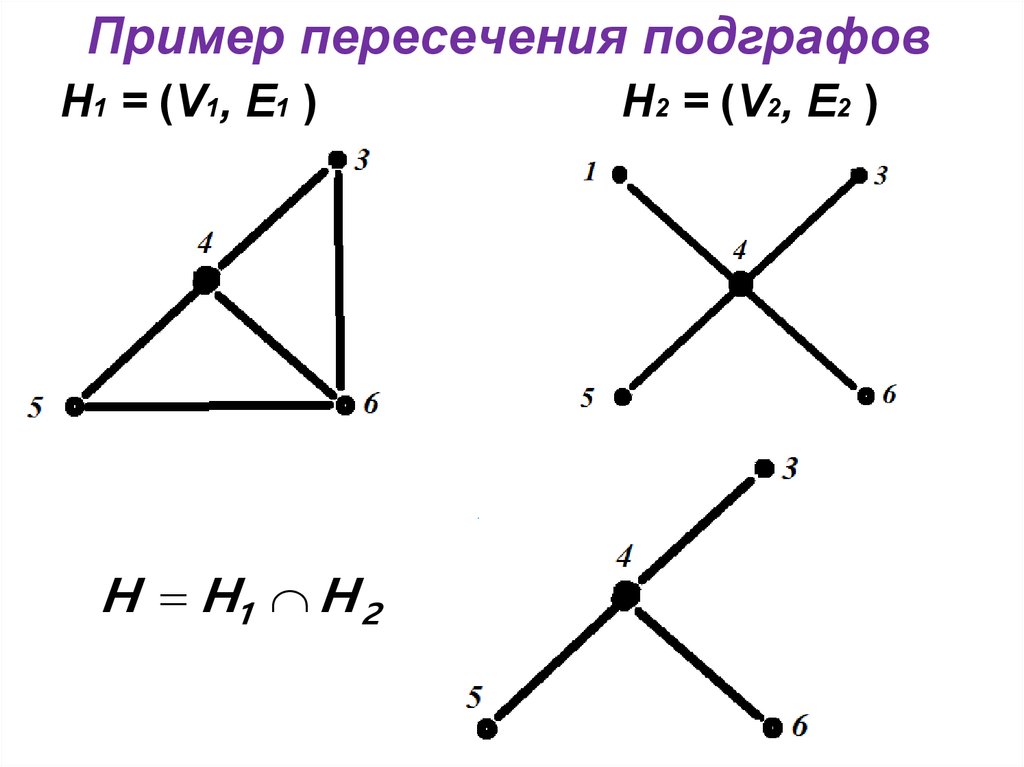
17. Пример пересечения подграфов

Н1 = (V1, E1 )
H H1 H 2
Н2 = (V2, E2 )

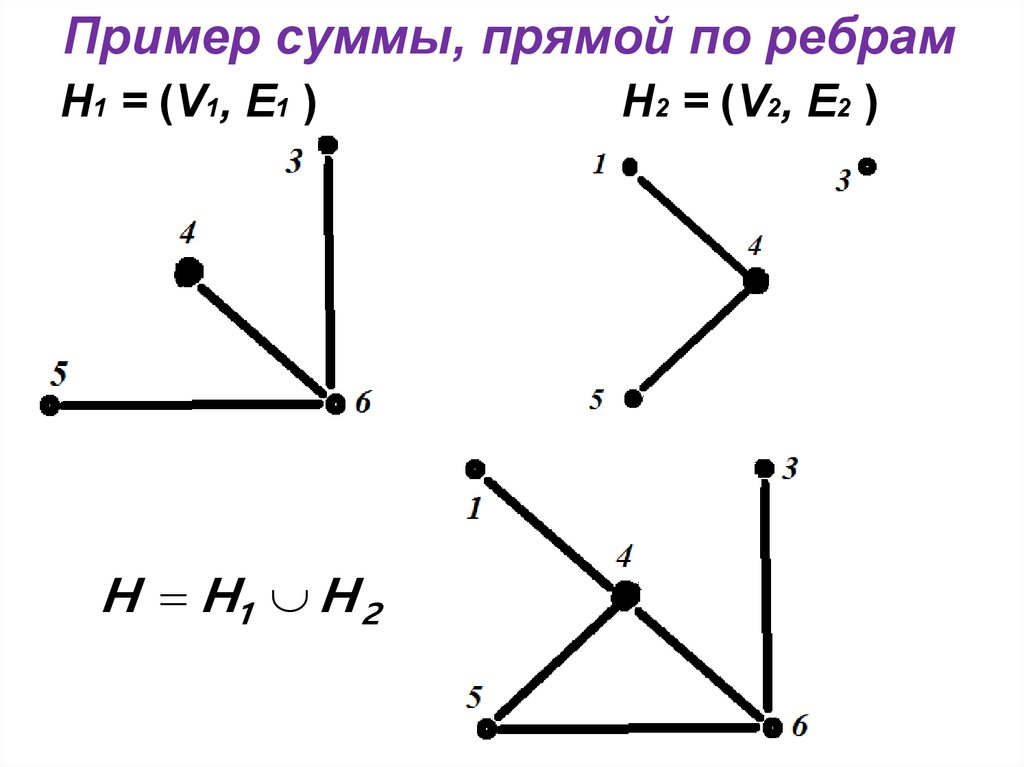
18. Пример суммы, прямой по ребрам

Н1 = (V1, E1 )
H H1 H 2
Н2 = (V2, E2 )

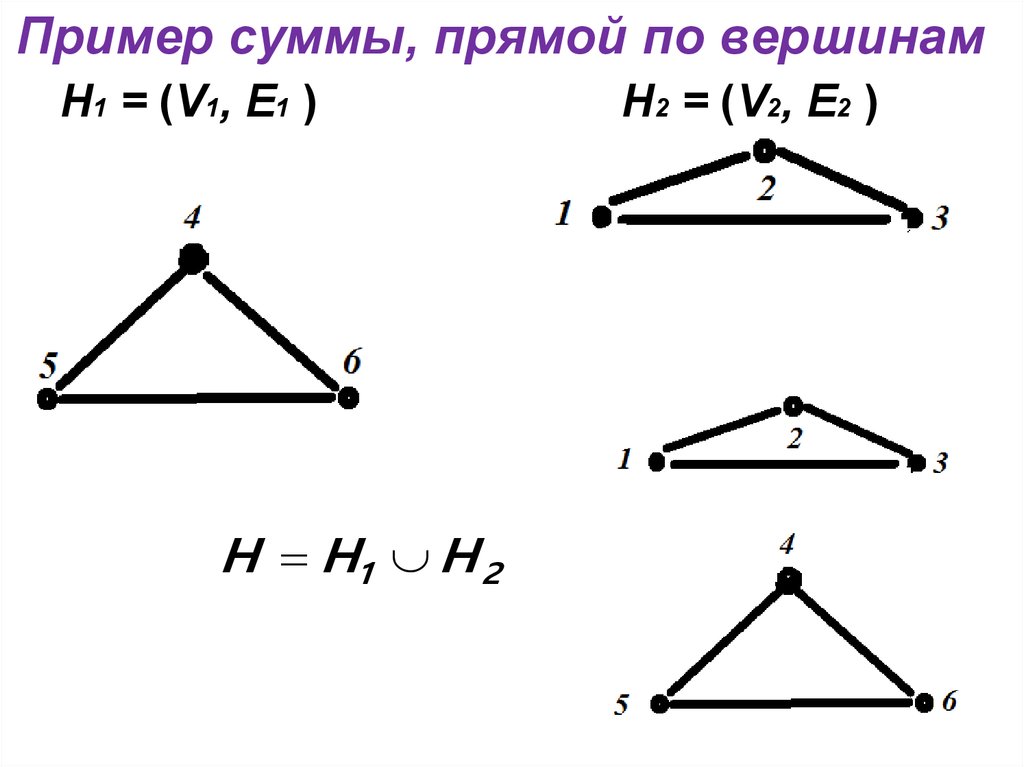
19. Пример суммы, прямой по вершинам

Н1 = (V1, E1 )
H H1 H 2
Н2 = (V2, E2 )

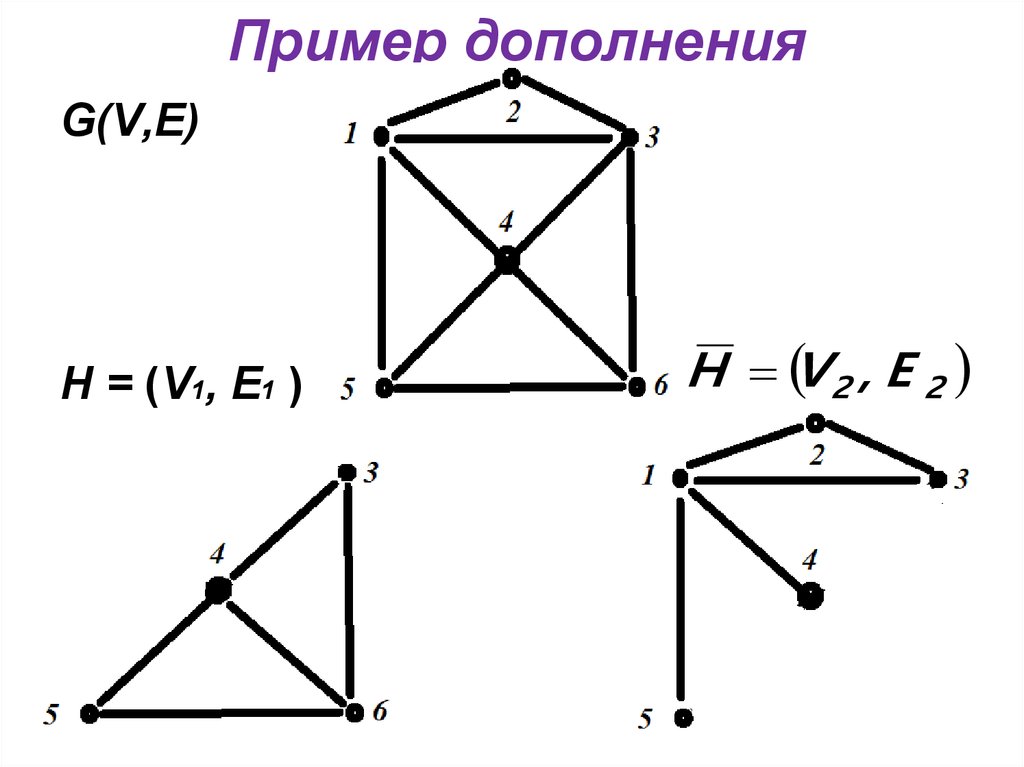
20. Пример дополнения

G(V,E)
Н = (V1, E1 )
H V 2 , E 2

21. Замечание

Подграф и его дополнение
являются прямой суммой по
ребрам:
Н H G