Similar presentations:
Дискретная математика. Курс лекций (часть 1)
1. Федеральное государственное бюджетное образовательное учреждение высшего образования «КЕМЕРОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Кафедра прикладной математикиДИСКРЕТНАЯ МАТЕМАТИКА
Часть 1
курс лекций
Кемерово
2018
© Гутова С. Г. , 2018
© Кемеровский государственный
университет, 2018
ISBN 978-5-8353-1686-1
Об издании – 1, 2, 3
1
2.
ББК В19я73-5УДК 519.6(075.8)
Г 89
Издается по решению редакционно-издательского совета
Кемеровского государственного университета
Составитель:
Гутова Светлана Геннадьевна – кандидат технических наук, доцент кафедры
прикладной математики
Г 89
Гутова, С. Г. Дискретная математика. Ч. 1: электронное учебнометодическое пособие [Электронный ресурс]: / С. Г. Гутова; КемГУ. – Электрон.
дан. (1 Мб). – Кемерово: КемГУ, 2018. – 1 электрон. опт. диск (СD-ROM). –
Систем. требования: Intel Pentium (или аналогичный процессор других
производителей), 12 ГГц; 512 Мб оперативной памяти; видеокарта SVGA,
1280x1024 High Color (32 bit); 2 Мб свободного дискового пространства; операц.
система Windows ХР/7/8; Power Point. – Загл. с экрана.
ISBN 978-5-8353-1686-1
2
3.
Конспект лекций разработан по дисциплине «Дискретная математика»для направления подготовки 01.03.02 Прикладная математика и информатика
в соответствии с требованиями ФГОС ВО и включает теоретический
материал, примеры, снабженные анимацией. Может быть использован для
обеспечения лекционных занятий по дисциплине «Дискретная математика»
студентами направлений 02.03.02 Фундаментальная информатика
и
информационные технологии и 02.03.03 Математическое обеспечение и
администрирование информационных систем и по дисциплине «Дискретная
математика и математическая логика» студентами направления 02.03.01
Математика и компьютерные науки.
Утверждено на заседании
кафедры прикладной математики
Рекомендовано научно-методическим
советом института фундаментальных наук
Протокол № 7 от «26 » февраля
2018 г.
Заведующий кафедрой,
__________________ Е. С. Каган
Рекомендовано
Протокол № 7 от «19» марта 2018 г.
Председатель совета доцент
_____________С. М. Сирик
3
4.
Текстовое электронное изданиеМинимальные системные требования:
Компьютер: Pentium 3 и выше, 12 ГГц; ОЗУ 512 Мб; 2 Мб на жестком
диске; видеокарта SVGA, 1280x1024 High Color (32 bit); привод
CD-ROM
Операционная система: Windows ХР/7/8
Программное обеспечение: Adobe Reader
© Гутова С. Г. , 2018
© Кемеровский государственный
университет, 2018
4
5.
ВведениеКонспект
лекций
разработан
по
дисциплине
«Дискретная математика» для направления подготовки
01.03.02 Прикладная математика и информатика в
соответствии с требованиями ФГОС ВО и включает
теоретический материал и примеры решения задач,
снабженные анимацией.
В
результате
освоения
данной
дисциплины
формируется компетенция учебного плана по направлению
подготовки 01.03.02 Прикладная математика и информатика:
- способен применять фундаментальные знания, полученные
в области математических и (или) естественных наук, и
использовать их в профессиональной деятельности.
5
6.
Конспект лекций может быть использован дляобеспечения лекционных занятий по дисциплине
«Дискретная математика» студентами направлений
подготовки 02.03.02 Фундаментальная информатика и
информационные технологии и 02.03.03 Математическое
обеспечение и администрирование информационных
систем и по дисциплине «Дискретная математика и
математическая
логика»
студентами
направления
подготовки 02.03.01 Математика и компьютерные науки.
6
7. Оглавление
ВведениеЛекция 1
Лекция 2
Лекция 3
Лекция 4
Лекция 5
Лекция 6
Лекция 7
Лекция 8
Лекция 9
Лекция 10
Лекция 11
Лекция 12
Лекция 13
Лекция 14
Лекция 15
Лекция 16
Лекция 17
7
8. Лекция 1
Множества9.
Множество – это совокупностьопределенных различаемых объектов
таких, что для любого объекта можно
установить, принадлежит объект
данному множеству или нет [1, 2].
Множество, которое подчиняется лишь
такому ограничению, может содержать
объекты почти любой природы.
9
10.
Георг Кантор определил множество так:Множество – это многое,
мыслимое как целое.
10
11.
Например:• множество всех станций Московского
метро;
• множество левых ботинок;
• множество натуральных чисел: 1, 2, 3, 4 и
т. д.;
• множество символов, доступных
специальному печатающему устройству;
• множество кодов операций конкретного
компьютера.
11
12.
• множество всех натуральных чисел: 1, 2, 3, . .Обозначим N. Часто 0 считают натуральным
числом. Множество N с добавлением 0
обозначается N 0 .
• множество всех натуральных чисел, не
превосходящих 100.
• множество всех решений уравнения
sin x 1
12
13.
Множество обозначают заглавнымибуквами, а его элементы – прописными.
А а1 , а2 , ..., аn
Говоря об определенном множестве, мы
полагаем, что для каждого объекта имеется
две возможности: элемент либо входит в
множество x X , либо нет x X .
Мощность множества – количество его
элементов.
Обозначение мощности: А .
13
14.
Множество, не содержащее элементов,называется пустым множеством и
обозначается Ø.
Ø 0.
В зависимости от их мощности
множества различают как конечные или
бесконечные. Конечные множества могут
состоять из одного или нескольких
элементов.
14
15. Способы задания множества
Перечисление всех элементов множества(список), например множество однозначных
неотрицательных чисел
X 0,1,2,3,...9 .
Множества часто рассматриваются как
«неупорядоченные совокупности элементов»,
хотя иногда полезно подчеркнуть, что,
например
X 0,1,2 2,1,0 2,0,1 .
15
16.
Выяснить, какие из приведенныхопределений верные?
В 1,2,3 .
С 5,6,6,7 .
D В , С .
16
17. Порождающая процедура
Описывает способ получения элементовмножества из уже полученных элементов
либо других объектов. Тогда элементы
множества – все объекты, которые могут
быть получены (построены) с помощью такой
процедуры.
17
18.
Множество М 2n натуральных степенейдвойки: 2, 4, 8, 16, 32, 64, 128…
Порождающую процедуру зададим
рекуррентно:
1 1 M 2n
2) m М 2 n ; 2m М 2n
18
19. Пример 2
Какое множество задается рекуррентнойформулой: x1 1, xn xn 1 n
при n 2, x2 x1 2 1 2 2!
при n 3, x3 x2 3 2! 3 = 3!
при n 4, x4 x3 4 3! 4 = 4!
Множество, состоящее
из факториалов :1!, 2!, 3!, 4!,..., n!,...
19
20. Задание множества описанием его элементов (разрешающая процедура)
указание общего свойства, которымобладают все элементы множества,
например множество четных
натуральных чисел
или
X {2,4,6,8,10,12...}
X {x : x 2n, n N };
20
21.
Множество А называют подмножествоммножества В (обозначается A B ), если
каждый элемент множества А является также
элементом множества В.
Рис.1. Подмножество
21
22.
Множества А и В называют равными(А = В), если каждый элемент множества А
является одновременно элементом
множества В и наоборот,
то есть если A B и B A .
Другими словами, два множества равны,
если они состоят из одних и тех же
элементов.
22
23.
Множество U называетсяуниверсальным множеством (множество
элементов всех подмножеств) для некоторой
системы множеств, если каждое множество
этой системы является подмножеством U, то
есть
A U , B U ,C U ...
23
24.
Дополнением множества A называетсямножество A , состоящее из тех и только тех
элементов универсального множества,
которые не входят в множество А.
Рис.2. Дополнение
множества
24
25.
Объединением двух множеств А и Вназывается множество A U B , состоящее из
тех элементов, которые принадлежат или
множеству А, или В, или А и В
одновременно.
Рис.3.
Объединение
множеств
25
26.
Пересечением двух множеств А и Вназывается множество A I B , состоящее из
тех и только тех элементов, которые
принадлежат множествам
А
и
В
одновременно.
Рис.4.
Пересечение
множеств
26
27.
Разностью двух множеств А и В( A B или A \ B ) называется множество тех
элементов множества А, которые не
принадлежат множеству В:
A B AI B
Рис.5.
Разность множеств
27
28.
Прямым (декартовым) произведениемдвух множеств А и В называется множество,
состоящее из упорядоченных пар элементов,
в которых первый элемент принадлежит
множеству А, а второй – множеству В.
A B a,b : a A,b B
28
29. Пример 3
Заданы два множества: А = {-2, -1, 0, 1, 2}и B = {0, 2, 4, 5}. Определить множества A B ;
A B ; A\ B ; B \ A и их мощность.
Решение:
Множество А = {-2, -1, 0, 1, 2} состоит из
пяти элементов, следовательно мощность этого
множества равна 5:
Аналогично, B = {0, 2, 4, 5} содержит 4
элемента:
29
30.
По определению пересечение двухмножеств состоит только из общих для обоих
множеств элементов, следовательно,
A B {0, 2} и
Пояснение:
A I B 0, 2
30
31.
По определению объединение двухмножеств состоит из всех элементов, которые
принадлежат только множеству А, или только
множеству В, или множествам А и В
одновременно, следовательно,
A B = {-2, -1, 0, 1, 2, 4, 5} и
Пояснение:
A U B 0, 2, 2, 1, 1, 4, 5
.
31
32.
Множество A\ B является разностью двухмножеств А и В и состоит из элементов
множества А, которые одновременно не
принадлежат множеству В, следовательно
Пояснение:
A\ B 2, 1, 1 .
32
33.
Аналогично,Пояснение:
B \ A 4, 5 .
33
34. Пример 4:
A 2, 1, 0,1, 2 , B 0, 2, 4, 5• Прямое (декартово) произведение:
A B = {(-2, 0); (-2, 2); (-2, 4); (-2, 5);(-1, 0);
(-1, 2); (-1, 4); (-1, 5);(0, 0); (0, 2);(0, 4);(0, 5);
(1, 0); (1, 2); (1, 4); (1, 5); (2, 0); (2, 2); (2, 4);
(2, 5)};
• B A = {(0, -2); (0, -1); (0, 0); (0, 1); (0, 2);
(2, -2); (2, -1); (2, 0); (2, 1); (2, 2); (4, -2); (4, 1); (4, 0); (4, 1); (4, 2); (5, -2); (5, -1); (5, 0).
(5, 1); (5, 2)}
34
35.
Из примера 2 видно, чтоA B B A
A B B A A B 5 4 20.
35
36. Пример 5
На диаграмме Вьенна-Эйлера изобразитьрезультат действия А В С.
Решение:
Решаем по действиям. На каждой копии
диаграммы
необходимо
восстановить
контуры всех множеств, участвующих в
задании. Они должны пересекаться в самом
общем виде. Самый большой контур –
универсальное множество. Оно содержит в
36
себе все множества задачи.
37.
Основа диаграммыкаждого действия.
для
выполнения
Рис.6.
Основа диаграммы
для тех множеств
37
38.
1) Изобразим на 1 диаграммемножества, вступающие в 1 действие
(действие в скобках). Каждое множество
заштриховываем штриховкой своего вида
(с наклоном влево, с наклоном вправо,
горизонтальной
или
вертикальной).
Множества
штрихуются
целиком,
независимо от их пересечения с другими
множествами диаграммы.
38
39.
AB
C
U
Рис.7. Множества, вступающие в 1 действие 39
40.
2) На 2 копии диаграммы надозаштриховать множества, вступающие
во второе действие: это результат
первого действия и С. У каждого из
этих множеств на рисунке одинарная
штриховка своего вида (цвета).
40
41.
AB
C
U
Рис.8. Множества, вступающие во 2 действие41
42.
3) На 3 копии диаграммы надозаштриховать множество, которое
будет являться ответом.
Штриховка – одинарная.
Заметим, что на каждой копии
диаграммы, кроме последней, должно
быть ровно два вида штриховки, а на
последней копии – один вид.
42
43.
AB
C
Рис.9. Ответ
U
43
44. Лекция 2
Векторы и прямыепроизведения множеств.
Проекция вектора на ось
45.
ВекторыВектор – это упорядоченный набор
элементов [2]. Его элементы зазываются
координатами или компонентами вектора.
Длина (размерность) вектора – число
координат вектора.
В отличие от элементов множества, его
координаты могут совпадать. Обозначение
вектора: в круглых скобках, координаты –
через запятую (0, 5, 4, 5, 0, 1). Иногда скобки и
даже запятые опускаются.
45
46.
Векторы длины 2 называютупорядоченными парами; длины 3 –
тройками; и так далее, длины n – n-ками.
Два вектора равны, если они имеют
одинаковую длину, и соответствующие
координаты равны, то есть.
a1 , a2 , ..., am b1 ,b2 , ...,bn
если m n и
a1 b1 , a2 b2 ,..., am bn .
46
47.
Прямое произведение n множествПрямое произведение множеств
A1 , A2 ,..., An
называется множеством всех векторов
(a1 , a2 ,..., an ), длины n таких, что
a1 A1 , a2 A2 ,..., an An .
Иначе говоря
A1 A2 ... An
a1 ,a2 ,...,an : a1 A1 ,a2 A2 ,...,an An .
47
48. Пример 1:
Найти прямое произведение множествA1 , A2 и A3 где
A1 0,1 , A2 т, п , A3 1,3 .
Перечисляем тройки элементов в лексикографическом порядке.
A1 A2 A3 0, т,1 , 0, т,3 , 0, п,1 ,
0, п,3 , 1, т,1 , 1, т,3 , 1, п,1 , 1, п,3 .
48
49.
Пусть А – конечное множество, элементамикоторого являются символы (буквы, цифры,
знаки препинания, знаки операций и т. д.).
Такие множества обычно называют
алфавитом.
Примеры алфавитов:
1) 33 русских буквы,
2) 26 латинских букв,
3) 10 арабских цифр;
4) список символов клавиатуры компьютера.
49
50.
Слова длины n в алфавите А – это элементымножества An . Множество всех слов в
алфавите А – это множество
A U A A U A U ... U A U ...
i
1
2
n
i N
Здесь слово определено как вектор.
При написании слова не принято
пользоваться разделителями: скобками,
запятыми; они могут оказаться символами
самого алфавита. Поэтому слово в алфавите
обозначается как конечная последовательность
символов из алфавита А.
50
51. Пример 2:
1. Десятичное число – слово в алфавите цифр{0, 1, 2, 3, ... , 9}.
2. Двоичное слово в алфавите {0, 1}.
3. Текст, отпечатанный на машинке – слово в
алфавите, определяемом клавиатурой этой
машинки.
51
52. Теорема (о мощности прямого произведения множеств)
Пусть A1 , A2 ,..., Anконечные множества и
A1 m1 , A2 m2 ,..., An mn .
Тогда мощность множества A1 A2 ... An
равна произведению мощностей множеств:
A1 A2 ... An m1 m2 ... mn .
52
53. Следствие:
A A .n
n
Например, множество B3 двоичных
векторов длины 3, содержит
3
B3 B B 2 .
3
3
53
54. Проекции множества векторов на оси
Проекцией вектораv a1 , a2 , ...,an
длины n на i-ю ось называется его i-я
координата. Обозначается это так:
прi v ai
Например:
v в , п , л , тогда пр1 v в , пр3 v л.
54
55.
Проекцией вектора v a1 , a2 , ...,anдлины n на оси с номерами i1 , i2 ,...,ik
называется вектор, составленный из
соответствующих координат. Обозначается
это так: прi1 , i2 , ...ik v ai1 , ai2 , ..., aik .
Например:
v в, п, л , тогда пр1,2 v в , п .
55
56. Пусть дано множество V векторов одинаковой длины.
Проекцией множества векторов на iю ось называется множество проекций наi-ю ось всех его векторов. Обозначается
это так: прi V прi v : v V .
Например:
V a, b, c , d , c, a ,
пр2 V b, c , пр3 V c, a .
56
57.
Проекцией множества векторов на осис номерами i1 , i2 ,...,ik
называется
множество проекций на оси с номерами
i1 , i2 ,...,ik всех его векторов. Обозначается:
прi1 , i2 , ...ik V прi1 , i2 , ...ik v : v V .
a, b, c , d , c, a , тогда
пр1,2 V a ,b d ,c .
Например:V
57
58. Пример 3:
Дано множество векторов:V = {(Иванов Александр Николаевич),
(Иванов Михаил Александрович),
(Иванов Сергей Александрович)}.
пр1 V = {Иванов},
пр2 V = {Александр, Михаил, Сергей},
пр23 V = {(Александр Николаевич), (Михаил
Александрович), (Сергей Александрович)}.
58
59. Пример 4
Дано множество векторовV v1 (a, b, d ); v2 (c, b, d ); v3 (d , b, b) .
Тогда
пр1v1 a – это вектор из одной координаты вектора v1 , а именно, первой
координаты;
пр3v2 d – это вектор из одной координаты вектора v2 , а именно, третьей;
пр 2 v 3 b – это вектор из одной координаты вектора v3 , а именно, второй;
59
60. Пример 4
V v1 (a, b, d ); v2 (c, b, d ); v3 (d , b, b)пр1,2v2 c , b – это вектор из двух коор-
динат вектора v2 , а именно первой и
второй;
пр2,3v3 b, b – это вектор из двух координат вектора v3 , а именно второй и
третьей;
пр1,3v1 a , d – это вектор из двух координат вектора v1 , а именно первой и
60
третьей;
61. Пример 4
V v1 (a, b, d ); v2 (c, b, d ); v3 (d , b, b)пр1V a , c , d
– это множество векторов,
составленных из первых координат элементов
V. Они все различны, поэтому пр1V 3 ;
пр2V b
– это множество векторов,
составленных из вторых координат элементов
V. Они все одинаковы, поэтому пр2V 1 ;
пр3V d , b –
это множество векторов,
составленных из третьих координат элементов
V. Две из трех одинаковы, поэтому пр3V 2 ;
61
62. Пример 4
V v1 (a, b, d ); v2 (c, b, d ); v3 (d , b, b)пр1,2V a , b , c , b , d , b – это множество
векторов, составленных из 1-х и 2-х координат
векторов множества V.
пр2 ,3V b, d , b, b
– это множество
векторов, составленных из 2-х и 3-х координат
векторов множества V.
пр1,3V a , d , c , d , d , b – это множество
векторов, составленных из 1-х и 2-х координат
векторов множества V.
62
63. Лекция 3
Комбинаторика64. Правило суммы
Классическая формулировкаЕсли элемент α можно выбрать k
способами, а элемент β можно
выбрать m способами [1].
Тогда α или β можно выбрать
k + m способами.
64
65.
Теорема о мощности объединениямножеств (современная формулировка)
Количество элементов объединения двух
множеств равно сумме количества
элементов в первом и во втором множестве,
за вычетом количества элементов их
пересечения:
А В А B A B
65
66.
Причем, если множества непересекаются, то теорема приобретает
вид, аналогичный классической
формулировке:
А В А В
66
67.
Для трех множеств теорема имеет вид:А В С А В С
А В А С В С А В С
67
68.
Пример 1Из 35 учащихся класс по итогам года имели
«5» по математике – 14 человек; по физике –
15 человек; по химии – 18 человек;
по математике и физике – 7 человек;
по математике и химии – 9 человек; по физике и
химии – 6 человек; по всем трем предметам –
4 человек.
Сколько человек имеют “5” по указанным
предметам? Сколько человек не имеет “5” по
указанным предметам? Имеет “5” только по
математике? Имеет “5” только по двум
68
предметам?
69.
Пример 1Введем обозначения. Обозначим буквой U
множество всех учеников класса, буквой М
множество учеников, имеющих «5» по
математике, буквой Ф – имеющих «5» по
физике, Х – имеющих «5» по химии. Тогда,
согласно условию,
69
70.
Пример 1На рисунке 1 приведено множество,
состоящее из учеников, имеющих «5» хотя бы
по одному из указанных предметов.
Рис.1. Множество
учеников, имеющих
«5» хотя бы по
данному предмету
70
71.
Пример 1Очевидно, что это объединение множеств
М, Ф и Х. Для нахождения количества
элементов объединения воспользуемся
правилом суммы.
71
72.
Пример 1На рисунке 2 приведено множество,
состоящее из учеников, не имеющих «5» ни по
одному из указанных предметов. Обозначим его
буквой Н.
Рис. 2. Множество
учеников, не имеющих
«5» по указанным
предметам
72
73.
Пример 1Очевидно, что это разность между
универсальным множеством U и объединением
множеств М, Ф и Х.
73
74.
Пример 1На рисунке 3 приведено множество,
состоящее из учеников, имеющих «5» только по
математике. Обозначим его буквами ТМ.
Рис. 3. Множество
учеников, имеющих
«5» только по
математике
74
75.
Пример 1Очевидно, что это разность между
множеством М и множествами ТМФ – имеющих
«5» только по математике и физике, ТМХ –
имеющих «5» только по математике и химии, и
75
76.
Пример 1На рисунке 4 приведено множество,
состоящее из учеников, имеющих «5» только по
двум предметам. Обозначим его Т2. Очевидно,
что Т2 является суммой трех непересекающихся
множеств ТМФ,
ТМХ, ТФХ.
Рис. 4. Множество
учеников, имеющих
«5» только по двум
предметам
76
77. Найдем мощность каждой части искомого множества:
ТМФ М Ф М Ф Х ;ТМХ М Х М Ф Х ;
ТФХ М Ф М Ф Х .
Тогда искомая мощность примет вид:
Т 2 ТМФ ТМХ ТФХ
М Ф М Х Ф Х 3 М Ф Х .
77
78. Правило произведения
Классическая формулировкаЕсли элемент α можно выбрать k
способами, а элемент β можно выбрать
m способами.
Тогда пару α и β можно выбрать km
способами.
78
79.
Теорема о мощности прямогопроизведения множеств (современная
формулировка)
А В А В
79
80. Пример 2:
Из 3 экземпляров учебника алгебры, 7экземпляров учебника геометрии и 6
экземпляров учебника физики, надо выбрать
комплект, содержащий все учебники по
одному разу. Сколькими способами это
можно сделать?
Ответ: 3 ⨉ 7 ⨉ 6 = 126.
80
81. Пример 3:
Из 10 арабских цифр составляют 5-значныйкод. Сколькими способами это можно сделать
так, чтобы: а) все цифры были разными; б) на
последнем месте четная цифра.
а) 10 ⨉ 9 ⨉ 8 ⨉ 7 ⨉ 6;
б) 10 ⨉ 10 ⨉ 10 ⨉ 10 ⨉ 5.
81
82. Число размещений без повторений
Число размещений без повторений из n поk – это число способов, сколькими можно из n
различных элементов построить векторов с k
различными координатами.
Число размещений без повторений
находится по формуле:
k
Аn
n!
n k !
82
83. Пример 4:
Сколькими способами можно построить 3значное число с различными цифрами, несодержащее цифры 0?
9!
9! 1 2 ... 6 7 8 9
А
7 8 9.
9 3 ! 6!
1 2 ... 6
3
9
83
84. Число размещений с повторениями
Число размещений с повторениями из nпо k – это число способов, сколькими можно
из n различных элементов построить
векторов с k координатами, среди которых
могут быть одинаковые.
Число размещений с повторениями
находится по формуле:
k
k
Вn n
84
85. Пример 5:
Сколько слов длины 6 можно составить из26 букв латинского алфавита?
6
6
В26 26
85
86. Число перестановок без повторений
Число перестановок без повторений из nэлементов – это число способов, сколькими
можно расположить на n различных местах n
различных элементов.
Число перестановок без повторений
находится по формуле:
Рn n!
86
87. Задача на рассадки и расстановки
В задачах на рассадки и расстановкииспользуется тот факт, что
n различных элементов на
n различных местах
можно расставить n!
различными способами
87
88. Пример 6:
Сколькими способами можно расставить накнижной полке 5 различных книг? В скольких
случаях две определенные книги А и В
окажутся рядом?
Всего вариантов расстановки 5 книг на 5
местах :
5!=120
88
89. Замечание:
В задаче на рассадки и расстановки числоэлементов множества А ищут по формуле:
А х1 х2 х3 ,
где х1 – число способов выбрать нужные
места;
х2 – число способов расположить на них
нужные элементы;
х3 – число способов расположить
остальные элементы на оставшихся местах.
89
90. Рис. 5. Схема расстановки
12
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
Рис. 5. Схема расстановки
х1 4;
х2 2!; х3 3!;
A 4 2! 3!
90
91. Число сочетаний без повторений
Число сочетаний без повторений из nпо k – это число способов, сколькими можно
из n различных элементов выбрать k штук
без учета порядка.
Число сочетаний без повторений
находится по формуле:
n!
С
.
k! n k !
k
n
91
92. Свойства числа сочетаний
01.C n 1 ;
n
2. C n 1 ;
1
3. C n n ;
n 1
4. C n n ;
k
n k
5. C n C n ;
n( n 1 )
2
6. C n
;
2
n n 1 n 2
3
7. C n
3!
92
.
93. Урновая задача
Урновая задача – это задача, в которойпроизводится выбор сразу нескольких
элементов из заданной совокупности.
Пример 7:
В урне 7 шаров. Из них 3 белых, 4 черных.
Наугад выбирают 3 шара. Сколькими
способами это можно сделать? В скольких
случаях среди них будет: 1) один белый;
2) два белых; 3) все белые.
93
94. Схема урновой задачи
9495. Общее число исходов эксперимента найдем по общей формуле
n!С
.
k! n k !
k
n
7! 5 6 7
U С
5 7 35
3! 4! 1 2 3
3
7
95
96. Количество элементов множества А1 найдем по формуле:
4 3А1 С С 3
3 6 18.
2
1
3
2
4
96
97. Количество элементов множества А2 найдем по формуле:
21
А2 С3 С4 3 4 12.
97
98. Количество элементов множества А3 найдем по формуле:
30
А3 С3 С4 1 1 1.
98
99. Лекция 4
Соответствия100.
Соответствия и функцииСоответствием множеств А и В [2, 3]
называется подмножество G такое, что
G A B.
Если (a, b) G, то говорят, что
«b соответствует a при соответствии G».
Область определения соответствия G –
множество пр1 G A.
Область значений соответствия G –
множество пр2 G B.
100
101.
Соответствие G называется всюду(полностью) определенным – если пр1 G = А
(в противном случае – частично
определенное соответствие).
Соответствие G называется
сюрьективным, если пр2 G = B.
101
102.
Образ элемента a пр1G в множестве Bпри соответствии G – это множество всех
элементов b пр2G которые соответствуют a.
Прообраз элемента b пр2G в множестве
А при соответствии G – это множество всех
a пр1G которым соответствует b.
102
103.
Образом множества C пр1Gназывается объединение образов всех
элементов С.
Прообразом множества D пр2G
называется объединение прообразов всех
элементов D.
103
104.
Соответствие G называетсяфункциональным (однозначным)
соответствием, если образом любого
элемента из пр1 G является единственный
элемент из пр2 G.
Соответствие G называется инъективным
соответствием, если прообразом любого
элемента из пр2 G является единственный
элемент из пр1 G.
104
105.
Соответствие F является функцией типаF : A B, если оно функционально
(однозначно)
F ( a ) b.
105
106.
Соответствие G является отображениемфункционально и полностью определено.
Соответствие G является отображением
множества А в множество В, если оно не
сюрьективно.
Соответствие G является отображением
множества А на множество В, если оно
сюрьективно.
106
107.
Соответствие G является взаимнооднозначным, если оно:
1) всюду определено;
2) сюрьективно;
3) функционально;
4) инъективно.
107
108. Пример 1:
Определить свойства соответствия G междумножествами A и B.
A = {a, b, c}, B = {1, 2, 3}.
G = {(a, 2), (b, 2), (c,3)}.
108
109.
Область определения:D(G) = пр1G = {a, b, c} = A, значит
полностью определено.
Область значения:
Е(G) = пр2G = {2, 3} ≠ B, значит не
сюрьективно.
109
110.
Образы элементов области определения:G (a) = {2}; G (b) = {2}; G (c) = {3}.
Видим, что есть единственность образа,
значит соответствие функционально.
110
111.
Прообразы элементов области значений:G
1
2 a,b ; G 3 c .
1
Нет единственности прообраза, значит не
инъективно.
111
112. Выводы:
1. Соответствие является функцией, так какфункционально.
2. Соответствие является отображением, так
как полностью определено и функционально.
3. Соответствие является отображением А в В,
так как не сюрьективно.
4. Соответствие не является взаимно
однозначным, так как не сюрьективно и не
инъективно.
112
113. Пример 2:
Определить свойства соответствия G междумножествами A и B.
A = {a, b, c}, B = {1, 2, 3}.
G = {(b, 1), (b, 2), (c,3)}.
113
114.
Область определения:D(G) = пр1G = {b, c} ≠ A, значит не
полностью определено.
Область значения:
Е(G) = пр2G = {1, 2, 3} = B, значит
сюрьективно.
114
115.
Образы элементов области определения:G (b) = {1, 2}; G (c) = {3}.
Видим, что нет единственности образа,
значит соответствие не функционально.
115
116.
Прообразы элементов области значений:G-1 (1) = {b}, G-1 (2) = {b}, G-1 (3) = {c}
Есть единственность прообраза, значит
инъективно.
116
117. Выводы:
1. Соответствие не является функцией, таккак не функционально.
2. Соответствие является отображением, так
как не полностью определено и не
функционально.
3. Соответствие не является взаимно
однозначным, так как не функционально и не
полностью определено.
117
118.
Преобразованием множества Аназывается отображение типа A A.
Функция типа A1 A2 ... An B
называется n-местной функцией
f (a1 , a2 ,..., an ) b.
118
119.
Соответствие H B A называетсяобратным к G A B, если Н таково, что
(b, a ) H (a, b) G.
119
120.
Если соответствие, обратное к функцииf : A B является функциональным, то оно
называется функцией, обратной к f,
f
1
: B A.
120
121.
Пусть дана функция f : A B.Соответствие
f
1
: B A.
является функцией тогда и только тогда, когда
1
f
f инъективна, и
является отображением
тогда и только тогда, когда f инъективна и
сюрьективна, то есть биективна.
121
122.
Утверждение:Для функции
f : A B
существует
1
обратная функция f
тогда и только тогда,
когда f является взаимно однозначным
соответствием между своей областью
определения и областью значений.
122
123.
Пусть даны функцииf : A B и g : B C.
Функция h : A C называется
композицией функций f и g, если
f g h( x) g ( f ( x)), x ∈ A.
Часто говорят, что h получена подстановкой
f в g.
123
124.
Для многоместных функцийf : A B и g : B n C возможны
m
различные варианты подстановки f в g,
задающие функции различных типов.
Например, при m = 3 и n = 4 функция
имеет 6 аргументов и тип B A B C ,
3
2
h g (b1 , f (a1 , a2 , a3 ), b3 , b4 ).
124
125.
Для множества многоместныхf1 : A A, ... f n : A
m1
mn
A
функций типа возможны любые
подстановки функций друг в друга, а также
любые переименования аргументов.
Например, переименование x3 в x2 из
функции четырёх аргументов порождает
функцию трёх аргументов:
f ( x1 , x2 , x2 , x4 ) g ( x1 , x2 , x4 ).
125
126.
Функция, полученная из функцийf1 , ..., f n
некоторой подстановкой их друг в друга и
переименованием аргументов, называется
суперпозицией.
Выражение, задающее эту суперпозицию и
содержащее функциональные знаки, скобки и
символы аргументов, называется формулой.
126
127. Взаимно однозначные соответствия и мощность множеств
Утверждение (о взаимно однозначномсоответствии равномощных множеств):
Если между конечными множествами А и
В существует взаимно однозначное
соответствие, то
А В.
127
128. Взаимно однозначные соответствия и мощность множеств
Доказательство:1. Пусть мощность А больше, чем мощность В.
128
129. Взаимно однозначные соответствия и мощность множеств
Тогда если выполняется свойство полнойопределенности, то не выполняется свойство
инъективности.
129
130. Взаимно однозначные соответствия и мощность множеств
Доказательство:2. Пусть мощность А меньше, чем
мощность В.
130
131. Взаимно однозначные соответствия и мощность множеств
Тогда если выполняется свойствофункциональности, то не выполняется
свойство сюрьективности, и наоборот.
131
132. Взаимно однозначные соответствия и мощность множеств
Таким образом, получили противоречие,что доказывает истинность
сформулированного утверждения.
132
133.
Этот факт:1) позволяет установить равенство
мощностей двух множеств, не вычисляя
мощностей этих множеств;
2) дает возможность вычислить мощность
множества, установив его взаимно
однозначное соответствие с множеством,
мощность которого известна или легко
вычисляется.
133
134.
На понятии взаимно однозначногосоответствия строится доказательство многих
важных теорем в теории множеств.
Теорема о числе подмножеств
конечного множества
Если мощность конечного
множества U равна n, то число
его подмножеств равно 2n .
134
135.
Доказательство:Пусть элементы множества U
перенумерованы:
U = {a1 , a2 , a3 ,…, an }.
Установим взаимно однозначное
соответствие между множеством всех
подмножеств U –
булеаном ℬ (U) и множеством двоичных
векторов длины n – Вn.
135
136.
Доказательство:Двоичный вектор
v = (v1 , v2 , v3 ,…, vn ), соответствующий
подмножеству М множества U: имеет
координату
vi = 0, если ai не принадлежит U;
vi = 1, если ai принадлежит U.
136
137.
Например:Элементу булеана Ø соответствует
двоичный вектор (0, 0, …, 0);
подмножеству {a1} – (1, 0,…,0);
подмножеству {a2} – (0, 1,…,0);
подмножеству {a1 , a2 } – (1, 1,…,0);
подмножеству U – (1, 1,…,1).
137
138. Теорема о числе подмножеств конечного множества
Таким образом, между множествамиℬ (U) и Вn установлено взаимно
однозначное соответствие.
Согласно утверждению, их мощности
равны:
ℬ (U)│= │Вn │= 2n .
138
139. Лекция 5
Отношения140. Определение:
nПодмножество R M называется
n – местным отношением
на множестве М [2, 3].
Говорят, что a1 , a 2 , , a n находится
в отношении R, если a1 , a2 , , an R .
140
141.
Одноместное отношение – это простоподмножество М. Такие отношения называют
признаками: элемент а – обладает признаком
R, если R⊆ M и a ∈ R.
Свойства одноместных отношений – это
свойства подмножеств М, поэтому для случая
n = 1 термин «отношение» употребляется
редко.
141
142.
Примером трехместного (тернарного)отношения является множество троек
нападающих в хоккейной команде. Любой из
нападающих находится в этом отношении со
всеми теми игроками, с которыми он играет в
одной тройке (один нападающий может,
вообще говоря, участвовать более, чем в
одной тройке).
142
143.
При n = 2 – отношения называютсядвуместными или «бинарными».
Если a и b находятся в отношении R,
это записывается aRb.
Таким образом, бинарное отношение,
заданное на множестве М, это любое
2
подмножество R ⊆ M .
143
144. Способы задания
Бинарные отношения задаются:1) cписком;
2) матрицей бинарного отношения;
3) графом.
144
145. Список
Списком задаются отношения, где М –конечное множество, а R содержит небольшое
количество пар.
Пример 1:
M а , b , c – алфавит из трех букв, отношение
R – предшествования букв в алфавите. Тогда R
содержит пары:
R а, b , a, c , b, c .
145
146.
Матрица бинарного отношения,заданного на множестве M {a1 , a2 , , an }
– это квадратная матрица С порядка n,
элементами:
1, если ai Ra j ;
cij
0, в противном случае.
Здесь i – номер строки, j - номер столбца.
146
147. Пример 2:
M 1, 2, 3, 4Отношение R – «быть больше или равно»
1
2
3
4
1
1
1
1
1
2
0
1
1
1
3
0
0
1
1
4
0
0
0
1
147
148. Задание графом
При задании графом, элементы Мсопоставляются одноименным точкам. Точки a
и b соединяются стрелками, если aRb.
Пример 3:
M 1, 2, 3 .
Отношение –
быть меньше.
Рис. 1. Задание
отношения графом
148
149. Свойства бинарных отношений
Отношение R на М называетсярефлексивным, если для любого a ∈ M
выполняется a Ra.
Главная диагональ матрицы такого
отношения содержит только единицы, граф –
петлю в каждой вершине.
Пример 4: Отношение «быть делителем»,
заданной на множестве N. 1 делитель 1; 2
делитель 2; 3 делитель 3; и т. д.
149
150. Свойства бинарных отношений
Отношение R на М называетсяантирефлексивным, если для любого a ∈ M
выполняется aRa.
Главная диагональ матрицы такого
отношения содержит только нули, граф – не
имеет петель.
Пример 5: Отношение «быть больше»,
заданной на множестве N. 1 не больше 1; 2 не
больше 2; 3 не больше 3; и т.д.
150
151. Свойства бинарных отношений
Отношение R на М называетсясимметричным, если для любой пары
a ,b ∈ M из aRb следует bRa (то есть для
любой пары отношение R выполняется в обе
стороны или не выполняется вообще).
Матрица симметричного отношения –
симметрична относительно главной диагонали,
у графа все стрелки парные, симметричные.
151
152. Пример 6:
• Отношение «жить в одной комнате вобщежитии».
• Если А живет в одной комнате с В, то и
В живет в одной комнате с А.
• Если С живет в одной комнате с D, то и
D живет в одной комнате с C.
• И так далее.
152
153. Свойства бинарных отношений
Отношение R на М называетсяантисимметричным, если для любой пары
a ,b ∈ M из того, что одновременно выполняется:
aRb и bRa следует что a = b .
Матрица антисимметричного отношения не
имеет ни одной симметричной 1, у графа все
стрелки непарные, направлены лишь в одну
строну.
153
154. Пример 7:
• Отношение «быть начальником».• Если А начальник В, то В не является
начальником А.
• Если C начальник D, то D не является
начальником C.
• И так далее.
154
155. Свойства бинарных отношений
Отношение R на М называетсятранзитивным, если для любых трех
a ,b ,c ∈ M из того, что выполняется aRb и
одновременно bRc следует, что aRc.
Пример 8: Отношение «быть больше»,
заданной на множестве N.
если 3 больше 2 и 2 больше 1, то 3 больше 1;
если 5 больше 3 и 3 больше 1, то 5 больше 1;
и т.д.
155
156. Отношение эквивалентности
Отношение R на М называется отношениемэквивалентности, если оно
Рефлексивно,
симметрично,
транзитивно.
156
157. Пример 9:
На множестве натуральных чиселзадано отношение R – иметь одинаковый
остаток от деления на 3.
R – рефлексивно, так как каждое число
само с собой имеет одинаковый остаток
от деления на 3,
например 1 и 1, 2 и 2, 3 и 3, и так далее.
157
158. Отношение: иметь одинаковый остаток от деления на 3
R – симметрично, так как каждое если число аимеет с числом b одинаковый остаток от
деления на 3, то и число b с числом а тоже имеет
одинаковый остаток от деления на 3. Например,
1 и 4 имеют одинаковый остаток от деления на 3,
то и 4 и 1 тоже имеют одинаковый остаток;
2 и 5 имеют одинаковый остаток от деления на 3,
то и 5 и 2 тоже имеют одинаковый остаток;
3 и 12 имеют одинаковый остаток от деления на
3, то и 12 и 3 тоже имеют одинаковый остаток, и
158
так далее.
159. Отношение: иметь одинаковый остаток от деления на 3
R – транзитивно, так для каждых чисела , b и с если а с b имеют одинаковый остаток
от деления на 3, и b с с имеют одинаковый
остаток от деления на 3, то и а с с тоже
имеют одинаковый остаток от деления на 3,
например 1 и 4 имеют одинаковый остаток от
деления на 3, и 4 и 13 тоже имеют одинаковый
остаток от деления на 3, тогда 1 и 13 тоже
имеют одинаковый остаток.
159
160. Отношение: иметь одинаковый остаток от деления на 3
Таким образом, отношение R –рефлексивно, симметрично и
транзитивно, то есть является
отношением эквивалентности.
160
161. Разбиение на классы эквивалентности
Если отношение R – отношениеэквивалентности, то оно разбивает
множество, на котором задано, на
классы эквивалентности.
161
162. Разбиение на классы эквивалентности
Для разбиения на классы надо:1) выбрать из М произвольный элемент a1 и
поместить его в класс C1 , затем поместить в этот
класс все элементы, эквивалентные ему;
2) затем из оставшихся элементов М выбрать
элемент a2 и поместить его в класс C 2 , затем
поместить в этот класс все элементы,
эквивалентные ему;
3) делать, пока останутся нераспределенные по
классам элементы.
Число классов разбиения – индекс разбиения I.
162
163. Отношение: иметь одинаковый остаток от деления на 3
Для разбиения на классы надо:1) выбрать произвольный элемент 1 и поместить его
в класс C1 , затем поместить в этот класс все
элементы, эквивалентные ему: 4, 7, 10, 13, ... ;
2) затем из оставшихся элементов М выбрать элемент
2 и поместить его в класс C 2 , затем поместить в
этот класс все элементы, эквивалентные ему: 5, 8,
11, 14, 17, … ;
3) затем из оставшихся элементов М выбрать элемент
3 и поместить его в класс C 3 , затем поместить в
этот класс все элементы, эквивалентные ему: 6, 9,
12, 15, … Индекс разбиения равен 3.
163
164. Отношение порядка
Отношение R – отношениепорядка [4], если оно
антисимметрично и
транзитивно.
164
165. Отношение порядка
Отношение порядка R –отношение строгого порядка,
если оно антирефлексивно,
антисимметрично и
транзитивно.
165
166. Отношение порядка
Отношение порядка R –отношение нестрогого
порядка, если оно
рефлексивно,
антисимметрично и
транзитивно.
166
167. Отношение порядка
Если элементы a и b связаны отношениемпорядка, то есть aRb или bRa, то a и b
сравнимы по отношению порядка R.
167
168. Отношение порядка
Если любые два элемента a и b сравнимыпо отношению порядка R, то R отношение
полного или линейного порядка, а М
называется полностью упорядоченным.
168
169. Пример 10: отношение «быть делителем», задано на N
R – рефлексивно, так как каждое числоявляется делителем самого себя:
1 делитель 1;
2 делитель 2;
3 делитель 3, и так далее.
169
170. Отношение «быть делителем», задано на N
R – антисимметрично, так как если числаразные и a делитель b,то b не является
делителем a:
если 1 делитель 2 и 2 не делитель 1;
если 4 делитель 8, то 8 не делитель 4;
если 3 делитель 9, то 9 не делитель 3,
и так далее.
170
171. Отношение «быть делителем», задано на N
R – транзитивно, так как если числа разныеи a делитель b и b делитель с, то а тоже
является делителем с:
если 1 делитель 2 и 2 делитель 4, то 1 –
делитель 4;
если 4 делитель 8 и 8 делитель 24, то 4 –
делитель 24, и так далее.
171
172. Отношение «быть делителем», задано на N
R – рефлексивно, антисимметрично итранзитивно, значит
R – отношение нестрогого порядка.
172
173. Отношение «быть делителем», задано на N
R – задает неполный порядок,так как можно найти хотя бы одну пару
несравнимых элементов,
например: 2 и 3; 7 и 11; 4 и 9, и так
далее.
173
174. Лекция 6
Операции и алгебры175. Определение операции
N-арная операция на множестве М –это функция типа
n
: М M,
где n – арность операции [2, 3, 5].
Операция замкнута относительно
множества М по определению, то есть
операция над элементами множества М,
и результат тоже элемент М.
175
176. Определение алгебры
Алгеброй называется множество М,вместе с заданной на нем
совокупностью операций
1 , 2 , ... , n ,
то есть система
А M ; 1 , 2 , ... , n
176
177.
М – основное (несущее) множество(носитель алгебры) алгебры А.
Тип алгебры – вектор арностей
операций.
Сигнатура – совокупность
операций Σ.
177
178.
МножествоM М называется
замкнутым относительно n-арной
операции на М, если
М M ,
n
то есть, если значения на аргументе
из М' принадлежат М' .
178
179.
Если М' замкнуто относительновсех операций 1 , 2 , ... , n ,
алгебры А с носителем М, то система
А M ; 1 , 2 , ... , n
называется подалгеброй алгебры А.
179
180. Пример 1:
Алгебра R, , – называется полемдействительных чисел.
Обе операции бинарные, поэтому тип
этой алгебры (2, 2).
Сигнатура
Σ , .
Подалгеброй этой алгебры является,
например, поле рациональных чисел.
180
181. Примеры 2:
Пусть N p 0, 1, 2, ... , p 1 .Определим на N p операции:
– «сложение по модулю р»,
– «умножение по модулю р»,
следующим образом:
a b c и a b d,
где с и d – остатки от деления на р чисел
а + b и а b соответственно.
181
182. Пример 2:
Пусть, например, р = 7, тогдаN p = { 0,1, 2, 3, 4, 5, 6 } и
3 4 0, 3 4 5, 4 6 3.
Часто обозначают:
a + b = с (mod p) и a b = d (mod p).
182
183.
Конечным полем характеристики рназывается алгебра
N p , , ,
если р – простое число.
183
184. Пример 3:
Булеаном U называется множество всехподмножеств множества U
(обозначается ℬ(U)).
Булева алгебра множеств над U или
алгебра Кантора – алгебра (ℬ(U), , , )
Ее тип (2, 2, 1), сигнатура
Σ = ( , , ).
184
185. Пример 3:
Для любого U ′ ⊂ UB' = (ℬ(U'), U, ∩, ¬ )
– является подалгеброй В.
185
186. Пример 3:
Множество U={a, b, c, d}тогда основное множество алгебры В
содержит 16 элементов.
B՛=(ℬ({a, b}),U, ∩, ¬ ).
является подалгеброй В.
186
187. Свойства бинарных алгебраических операций
Операция φ называетсяассоциативной, если для любых
элементов а, b, с .
a b c a b c a b c.
187
188. Пример 4:
1. Сложение и умножение чиселассоциативны, что позволяет не ставить
скобки в выражениях a b c a b c,
a b c a b c.
2. Возведение в степень a
b
a b
– не ассоциативна,
a b c a a
не равно
bc
a b c a .
так как
b c
bc
188
189. Пример 4:
3. Прямое произведение множеств неассоциативно: A 1, 2 , B a, b , C z .
A B C
1, a , z , 1, b , z , 2, a , z , 2, b , z ;
A B C
1, a, z , 1, b, z , 2, a, z , 2, b, z .
189
190. Свойства бинарных алгебраических операций
Операция φ называетсякоммутативной, если для любых
элементов a, b
a b b a.
190
191. Пример 5:
1. Сложение чисел коммутативно(«от перемены мест слагаемых сумма не
меняется»):
a b b a.
2. Умножение чисел коммутативно («от
перемены мест множителей произведение
не меняется»):
a b b a.
191
192. Пример 5:
3. Вычитание и деление – некоммутативныеоперации: a b b a ; a / b b / a .
4. Умножение матриц – некоммутативная
операция, например:
1 2 2 2 2 3
;
0 1 0 1 0 1
2 2 1 1 2 4
.
0 1 0 1 0 1
192
193. Свойства бинарных алгебраических операций
Операция φ называетсядистрибутивной слева относительно
операции ψ, если для любых a, b, с
a b c a b a c .
193
194. Свойства бинарных алгебраических операций
Операция φ называетсядистрибутивной справа относительно
операции ψ, если для любых a, b, с
a b c a с b c .
194
195. Пример 6:
1. Умножение дистрибутивно относительносложения слева и справа
a b c a b a c ;
a b c a c b c .
195
196. Пример 6:
2. Возведение в степень дистрибутивноотносительно умножения справа.
a b c a b
c
a b a с b c .
c
c
196
197. Пример 6:
но не слева, так какa b c a
b c
a b a c a a a
b
c
b c
197
.
198. Пример 6:
3. Сложение не дистрибутивноотносительно умножения
a b c a b a c ;
a b c a c b c .
198
199. Лекция 7
Гомоморфизм алгебр200.
Алгебры разного типа, очевидно, имеютсущественно различное строение. Если же алгебры
имеют одинаковый тип, то наличие у них сходства
характеризуется с помощью вводимых ниже
понятий гомоморфизма и изоморфизма.
Пусть даны две алгебры
А K ; 1 , 2 , ... , n и В M ; 1 , 2 , ... , n
одинакового типа, т. е. арности 1 и ψ1 ; 2 и
ψ 2 , ...; п и ψ п – одинаковы.
200
201.
Гомоморфизмом алгебры А в алгебру Вназывается отображение
Γ : K М ,
удовлетворяющее условию:
i k1 , k2 , ... , kl i i k1 , k2 , ... , kl i
для всех i 1, 2, ..., n, ,
i m1 , m2 , ... , ml i
где l i – арность операций i и ψ i ).
201
202.
Смысл условия гомоморфизма:a , b, c ∈ K ; Γ (a), Γ (b), Γ (c) ∈ M
независимо от того, выполнена ли сначала операция i в
множестве K и затем произведено отображение Г, либо
сначала произведено отображение Г, а затем в
множестве M выполнена соответствующая операция i ,
результат будет одинаков.
202
203.
Изоморфизмом алгебры А на алгебру Вназывается взаимно однозначный гомоморфизм.
В этом случае существует обратное отображение
1: K M , так же взаимно однозначное.
1
m j .
k
Пусть k j m j , m j M . Тогда j
Поменяем в условии гомоморфизма левые части
1
к
этих равенств на правые и применим
обеим частям получившегося равенства. Так как
1 k k , то получим:
1 i k1, k2 , ..., kl (i ) 1 i m1, m2 , ..., ml (i ) ,
1
, получим
учитывая, что
i 1 m1 , 1 m2 , ..., 1 ml (i ) 1 i m1, m2 , ..., ml (i ) .
203
204.
Это тоже равенство с заменой Г на1
, элементов множества K на
элементы множества М и переменой
1
ψ
местами i и i . Иначе говоря, – это
изоморфизм В на А.
Утверждение 1.
Если существует изоморфизм А на В,
то существует изоморфизм В на А; при
этом алгебры А и В называются
изоморфными.
204
205.
Утверждение 2.Мощности несущих множеств
изоморфных алгебр равны (при
гомоморфизме это равенство может не
выполняться).
Автоморфизм на себя или
автоморфизм – это гомоморфизм при
условии, что А = В.
Изоморфизм
в
себя
–
изоморфизм В ⊂ А .
205
206.
Пример 1:Пусть Q N – множество целых чисел;
Q2 N – множество четных чисел.
Алгебры (QN ;+ ) и
является отображение
(Q2 N ;+) изоморфны. Изоморфизмом
: n 2n .
Условие гомоморфизма имеет вид:
a b a b .
Поскольку
a b 2 a b ,
a 2a; b 2b,
то условие изоморфизма примет вид истинного равенства:
2 (a + b) = 2a + 2b.
206
207.
Пример 1.Пусть QN – множество всех целых чисел;
Q2 N – множество всех четных чисел.
(QN ;+)
(Q2 N ;+)
Алгебры
и
изоморфны.
Изоморфизмом является отображение : n 2n , причем,
условие гомоморфизма здесь имеет вид:
Г(a + b) = Г(a) + Г(b).
Поскольку
nо условие
равенства:
Г(a + b) = 2 (a + b),
Г(a) = 2a, Г(b) = 2b,
гомоморфизма примет
вид
истинного
2 (a + b) = 2a + 2b.
Поскольку Q2 N QN , то Г – изоморфизм алгебры
(QN ;+) в себя.
207
208.
Пример 2.Пусть QZ – множество всех целых чисел;
Отображение:
: n 2n ,
является для алгебры QZ ; автоморфизмом.
Условие гомоморфизма здесь имеет вид:
Г(a + b) = Г(a) + Г(b).
Поскольку
Г(a + b) = – (a + b),
Г(a) = – a, Г(b) = – b,
то условие гомоморфизма примет вид истинного
равенства:
– (a + b) = (– a) + (– b).
208
209.
Пример 3.Отображение:
: n ( n)
для алгебры (QN ;+) не является автоморфизмом, так как
условие гомоморфизма имеет вид:
a b a b .
Поскольку
a b a b ,
a a, b b,
то условие
равенства:
гомоморфизма
принимает
вид
ложного
a b a b .
209
210.
Пример 4.Изоморфизмом между алгебрами R ; и R; , где
R+ – положительное подмножество R, является отображение:
а log a.
Условие гомоморфизма имеет вид:
a b a b .
и поскольку
a b log a b ,
то условие
равенства:
a log a, b logb,
гомоморфизма принимает
вид
истинного
log a b log a log b.
210
211.
Булевы алгебры КантораB = ( B(U), , , ), и B′ = ( B(U ′ ), , , ),
образованные двумя различными
множествами U и U΄ одинаковой мощности,
изоморфны. Операции у них просто
одинаковы, а отображением Г может служить
любое взаимно однозначное соответствие
между U и U΄ .
212.
Утверждение 3.Отношение изоморфизма является
отношением эквивалентности на множестве
алгебр:
– рефлексивность отношения изоморфизма
очевидна;
– симметричность следует из существования
обратного изоморфизма;
– транзитивность устанавливается следующим
образом: если Г1 – изоморфизм А на В, Г2 –
изоморфизм В на С, то изоморфизмом А на С
будет композиция Г1 и Г2.
212
213.
Классами эквивалентности в разбиениипо отношению изоморфизма являются
классы изоморфных между собой алгебр.
Понятие изоморфизма – одно из
важнейших в математике. Его сущность,
как видно из примеров можно выразить
так: если алгебры А и В изоморфны, то
элементы и операции в В можно
переименовать так, что В совпадет с А.
213
214.
• Из условия изоморфизма следует, что любоеэквивалентное соотношение в алгебре А
сохраняется в любой изоморфной ей алгебре.
• Это позволяет получить такие соотношения в
алгебре А и автоматически распространить их на
все алгебры, изоморфные А. Распространенное в
математике выражение «рассматривать с
точностью до изоморфизма» означает, что
рассматриваются только те свойства объектов,
которые сохраняются при изоморфизме, то есть
являются общими для всех изоморфных объектов.
• В частности, изоморфизм сохраняет
ассоциативность, коммутативность,
дистрибутивность.
214
215. Лекция 8
Графы. Определения,способы задания.
Виды графов.
216. Определение графа
Пусть V – множество вершин,а Е – множество ребер.
Графом G называется пара объектов
(V, E) между которыми задано отношение
инцидентности:
Г : е → (v, w),
где вершина v и ребро e инцидентны друг
другу, если вершина является для этого ребра
концевой точкой.
216
217. Определение графа
Вершины v' и v" называются смежными,если существует ребро, соединяющее их, то
есть они инцидентны одному и тому же
ребру.
Ребра e' и e" называются смежными, если
они имеют, по крайней мере, одну общую
вершину (инцидентны одной вершине).
217
218. Определение графа
Граф, содержащий направленные ребра(дуги) с началом v' и концом v" , называется
ориентированным графом (ор-графом). Для
ор-графа
v , v v , v .
Граф, содержащий ненаправленные ребра
с конами v' и v" , называется
неориентированным графом (н-графом).
Для н-графа
v , v v , v .
218
219. Определение графа
Вершина, у которой нет инцидентныхребер, называется изолированной.
219
220. Определение графа
Рис.1. Неориентированное ребро (a, b)Рис.2. Ориентированное ребро (a, b)
220
221. Определение графа
Ребро, концевые вершины которогосовпадают, называется петлей.
Рис.3.
Неориентированная
петля
Рис.4. Ориентированная
петля
221
222. Определение графа
Ребра (дуги), имеющие одинаковые начало иконец, называются параллельными или
кратными.
Рис.5. Кратные неориентированные ребра
222
223. Определение графа
Рис. 6. Кратные ориентированные ребра223
224. Определение графа
Ребра ор-графа, соединяющие одну и тужепару вершин в разных направлениях
называются симметричными или
противоположно-направленными.
Рис. 7. Симметричные ребра
224
225. Определение графа
Граф называется конечным, еслимножество его элементов (вершин и ребер)
конечно.
Рис. 8. Конечный граф
225
226. Определение графа
Граф называется бесконечным, еслибесконечно множество вершин или
множество его ребер.
Рис. 9. Граф с бесконечным числом вершин
226
227. Определение графа
Рис. 10. Граф с бесконечным числом ребер227
228. Определение графа
Рис. 11. Бесконечный граф228
229. Каноническое соответствие
Каждому неориентированному графуканонически соответствует
ориентированный граф с тем же множеством
вершин, в котором каждое ребро заменено
двумя ориентированными ребрами,
инцидентными тем же вершинам и
имеющим противоположные направления.
229
230. Каноническое соответствие
Рис. 12. Канонически соответствующие графы230
231. Способы задания
Задать граф – значит описать множестваего вершин и ребер, а также отношение
инцидентности.
Пусть вершины графа v1 , v2 , , vn ;
e1 , e2 , , em ребра графа G.
Граф задают:
1) матрицей инцидентности.
2) матрицу смежности.
3) списком ребер.
4) рисунком.
231
232. Матрица инцидентности
матрица инцидентностиij
размера m n (строкам соответствуют
ребра, столбцам – вершины графа), в которой
для н-графа элементы имеют вид:
1, ребро ei инциндентно вершине v j ;
ij
0 , в противном случае.
232
233. Матрица инцидентности
для ор-графа –1, если вершина v j начало ребра ei ;
1, если вершина v j конец ребра ei ;
ij
, если ei петля вокруг вершины v j ;
0 в остальных случаях.
233
234. Пример 1:
ab c d
1 1
0 0 0
2 1 0 1 0
3 1 0 1 0
4 1
1 0 0
5 0
1 1 0
Рис.13. Матрица инцидентности н-графа
234
235. Пример 2:
a b c d1 α 0 0 0
2 1 0 -1 0
3 1 0 -1 0
4 -1 1 0 0
5 0 -1 1 0
6 0 1 -1 0
Рис. 14. Матрица инцидентности ор-графа
235
236. Матрица смежности
Матрица смежностиij
размера n n , столбцам и строкам которой
соответствуют вершины графа.
Для н-графа ij равно количеству ребер,
связывающих i-ю и j-ю вершины,
для ор-графа ij равно количеству ребер
выходящих из i-й и входящих в j-ю вершину.
236
237. Матрица смежности
• Матрица смежности н-графа всегдасимметрична.
• Матрица смежности ор-графа в общем
случае не симметрична.
• Она симметрична, если данному орграфу
есть канонически соответствующий н-граф.
237
238. Пример 3:
a ba 1
b
c d
1 2 0
1 0 1 0
c 2
1 0 0
d 0
0 0
Рис. 15. Матрица смежности н-графа
0
238
239. Пример 4:
a b c da
1
1 0 0
b 0 0 1 0
c
2
1 0 0
d 0 0 0 0
Рис. 16. Матрица смежности ор-графа
239
240. Список ребер
• Списком ребер можно задать граф безкратных ребер.
• Ребро представляется парой вершин,
инцидентных ему, например е = (v, w).
• Для н-графа порядок вершин в строке
произволен, для ор-графа первым стоит
номер вершины – начала ребра.
240
241. Рисунок
• Рисунок или геометрическая интерпретацияпоявляется, если сопоставить вершинам
точки плоскости, ребрам – линии на
плоскости, причем, линия соединяет только
те точки, которые соответствуют
вершинам, инцидентным данной линииребру.
241
242. Пример 5:
E = {(a,a), (a,b), (a,c), (b,c)}.Рис. 17. Список ребер н-графа
242
243. Пример 6:
E={(a,a), (a,b), (a,c), (с,a), (b,c)}.Рис. 18. Список ребер ор-графа
243
244. Планарные графы
– это графы, допускающие геометрическуюреализацию на плоскости без пересечения
ребер.
Далеко не все графы являются планарными.
В трехмерном пространстве можно
геометрически реализовать без пересечения
ребер любой граф.
244
245. Планарные графы
• На рисунке приведен пример непланарного графа
Рис. 19. Граф «три дома – три колодца»
245
246. Изоморфные графы
Графы, отличающиеся тольконумерацией вершин, называются
изоморфными.
246
247. Изоморфные графы
Рис.20. Изоморфные графы247
248. Пустой и полный граф
Граф называется пустым, еслимножество ребер пусто: E Ø.
Рис. 21. Пустой граф
248
249. Пустой и полный граф
Н-граф называется полным, еслилюбые две вершины связаны ребром:
E V .
2
Рис. 22. Полный
н-граф
249
250. Пустой и полный граф
Ор-граф называется полным, еслилюбые две вершины связаны парой
симметричных
ребер:
Рис. 23. Полный
ор-граф
250
251. Двудольный граф
Граф называется двудольным еслимножество его ребер разбито на два
подмножества,
V V1 V2 , V1 V2 Ø
и ребрами связаны только вершины из
разных подмножеств.
251
252. Двудольный граф
V1 a, bV2 c, d , g
Рис. 24. Двудольный
граф
252
253. Двудольный граф
Граф называется полным двудольным,если каждая
Вершина V1
cвязана ребром
с каждой
вершиной V2 .
Рис. 25. Полный
двудольный граф
253
254. Двудольный граф
Если V1 n1 , а V2 n2 , тополный двудольный граф обозначается:
K n1 ,n2
254
255. Двудольный граф
Рис. 26. Полныйдвудольный граф K1,2
255
256. Двудольный граф
На рис. 24 приведенпример K2,3.
На рис. 19 приведен
пример K3,3.
Рис. 26. Полный двудольный
граф K2,2
256
257. Лекция 9
Локальные степени вершин258. Локальные степени вершин н-графа
Пусть G = (V, E) – н-граф.Локальной степенью вершины v V
называется число ρ v равное числу
ребер, инцидентных вершине v.
При этом вклад петли в степень
вершины равен 2.
258
259. Локальные степени вершин н-графа
Вектор степеней н-графаG = (V, E) – вектор размерности n,
составленный из степеней вершин графа,
расположенных по убыванию.
259
260. Локальные степени вершин н-графа
ρ(a) = 5ρ(b) = 2
ρ(c) = 3
ρ(d) = 0
Вектор
степеней
ρ = (5, 3, 2, 0)
Рис. 1. Степени вершин н-графа
260
261. Локальные степени вершин н-графа
Замечание 1: векторы степенейизоморфных графов одинаковы:
ρ = (5,3,2,0)
Рис. 2. Граф, изоморфный графу на рис.1
261
262. Локальные степени вершин н-графа
Замечание 2:Сумма всех локальных степеней вершин нграфа равна удвоенному количеству ребер.
n
vi 2 e
i 1
e – число ребер н-графа.
262
263. Локальные степени вершин н-графа
Теорема(о числе вершин нечетной степени)
Число вершин нечетной степени –
четно.
263
264. Локальные степени вершин н-графа
Доказательство:vi 2 e .
Сумма в левой части равенства –
четна.
Если убрать все четные слагаемые,
сумма останется четной.
Сумма нечетных слагаемых четна,
если их четное число.
264
265. Локальные степени вершин н-графа
Однородным степени k называетсян-граф, локальные степени которого
одинаковы и равны k.
Для однородного графа степени k:
vi k v 2 e ,
k
e v , v число вершин.
2
265
266. Локальные степени вершин н-графа
Локально-конечным называетсян-граф, все локальные степени которого
конечны.
Рис. 3.
Локальноконечный,
бесконечный
однородный
граф степени 4
266
267. Локальные степени вершин ор-графа
Пусть G = (V, E) – ор-граф.Локальной степенью исхода вершины
v V
называется число
ρ v ,
равное числу ребер, выходящих из
вершины v.
267
268. Локальные степени вершин ор-графа
Локальной степенью заходавершины v V называется число
ρ v равное числу ребер, входящих
в вершину v.
268
269. Локальные степени вершин ор-графа
Вектор степеней исходаор-графа G = (V, E) – вектор
размерности n, составленный из
степеней исхода вершин графа,
расположенных по убыванию.
269
270. Локальные степени вершин ор-графа
Вектор степеней заходаор-графа – вектор размерности n,
составленный из степеней захода
вершин графа, расположенных по
убыванию.
270
271. Локальные степени вершин ор-графа
ρ a 1; ρ a 3;ρ b 1; ρ b 1;
ρ c 2; ρ c 1;
ρ d 0; ρ d 0.
ρ 2,1,1, 0 ,
ρ 3,1,1, 0 .
271
272. Локальные степени вершин ор-графа
Замечание 3:Векторы степеней исхода и степеней
захода изоморфных графов одинаковы.
272
273.
ρ 2,1,1, 0 ; ρ 3,1,1, 0 .273
274. Локальные степени вершин н-графа
Замечание 4:Сумма всех локальных степеней
исхода вершин и сумма всех
локальных степеней захода ор-графа
равна количеству ребер.
vi vi e .
n
i 1
n
i 1
274
275. Локальные степени вершин ор-графа
Однородным степени kназывается ор-граф, локальные
степени исхода и степени захода
которого одинаковы и равны k.
Для однородного графа степени k:
vi vi k v e ,
e k v .
275
276. Локальные степени вершин ор-графа
Локально-конечным называется орграф, все локальные степени исхода изахода которого конечны.
Рис. 6.
Локальноконечный,
бесконечный
однородный
граф степени 2
276
277. Лекция 10
Части графа.Операции над частями графа
278. Часть графа
Пусть G = (V, E) – н-граф.Частью (подграфом) графа G
называется граф Н = (V', E' ),
где V' V, E' E ,
причем все ребра множества E' входят
в граф Н вместе со своими концами.
278
279. Суграф
Подграф Н = (V', E' ) называетсясуграфом, если V' = V.
Суграф называется покрывающим,
если каждая вершина инцидентна хотя
бы одному ребру графа G.
279
280. Подграф, порожденный множеством вершин
Подграф Н = (A, E' ), называетсяподграфом, порожденным
множеством вершин А ⸦ V,
если множество вершин V' = А,
множество ребер E' состоит из ребер
множества Е, соединяющих вершины
множества А.
280
281. Звездный граф
Подграф Н = (V', E' ), называетсязвездным графом вершины
v V
если V' составляют вершина v и все
смежные ей вершины,
E' состоит из ребер множества Е,
инцидентных вершине v.
281
282. Пример покрывающего суграфа
G(V,E)Н1 = (V', E' )
Рис. 1. Покрывающий суграф
282
283. Пример непокрывающего суграфа
G(V,E)Н2 = (V', E' )
Рис. 2. Непокрывающий суграф
283
284. Пример подграфа, порожденного множеством А
G(V,E)Н3 = (А, E' ), А={3,4,5,6}
Рис. 3. Подграф, порожденный множеством А 284
285. Пример звездного графа
G(V,E)Н4 = (V', E' ) = Z(4)
Рис. 4. Звездный граф
285
286. Операции над частями графа
Суммой подграфовН1 = (V1, E1 ) и Н2 = (V2, E2 ) называется
граф Н = (V, E ),
такой что
V V1 V2 ,
Обозначается:
Е Е1 Е2 .
H H1 H 2 .
286
287. Операции над частями графа
Пересечением подграфовН1 = (V1, E1 ) и Н2 = (V2, E2 )
называется граф D = (V, E ),
такой что
V V1 V2 , Е Е1 Е2 .
Обозначается:
D H1 H 2 .
287
288. Операции над частями графа
Сумма подграфовН1 = (V1, E1 ) и Н2 = (V2, E2 )
называется прямой по ребрам, если у
них нет общих ребер:
E1 E2 Ø.
288
289. Операции над частями графа
Сумма подграфовН1 = (V1, E1 ) и Н2 = (V2, E2 ) называется
прямой по вершинам, если у них нет
общих вершин:
V1 V2 Ø.
289
290. Операции над частями графа
Дополнением подграфаН = (V1, E1 ) до графа G = (V, E )
называется подграф H V2 , E 2 ,
где множество его ребер:
E2 E E1 ,
290
291. Операции над частями графа
а множество вершин V2 состоит из всехвершин множества V, инцидентных
ребрам из Е2 и всех
изолированных вершин, не попавших
в множество V1.
291
292. Пример суммы подграфов
Н1 = (V1, E1 )Н2 = (V2, E2 )
H H1 H 2
Рис. 5. Сумма подграфов
292
293. Пример пересечения подграфов
Н1 = (V1, E1 )Н2 = (V2, E2 )
H H1 H 2
Рис. 6. Пересечение
подграфов
293
294. Пример суммы, прямой по ребрам
Н1 = (V1, E1 )Н2 = (V2, E2 )
H H1 H 2
Рис. 7. Прямая по ребрам
сумма подграфов
294
295. Пример суммы, прямой по вершинам
Н1 = (V1, E1 )Н2 = (V2, E2 )
H H1 H 2
Рис. 8. Прямая сумма
подграфов
295
296. Пример дополнения
Н = (V1, E1 )G(V,E)
H V2 , E 2
Рис. 9. Дополнение
296
297. Замечание:
Подграф и его дополнение являютсяпрямой суммой по ребрам:
Н H G.
297
298. Лекция 11
Маршруты.Расстояние в графе
299. Маршруты
Пусть G = (V, E) – н-граф.Маршрутом в графе G называется
чередующаяся последовательность
вершин и ребер
M v0 , e1 , v1 , e2 , ..., en , vn
где ребро ei инцидентно вершинам
vi -1 , vi .
299
300. Маршруты
Вершина v0 – начальная вершинамаршрута М,
vn – конечная,
vi – внутренняя вершина,
M(v0 , vn ) – маршрут,
соединяющий v0 и vn .
Дина маршрута – число его ребер.
300
301. Маршруты
Маршрут М называетсямаршрутом общего вида, если
вершины и ребра повторяются,
цепью – если его ребра не повторяются,
простой цепью – если его вершины не
повторяются.
301
302. Маршруты
Маршрут М называется циклическим,если начальная и конечная вершина
совпадают.
Замечание: совпадают, не значит
повторяются.
302
303. Маршруты
Циклический маршрут М называетсямаршрутом общего вида, если
вершины и ребра повторяются,
циклом – если его ребра не
повторяются,
простым циклом – если его вершины
не повторяются (кроме начала и конца).
303
304. Пример 1
М1 = (1, 2, 3, 4, 1, 3, 4, 5) – общего вида.М2 = (1, 2, 3, 4, 1, 5) – цепь
М3 = (5, 6, 3, 4, 1) –
простая цепь.
Рис. 1. Маршруты
304
305. Маршруты
М1 =(1, 2, 3, 1, 2, 3, 1) – циклическиймаршрут общего вида.
М1 =(1, 3, 4, 5, 6, 4, 1) – цикл
(не простой)
М1 =(1, 2, 3, 4, 1) –
простой цикл.
Рис. 2. Циклические
маршруты
305
306. Расстояния в графе
Расстоянием между вершинами a иb называется длина минимальной
простой цепи, связывающей их.
Расстояние обозначается d(a, b).
Аксиомы метрики:
1) d(a, b) = d(b, a);
2) d(a, b) ≥ 0, d(a, b) = 0 ↔ a = b;
3) d(a, b) ≤ d(a, c) + d(c, b)
306
307. Расстояния в графе
Пример 21 2 3 4 5
Рис. 3. Расстояния в
графе
1
2
3
4
5
0 1 1 2 1
1 0 2 1 1
1 2 0 1 1
2 1 1 0 1
1 1 1 1 0
307
308. Расстояния в графе
ri – эксцентриситет i-ой вершины– расстояние от этой вершины до
наиболее удаленной от нее вершины.
ri = max d(vi,vj)
по всем j от 1 до n.
308
309. Расстояния в графе
Диаметр графа G – максимальноерасстояние между вершинами графа
d(G)= max d(vi,vj)
по всем i и j от 1 до n, или
d(G)=max ri по всем i от 1 до n.
309
310. Расстояния в графе
Центр графа G – это вершина,расстояние от которой до наиболее
удаленной вершины – минимальное.
Чтобы найти центр, надо сначала
найти радиус графа.
310
311. Расстояния в графе
Радиус графа G – расстояние отцентра графа до наиболее удаленной
вершины.
r (G) = min ri
по всем i от 1 до n.
311
312. Расстояния в графе
Центр графа G – такая вершина vi,для которой
ri = r(G).
Замечание:
Центр в графе может быть не
единственный.
312
313. Расстояния в графе
В нашемпримере
центром
является
вершина 5.
Радиус – 1,
диаметр – 2.
1 2 3 4 5 ri
1 0
2 1
3 1
4 2
5 1
1 1 2 1 2
0 2 1 1 2
2 0 1 1 2
1 1 0 1 2
1 1 1 0 1
313
314. Расстояния в графе
Диаметральные цепи графа G –простые цепи, длина которых равна
d(G), соединяющие наиболее
удаленные вершины графа.
314
315. Расстояния в графе
Радиальные цепи графа G –простые цепи, длина которых равна
r(G), соединяющие центр и наиболее
удаленные от него вершины графа.
315
316. Расстояния в графе
D1=(1,5,4), D2=(1,3,4),D3=(1,2,4), D4=(2,5,3),
D5=(2,1,3), D6=(2,4,3),
R1=(5,1), R2=(5,2),
R3=(5,3), R4=(5,4).
Рис. 4. Диаметральные
и радиальные цепи
316
317. Лекция 12
Связные компоненты графа318. Связность
Пусть G = (V, E) – н-граф.связными называются вершины a и b
если существуют маршрут,
связывающий их.
Н-граф G называется связным, если
все его вершины связны.
318
319. Связность
Утверждение: отношение связностиявляется отношением эквивалентности.
Доказательство:
1. Каждая вершина связана сама с
собой маршрутом нулевой длины,
значит отношение связности
рефлексивно.
319
320. Связность
2. Если вершина a связна с b, то и bсвязна с a. Если a с b связаны
маршрутом М(a,b), то b с a связаны
маршрутом М(b,a), где ребра и
вершины идут в обратном порядке.
Значит отношение связности
симметрично.
320
321. Связность
3. Если вершина a связана маршрутомс b, b связана с с, то и a связана
маршрутом с с.
Это маршрут, начало которого
М(a,b), окончание – M(b,c), вершина b
– общая.
Значит отношение связности
транзитивно.
321
322. Связность
Отношение рефлексивно,симметрично и транзитивно,
значит является отношением
эквивалентности.
Множество вершин V разбивается
отношением связности на классы
эквивалентности – подмножества
связных вершин.
322
323. Связность
Связными компонентами графа Gназываются подграфы, порожденные
классами эквивалентности по
отношению связности.
Замечание: В связном графе одна
связная компонента.
323
324. Связные компоненты
V={a,b,c,d,g},класс V1 = { a,c,d },
класс V2 = {b,g}.
Рис. 1. Связные
компоненты
324
325. Разделяющие множества
Разделяющим множествомн-графа G = (V, E) называется
множество ребер, при удалении
которых число компонент связности
графа увеличивается.
325
326. Разделяющие множества
Разрезом в н-графе G =(V, E)называется разделяющее множество в
котором нет лишних ребер, то есть
минимальное разделяющее
множество.
326
327. Разделяющие множества
Мостом или перешейкомв н-графе G = (V, E) называется
разрез, состоящий из одного ребра.
327
328. Рис.2. Разделяющее множество
Разделяющее множество:{(1,4), (2,3), (7,8)};
разрез:{(1,4), (2,3)}, (7,8) – лишнее;
мост :{(4,5) }.
328
329. Шарнир
Вершина v0 н-графа G = (V, E)называется шарниром, если удаление
этой вершины и всех инцидентных ей
ребер приводит к увеличению числа
компонент связности графа.
329
330. Шарнир
Рис. 3. Шарнир в графеШарниром является вершина 4.
330
331. Лекция 13
Задачи об обходах332. Задача о мостах Кёнигсберга
Рис. 1. Карта мостов Кенигсбергаво времена Эйлера
332
333. Граф – схема мостов
Части города – вершины, мосты – ребра.Из рисунка видно,
что задача,
поставленная
Эйлером,
не выполнима.
Рис. 2. Граф,
соответствующий схеме мостов
333
334. Известные головоломки
Рис. 3. Сабли МагомедаРис. 4. Пентаграмма334
335. Эйлеров граф
Эйлеровым циклом в н-графеназывается цикл, обходящий все ребра
графа (ровно по одному разу).
Эйлеров граф – граф, в котором есть
эйлеров цикл.
335
336. Полуэйлеров граф
Эйлеровой цепью в н-графеназывается цепь, обходящая все ребра
графа (ровно по одному разу).
Полуэйлеров граф – граф, в котором
есть эйлерова цепь.
336
337. Теорема Эйлера (условие эйлеровости графа)
Для того, чтобы произвольныйн-граф был эйлеровым, необходимо и
достаточно, чтобы
1) он был связен;
2) локальные степени всех его вершин
были четными.
337
338. Теорема (условие полуэйлеровости графа)
Для того, чтобы произвольныйн-граф был полуэйлеровым, необходимо и
достаточно, чтобы:
1) он был связен;
2) локальные степени всех его вершин,
кроме двух, были четными.
Вершины с нечетными степенями являются
началом и концом эйлеровой цепи.
338
339. Эйлеров, полуэйлеров, не эйлеров графы
Рис. 6. Полуэйлеров графРис. 5. Эйлеров граф
Рис. 7. Не эйлеров граф
339
340. Алгоритм Флери
При построении эйлерова цикланачинаем с произвольной вершины и
двигаемся в произвольном направлении
выполняя два условия:
1) стираем пройденные ребра и
изолированные вершины, которые при этом
появляются;
2) идем по мосту, только если нет другой
340
возможности.
341. Рис. 8. Пример построения эйлерова цикла
Рис. 8. Пример построения эйлерова цикла341342. Гамильтонов граф
Гамильтоновым циклом в н-графеназывается простой цикл, обходящий
все вершины графа (ровно по одному
разу).
Гамильтонов граф – граф, в котором
есть гамильтонов цикл.
342
343. Полугамильтонов граф
Гамильтоновой цепью в н-графеназывается простая цепь, обходящая
все вершины графа (ровно по одному
разу).
Полугамильтонов граф – граф, в
котором есть гамильтонова цепь.
343
344. Гамильтонов, полугамильтонов графы
Рис. 9. Гамильтонов графРис. 10. Полугамильтонов граф
344
345. Задача о кратчайшем пути
Пусть G = (V, E) – н-граф.Пусть каждому ребру e графа
приписано положительное число –
длина ребра L(e).
Задача заключается в нахождении
маршрута от вершины a к вершине b,
наименьшей длины.
345
346. Алгоритм
Присвоим всем вершинам меткиs(v) = +∞, причем метка s(а) = 0.
Проверим каждое ребро (vi , vj) на
выполнение условия пересчета:
s(vj) - s(vi) > L(vi,vj).
Если это так, пересчитаем метку конца
ребра:
s(vj) = s(vi) + L(vi,vj).
346
347. Алгоритм
Совершаем пересчет меток до техпор, пока не перестанет выполнятся
указанное условие. Метка, которую
получила вершина b является длиной
искомого маршрута.
347
348. Пример 1
Рис. 11. Задача о кратчайшем пути348
349. Задача о кратчайшем пути
1. 2,1 : s 1 s 2 L 2,1s 1 s 2 L 2,1 0 1 1;
1
2
3
4
5
6
7
0
1 0
349
350. Пример 1
Рис. 11. Задача о кратчайшем пути350
351. Задача о кратчайшем пути
1. 2,1 : s 1 s 2 L 2,1s 1 s 2 L 2,1 0 1 1;
2. 2,3 : s 3 s 2 L 2,3
s 3 s 2 L 2,3 0 3 3;
1
2
3
4
5
6
7
0
1 0
1 0 3
351
352. Пример 1
Рис. 11. Задача о кратчайшем пути352
353. Задача о кратчайшем пути
1. 2,1 : s 1 s 2 L 2,1s 1 s 2 L 2,1 0 1 1;
2. 2,3 : s 3 s 2 L 2,3
s 3 s 2 L 2,3 0 3 3;
3. 1,3 : s 3 s 1 2 L 1,3
s 3 3;
1
2
3
4
5
6
7
0
1 0
1 0 3
1 0 3
353
354. Пример 1
Рис. 11. Задача о кратчайшем пути354
355. Задача о кратчайшем пути
1. 2,1 : s 1 s 2 L 2,1s 1 s 2 L 2,1 0 1 1;
2. 2,3 : s 3 s 2 L 2,3
s 3 s 2 L 2,3 0 3 3;
3. 1,3 : s 3 s 1 2 L 1,3
s 3 3;
4. 1,5 : s 5 s 1 L 1,5
1
2
3
4
5
6
7
0
1 0
1 0 3
1 0 3
1 0 3 3
s 5 s 1 L 1,5 1 2 3;
355
356. Пример 1
Рис. 11. Задача о кратчайшем пути356
357. Задача о кратчайшем пути
1. 2,1 : s 1 s 2 L 2,1s 1 s 2 L 2,1 0 1 1;
2. 2,3 : s 3 s 2 L 2,3
s 3 s 2 L 2,3 0 3 3;
3. 1,3 : s 3 s 1 2 L 1,3
s 3 3;
4. 1,5 : s 5 s 1 L 1,5
1
2
3
4
5
6
7
1 0 3 4
3
0
1 0
1 0 3
1 0 3
1 0 3 3
s 5 s 1 L 1,5 1 2 3;
5. 1,4 : s 4 s 1 L 1,4
s 4 s 1 L 1,4 1 3 4;
357
358. Пример 1
Рис. 11. Задача о кратчайшем пути358
359. Задача о кратчайшем пути
1. 2,1 : s 1 s 2 L 2,1s 1 s 2 L 2,1 0 1 1;
2. 2,3 : s 3 s 2 L 2,3
s 3 s 2 L 2,3 0 3 3;
3. 1,3 : s 3 s 1 2 L 1,3
s 3 3;
4. 1,5 : s 5 s 1 L 1,5
s 5 s 1 L 1,5 1 2 3;
1
2
3
4
5
6
7
0
1 0
1 0 3
1 0 3
1 0 3 3
1 0 3 4
1 0 3 4
3
3
5. 1,4 : s 4 s 1 L 1,4
s 4 s 1 L 1,4 1 3 4;
6. 4,5 : s 5 s 4 1 L 4,5
s 5 3;
359
360. Пример 1
Рис. 11. Задача о кратчайшем пути360
361. Задача о кратчайшем пути
7. 3,4 : s 4 s 3 1 L 3,4s 4 4;
1
2
3
4
5
6
7
0
1 0
1 0 3
1 0 3
1 0 3 3
1 0 3 4 3
1 0 3 4 3
362. Пример 1
Рис. 11. Задача о кратчайшем пути362
363. Задача о кратчайшем пути
7. 3,4 : s 4 s 3 1 L 3,4s 4 4;
8. 3,7 : s 7 s 3 L 3,7
s 7 s 3 L 3,7 3 2 5;
1
2
3
4
5
6
7
0
1 0
1 0 3
1 0 3
1 0 3 3
1 0 3 4 3
1 0 3 4 3
1 0 3 4 3 5
364. Пример 1
Рис. 11. Задача о кратчайшем пути364
365. Задача о кратчайшем пути
7. 3,4 : s 4 s 3 1 L 3,4s 4 4;
8. 3,7 : s 7 s 3 L 3,7
s 7 s 3 L 3,7 3 2 5;
9. 4,7 : s 7 s 4 L 4,7
s 7 5;
1
2
3
4
5
6
7
0
1 0
1 0 3
1 0 3
1 0 3 3
1 0 3 4 3
1 0 3 4 3
1 0 3 4 3 5
1 0 3 4 3 5
366. Пример 1
Рис. 11. Задача о кратчайшем пути366
367. Задача о кратчайшем пути
7. 3,4 : s 4 s 3 1 L 3,4s 4 4;
8. 3,7 : s 7 s 3 L 3,7
s 7 s 3 L 3,7 3 2 5;
9. 4,7 : s 7 s 4 L 4,7
s 7 5;
10. 5,7 : s 7 s 5 2 L 5,7
s 7 s 5 L 5,7 3 1 4;
1
2
3
4
5
6
7
0
1 0
1 0 3
1 0 3
1 0 3 3
1 0 3 4 3
1 0 3 4 3
1 0 3 4 3 5
1 0 3 4 3 5
1 0 3 4 3 4
368. Пример 1
Рис. 11. Задача о кратчайшем пути368
369. Задача о кратчайшем пути
7. 3,4 : s 4 s 3 1 L 3,4s 4 4;
8. 3,7 : s 7 s 3 L 3,7
s 7 s 3 L 3,7 3 2 5;
9. 4,7 : s 7 s 4 L 4,7
s 7 5;
10. 5,7 : s 7 s 5 2 L 5,7
s 7 s 5 L 5,7 3 1 4;
11. 5,6 : s 6 s 5 L 5,6
s 6 s 5 L 5,6 3 4 7;
1
2
3
4
5
6
7
0
1 0
1 0 3
1 0 3
1 0 3 3
1 0 3 4 3
1 0 3 4 3
1 0 3 4 3 5
1 0 3 4 3 5
1 0 3 4 3 4
1 0 3 4 3 7 4
370. Пример 1
Рис. 11. Задача о кратчайшем пути370
371. Задача о кратчайшем пути
7. 3,4 : s 4 s 3 1 L 3,4s 4 4;
8. 3,7 : s 7 s 3 L 3,7
s 7 s 3 L 3,7 3 2 5;
9. 4,7 : s 7 s 4 L 4,7
s 7 5;
10. 5,7 : s 7 s 5 2 L 5,7
s 7 s 5 L 5,7 3 1 4;
11. 5,6 : s 6 s 5 L 5,6
s 6 s 5 L 5,6 3 4 7;
12. 7 ,6 : s 6 s 7 3 L 7 ,6
s 6 s 7 L 7,6 4 1 5.
1
2
3
4
5
6
7
0
1 0
1 0 3
1 0 3
1 0 3 3
1 0 3 4 3
1 0 3 4 3
1 0 3 4 3 5
1 0 3 4 3 5
1 0 3 4 3 4
1 0 3 4 3 7 4
1 0 3 4 3 5 4
372. Задача о кратчайшем пути
Таким образом, длина кратчайшегопути равна 5.
Возвращаясь от вершины 6 переходя
к вершинам, инцидентным ребрам,
ведущим в вершину 6, доходим до
вершины 2.
μ = ( 2, 1, 5, 7, 6)
372
373. Лекция 14
Деревья374. Определения дерева
Пусть G =(V, E) – н-граф.Деревом называется связный
ациклический граф [2-5].
Рис. 1. Дерево
374
375. Определение леса
Лесом называется несвязныйациклический граф.
Рис. 2. Лес
375
376. Теорема 1 (о деревьях)
Граф будет дерево тогда и только тогда,когда любые две его вершины связаны
единственной простой цепью.
Связность дает наличие
такой цепи, ацикличность
– ее единственность.
Рис. 3. Теорема 1
376
377. Терема 2 (о деревьях)
Граф с n вершинами будет деревомтогда и только тогда, в нем ровно n-1
ребро.
Если ориентировать
дерево о выбранной
вершины,
то в каждую вершину
будет входить 1 ребро,
а в а0 – 0.
Рис. 4. Теорема 2
377
378. Вершины максимального типа
Дано неориентированное дерево Т.Концевые вершины дерева – вершины,
локальная степень которых равна 1.
Назовем их вершинами первого типа
дерева Т.
Рис. 5. Вершины
1 типа
378
379. Вершины максимального типа
Удалим из дерева Т ребра,инцидентные концевым вершинам –
концевые ребра. Получим дерево Т1.
Концевые вершины
дерева Т1 – Вершины
типа 2.
Рис. 6. Вершины
2 типа
379
380. Вершины максимального типа
Удалим из дерева Т1 концевые ребра.Получим дерево Т2.
Концевые вершины дерева Т2 –
Вершины типа 3.
Рис. 7. Вершины максимального типа
380
381. Вершины максимального типа
Утверждение 1:В конечном дереве есть вершины
только конечного числа типов.
Утверждение 2:
Вершин максимального типа k одна
или две.
381
382. Вершины максимального типа
Утверждение 3:Центрами деревьев являются вершины
максимального типа k и только они. Все
диаметральные цепи проходят через
центры.
Длина диаметральной цепи равна
2k-1, если центра два и 2k-2, если центр
один.
382
383. Вершины максимального типа
k = 3 , центров два, длина диаметральнойцепи 2k-1=5.
Рис. 8. Диаметральная цепь 383
384. Корень дерева
Если дерево не ориентировано,то его можно ориентировать от
корня.
Корень – это один из центров
дерева.
384
385. Корень дерева
У всех вершин дерева локальныестепени захода равны 1, а у корня – 0.
Вершины, степени исхода которых
равны 0 называются листьями.
Высотой дерева называется
наибольшее расстояние от корня до
листа.
385
386. Рис. 9. Листья
386387. Бинарное дерево
Бинарным деревом называетсяориентированное дерево с корнем,
где каждая вершина имеет локальную
степень исхода, равную 2.
387
388. Ветвь дерева
Ветвью вершины а в дереве Т скорнем а0 называется подграф,
порожденный множеством
вершин В(а), состоящим из
вершин, связанных с корнем цепь,
проходящей через а.
388
389. Ветвь
tРис. 10. Ветвь дерева
389
390. Лекция 15
Характеристическиечисла графа
391. Цикломатическое число
Цикломатическим числомграфа G называется число ребер,
которые надо убрать, что бы граф
стал ацикличным.
391
392. Цикломатическое число
1.11.2
Рис. 1. Цикломатическое число
392
393. Цикломатическое число
Цикломатическое число графа Gнаходится по формуле:
γ G e v с
e число ребер,
v число вершин,
с число компонент связности.
393
394. Цикломатическое число
Замечание 1: Цикломатическоечисло дерева равно 0.
Замечание 2: Цикломатическое
число леса равно 0.
Замечание 3: Если цикломатическое
число графа равно 1, то в графе ровно
1 цикл.
394
395. Цикломатическое число
Пример 1:Рис. 3. Нахождение цикломатического числа
γ G e v с
7 5 1 3.
395
396. Цикломатическое число
Пример 2:γ G e v с
10 7 2 5.
Рис. 4. Цикломатическое число несвязного графа
396
397. Число внутренней устойчивости
Внутренне устойчивым множествомграфа G называется множество вершин S,
все вершины которого попарно
несмежны.
Число внутренней устойчивости:
α G max S .
S V
397
398. Число внутренней устойчивости
Пример 3:Рис.5.
Нахождение α(G)
S1 a , S 2 a, c , S3 g , c , S 4 a, d .
G max Si 2.
398
399. Число внешней устойчивости
Внешне устойчивым множествомграфа G называется множество вершин
Q, таких, что из всех вершин
множества Q ведут ребра в вершины
множества Q.
Число внутренней устойчивости:
G min Q .
Q V
399
400. Число внешней устойчивости
Пример 4:Рис.6.
Нахождение β(G)
Q1 a, b, c , Q2 g , d , Q2 b
G min Qi 1.
400
401. Хроматическое число
Граф G называется h- хроматическим,если его вершины можно раскрасить h
различными красками так, чтобы
никакие две смежные (различные)
вершины не были окрашены в один цвет.
Хроматическое число графа – это
наименьшее число красок.
G min h.
401
402. Хроматическое число
Пример 5:Рис.7.
Нахождение χ(G)
H1 a, d , H 2 g , c , H 3 b .
G min h 3.
402
403. Хроматическое индекс
Граф G называется kраскрашиваемым, если его ребраможно раскрасить k различными
красками так, чтобы никакие два
смежные ребра не были окрашены в
один цвет. Хроматический индекс
графа – это наименьшее число красок.
G min k .
403
404. Хроматическое индекс
Согласно теореме Визинга, еслимаксимальная локальная степень
вершины графа равна k, то
хроматический индекс подчиняется
условию:
k G k 1.
404
405. Хроматическое индекс
Пример 6:Рис.8.
Нахождение χ'(G)
k max v b 4;
4 G 5;
G 4.
405
406. Пример 7:
В пунктах Х1, Х2, Х3, Х4, Х5, Х6 могутбыть источники излучения. Если
источники расположены в пунктах Xi и
Xj влияют друг на друга (поражают друг
друга), то на графе они соединены
ребром (Xi, Xj).
Можно ли расположить в каких-либо
из данных пунктов 4 или 3 источника, не
поражающих друг друга?
406
407.
S1={X2, X5},S2={X1, X4},
S3={X3, X6},
S4={X2, X4, X6}.
Рис. 9. Нахождение максимального внутренне
устойчивого множества
407
408. Пример 8:
Объекты Х1, Х2, … , Х9 расположенытак, как показано на графе. Объекты,
которые просматриваются друг из
друга соединены ребрами. Определить
в каких объектах достаточно
поставить камеры наблюдения, чтобы
они в совокупности просматривали
все объекты.
408
409.
Рис. 10. Нахождениеминимального
внешне устойчивого множества
409
410.
Пример 9: Дана политическая картаконтинента. Найти минимальное число
цветов, чтобы раскрасить карту.
Рис. 11. Раскраска
географической карты
410
411.
Найдемхроматическое
число графа.
χ(G) = 3.
Рис. 12. Замена стран
на вершины,
границ между ними
на ребра
411
412.
Рис. 13. Раскраска карты в три цвета412
413. Лекция 16
Сети,потоки в сетях
414. Введение
Сети – это графы, которыемоделируют реальные
транспортные и
коммуникационные сети.
414
415. Введение
Задача о максимальном потоке в сетизаключается в том, чтобы подсчитать
максимальное количество некоторых
объектов, которые могут двигаться от
одного конца сети к другому. При этом
пропускная способность узлов сети
ограничена.
415
416. Введение
Под объектами могут пониматься –пакеты данных, путешествующих по
Интернету;
– коробки с товарами, которые везут
по автомагистрали; и так далее.
416
417. Введение
Эта задача может использоваться присоставлении расписания авиарейсов,
распределения задач в суперкомпьютерах,
обработке цифровых изображений и
расположении последовательности ДНК.
417
418. Введение
Перемещение объектов могутограничено пропускной способностью
соединений сети или скоростью
транспорта на загруженных дорогах.
418
419. Введение
В задаче о максимальном потоке одна ихвершин графа назначается истоком –
точкой, в которой все объекты начинают
свой путь, а другая – стоком, точкой, в
которую они все направляются. Пропускная
способность каждого ребра ограничена.
В вершинах вещество не накапливается –
сколько пришло, столько и ушло.
419
420. Сети
Сетью называется частичноориентированный граф G(V, E).
Истоком и стоком (входным и
выходным полюсом) называются
некоторые отмеченные вершины.
420
421. Сети
Исток – вершина, локальная степеньзахода которой равна 0.
Сток – вершина, локальная степень
исхода которой равна 0.
421
422. Сети
Если в сети k истоков иm стоков – сеть называется
(k,m)-полюсником.
Если в сети 1 исток и 1 сток, сеть
называется двухполюсной.
Далее будем рассматривать только
двухполюсные сети.
422
423. Сети
Пусть s – исток, t – сток, так чтолюбая другая вершина лежит на пути
из вершины s в t. Вершины, не
являющиеся истоком и стоком
называются внутренними вершинами
сети.
423
424. Сети
Разобьем множество вершин V надва подмножества Х и Х таких, что
s Х , а t Х.
Множество ребер, реализующих это
разбиение назовем разрезом в сети
R X, Х .
424
425. Сети
Ориентированные ребра с началомв Х и концом в Х называются
прямыми.
Множество прямых ребер
обозначим
E R .
-
425
426. Сети
Ориентированные ребра сначалом в Х и концом в Х
называются обратными.
Множество обратных ребер
обозначим
E R .
426
427. Сети
Все неориентированные ребраявляются прямыми.
Их ориентация произвольна,
и определяется при задании
потока в сети.
427
428. Сети
Замечание 1:Прямым или обратным ребро
будет в зависимости от вида
разреза в сети.
428
429. Пример 1
Дана частично ориентированнаядвухполюсная сеть.
429
430.
X s,1, 3 ; X t , 2, 4 .R X , X 1,2 , 3,4 , 4,1 .
E R 1,2 , 3,4 ; E R 4,1 .
430
431.
X s, 3, 4 ; X t ,1, 2 .R X , X s,1 , 1,3 , 4,1 , 2,4 , 4, t .
E R s,1 , 1,3 , 4,1 , 2,4 , 4, t ;
E R пусто .
431
432.
X s,1, 2 ; X t, 3, 4 .R X, X s,3 , 1,3 , 4,1 , 2,4 , 2, t .
E R s,3 , 1,3 , 2,4 , 2, t ;
E R 4,1 .
432
433.
X s,1, 3, 4 ; X t, 2 .R X, X 1,2 , 2,4 , 4, t .
E R 1,2 , 2,4 , 4, t ;
E R пусто
433
434. Поток в сети
Пусть S произвольная частичноориентированная сеть.
Пусть каждому ребру сети e E
приписано число
с(e) 0,
– пропускная способность ребра е.
434
435. Поток в сети
Потоком в сети S называется пара,составленная из числовой и
нечисловой функций ( f ,w):
w – ориентация всех
неориентированных ребер сети,
f = f(e) – функция значений потока
на ребрах.
435
436. Поток в сети
Функция f удовлетворяетусловиям:
1) 0 f (e) c(e), e E;
2) выполняется закон Киргоффа:
дивергенция любой внутренней
вершины сети равна 0.
436
437. Поток в сети
Дивергенция вершины сети – числонаходимое по формуле:
R(a) f e f e .
e a
e a
a ребра, выходящие из а;
a ребра, входящие в а.
437
438. Поток в сети
Величина потока в сети S –равна дивергенции потока в вершине
s (дивергенция истока).
R R(s).
438
439. Поток в сети
Замечание 2:R s R t .
439
440. Поток в сети
Замечание 3:Величина потока в сети есть
величина переменная, зависящая
от значений функции f(e).
440
441. Пример 2
Дана частично ориентированнаядвухполюсная сеть. Найти величину
потока в сети.
441
442.
с(a)=2; c(b)=3; c(h)=1; c(d)=2; c(q)=1;c(w)=1; c(x)=3; c(y)=2; c(z)=2.
442
443.
443444.
444445. Поток в сети
Каждому разрезу R ставится всоответствие пропускная
способность разреза с(R), равная
сумме пропускных способностей
всех прямых ребер разреза.
445
446.
с(a) = 2; c(b) = 3; c(h) = 1; c(d) = 2;c(q) = 1; c(w) = 1; c(x) = 3; c(y) = 2;
c(z) = 2. C = c(w) + c(d) = 3 + 1 = 4.
446
447.
C = c(b) + c(h) + c(x) + c(y) == 3 + 1 + 3 + 2 = 9.
447
448. Поток в сети
Теорема Форда-ФалкерсонаМаксимальная величина потока в
сети S равна минимальной
пропускной способности среди
всех ее разрезов.
448
449. Лекция 17
Основытеории кодирования
450. Основы теории кодирования
Кодом называется система условных знаков (символов),для передачи, обработки и хранения информации.
Пусть А – произвольный алфавит. Элементы алфавита А
называются буквами, а конечные вектора, составленные из
букв – словами.
Длина слова – число букв в слове , обозначается .
Соединение слов 1 и 2 обозначим через 1 2 , а
соединение n одинаковых слов α – через n . Слово 1
называется началом слова α, если существует слово 2 ,
такое что 1 2 .
450
451. Основы теории кодирования
Пример 1:Алфавит А={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Слова: натуральные числа, составленные их
цифр.
n1=23421, n2= 5600976, и так далее.
Двоичный код натуральных: разложение по
неотрицательным степеням 2.
код числа m1 = 3 – v1 =11;
код числа m2 = 4 – v2 =100;
код числа m3 = 6 – v3 =110;
код числа m4 = 12 – v4 =1100; и так далее.
451
452.
Рассмотрим алфавит Bk 0 , 1, 2 , ... , k 1 .Произвольное
отображение
произвольного
множества М в множество слов в алфавите Bk
называется k-ичным кодированием множества М.
При k = 2, B2 B 0,1 – двоичное множество.
452
453.
Кодирование (отображение) Е – двоичная записьнатуральных чисел с помощью минимального количества
букв.
Числу n N 0 ставится в соответствие слово
b( n ) b1b2 ...bl( n ) ,
наименьшей длины, удовлетворяющее условию:
l( n )
n bi 2l( n ) i .
i 1
При этом b1 1, а длина слова l( n ) log2 n . Последнее
условие означает, что n удовлетворяет неравенству
2l( n ) 1 n 2l( n ) .
453
454.
Пример 2:Пусть n = 12.
log2 12 3,59 , т. е. это дробное число между 3 и 4.
Инкремент этого логарифма равен l( 12 ) log2 12 4 , так
как это следующее целое, идущее за ним.
4
4 i
12
b
2
i
Аналогично 2 12 2 . Значит,
.
3
4
i 1
12 b1 2 b2 2 b3 2 b4 2
3
2
1
0
1 8 b2 4 b3 2 b4 1
1 8 1 4 0 2 0 1.
Таким образом, двоичный код числа 12 имеет вид:
b(12) = 1100 .
454
455.
Кодирование E m – двоичная запись натуральных чиселс помощью m букв.
Числу n N 0 , удовлетворяющему условию
0 n 2m
ставится в соответствие слово
bm ( n ) 0m l( n ) b( n ) .
Пусть n = 12, m = 3.
Так как неверно то, что 0 12 2 , то это означает, что
3
код b3 ( 12 ) построить невозможно.
455
456.
Пример 3:Пусть n = 12, m = 6.
6
0
12
2
Так как верно то, что
, то это означает,
что код b3 ( 12 ) построить можно, его вид:
b6 ( 12 ) 0
6 4
b( 12 ) 001100.
456
457. Побуквенное кодирование
Кодирование является побуквенным,если каждой букве алфавита ставиться
в соответствие двоичный код.
Код слова получается из
последовательной записи кодов букв.
457
458. Побуквенное кодирование
Пример 4: Алфавит А={a, b, c, d}Двоичный код букв:
код буквы a – v1 =0;
код буквы b – v2 =11;
код буквы c – v3 =01;
код буквы d – v4 =011.
Тогда слово bc имеет код 1101. Его можно
однозначно разделит на коды букв.
Тогда слово ab имеет код 011. Его можно
декодировать как ab или как d.
458
459. Побуквенное кодирование
Побуквенный код называетсяравномерным, если коды букв имеют
одинаковую длину [2].
Пример 5: Алфавит А={a, b, c, d}
Двоичный код букв:
код буквы a – v1 =000;
код буквы b – v2 =110;
код буквы c – v3 =010;
код буквы d – v4 =011.
459
460. Побуквенное кодирование
Побуквенный код называетсяпрефиксным, если ни одно кодовое слово не
является началом другого кодового слова.
Пример 6: Алфавит А={a, b, c, d}
Двоичный код букв:
код буквы a – v1 =00;
код буквы b – v2 =10;
код буквы c – v3 =010;
код буквы d – v4 =011.
460
461. Побуквенное кодирование
Побуквенный код называетсяразделимым,
если код слова можно однозначно
разделить на коды букв.
461
462. Побуквенное кодирование
Утверждение 1:Равномерный код всегда разделим.
Утверждение 2:
Префиксный код всегда разделим.
Утверждение 3:
Префиксный код всегда является разделимым,
но разделимый код не обязательно является
префиксным, то есть префиксность является
достаточным условием разделимости, но не
является необходимым условием.
462
463.
Оптимальное кодированиеПусть источник случайным образом генерирует
буквы алфавита А а1 , а2 , ... , аm , причем вероятность
появления каждой буквы известна. Таким образом
задано распределение вероятностей Р вида:
… a
a
a
a
i
1
2
pi
p1
p2
m
…
pm
Так как алфавит фиксирован, то это распределение
можно записать в виде:
m
P p1 , p2 , ... , pm , p i 0, pi 1 463
.
i 1
464.
Оптимальное кодированиеСтоимостью
кода
распределении P назовем число
V
при
m
LV P vi pi .
i 1
Оно характеризует среднее количество
букв кодирующих слов, приходящихся на
одну букву алфавита А при кодировании V.
Очевидно, что при различных кодированиях
одного и того же алфавита, стоимость кодов
464
будет различной.
465.
Префиксный код V v1 , v2 , ..., vmназывается оптимальным при распределении
Р р1 , р2 , ..., рm , если его стоимость
минимальна по сравнению с другими кодами
алфавита А при распределении Р.
465
466.
Код ФаноКод Р. Фано, близкий к оптимальному,
заключается в следующем. Упорядоченный (в
порядке не возрастания вероятностей) список букв
алфавита делится на две последовательные части
так, чтобы суммы вероятностей входящих в них
букв отличались как можно меньше. Буквам из 1-й
части присваивается символ 0, из 2-й – 1. С каждой
частью поступают аналогично. Так делается пока, в
каждой из частей не окажется по одной букве.
Полученные последовательности нулей и единиц
является кодом Фано данного алфавита [2].
466
467. Пример 6:
Дано распределение частот для буквалфавита. Построить код Фано. Найти
стоимость кода.
A
B
C
D
E
F
G
H
0,17 0,13 0,04 0,29 0,15 0,07
0,1
0,05
467
468. Код Фано
1. Упорядочить буквы по невозрастанию частот.
A
B
C
D
E
F
G
H
0,17 0,13 0,04 0,29 0,15 0,07
0,1
0,05
468
469.
АB
C
D
E
F
G H
0,17 0,13 0, 04 0, 29 0,15 0, 07 0,1 0, 05
469
470. Код Фано
1. Упорядочить буквы по невозрастанию частот.
2. Разделить список на две
последовательные части так, чтобы
разница между суммами частот этих
частей была минимальна.
470
471.
DА
E
B
G
F
H
C
0, 29
0,17
0,15
0,13
0,1
0, 07
0, 05
0, 04
0, 29 0,71 0, 42;
0, 46 0,54 0,08;
0, 46
0,54
0,61 0,39 0, 22.
471
472. Код Фано
1. Упорядочить буквы по не возрастаниючастот.
2. Разделить список на две
последовательные части так, чтобы разница
между суммами частот этих частей была
минимальна.
3. Сопоставить частотам первой части
символ 0, второй части сопоставить 1.
472
473.
D0,29
A
0,17
E
0,15
B
0,13
G
0,1
F
0,07
H
0,05
C
0,04
0,46
0,54
473
474. Код Фано
1. Упорядочить буквы по не возрастаниючастот.
2. Разделить список на две последовательные
части так, чтобы разница между суммами
частот этих частей была минимальна.
3. Сопоставить частотам первой части символ
0, второй части сопоставить 1.
4. С каждой из полученных частей произвести
аналогичное деление.
474
475.
D0,29
A
0,17
E
0,15
B
0,13
G
0,1
F
0,07
H
0,05
C
0,04
0,46
0,28
0,54
0,26
475
476.
D0,29
A
0,17
E
0,15
B
0,13
G
0,1
F
0,07
H
0,05
C
0,04
0,46
0,28
0,54
0,26
476
477.
D0,29
A
0,17
E
0,15
B
0,13
G
0,1
F
0,07
H
0,05
C
0,04
0,46
0,28
0,54
0,26
477
478.
D0,29
A
0,17
E
0,15
B
0,13
G
0,1
F
0,07
H
0,05
C
0,04
0,46
0,28
0,54
0,26
478
479.
D0,29
A
0,17
E
0,15
B
0,13
G
0,1
F
0,07
H
0,05
00
01
100
101
110
1110
11110
C
0,04
11111
479
480. Стоимость кода
Стоимость кода V при распределении Рнаходится по формуле:
Здесь λ(vi) – длина кодирующего слова vi ;
pi – частота появления слова vi .
480
481.
DA
E
B
G
F
H
C
0, 29
0,17
0,15
0,13
0,1
0, 07
0, 05
0, 04
L
2
2
3
3
3
4
5
00
01
100
101
110
1110
11110
11111
5
2, 79
481
482.
Код ХаффменаТеорема Хаффмена
Если V v1 , v2 , ..., vm – оптимальный двоичный код
при распределении P p1 , p2 , ... , pm ,
и некоторая вероятность p j = q1 + q2 , причем
р1 р2 ... p j 1 p j p j 1 рm q1 q2 ,
то код V v1, v2 , ..., v j 1, v j 1, ..., vm , v j 0, v j1
так же является оптимальным при распределении
P p1 , p2 , ... , p j 1 , p j 1 , ... , pm , q1 , q2 .
Код V является расширением кода V .
482
483.
Код ХаффменаПостроение оптимального кода Хаффмена
заключаются в следующем. Пусть в упорядоченном по
невозрастанию вероятностей списке две последние
вероятности pm-1 и pm .
Эти вероятности из списка исключаются, а их сумма
вставляется в список таким образом, чтобы
вероятности по-прежнему не убывали. Делаем так,
пока в списке не останется две вероятности. Первой из
них присваивается символ 0, второй – символ 1.
Получаем оптимальный код, состоящий из 2 кодовых
слов. Далее, используя теорему расширяем его до кода
из 3 слов, и т. д., пока не получим список исходных
вероятностей [2].
483
484.
aipi
xi
,5 0,5 0,5 0
a 00,5
,2 0,3
b 00,2
1
c 0,2
d 0,1
1
1
00
0
01
01
0 000
1 001
484
485. Стоимость кода
Найдем стоимость полученного кода.4
LV P vi pi
i 1
0,5 2 0,2 3 0,2 0,1 1,8.
.
485
486.
Рассмотрим равномерный код собнаружением и исправлением ошибок [4].
Однозначной ошибкой типа замещения
называют результат замены одного из
символов 0 на 1 или 1 на 0.
Кратностью ошибки s называется число
ошибок одного типа. Например, если
передаваемое слово x = 1011, а на приемной
станции получено y = 0011, то в слове
произошла ошибка типа замещения.
486
487.
Функция Хемминга H(x), задается на двоичныхn
B
∈
x
. Это вектор минимальной длины l,
векторах
полученный в результате покоординатного сложения по
модулю 2 двоичных кодов номеров тех координат
вектора х, которые равны 1.
Здесь l – та длина двоичного кода, которой
достаточно, чтобы закодировать номера всех координат
слова х.
l log 2 n 1 .
Таким образом,
H x x1 bl 1 x 2 bl 2 ... x n bl n .
487
488.
Пример 8:Найти функцию Хемминга для двоичного слова
x = 1011. Так как n = 4 , то
l log 2 4 1 log 2 5 3 . Найдем двоичные
коды длины 3 для всех номеров координат слова х .
1
2
3
4
n
b3 (n)
001
010
011
100
Тогда
H x 1 001 ⊕0 010 ⊕1 011 ⊕1 100 =
= (001) ⊕(011) ⊕(100) =
= (0 ⊕0 ⊕1, 0 ⊕1⊕0, 1⊕1⊕0)= (110) .
488
489.
489490.
Пример 9:Пусть при передаче по каналу связи в двоичном
слове x = 010101∈ H 6 произошло замещение 5-го
символа, в результате чего получилось слово
y = 010111. Найдем функцию Хемминга H ( y) .
l log 2 6 1 log 2 7 3 .
Сложим по модулю 2 двоичные коды номеров
только тех координат вектора у, которые равны 1.
H у 010 ⊕ 100 ⊕ 101 ⊕ 110 101 b3 5 .
Полученный результат является двоичным кодом
номера того места, на котором произошло
замещение.
490
491.
Литература1.
1. Теория
вероятностей и математическая статистика
[Текст]: практикум / Кемеровский гос. ун-т; [сост. С. Г. Гутова].
– Кемерово: КемГУ, 2017. - 185 с.: рис., табл.
2. Дискретная математика: учеб.-метод. пособие [Текст] /
сост. С. Г. Гутова, Т. А. Невзорова. – Кемерово, 2011. – 128 с.
3. Кузнецов, О. П. Дискретная математика для инженера
[Текст] / О. П. Кузнецов, Г. М. Адельсон-Вельский. – М.:
Энергоатомиздат, 1986. – 480 с.
4. Чуешева, О. А. Математическая логика: учеб.-метод.
пособие [Текст] / сост. О. А. Чуешева. – Кемерово, 2006. – 48 с.
5. Щекочихина, С. Г. Дискретная математика: вопросы для
самостоятельного изучения для студентов 1 курса МФ спец.
01.02
[Текст] / С. Г. Щекочихина. – Кемерово:
Кузбассвузиздат, 2003. – 64 с.
491
492.
Учебное изданиеГУТОВА
Светлана Геннадьевна
ДИСКРЕТНАЯ МАТЕМАТИКА
Часть 1
конспект лекций
492




















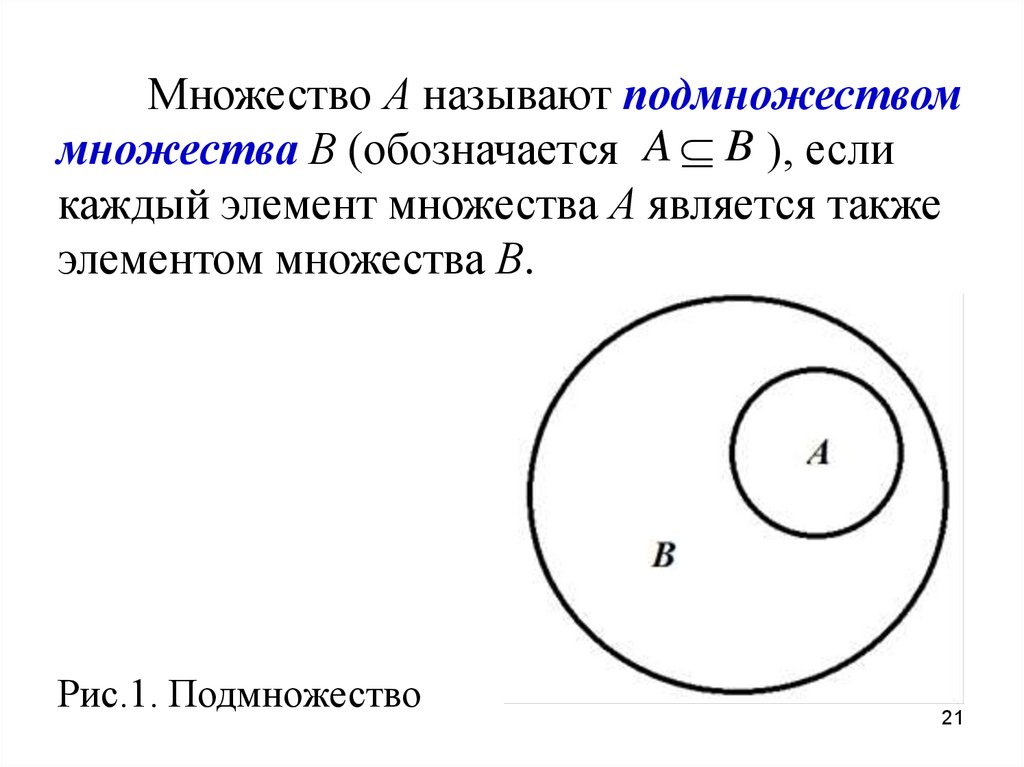



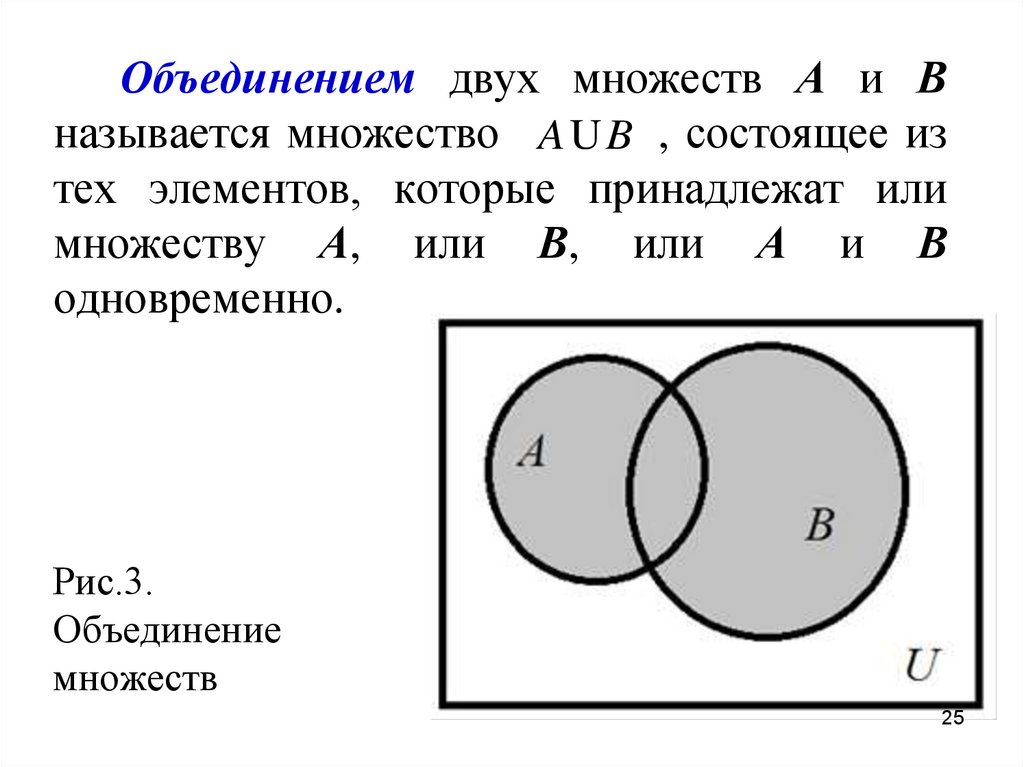
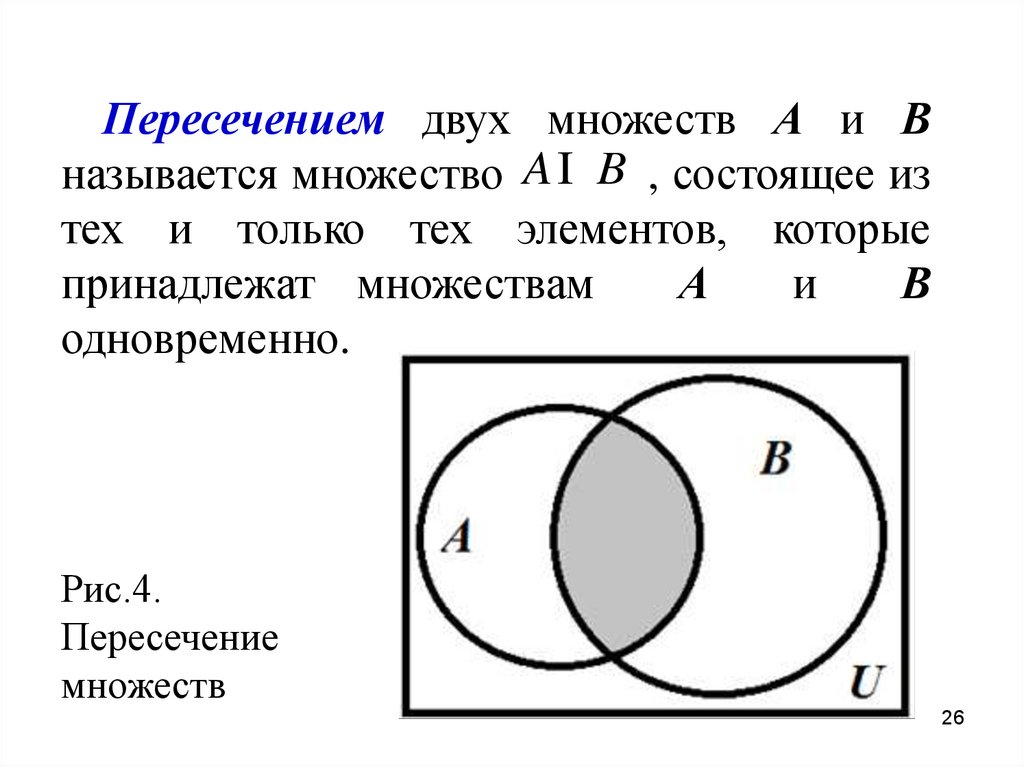
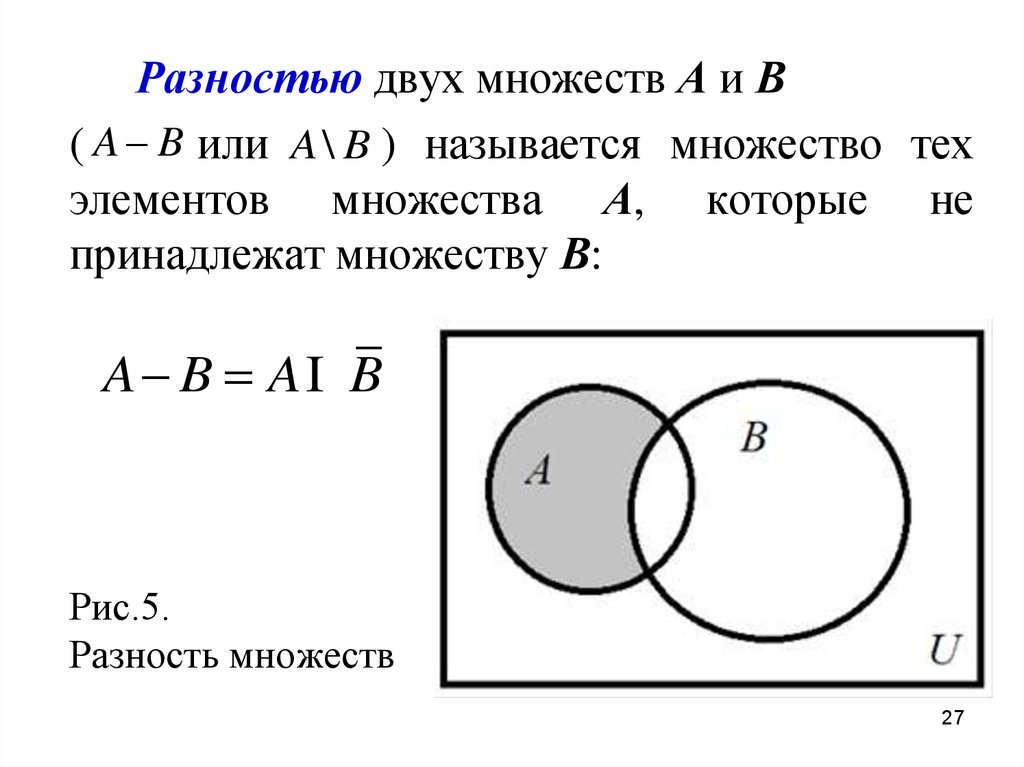











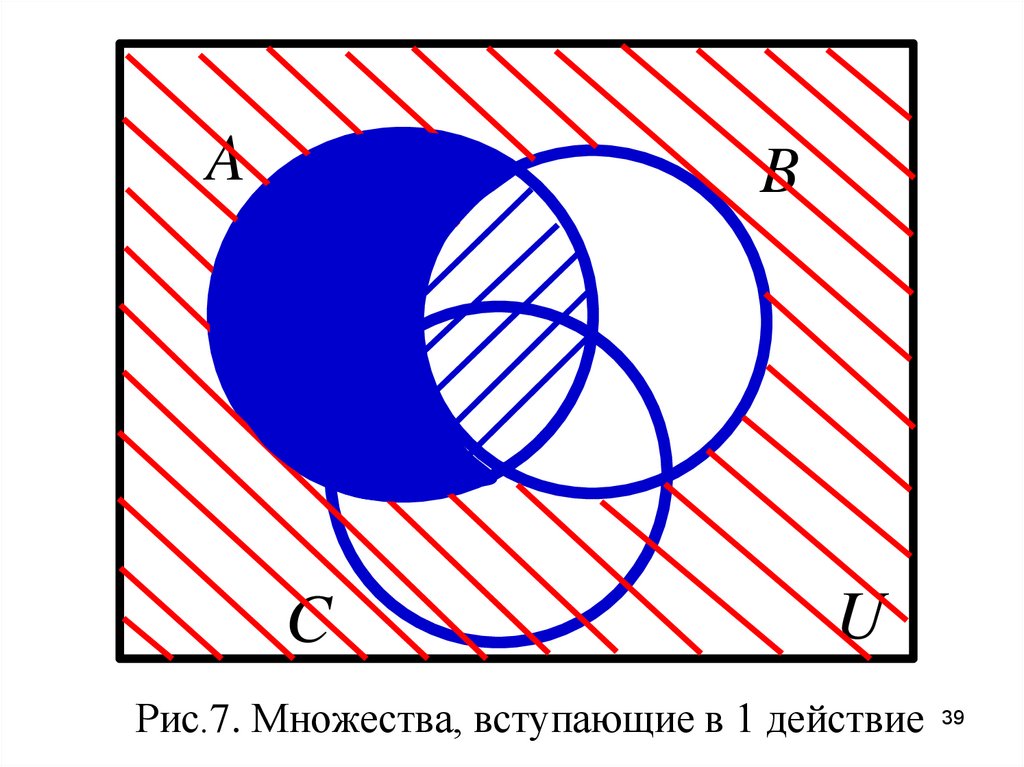

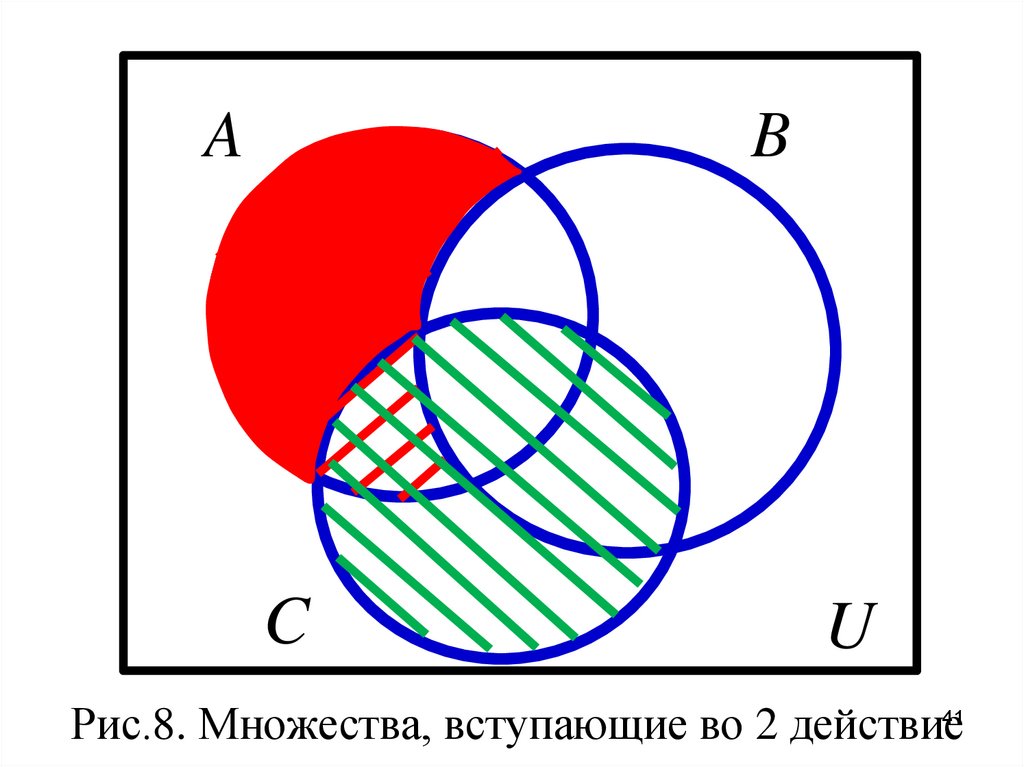




























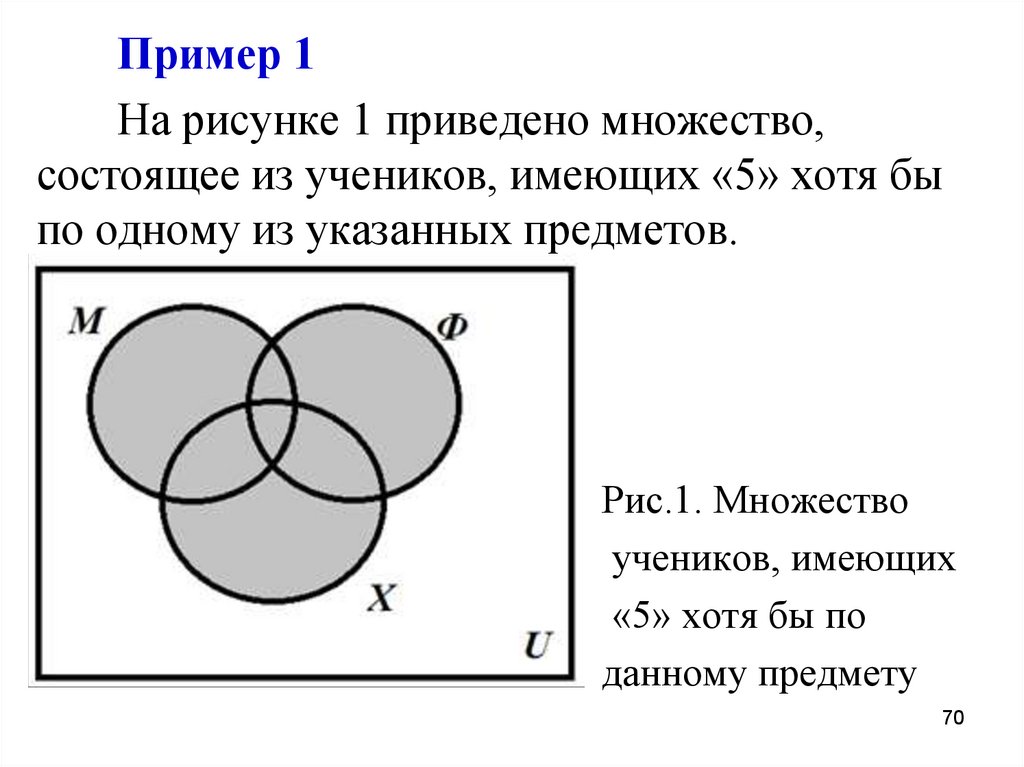

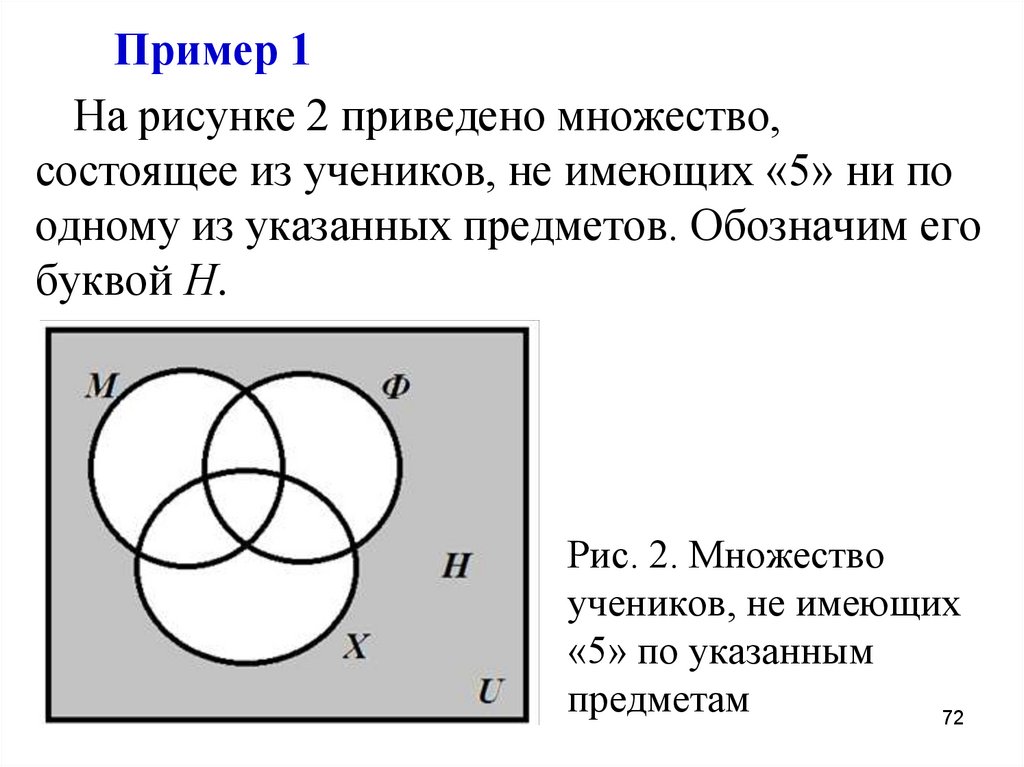

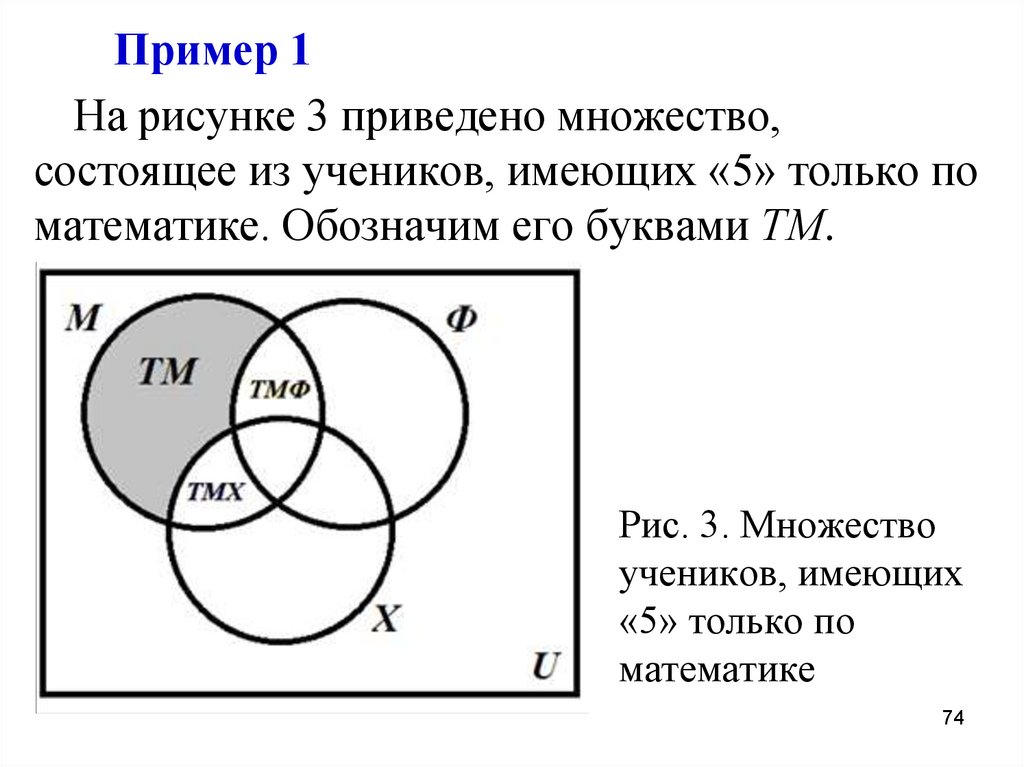



















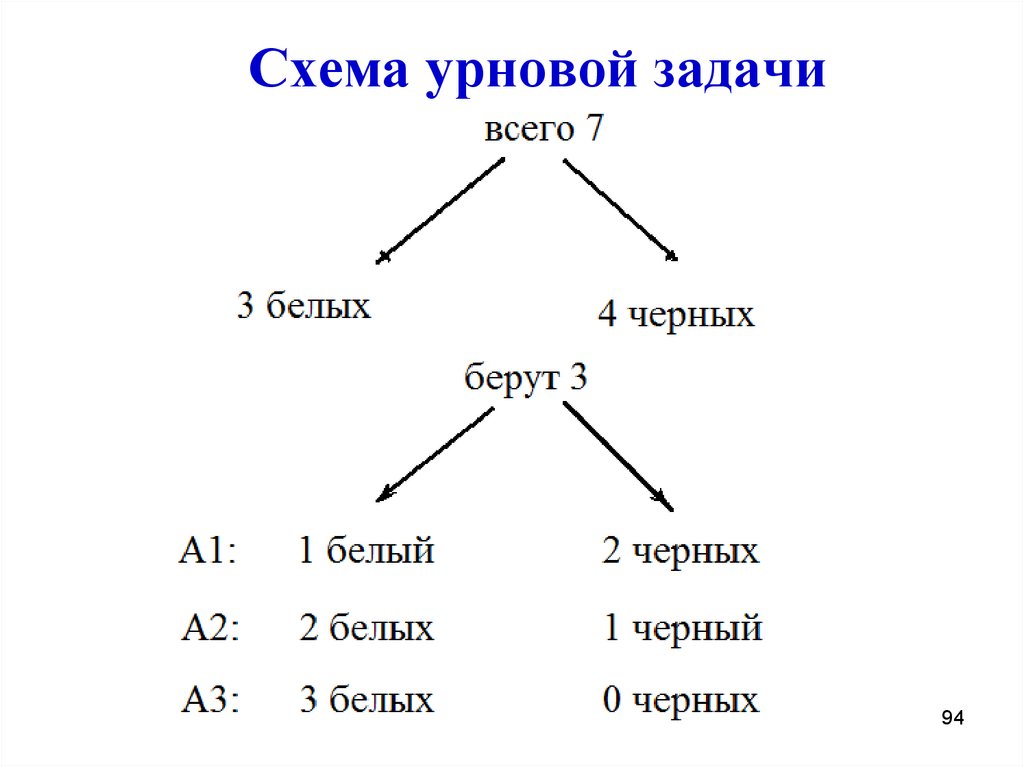
















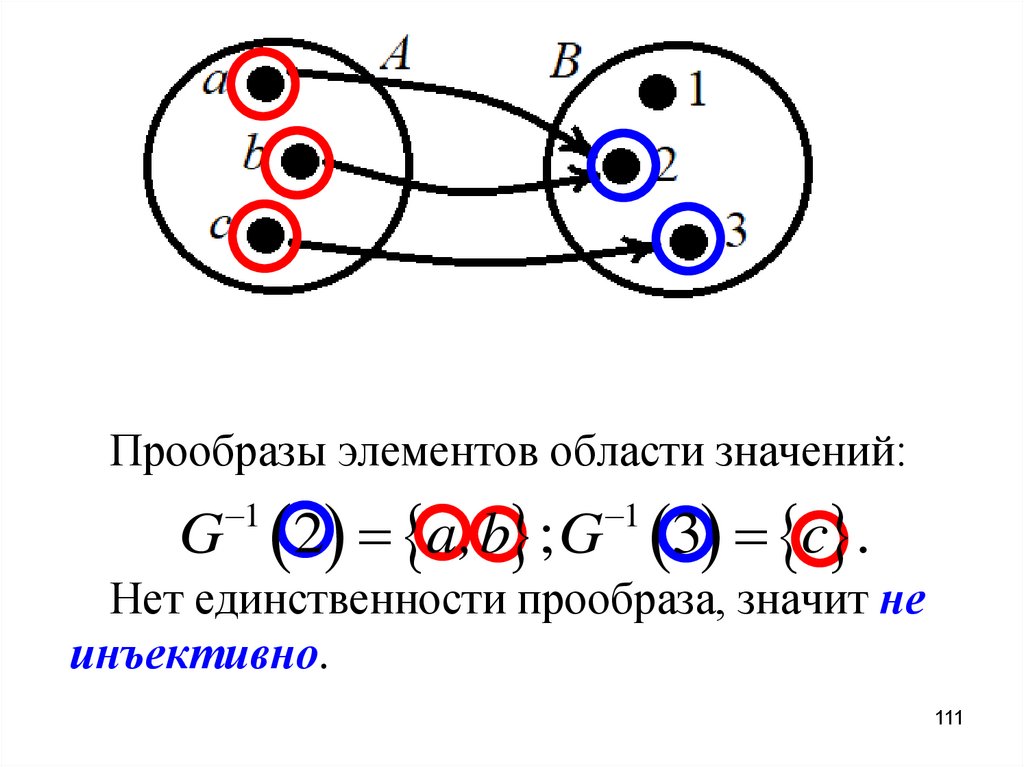


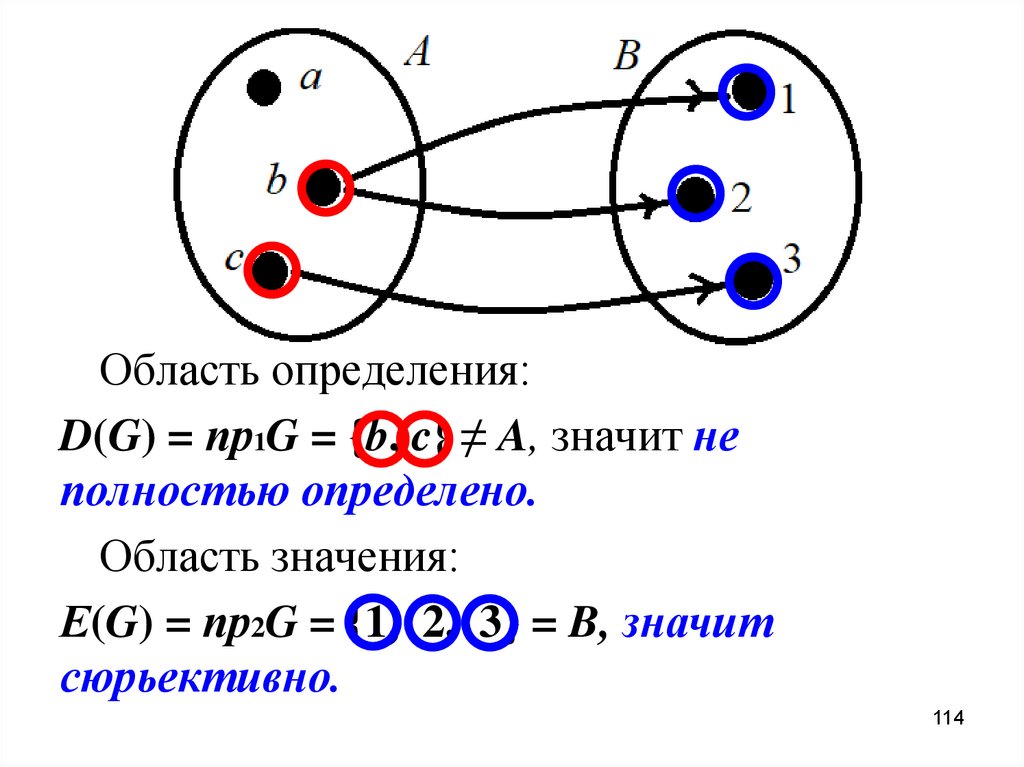
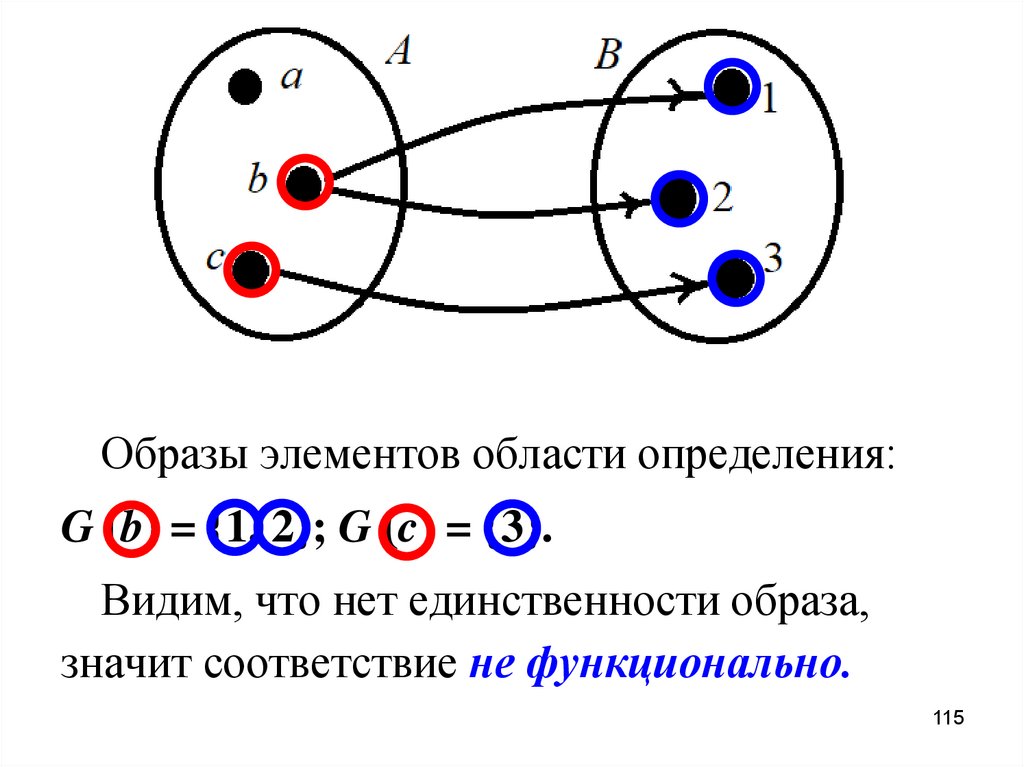
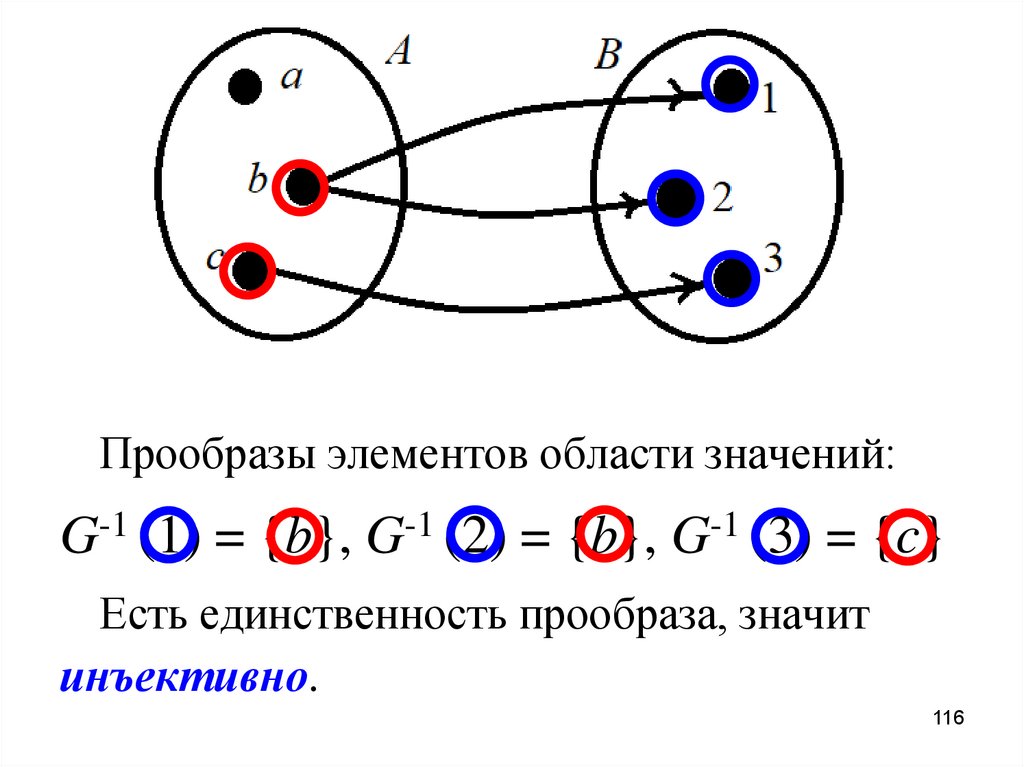











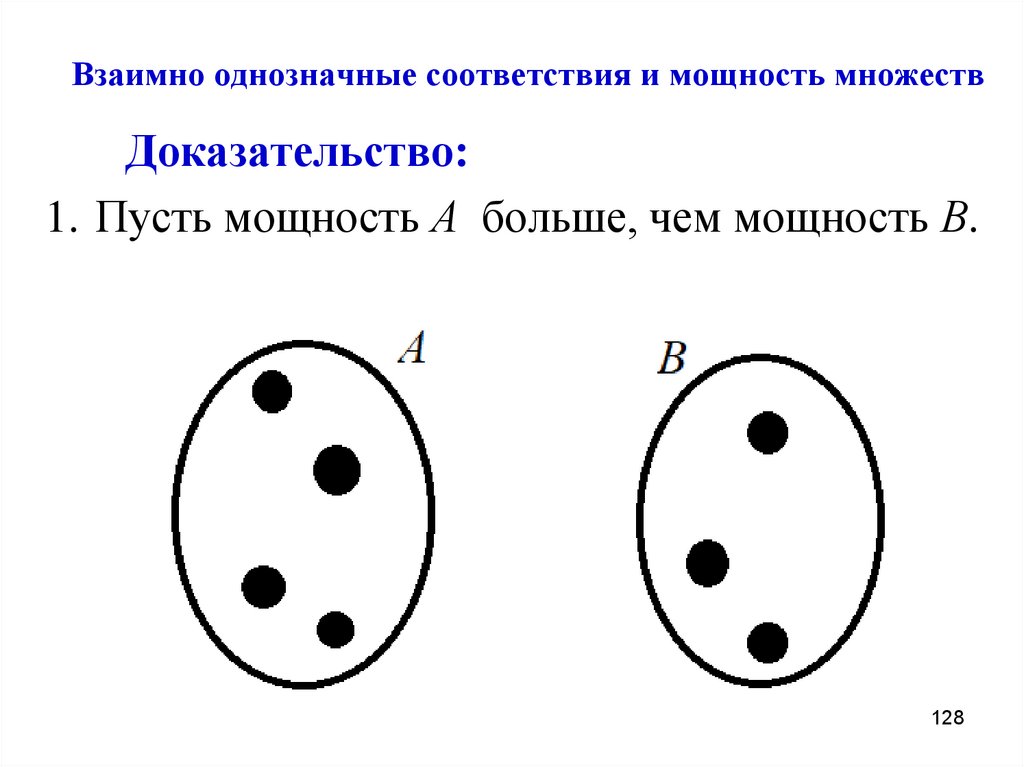
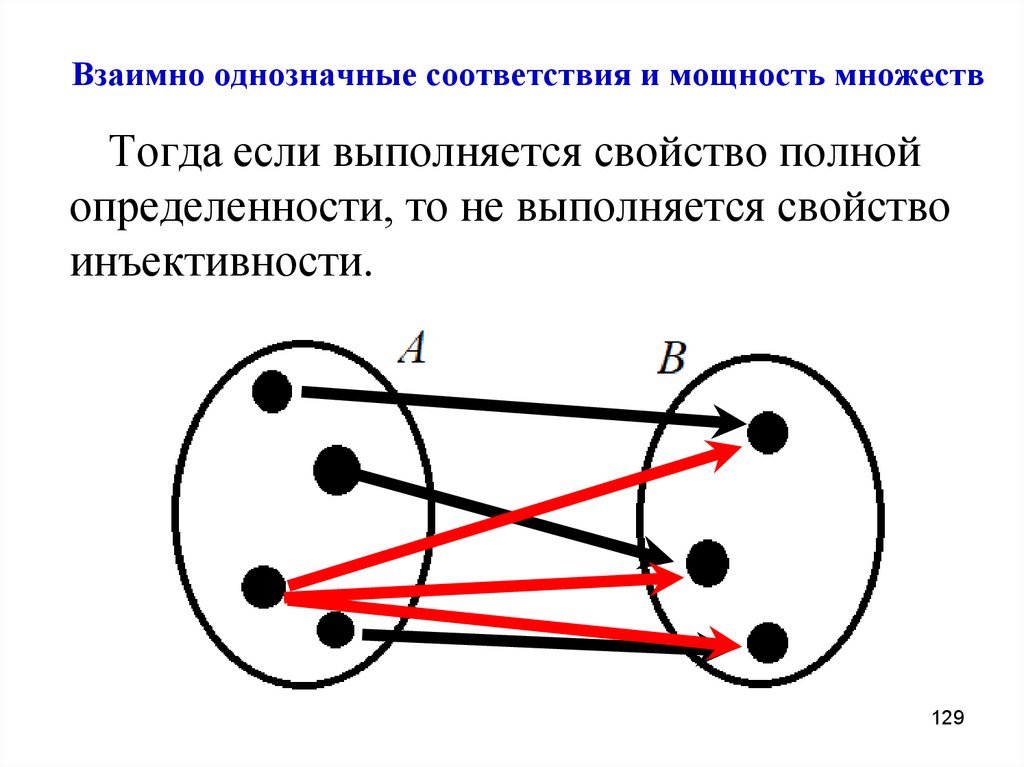


















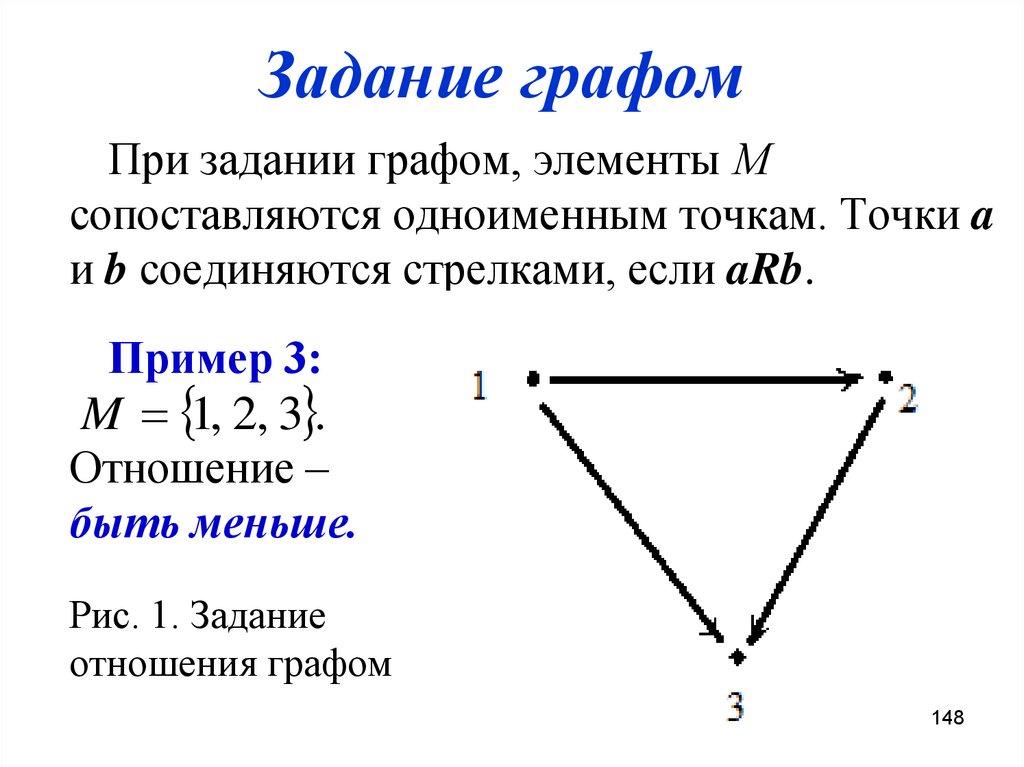





















































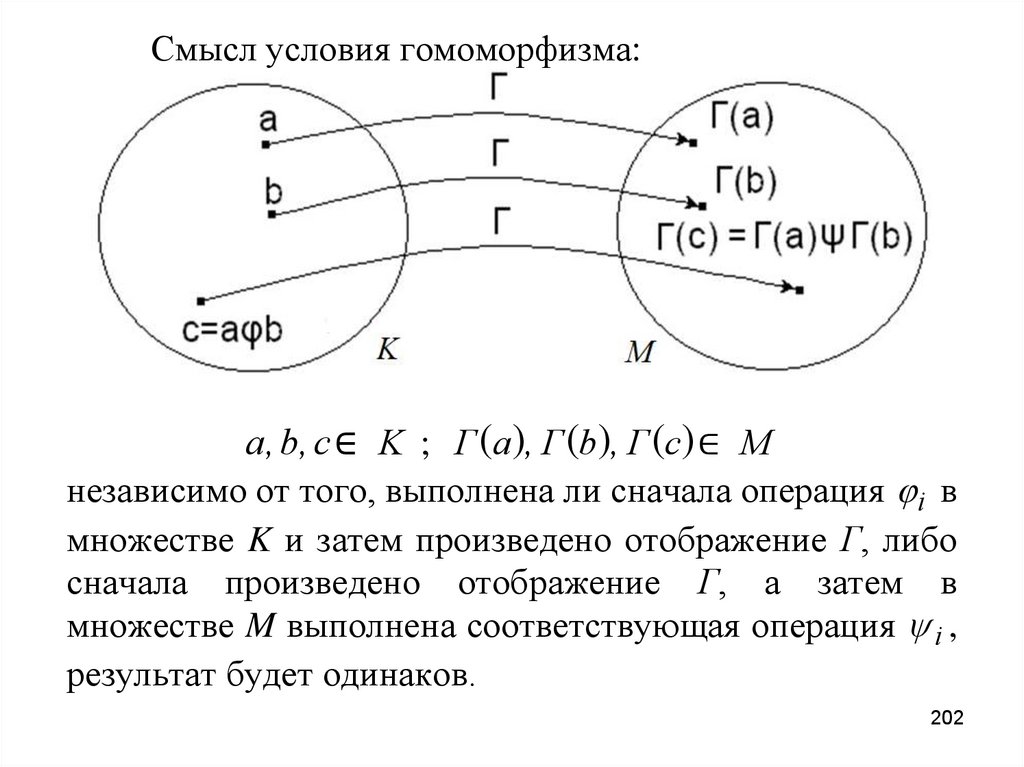

















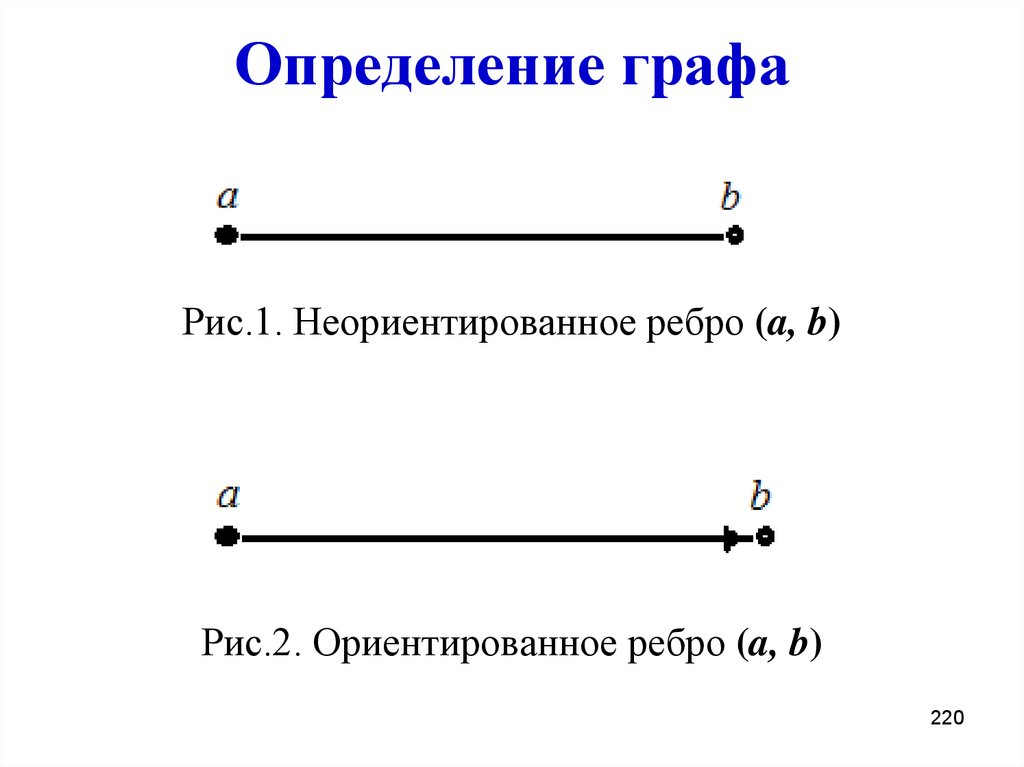
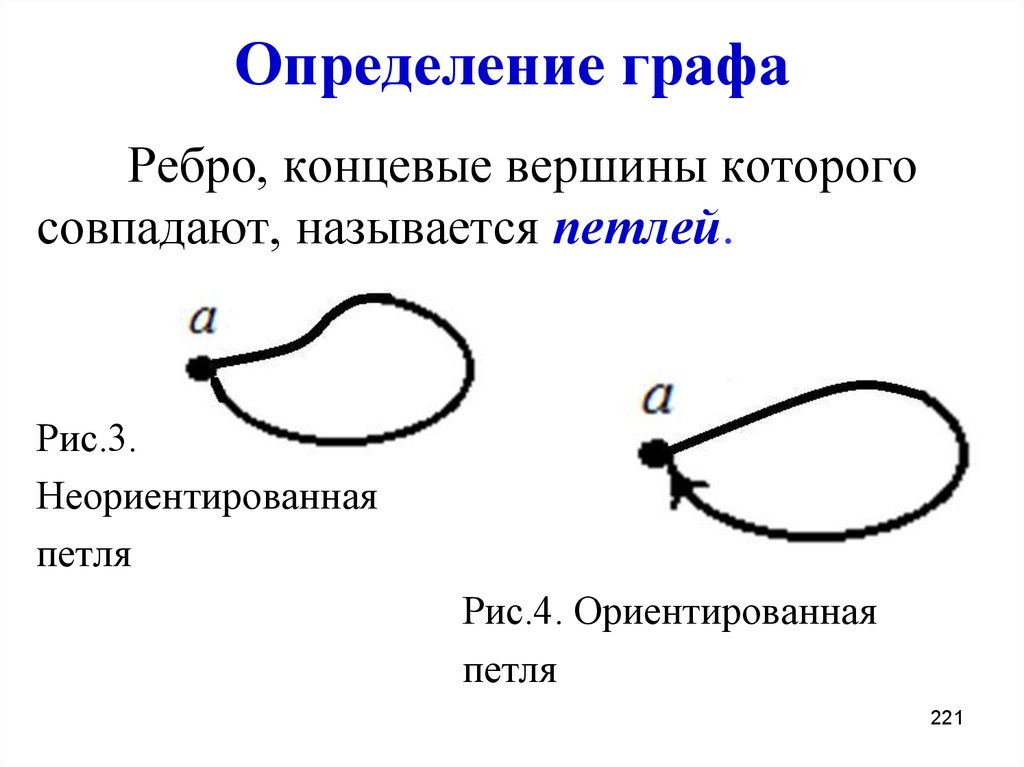
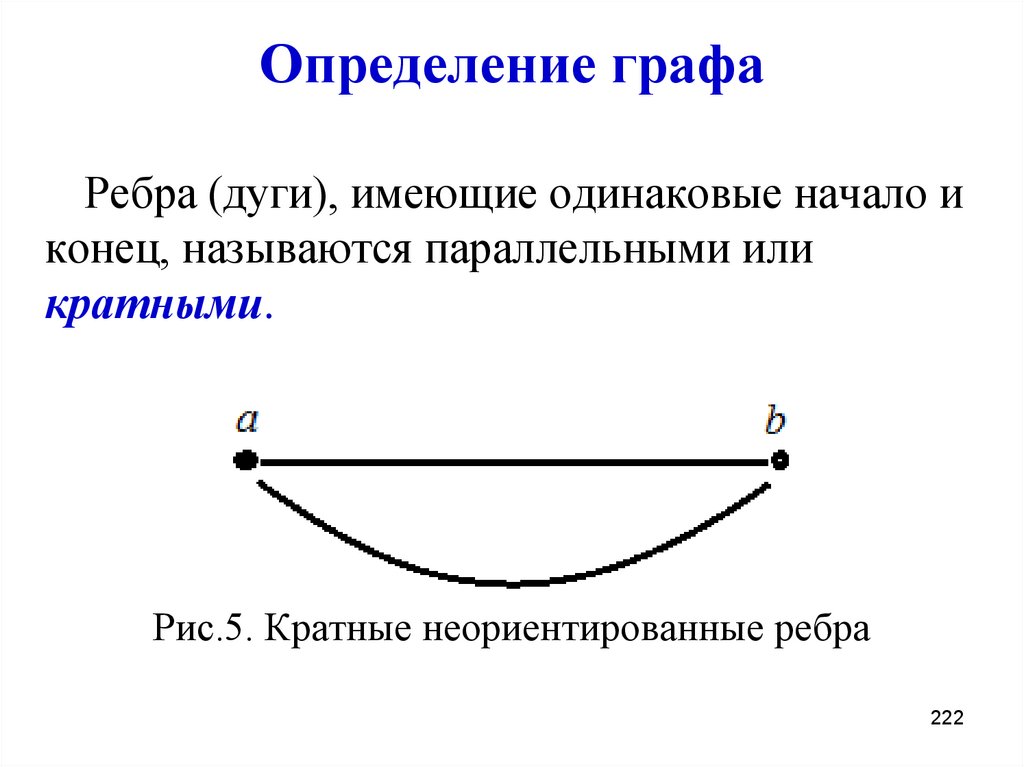

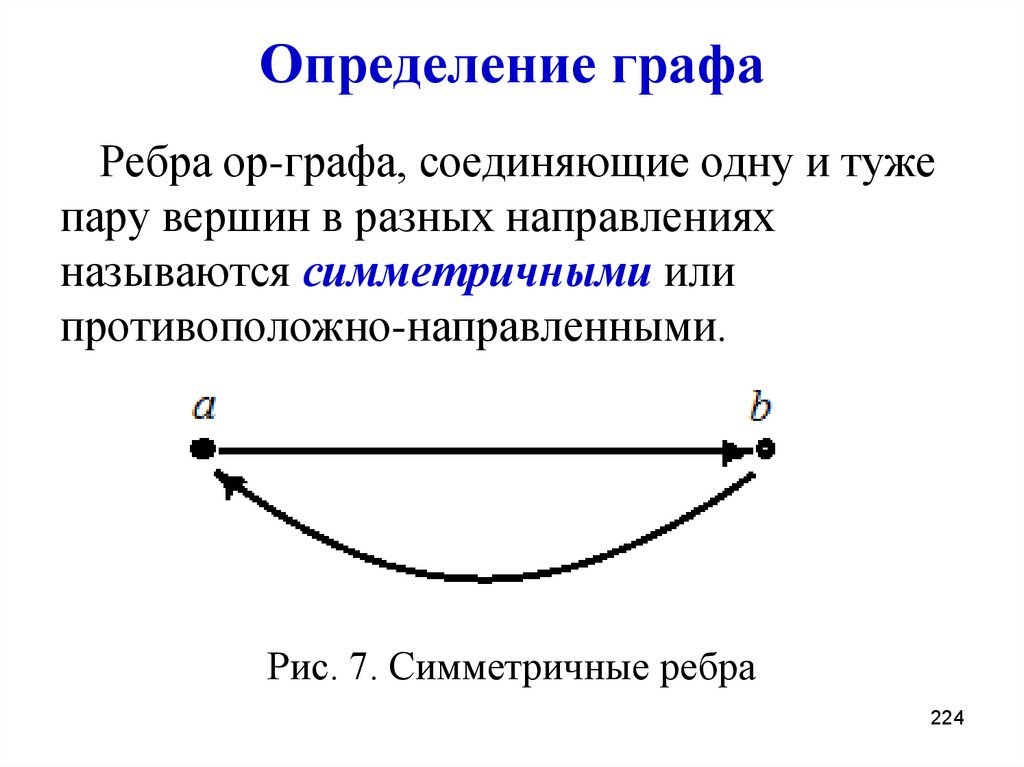
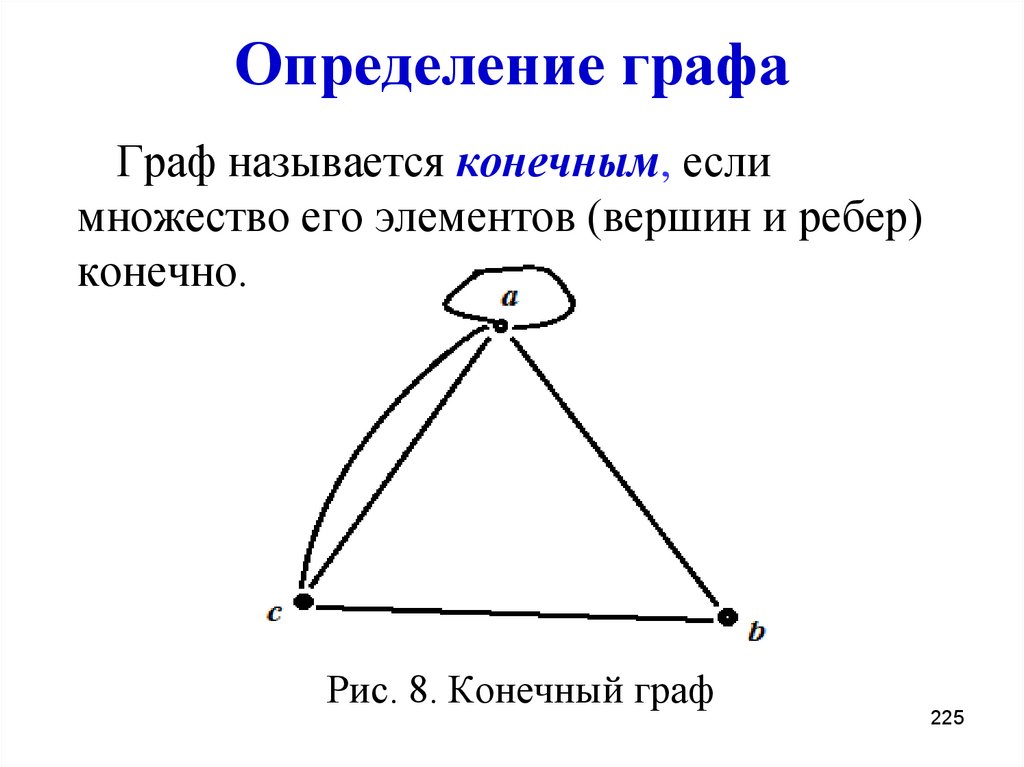
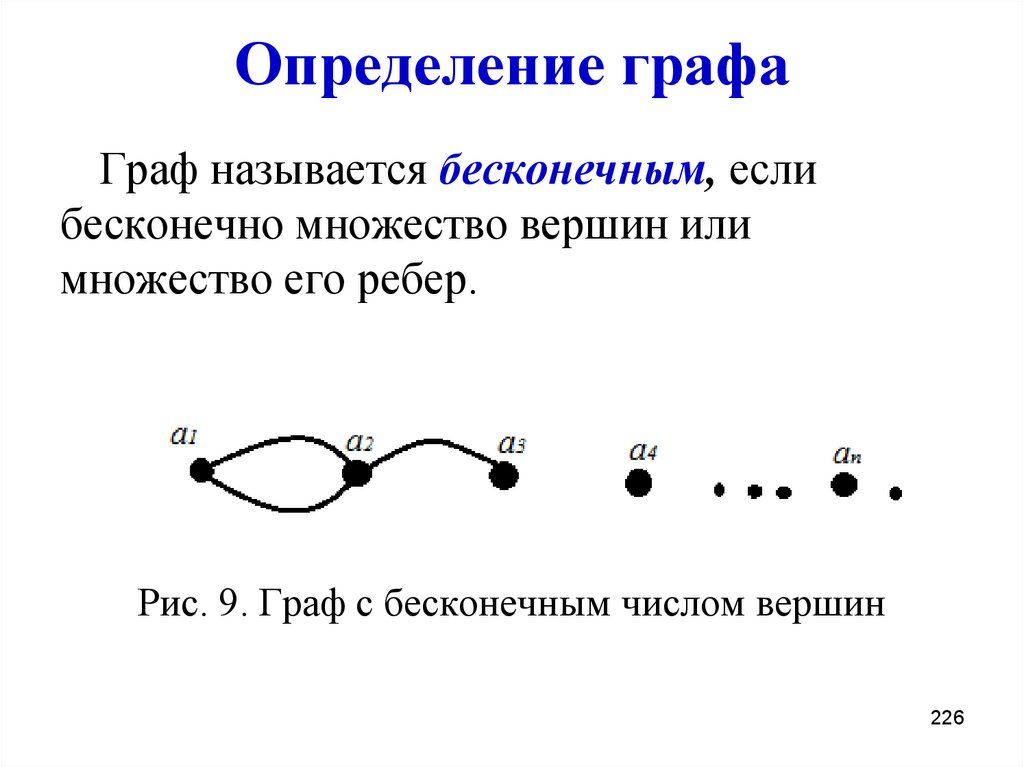
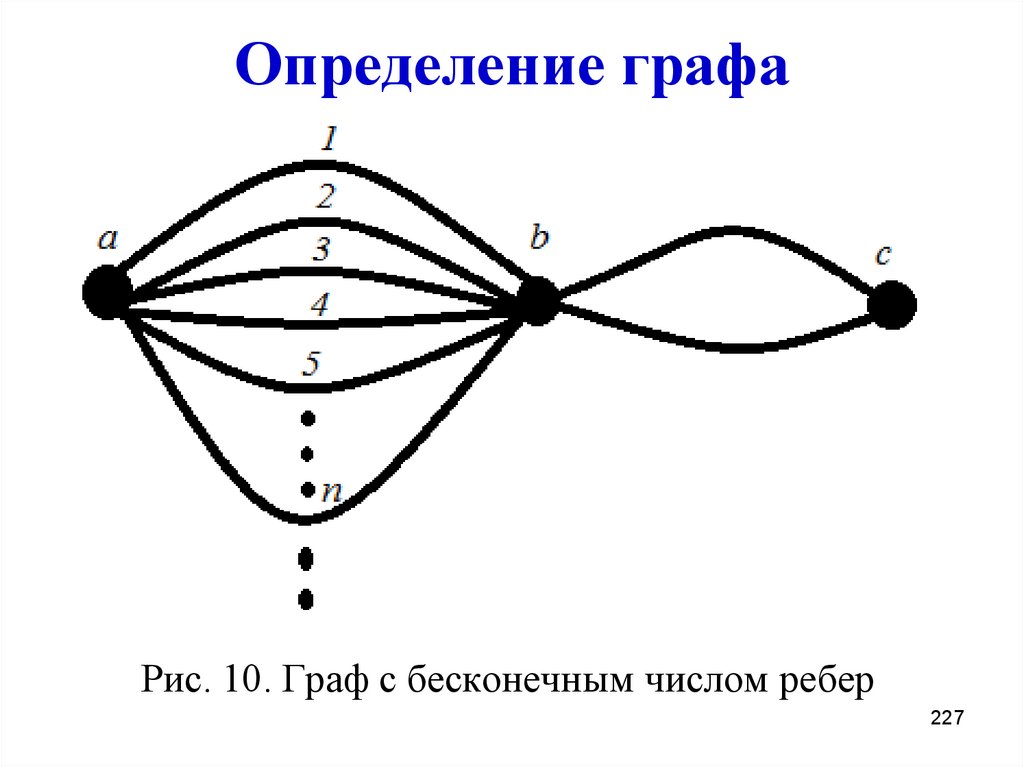


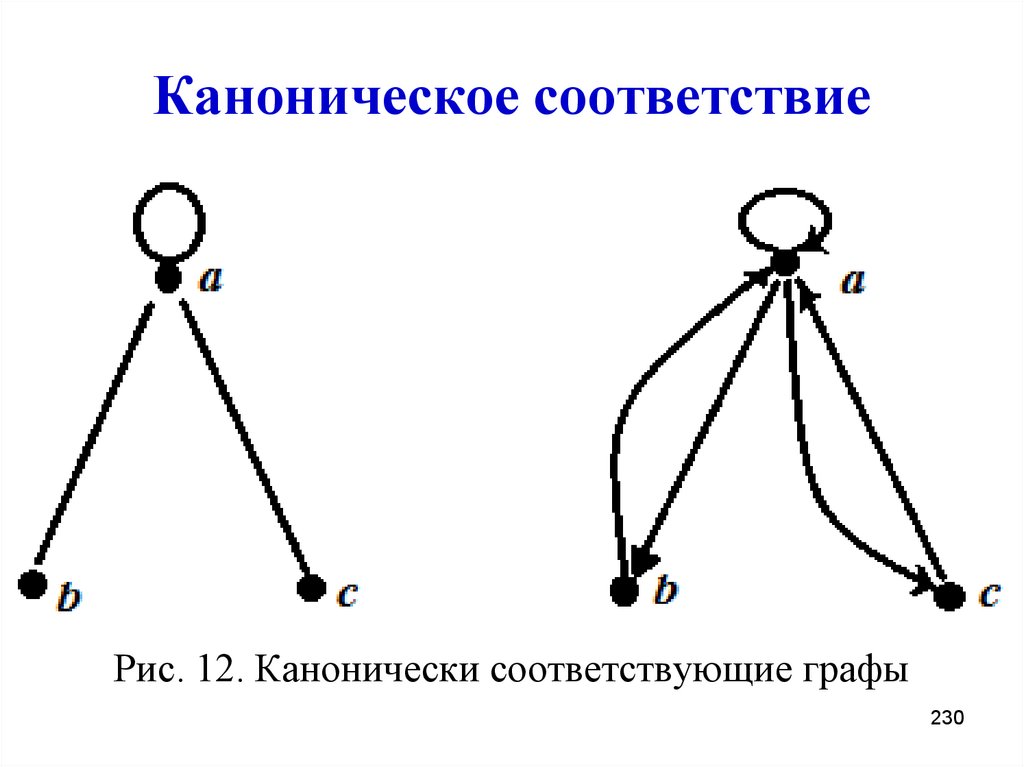




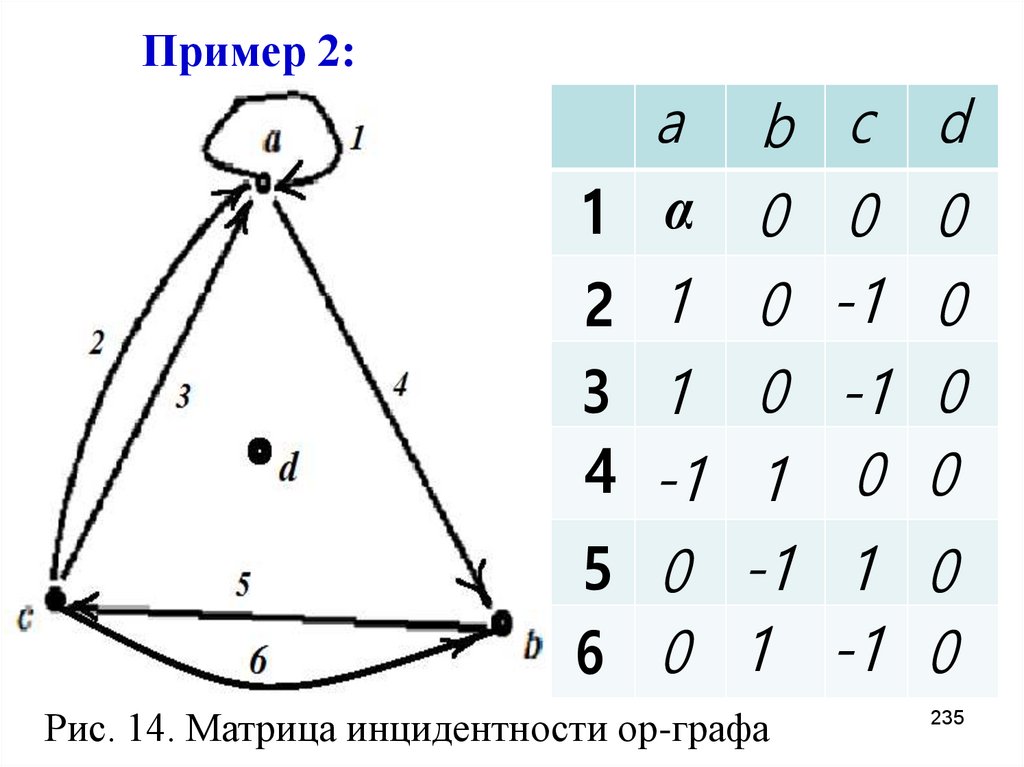


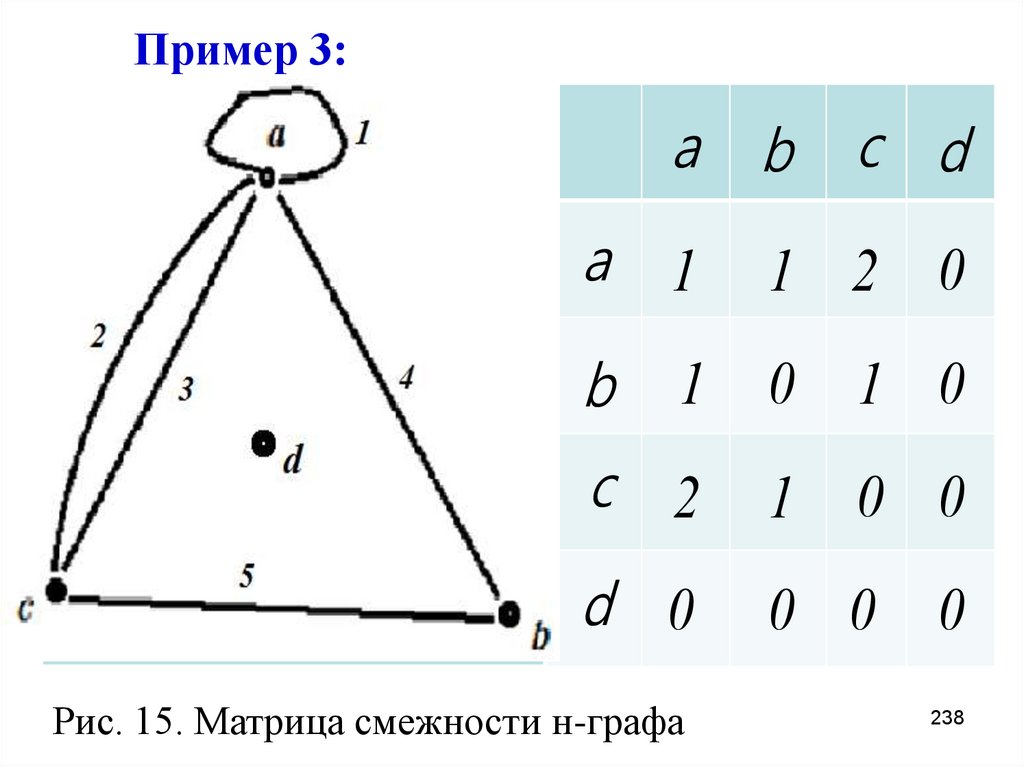
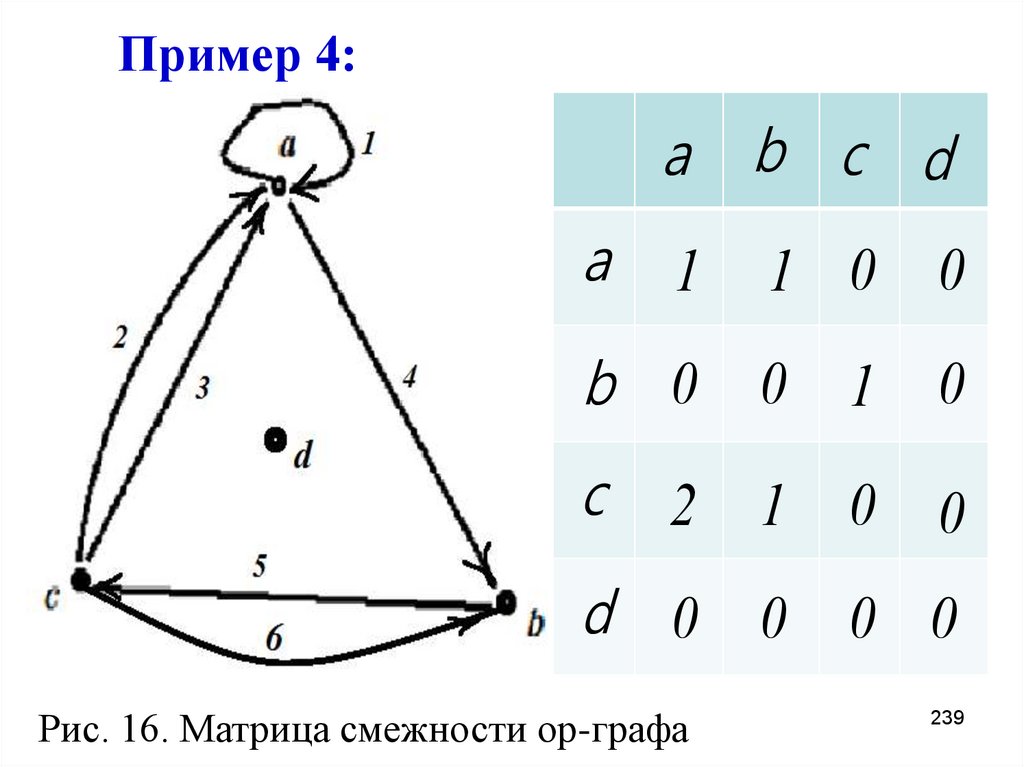







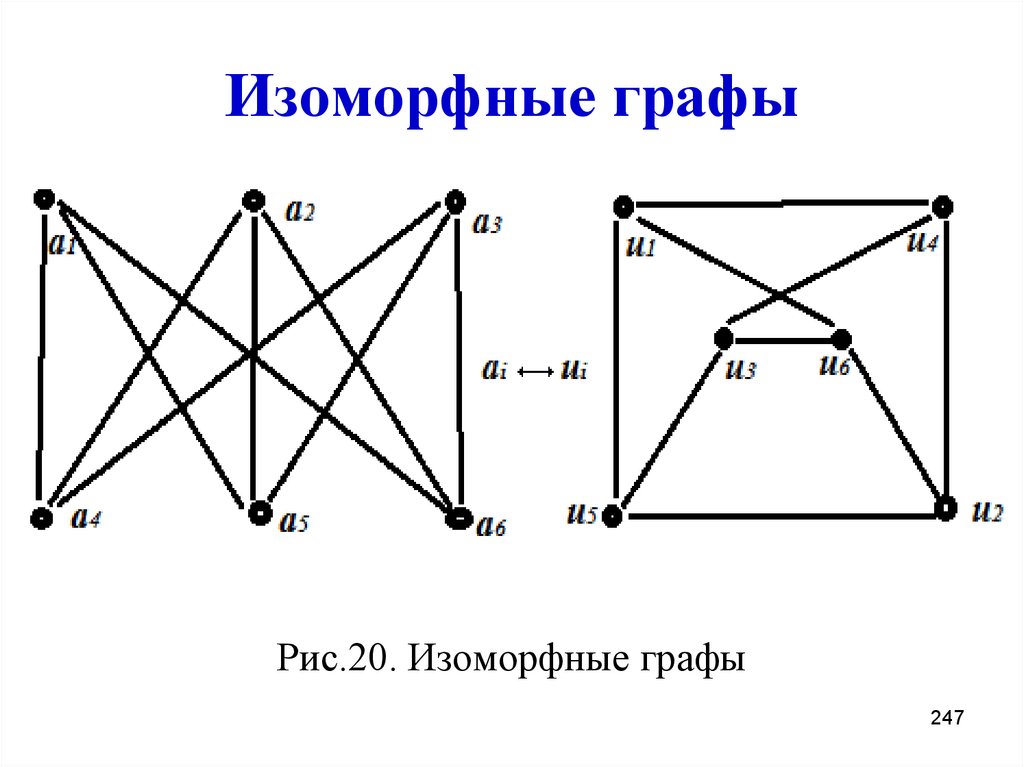

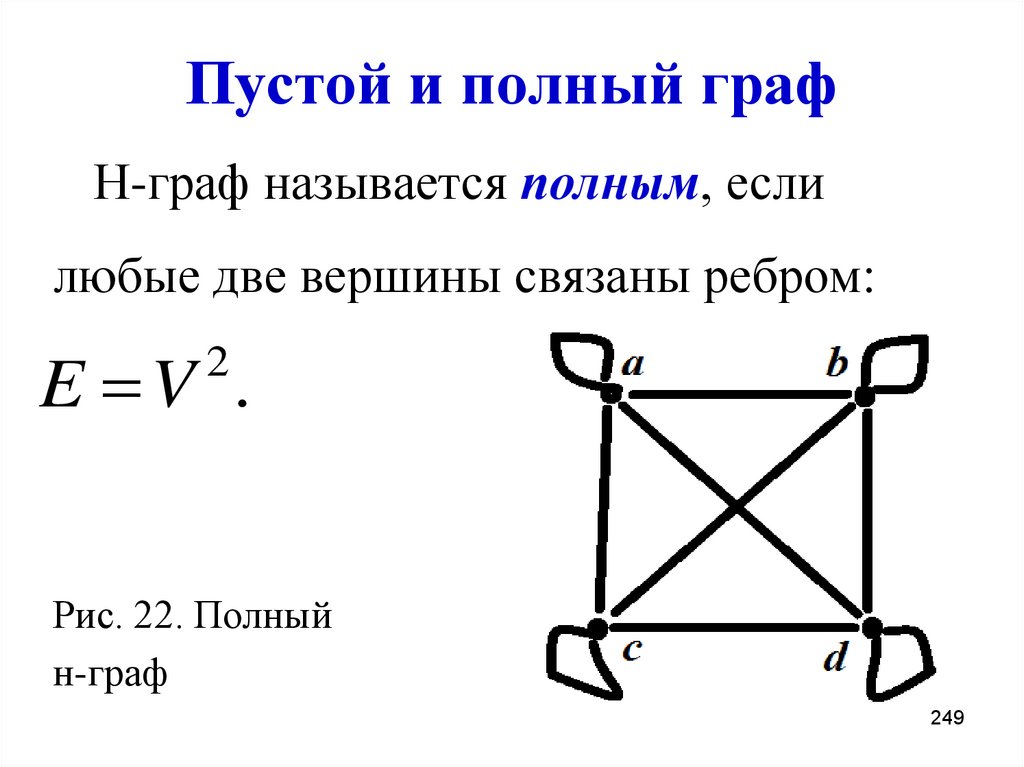
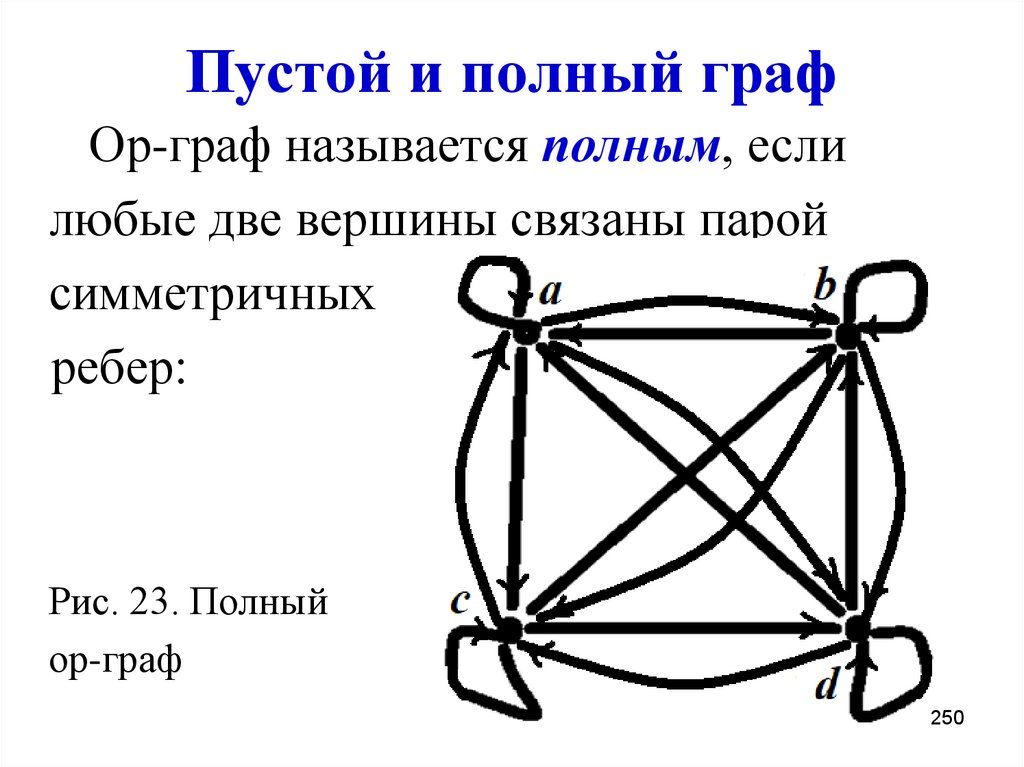


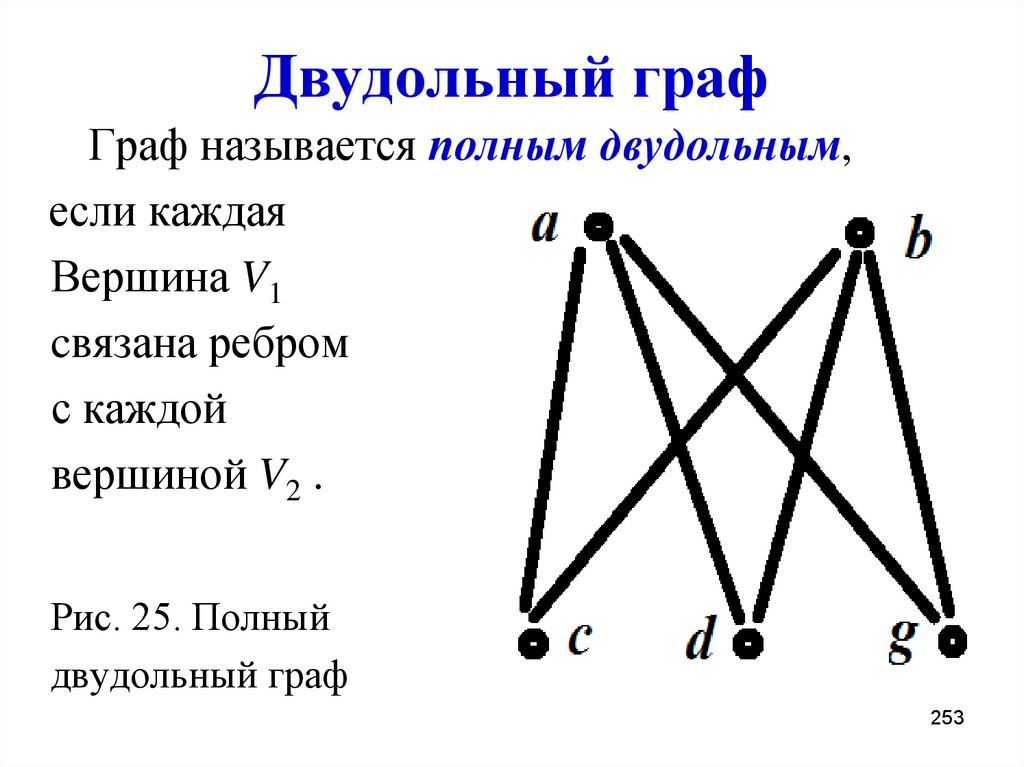


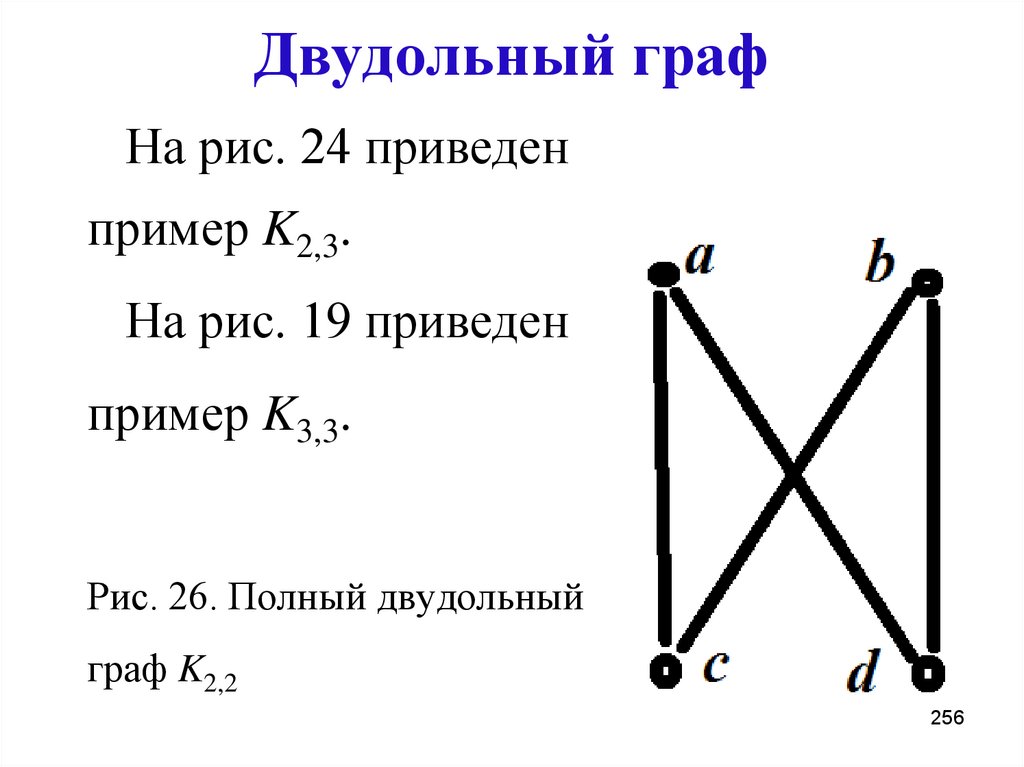



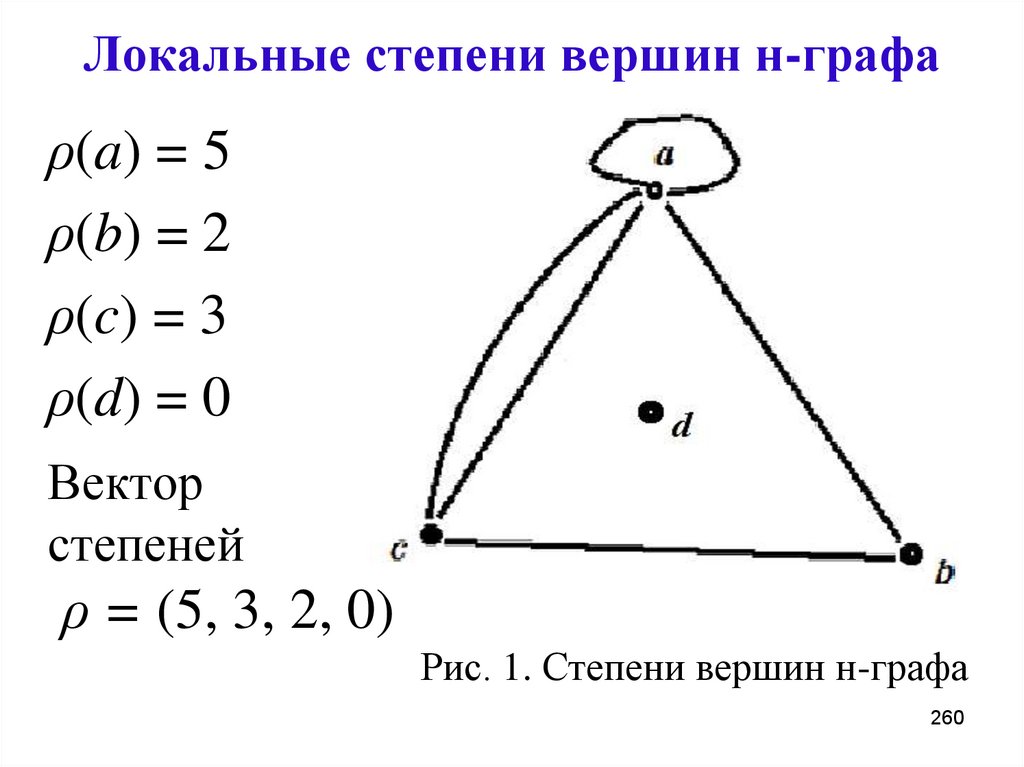
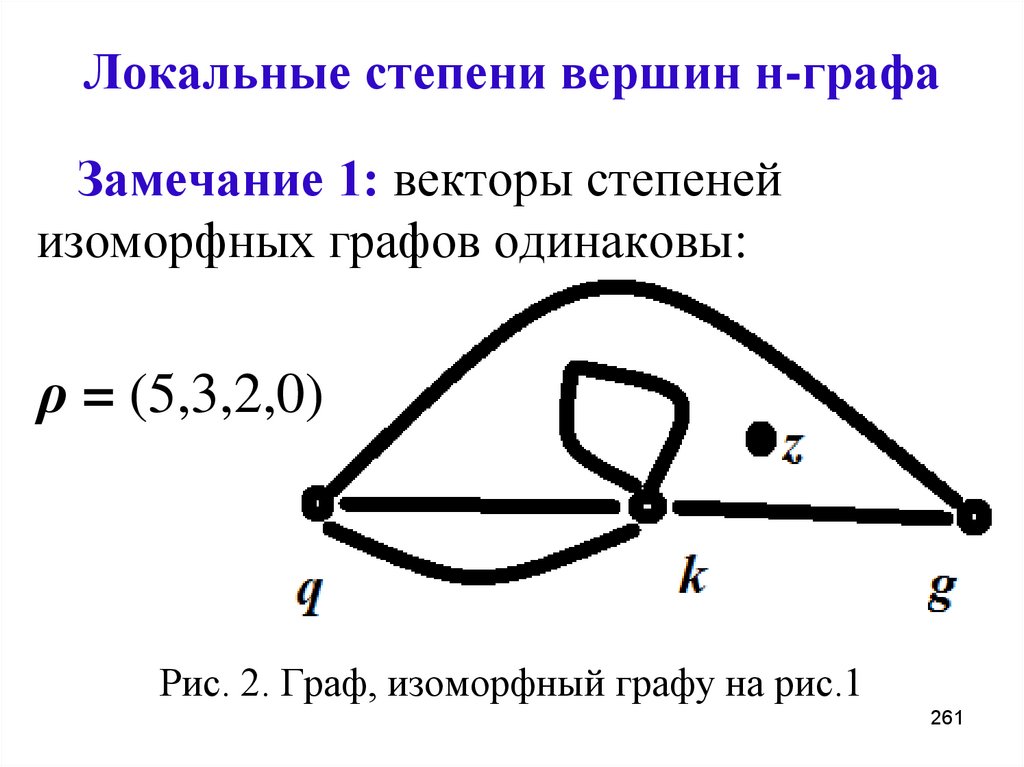




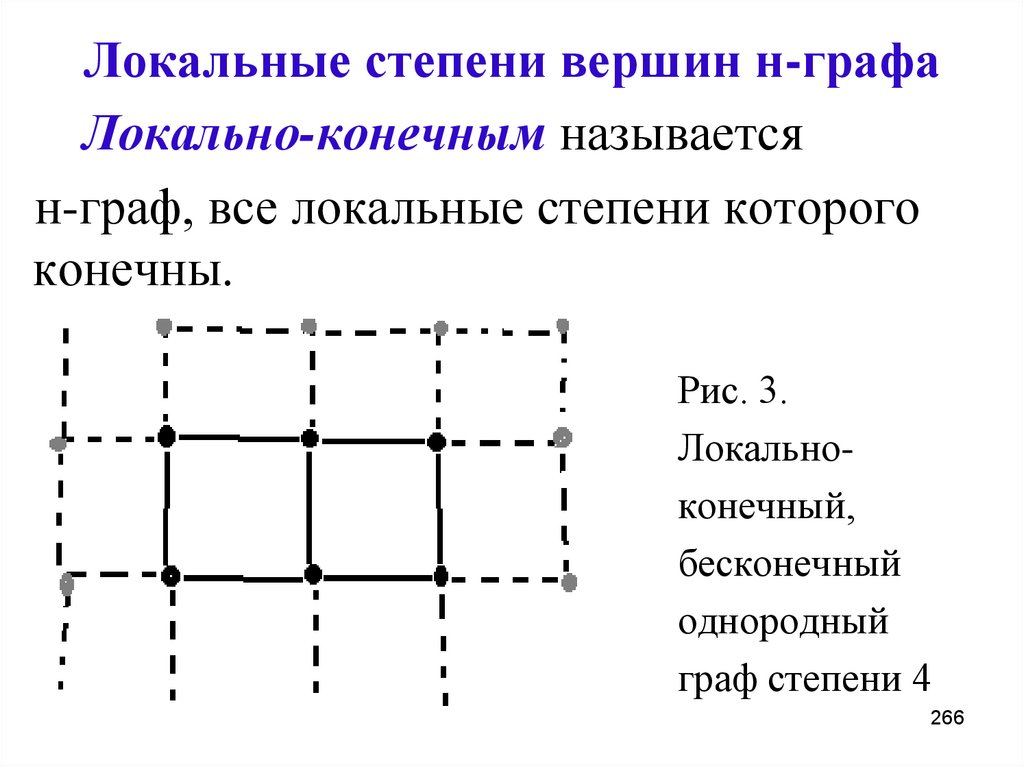




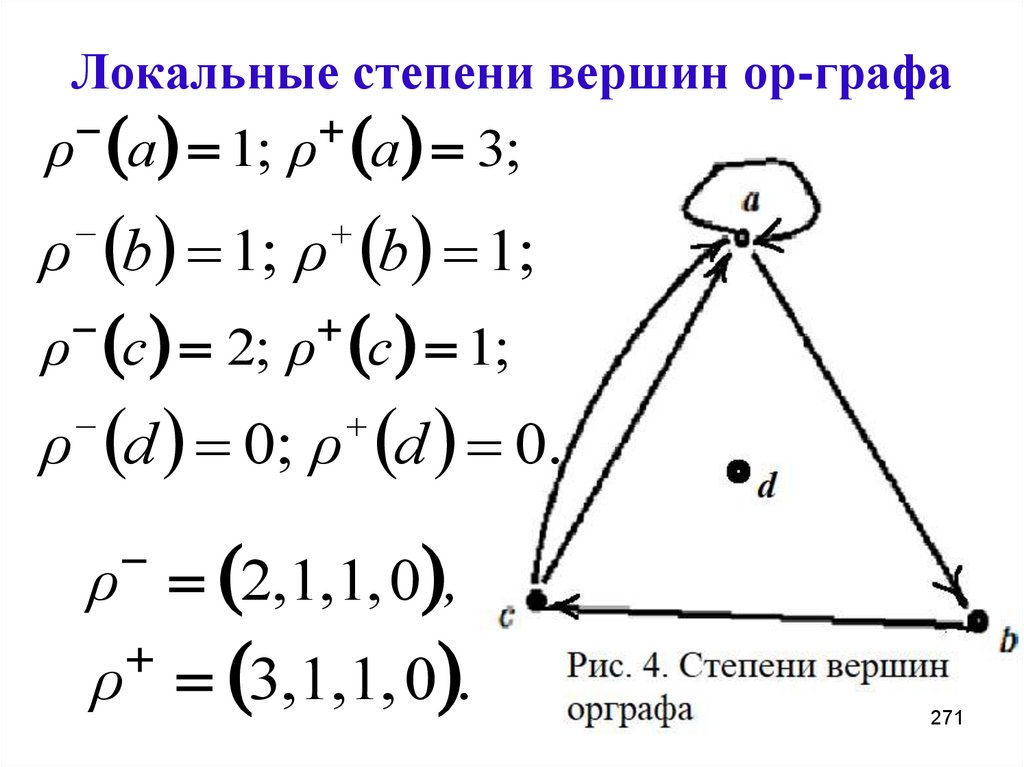




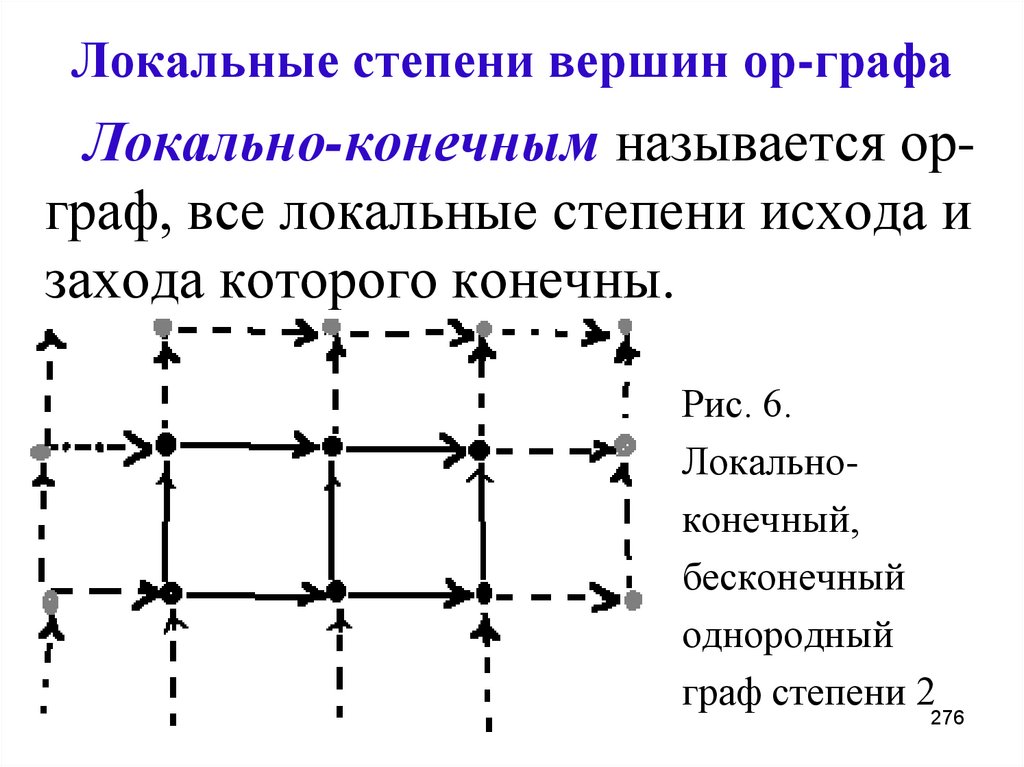






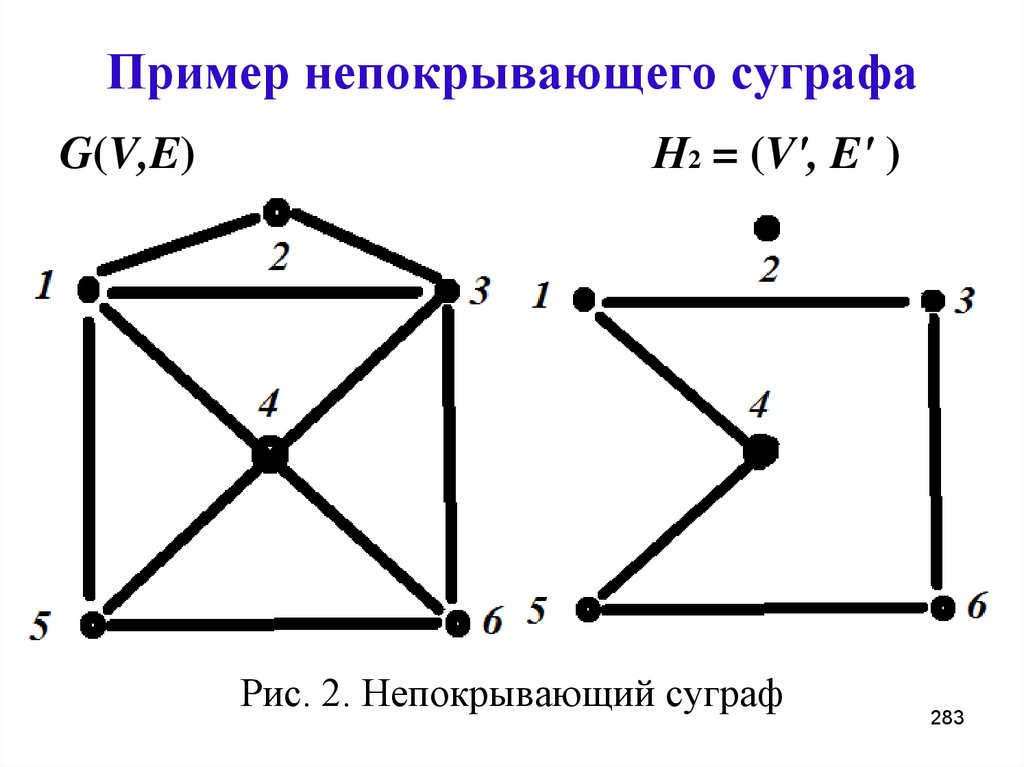
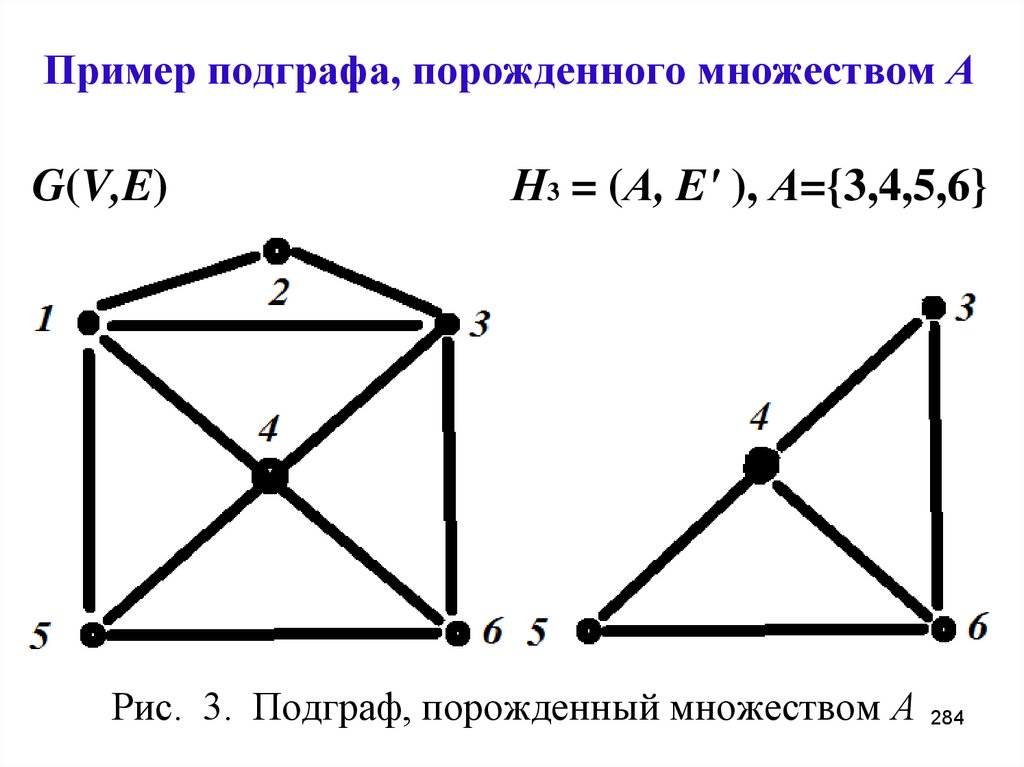
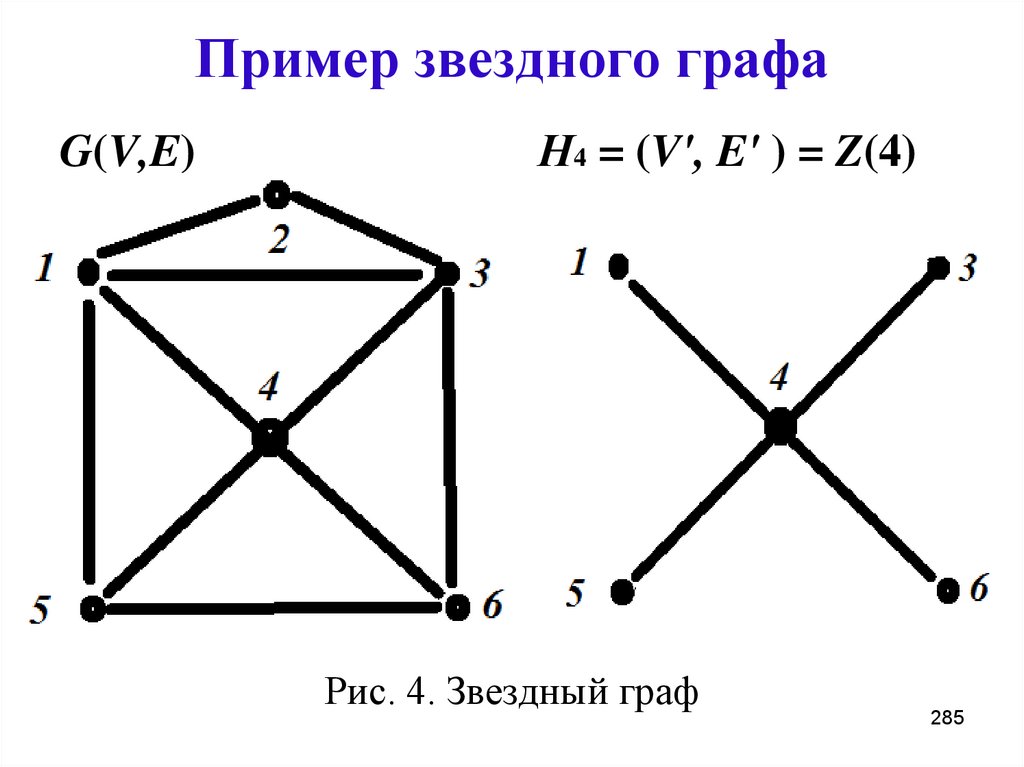






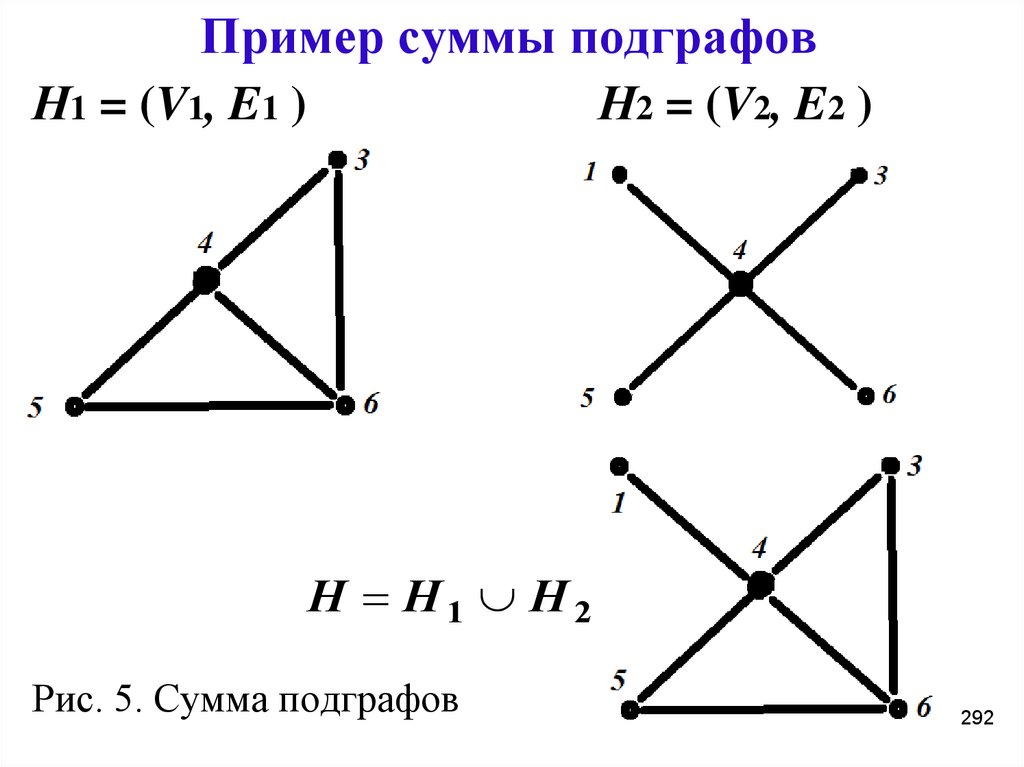
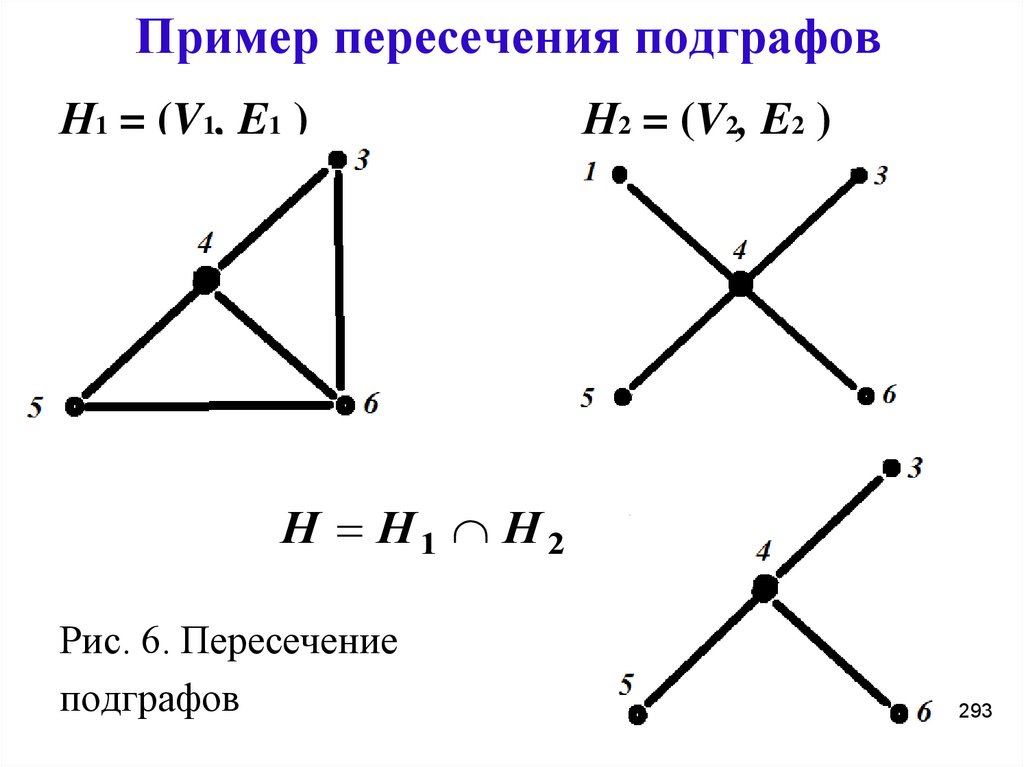











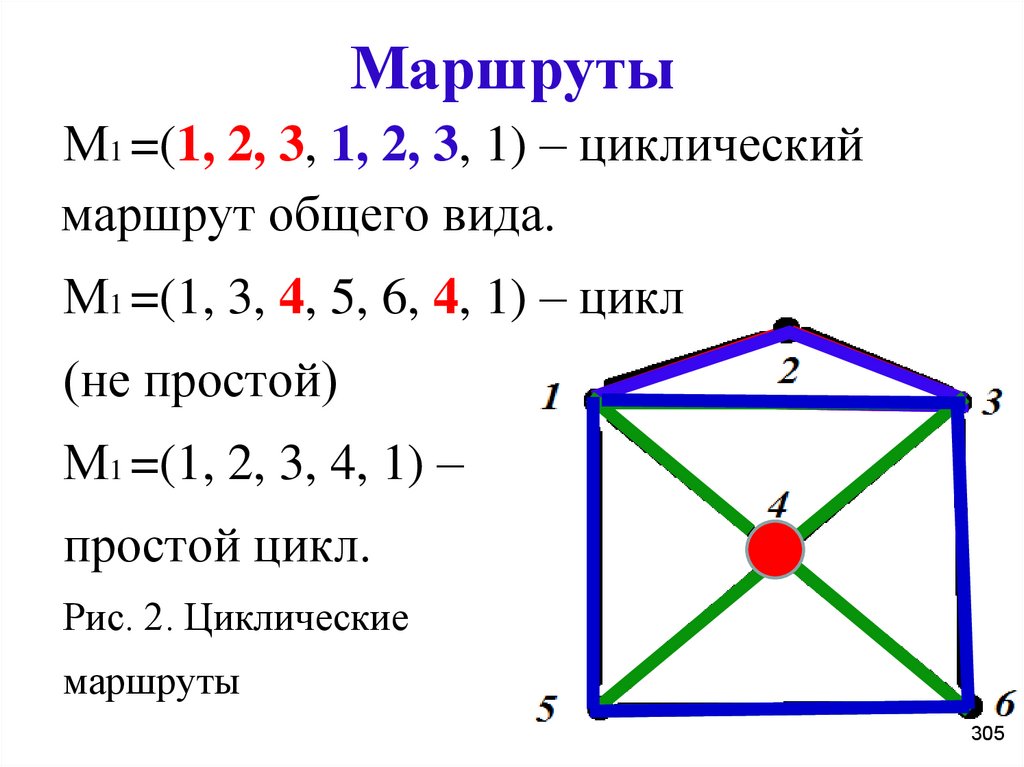

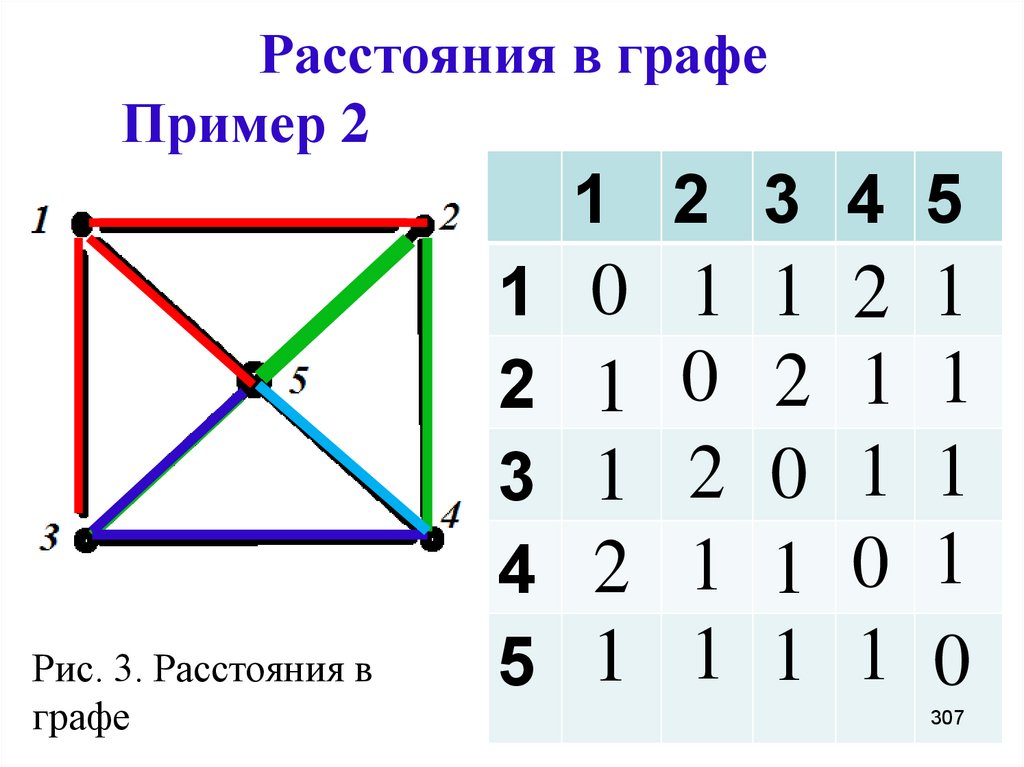




















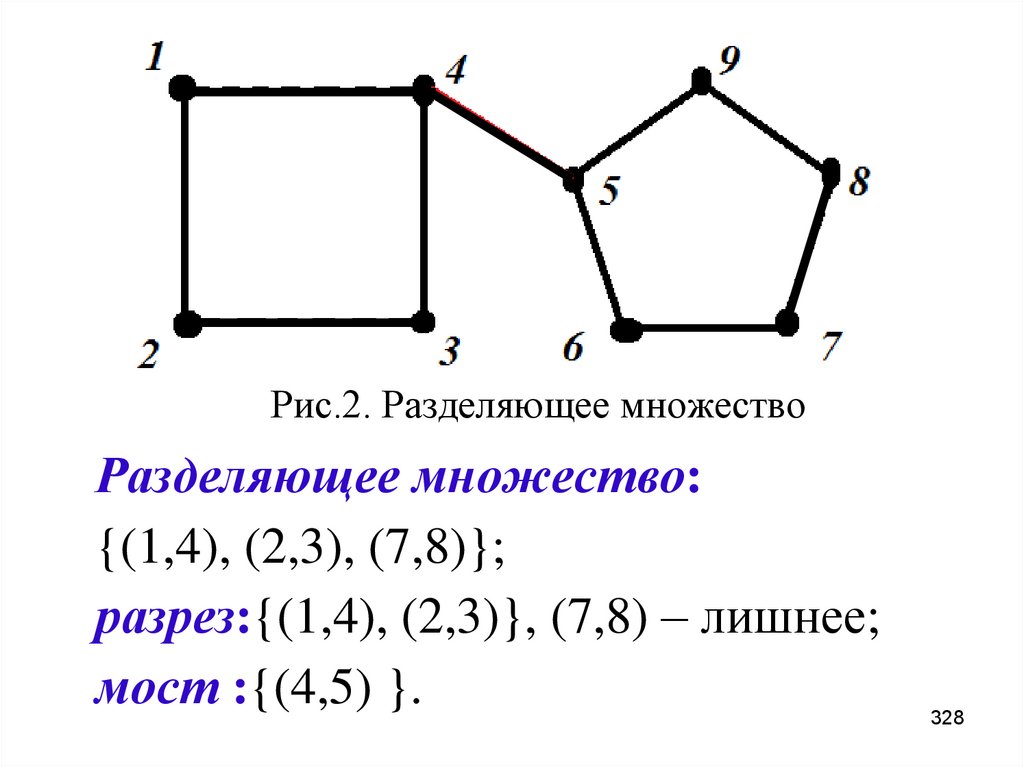

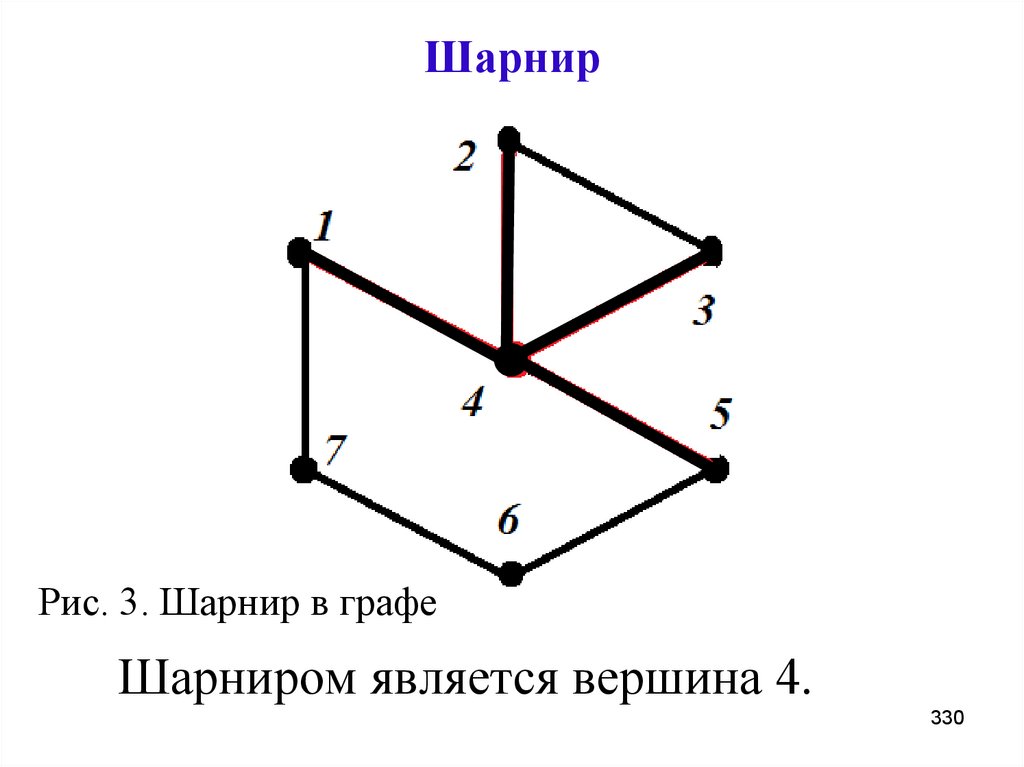



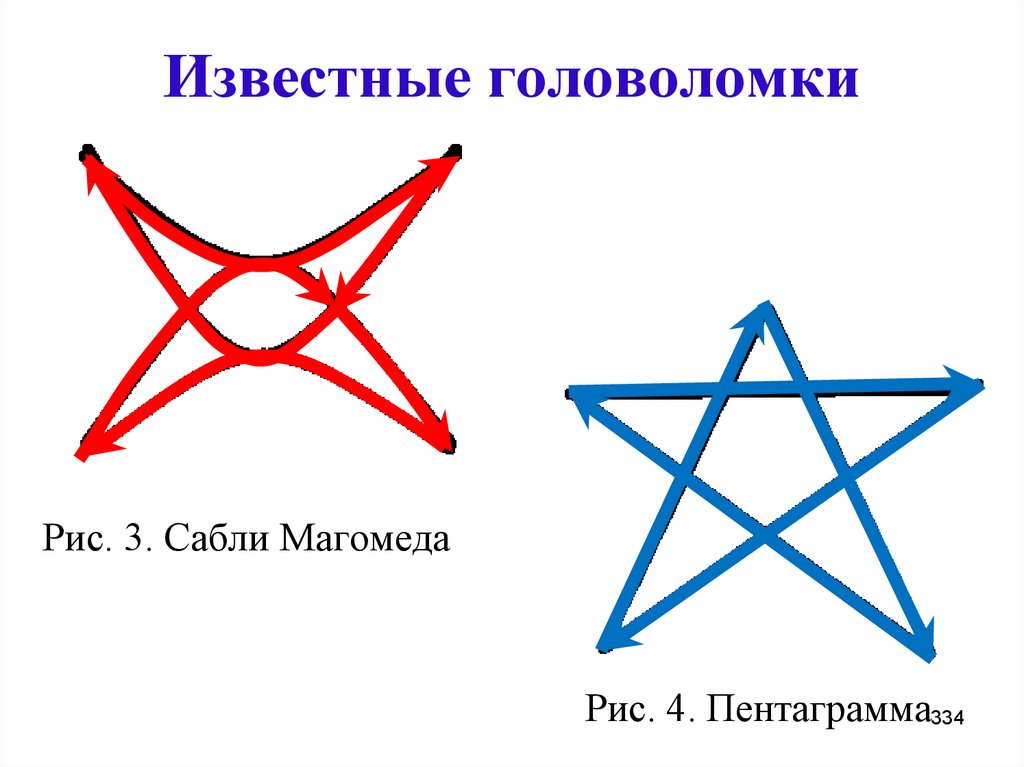






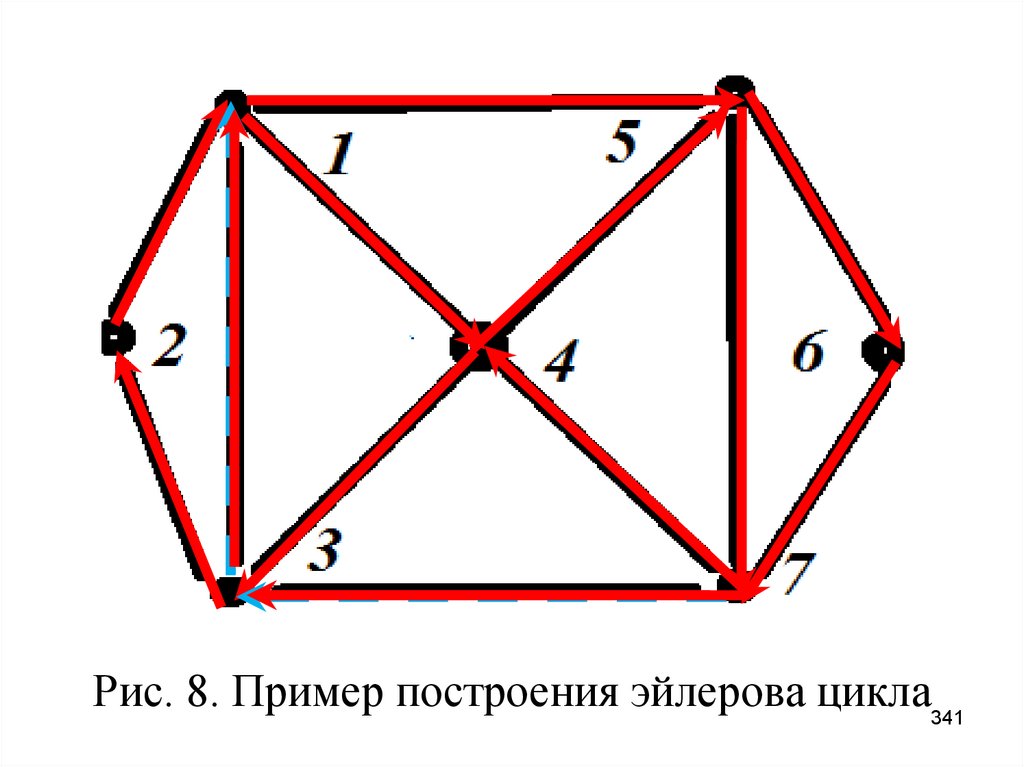


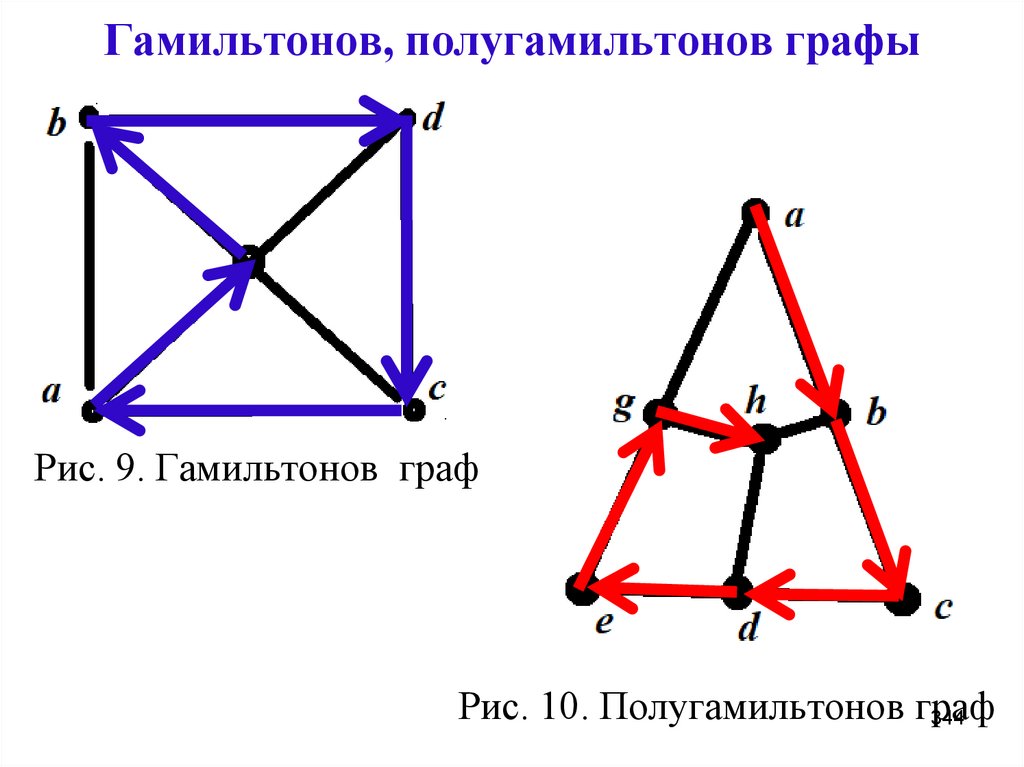





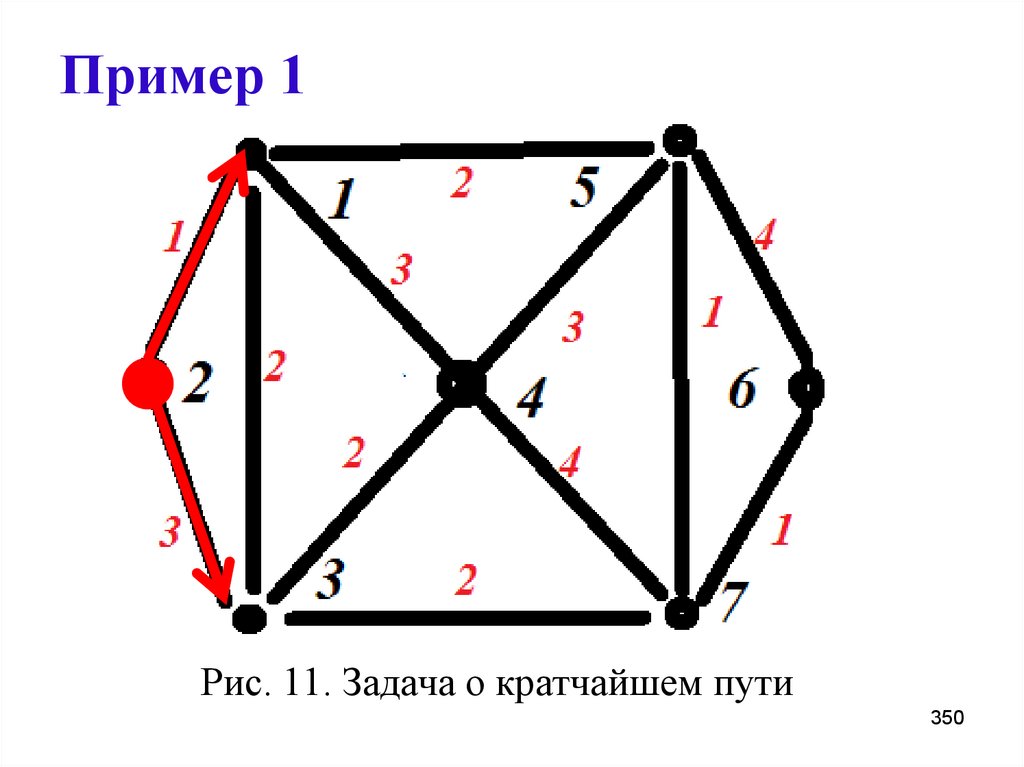
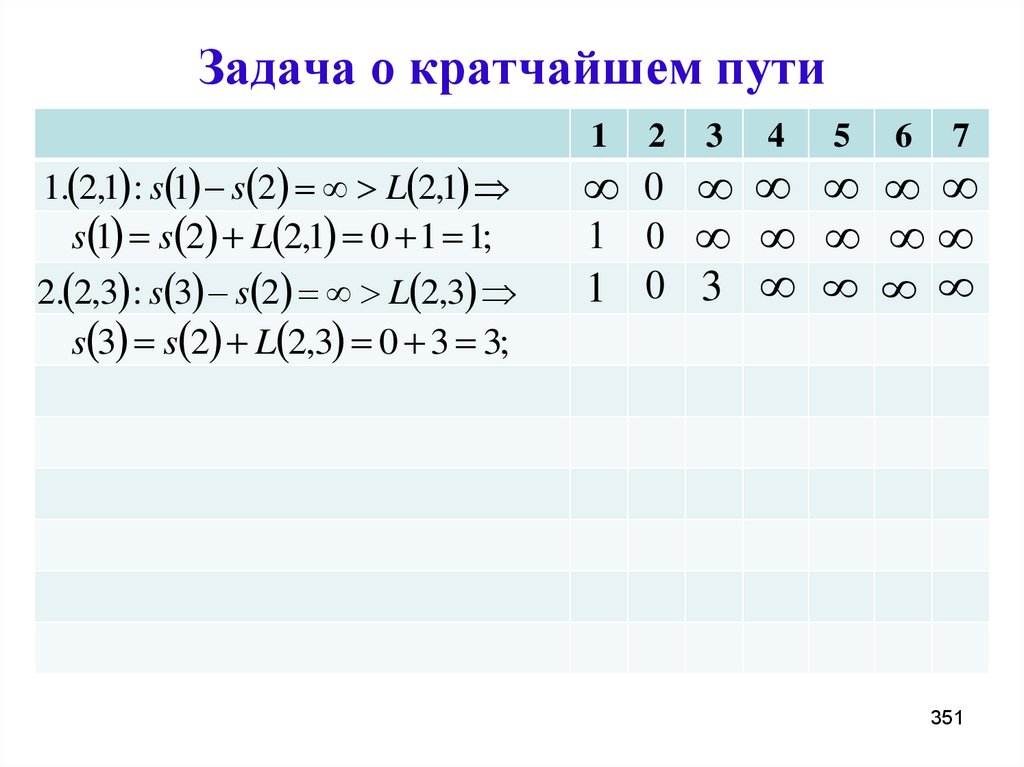
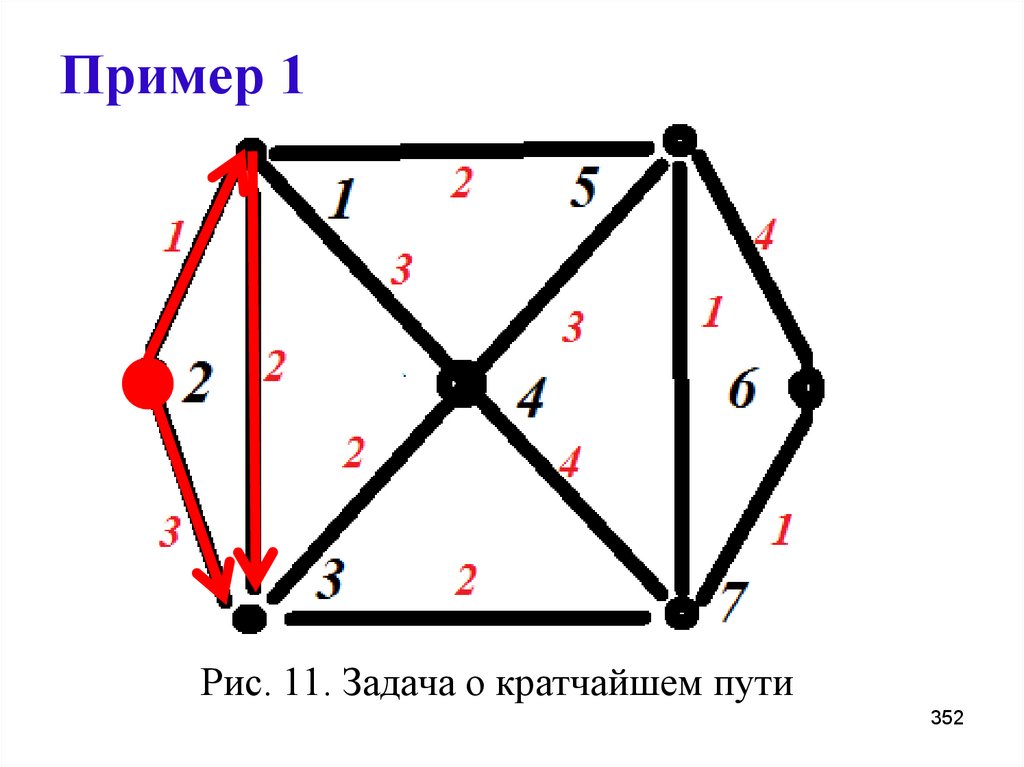
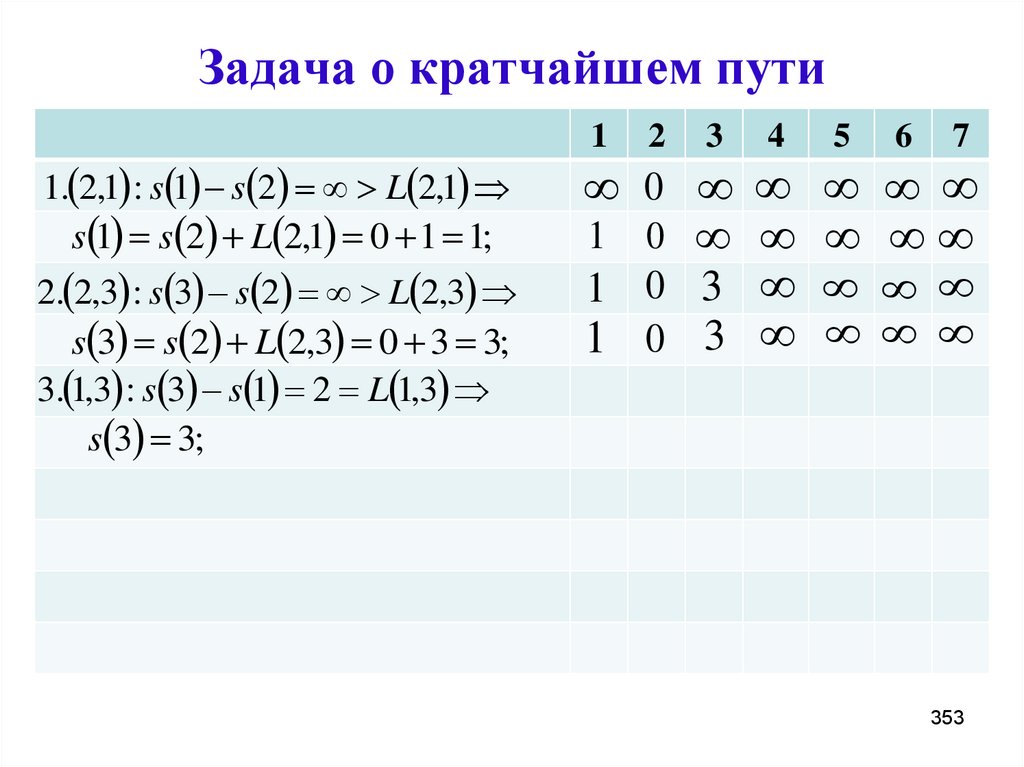
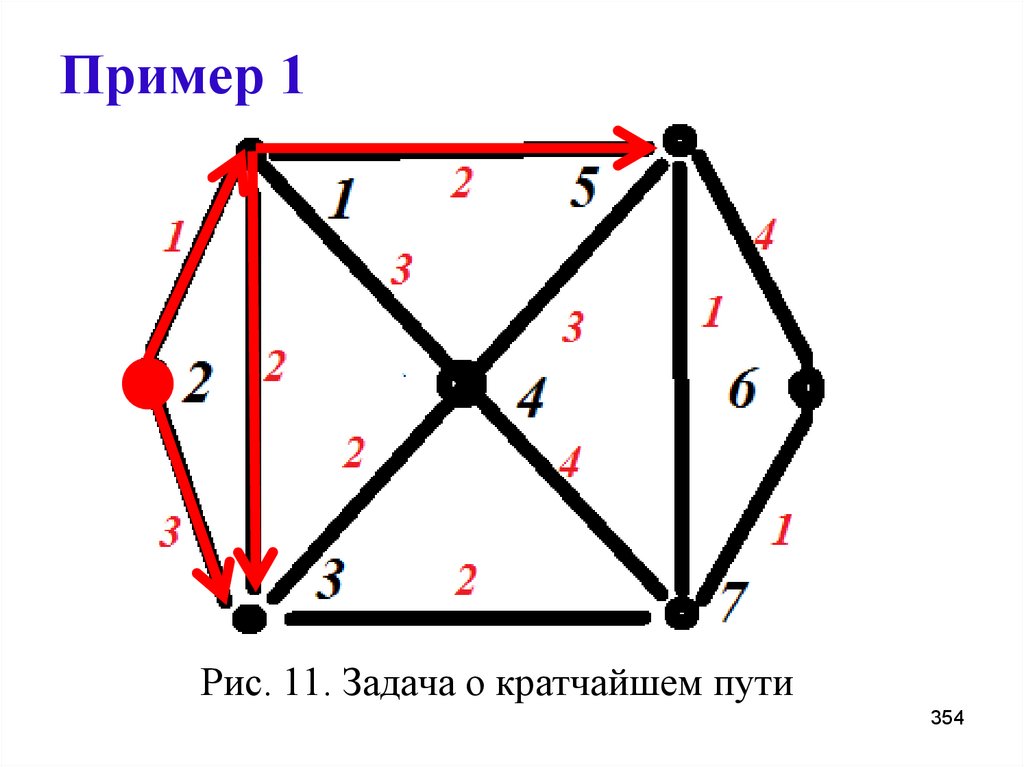
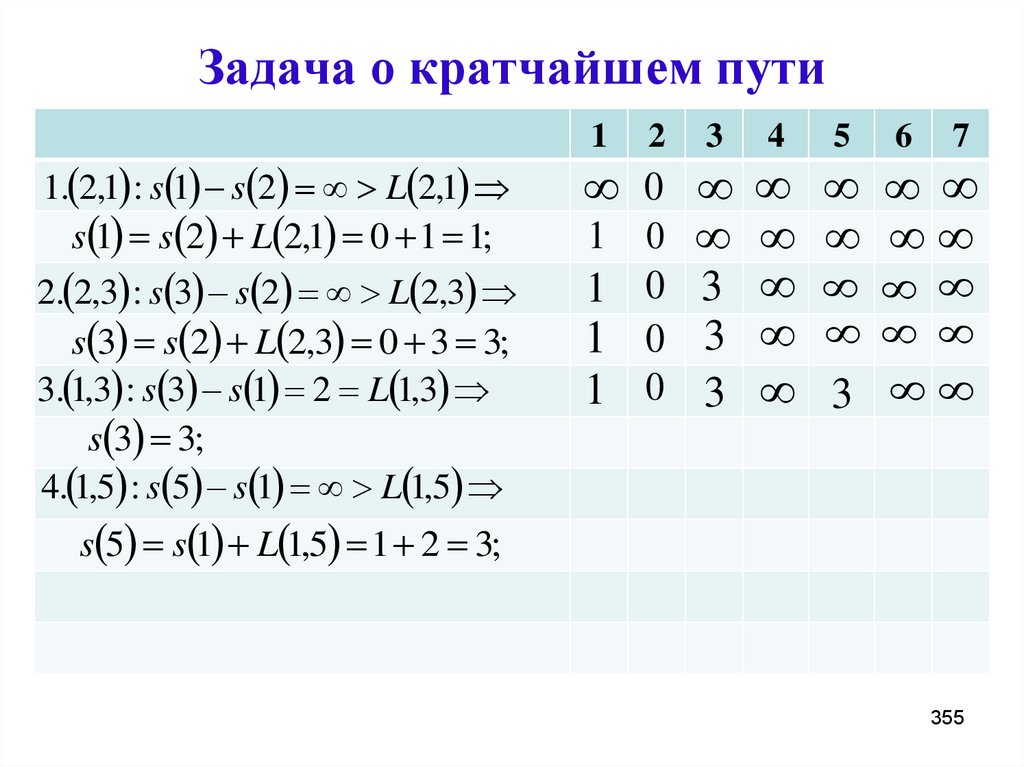
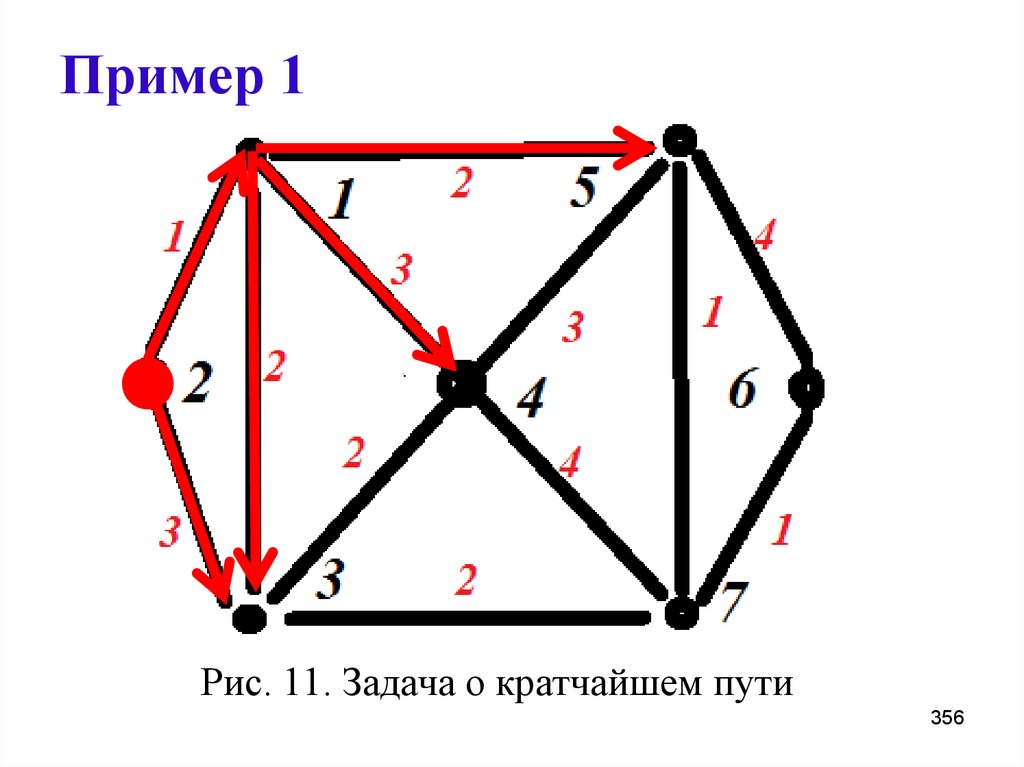
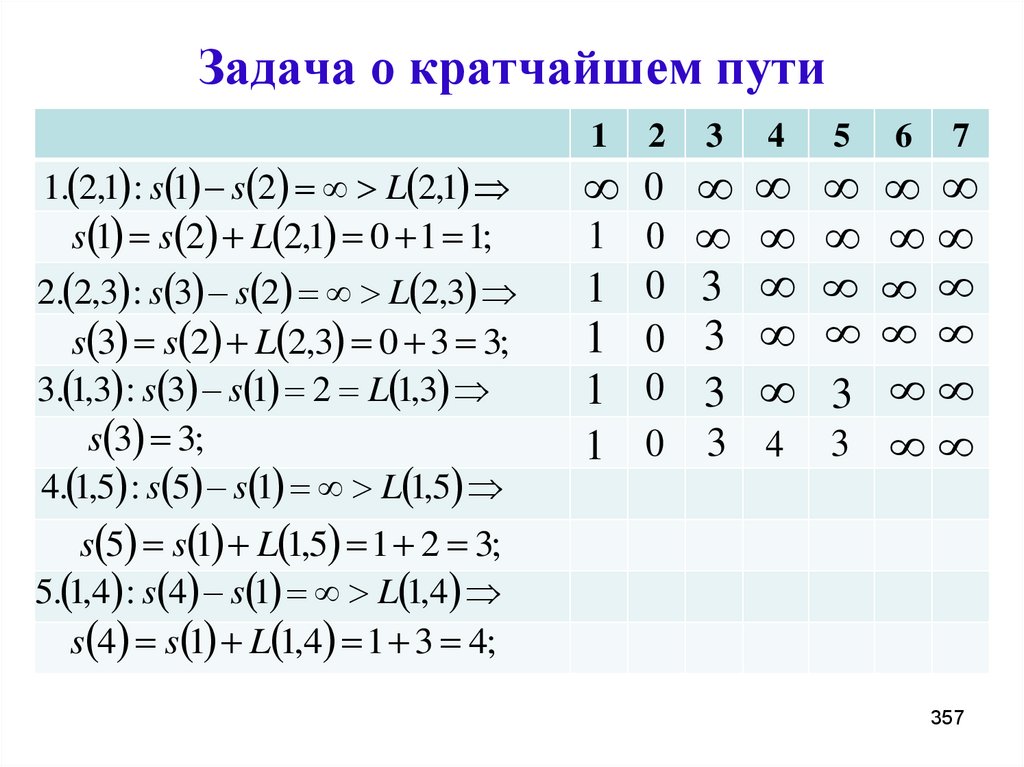
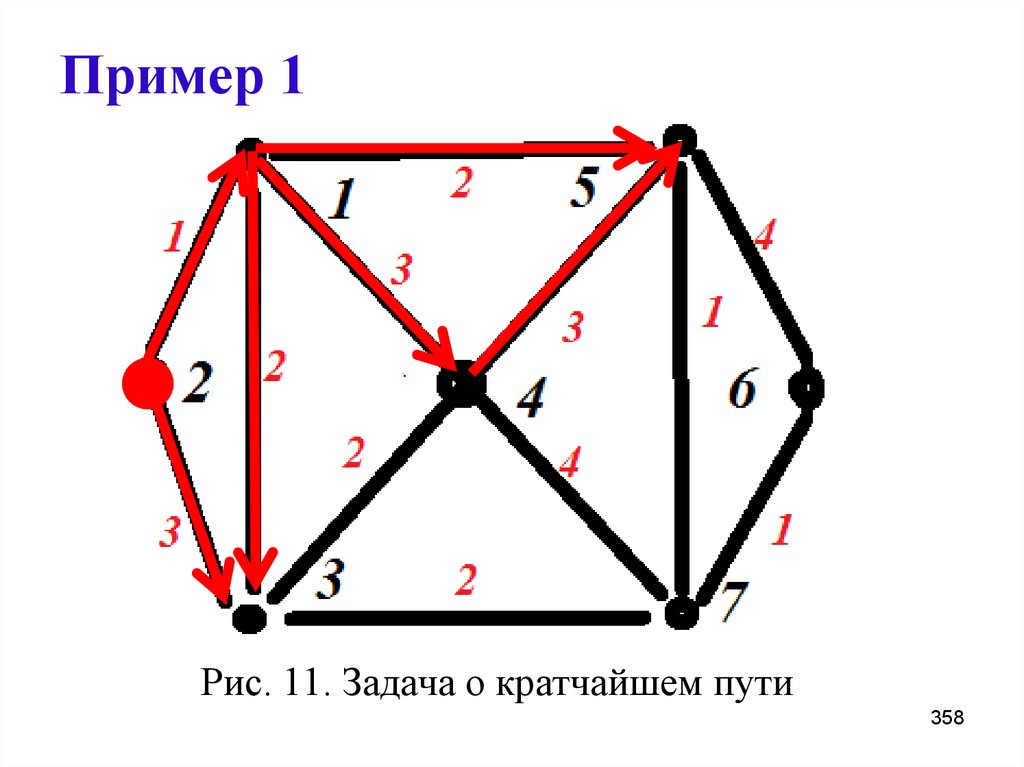
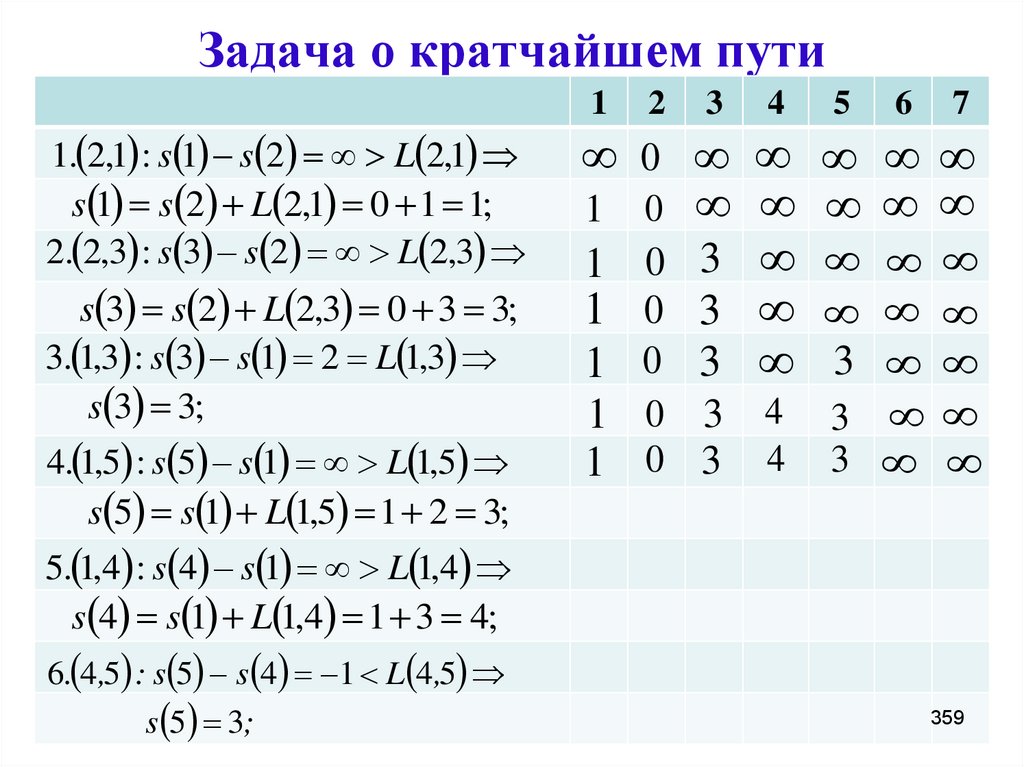
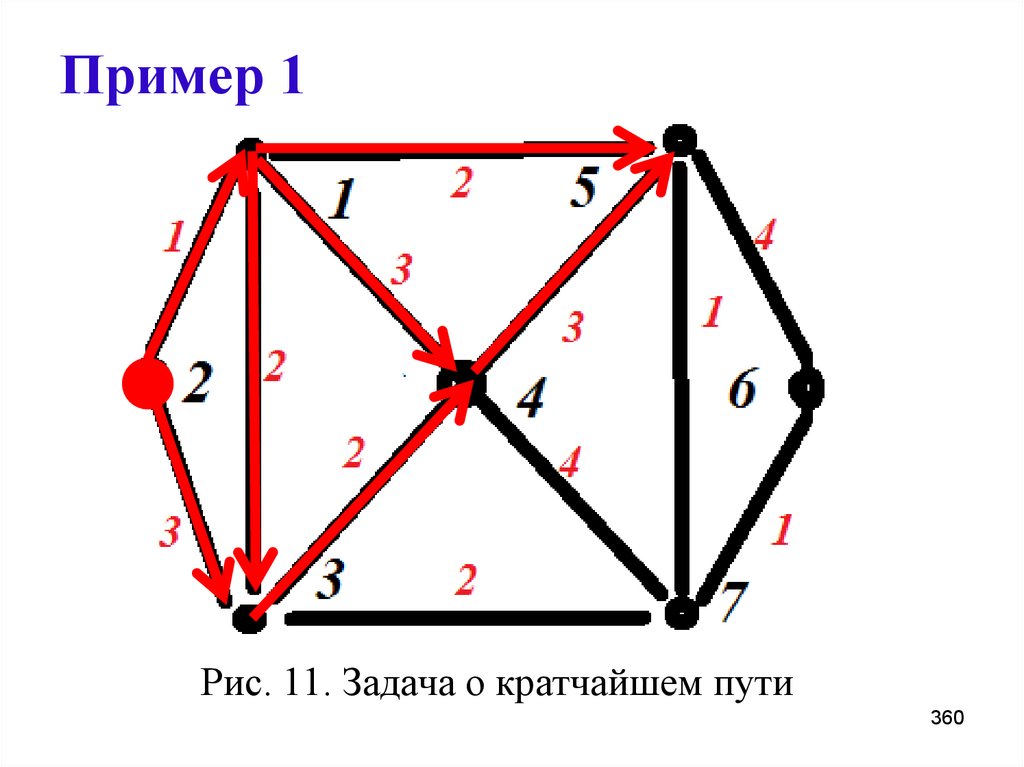

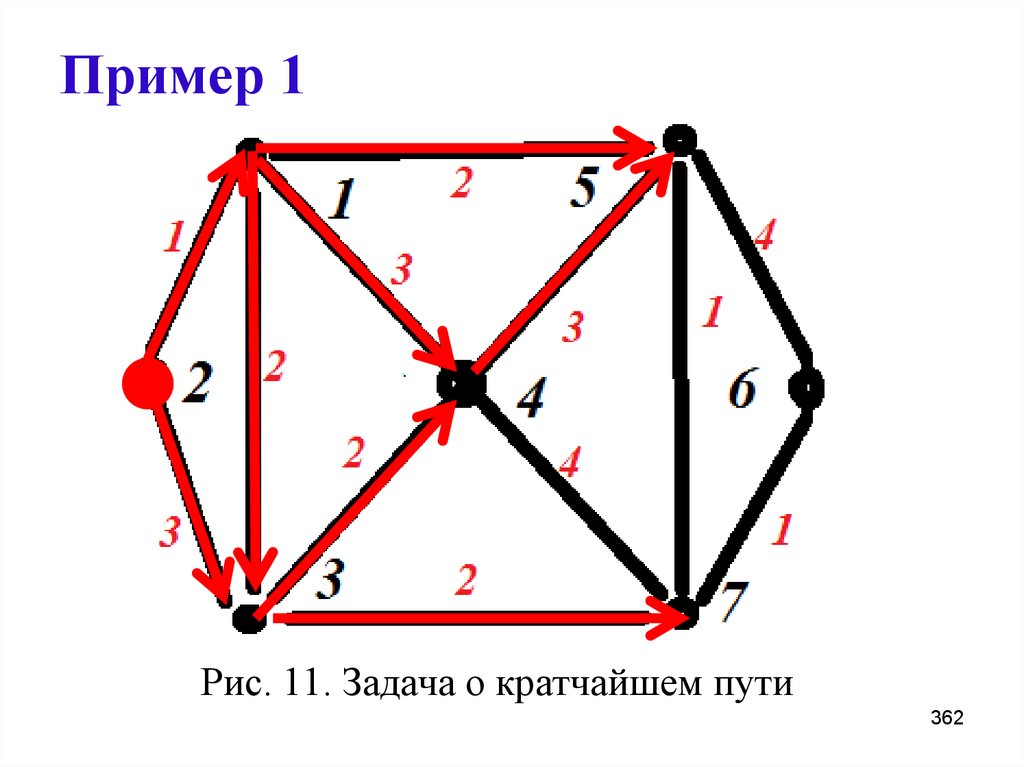
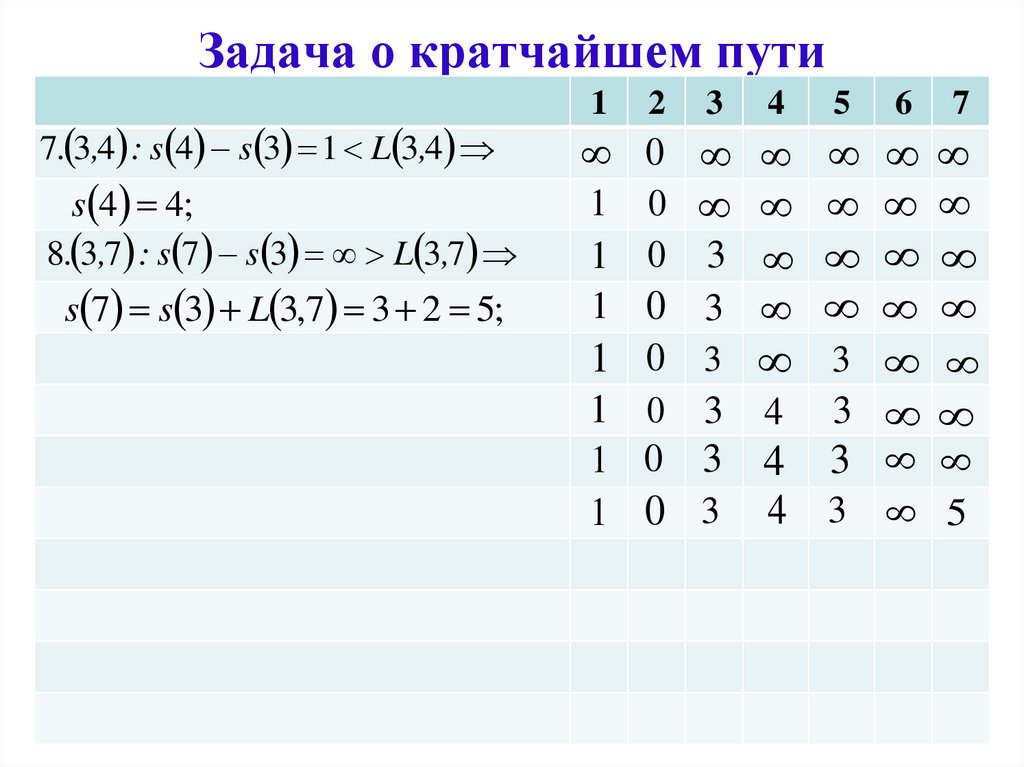
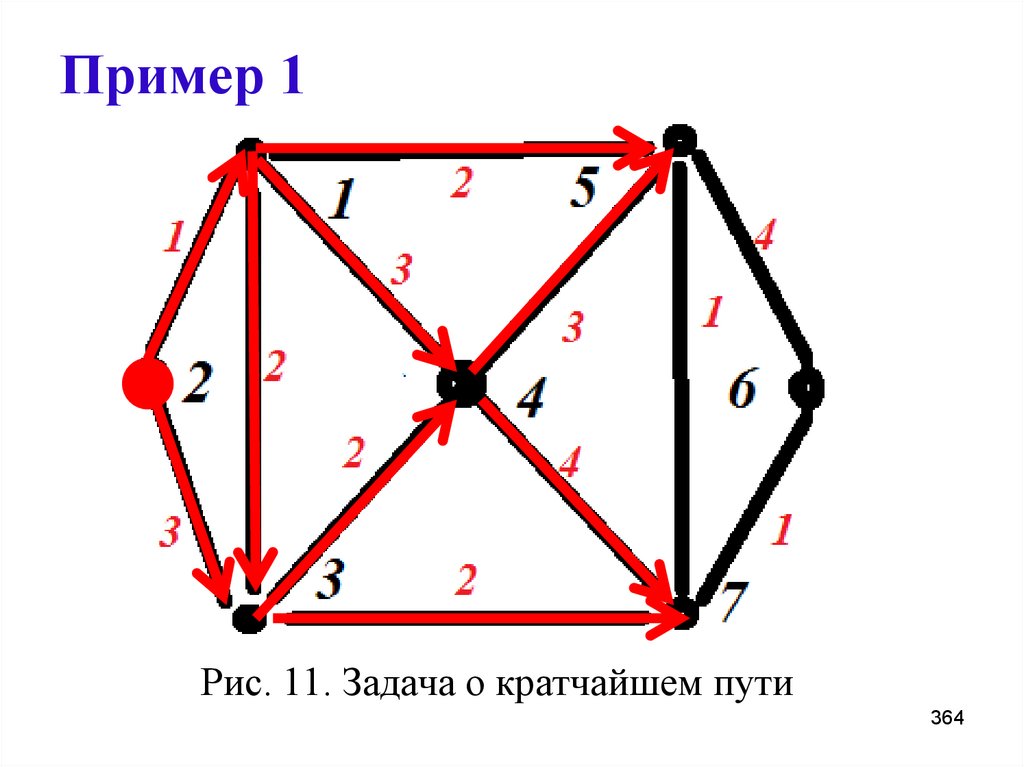


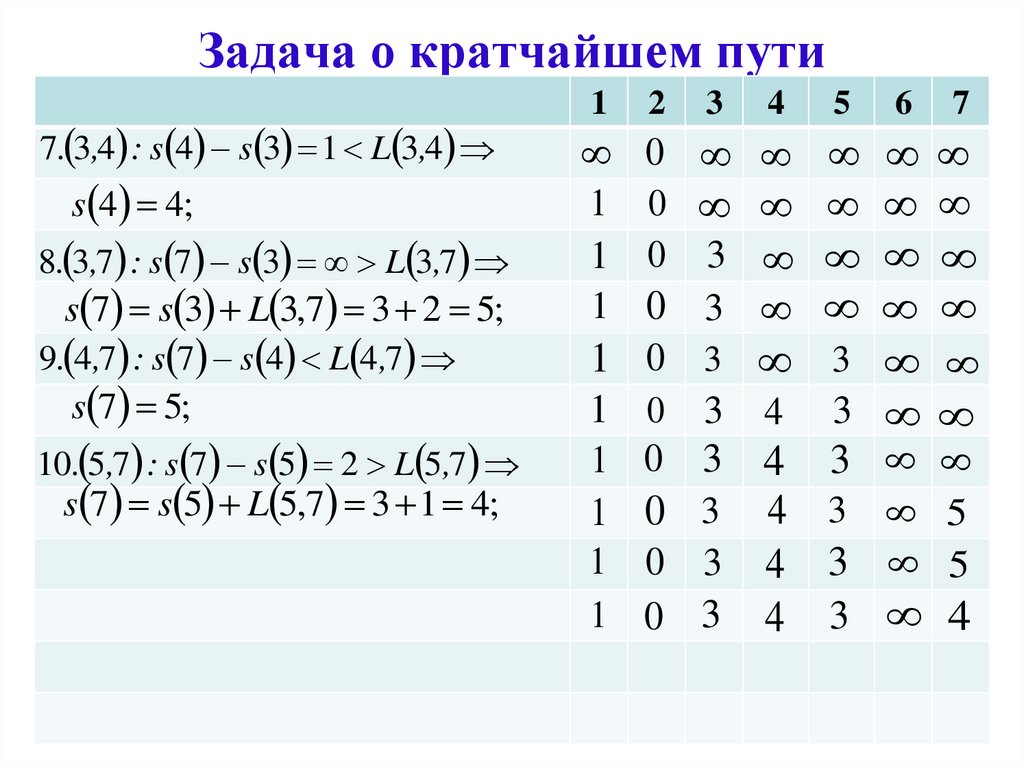
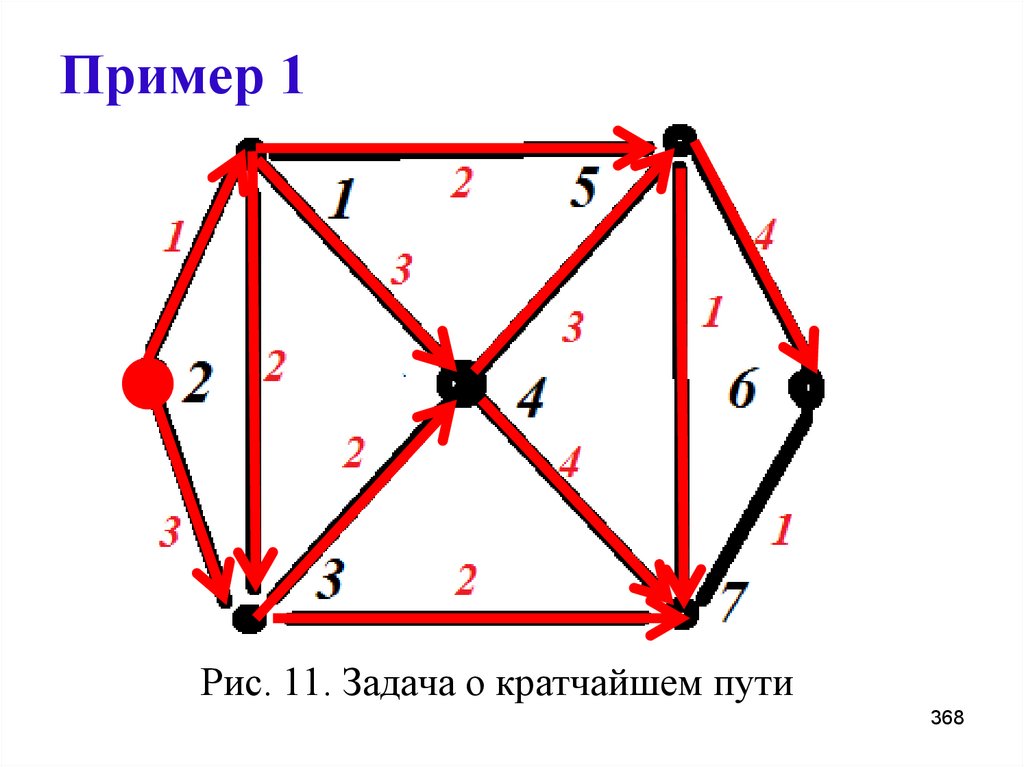


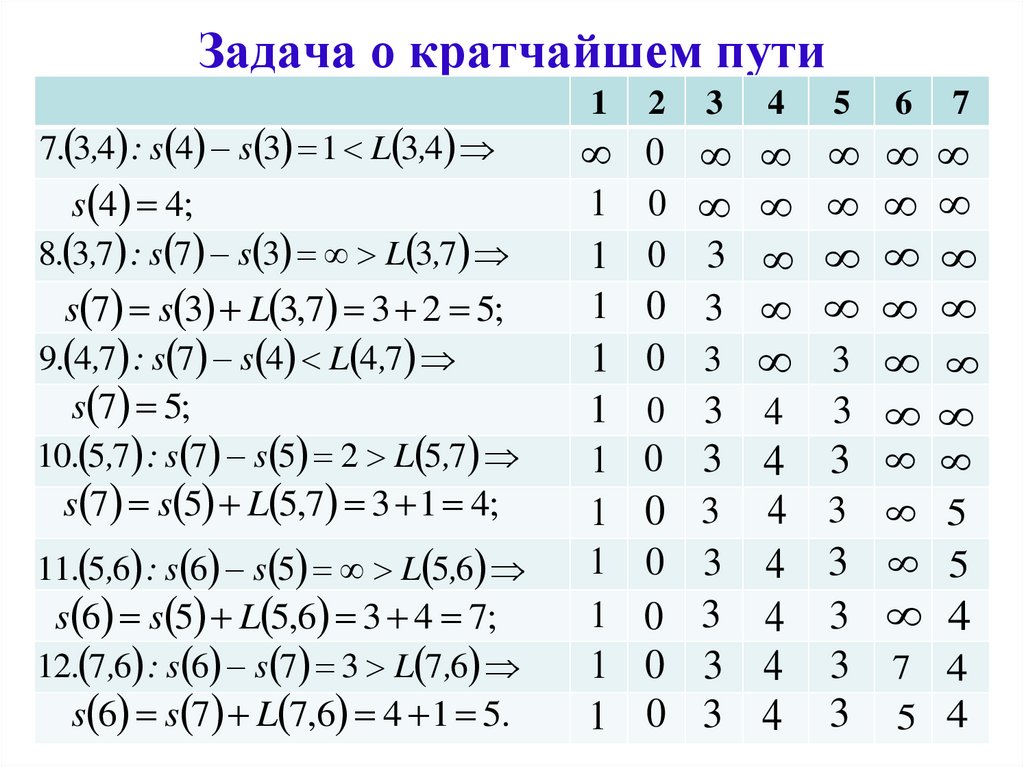




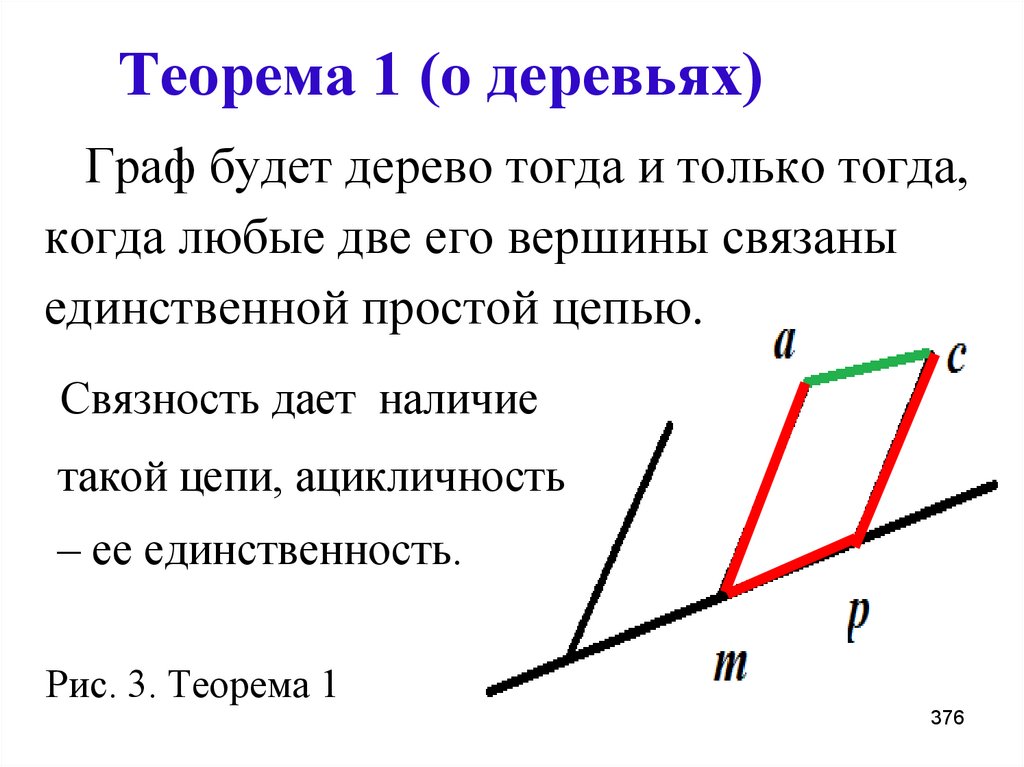
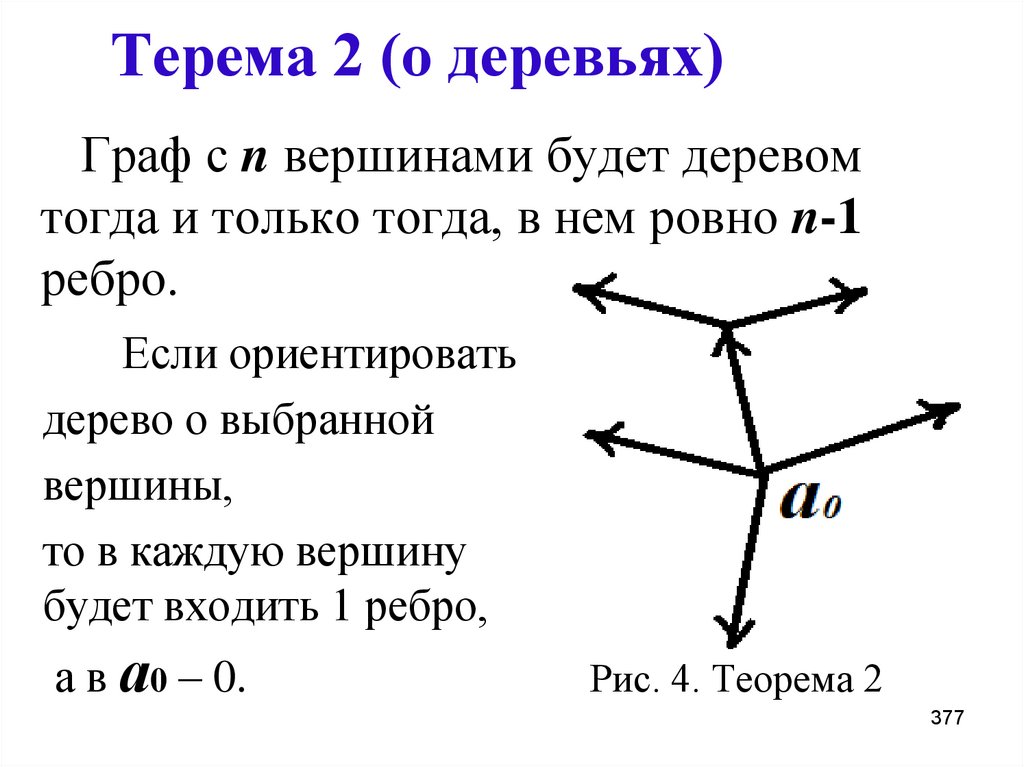
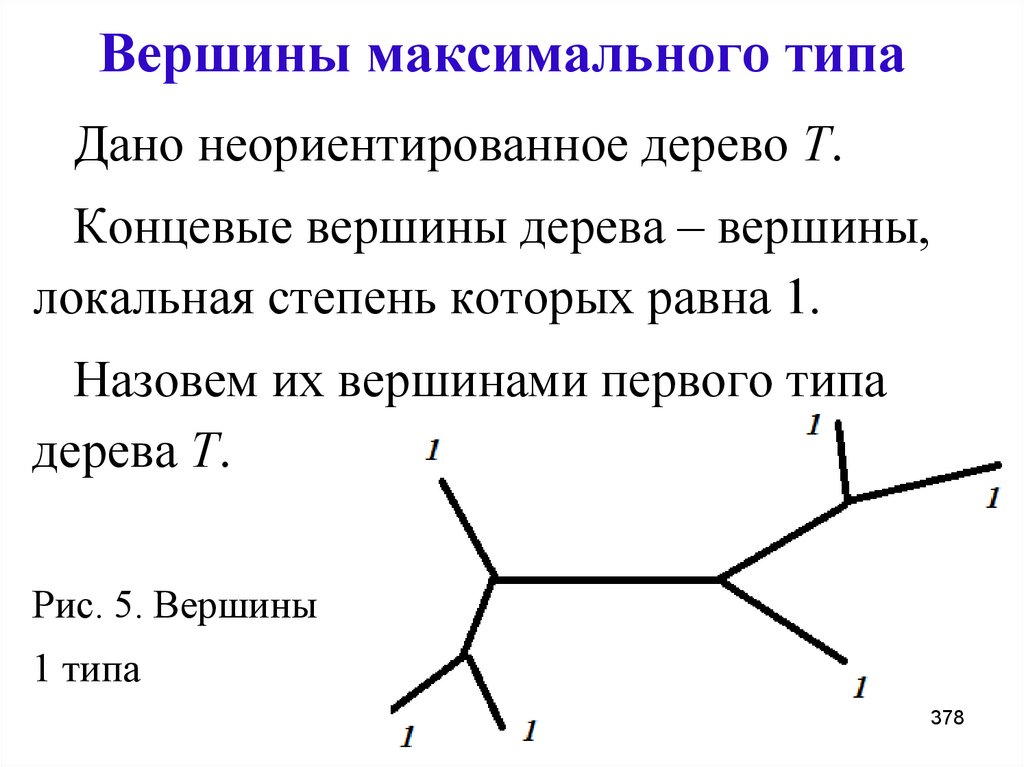
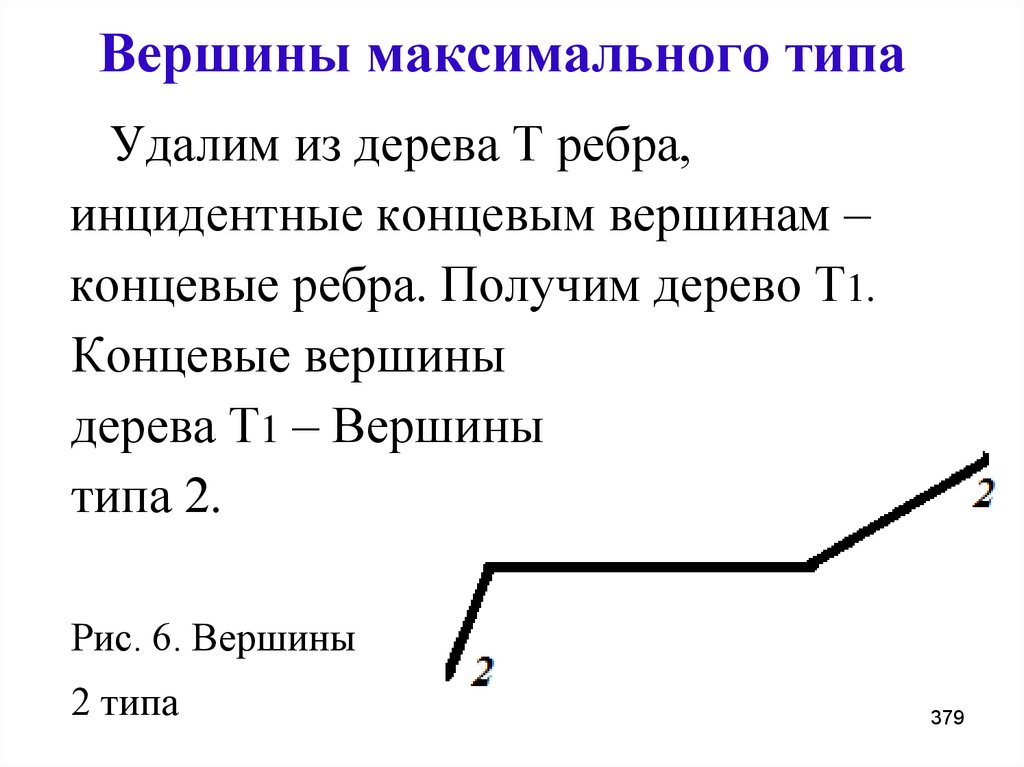









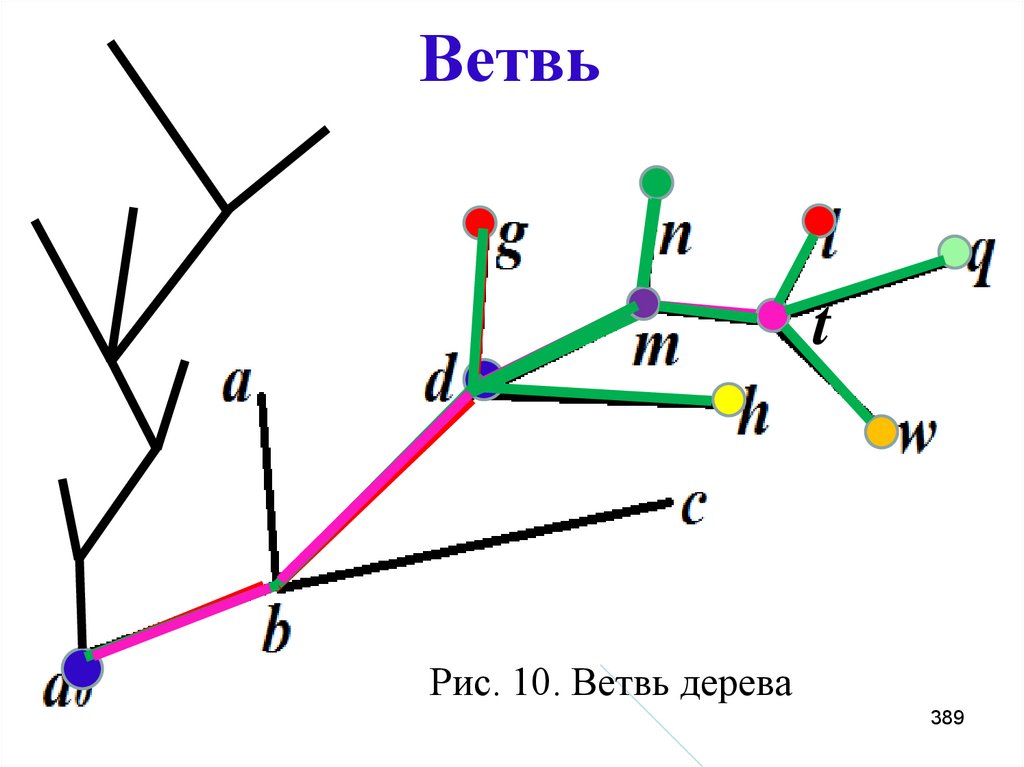


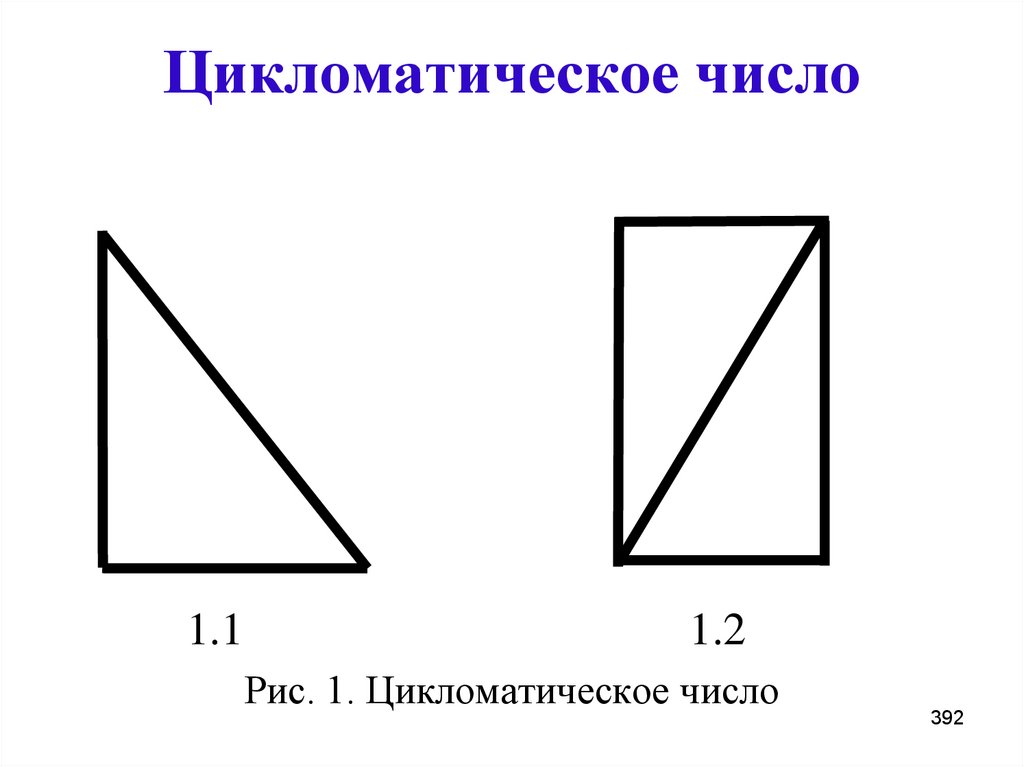

















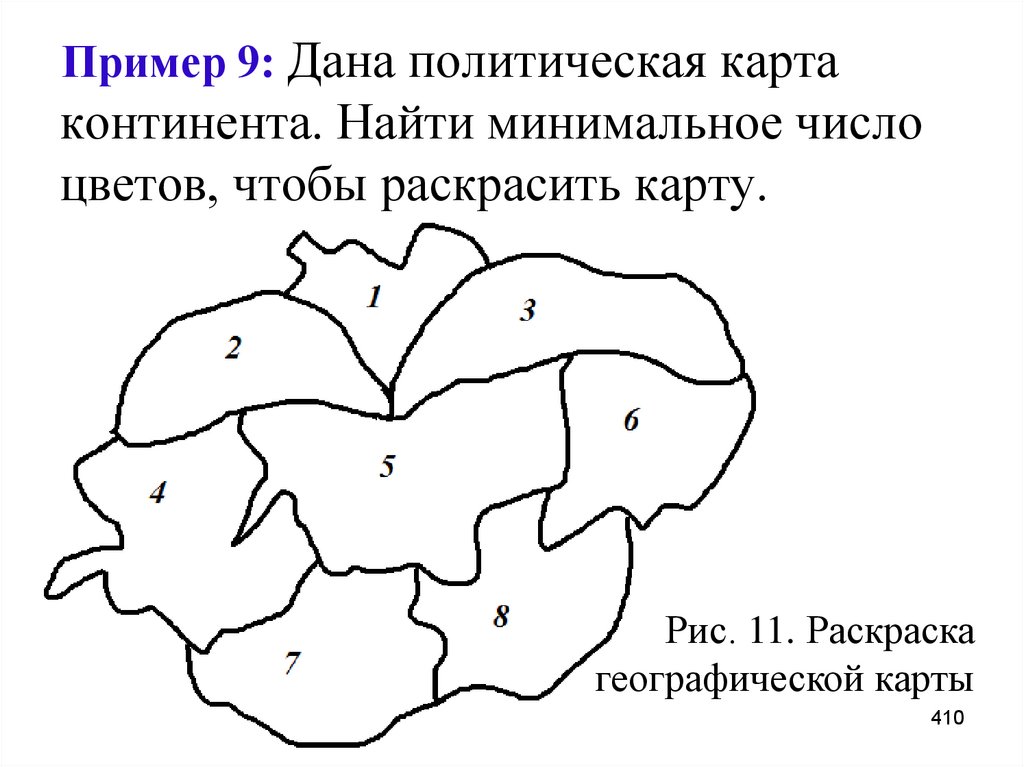



















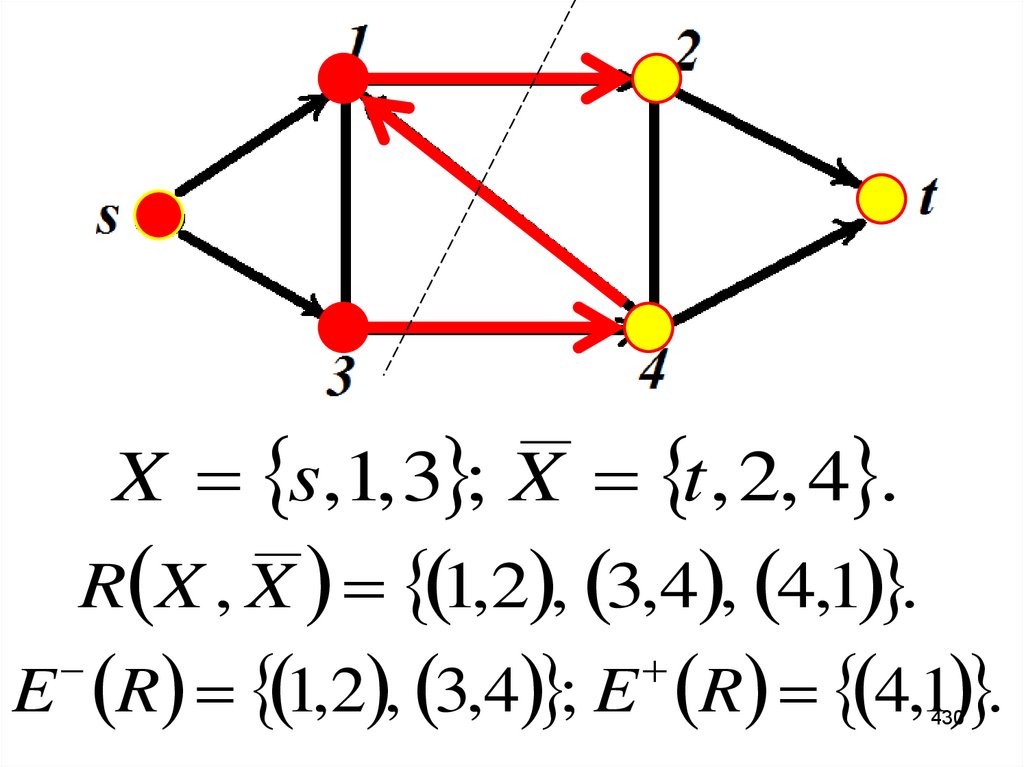
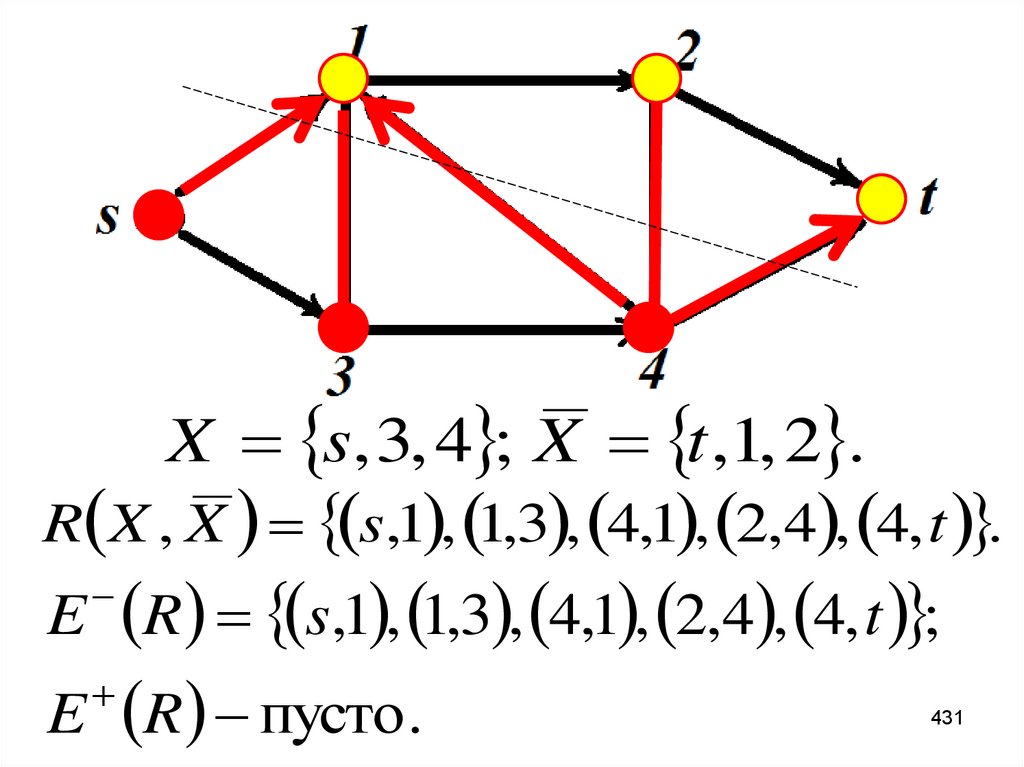
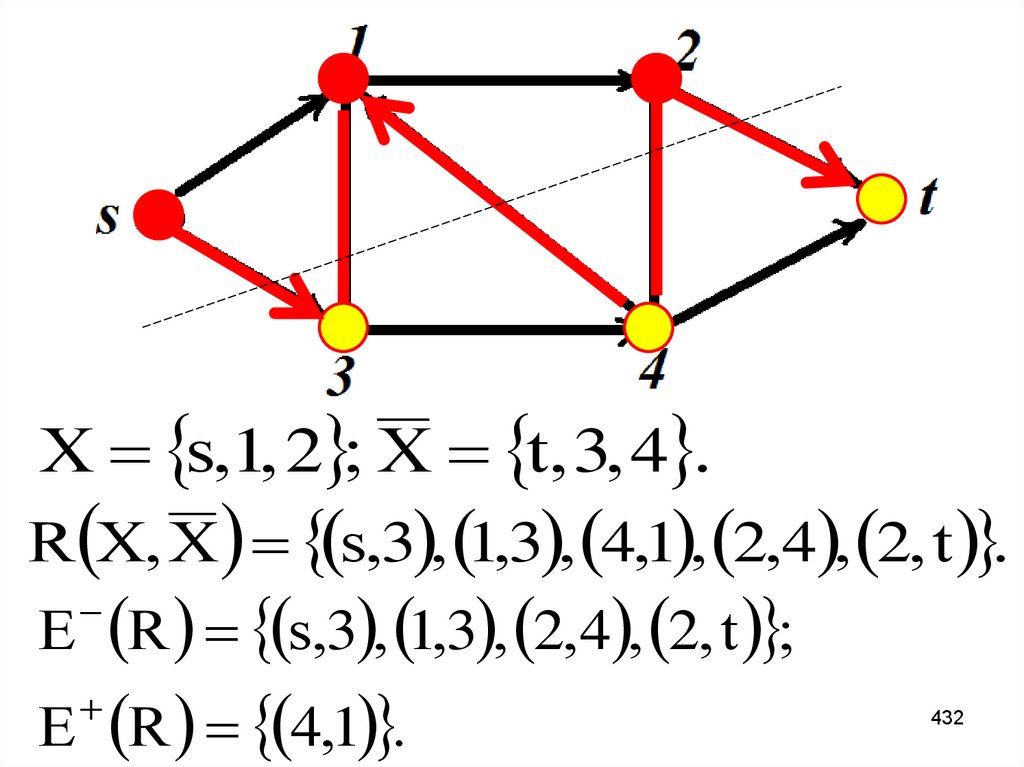










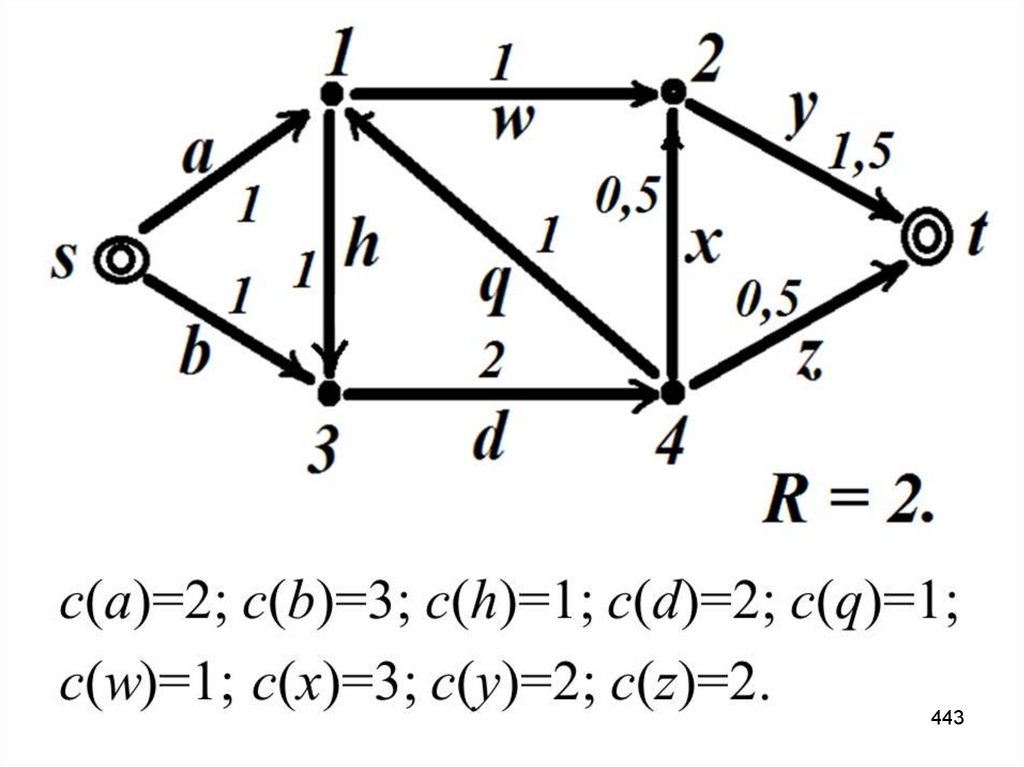
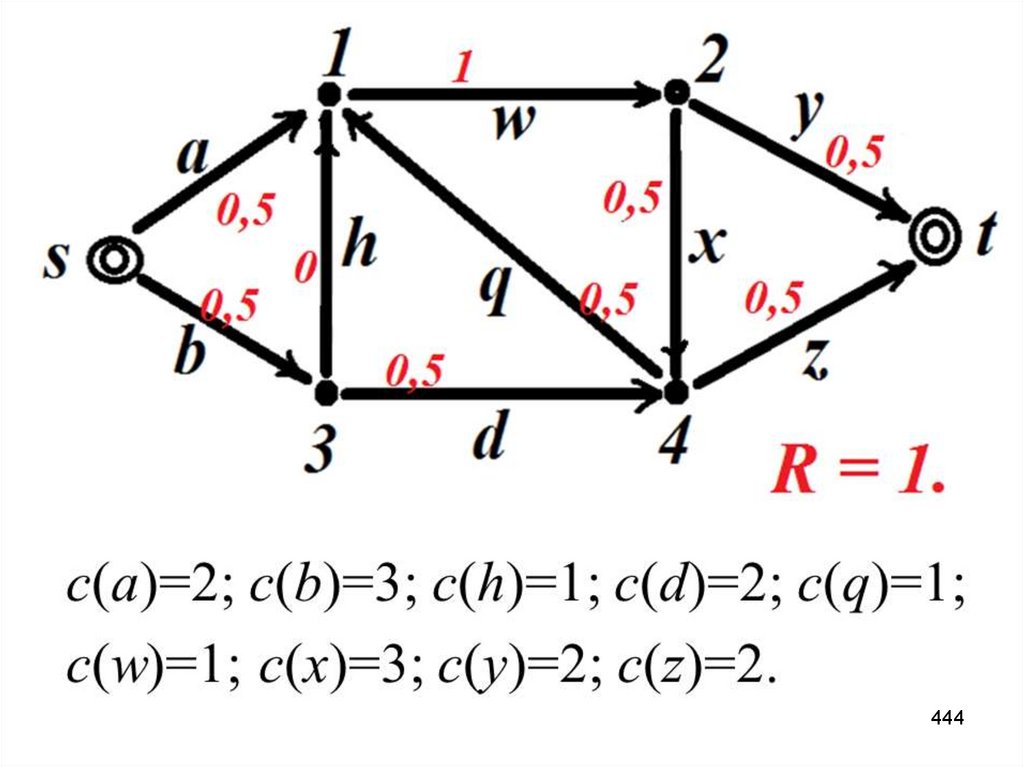
























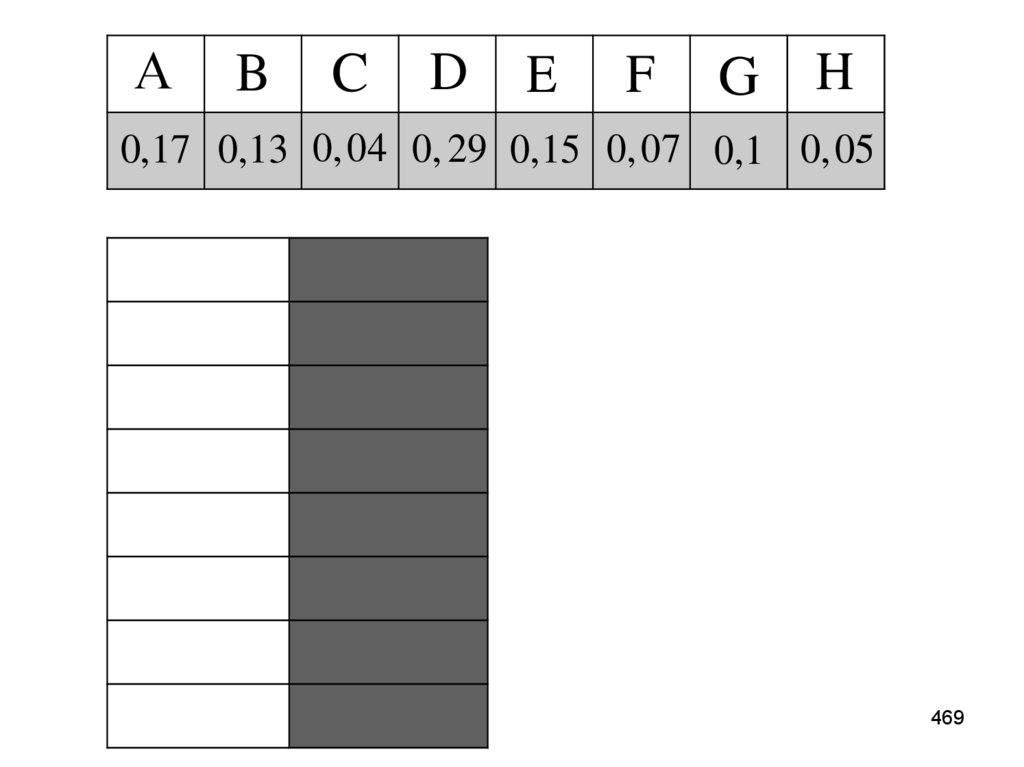



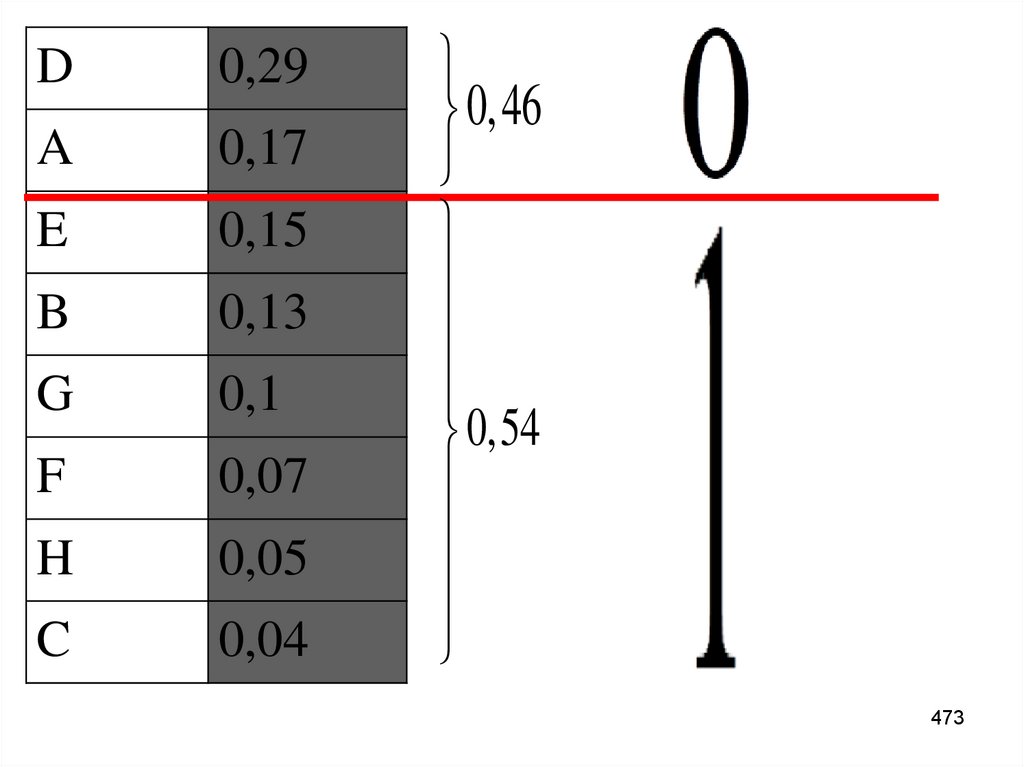

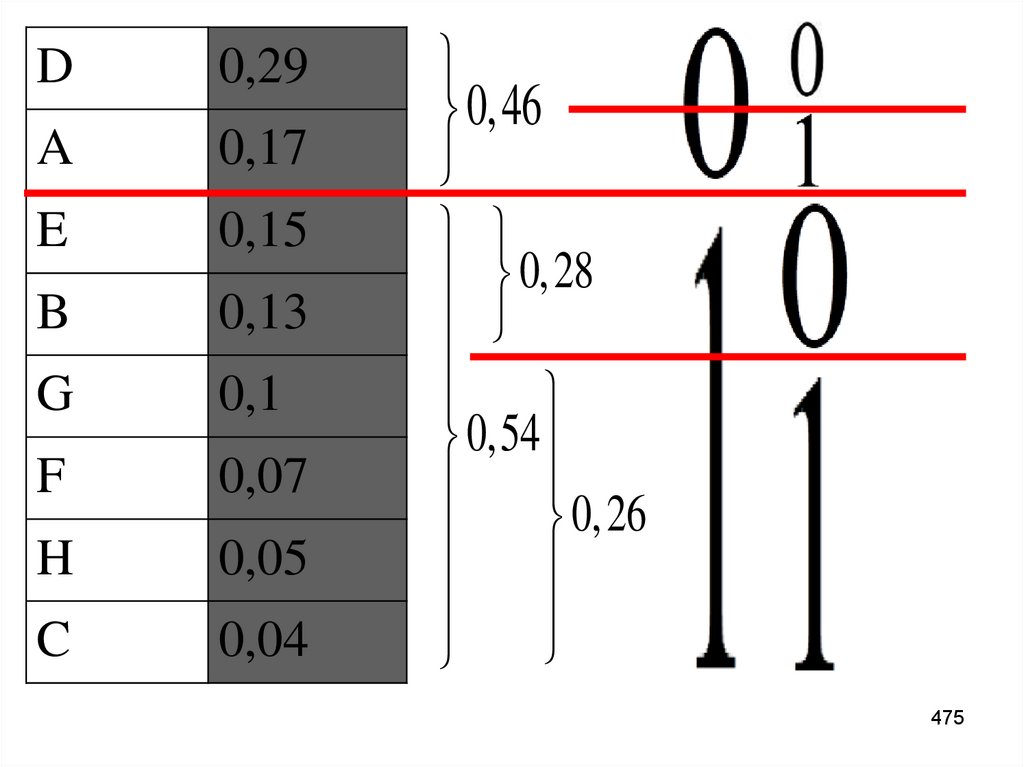
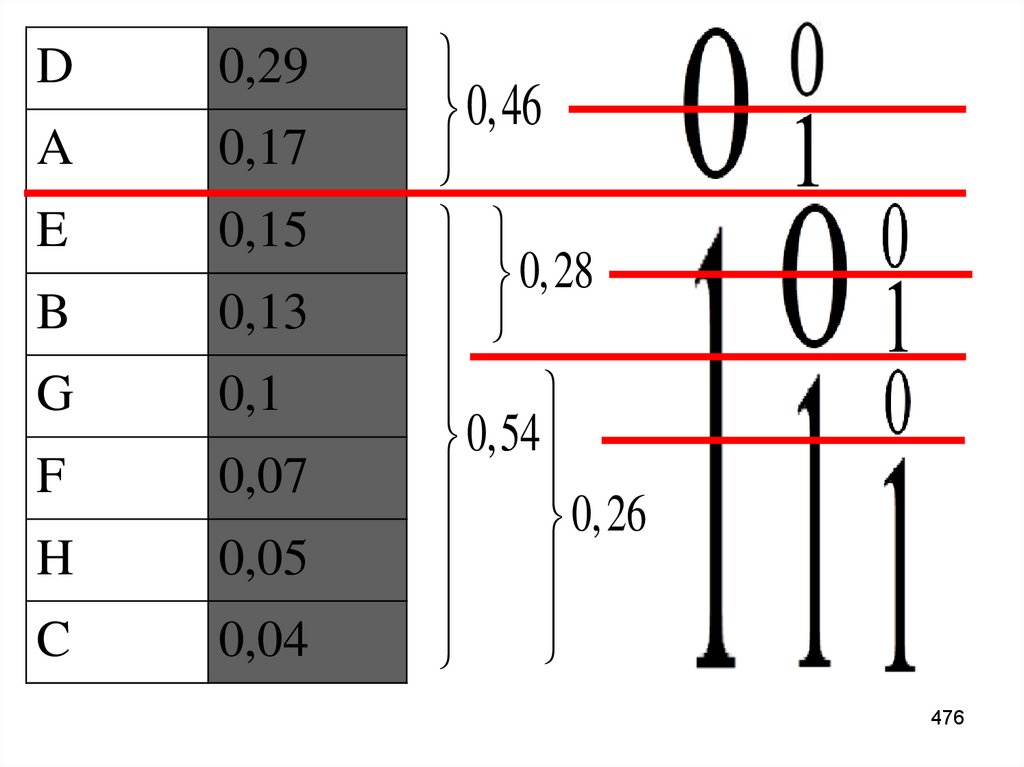

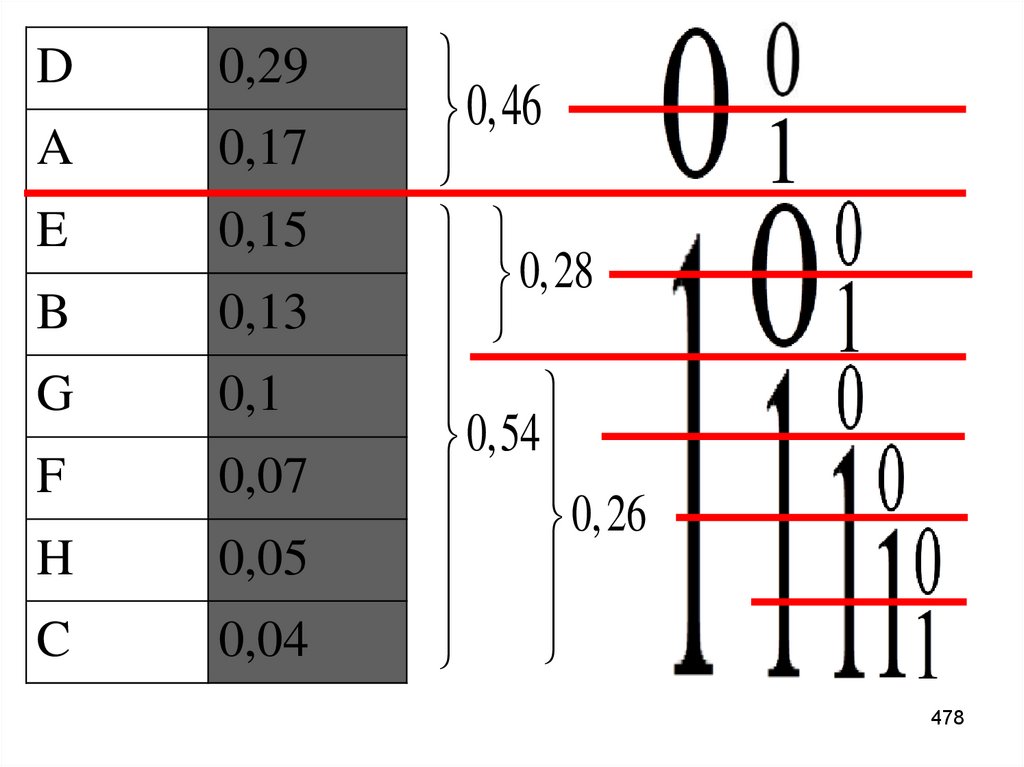














 mathematics
mathematics








