Similar presentations:
Дискретная математика. Графы. Основные определения, способы задания
1. Дискретная математика
Графы.Основные определения,
способы задания
2. Определение графа
• Пусть V – множество вершин,а Е – множество ребер.
• Графом G называется пара объектов
(V, E) между которыми задано
отношение инцидентности:
Г : е → (v, w),
где вершина v и ребро e инцидентны
друг другу, если вершина является для
этого ребра концевой точкой.
3. Определение графа
• Вершины v' и v" называютсясмежными, если существует ребро,
соединяющее их, т.е. они инцидентны
одному и тому же ребру.
• Ребра e' и e" называются смежными,
если они имеют, по крайней мере, одну
общую вершину (инцидентны одной
вершине).
4. Определение графа
• Граф, содержащий направленныеребра (дуги) с началом v' и концом v" ,
называется ориентированным
графом (орграфом). Для орграфа
v ,v v ,v
• Граф, содержащий ненаправленные
ребра с конами v' и v" , называется
неориентированным графом
(нрграфом). Для нрграфа
v ,v v ,v
5. Определение графа
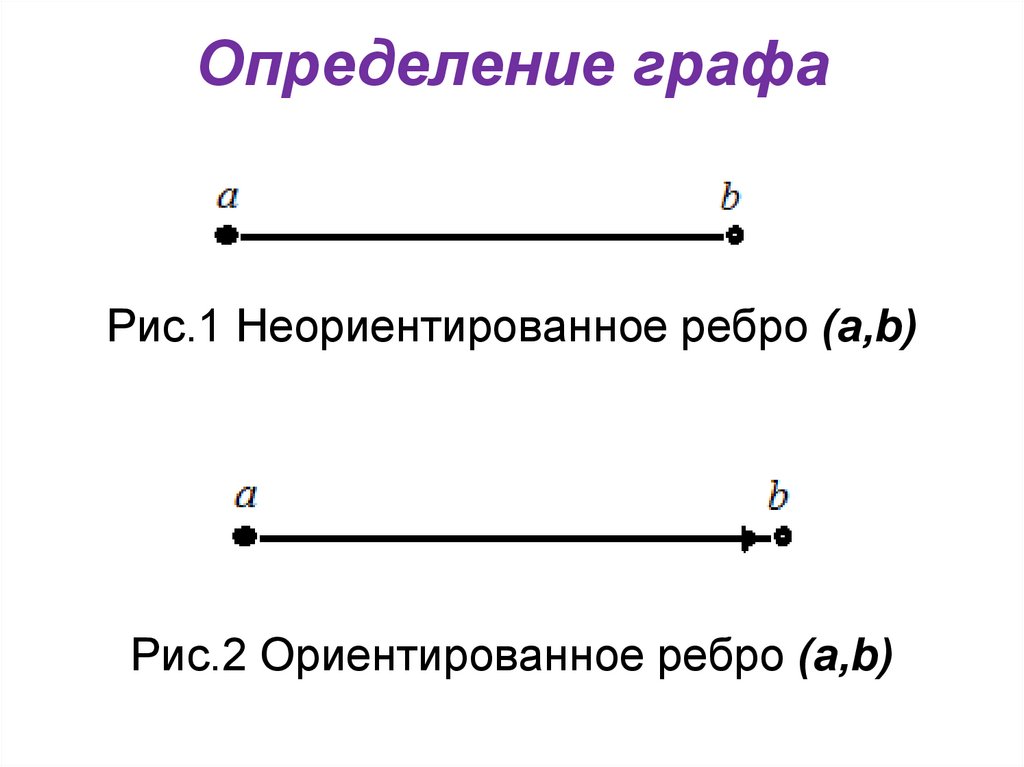
Рис.1 Неориентированное ребро (a,b)Рис.2 Ориентированное ребро (a,b)
6. Определение графа
• Ребро, концевые вершины которогосовпадают, называется петлей.
Рис.3.
Неориентированная
петля
Рис.4. Ориентированная
петля
7. Определение графа
• Ребра (дуги), имеющие одинаковыеначало и конец, называются
параллельными или кратными.
Рис.5 Кратные неориентированные ребра
8. Определение графа
Рис. 6. Кратные ориентированные ребра9. Определение графа
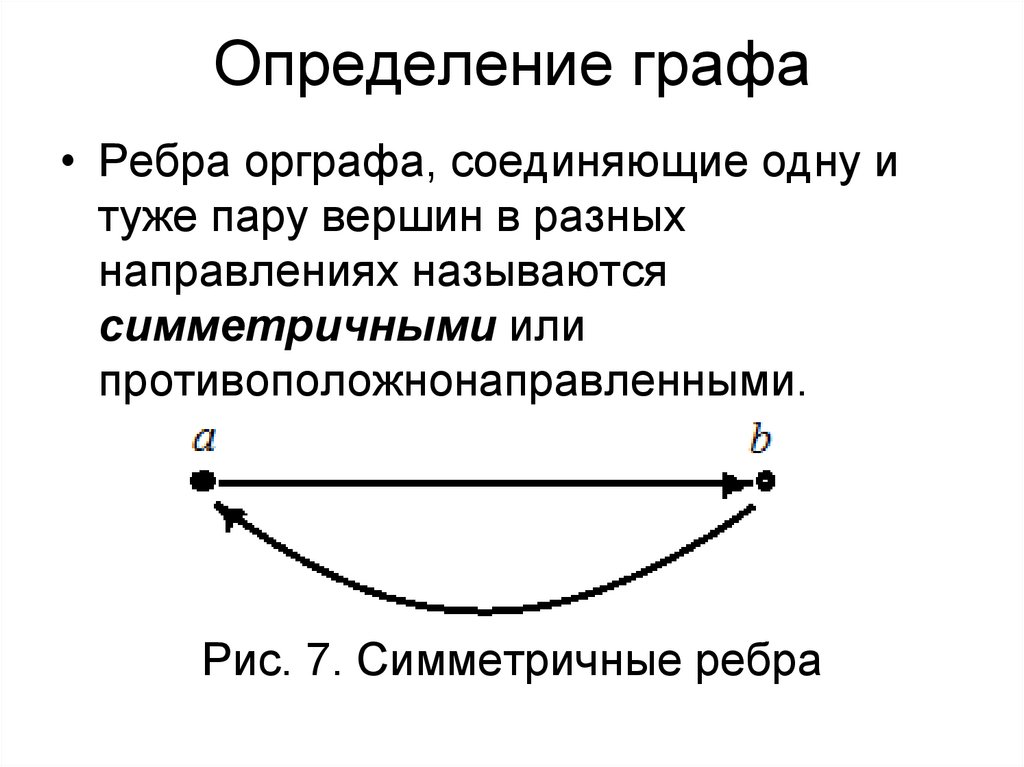
• Ребра орграфа, соединяющие одну итуже пару вершин в разных
направлениях называются
симметричными или
противоположнонаправленными.
Рис. 7. Симметричные ребра
10. Определение графа
• Граф называется конечным, еслимножество его элементов (вершин и
ребер) конечно.
Рис. 8. Конечный граф
11. Определение графа
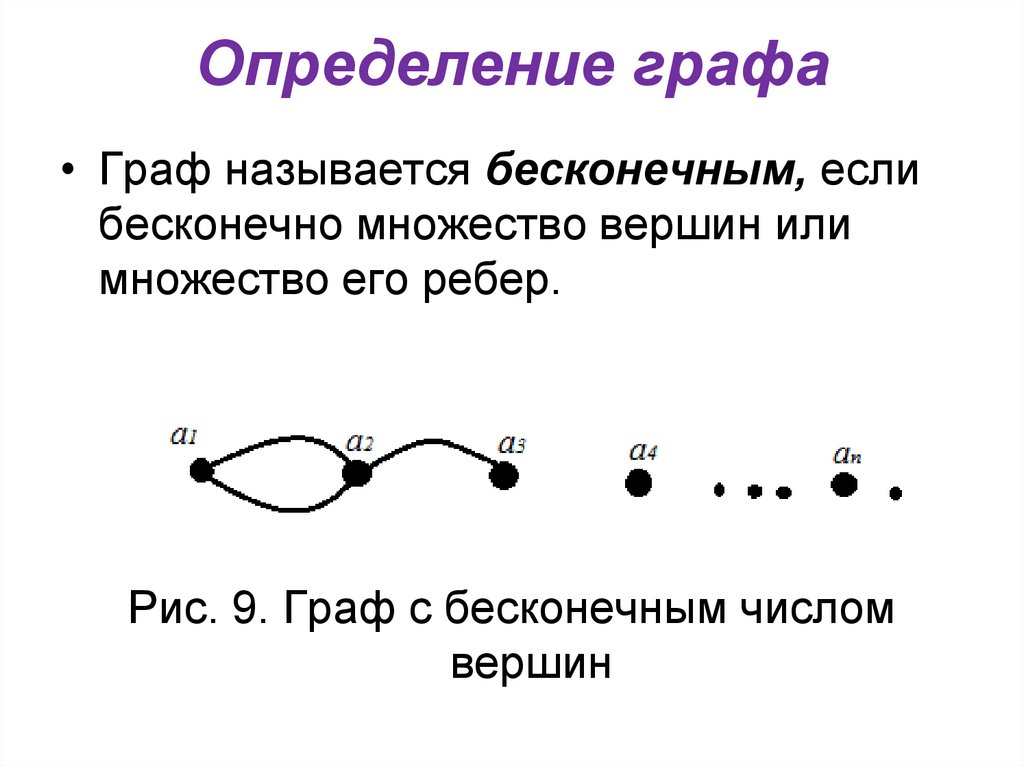
• Граф называется бесконечным, еслибесконечно множество вершин или
множество его ребер.
Рис. 9. Граф с бесконечным числом
вершин
12. Определение графа
Рис. 10. Граф с бесконечным числом ребер13. Определение графа
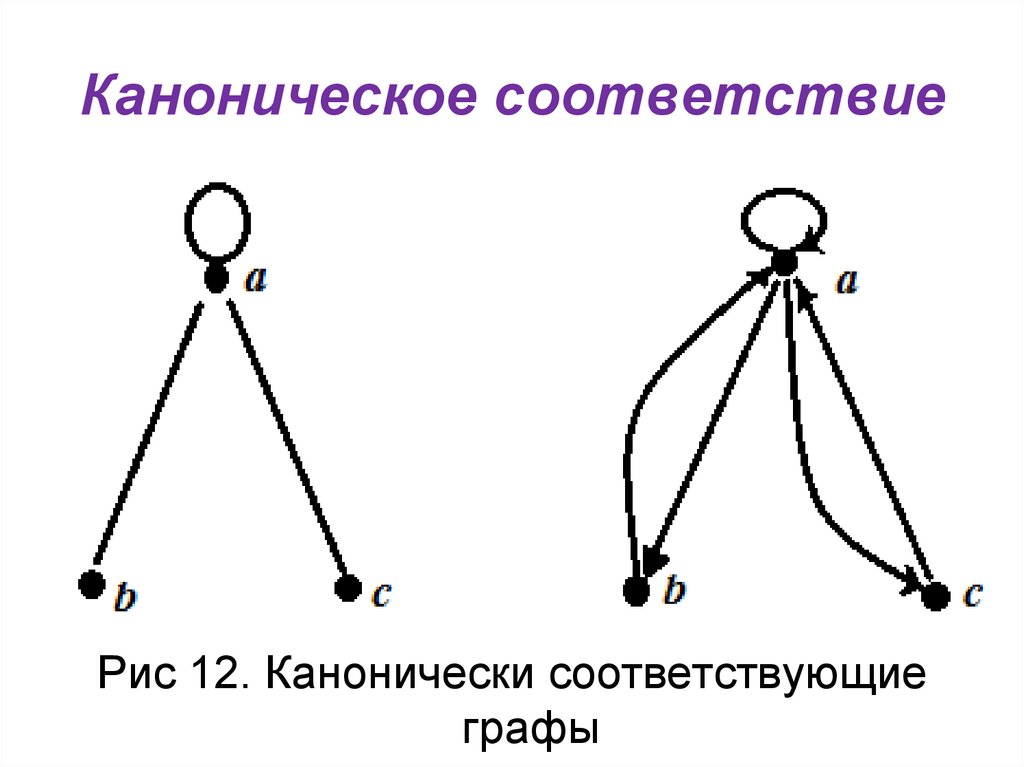
Рис. 11. Бесконечный граф14. Каноническое соответствие
• Каждому неориентированному графуканонически соответствует
ориентированный граф с тем же
множеством вершин, в котором каждое
ребро заменено двумя
ориентированными ребрами,
инцидентными тем же вершинам и
имеющим противоположные
направления.
15. Каноническое соответствие
Рис 12. Канонически соответствующиеграфы
16. Способы задания
Задать граф – значит описать множестваего вершин и ребер, а также отношение
инцидентности.
Пусть вершины графа v 1, v 2 , ,v n
;
e1, e 2 , , e m ребра графа G.
Граф задают:
1) Матрицей инцидентности
2) Матрицу смежности
3) Списком ребер
3) Рисунком
17. Матрица инцидентности
матрица инцидентности ijразмера m n (строкам
соответствуют ребра, столбцам –
вершины графа), в которой
для нграфа
1, ребро e i инциндентно вершине v j ;
ij
0 в противном случае .
18. Матрица инцидентности
• для орграфа1, если вершина v j начало ребра e i ;
1, если вершина v j конец ребра e i ;
ij
2, если e i петля вокруг вершины v j ;
0 в остальных случаях .
19. Пример: матрица инцидентности н-графа
ab c d
1 1
2 1
0 0 0
3 1
0 1 0
0 1 0
4 1 1 0 0
5 0 1 1 0
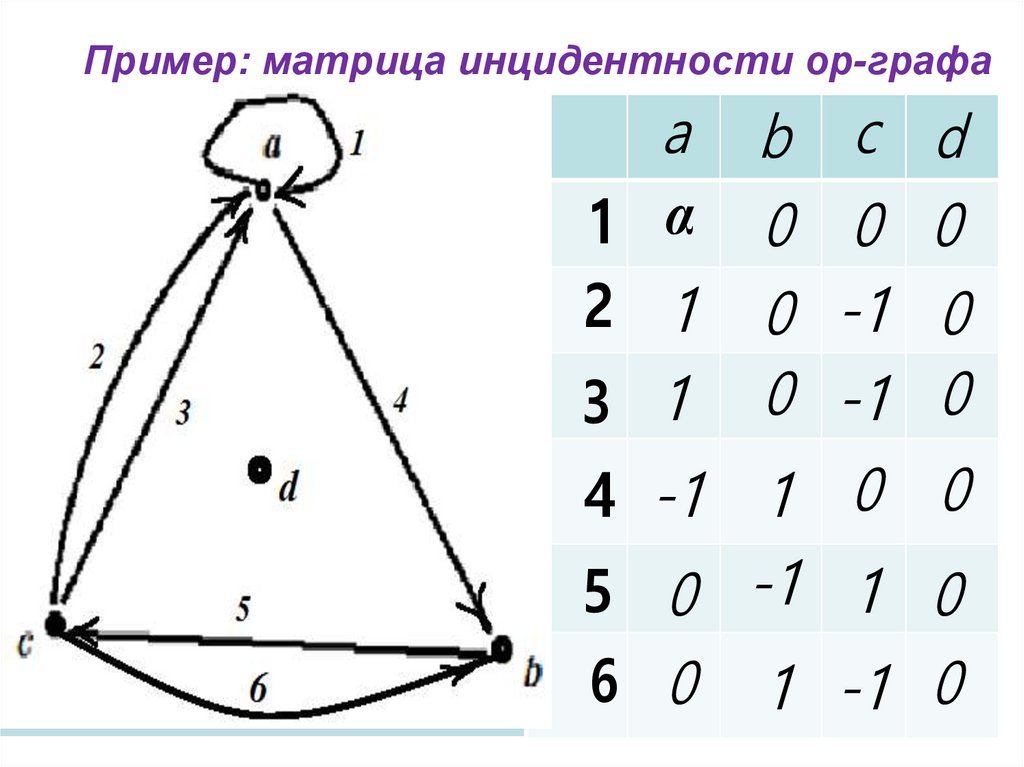
20. Пример: матрица инцидентности ор-графа
a b c d1 α 0 0 0
2 1 0 -1 0
3 1 0 -1 0
4 -1 1 0 0
5 0 -1 1 0
6 0 1 -1 0
21. Матрица смежности
Матрица смежностиij
размера n n , столбцам и строкам
которой соответствуют вершины графа.
Для нграфа ij равно количеству ребер,
связывающих i-ю и j-ю вершины,
для орграфа ij равно количеству ребер
выходящих из i-й и входящих в j-ю
вершину.
22. Матрица смежности
• Матрица смежности нграфа всегдасимметрична.
• Матрица смежности орграфа в общем
случае не симметрична.
• Она симметрична, если данному
орграфу есть канонически
соответсвующий нграф.
23. Пример: матрица смежности н-графа
ab c d
a
1
1 2 0
b
1 0
c
2
1 0 0
d
0
0
1 0
0 0
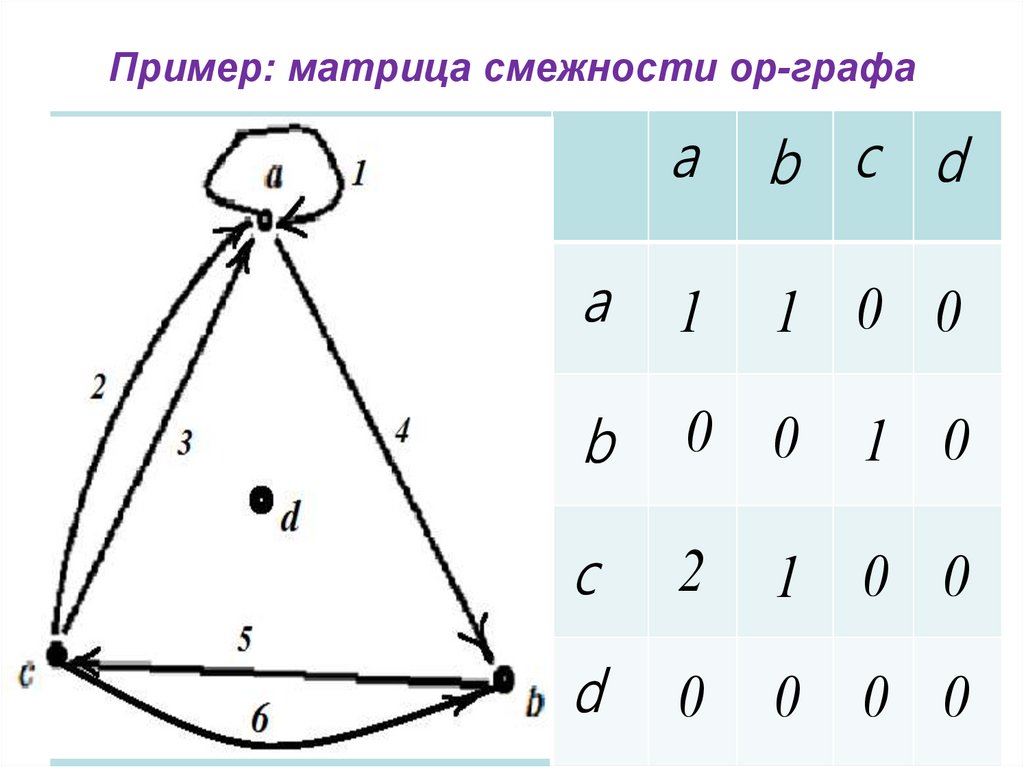
24. Пример: матрица смежности ор-графа
ab c d
a
1
1 0 0
b
0 0
c
2
1 0 0
d
0
0
1 0
0 0
25. Список ребер
• Списком ребер можно задать граф безкратных ребер.
• Ребро представляется парой вершин,
инцидентных ему, например е =(v, w).
• Для н-графа порядок вершин в строке
произволен, для ор-графа первым стоит
номер вершины–начала ребра.
26. Рисунок
• Рисунок или геометрическаяинтерпретация появляется, если
сопоставить вершинам точки плоскости,
ребрам – линии на плоскости, причем,
линия соединяет только те точки,
которые соответствуют вершинам,
инцидентным данной линии-ребру.
• Граф для которого возможна
геометрическая интерпретация на
плоскости, называется планарным.
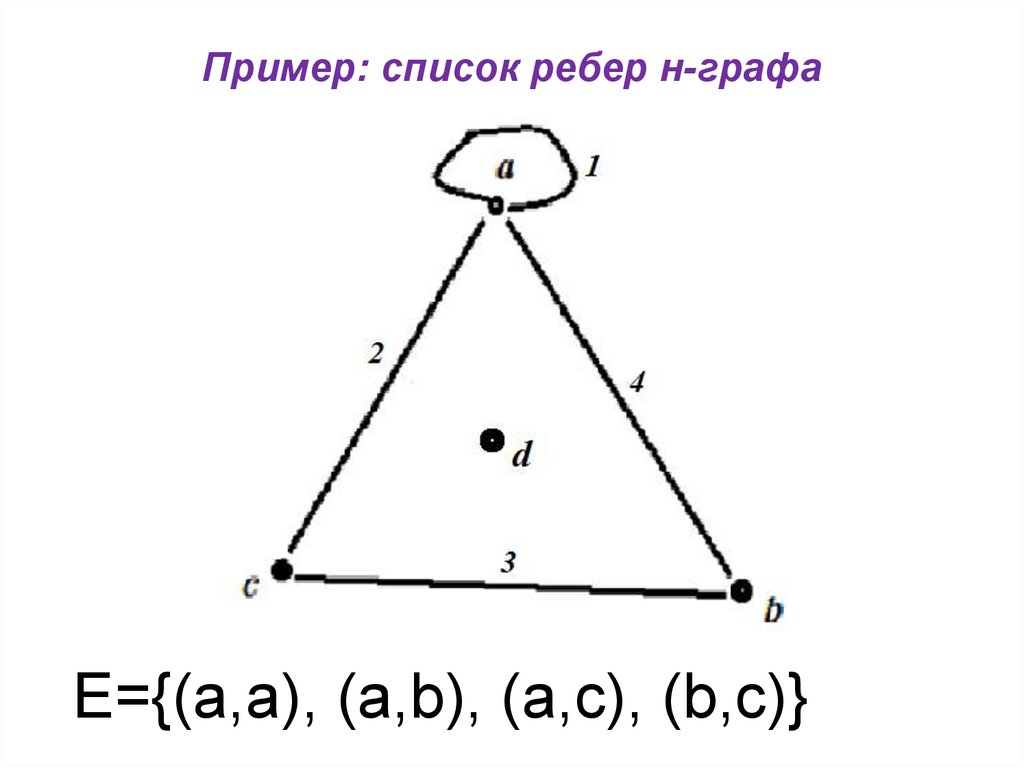
27. Пример: список ребер н-графа
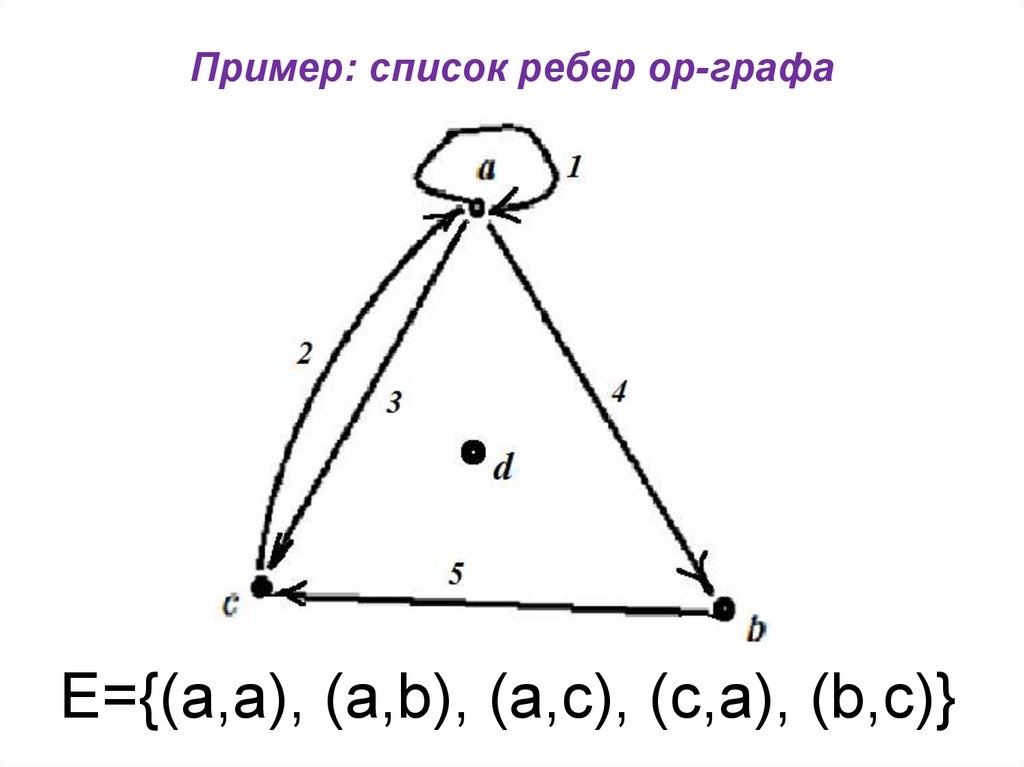
E={(a,a), (a,b), (a,c), (b,c)}28. Пример: список ребер ор-графа
E={(a,a), (a,b), (a,c), (с,a), (b,c)}29. Планарные графы
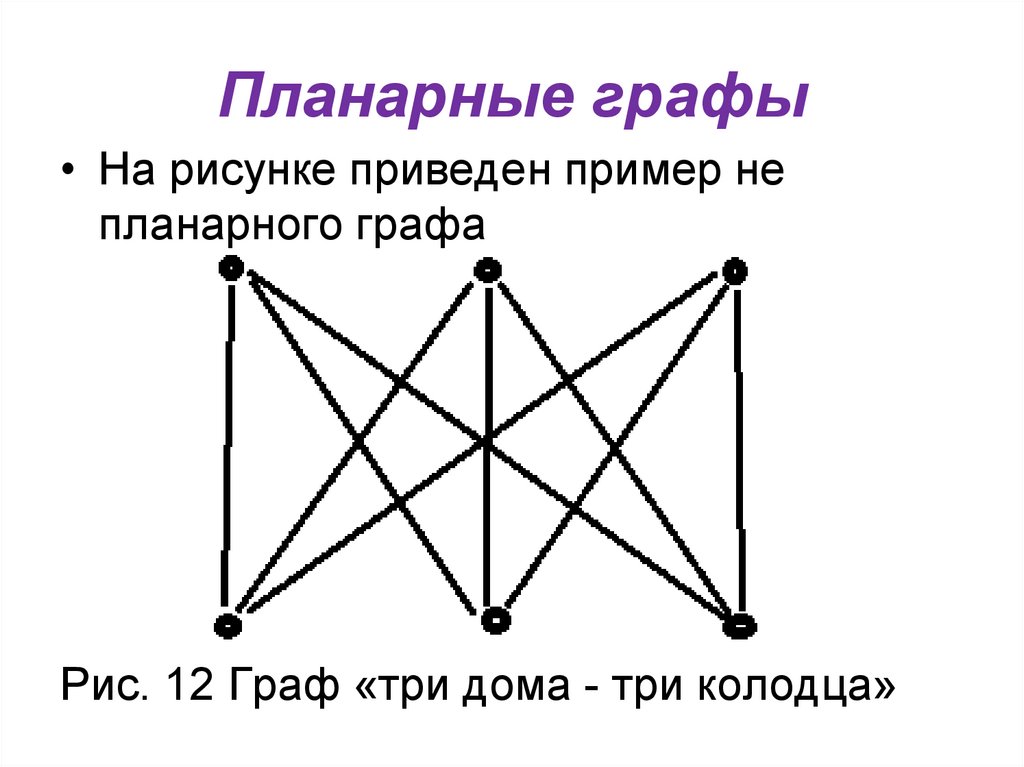
• На рисунке приведен пример непланарного графа
Рис. 12 Граф «три дома - три колодца»
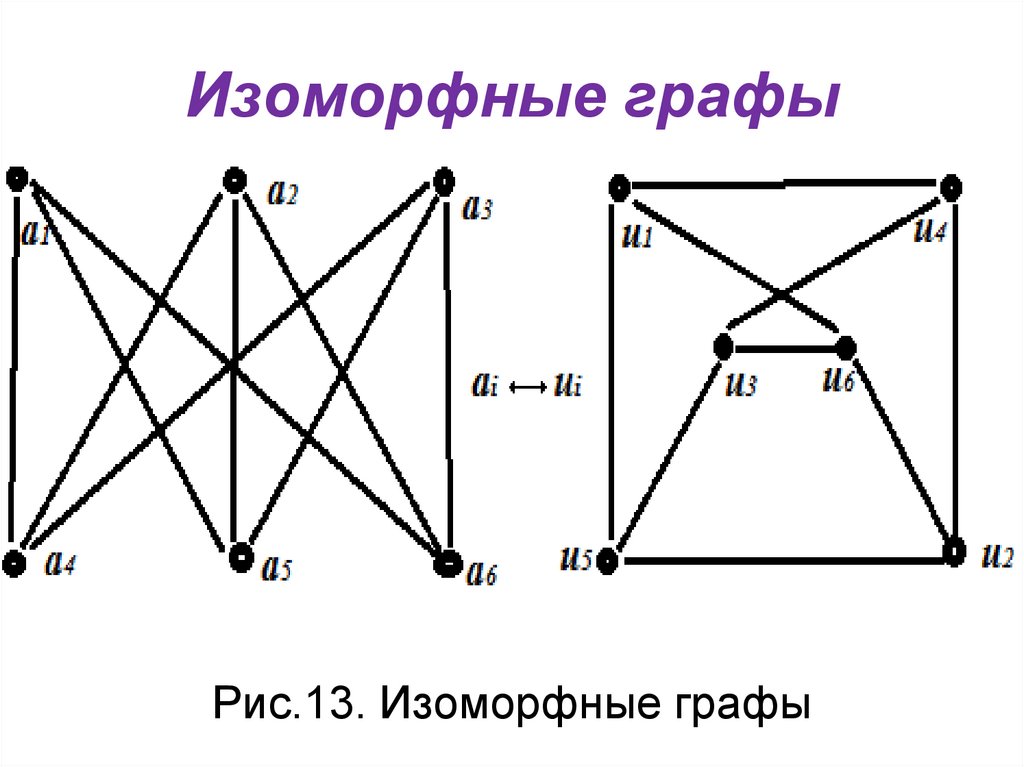
30. Изоморфные графы
• Графы, отличающиеся тольконумерацией вершин,
называются изоморфными.





















 mathematics
mathematics