Similar presentations:
Основные понятия и определения графа и его элементов
1.
ОСНОВНЫЕПОНЯТИЯ И
ОПРЕДЕЛЕНИЯ
И ЕГО
ЭЛЕМЕНТОВ
2.
ГРАФОМG
=
(V,
X)
НАЗЫВАЕТСЯ ПАРА ДВУХ
КОНЕЧНЫХ
МНОЖЕСТВ:
МНОЖЕСТВО
ТОЧЕК
И
МНОЖЕСТВО
ЛИНИЙ,
СОЕДИНЯЮЩИХ НЕКОТОРЫЕ
ПАРЫ ТОЧЕК.
ВПЕРВЫЕ
ПОНЯТИЕ
«ГРАФ»
ВВЕЛ
В
1936
г.
ВЕНГЕРСКИЙ
МАТЕМАТИК
ДЕННИ КЁНИГ. НО ПЕРВАЯ
РАБОТА ПО ТЕОРИИ ГРАФОВ
ПРИНАДЛЕЖАЛА
ПЕРУ
3.
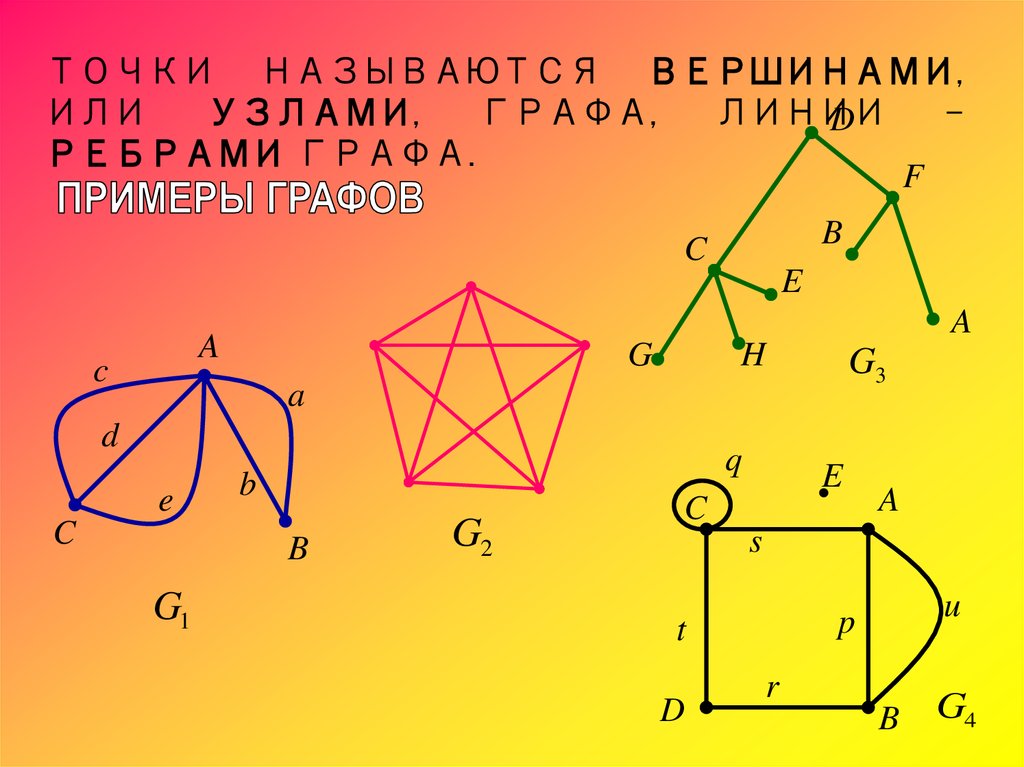
ТОЧКИ НАЗЫВАЮТСЯ ВЕРШИНАМИ,ИЛИ
УЗЛАМИ,
ГРАФА,
ЛИНИИ
–
D
РЕБРАМИ ГРАФА.
F
B
C
E
A
A
c
G
H
G3
a
d
e
C
q
b
B
G1
G2
E
C
A
s
t
D
u
p
r
B
G4
4.
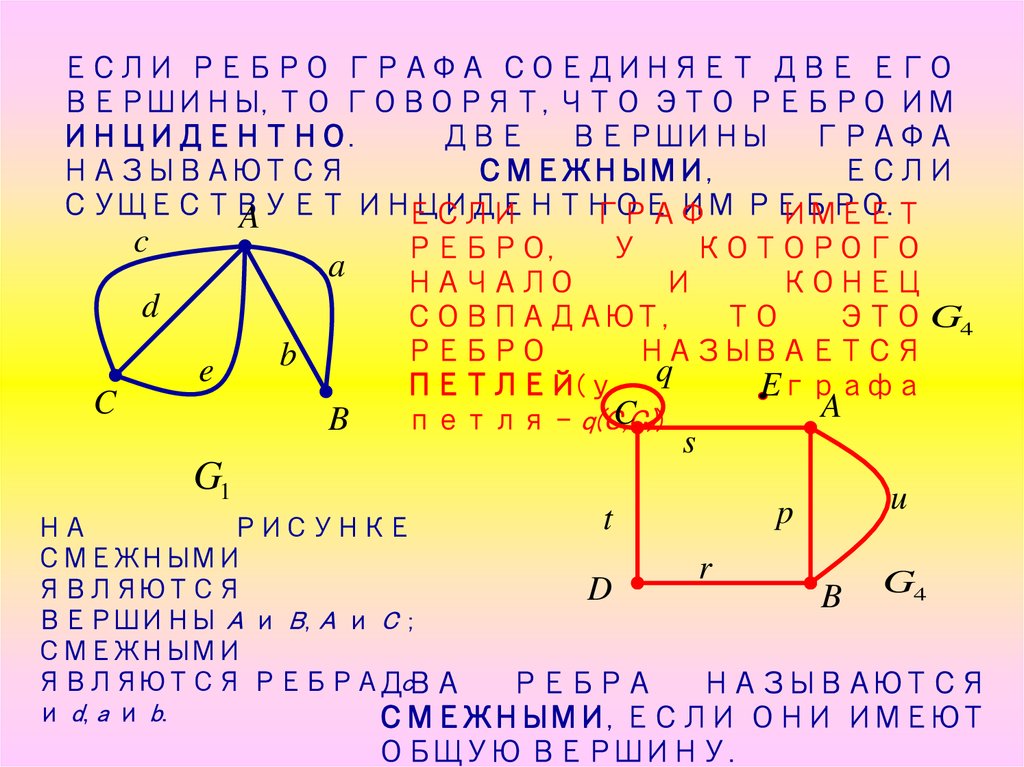
ЕСЛИ РЕБРО ГРАФА СОЕДИНЯЕТ ДВЕ ЕГОВЕРШИНЫ, ТО ГОВОРЯТ, ЧТО ЭТО РЕБРО ИМ
ИНЦИДЕНТНО.
ДВЕ ВЕРШИНЫ
ГРАФА
НАЗЫВАЮТСЯ
СМЕЖНЫМИ,
ЕСЛИ
СУЩЕСТВУЕТ
ИНЦИДЕНТНОЕ
ИМ РЕБРО.
ЕСЛИ
ГРАФ
ИМЕЕТ
A
c
РЕБРО,
У
КОТОРОГО
a
НАЧАЛО
И
КОНЕЦ
d
СОВПАДАЮТ,
ТО
ЭТО G4
РЕБРО
НАЗЫВАЕТСЯ
b
e
ПЕТЛЕЙ(у q
Eграфа
C
A
C ).
петля – q(C,C)
B
s
G1
p
u
t
НА
РИСУНКЕ
СМЕЖНЫМИ
r
ЯВЛЯЮТСЯ
D
B G4
ВЕРШИНЫ A и B, A и C ;
СМЕЖНЫМИ
ЯВЛЯЮТСЯ РЕБРАДВА
c
РЕБРА
НАЗЫВАЮТСЯ
и d, a и b.
СМЕЖНЫМИ, ЕСЛИ ОНИ ИМЕЮТ
ОБЩУЮ ВЕРШИНУ.
5.
qA
c
a
d
e
C
b
E
C
КРАТНЫЕ
РЕБРА
s
G1
ЧИСЛО
РЕБЕР,
ИНЦИДЕНТНЫХ
ВЕРШИНЕ
A
,
НАЗЫВАЕТСЯ
СТЕПЕНЬЮ
ЭТОЙ
ВЕРШИНЫ
И
ОБОЗНАЧАЕТСЯ deg(A).
ЕСЛИ ВЕРШИНЕ
ИНЦИДЕНТНА ПЕТЛЯ, ОНА
D
u
p
t
B
A
r
B
deg(A)= 3;
deg(B) = 3;
deg(C) = 4;
deg(D) = 2;
deg(E) = 0.
G4
6.
qE
deg(E) = 0
A
C
s
E–
u
p
t
r
D
B
ИЗОЛИРОВАН
НАЯ ВЕРШИНА
G4
D
F
B
C
E
G
H
G3
deg(G) = 1
deg(H) = 1
deg(E) = 1
deg(B) = 1
A
deg(A) = 1
G, H, E, B, A
ВИСЯЧ
ИЕ
ВЕРШИН
Ы
7.
ВГРАФЕ
G(V,
X)
СУММА
СТЕПЕНЕЙ
ВСЕХ
ЕГО
ВЕРШИН – ЧИСЛО ЧЕТНОЕ,
РАВНОЕn
УДВОЕННОМУ
ЧИСЛУ РЕБЕР
deg(Vi ) ГРАФА:
2m
i 1
ВЕРШИНА НАЗЫВАЕТСЯ ЧЕТНОЙ
(НЕЧЕТНОЙ), ЕСЛИ ЕЕ СТЕПЕНЬ –
ЧЕТНОЕ(НЕЧЕТНОЕ) ЧИСЛО.
ЧИСЛО
НЕЧЕТНЫХ
ВЕРШИН ЛЮБОГО ГРАФА –
ЧЕТНО.
НЕВОЗМОЖНО
НАЧЕРТИТЬ ГРАФ С
НЕЧЕТНЫМ ЧИСЛОМ
НЕЧЕТНЫХ ВЕРШИН.
8.
ГРАФНАЗЫВАЕТСЯ
ПОЛНЫМ,
ЕСЛИ
ЛЮБЫЕ ДВЕ ЕГО
РАЗЛИЧНЫЕ
ВЕРШИНЫ
СОЕДИНЕНЫ
ОДНИМ
И
ТОЛЬКО ОДНИМ
ДОПОЛНЕНИЕМ
РЕБРОМ.
ГРАФА
НАЗЫВАЕТСЯ
ГРАФ С ТЕМИ ЖЕ
ВЕРШИНАМИ
И
ИМЕЮЩИЙ
ТЕ
И
ТОЛЬКО ТЕ РЕБРА,
КОТОРЫЕ
G2
G5
ДОПОЛНЕНИЕ
G5
ГРАФА
ДО
G2
ГРАФА
9.
КОНЕЦДУГИ (A,B)
B
r
A
СТЕПЕНИ ВХОДА
ВЕРШИН ГРАФА
u (см. рис.):
t
deg ( A) 1
s
C
НАЧАЛО
ДУГИ (A,B)
ДУГИ
СТЕПЕНЬЮ
ВХОДА
(ВЫХОДА)
ВЕРШИНЫ
ОРГРАФА
НАЗЫВАЕТСЯ
ЧИСЛО
РЕБЕР,
ДЛЯ
КОТОРЫХ ЭТА ВЕРШИНА
ЯВЛЯЕТСЯ
КОНЦОМ
deg ( B ) 1
deg (C ) 2
СТЕПЕНИ ВЫХОДА
ВЕРШИН:
deg ( A) 1
deg ( B) 2
deg (C ) 1
10.
ПОСЛЕДОВАТЕЛЬНОСТЬРЕБЕР
НЕОРИЕНТИРОВАННОГО ГРАФА, В КОТОРОЙ
ВТОРАЯ
ВЕРШИНА
ПРЕДЫДУЩЕГО
РЕБРА
СОВПАДАЕТ
С
ПЕРВОЙ
ВЕРШИНОЙ
СЛЕДУЮЩЕГО, НАЗЫВАЕТСЯ МАРШРУТОМ.
ЧИСЛО РЕБЕР МАРШРУТА
ДЛИНОЙ МАРШРУТА.
НАЗЫВАЕТСЯ
ЕСЛИ НАЧАЛЬНАЯ ВЕРШИНА МАРШРУИА
СОВПАДАЕТ
С
КОНЕЧНОЙ,
ТО
ТАКОЙ
МАРШРУТ
НАЗЫВАЕТСЯ
ЗАМКНУТЫМ
ИЛИ
ЦИКЛОМ.
q
D
(t, s, p, r) – 4-
E A
ЕСЛИ РЕБРО ВСТРЕТИЛОСЬ ТОЛЬКО ОДИН
цикл
F
C s
РАЗ,
ТО
МАРШРУТ
НАЗЫВАЕТСЯ
ЦЕПЬЮ.
C
B
u
p
E
t
(t, s, u, r, t, s, p, r) –
A
H
r
G
D
8-цикл
B
HCDFD
–
МАРШРУТ
ДЛИНОЙ 4.
петля (q) – 1(t, s, p) – 3цикл
цепь
11.
ПУТЬ–
(u, s, r, t) – 4УПОРЯДОЧЕННАЯ
ПОСЛЕДОВАТЕЛЬНОС путь
ТЬ
РЕБЕР
ОРИЕНТИРОВАННОГО (r, u) – 2-путь
ГРАФА,
В
КОТОРОЙ (s, r, t) и (u, s, r) –
КОНЕЦ ПРЕДЫДУЩЕГО
3-циклы
РЕБРА СОВПАДАЕТ С
НАЧАЛОМ
СЛЕДУЮЩЕГОB И ВСЕ
РЕБРА
u
ЦИКЛ В ОРГРАФЕ –
ЕДИНСТВЕННЫ.
r
t
ПУТЬ, У КОТОРОГО
A
s
C
СОВПАДАЮТ
НАЧАЛО И КОНЕЦ.
12.
ЦЕПЬ, ПУТЬ И ЦИКЛ ВГРАФЕ НАЗЫВАЮТСЯ
ПРОСТЫМИ, ЕСЛИ ОНИ
ПРОХОДЯТ ЧЕРЕЗ ЛЮБУЮ
ИЗ ВЕРШИН НЕ БОЛЕЕ
ОДНОГО РАЗА.
НЕОРИЕНТИРОВАННЫЙ
ГРАФ НАЗЫВАЕТСЯ
СВЯЗНЫМ, ЕСЛИ МЕЖДУ
ЛЮБЫМИ ДВУМЯ ЕГО
ДЛЯ
ТОГО,
ВЕРШИНАМИ
ЕСТЬ ЧТОБЫ
СВЯЗНЫЙ
ГРАФ
МАРШРУТ.
ЯВЛЯЛСЯ
ПРОСТЫМ
ЦИКЛОМ,
НЕОБХОДИМО
И
ДОСТАТОЧНО, ЧТОБЫ
КАЖДАЯ
ЕГО
13.
ГРАФG
НАЗЫВАЕТСЯ
ПЛАНАРНЫМ(ПЛОСКИМ),
ЕСЛИ
СУЩЕСТВУЕТ ТАКОЙ ГРАФ G' , В
ИЗОБРАЖЕНИИ
КОТОРОГО
НА
D
ПЛОСКОСТИ
РЕБРА
A
FВ
c
ПЕРЕСЕКАЮТСЯ
ТОЛЬКО
a
B
ВЕРШИНАХ.
C
d
E
b
A
e
H
C
G
B
ПЛАНАРНЫЕ ГРАФЫ
ПЕРВОНАЧАЛЬН
ИЗОБРАЖЕННЫЙ
14.
ЭЙЛЕРОВЫМ ПУТЕМ(ЦИКЛОМ)ГРАФА
НАЗЫВАЕТСЯ
ПУТЬ(ЦИКЛ),
КОТОРЫЙ
СОДЕРЖИТ
ВСЕ
РЕБРА
ГРАФА ТОЛЬКО ОДИН РАЗ.
ГРАФ,
ОБЛАДАЮЩИЙ
ЭЙЛЕРОВЫМ
ЦИКЛОМ,
НАЗЫВАЕТСЯ ЭЙЛЕРОВЫМ.
ГРАФ ЯВЛЯЕТСЯ
ЭЙЛЕРОВЫМ ТОГДА
И ТОЛЬКО ТОГДА,
КОГДА ОН –
СВЯЗНЫЙ ГРАФ,
ИМЕЮЩИЙ ВСЕ
ЧЕТНЫЕ ВЕРШИНЫ.
15.
ГАМИЛЬТОНОВЫМПУТЕМ(ЦИКЛОМ) ГРАФА
НАЗЫВАЕТСЯ
ПУТЬ(ЦИКЛ),
ПРОХОДЯЩИЙ ЧЕРЕЗ
КАЖДУЮ ЕГО ВЕРШИНУ
ТОЛЬКО ОДИН РАЗ.
ГРАФ, СОДЕРЖАЩИЙ
ГАМИЛЬТОНОВ
ЦИКЛ,
A
НАЗЫВАЕТСЯ
B
(C, D, A, B, E) –
D ГАМИЛЬТОНОВЫМ.
E
C
гамильтон
ов путь
16.
МАТРИЦЕЙ ИНЦИДЕНТНОСТИ ГРАФАG НАЗЫВАЮТ ТАБЛИЦУ B, СОСТОЯЩУЮ
ИЗ n СТРОК(ВЕРШИНЫ) И m
СТОЛБЦОВ(РЕБРА), В КОТОРОЙ:
•ДЛЯ НЕОРИЕНТИРОВАННОГО
ГРАФА:
Vi ИНЦИДЕНТНА X j
bij 1 , ЕСЛИ
РЕБРУ
Vi ИНЦИДЕНТНА
Xj
, ЕСЛИ ВЕРШИНА
РЕБРУ
bij 0 ВЕРШИНА
•ДЛЯ ОРИЕНТИРОВАННОГО
bГРАФА:
1, ЕСЛИ ВЕРШИНА
V ЯВЛЯЕТСЯ
ij
i
Xj
ДУГИ X ДУГ
Vi НАЧАЛОМ
НЕ ИНЦИДЕНТНА
bij 0, ЕСЛИ ВЕРШИНА
j
X jД
bij 1 , ЕСЛИ ВЕРШИНА Vi ЯВЛЯЕТСЯ КОНЦОМ
17.
МАТРИЦЕЙ СМЕЖНОСТИ ГРАФАG(V,X)
БЕЗ
КРАТНЫХ
РЕБЕР
НАЗЫВАЮТ
КВАДРАТНУЮ
МАТРИЦУ
A
ПОРЯДКА
n,
В
КОТОРОЙ:
a 1,
(V ,V ) X
ij
aij
i
j
ЕСЛ
И
0 , ЕСЛИ(Vi ,V j ) X
18.
ЗАДАЙТЕ СЛЕДУЮЩИЙ ОРГРАФТАБЛИЦЕЙ ИНЦИДЕНТНОСТИ
B
u
r
A
t
s
C
A
B
C
r
1
-1
0
s
-1
0
1
t
0
1
-1
u
0
1
-1
19.
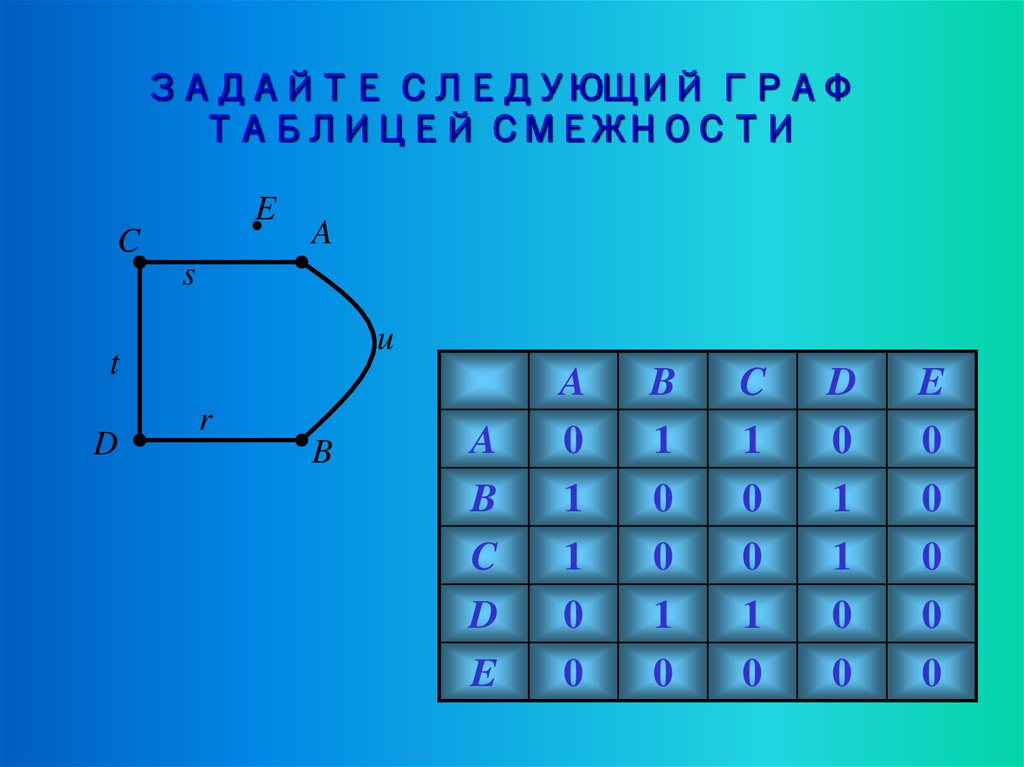
ЗАДАЙТЕ СЛЕДУЮЩИЙ ГРАФТАБЛИЦЕЙ СМЕЖНОСТИ
E
C
A
s
u
t
D
r
B
A
B
C
D
E
A
0
1
1
0
0
B
1
0
0
1
0
C
1
0
0
1
0
D
0
1
1
0
0
E
0
0
0
0
0
20.
Автор: Оркина Марина Александровна,преподаватель ГОУ СПО
«Зубово-Полянский педагогический колледж»
Республика Мордовия

















 mathematics
mathematics








