Основы теории графов. Основные понятия и определения. Тема 3.1

1. Раздел 3: Основы теории графов

Тема 3.1. Основные понятия и определения
Преподаватель ОЯТЦ ИЯТШ
Егорова О.В.

2. План лекций

2
План лекций
понятие графа, основные типы графов
способы задания графов
основные операции над графами
понятие подграфа
пути, дороги в графах
обход графов
связность графов
метрические характеристики графов

3. Понятие графа

3
Понятие графа
Граф G = (V, E) -
совокупность двух множеств:
множества точек V, называемых вершинами,
и множества линий E, называемых ребрами
любое ребро инцидентно
(присоединено к) двум вершинам
Пример: граф с множеством вершин V a, b, c
и множеством ребер E a, b , b, c
[ ребра графа можно задать парами
инцидентных им вершин, т.е. E V V ]
ИЛИ
два ребра, инцидентные одной
вершине, называются смежными
a
две вершины инцидентные одному
ребру, также называются смежными
обычно граф изображают в виде
диаграммы, - на которой вершины
обозначаются точками, а ребра линиями
b
Число вершин графа G (V , E ) равно V n
Число ребер графа G (V , E ) равно E m
граф с n вершинами и m ребрами
называется (n, m)-графом

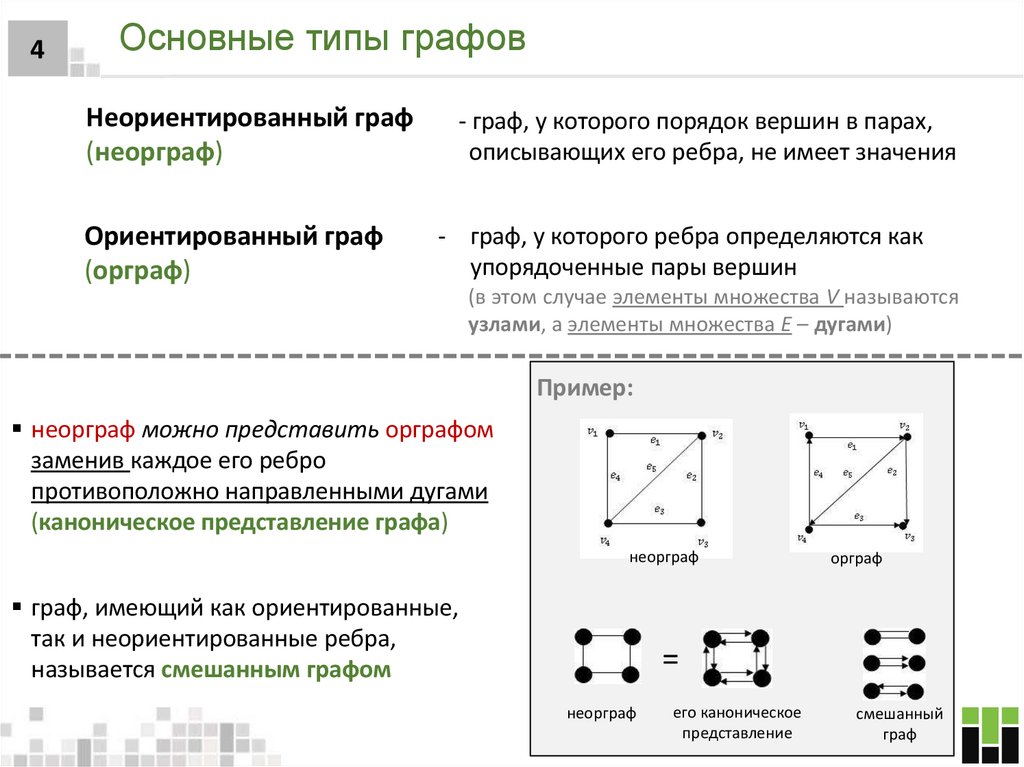
4. Основные типы графов

4
Основные типы графов
Неориентированный граф
(неорграф)
Ориентированный граф
(орграф)
- граф, у которого порядок вершин в парах,
описывающих его ребра, не имеет значения
- граф, у которого ребра определяются как
упорядоченные пары вершин
(в этом случае элементы множества V называются
узлами, а элементы множества E – дугами)
Пример:
неорграф можно представить орграфом
заменив каждое его ребро
противоположно направленными дугами
(каноническое представление графа)
неорграф
граф, имеющий как ориентированные,
так и неориентированные ребра,
называется смешанным графом
орграф
=
неорграф
его каноническое
представление
смешанный
граф

5. Некоторые разновидности графов

5
Некоторые разновидности графов
Примеры
Пустой граф – граф с пустым множеством ребер (E)
Нуль-граф – граф с пустыми множествами ребер (E) и вершин (V)
Тривиальный граф – пустой граф, имеющий лишь одну вершину
Граф с петлями – граф, имеющий петлевые дуги или ребра
[петля - это ребро, которое соединяет вершину саму с собой]
Мультиграф – граф, имеющий кратные ребра
[кратные ребра - это ребра, между двумя одинаковыми вершинам
(дуги считаются кратными, если они имеют одинаковое направление)]
Простой граф – граф, не содержащий петель и кратных ребер
Бесконечный граф – граф, определяющийся некоторой процедурой
порождения бесконечных множеств его
вершин и ребер

6. Понятие степени вершины графа

6
Понятие степени вершины графа
Локальная степень – число ребер, инцидентных вершине v,
вершины v
принадлежащей графу G(V, E)
[обозначение: deg v]
для орграфов используются понятия
«полустепень исхода» и «полустепень захода»:
Пример:
• «полустепень исхода» - число дуг исходящих из
узла v
• «полустепень захода» - число дуг входящих в
узел v
вершина v называется изолированной, если
deg v = 0, и концевой, если deg v = 1
ребро, инцидентное концевой вершине, также
называют концевым
минимальную степень вершины графа G
обозначают (G) , а максимальную – (G )
список степеней всех вершин называют
степенной последовательностью графа
deg v1 = 3
deg v4 = 3
deg v2 = 3
deg v5 = 2
deg v3 = 3

7. Понятие степени вершины графа

7
Понятие степени вершины графа
Теорема 1: сумма степеней вершин (n, m) – графа равна удвоенному числу
его ребер: n
deg vi 2 E 2 m
i 1
Доказательство: каждое ребро графа инцидентно двум вершинам, следовательно
каждое ребро добавляет 2 в сумму степеней вершин графа, что
соответствует утверждению теоремы
!!! Петля при учете степеней вершин
считается два раза
Теорема 2: в любом графе число вершин нечетной степени четно
Доказательство:
согласно вышерассмотренной теореме, сумма степеней вершин графа четна
так как сумма четных степеней вершин тоже четна, то для четности суммы
степеней всех вершин число вершин нечетной степени должно быть четно
ч.т.д.
[САМ. Найти неформальную формулировку леммы о рукопожатиях]
Граф G называется d – однородным, или однородным степени d, если (G) (G) d
!!! В однородном графе все вершины
имеют одинаковую степень

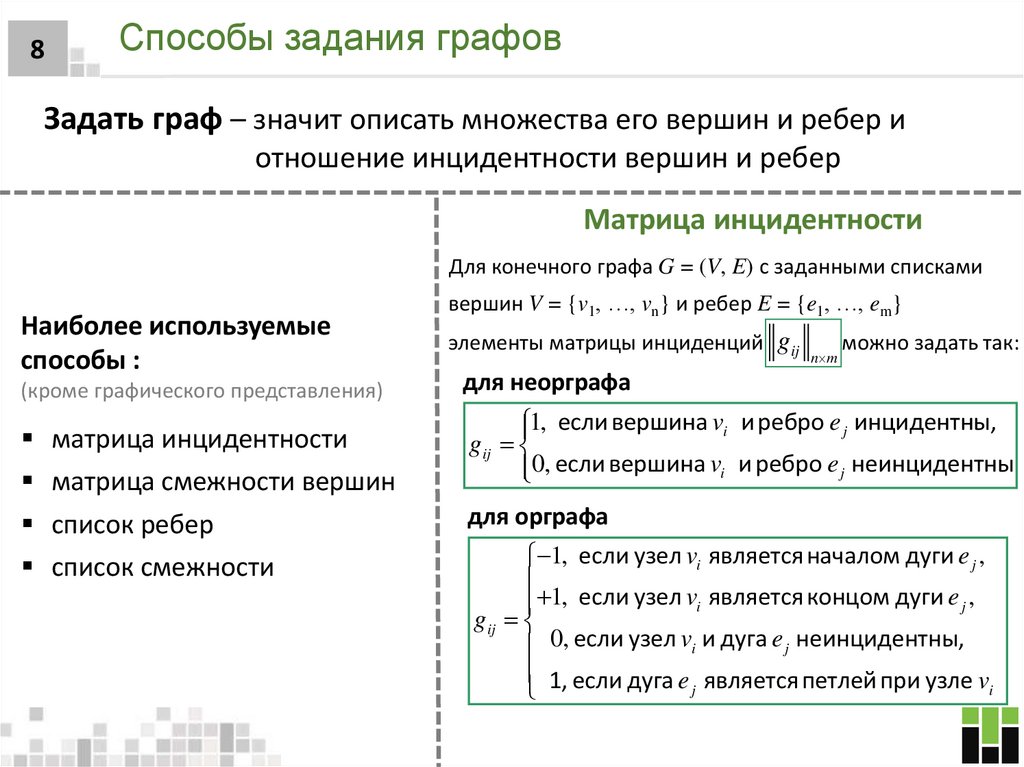
8. Способы задания графов

8
Способы задания графов
Задать граф – значит описать множества его вершин и ребер и
отношение инцидентности вершин и ребер
Матрица инцидентности
Для конечного графа G = (V, E) с заданными списками
Наиболее используемые
способы :
(кроме графического представления)
матрица инцидентности
матрица смежности вершин
список ребер
список смежности
вершин V = {v1, …, vn} и ребер E = {e1, …, em}
элементы матрицы инциденций gij
n m
можно задать так:
для неорграфа
1, если вершина vi и ребро e j инцидентны,
gij
0, если вершина vi и ребро e j неинцидентны
для орграфа
1, если узел vi является началом дуги e j ,
1, если узел vi является концом дуги e j ,
gij
0, если узел vi и дуга e j неинцидентны,
1, если дуга e является петлей при узле v
j
i

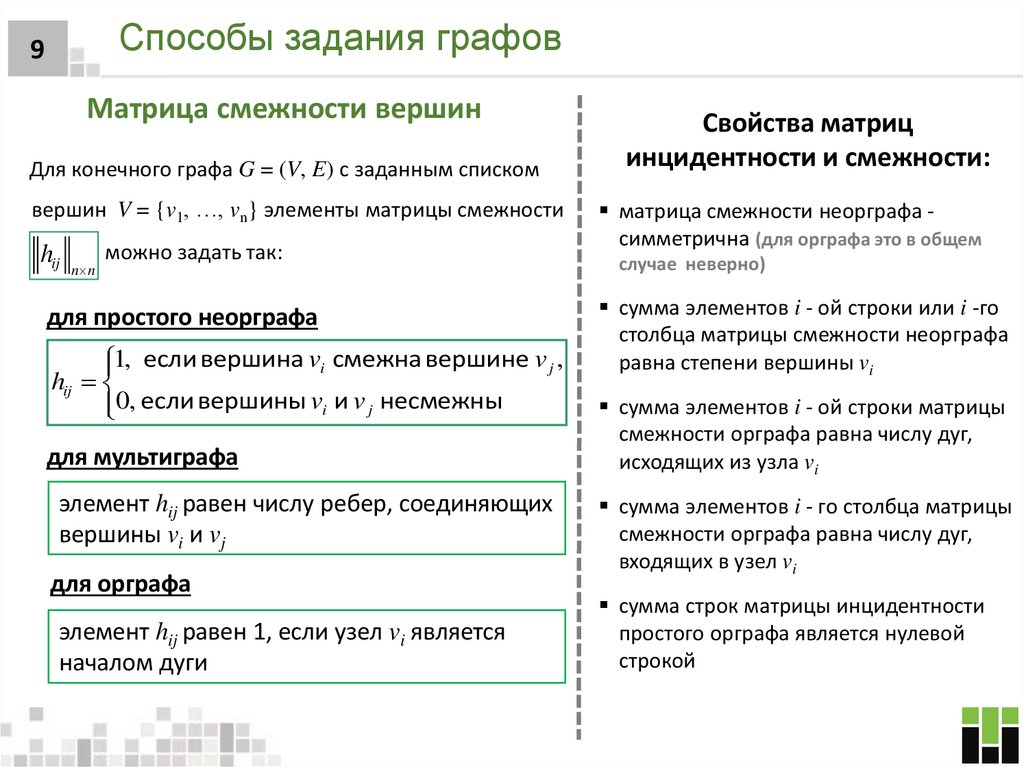
9. Способы задания графов

9
Матрица смежности вершин
Для конечного графа G = (V, E) с заданным списком
вершин V = {v1, …, vn} элементы матрицы смежности
hij
n n
можно задать так:
для простого неорграфа
1, если вершина vi смежна вершине v j ,
hij
0, если вершины vi и v j несмежны
для мультиграфа
элемент hij равен числу ребер, соединяющих
вершины vi и vj
для орграфа
элемент hij равен 1, если узел vi является
началом дуги
Свойства матриц
инцидентности и смежности:
матрица смежности неорграфа симметрична (для орграфа это в общем
случае неверно)
сумма элементов i - ой строки или i -го
столбца матрицы смежности неорграфа
равна степени вершины vi
сумма элементов i - ой строки матрицы
смежности орграфа равна числу дуг,
исходящих из узла vi
сумма элементов i - го столбца матрицы
смежности орграфа равна числу дуг,
входящих в узел vi
сумма строк матрицы инцидентности
простого орграфа является нулевой
строкой

10. Способы задания графов

10
Способы задания графов
Список ребер
Пример:
в списке ребер, каждое ребро представляется
парой вершин
орграф G2
неорграф G1
в неорграфе порядок вершин не имеет
значения и не учитывается
Матрицы инциденций для G1 и G2:
в орграфе первым в паре указывается узел,
являющийся началом дуги, а вторым – узел,
являющийся ее концом
v1
G1 v2
v3
v4
e1 e2
1 0
1 1
0 1
0 0
e3
0
0
1
1
e4
1
0
0
1
e5
0
1
0
1
v1
G2 v2
v3
v4
e1 e2 e3 e4 e5
1 0 0 1 0
1 1 0 0 1
0 1 1 0 0
0 0 1 1 1
Матрицы смежности для G1 и G2:
Список (структура) смежности
список смежности состоит из списков A[v]
вершин графа смежных с вершиной v
списки A[v] составляются для каждой
вершины графа
[САМ. Cоставить список ребер для графа G1 и
списко смежности для графа G2]
v1
G1 v2
v3
v4
v1 v2
0 1
1 0
0 1
1 1
v3
0
1
0
1
v4
1
1
1
0
v1
G2 v2
v3
v4
v1 v2
0 1
0 0
0 0
1 0
v3
0
1
0
1
v4
0
1
0
0
Список дуг для G2 : v1, v2 , v2 , v3 , v2 , v4 , v4 , v1 , v4 , v3
Список смежности для G1 :
v
1
2
3
4
A[v]
2, 4
1, 3, 4
2, 4
1, 2, 3

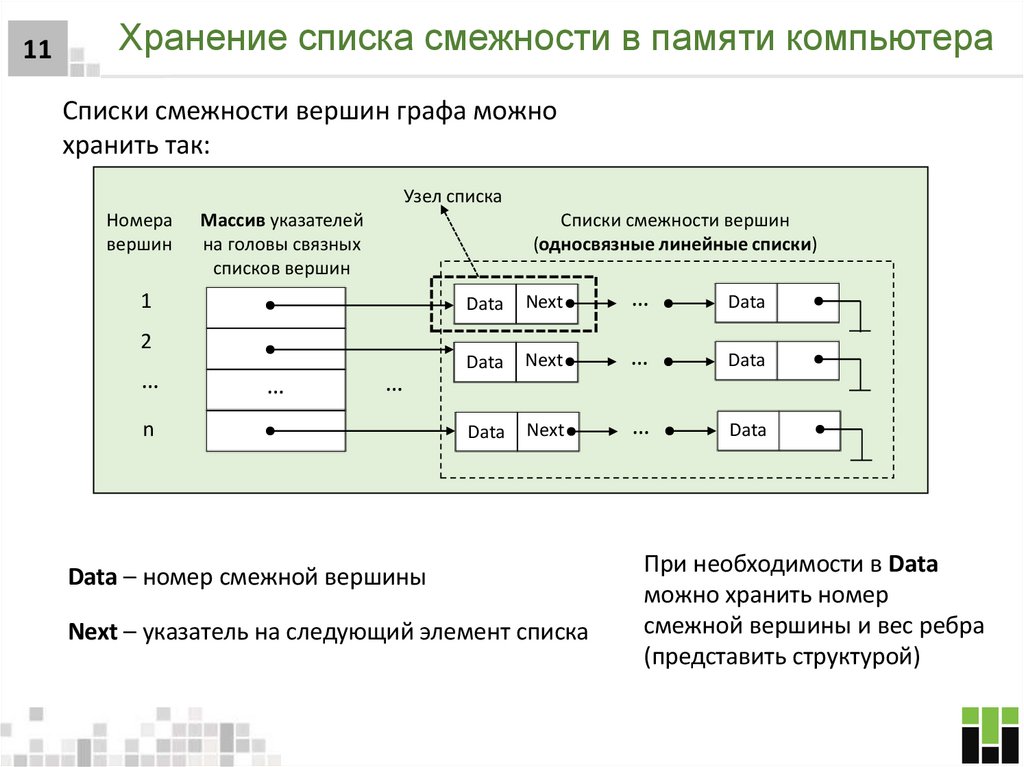
11. Хранение списка смежности в памяти компьютера

11
Хранение списка смежности в памяти компьютера
Списки смежности вершин графа можно
хранить так:
Узел списка
Номера
вершин
Списки смежности вершин
(односвязные линейные списки)
Массив указателей
на головы связных
списков вершин
1
2
…
…
…
n
Data
Next
…
Data
Data
Next
…
Data
Data
Next
…
Data
Data – номер смежной вершины
Next – указатель на следующий элемент списка
При необходимости в Data
можно хранить номер
смежной вершины и вес ребра
(представить структурой)

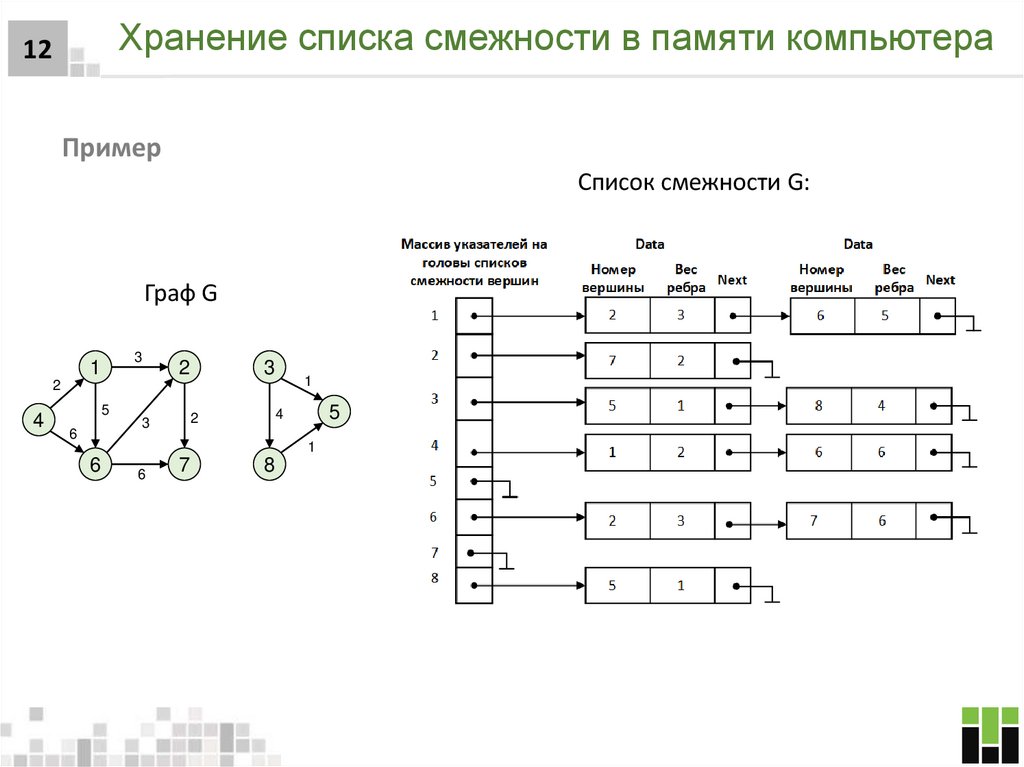
12. Хранение списка смежности в памяти компьютера

12
Пример
Список смежности G:
Граф G
3
1
2
3
1
2
4
5
6
5
4
2
3
1
6
6
7
8

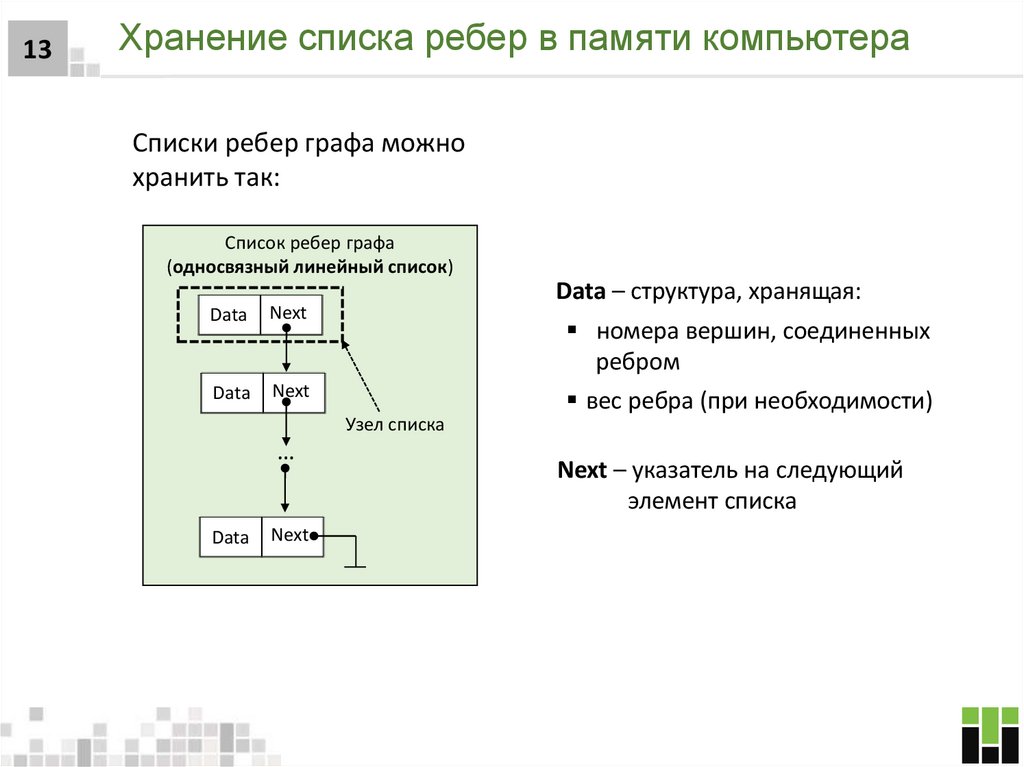
13. Хранение списка ребер в памяти компьютера

13
Хранение списка ребер в памяти компьютера
Списки ребер графа можно
хранить так:
Список ребер графа
(односвязный линейный список)
Data
Next
Data
Next
Data – структура, хранящая:
номера вершин, соединенных
ребром
вес ребра (при необходимости)
Узел списка
…
Data
Next
Next – указатель на следующий
элемент списка

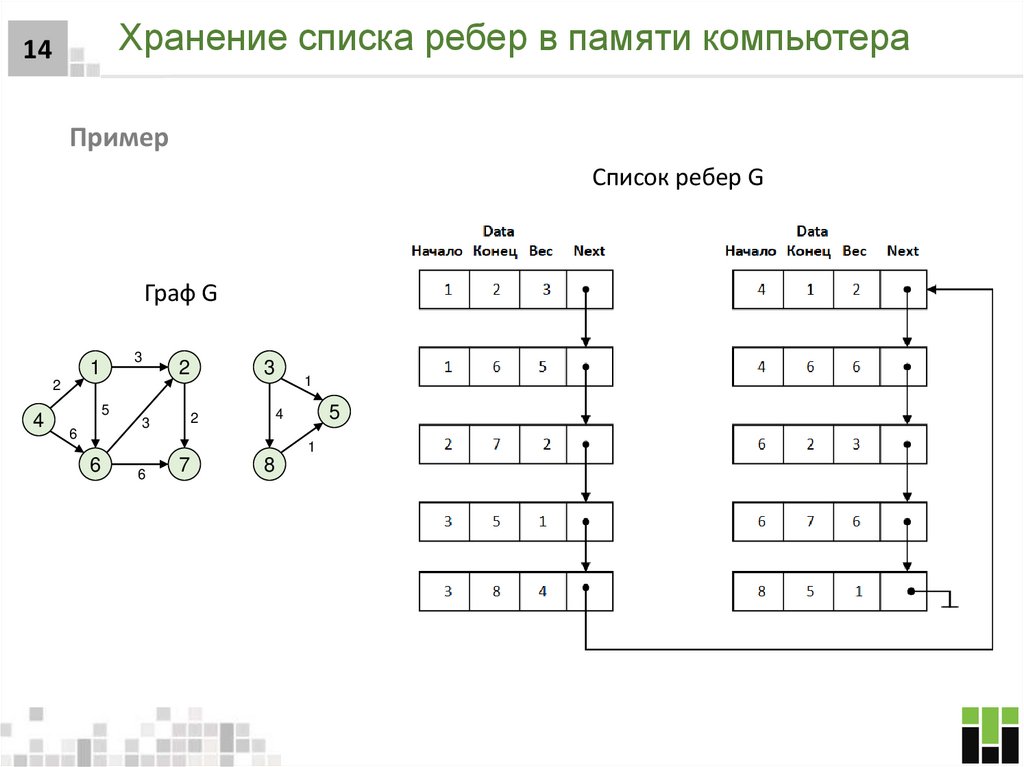
14. Хранение списка ребер в памяти компьютера

14
Пример
Список ребер G
Граф G
3
1
2
3
1
2
4
5
6
5
4
2
3
1
6
6
7
8

15. Сравнение разных способов задания графов

15
Сравнение разных способов задания графов
Способ задания
Удобно
Неудобно
Матрица
смежности
добавлять и удалять ребра
добавлять и удалять вершины
проверять смежность
вершин
работать с разреженными
графами
Матрица
инцидентности
менять нагрузку (вес) на
ребра
добавлять и удалять вершины
проверять инцидентность
Список
смежности
искать вершины, смежные
с данной
работать с разреженными
графами
проверять наличие ребер
удалять ребра и вершины
добавлять ребра и
вершины
работать с разреженными
графами
Список ребер
добавлять и удалять
ребра
определять смежность вершин
и ребер
упорядочивать ребра по
возрастанию нагрузки
осуществлять перебор
инцидентных заданной
вершине ребер
представлять сильно
разреженные графы

16. Операции над графами

16
Операции над графами
Удаление вершины
результатом удаления вершины v в графе G = (V, E) является
граф, остающийся после удаления из графа G = (V, E)
вершины v и всех инцидентных ей ребер
Удаление ребра
результатом удаления ребра e в графе G = (V, E) является
граф, остающийся после удаления из графа G = (V, E) ребра
e без удаления инцидентных ему вершин
Объединение графов
обозначение: G G1 G2
Результатом объединения графов G1 = (V1, E1) и G2 = (V2, E2)
является граф G = (V, E) , где V V1 V2 и E E1 E2
Пересечение графов
Результатом пересечения графов G1 = (V1, E1) и G2 = (V2, E2)
обозначение: G G1 G2 является граф G = (V, E) , где V V1 V2 и E E1 E2
Дополнение графа
обозначение: G
Результатом дополнения простого графа G = (V, E) есть граф
G V , E такой, что vi , v j E тогда и только тогда, когда
v , v E (иначе говоря, вершины v и v (i не равно j) смежные
i
j
i
j
в графе G тогда и только тогда, когда они несмежны
в графе G)

17. Операции над графами

17
Операции над графами
Отождествление
вершин
результатом отождествления вершин vi и vj в графе G
является граф G’, полученный из графа G заменой пары
вершин vi и vj одной вершиной v, инцидентной всем тем
ребрам, которым были инцидентны вершины vi и vj
Стягивание ребра
результатом стягивания ребра е в графе G является граф G’,
полученный из графа G удалением из него ребра е и
отождествлением его концевых вершин
[говорят, что граф G стягивается к графу H, если граф H можно
получить из графа G последовательным стягиванием его ребер]

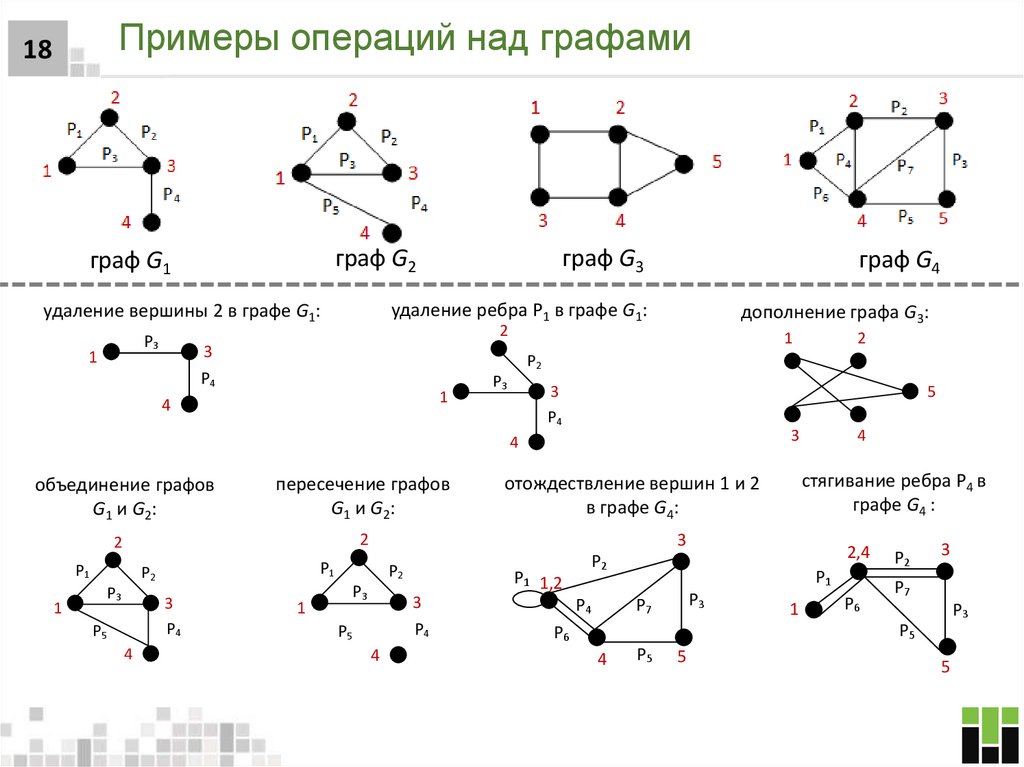
18. Примеры операций над графами

18
удаление вершины 2 в графе G1:
P3
1
граф G3
граф G4
удаление ребра P1 в графе G1:
дополнение графа G3:
граф G2
граф G1
2
3
P4
1
P2
1
4
P3
3
P4
5
3
4
объединение графов
G1 и G2 :
пересечение графов
G1 и G2 :
2
2
P1
1
3
P4
P5
4
P2
P3
1
4
стягивание ребра P4 в
графе G4 :
отождествление вершин 1 и 2
в графе G4:
3
P1
P2
P3
2
P1 1,2
3
P4
P5
4
2,4
P2
P4
P1
P3
P7
1
P6
P2
3
P7
P3
P5
P6
4
P5
5
5

19. Подграфы

19
Подграфы
Граф G‘ = (V’, E’) называется подграфом графа G = (V, E), если
V ' V , E ' E и обе вершины каждого ребра из Е’ принадлежат V’
Подграф G‘ = (V’, E’) графа G = (V, E) называется
собственным подграфом, когда V’ V или E’ E
Собственный подграф называется остовным (или суграфом),
если V’ = V, а E’ E
Пример:
все остовные подграфы графа G
!!!!Заметим, что любой остовной подграф G‘ = (V, E’)
графа G= (V, E) можно получить путем удаления
подмножества ребер E \ E ' из графа G= (V, E)

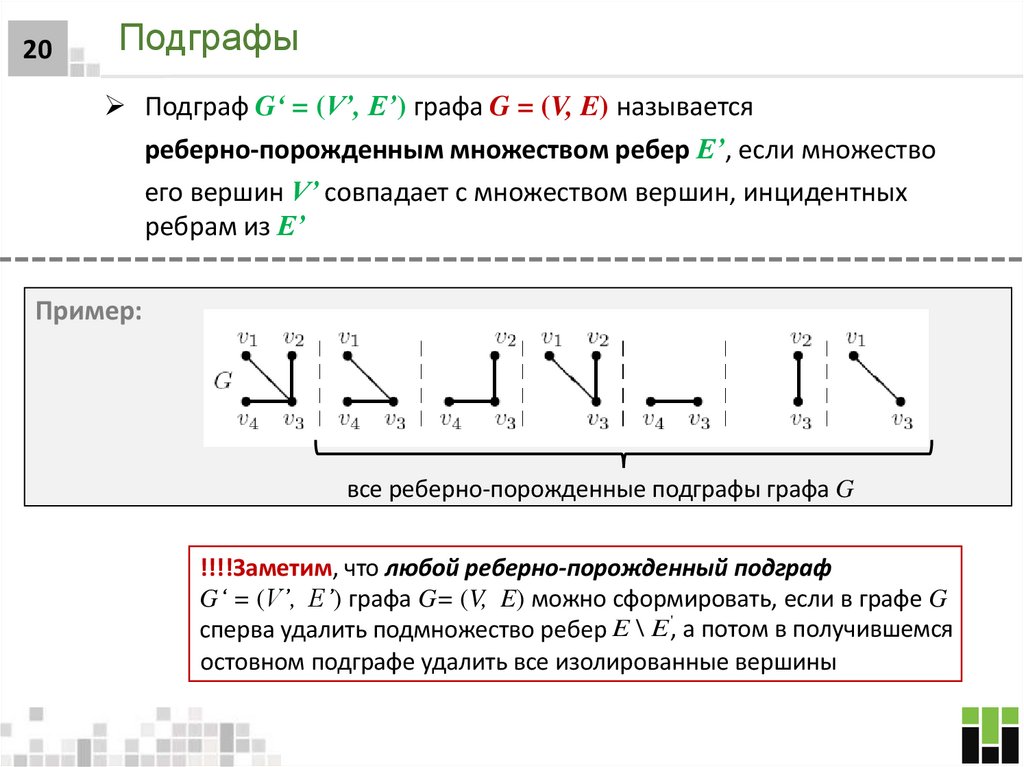
20. Подграфы

20
Подграфы
Подграф G‘ = (V’, E’) графа G = (V, E) называется
реберно-порожденным множеством ребер E’, если множество
его вершин V’ совпадает с множеством вершин, инцидентных
ребрам из E’
Пример:
все реберно-порожденные подграфы графа G
!!!!Заметим, что любой реберно-порожденный подграф
G‘ = (V’, E’) графа G= (V, E) можно сформировать, если в графе G
сперва удалить подмножество ребер E \ E ,' а потом в получившемся
остовном подграфе удалить все изолированные вершины

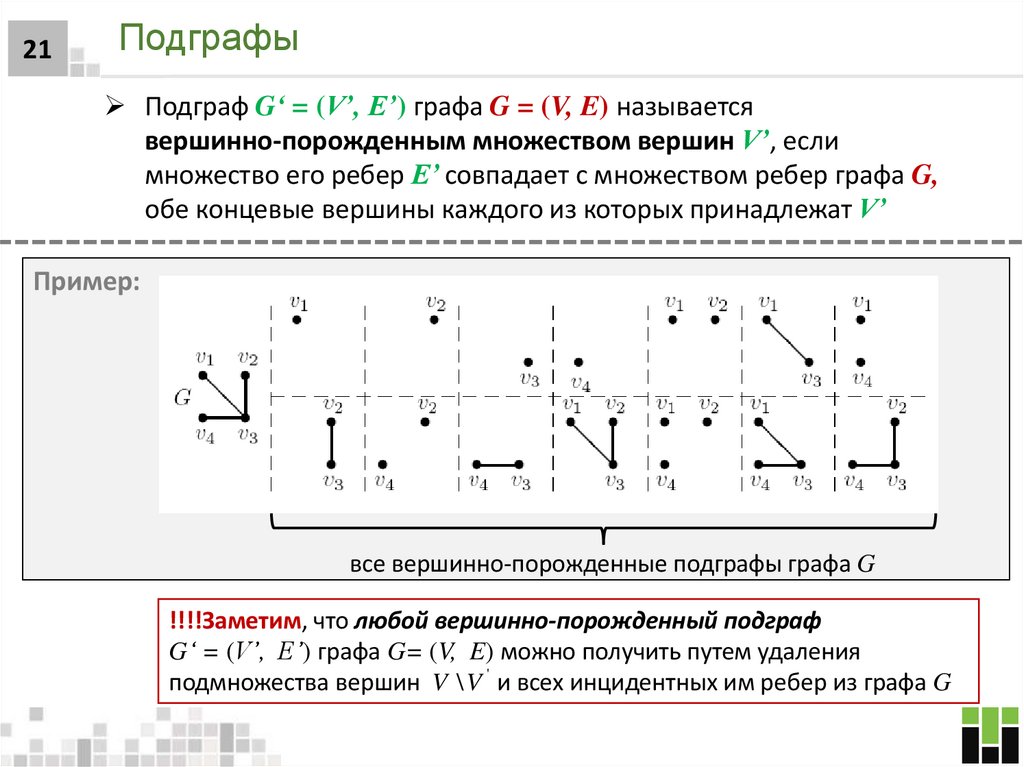
21. Подграфы

21
Подграфы
Подграф G‘ = (V’, E’) графа G = (V, E) называется
вершинно-порожденным множеством вершин V’, если
множество его ребер E’ совпадает с множеством ребер графа G,
обе концевые вершины каждого из которых принадлежат V’
Пример:
все вершинно-порожденные подграфы графа G
!!!!Заметим, что любой вершинно-порожденный подграф
G‘ = (V’, E’) графа G= (V, E) можно получить путем удаления
подмножества вершин V \ V ' и всех инцидентных им ребер из графа G

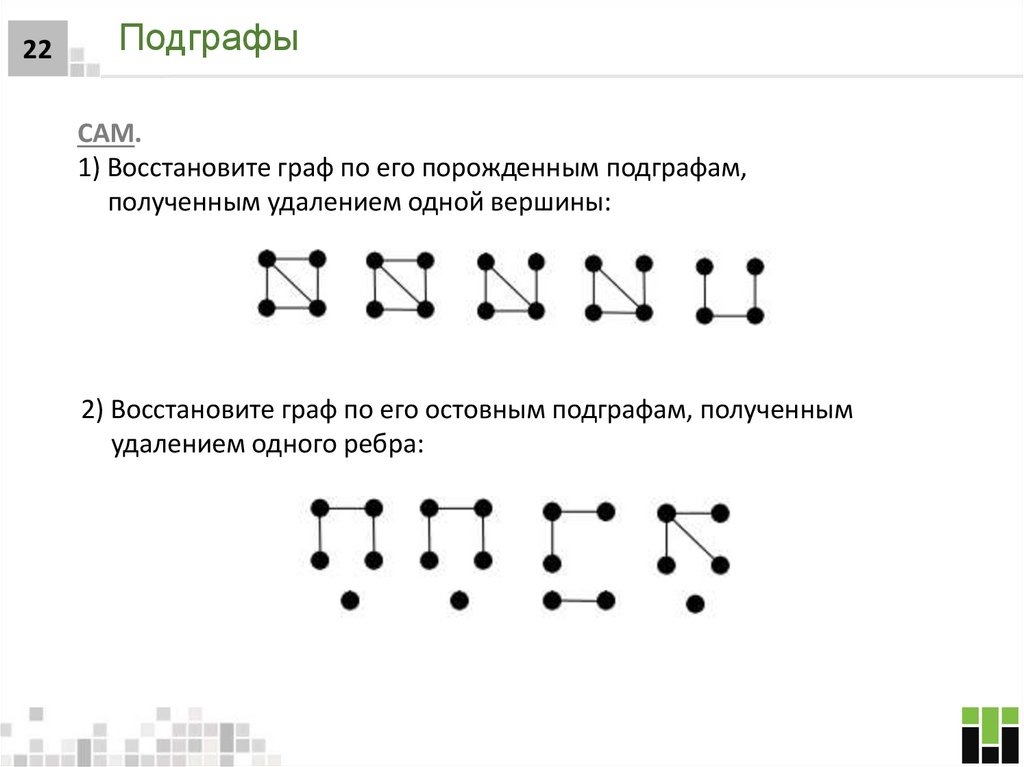
22. Подграфы

22
Подграфы
САМ.
1) Восстановите граф по его порожденным подграфам,
полученным удалением одной вершины:
2) Восстановите граф по его остовным подграфам, полученным
удалением одного ребра:

23. Подграфы

23
Подграфы
Подграф G‘ = (V’, E’) графа G = (V, E) называется
максимальным подграфом со свойством p, если никакой другой
подграф графа G = (V, E) , строго включающий G‘ = (V’, E’), не
обладает свойством p
Подграф G‘ = (V’, E’) графа G = (V, E) называется
минимальным подграфом со свойством p, если никакой другой
собственный подграф графа G‘ = (V’, E’), не обладает свойством p

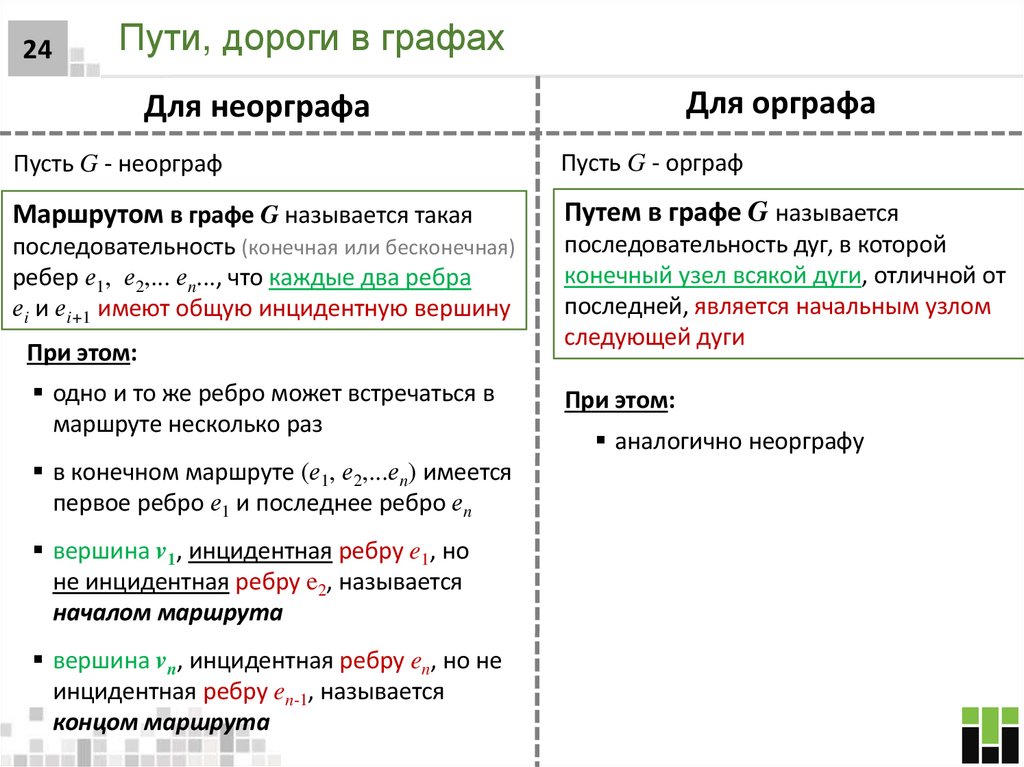
24. Пути, дороги в графах

24
Пути, дороги в графах
Для орграфа
Для неорграфа
Пусть G - неорграф
Пусть G - орграф
Маршрутом в графе G называется такая
Путем в графе G называется
последовательность (конечная или бесконечная)
ребер е1, е2,... еn..., что каждые два ребра
еi и еi+1 имеют общую инцидентную вершину
последовательность дуг, в которой
конечный узел всякой дуги, отличной от
последней, является начальным узлом
следующей дуги
При этом:
одно и то же ребро может встречаться в
маршруте несколько раз
в конечном маршруте (е1, е2,...еn) имеется
первое ребро е1 и последнее ребро еn
вершина v1, инцидентная ребру e1, но
не инцидентная ребру e2, называется
началом маршрута
вершина vn, инцидентная ребру en, но не
инцидентная ребру en-1, называется
концом маршрута
При этом:
аналогично неорграфу

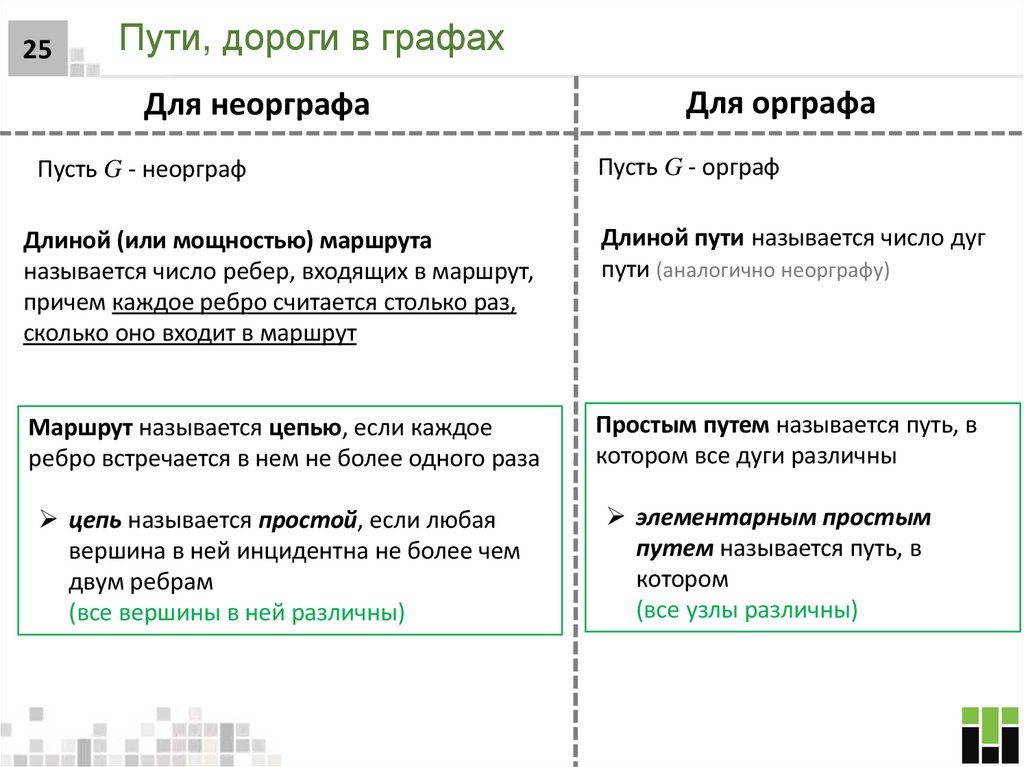
25. Пути, дороги в графах

25
Пути, дороги в графах
Для неорграфа
Для орграфа
Пусть G - неорграф
Пусть G - орграф
Длиной (или мощностью) маршрута
называется число ребер, входящих в маршрут,
причем каждое ребро считается столько раз,
сколько оно входит в маршрут
Длиной пути называется число дуг
пути (аналогично неорграфу)
Маршрут называется цепью, если каждое
ребро встречается в нем не более одного раза
Простым путем называется путь, в
котором все дуги различны
цепь называется простой, если любая
вершина в ней инцидентна не более чем
двум ребрам
(все вершины в ней различны)
элементарным простым
путем называется путь, в
котором
(все узлы различны)

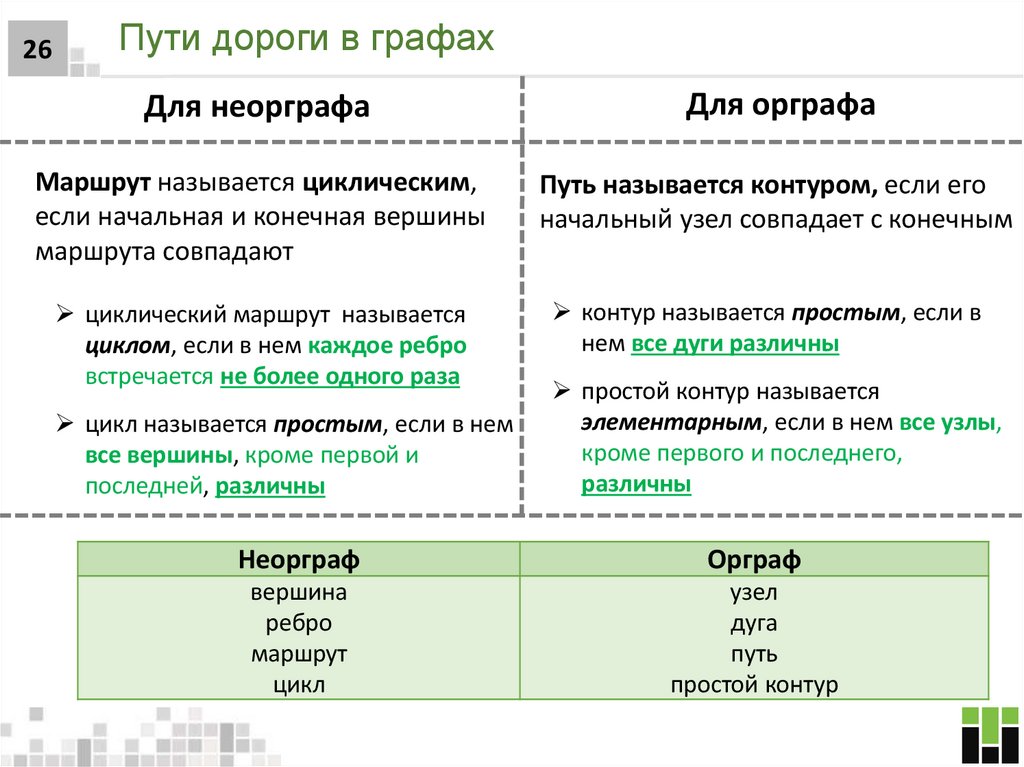
26. Пути дороги в графах

26
Пути дороги в графах
Для неорграфа
Для орграфа
Маршрут называется циклическим,
если начальная и конечная вершины
маршрута совпадают
Путь называется контуром, если его
начальный узел совпадает с конечным
циклический маршрут называется
циклом, если в нем каждое ребро
встречается не более одного раза
контур называется простым, если в
нем все дуги различны
цикл называется простым, если в нем
все вершины, кроме первой и
последней, различны
простой контур называется
элементарным, если в нем все узлы,
кроме первого и последнего,
различны
Неорграф
Орграф
вершина
ребро
маршрут
цикл
узел
дуга
путь
простой контур

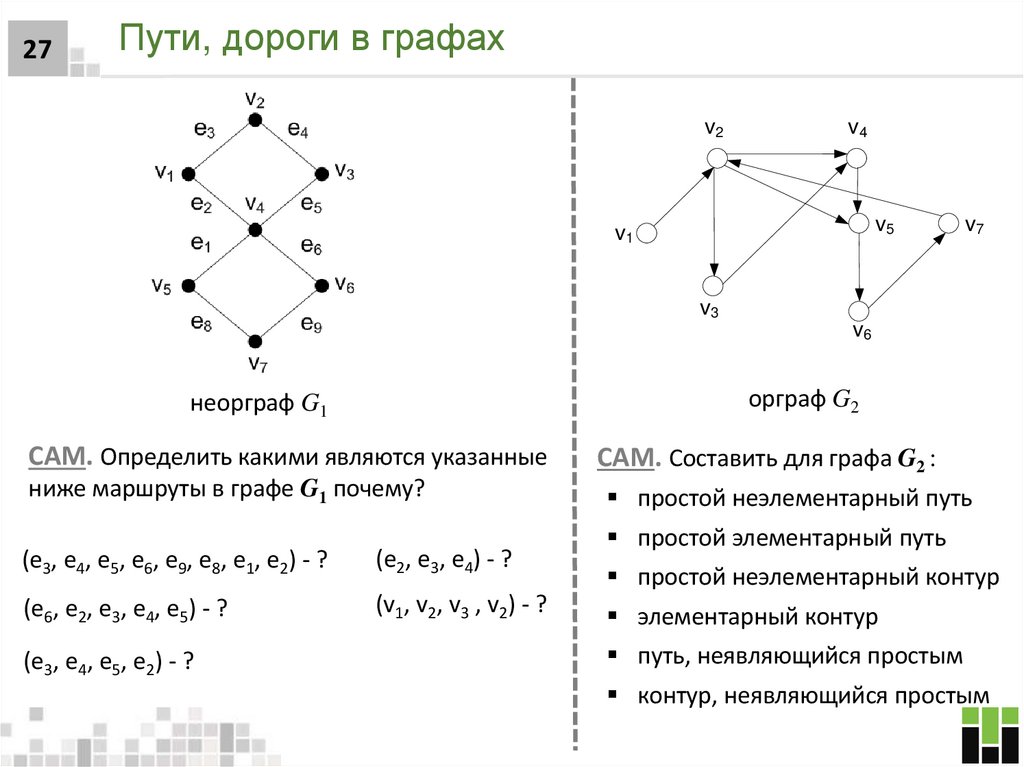
27. Пути, дороги в графах

27
Пути, дороги в графах
v2
v4
v5
v1
v7
v3
v6
орграф G2
неорграф G1
САМ. Определить какими являются указанные
САМ. Составить для графа G2 :
ниже маршруты в графе G1 почему?
простой неэлементарный путь
(e3, e4, e5, e6, e9, e8, e1, e2) - ?
(e2, e3, e4) - ?
(e6, e2, e3, e4, e5) - ?
(v1, v2, v3 , v2) - ?
(e3, e4, e5, e2) - ?
простой элементарный путь
простой неэлементарный контур
элементарный контур
путь, неявляющийся простым
контур, неявляющийся простым

28. Алгоритмы обхода графов

28
Алгоритмы обхода графов
Под обходом графа будем понимать
процесс систематического просмотра всех вершин графа с целью
отыскания вершин, удовлетворяющих некоторому условию
Обход в глубину
Обход в ширину
(от англ. "depth first search")
(от англ. "breadth first search")
находясь в вершине v выбираем произвольную,
но еще не просмотренную вершину u, смежную
с вершиной v
отмечаем u как просмотренную
эту новую вершину u рассматриваем теперь уже
как v и, начиная с нее, продолжаем обход
если не существует еще не просмотренной
вершины, смежной с v, то говорят, что вершина v
просмотрена и возвращаются в вершину, из
которой попали в v
поиск закончен, когда v = v0 (v0 – вершина , с
которой был начат обход) и просмотрены все
вершины или продолжение поиска невозможно
находясь в вершине v, отмечаем ее как
просмотренную
затем просматриваем ее список
смежности A[v] и отмечаем все ранее не
отмеченные вершины списка
после того как отмечены все вершины из
списка смежности A[v], вершину v
считаем полностью обработанной
продолжаем обработку вершин из списка
смежности A[v] по очереди согласно
описанным выше правилам
поиск заканчивается, когда все вершины
полностью обработаны или продолжение
поиска невозможно

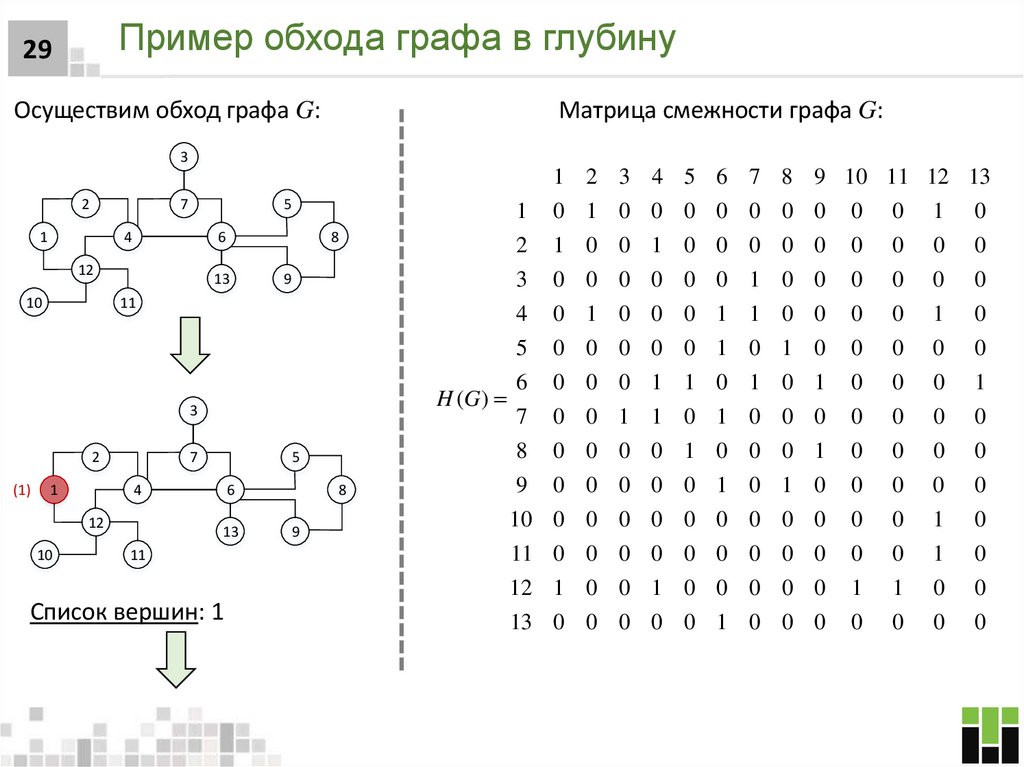
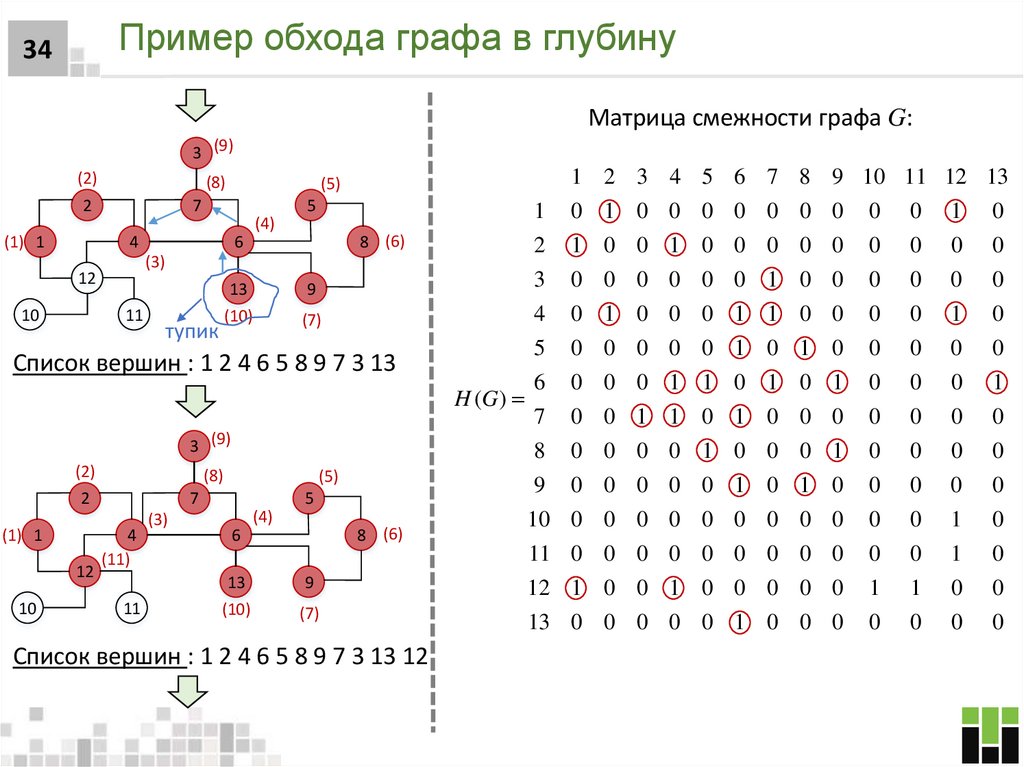
29. Пример обхода графа в глубину

29
Осуществим обход графа G:
Матрица смежности графа G:
3
2
7
1
5
4
6
12
10
8
13
9
11
3
2
(1)
1
7
4
12
10
5
6
13
11
Список вершин: 1
8
9
1
2
3
4
5
6
H (G )
7
8
9
10
11
12
13
1
0
1
0
0
0
0
0
0
0
0
0
1
0
2
1
0
0
1
0
0
0
0
0
0
0
0
0
3
0
0
0
0
0
0
1
0
0
0
0
0
0
4
0
1
0
0
0
1
1
0
0
0
0
1
0
5
0
0
0
0
0
1
0
1
0
0
0
0
0
6
0
0
0
1
1
0
1
0
1
0
0
0
1
7
0
0
1
1
0
1
0
0
0
0
0
0
0
8
0
0
0
0
1
0
0
0
1
0
0
0
0
9 10 11 12 13
0 0 0 1 0
0 0 0 0 0
0 0 0 0 0
0 0 0 1 0
0 0 0 0 0
1 0 0 0 1
0 0 0 0 0
1 0 0 0 0
0 0 0 0 0
0 0 0 1 0
0 0 0 1 0
0 1 1 0 0
0 0 0 0 0

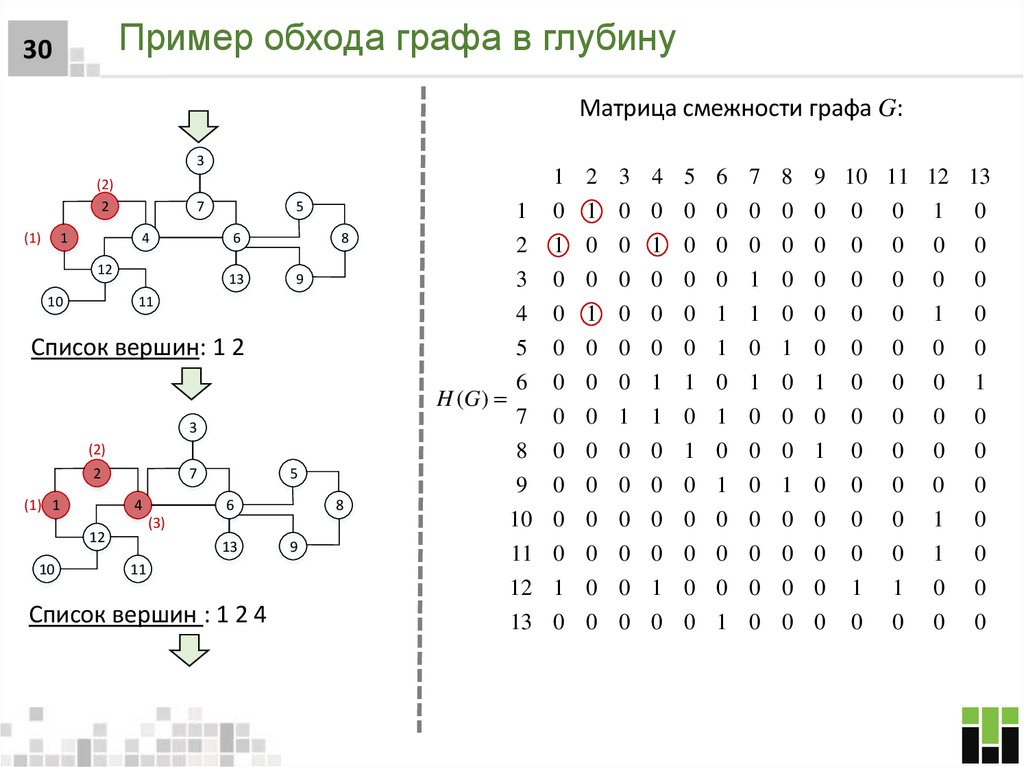
30. Пример обхода графа в глубину

30
Матрица смежности графа G:
3
(2)
2
(1)
1
7
4
6
12
10
5
13
8
9
11
Список вершин: 1 2
3
(2)
2
(1) 1
7
4
6
8
(3)
12
10
5
13
11
Список вершин : 1 2 4
9
1
2
3
4
5
6
H (G )
7
8
9
10
11
12
13
1
0
1
0
0
0
0
0
0
0
0
0
1
0
2
1
0
0
1
0
0
0
0
0
0
0
0
0
3
0
0
0
0
0
0
1
0
0
0
0
0
0
4
0
1
0
0
0
1
1
0
0
0
0
1
0
5
0
0
0
0
0
1
0
1
0
0
0
0
0
6
0
0
0
1
1
0
1
0
1
0
0
0
1
7
0
0
1
1
0
1
0
0
0
0
0
0
0
8
0
0
0
0
1
0
0
0
1
0
0
0
0
9 10 11 12 13
0 0 0 1 0
0 0 0 0 0
0 0 0 0 0
0 0 0 1 0
0 0 0 0 0
1 0 0 0 1
0 0 0 0 0
1 0 0 0 0
0 0 0 0 0
0 0 0 1 0
0 0 0 1 0
0 1 1 0 0
0 0 0 0 0

31. Пример обхода графа в глубину

31
Матрица смежности графа G:
3
(2)
2
7
5
(4)
(1) 1
4
12
10
6
8
(3)
13
9
11
Список вершин: 1 2 4 6
3
(2)
(5)
2
7
5
(4)
(1) 1
4
12
10
6
8
(3)
13
11
Список вершин: 1 2 4 6 5
9
1
2
3
4
5
6
H (G )
7
8
9
10
11
12
13
1
0
1
0
0
0
0
0
0
0
0
0
1
0
2
1
0
0
1
0
0
0
0
0
0
0
0
0
3
0
0
0
0
0
0
1
0
0
0
0
0
0
4
0
1
0
0
0
1
1
0
0
0
0
1
0
5
0
0
0
0
0
1
0
1
0
0
0
0
0
6
0
0
0
1
1
0
1
0
1
0
0
0
1
7
0
0
1
1
0
1
0
0
0
0
0
0
0
8
0
0
0
0
1
0
0
0
1
0
0
0
0
9 10 11 12 13
0 0 0 1 0
0 0 0 0 0
0 0 0 0 0
0 0 0 1 0
0 0 0 0 0
1 0 0 0 1
0 0 0 0 0
1 0 0 0 0
0 0 0 0 0
0 0 0 1 0
0 0 0 1 0
0 1 1 0 0
0 0 0 0 0

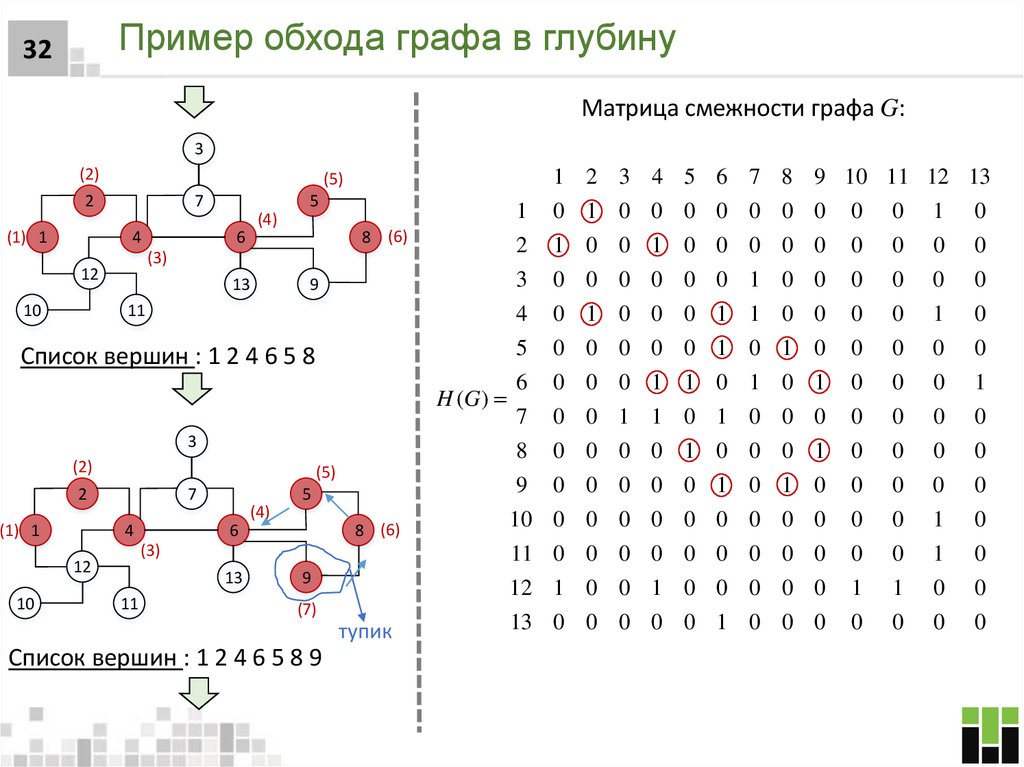
32. Пример обхода графа в глубину

32
Матрица смежности графа G:
3
(2)
(5)
2
7
5
(4)
(1) 1
4
(3)
12
10
8 (6)
6
13
9
11
Список вершин : 1 2 4 6 5 8
3
(2)
(5)
2
7
5
(4)
(1) 1
4
12
10
8 (6)
6
(3)
13
11
9
(7)
тупик
Список вершин : 1 2 4 6 5 8 9
1
2
3
4
5
6
H (G )
7
8
9
10
11
12
13
1
0
1
0
0
0
0
0
0
0
0
0
1
0
2
1
0
0
1
0
0
0
0
0
0
0
0
0
3
0
0
0
0
0
0
1
0
0
0
0
0
0
4
0
1
0
0
0
1
1
0
0
0
0
1
0
5
0
0
0
0
0
1
0
1
0
0
0
0
0
6
0
0
0
1
1
0
1
0
1
0
0
0
1
7
0
0
1
1
0
1
0
0
0
0
0
0
0
8
0
0
0
0
1
0
0
0
1
0
0
0
0
9 10 11 12 13
0 0 0 1 0
0 0 0 0 0
0 0 0 0 0
0 0 0 1 0
0 0 0 0 0
1 0 0 0 1
0 0 0 0 0
1 0 0 0 0
0 0 0 0 0
0 0 0 1 0
0 0 0 1 0
0 1 1 0 0
0 0 0 0 0

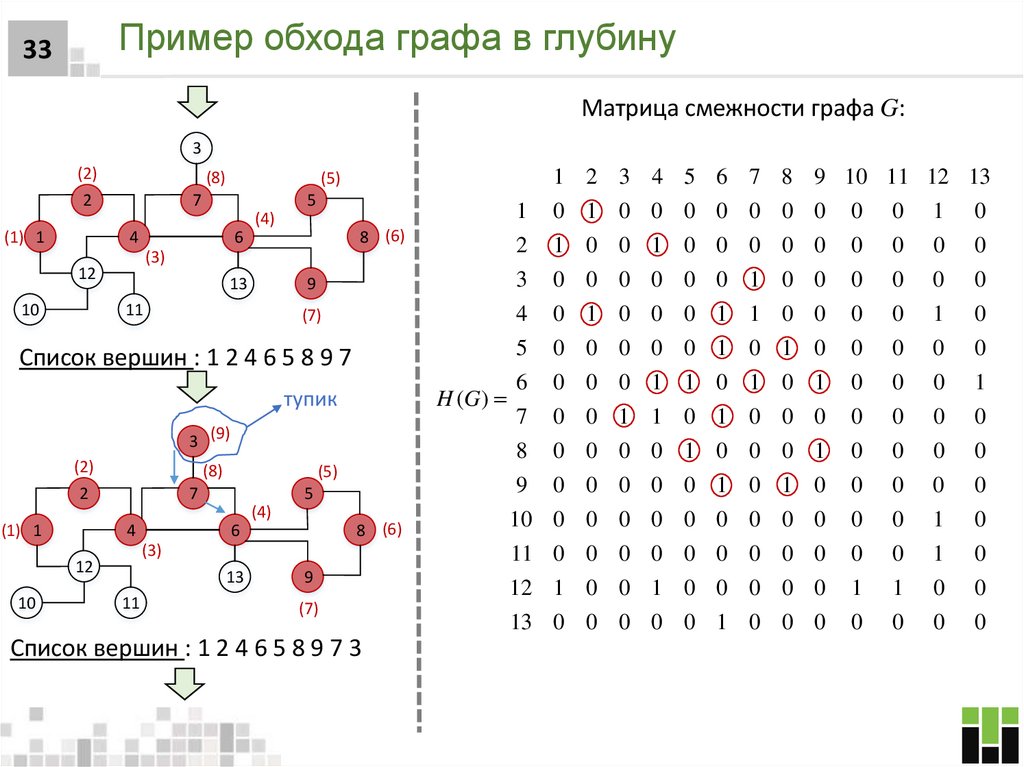
33. Пример обхода графа в глубину

33
Матрица смежности графа G:
3
(2)
(8)
2
(5)
7
5
(4)
(1) 1
4
(3)
12
10
8 (6)
6
13
9
11
(7)
Список вершин : 1 2 4 6 5 8 9 7
тупик
3 (9)
(2)
(8)
2
(5)
7
5
(4)
(1) 1
4
(3)
12
10
8 (6)
6
13
11
9
(7)
Список вершин : 1 2 4 6 5 8 9 7 3
1
2
3
4
5
6
H (G )
7
8
9
10
11
12
13
1
0
1
0
0
0
0
0
0
0
0
0
1
0
2
1
0
0
1
0
0
0
0
0
0
0
0
0
3
0
0
0
0
0
0
1
0
0
0
0
0
0
4
0
1
0
0
0
1
1
0
0
0
0
1
0
5
0
0
0
0
0
1
0
1
0
0
0
0
0
6
0
0
0
1
1
0
1
0
1
0
0
0
1
7
0
0
1
1
0
1
0
0
0
0
0
0
0
8
0
0
0
0
1
0
0
0
1
0
0
0
0
9 10 11 12 13
0 0 0 1 0
0 0 0 0 0
0 0 0 0 0
0 0 0 1 0
0 0 0 0 0
1 0 0 0 1
0 0 0 0 0
1 0 0 0 0
0 0 0 0 0
0 0 0 1 0
0 0 0 1 0
0 1 1 0 0
0 0 0 0 0

34. Пример обхода графа в глубину

34
Матрица смежности графа G:
3 (9)
(2)
(8)
2
(5)
7
5
(4)
(1) 1
4
(3)
12
10
8 (6)
6
11
тупик
13
9
(10)
(7)
Список вершин : 1 2 4 6 5 8 9 7 3 13
3 (9)
(2)
(8)
2
(1) 1
12
10
(5)
7
4
(11)
11
(3)
5
(4)
8 (6)
6
13
9
(10)
(7)
Список вершин : 1 2 4 6 5 8 9 7 3 13 12
1
2
3
4
5
6
H (G )
7
8
9
10
11
12
13
1
0
1
0
0
0
0
0
0
0
0
0
1
0
2
1
0
0
1
0
0
0
0
0
0
0
0
0
3
0
0
0
0
0
0
1
0
0
0
0
0
0
4
0
1
0
0
0
1
1
0
0
0
0
1
0
5
0
0
0
0
0
1
0
1
0
0
0
0
0
6
0
0
0
1
1
0
1
0
1
0
0
0
1
7
0
0
1
1
0
1
0
0
0
0
0
0
0
8
0
0
0
0
1
0
0
0
1
0
0
0
0
9 10 11 12 13
0 0 0 1 0
0 0 0 0 0
0 0 0 0 0
0 0 0 1 0
0 0 0 0 0
1 0 0 0 1
0 0 0 0 0
1 0 0 0 0
0 0 0 0 0
0 0 0 1 0
0 0 0 1 0
0 1 1 0 0
0 0 0 0 0

35. Пример обхода графа в глубину

35
Матрица смежности графа G:
3
(2)
(8)
2
(5)
7
(1) 1
12
5
(4)
(3)
4
(11)
10
11
(12)
тупик
8 (6)
6
13
9
(10)
(7)
Вершины: 1 2 4 6 5 8 9 7 3 13 12 10
3
(2)
(8)
2
(1) 1
12
10
(12)
(5)
7
4
(11)
11
(13)
(3)
5
(4)
8 (6)
6
13
9
(10)
(7)
Вершины: 1 2 4 6 5 8 9 7 3 13 12 10 11
1
2
3
4
5
6
H (G )
7
8
9
10
11
12
13
1
0
1
0
0
0
0
0
0
0
0
0
1
0
2
1
0
0
1
0
0
0
0
0
0
0
0
0
3
0
0
0
0
0
0
1
0
0
0
0
0
0
4
0
1
0
0
0
1
1
0
0
0
0
1
0
5
0
0
0
0
0
1
0
1
0
0
0
0
0
6
0
0
0
1
1
0
1
0
1
0
0
0
1
7
0
0
1
1
0
1
0
0
0
0
0
0
0
8
0
0
0
0
1
0
0
0
1
0
0
0
0
9 10 11 12 13
0 0 0 1 0
0 0 0 0 0
0 0 0 0 0
0 0 0 1 0
0 0 0 0 0
1 0 0 0 1
0 0 0 0 0
1 0 0 0 0
0 0 0 0 0
0 0 0 1 0
0 0 0 1 0
0 1 1 0 0
0 0 0 0 0

36. Пример обхода графа в ширину

36
Осуществим обход графа G:
3
(2)
(1) 1
(3)
7
4
(4)
(7)
12
(5) 10
(9)
(8)
2
11 (6)
Список смежности:
1: 2 12
2: 1 4
3: 7
4: 2 6 7 12
5: 6 8
6: 4 5 7 9 13
7: 3 4 6
8: 5 9
9: 6 8
10: 12
11: 12
12: 1 4 10 11
13: 6
Матрица смежности графа G:
(12)
5
8 (13)
6
13
9
(11)
(10)
1
2
3
4
5
6
H (G )
7
8
9
10
11
12
13
1
0
1
0
0
0
0
0
0
0
0
0
1
0
2
1
0
0
1
0
0
0
0
0
0
0
0
0
3
0
0
0
0
0
0
1
0
0
0
0
0
0
4
0
1
0
0
0
1
1
0
0
0
0
1
0
5
0
0
0
0
0
1
0
1
0
0
0
0
0
6
0
0
0
1
1
0
1
0
1
0
0
0
1
7
0
0
1
1
0
1
0
0
0
0
0
0
0
8
0
0
0
0
1
0
0
0
1
0
0
0
0
9 10 11 12 13
0 0 0 1 0
0 0 0 0 0
0 0 0 0 0
0 0 0 1 0
0 0 0 0 0
1 0 0 0 1
0 0 0 0 0
1 0 0 0 0
0 0 0 0 0
0 0 0 1 0
0 0 0 1 0
0 1 1 0 0
0 0 0 0 0
Список вершин: 1 2 12 4 10 11 6 7 5 9 13 3 8

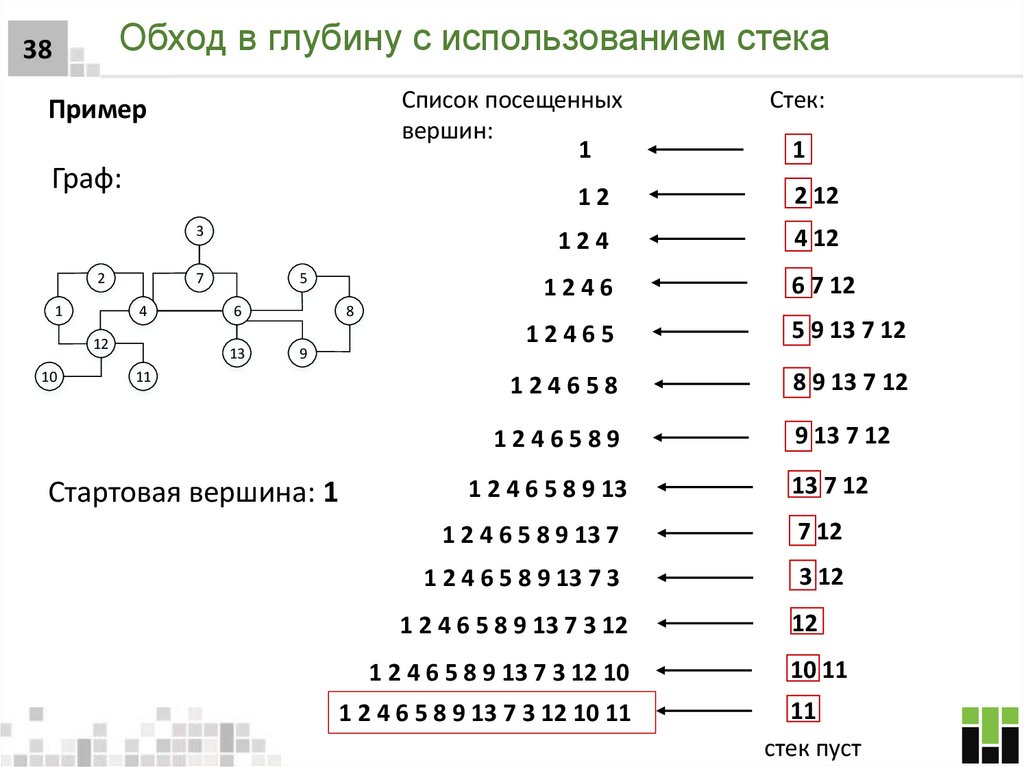
37. Обход в глубину с использованием стека

37
Обход в глубину с использованием стека
Итеративная реализация
(один из вариантов):
Шаг 1. Разместить любую вершину графа на вершине стека
Шаг 2. Взять верхний элемент стека и добавьте его в список
посещенных вершин
Шаг 3. Создать список смежных вершин этой вершины
Шаг 4. Добавить те, которых нет в списке посещенных, в
начало стека
Шаг 5. Продолжить повторять шаги 2 и 3, пока стек не
станет пустым
В случае если стек пуст, а в списке просмотренных
вершин не все вершины (значит граф несвязный),
необходимо повторить данный алгоритм для
оставшихся не просмотренных вершин, стартуя от
какой-либо из них

38. Обход в глубину с использованием стека

38
Список посещенных
вершин:
1
Стек:
12
2 12
124
4 12
1246
6 7 12
12465
5 9 13 7 12
124658
8 9 13 7 12
1246589
9 13 7 12
1 2 4 6 5 8 9 13
13 7 12
1 2 4 6 5 8 9 13 7
7 12
1 2 4 6 5 8 9 13 7 3
3 12
1 2 4 6 5 8 9 13 7 3 12
12
1 2 4 6 5 8 9 13 7 3 12 10
10 11
1 2 4 6 5 8 9 13 7 3 12 10 11
11
стек пуст
Пример
Граф:
3
2
1
7
4
12
10
5
6
13
8
9
11
Стартовая вершина: 1
1

39. Рекурсивная реализация обхода графа в глубину

39
Рекурсивная реализация обхода графа в глубину
при рекурсивном вызове функции используется аппаратный стек, в
котором сохраняются значения аргументов и локальных переменных
каждого рекурсивного вызова функции
при завершении текущего вызова и возврате на предыдущий имеется
доступ к предыдущим значениям аргументов и локальных
переменных функции
это делает возможным рекурсивную реализацию алгоритм обхода
графа в глубину
рекурсивная реализация выглядит более компактно в сравнении с
итеративной и позволяет не организовывать программный стек для
хранения смежных вершин текущей просматриваемой вершины (для
этого неявно используется аппаратный стек)
недостатком такой реализации является ограниченная емкость
аппаратного стека, что может при существенных размерах графа
привести к переполнению аппаратного стека

40. Описание рекурсивной реализации алгоритма обхода графа в глубину

40
Описание рекурсивной реализации алгоритма
обхода графа в глубину
Шаг 1. Помечаем вершину v как просмотренную
Шаг 2. Обрабатываем вершину v
Шаг 3. Ищем вершину u, смежную v, которая еще не
была отмечена как просмотренная
Шаг 4. Повторяем рекурсивно шаги 1-3 для вершины u

41. Обход в ширину с использованием очереди

41
Обход в ширину с использованием очереди
Шаг 1. Выбирается любая вершина графа, помечается как
посещенная и заносится в очередь
Шаг 2. Просматривается первая вершина из очереди, если
она не помечена как посещенная, то помечается. Все
смежные ей непомеченные вершины заносятся в очередь.
После этого она удаляется из очереди
Шаг 3. Повторяется шаг 2 до тех пор, пока очередь не пуста
В случае если очередь пуста, а в списке просмотренных
вершин не все вершины (значит граф несвязный),
необходимо повторить данный алгоритм для
оставшихся не просмотренных вершин, стартуя от
какой-либо из них

42. Обход в ширину с использованием очереди

42
Список посещенных
вершин:
Пример
Граф:
1
3
2
1
7
4
12
10
12
5
6
13
8
9
11
Стартовая вершина: 1
Очередь:
1
1 2 12
2 12 4
12 4 10 11
1 2 12
1 2 12 4
4 10 11 6 7
1 2 12 4 10
10 11 6 7
1 2 12 4 10 11
11 6 7
1 2 12 4 10 11 6
6 7 5 9 13
1 2 12 4 10 11 6 7
7 5 9 13 3
1 2 12 4 10 11 6 7 5
5 9 13 3 8
1 2 12 4 10 11 6 7 5 9
1 2 12 4 10 11 6 7 5 9 13
1 2 12 4 10 11 6 7 5 9 13 3
1 2 12 4 10 11 6 7 5 9 13 3 8
9 13 3 8
13 3 8
38
8
очередь пуста

43. Временная эффективность (трудоемкость) алгоритмов обхода графов

43
Временная эффективность (трудоемкость)
алгоритмов обхода графов
Алгоритмы обхода графа в глубину и ширину в худшем
случае имеют одинаковые верхние оценки функции
трудоемкости (О-оценки)
Трудоемкость алгоритмов зависит от
способа представления графа:
в случае использования матрицы
смежности:
O(n2)
в случае использования списка
смежности:
O(n+m)
где n – число вершин графа, m – число ребер графа

44. Обход графа

44
Обход графа
0
1
6
3
5
7
2
4
САМ. Стартуя с вершины 0 выполнить обход графа,
представленного диаграммой выше, в глубину и ширину.
Результат представить в виде списка просмотренных вершин

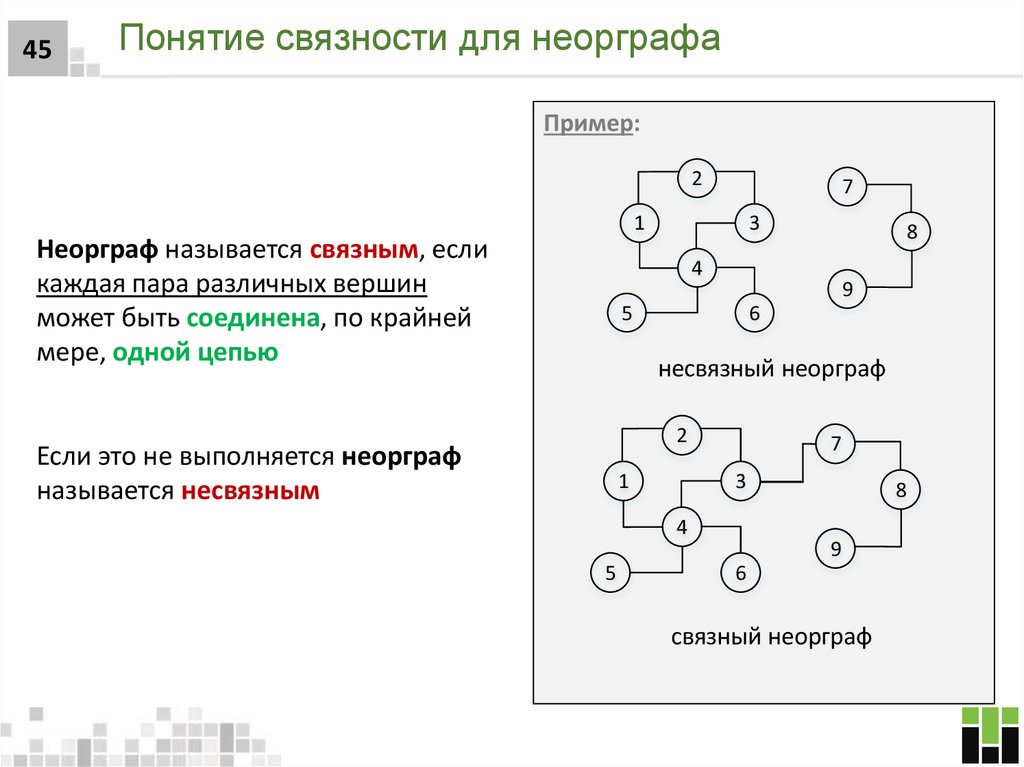
45. Понятие связности для неорграфа

45
Понятие связности для неорграфа
Пример:
2
7
1
Неорграф называется связным, если
каждая пара различных вершин
может быть соединена, по крайней
мере, одной цепью
3
8
4
9
5
6
несвязный неорграф
2
Если это не выполняется неорграф
называется несвязным
1
7
3
4
5
8
9
6
связный неорграф

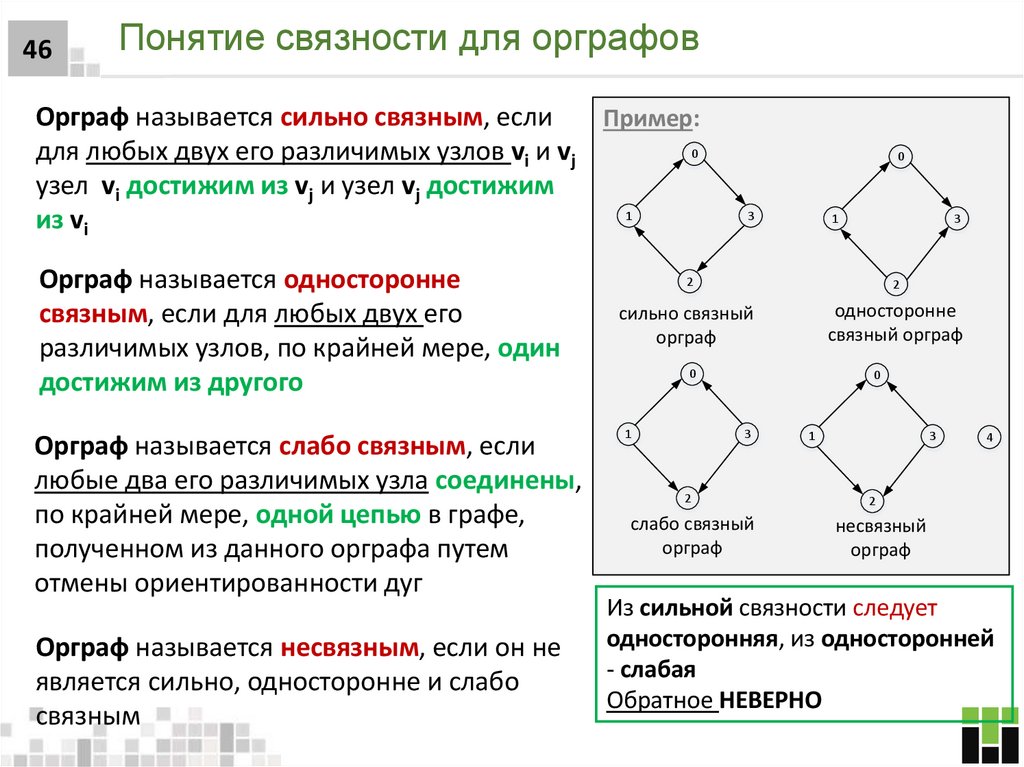
46. Понятие связности для орграфов

46
Понятие связности для орграфов
Орграф называется сильно связным, если
Пример:
0
для любых двух его различимых узлов vi и vj
узел vi достижим из vj и узел vj достижим
1
из vi
Орграф называется односторонне
связным, если для любых двух его
различимых узлов, по крайней мере, один
достижим из другого
Орграф называется слабо связным, если
любые два его различимых узла соединены,
по крайней мере, одной цепью в графе,
полученном из данного орграфа путем
отмены ориентированности дуг
Орграф называется несвязным, если он не
является сильно, односторонне и слабо
связным
0
3
1
3
2
2
сильно связный
орграф
односторонне
связный орграф
0
1
0
3
1
3
2
2
слабо связный
орграф
несвязный
орграф
4
Из сильной связности следует
односторонняя, из односторонней
- слабая
Обратное НЕВЕРНО

47. Компоненты связности графов

47
Компоненты связности графов
Любой граф можно разбить на
непересекающиеся связные подграфы, называемые
компонентами связности
Для неорграфа
Компонентой связности называется
его связный подграф, не являющийся
собственным подграфом никакого
другого связного подграфа данного
графа
(максимально связный подграф)
Для орграфа
Компонентой сильной (односторонней,
слабой) связности
называется его сильно (односторонне,
слабо) связный подграф,
не являющийся собственным
подграфом никакого другого сильно
(односторонне, слабо) связного
подграфа данного графа
(максимально сильно [односторонне,
слабо] связный подграф)

48. Отношение достижимости на графах

48
Отношение достижимости на графах
При решении задач на графах часто возникает вопрос о существовании путей
между заданными или всеми парами вершин
Ответ на этот вопрос дает отношение достижимости, заданное на множестве
вершин неорграфа или орграфа G=(V, E)
Отношение достижимости: вершина w достижима из вершины v, если
v = w или в G есть маршрут (путь) из v в w
(иначе говоря, отношение достижимости является рефлексивным и
транзитивным замыканием отношения E)
Для неорграфа:
Для орграфа:
отношение достижимости
рефлексивно, транзитивно и симметрично
(т.е. является отношением эквивалентности на
множестве V)
отношение достижимости не всегда
симметрично
классы эквивалентности по отношению
достижимости соответствуют компонентам
связности (если классов эквивалентности больше 1,
то неорграф не является связным)
симметричным является только лишь
отношение взаимной достижимости

49. Отношение достижимости на графах

49
Отношение достижимости на графах
Отношение взаимной достижимости: узлы v и w орграфа G=(V, E)
взаимно достижимы, если в G=(V, E) есть путь из v и w и путь из w в v
отношение взаимной достижимости
рефлексивно, симметрично и транзитивно
(следовательно, является отношением эквивалентности на
множестве узлов орграфа G)
классы эквивалентности по отношению взаимной достижимости
соответствуют компонентам сильной связности (двусвязным
компонентам) орграфа

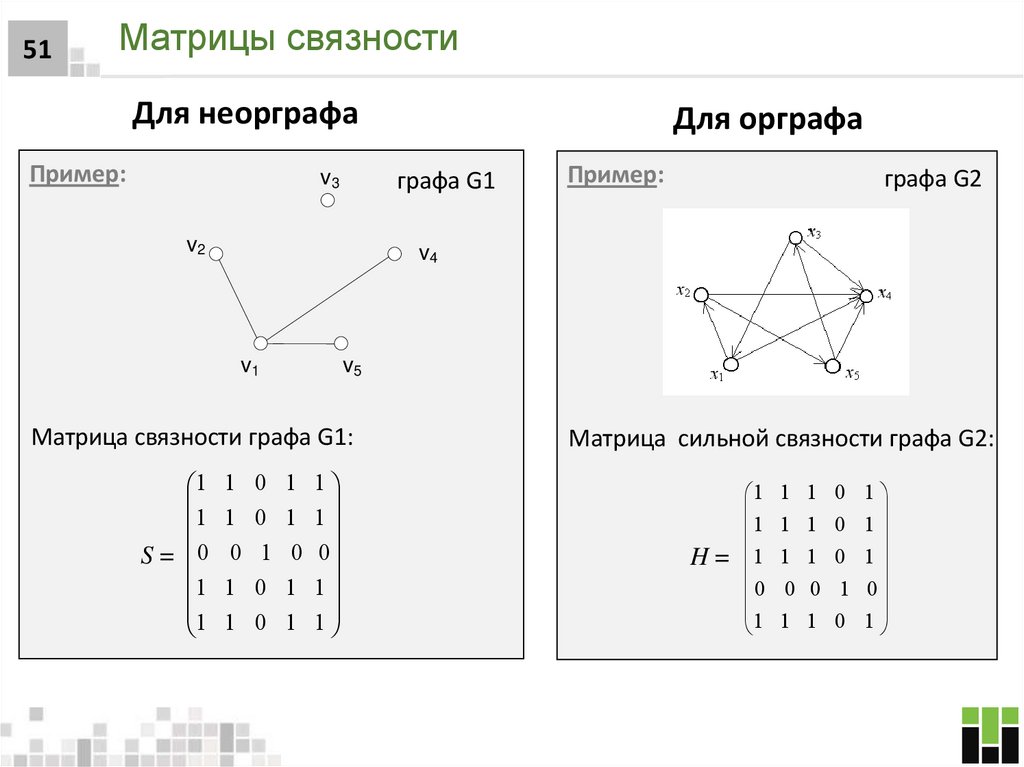
50. Матрицы связности

50
Матрицы связности
Отношение достижимости можно представить
бинарной матрицей связности
Для неорграфа
Для орграфа
Матрица односторонней связности для
Матрица связности для неорграфа G = (V, E)
с множеством вершин V v1 ,..., vn - это
матрица S sij n n
если вершины vi и v j принадлежат
1,
,
sij одной компоненте связности
0 в противном случае
орграфа G = (V, E) с множеством узлов
V v1 ,..., vn - это матрица T tij
n n
1, если существует путь из vi в v j ,
tij
0 в противном случае
Матрица сильной связности для
орграфа G = (V, E) с множеством узлов
V v1 ,..., vn - это матрица H hij
n n
если существует путь из vi в v j и
1,
,
hij из v j в vi
0 в противном случае

51. Матрицы связности

51
Матрицы связности
Для неорграфа
Пример:
v3
Для орграфа
графа G1
v2
Пример:
графа G2
v4
v1
v5
Матрица связности графа G1:
1 1 0 1 1
1
1
0
1
1
0 0 1 0 0
S=
1 1 0 1 1
1 1 0 1 1
Матрица сильной связности графа G2:
1 1 1 0 1
1
1
1
0
1
H = 1 1 1 0 1
0 0 0 1 0
1 1 1 0 1

52. Вершинная и реберная связность графов

52
некоторые связные графы можно сделать несвязными, удалив одну
вершину или одно ребро
вершина, обладающая таким свойством, называется точкой сочленения, а
ребро с таким свойством – мостом
неразделимым называется непустой граф, не имеющий точек сочленения
блоком графа называется максимальный неразделимый его подграф
Пример разделимого графа:
G – граф
ребро (v1, v2) – мост
вершины v1 и v2 – точки
сочленения
В1, В2, В3 – блоки графа G
v1
v2
G
B1
B2
B3

53. Вершинная и реберная связность графов

53
Вершинная и реберная связность графов
Теорема 3. Пусть v – вершина связного графа G=(V, E). Вершина v является
точкой сочленения графа G=(V, E) тогда и только тогда, когда в
графе G=(V, E) существуют вершины v1 и v2, отличные от v, и такие,
что v принадлежит каждой простой (v1 - v2) – цепи
Теорема 4. Ребро e – мост связного графа G=(V, E) тогда и только тогда, когда в
графе G=(V, E) существуют вершины v1 и v2 такие, что ребро e
принадлежит каждой простой (v1 - v2) – цепи, или ребро e не
принадлежит ни одному циклу графа G=(V, E)
Теорема 5. Пусть G=(V, E) – связный граф, имеющий не менее трех вершин.
Граф G=(V, E) является блоком тогда и только тогда, когда любая
вершина и любое ребро графа G=(V, E) принадлежат некоторому
общему для них простому циклу
[ доказательства этих теорем смотрите в книге
Свами М. и др., Графы, сети и алгоритмы: пер. с
анг. – М.: Мир, 1984]

54. Вершинная и реберная связность графов

54
Вершинная и реберная связность графов
Вершинная связность графа G - наименьшее число вершин, при удалении
которых граф G становится несвязным или
(G)
тривиальным
(вершинная связность несвязного графа равна 0, а
графа, имеющего точку сочленения, равна 1)
Реберной связностью графа G - наименьшее количество ребер, удалением
которых можно получить несвязный граф
(G)
(реберная связность несвязного графа равна 0, а
связность графа, имеющего мост равна 1)
Теорема 6. Для любого графа G выполняется (G) (G) (G)
[ САМ. ознакомится с доказательством данной теоремы
(расположенном в:
S:\_Студентам\ИЯТШ\ОЯТЦ\Дискретная_математика\!1_Сам_изуч\3_Основы
теории графов]

55. Метрические характеристики графов

55
Метрические характеристики графов
Расстояние r(vi, vj) между вершинами - длина кратчайшей цепи
(сама кратчайшая цепь называется
vi и vj в связном графе G = (V, E)
геодезической)
Определенное таким образом расстояние удовлетворяет
всем аксиомам метрики:
2) r v , v r v , v (в неориентированном графе)
1) r vi , v j 0, причем r (vi , v j ) 0 только при v i v j
i
j
j
i
3) r vi , v j r v j , vk r vi , vk (правило треугольника)
поэтому расстояние можно рассматривать как метрику графа, а множество
вершин – как метрическое пространство
то, что расстояние удовлетворяет первым двум
аксиомам – очевидно
докажем, что оно удовлетворяет третьей аксиоме (3)

56. Метрические характеристики графов

56
Метрические характеристики графов
Доказательство удовлетворения расстояния
3-й аксиоме метрики:
1-ый случай: если vi и vj или vj и vk не связаны маршрутом, тогда r vi , v j
или r v j , vk , тогда соответствие r третьей аксиоме метрики
очевидно
2-ой случай: если vi и vk не связаны маршрутом, тогда либо vi и vj, либо
vj и vk не связаны, получим первый случай
3-й случай: если vi и vj связаны и vj и vk связаны, то в этом случае,
• когда vj лежит на кратчайшем маршруте, соединяющем vi и vk , то
r vi , v j r v j , vk r vi , vk
• в остальных случаях очевидно, что
j
r(i, j)
i
r vi , v j r v j , vk r vi , vk
j
r(j, k)
r(i, j)
k
r vi , vk r vi , v j r v j , vk
i
r(j, k)
r(i, k)
k
r vi , v j r v j , vk r vi , vk

57. Метрические характеристики графов

57
Метрические характеристики графов
Диаметр связного графа G (d(G)) - длина длиннейшей геодезической цепи
(наибольшее расстояние между вершинами
графа)
Теорема 7. В связном графе любые две простые цепи максимальной длины
имеют общую вершину
[САМ. ознакомится с доказательством данной теоремы, расположенном в:
S:\_Студентам\ИЯТШ\ОЯТЦ\Дискретная_математика\!1_Сам_изуч\3_Основы теории
графов\Доказательство теоремы 7)]
Эксцентриситет (e(v)) вершины v в связном графе G - максимальное
расстояние от вершины v до других вершин графа G
(наиболее эксцентричные вершины – это концы диаметра)
Радиус (R(G)) графа G - наименьший из эксцентриситетов вершин
Вершина v называется центральной, если ее эксцентриситет совпадает с
радиусом графа
(центр не обязательно должен быть единственным)
Множество центральных вершин графа G
называется его центром и обозначается С(G)

58. Пример поиска метрических характеристик графа

58
Пример поиска метрических характеристик графа
Найдем метрические характеристики графа (G), заданного диаграммой:
3
2
4
5
1
1) Найдем все расстояния, учитывая, что r(v, w) = r(w, v):
число расстояний можно вычислить, используя формулу для
n!
5!
2
расчета числа сочетаний из n по k: C k
C
10
n
k !(n k )!
5
2!3!
расстояния: r(1, 2)=1; r(1, 3)=2; r(1, 4)=2; r(1, 5)=3; r(2, 3)=1; r(2, 4)=1;
r(2, 5)=2; r(3, 4)=1; r(3, 5)=2; r(4, 5)=1
2) Диаметр: d(G)=3
3) Эксцентриситеты вершин: e(1)=3; e(2)=2; e(3)=2; e(4)=2; e(5)=3
4) Радиус графа: R(G)=2
5) Центры графа: 2, 3, 4

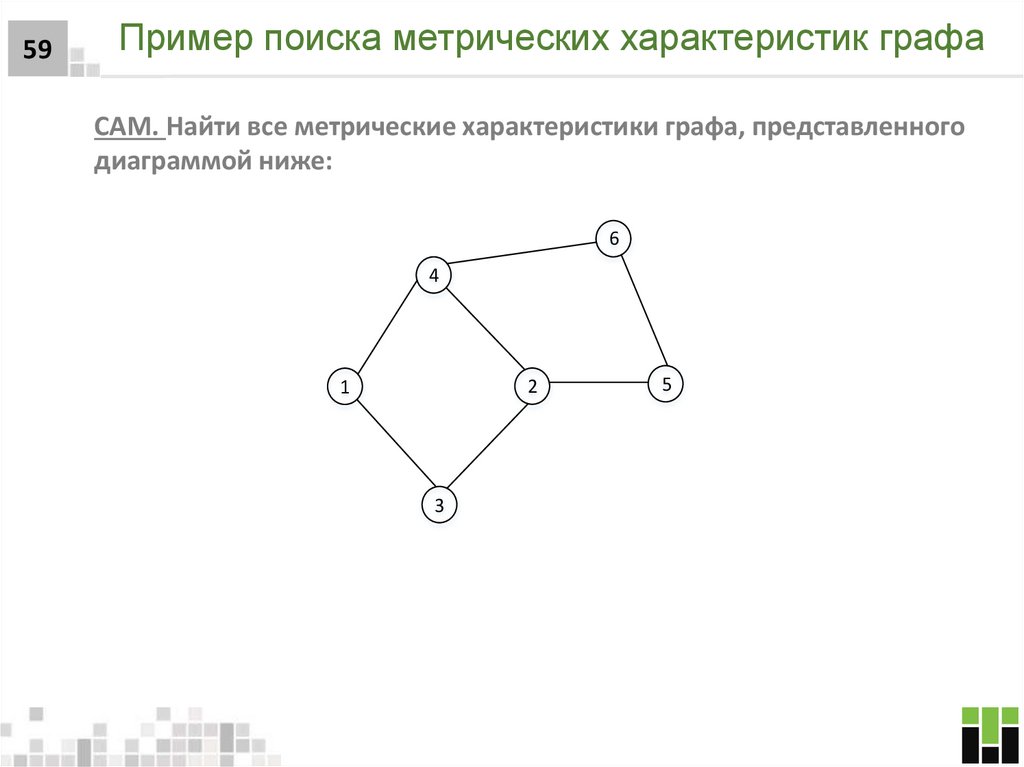
59. Пример поиска метрических характеристик графа

59
Пример поиска метрических характеристик графа
САМ. Найти все метрические характеристики графа, представленного
диаграммой ниже:
6
4
2
1
3
5