Введение в теорию графов

1. Введение в теорию графов

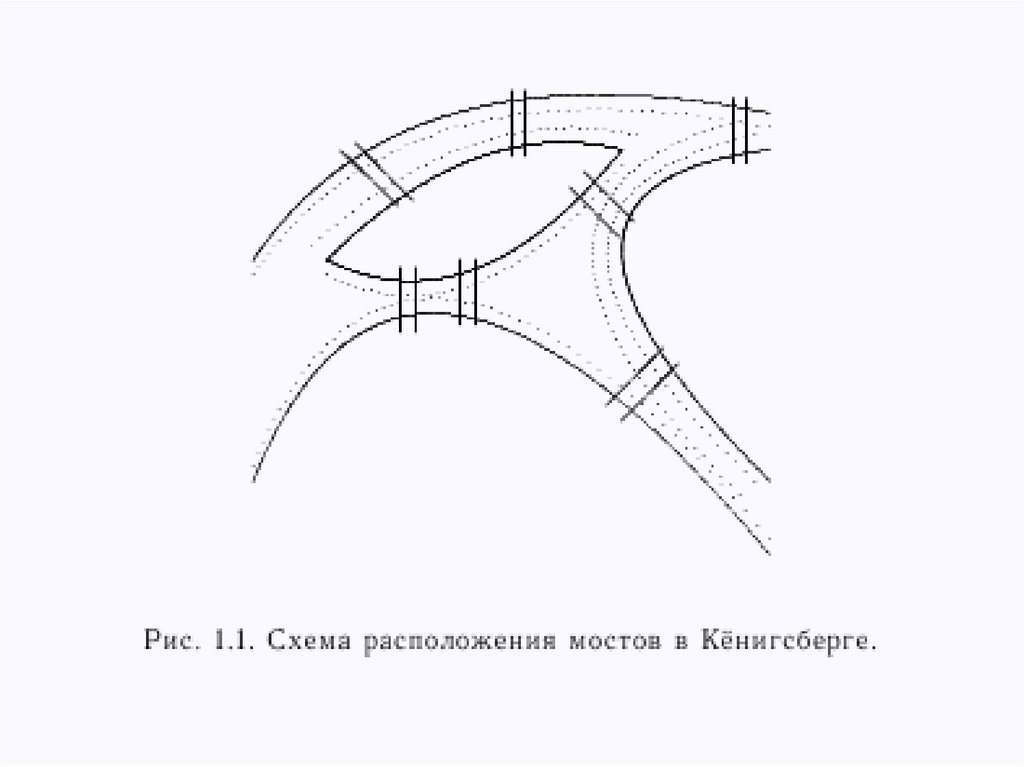
2. Задача о Кёнигсберских мостах:

Может ли пешеход обойти все мосты,
пройдя по каждому из них только один раз,
и вернуться в исходную точку?

3.

4. Задача четырёх красок:

Можно ли любую карту так раскрасить
четырьмя красками, чтобы никакие две
области, имеющие общий участок
границы, не были окрашены в один и тот
же цвет?

5. Задача о домиках и колодцах:

Имеются три домика и три колодца.
Можно ли проложить тропинки от каждого
домика к каждому колодцу так, чтобы
тропинки не пересекались?

6.

Понятие неориентированного
графа

7.

Граф – это система некоторых объектов
вместе с некоторыми парами этих
объектов, изображающая отношение
связи между ними.

8.

Неориентированный граф – это система
G (V , E , Г )
состоящая из множества V с элементами
v, называемыми вершинами графа,
множества E с элементами e,
называемыми рёбрами графа и
отображения Г : E V 2 , ставящего в
соответствие каждому элементу e E
неупорядоченную пару элементов v1 , v2 V
называемых концами ребра e.

9.

Если ребро e u, v , то говорят, что
ребро e соединяет вершины u и v.

10.

Ребро e называют инцидентным
вершине v, если она является одним из
его концов.

11.

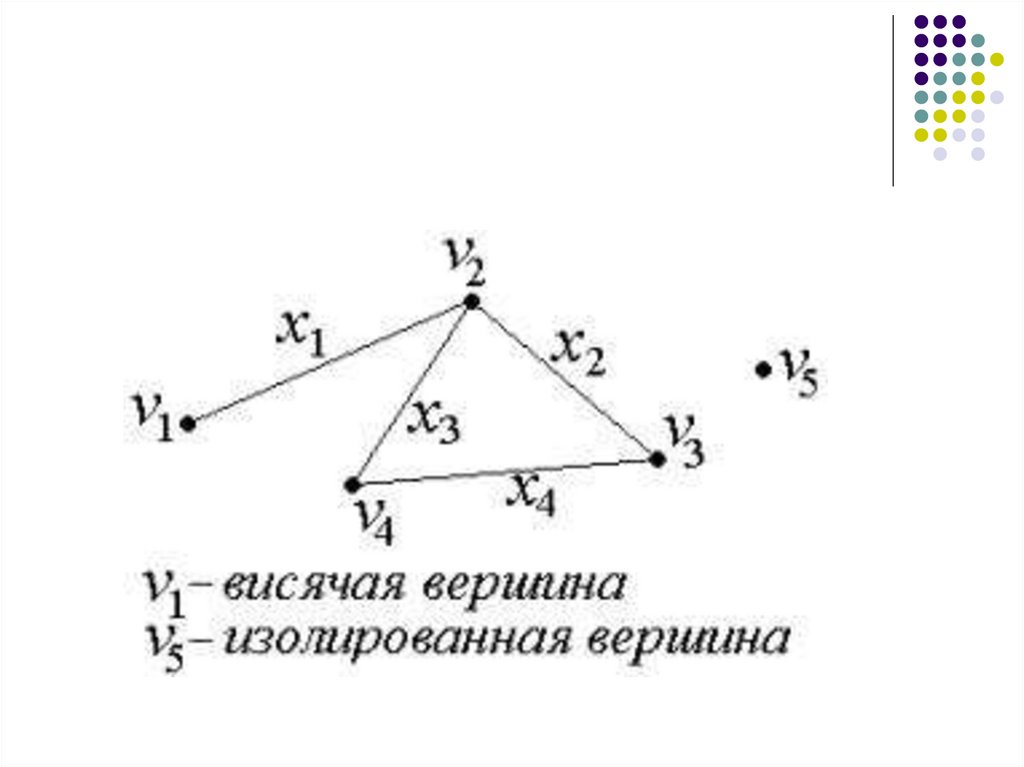
Вершина, не инцидентная ни одному
ребру, называется изолированной.

12.

Вершина, инцидентная ровно одному
ребру, называется концевой, а данное
ребро концевым (висячим).

13.

14.

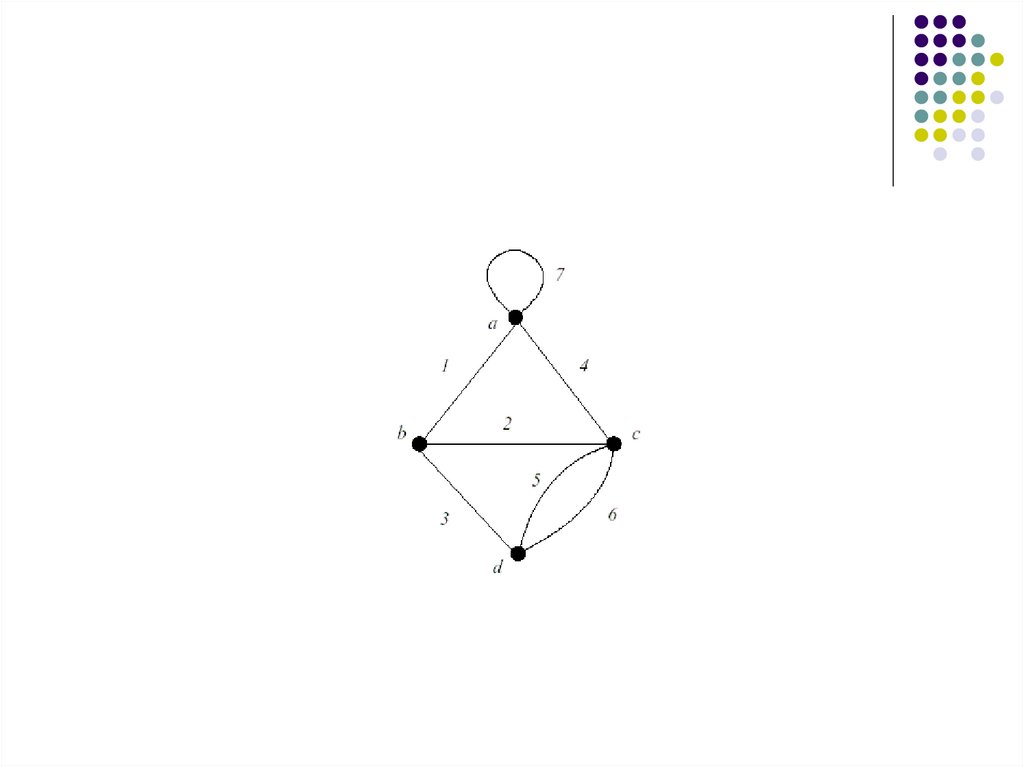
Ребро с совпадающими концами
называется петлёй

15.

16.

Две вершины, инцидентные одному и тому
же ребру, называются смежными
(соседними).
Два ребра, имеющие общую инцидентную
вершину, называются смежными.

17.

Ребра, которым поставлена в
соответствие одна и та же пара вершин,
называются кратными
(параллельными).

18.

19.

Понятие ориентированного графа

20.

Ориентированный граф –
это система G (V , E , Г ) , состоящая из
множества V с элементами v,
называемыми вершинами графа,
множества E с элементами e,
называемыми ребрами графа и
отображения Г : E V 2, ставящего в
соответствие каждому элементу e E
упорядоченную пару элементов v1 , v2 V ,
называемых концами ребра e.

21.

Если Г (e) (u, v) - упорядоченная пара,
т.е. (u, v) (v, u ), , то ребро e называют
ориентированной дугой, u - начало дуги,
v - конец дуги. Обозначение u v .
Вершины u и v в этом случае называют
смежными.

22.

23.

Дугу (u,v) называют заходящей в вершину
v и исходящей из вершины u.

24.

Дугу называют инцидентной вершине v,
если она заходит в v или исходит из v.

25.

Вершина, не являющаяся ни началом ни
концом ни одной дуги, называется
изолированной.

26.

Дугу, начало и конец которой есть одна и
та же вершина, называют петлёй

27.

28.

Дуги, которым поставлена в соответствие
одна и та же пара вершин и если они
имеют одинаковую ориентацию,
называются кратными (параллельными)

29.

30.

Дуги, которым поставлена в соответствие
одна и та же пара вершин, но
направленные противоположно,
называются противоположно
направленными (симметричными)

31.

32.

Способы задания графа
(неориентированного)

33.

1. Перечислением (или списком) рёбер с
указанием их концов и добавлением
списка изолированных вершин.

34. 2. В виде геометрического объекта.

Вершинам соответствуют выделенные
точки, рёбрам – отрезки кривых,
связывающие соответствующие точки и
не проходящие через вершины,
отличные от их концов.

35. 3. Матрицей инцидентности

Это матрица A aij размером n m , в
которой строкам поставлены в
соответствие вершины графа, а столбцам
– рёбра. Каждый элемент матрицы
определяется следующим образом: a ij 1,
если вершина v i инцидентна ребру e j ,
и a ij 0 в противном случае.

36. 4. Матрицей смежности

Это матрица B bij
размером n n ,
в которой и строкам и столбцам
поставлены в соответствие вершины
графа. Каждый элемент матрицы
определяется следующим образом: bij число рёбер, связывающих v i и v j

37.

Способы задания орграфа

38. 1. Перечислением (или списком) дуг с указанием их концов и добавлением списка изолированных вершин

39.

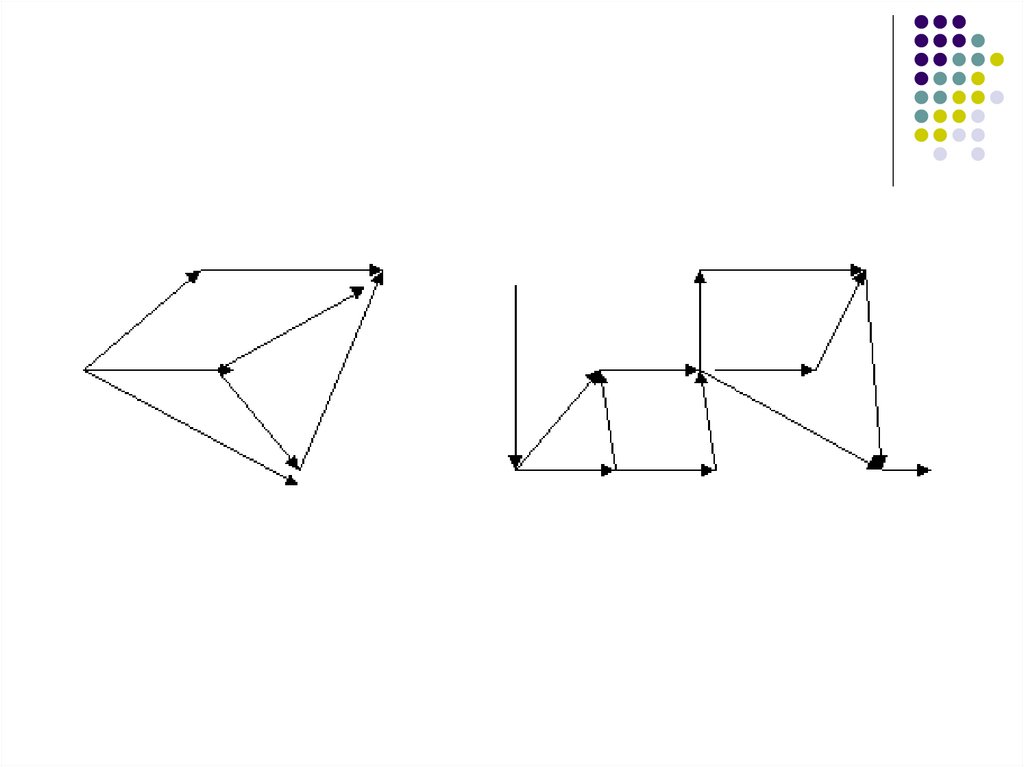
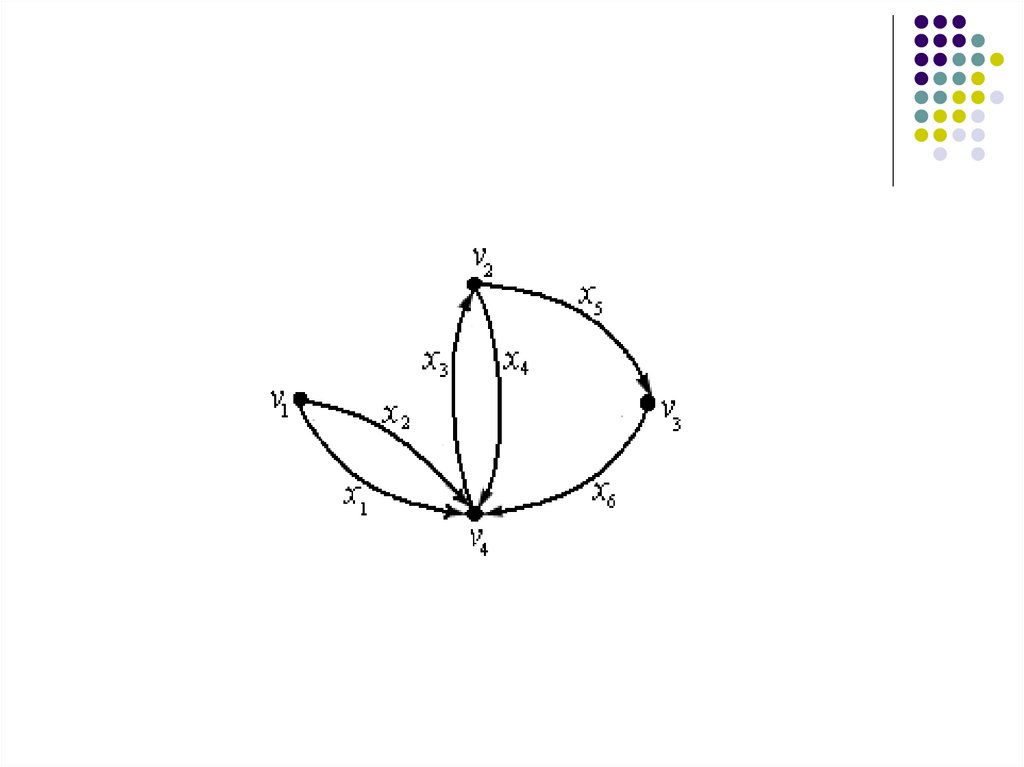
40. 2. В виде геометрического объекта

Вершинам соответствуют выделенные
точки, дугам – направленные отрезки
кривых, связывающие соответствующие
точки и не проходящие через вершины,
отличные от их концов.

41. 3. В виде матрицы инцидентности

Это матрица A aij размером n m, в
которой строкам поставлены в
соответствие вершины графа, а столбцам
– дуги. Каждый элемент матрицы
определяется следующим образом: aij 1 ,
если дуга e j выходит из вершины v i , a ij 1
если дуга e j заходит в вершину vi , a ij 0
если e j не инцидентна vi , и aij 2 , если e j
- петля вокруг vi

42. 4. В виде матрицы смежности

Это матрица B bij размером n n , в
которой и строкам и столбцам
поставлены в соответствие вершины
графа. Каждый элемент матрицы
определяется следующим образом: bij число рёбер, исходящих из v i и
входящих в v j

43.

Операции над графами

44.

Граф H (V ' , E ' ) называется подграфом
графа G (V , E ) , если V ' V , E ' E
При этом очевидно, что каждое ребро из
E’ входит в H вместе со своими концами

45. K1, K2, K3 — подграфы графа G

K1, K2, K3 — подграфы
графа G

46.

Подграф H, содержащий все вершины
графа G называется суграфом.

47.

48.

Подграфом, порожденным множеством
вершин A из V (натянутым на
множество A V ) называется подграф,
соединяющий все вершины из A и все
ребра графа G, соединяющего пары
вершин из A.

49. Объединение графов

50.

51.

52.

53. Пересечение графов

54.

55.

56. Кольцевая сумма графов

57.

58. Коммутативность операций

многоместность

59. Удаление вершины

Если хi -вершина графа G = (X, A), то G–хi порожденный подграф графа G на
множестве вершин X–хi , т. е. Gхi является графом, получившимся после
удаления из графа G вершины хi и всех
ребер, инцидентных этой вершине.

60.

61.

62. Удаление ребра или удаление дуги

Если ai - дуга графа G = (X, A), то G-ai –
подграф графа G, получающийся после
удаления из G дуги ai .
Заметим, что концевые вершины
дуги ai не удаляются.

63.

64. Замыкание или отождествление

Говорят, что пара
вершин хi и xj в графе G замыкается (или
отождествляется), если они заменяются
такой новой вершиной, что все дуги
в графе G, инцидентные хi и xj ,
становятся инцидентными новой вершине.

65.

66. Стягивание

Под стягиванием подразумевают
операцию удаления дуги или ребра и
отождествление его концевых вершин.

67.

68.

69.

Графы и бинарные отношения

70.

Бинарным отношением на множестве A
называется любое подмножество R
множества A2, состоящего из
всевозможных упорядоченных пар
элементов множества A.
Каждому такому отношению можно
поставить в соответствие граф
отношения G=(A,R).

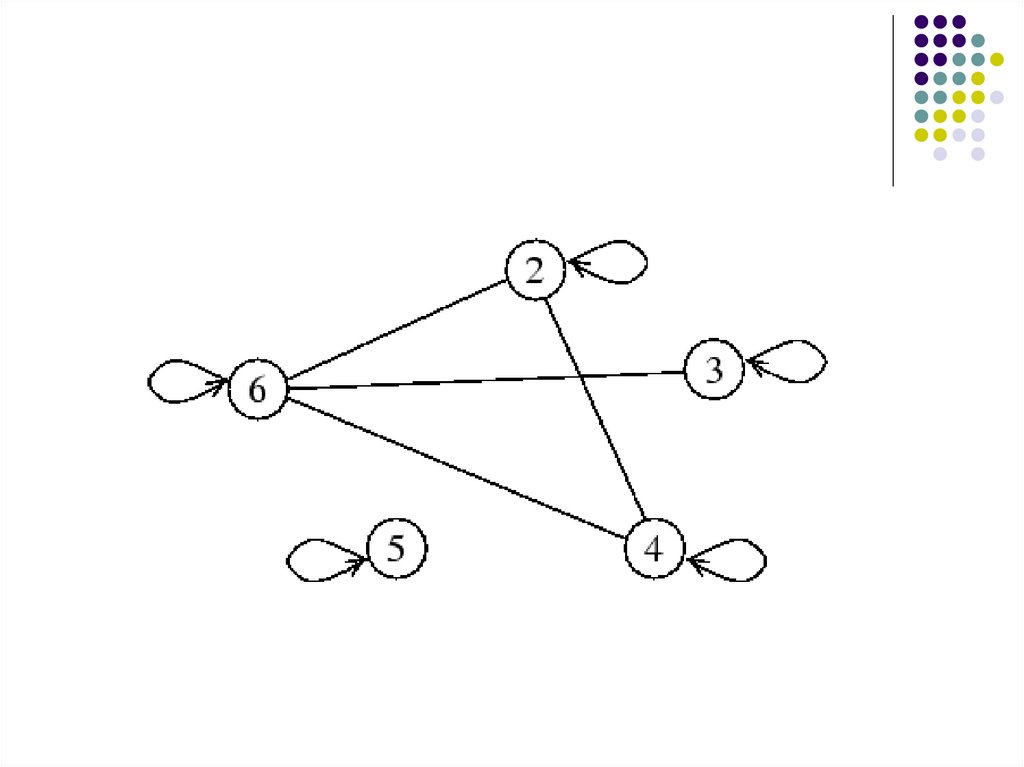
71.

В графе антирефлексивного и
симметричного отношения нет петель и
для каждой пары вершин либо нет ни
одного, либо есть два ребра,
соединяющих эти вершины

72.

Маршруты. Цепи. Циклы для
неориентированных графов

73.

Маршрутом графа G называется
чередующаяся последовательность
M v1 , e1 , v2 , e2 ,..., ek , vk 1
вершин и ребер графа, ei vi , vi 1

74.

Маршрут называется цепью, если все его
ребра различны, и простой цепью, если и
все его вершины различны.

75.

Замкнутый маршрут, являющийся цепью
называется циклом.

76.

Цикл, в котором все вершины, кроме
первой и последней, попарно различны,
называется простым циклом.

77.

Длиной маршрута называется количество
его ребер. В графе без петель и кратных
ребер длина всякого цикла не менее 3.

78.

Вершина v1 называется начальная, если
нет ребер, предшествующих e1 , v k 1 конечная, если нет ребер, следующих за ek
Любая вершина v l , инцидентная el и el 1
называется внутренняя.

79.

Связный неориентированный
граф

80.

Две вершины a и b называются
связными, если существует маршрут с
концами в вершинах a и b.

81.

Граф G называется связным, если
любая его пара вершин связана
маршрутом.

82.

Отношение связности является
отношением эквивалентности. Данное
отношение эквивалентности разбивает
множество вершин V графа G на классы
эквивалентности: V vi , i - количество
i
классов.

83.

Подграфы, порожденные (натянутые на)
множеством vi , называются связными
компонентами графа G.

84.

85. Методика выделения компонент связности в графе

1. Первоначальная разметка
2. Разметка соседних вершин
3. Завершение работы

86.

Маршруты. Цепи. Циклы в
ориентированном графе

87.

88.

Простой путь — это путь, все вершины
которого, кроме, быть может, первой и
последней, попарно различны.

89.

Простой путь ненулевой длины, начало и
конец которого совпадают, называют
контуром.

90.

Произвольный путь ненулевой длины,
начало и конец которого совпадают, будем
называть замкнутым путем.

91.

Ориентированный граф, не содержащий
контуров, называют бесконтурным
графом.

92.

93.

94.

95.

96.

97.

98.

99.

100.

101.

102.

103.

104.

105.

106.

107.

Числа внутренней и внешней
устойчивости

108. Внутренняя устойчивость графа

109. Алгоритм Магу

Шаг 1. Построить матрицу смежности
вершин графа G.
Шаг 2. По единицам матрицы смежности
построить парные дизъюнкты.
Шаг 3. Получить ДНФ.
Шаг 4. Для каждой конъюнкции выписать
недостающие вершины. Это и будут
множества внутренней устойчивости.

110. Внешняя устойчивость графа

111.

Число внутренней устойчивости – число
равное наименьшей из мощностей
множеств внешней устойчивости.

112. Алгоритм Магу:

Шаг 1. Построить матрицу смежности
вершин графа G.
Шаг 2. Поставить единицы по диагонали
матрицы смежности.
Шаг 3. Выписать дизъюнкты по единицам
и получить ДНФ.