Similar presentations:
Операции и алгебры
1. Дискретная математика
Операции и алгебры2.
N-арная операция на множестве М– это функция типа
n
φ:М → M ,
где n – арность операции.
Операция замкнута относительно
множества М по определению, т. е.
операция над элементами
множества М, и результат тоже
элемент М.
3.
Алгеброй называется множество, вместес заданной на нем совокупностью
операций
Ω = { φ1 , φ2 , ... , φn } , т. е.
система
А = (M ; φ1 , φ2 , ... , φn )
.
4.
М – основное (несущее)множество (носитель алгебры)
алгебры А.
Тип алгебры – вектор арностей
операций.
Сигнатура – совокупность
операций .
5.
МножествоM М называется
замкнутым относительно
n-арной операции на М, если
φ(М ′ )⊆ M ′
n
,
т. е. если значения на аргументе из
M′
принадлежат
M′
.
6.
ЕслиM ′ замкнуто относительно
всех операций
φ1 , φ2 , ... , φn ,
алгебры А с носителем М, то система
А′ = (M ′ ; φ1 , φ2 , ... , φn )
называется подалгеброй алгебры А
7. Примеры:
АлгебраR , , – называется полем
действительных чисел.
Обе операции бинарные, поэтому
тип этой алгебры (2,2).
Сигнатура
, .
Подалгеброй этой алгебры является,
например, поле рациональных
чисел.
8. Примеры:
N p = {0,1, 2, ... , p 1}.
Определим на N p операции:
– «сложение по модулю р»,
– «умножение по модулю р»,
следующим образом:
a b c и a b d ,
где с и d – остатки от деления на р чисел
а + b и а b соответственно.
Пусть
9. Примеры:
Пусть, например, р = 7, тогдаN p = { 0,1, 2, 3, 4, 5, 6 }
и
3 4 0 , 3 4 5,
4 6 3
.
Часто обозначают: a + b = с (mod p) и
a b = d (mod p).
10. Примеры:
Конечным полемхарактеристики р называется
алгебра
N p , ,
если р – простое число.
11. Пример:
Булеаном U называетсямножество всех подмножеств
множества U (обозначается B(U)).
Булева алгебра множеств над U
или алгебра Кантора – алгебра
В=(B(U), , , ). Ее тип (2,2,1),
сигнатура Ω = ( , , ).
Элементами основного множества
булевой алгебры являются
множества (подмножества U).
12. Пример:
U′ ⊂ UB B U , , ,
Для любого
– является подалгеброй В.
13. Пример:
МножествоU = {a , b , c , d }
тогда основное множество
алгебры В содержит 16
элементов.
B B a, b , , ,
является подалгеброй В.
14. Свойства бинарных алгебраических операций
Операция φ называетсяассоциативной, если для
любых элементов а, b, с
a b c a b c a b c
15. Пример:
1. Сложение и умножение чисел ассоциативны,что позволяет не ставить скобки в
выражениях
a +b+c
2. Возведение в степень
– не ассоциативна, так как
не равно
a b c a
и
a b c
.
b
a a b
b c
bc
a b c a a
b c.
16. Свойства бинарных алгебраических операций
Операция φ называетсякоммутативной, если для
любых элементов a, b
a b b a
17. Пример:
1 Сложение чисел коммутативно («от переменымест слагаемых сумма не меняется»):
a b b a
2. Умножение чисел коммутативно («от перемены
мест множителей произведение не меняется»):
a b b a
18. Пример:
3 Вычитание и деление – некоммутативныеоперации.
a b b a
a/b b/ a
2. Умножение матриц – некоммутативная
операция, например:
1 2 2 2 2 3 2 2 1 1 2 4
0 1 0 1 0 1 0 1 0 1 0 1
19. Свойства бинарных алгебраических операций
Операция φ называетсядистрибутивной слева
относительно операции ψ, если
для любых a, b, с
a b c a b a c
20. Свойства бинарных алгебраических операций
Операция φ называетсядистрибутивной справа
относительно операции ψ,
если для любых a, b, с
a b c a с b c
21. Пример:
1 Умножение дистрибутивно относительносложения слева и справа
a b c a b a c
a b c a c b c
22. Пример:
2 Возведение в степень дистрибутивноотносительно умножения справа.
a b c a b
c
a b a с b c
c
c
23. Пример:
но не слева, так какa b c a
b c
a b a c a
b
c
a a
b c
24. Пример:
3. Сложение не дистрибутивно относительноумножения
a b c a b a c
a b c a c b c






















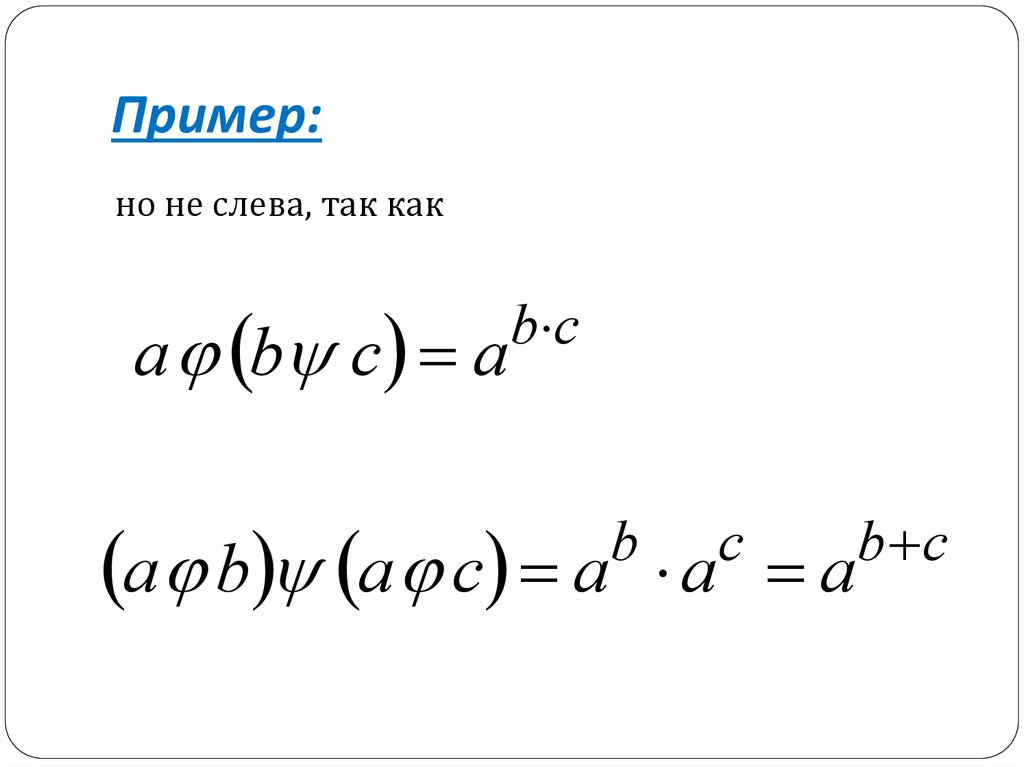

 mathematics
mathematics








