Similar presentations:
Подготовка к сдаче ГИА
1. Подготовка к сдаче ГИА
ОГЭ 9 КЛАСС2. При подготовке к ГИА учащимся необходимо:
2разъяснить особенности формулировок заданий;
познакомить с критериями, которыми
руководствуются эксперты при проверке тестовых
заданий;
рассмотреть самые распространенные ошибки;
отработать навыки тестирования;
научить распределять время на выполнение тестовых
заданий;
ознакомить, по каким темам больше всего вопросов в
тестах.
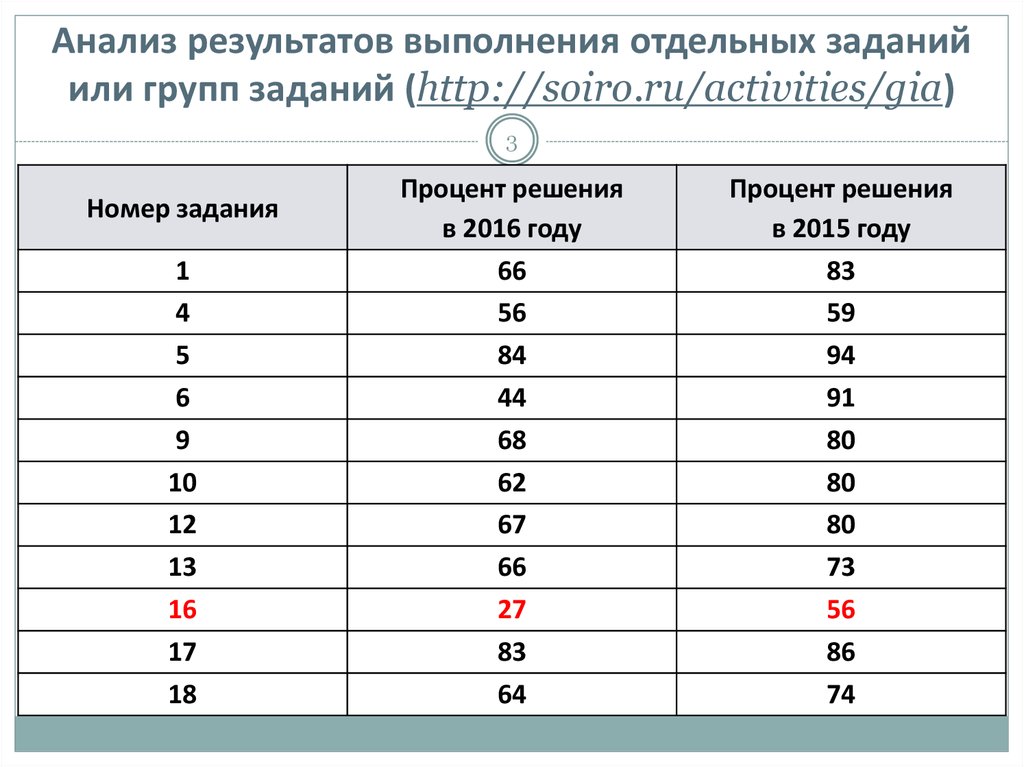
3. Анализ результатов выполнения отдельных заданий или групп заданий (http://soiro.ru/activities/gia)
3Номер задания
1
4
5
6
9
10
12
13
16
17
18
Процент решения
в 2016 году
66
56
84
44
68
62
67
66
27
83
64
Процент решения
в 2015 году
83
59
94
91
80
80
80
73
56
86
74
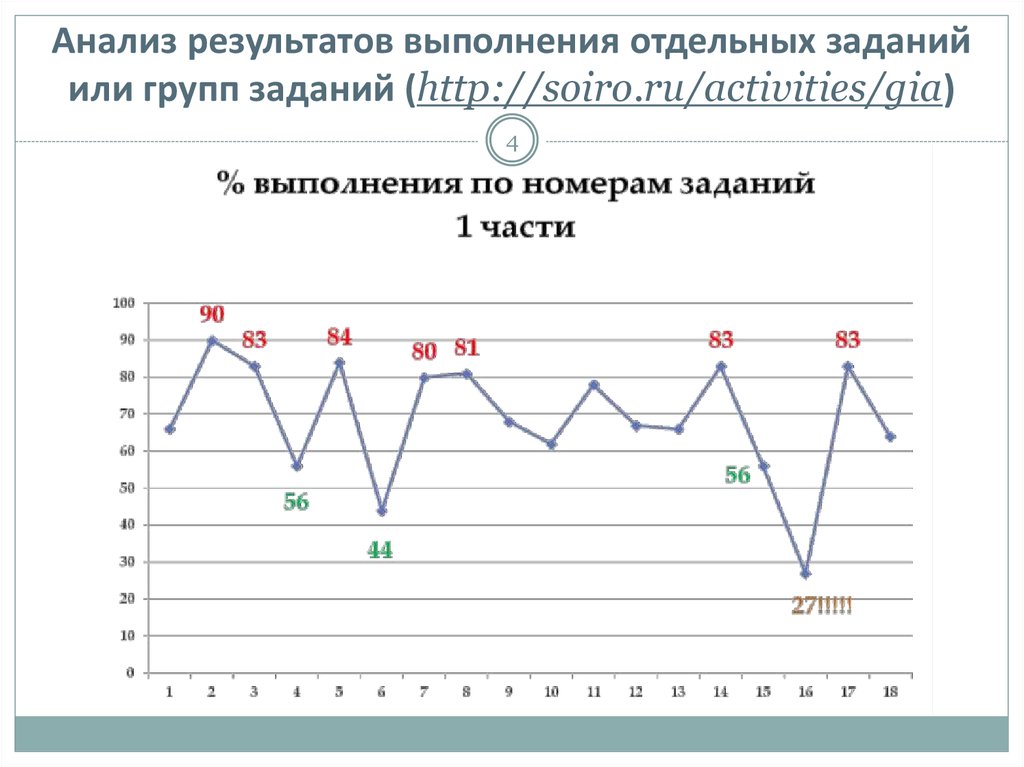
4. Анализ результатов выполнения отдельных заданий или групп заданий (http://soiro.ru/activities/gia)
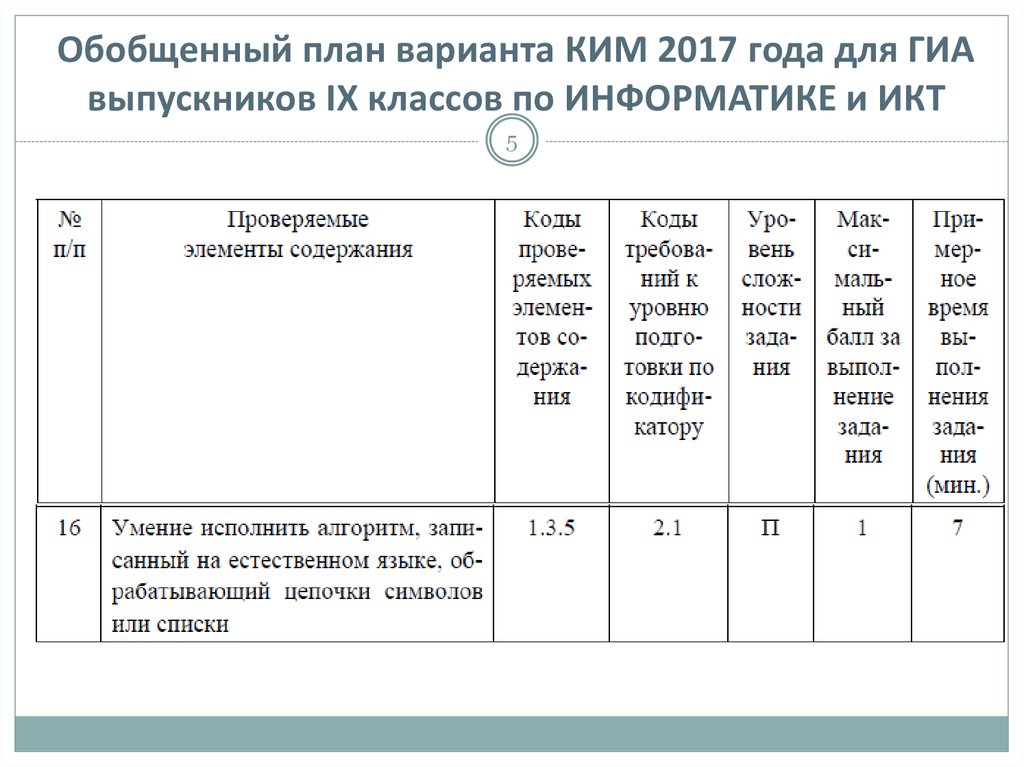
45. Обобщенный план варианта КИМ 2017 года для ГИА выпускников IХ классов по ИНФОРМАТИКЕ и ИКТ
56.
Раздел 1. Перечень элементов содержания, проверяемых наосновном государственном экзамене по ИНФОРМАТИКЕ и ИКТ
Раздел 2. Перечень требований к уровню подготовки
обучающихся, освоивших общеобразовательные программы
основного общего образования по ИНФОРМАТИКЕ и ИКТ
6
7. Алгоритмы, обрабатывающие цепочки символов или числа
7ЗАДАНИЕ №16 КИМ ГИА
8. Задание 16 (КИМ 2016)
89. Задание 16 (КИМ 2016)
В данной задаче проверяется умение разобраться в нестандартномалгоритме; увидеть ограничения, накладываемые на входные и
выходные данные, повторить алгоритм для некоторых входных
данных; проанализировать результаты его выполнения.
9
10.
Решение:1.
2.
3.
4.
выделение значений двух сумм (значение 0);
проверяем условие следования в порядке неубывания;
учитывая свойства суммы четных или нечетных цифр,
обращаем внимание на состав оставшихся чисел. Если
одно из чисел четное, делаем вывод, что второе является
суммой нечетных цифр;
проверяем возможность составить суммы, учитывая, что
если цифры четные, то в сумме может получиться
максимально число 8 (одна цифра), 16 (две цифры), 24 (три
цифры), 32 (четыре цифры), если же цифры нечетные, то
максимальное число составит 9 (одна цифра), 18 (две
цифры), 27 (три цифры) , 36 (четыре цифры).
10
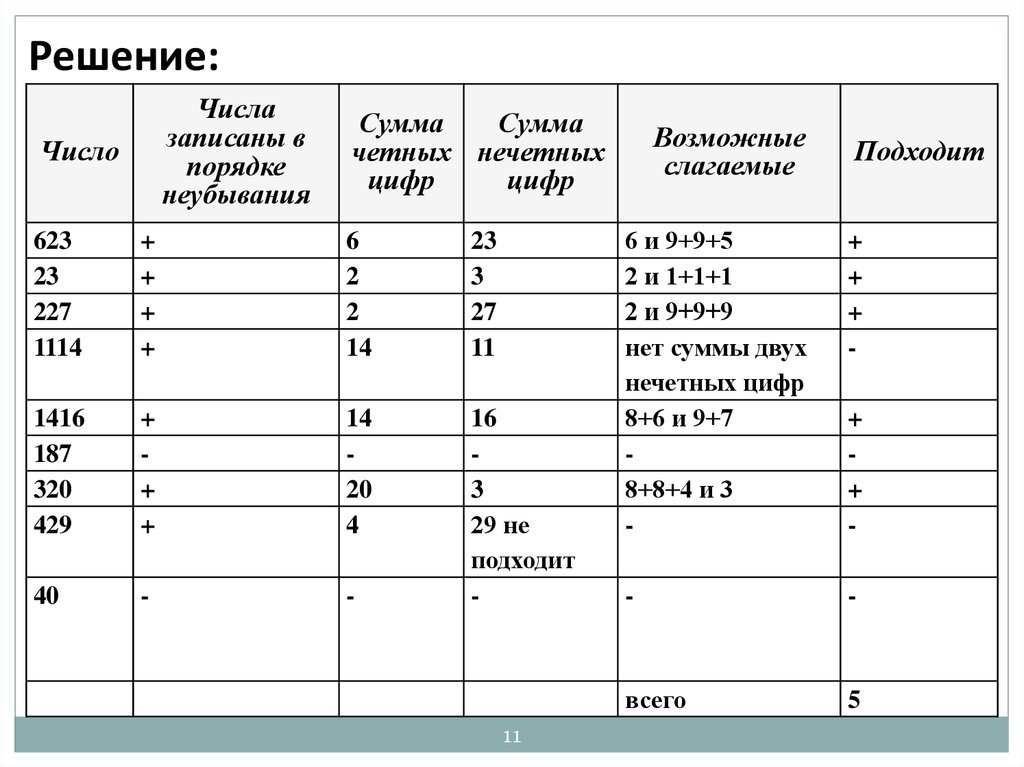
11.
Решение:Числа
записаны в
порядке
неубывания
Число
Сумма
Сумма
четных нечетных
цифр
цифр
623
23
227
1114
+
+
+
+
6
2
2
14
23
3
27
11
1416
187
320
429
+
+
+
14
20
4
40
-
-
16
3
29 не
подходит
-
11
Возможные
слагаемые
Подходит
6 и 9+9+5
2 и 1+1+1
2 и 9+9+9
нет суммы двух
нечетных цифр
8+6 и 9+7
8+8+4 и 3
-
+
+
+
-
-
-
всего
5
+
+
-
12. Задание 16 (КИМ 2016)
62323
227
1114
1416
12
187
320
429
40
13. Задание 16 (КИМ 2016)
1.2.
проверяем условие следования в порядке неубывания
(больше или равно);
учитывая свойства суммы четных или нечетных цифр,
обращаем внимание на состав оставшихся чисел. Если одно
из чисел четное, делаем вывод, что второе является суммой
нечетных цифр;
623
23
227 1114 1416 187
14: 8 и 6
13
11: сумма двух
нечетных цифр
– чётна
320 429
40
14. Задание 16 (КИМ 2016)
1.проверяем возможность составить суммы, учитывая, что
если цифры четные, то в сумме может получиться
максимально число 8 (одна цифра), 16 (две цифры), 24 (три
цифры), 32 (четыре цифры), если же цифры нечетные, то
максимальное число составит 9 (одна цифра), 18 (две
цифры), 27 (три цифры) , 36 (четыре цифры).
623
23
227
1416
320
429
623: 23:
6и2
23=7+7+9
1416: 14=7+7320:
и 3 и 20=8+6+6
и227:
3=1+1+1
2 и 27=9+9+9
429: 4 и 29≥27
16=8+814
Ответ: 5
14
15.
Задание 16 (http://distan-school.ru/oge/index.php?tap=3&var=23)Автомат получает на вход четырёхзначное десятичное число. По
полученному числу строится новое десятичное число по
следующим правилам:
1. Вычисляются два новых числа: сумма первых двух цифр, а
также сумма последних двух цифр
2. Полученные два числа записываются друг за другом в
порядке невозрастания (без разделителей).
Определите, сколько из приведённых ниже чисел могут
получиться в результате работы автомата:
1915 20 101 110 1213 1312 1819 312 1111
15
16.
Решение:1. проверяем условие следования сумм в порядке
невозрастания (меньше или равно);
2. четырёхзначное число лежит в диапазоне от 1000
до 9999, цифры-разряды этого числа принимают
значения от 0 до 9(за исключением первой цифры),
поэтому сумма двух цифр может быть от 0 до 18.
1915
20
101
110 1213 1312 1819 312
20: 1100101: 5501
110: 6500 1312: 7657
1111
1111: 9229
Ответ: 5
16
17.
Задание 16 (Д. М. Ушаков «Информатика. Новыйполный справочник для подготовки к ОГЭ»)
17
18.
Решение:1. проверяем условие следования сумм в порядке
невозрастания (меньше или равно);
2. трёхзначное число лежит в диапазоне от 100 до 999,
цифры-разряды этого числа принимают значения от
0 до 9 (за исключением первой цифры), поэтому
сумма двух цифр может быть от 0 до 18;
3. по условию при получении двух сумм цифрразрядов в обоих суммах используется одна и та же
цифра – средняя цифра числа, поэтому разница
предполагаемых сумм не должна превышать
значения 9.
1616
169
163
1916
18
1619
316
916
116
19.
Решение:1. по
условию при получении двух сумм цифрразрядов в обоих суммах используется одна и та же
цифра – средняя цифра числа, поэтому разница
предполагаемых сумм не должна превышать
значения 9.
1616
169
163
116
1616: 797
169: 790
163: 16-3=13
116: 560
Ответ: 3
19
20.
Задание 16 (Открытый банк задании ОГЭ)Автомат получает на вход пятизначное десятичное число. По
полученному числу строится новое десятичное число по
следующим правилам.
1. Вычисляются два числа – сумма первых трёх цифр и сумма
последних трёх цифр.
2. Полученные два числа записываются друг за другом в
порядке невозрастания (без разделителей).
Пример. Исходное число: 15177. Поразрядные суммы: 7, 15.
Результат: 157.
Определите, сколько из приведённых ниже чисел могут
получиться в результате работы автомата.
2525 256 2520 2528 2825 2025 625 106
В ответе запишите только количество чисел.
20
21.
Решение:1. проверяем
условие следования сумм в порядке
невозрастания (меньше или равно);
2. диапазоне возможных получаемых сумм для трех цифрразрядов от 0 до 27 (9+9+9);
3. по условию при получении двух сумм цифр-разрядов в обоих
суммах используется одна и та же цифра – средняя цифра
числа, поэтому разница предполагаемых сумм не должна
превышать значения 9.
2525
256
2520 2528
2825 2025
625
106
106: 33420
2525:256:
88997
25-6=19
2520: 88974
Ответ: 3
21
22.
Задание 16 (Открытый банк задании ОГЭ)Автомат получает на вход пятизначное десятичное число. По
полученному числу строится новое десятичное число по
следующим правилам.
1. Вычисляются два числа – сумма первой, третьей и пятой
цифр и сумма второй и четвёртой цифр заданного числа.
2. Полученные два числа записываются друг за другом в
порядке невозрастания (без разделителей).
Пример. Исходное число: 15177. Поразрядные суммы: 9, 12.
Результат: 129.
Определите, сколько из приведённых ниже чисел могут
получиться в результате работы автомата.
1220 120 210 2012 1920 2019 212 2919 1929
В ответе запишите только количество чисел.
22
23.
Решение:1. проверяем условие следования сумм в порядке
невозрастания (меньше или равно);
2. диапазоне возможных получаемых сумм для трех
цифр-разрядов от 0 до 27 (9+9+9), для двух от 0 до
18.
1220 120
210
2012 1920 2019
212 2919 1929
120: 30405
210: 90903
2012: 96962 2019: 202919:
212:
и 19≥18
92903
29≥27 и 19≥18
Ответ: 4
23
24.
Задание 16 (Открытый банк задании ОГЭ)Цепочка из трёх бусин, помеченных латинскими буквами,
формируется по следующему правилу:
– в начале цепочки стоит одна из бусин D, B, C;
– на третьем месте – одна из бусин A, C, D, E, которой нет на
первом месте;
– в середине – одна из бусин А, B, C, E, не стоящая на третьем
месте.
Определите, сколько из перечисленных цепочек созданы по
этому правилу?
BCE DAB CCE DCD CAA BAC ABC DCB DAE
В ответе запишите только количество цепочек
24
25.
Решение:– в начале цепочки стоит одна из бусин D, B, C;
– на третьем месте – одна из бусин A, C, D, E, которой
нет на первом месте;
– в середине – одна из бусин А, B, C, E, не стоящая на
третьем месте.
BCE DAB CCE DCD CAA BAC ABC
DCB DAE
Ответ: 4
25
26.
Задание 16 (Открытый банк задании ОГЭ)Некоторый алгоритм из одной цепочки символов получает новую
цепочку следующим образом. Сначала вычисляется длина исходной
цепочки символов; если она чётна, то дублируется левый символ
цепочки, а если нечётна, то в конец цепочки добавляется буква М. В
полученной цепочке символов каждая буква заменяется буквой,
следующей за ней в русском алфавите (А – на Б, Б – на В и т. д., а Я –
на А).
Получившаяся таким образом цепочка является результатом работы
описанного алгоритма.
Например, если исходной была цепочка ура, то результатом
работы алгоритма будет цепочка ФСБН, а если исходной была
цепочка КРОТ, то результатом работы алгоритма будет
цепочка ЛЛСПУ.
Дана цепочка символов РУКА. Какая цепочка символов получится,
если к данной цепочке применить описанный алгоритм дважды (т. е.
применить алгоритм к данной цепочке, а затем к результату вновь
применить алгоритм)?
Русский
алфавит: АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
26
27.
Решение:Для решения данной задачи требуется формально
исполнить предложенный алгоритм. Если алгоритм по
условию необходимо выполнить дважды, то второй раз
он применяется к результату выполнения, указанного
алгоритма первый раз.
Алгоритм:
1. Вычисляется длина исходной цепочки символов;
2. Если она чётна, то дублируется левый символ
цепочки;
3. Если нечётна, то в конец цепочки добавляется
буква М;
4. В полученной цепочке символов каждая буква
заменяется буквой, следующей за ней в русском
алфавите.
27
28.
Решение:1. Вычисляется длина исходной цепочки символов;
2. Если она чётна, то дублируется левый символ цепочки;
3. Если нечётна, то в конец цепочки добавляется буква М;
4. В полученной цепочке символов каждая буква заменяется
буквой, следующей за ней в русском алфавите.
алфавит: АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
РУКА
ССФЛБ
4
РРУКА
ССФЛБ
ССФЛБМ ТТХМВН
5
Ответ: ТТХМВН
28
29. Информационные ресурсы
1.2.
3.
4.
5.
6.
7.
http://www.alleng.ru/d/comp/comp380.htm - Информатика и ИКТ. 9кл.
Подготовка к ОГЭ-2016: 20 вариантов/ Л. Н. Евич – Ростов-наДону: Легион,
2016.
http://www.alleng.ru/d/comp/comp365.htm - ОГЭ 2016. По информатике и
ИКТ: типовые экзаменационные варианты(10 вариантов)/ С. С. Крылов,
Т. Е. Чуркина – М.: Национальное образование, 2016.
Демонстрационный вариант контрольных измерительных материалов
для проведения в 2017 году государственной (итоговой) аттестации (в
новой форме) по ИНФОРМАТИКЕ и ИКТ обучающихся.
Открытый банк заданий Федеральный институт педагогических
измерений – http://www.fipi.ru/
http://kpolyakov.spb.ru/ – сайт К. Ю. Полякова доктора технических наук,
учителя высшей категории.
http://www.videouroki.net/ – Видеоуроки в Интернет для учителей и
школьников.
http://distan-school.ru/oge/index.php?tap=3&var=23 – материалы для
подготовки к ОГЭ.
29

























 pedagogy
pedagogy








