Similar presentations:
Особливості пошуку екстремуму функції відгуку другого порядку
1. Особливості пошуку екстремуму функції відгуку другого порядку
2.
• Необхідною умовою існуванняекстремуму функції відгуку є виконання
умови:
y
0
x
i
• Відповідь на питання, чи буде мати
функція максимум чи мінімум у
“підозрілій” точці факторного простору,
потребує додаткового дослідження.
3. Приклад. Знайти екстремум функції
22
y 4 2x 1 2x 2 3x 1 x 2 0.5x 1 0.5x 2
• Точка, в якій може існувати екстремум,
знаходять з системи рівнянь:
y
- x 3x 2 0
1
2
x
1
y
3x x 2 0
1
2
x
2
2
x
1
2
2
x
2
2
4.
• Обчислення других похідних по кожній змінній свідчить,що в “підозрілій” на екстремум точці функція має
найбільше значення. Проте поверхня, що описується
вказаним рівнянням має вигляд сідла, і в підозрілій точці
функція не має ні максимуму, ні мінімуму.
2y
1
x 2
1
y
2y
1
x 2
2
x2
x1
5. Існують більш строгі методи дослідження цільової функції на екстремум.
1. Записується матриця Гессе (“гессіан”),елементи якої визначаються так:
2y
2y
a ij
a ji
x x
x x
i j
j i
a 11
a
21
A
...
a n1
a 12
a 22
...
a n2
... a 1n
... a 2 n
... ...
... a nn
i, j 1, ..., n
6. 2. Досліджуються знаки головних мінорів матриці:
• 2.1. Випадок двох змінних.2
y
1 a11
2
x1
2
a11
a12
a21 a22
2
2
y y
y
2
2
x1 x2
x1 x2
Достатньою умовою мінімуму є :
∆1 > 0;
∆2 > 0
Достатньою умовою максимуму є:
∆1 < 0;
∆2 > 0
7.
• 2.2. Випадок трьох змінних.1 a 11
2
a 11 a 12
a 21 a 22
a 11a 22 a 12
2
a 11 a 12 a 13
2
2
2
3 a 21 a 22 a 23 (a 11a 22 a 12 )a 33 a 13 a 22 a 23 a 11 2a 12 a 13a 23
a 13 a 23 a 33
Достатньою умовою мінімуму є :
∆1 > 0; ∆2 > 0, ∆3 > 0
Достатньою умовою максимуму є:
∆1 < 0; ∆2 > 0, ∆3 < 0
8.
22
y 4 2x 1 2x 2 3x 1 x 2 0.5x 1 0.5x 2
2
y
x1 x 2
3
1 3
A
3 1
2
y
x 2
1
1
2
y
2
1 (x1 x 2
)
2
x 2
2
Δ a 0; Δ 1 9 0;
1 11
2
Функція не має екстремуму .
9.
y 24 0.48x 0.91x 1.75x x 2.75x 2 3.06x 21
2
1 2
1
2
Якщо extr y існує, тт
y
0,48 1,75x 5,5x 0
2
1
x
1
y
0,91 1,75x 6,12x 0
1
2
x
2
x 0,242,
x 0,136
1
2
А
2y
2
x
1
2y
2y
x x
5.5
1
2
2
1.75
y
2
x x
x
1
2
2
2y
1 a11
5.5 0
2
x
1
1.75
6,12
2y 2y
2y
2
(
) 0
2
2
x
x
x
x
1
2
1
2
Отже, в точці х1 = -0,242; х2 = 0,136 функція має мінімум
10. Екстремум функції більшої кількості змінних:
• Мінімум: ∆і > 0;• Максимум:
парні головні мінори > 0;
непарні головні мінори < 0.







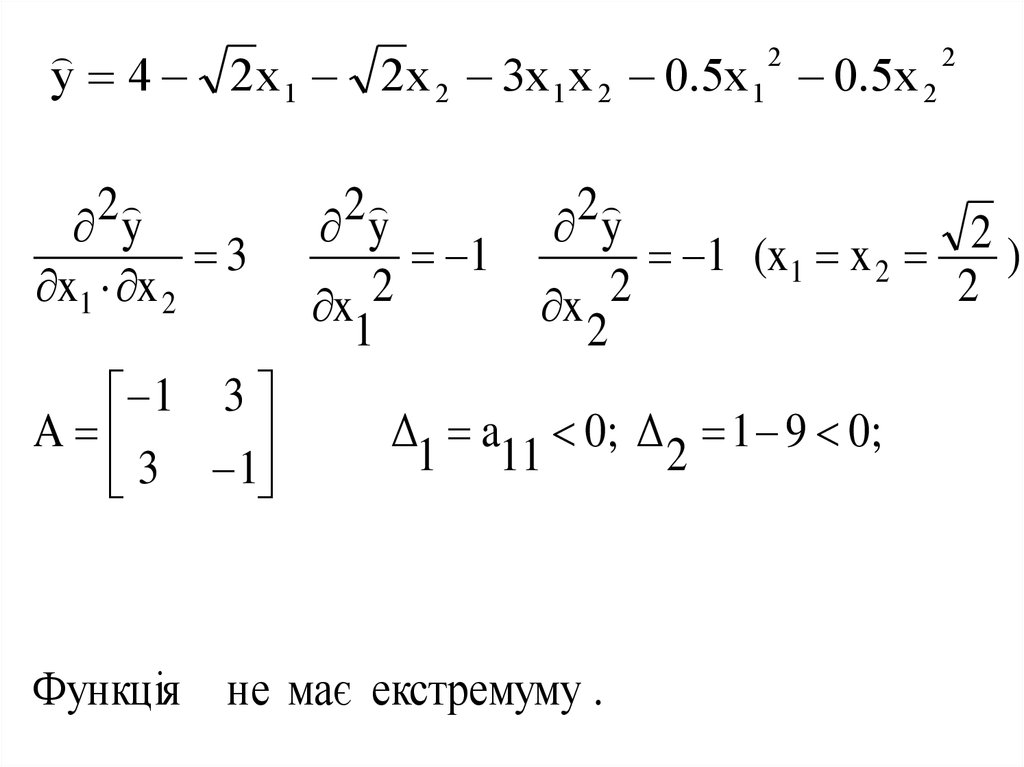


 mathematics
mathematics








