Расчёт показателей надёжности объектов теплоэнергетики при проектировании на основе теории случайных процессов

1. Лекция № 4. Расчёт показателей надёжности объектов теплоэнергетики при проектировании на основе теории случайных процессов

http://www.ribalco.exponenta.ru

2. Основные положения теории случайных процессов

Основные положения теории случайных
Дуга графа
процессов Вершина
графа
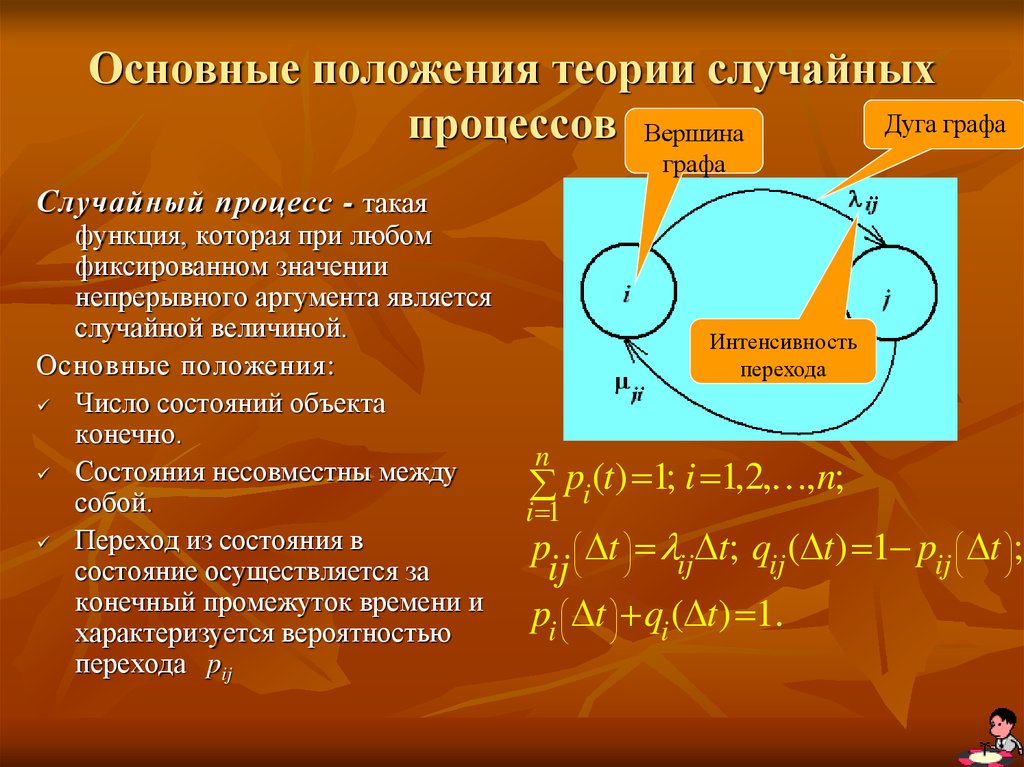
Случайный процесс - такая
функция, которая при любом
фиксированном значении
непрерывного аргумента является
случайной величиной.
Основные положения:
Число состояний объекта
конечно.
Состояния несовместны между
собой.
Переход из состояния в
состояние осуществляется за
конечный промежуток времени и
характеризуется вероятностью
перехода pij
Интенсивность
перехода
n
pi (t) 1; i 1,2, , n;
i 1
p t ij t; qij ( t) 1 pij t ;
ij
pi t qi ( t) 1.

3. Расчёт показателей надёжности проектируемого объекта Теоретические основы расчёта

Условия применения теории
марковских случайных процессов:
-
-
-
экспоненциальность потока событий;
переход из состояния в состояние
занимает конечный интервал времени;
интенсивность переходов не зависит от
момента его начала;
сумма вероятностей нахождения в
различных состояниях в любой момент
времени равна единице.
Система уравнений
Колмогорова
dpi
dt ij pi ji p j ;
dp
j p p ;
ji j
ij i
dt

4. Модель расчёта надёжности объектов при горячем резервировании элементов

dp0
dt
dp1
dt
dp2
dt
dp
3
dt
(2 1 2 ) p0 1 p1 2 p3 ;
S
dp
(0 3) p 2 p 2 p ;
(2
)
p
p
p
;
1
2
0
1
1
2
3
dt
1
2 p p ;
1
dp
2 1 p0 2 1 p2 ;
p
(p ;1 1 ) p1
dt
1
dp2 2 pS0 p ;
S1
1 2
1 1
dt
1
dp
3 2 p3 2 p0 ;
dt
1
1
1
2
1
2
3
1
0
1
2
S2
1 1
2
0
1

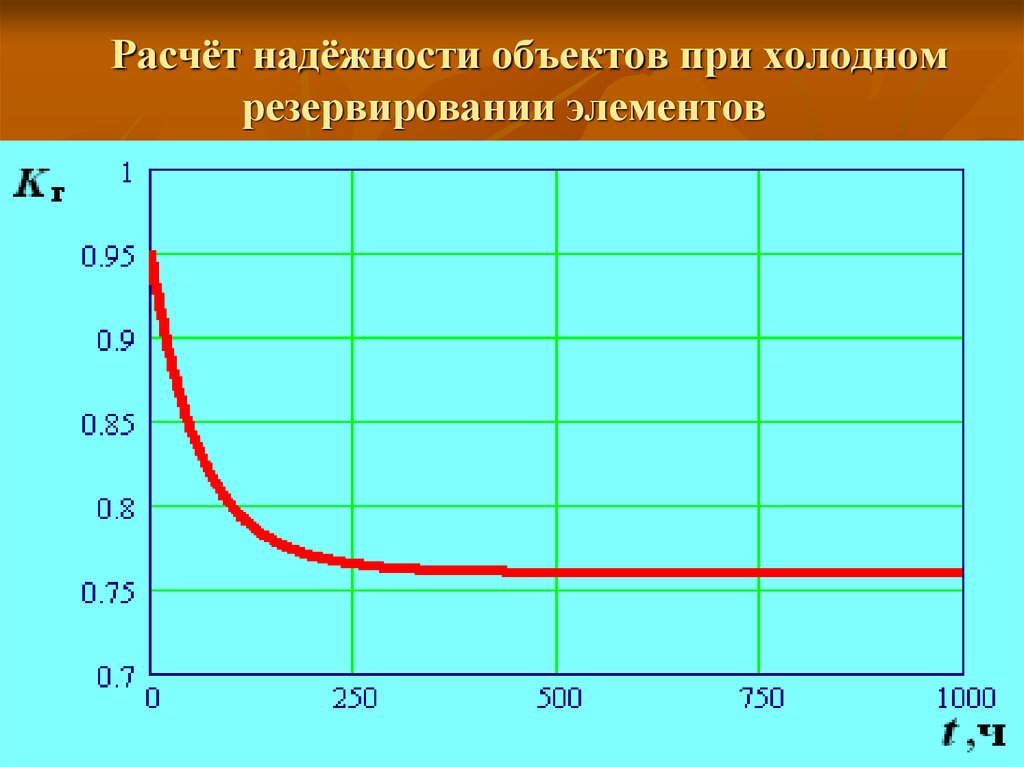
5. Расчёт надёжности объектов при холодном резервировании элементов

dp0
1 p1 2 p3
dt dp 0 ( (1 1 2 2))pp00
1 p1 2 p3
dt
dp 1 dp
1
2
( (1 1 1 1))pp11
21 p12 p2
11pp
0 0
dt dt
S3
dp2 2 p p
dp 2 dt 2 p1 2 1 p1
dt dp3 1 p2 1p 1
2 3
2 0
dp dt
3 2 p3 2 p0
dt
S2
1
1
S0
1
S1
1

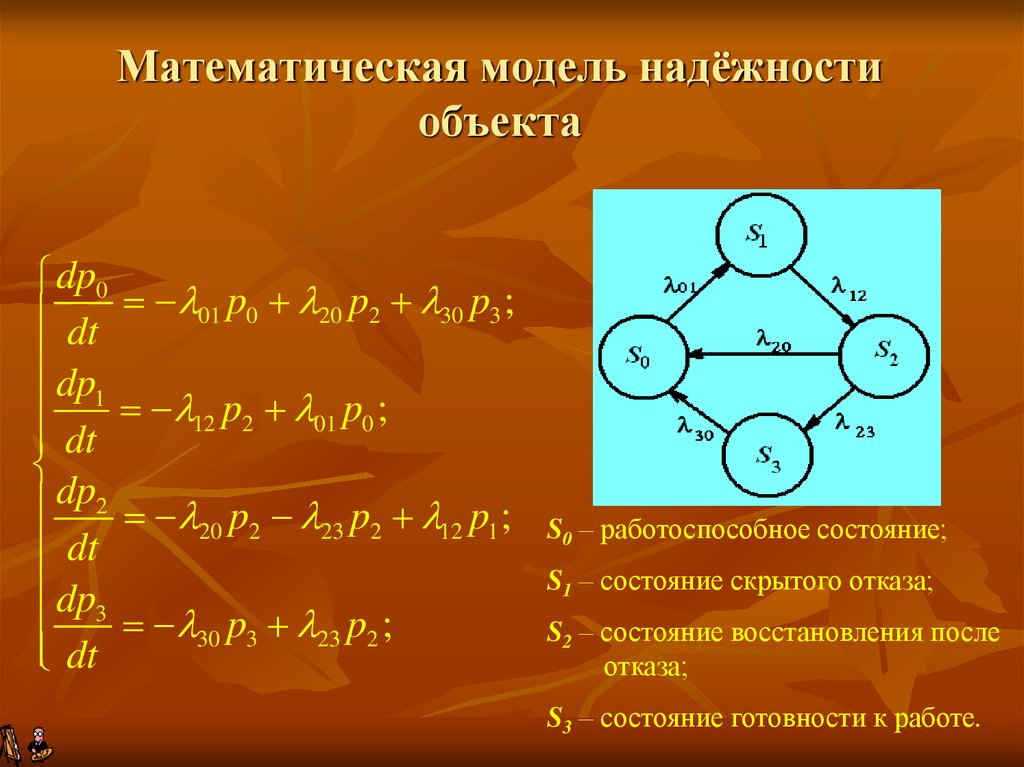
6. Математическая модель надёжности объекта

dp0
dt
dp1
dt
dp2
dt
dp
3
dt
01 p0 20 p2 30 p3 ;
12 p2 01 p0 ;
20 p2 23 p2 12 p1 ;
30 p3 23 p2 ;
S0 – работоспособное состояние;
S1 – состояние скрытого отказа;
S2 – состояние восстановления после
отказа;
S3 – состояние готовности к работе.

7. Результаты оценки надёжности объекта

Результаты получены при следующей исходной информации:
0, 0001 интенсивность отказа, 1/ч;
01
12 10
интенсивность обнаружения отказа, 1/ч;
20 23 0,1 интенсивность восстановления, 1/ч;
интенсивность приготовления к действию, 1/ч;
30 2

8.

Расчёт показателей надёжности проектируемого
объекта
Математическая модель надёжности установки как
структурно сложного объекта Структурная схема
Принципиальная схема
газотурбинного
энергоблока
газотурбинного
энергоблока
2 0 2 1 2 3 4 5 2 6 7 op p0 0 p1 1 p2 2 3 4 5 7 op p4 6 p3
0 0 p 2 0 p 2 0 p
1
0
4
1 1 p 2 1 p 2 1 p
D( t p )
2
0
4
6 6 p 2 6 p 2 6 p
3
0
4
Система уравнений
2 0 2 1 2 3 4 5 2 6 7 op p 0 p 1 p 2 3 4 5 7 op p 6 p
4
1
2
0
3
Колмогорова
Результаты решения

9.

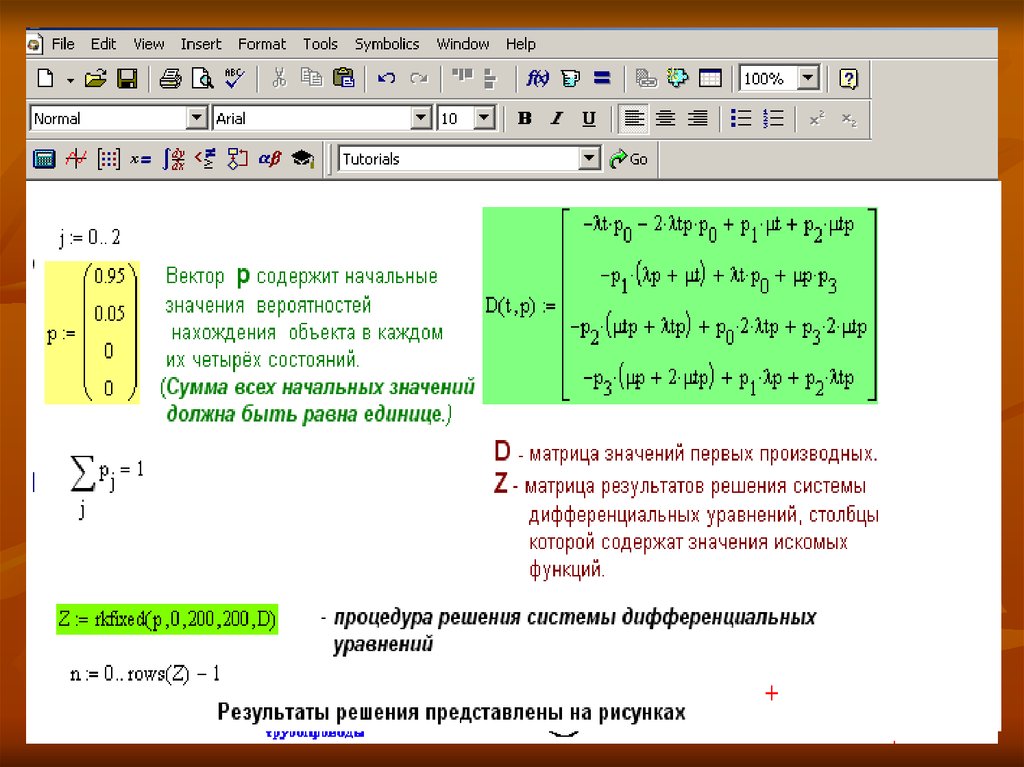
Интерфейс программы расчёта ПН с среде Mathcad

10. Присвоение исходной информации

11. Задание начальных условий

12.

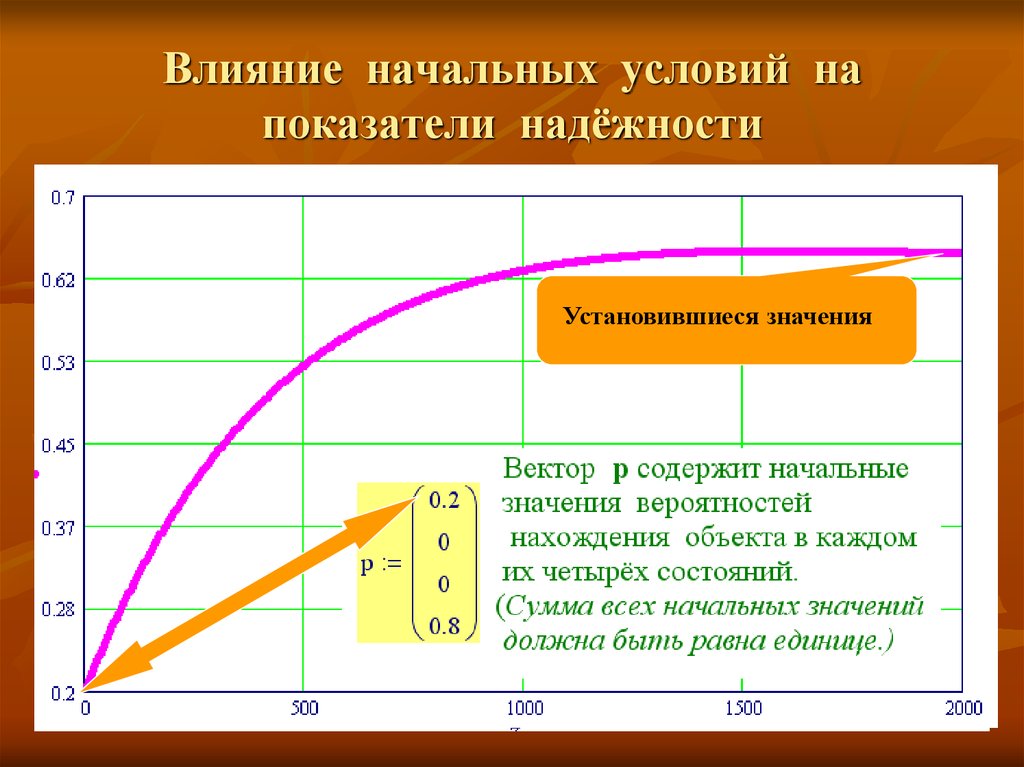
13. Влияние начальных условий на показатели надёжности

Нестационарные значения
Установившиеся значения
Установившиеся
(финальные) значения

14. Сравнение результатов расчёта для нагруженного и ненагруженного резерва

Нагруженный (горячий) резерв
1
2
3
1
2
3
Ненагруженный (холодный) резерв

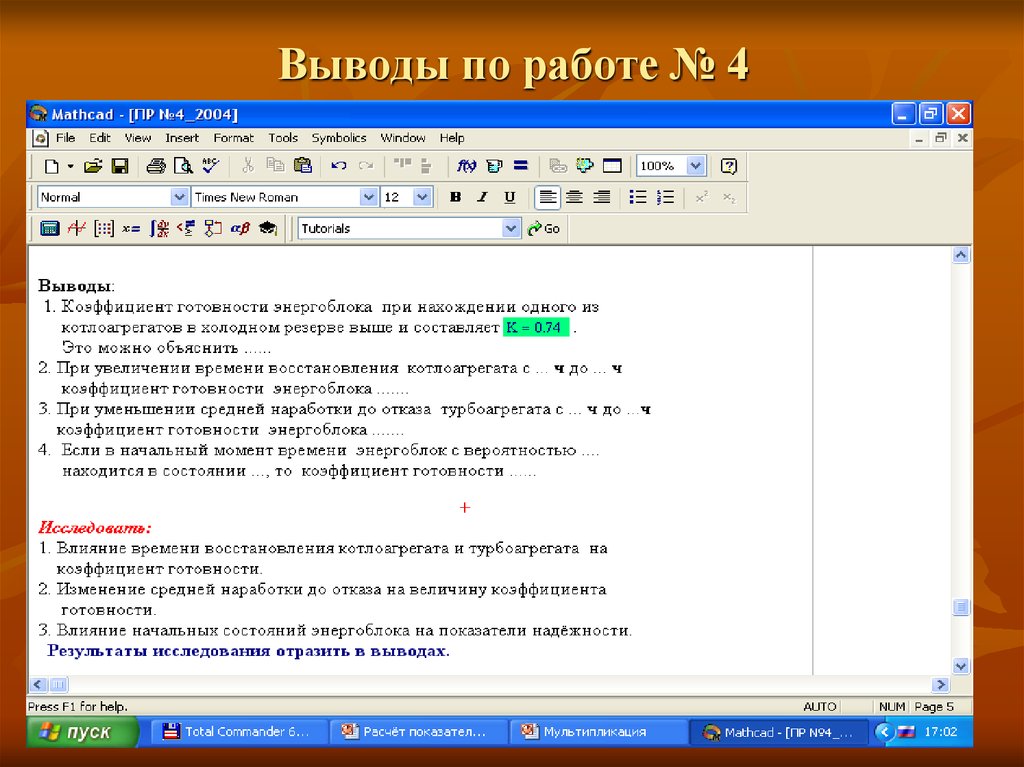
15. Выводы по работе № 4

16.

17. Результаты вычисления

18. Выводы по работе

19.

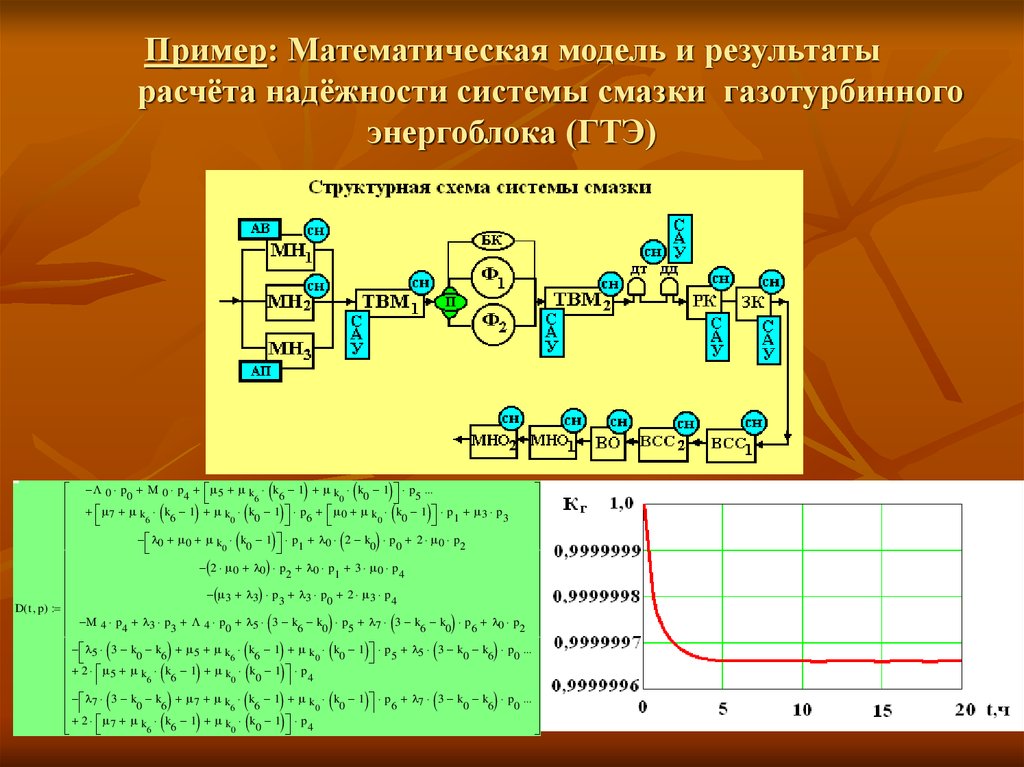
Пример: Математическая модель и результаты
расчёта надёжности системы смазки газотурбинного
энергоблока (ГТЭ)
0 p 0 0 p 4 5 k6 k6 1 k0 k0 1 p 5
k
1
k
1
p
k
1
p
p
7
k 6
k 0
0
k 0
3 3
6
1
6
0
0
0 0 k k 1 p 0 2 k p 2 0 p
0
1
0
0
2
0
2 0 0 p 0 p 3 0 p
2
1
4
3 3 p 3 p 2 3 p
3
0
4
D( t p )
p p p 3 k k p 3 k k p p
4 4
3 3
4 0
5
7
0 2
6
0
5
6
0
6
5 3 k k 5 k k 1 k k 1 p 5 3 k k p
0
6
6
0
0
6
0
6
0
5
2
k
1
k
1
p
5
k
k
6
0
4
6
0
7 3 k0 k6 7 k6 k6 1 k0 k0 1 p 6 7 3 k0 k6 p 0
2 7 k k 1 k k 1 p
6
0
6
0
4

20. Заключение

1.
2.
3.
4.
Расчёт надёжности проектируемых объектов энергетики
может быть выполнен с помощью специально
разработанных математических моделей на основе теории
марковских случайных процессов.
Для расчёта показателей надёжности требуется
определённая исходная информация, без которой расчёт
невозможен.
Путём сравнения рассчитанных и нормативных
показателей надёжности осуществляется контроль
достигнутого уровня надёжности проектируемого
объекта.
Методика на основе марковских случайных процессов
позволяет осуществлять частичный синтез объекта с
требуемым уровнем качества.

21. Благодарю за внимание!