Об одной двумерной модели поликристаллических сегнетоэлектриков

1.

Белоконь А.В., Герасименко Т.Е., Скалиух А.С.
Южный федеральный университет, Ростов-на-Дону
[email protected]

2. Предмет сообщения

Доклад посвящен построению определяющих соотношений в
поликристаллических сегнетоэлектрических материалах между
поляризацией и деформацией и электрическим полем при малых
механических напряжениях.

3. О моделях

1. Модели ориентационной поляризации и примыкающие к ним методы
энергетических условий переключения (Дудкевич В.П.);
2. Модели микромеханических поляризационных переключений, с учетом
объемных фракций различного сорта доменов (Chen X., Fang D.N.,
Hwang K.C., Li W.F., Weng G.J., Huo Y., Jiang Q.);
3. Модели Прейзаха (Турик А.В., Visintin A., Mayergoyz I.D., Fuzi J.,
J., Damjanovic D., Cardelli D., Torre E.D.);
Kadar
4. Модели эфективной среды (Алешин В.И., Лучанинов А.Г., Dunn M.L.,
Li J.Y., Michelitsch T., Levin V.M.);
5. Модели математической теории пластического течения (Landis C.M.,
McMeeking R.M., Hwang S.C., Huber J.E., Fleck N.A.);
6. Модели закрепленной доменной стенки (Jiles D.C., Atherton D.L., Smith
R.C., Hom C.L., Ounaies Z.A., Massad J.E).

4. Основные положения метода Джила-Атертона

1. Вывод предельной (ангистерезисной) зависимости.
2. Подсчет энергии, необходимой для слома механизмов
закрепления стенки домена.
3. Вычисление работы электрического поля.
4. Составление энергетического соотношения.
5. Вывод дифференциального уравнения (системы
уравнений).
6. Численные эксперименты.

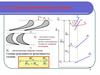
5. Вывод предельной зависимости (моделирование на уровне U2)

Строение керамики
Направление векторов спонтанной поляризации в
частице континуума уровня U2
Спонтанная поляризация домена (двумерный случай)
p s ps (i cos j sin )
Число доменов на окружности единичного радиуса
dN cdS

6. 2 основных положения, положенных в основу: поле Вейсса и статистика Больцмана

Эффективное электрическое поле Вейсса
E ef E αP0
Теорема Больцмана:
в консервативном поле распределение осей доменов в частице отличается от
их распределения в отсутствии поля на величину
e
U
kT
количество доменов, выходящих своими осями на элемент окружности
dN ce
U
kT
dS
Количество переключившихся доменов в частице
N c e
ps
Eef
kT
2
dS c e
0
ps
E ef
kT
d

7. Влияние коэрцитивного поля на процесс переключения

Суммарная поляризация доменов, выходящих своими осями на элемент площади ,
dP0 p s dN p s ce
U
kT
dS
Усредненное значение поляризации
E ef p s
c
P0 e kT p s dS
N
Переключения доменов происходит только при достижении некоторого
порогового значения E c . Предложены следующие соотношения:
P0 ,
d E 0, 0 E E c
E E c P0 , d E 0, E E c
ef
E
E E c P0 , d E 0, E E c
E P ,
d E 0, 0 E E c
0

8. Предельная поляризация

2
p1
PS
E1ef cos E2ef sin
a
e
cos d
0
2
E1ef cos E2ef sin
a
e
d
0
2
p2
PS e
E1ef cos E2ef sin
a
sin d
0
2
e
0
E1ef cos E2ef sin
a
d

9. Подсчет энергии, необходимой для слома механизмов закрепления стенок доменов (моделирование на уровне U1)

Для вывода соотношения для остаточной
поляризации рассмотрим энергию поворота домена
в эффективном поле
U (p s p's ) dEef
Полагаем, что энергия слома запирающей стенки
пропорциональна энергии поворота домена
U pin c(p s p's ) dEef
Определим постоянную из условия, 1800 поворота
домена
U π 2с ps | dE ef |

10. Подсчет энергии… (продолжение)

Полагая, что подобные соотношения справедливы для любого домена, усредним по объему
частицы уровня U1
U π | 2cps dEef | 2c ps | dEef |
Тогда энергию слома запирающей стенки можно выразить в виде
ΔU pin
Uπ
dp s dEef ,
2 ps | dEef |
Далее будет интересовать средняя по объему энергия
U pin
Uπ
Uπ
dp s dEef
dP0 dEef
2 ps | dEef |
2 ps | dEef |
Полная энергия в произвольном макро-объеме
U n U pin d n
dp s p s p's
Uπ
dP0 dEef d
2 ps | dEef |
где n обозначает среднюю плотность стенок запирания в частице

11. Оценка работы в поляризационном процессе

Работа поля при возникновении поляризации
A E dP d d (E P ) d P d Ed
d (E P ) d ( Pe P0 ) d Ed
d (E P ) d E ( P0 ) d Ed P0 d Ed
После дополнительных преобразований
P02
E E
A d E P d d
d αd
d
2
2
E d ( P0 ) E
d P0 d E ef d
2

12. Оценка работы… (продолжение)

Для циклического процесса (гармоническое изменение электрического поля) имеем
A A A A A3 A4 A5
1
Но
2
A 0, A 0, A 0.
2
1
3
Для симметричных гистерезисных зависимостей
A 0.
4
Таким образом, за потери отвечает пятый интеграл
A P0 d Eef d

13. Энергетический баланс

Если бы не приходилось затрачивать энергию для преодоления
механизмов затухания, то потери в системе определялись бы
предыдущим соотношением, где вместо остаточной поляризации надо
поставить поляризацию предельного случая.
A P dE ef d
В реальности же потери описываются интегралом
A5 P0 dE ef d
Потери в реальном процессе поляризации складываются из
потерь в идеальном (предельном) случае, плюс энергетические
затраты, необходимые для слома механизмов запирания стенок
доменов
или
Uπ
P0 dEef d P dEef d n
dP0 dEef d
2 p | dE |
s
ef

14. Энергетический баланс (продолжение)

В силу произвольности объема интегрирования и эффективного
электрического поля, получаем
dP0
P P0 k
| dEef |
Уравнение в дифференциалах относительно dP0
dP0
1
dE ef P P0
k

15. Решаем методом последовательных приближений

Перепишем уравнение в виде
( i 1)
dP0
( i 1 )
P0
Рассмотрим
положим
1
(i )
(i )
(i)
dE ef (P0 ) P (P0 ) P0
k
P0
(i )
dP0
( i 1 )
P Pe P0
Pe c(P P0 ) E
найдем
P (i 1) P0
(i 1)
c P (P0
( i 1)
) P0
( i 1)
E
( i 1)

16. Определение приращения остаточной деформации

Используя условие несжимаемости остаточных деформаций, и учитывая, что
элемент деформируется вдоль направления вектора остаточной поляризации,
можно определить предыдущее и текущее значения остаточной деформации в
локальных осях
ε 0 old
ε sat | P0 old |
(e 2 old e 2 old e1old e1old ),
2 psat
ε 0 new
ε sat | P0 new |
(e 2 newe 2 new e1newe1new ),
2 psat
Далее переходим к главным осям и находим приращение как разность деформаций этих двух
состояний
ε 0 ε 0new ε 0old

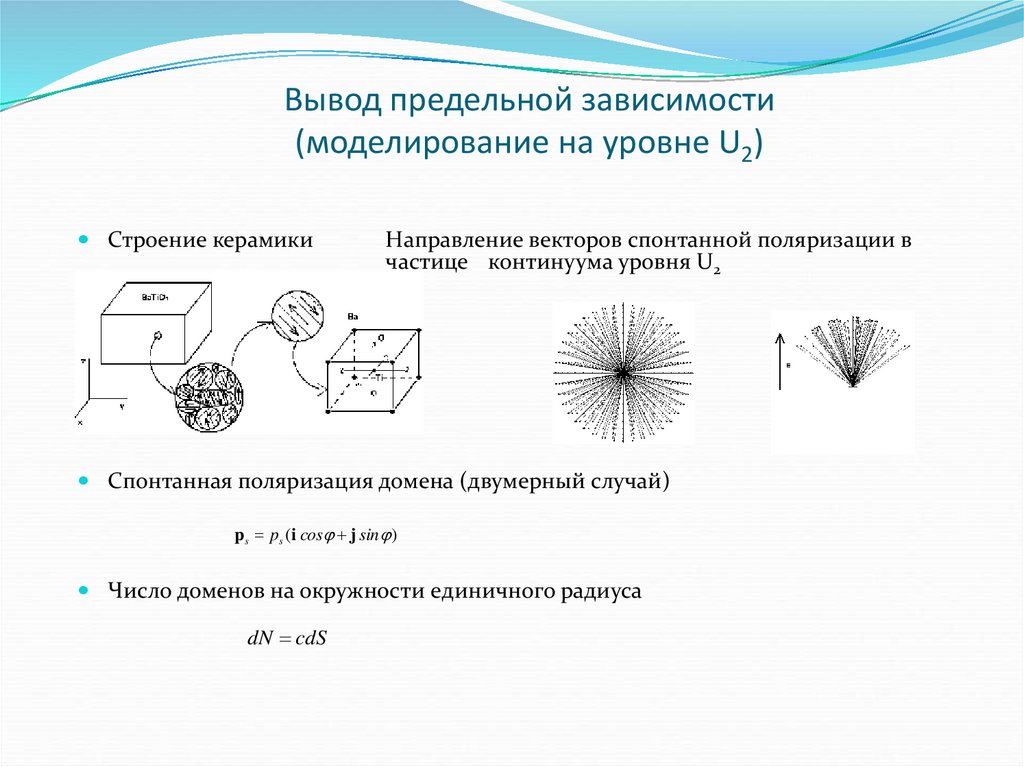
17. Численная реализация

Сравнение с экспериментом.
Выбраны следующие параметры:
a 9.79 105
в
м
7.3 106
вм
Кл
c 0.45
k 4.9 105
м
в
Ps 0.432
Кл
м2
1.4 10 8
Кл
мв
Ec 2.0 105
в
м

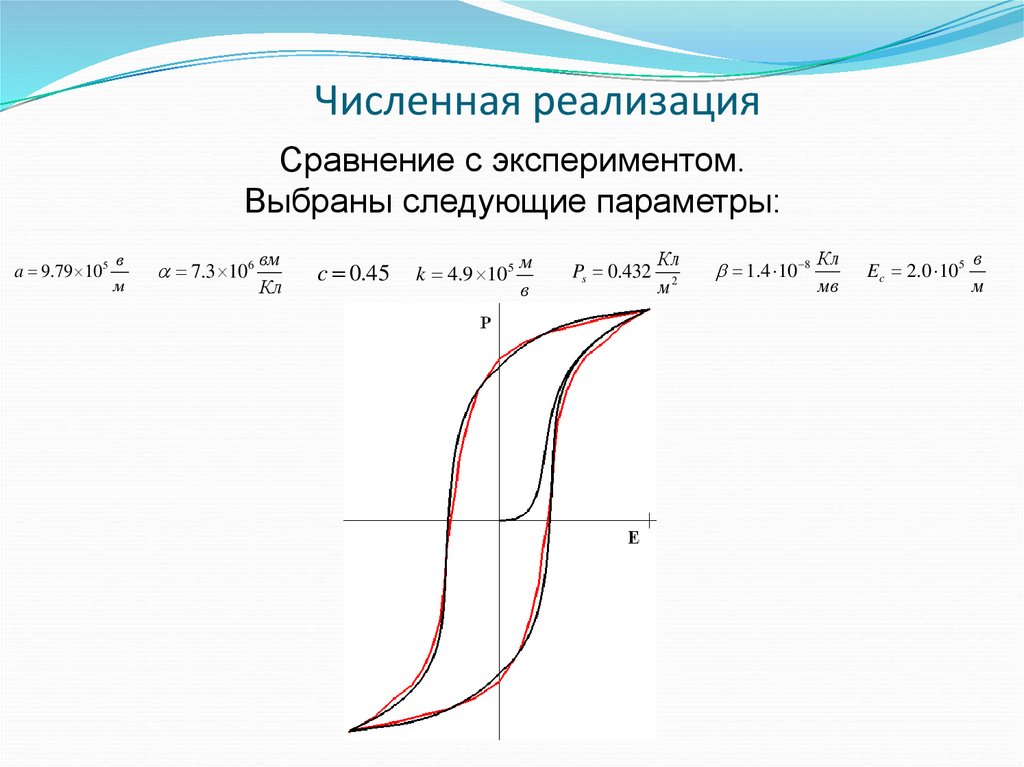
18. Сравнение малых петель диэлектрического гистерезиса

Малые петли гистерезиса
(эксперимент)
Малые петли гистерезиса
(модель)
Получено качественное совпадение для набора параметров:
a 8.79 105 6.1 106 c 0.15 k 4.9 105
Ps 0.55
0.8 10 9 Ec 6.0 105

19. Большая деформационная петля гистерезиса типа «бабочка»

20. Благодарю за внимание