Турбомашины АЭС

1.

ηoi, ηoe, ηoэ
p 0 , t0
G0
Ne
Ni
N0
Г
Nэ
SSS
T
qТУ
pк
К
FWP
qК
ηi, ηe, ηэ

2. Power and EF of the turbine and turbine equipment

EF
Power
Relative EF
Absolute EF
1
H 0 h0 hкt
t
qТУ h0 hпв
Ideal turbine
Power
N 0 GH 0
Internal
Ni H i
oi
N0 H 0
i
Ni
t oi
QТУ
Effective
Ne
oe
oi м
N0
e
Ne
t oe N e
QТУ
Electric
N
оэ э oi м эг
N0
Ni GH i N 0 oi
GH i м N 0 oe
N э GH 0 oi м эг
Nэ
э
t оэ
N0 оэ
QТУ

3.

Турбомашины АЭС

4.

а)
б)
2
1
3
в)
3
2
3
а) подливное колесо;
б) среднебойное колесо;
в) наливное колесо.
1. вал;
2. уровень воды в верхнем бьефе;
3. уровень воды в нижнем бьефе.

5.

6.

Gustaf de Laval
Charles Algernon Parsons
(1845-1913)
(1854 –1931)

7. Турбина Лаваля

8.

Давление пара
с1
Абсолютная
скорость пара
Схематический
разрез
одноступенчатой
активной турбины:
p0
с0
Разрез и
развертка
с2
p2=p1
p1
А-А
1 - вал; 2 - диск; 3 рабочие лопатки; 4 сопловая решетка; 5 корпус; 6 - выпускной
патрубок
4
А
А
3
2
1
3
4
5
d
6

9. Турбина Парсонса

Многоступенчатая реактивная турбина:
1 -корпус; 2 - барабан; 3 - подшипник; 4 - сопловые лопатки одной из ступеней; 5 рабочие лопатки одной из ступеней

10. Паровая турбина К-215-12,7

11.

Паровая турбина К-1000-5,8/50 для АЭС
на сборочно испытательном стенде ЛМЗ

12.

Продольный разрез турбины К-1200-6,8/25 ОАО “Силовые машины”
lпосл.ст = 1740 мм

13.

14.

Схематический чертеж радиальной турбины Юнгстрем.
1,2 — диски турбины; 3 — паропроводы свежего пара; 4, 5 — валы турбины;
6,7 — лопатки промежуточных ступеней.

15. Назначение турбины

NЭ
p0 , t0 , G0
MТ
n
N0 GH 0
MГ
pк
Турбина – двигатель, предназначенный для преобразования
потенциальной энергии теплоты в механическую энергию
вращения ротора турбины.

16.

2. ТЕЧЕНИЕ ГАЗА В КАНАЛАХ ТУРБИННЫХ
СТУПЕНЕЙ
p1
p0 , t0
p0 p2
p0 , t0
p2
p1
u
p2

17. Вопросы, рассматриваемые в разделе «2. ТЕЧЕНИЕ ГАЗА В КАНАЛАХ ТУРБИННЫХ СТУПЕНЕЙ»

2.1. Основные уравнения движения сжимаемой
жидкости.
2.2.Характеристики потока при изоэнтропийном
процессе расширения.
2.3. Реальное течение газа в каналах.
{ 2.4. Турбинные решетки. }

18. 2.1. Основные уравнения движения сжимаемой жидкости

Система уравнений (!!!), адекватно описывающая течение газа в
каналах:
Уравнение состояния
Уравнение неразрывности
Уравнение количества движения
Уравнение сохранения энергии

19. 2.1. Основные уравнения движения сжимаемой жидкости

Система уравнений (!!!), адекватно описывающая течение газа в
каналах:
Уравнение состояния
Уравнение неразрывности
Уравнение количества движения
Уравнение сохранения энергии

20.

2.1.1. Уравнение состояния
Состояние вещества однозначно определено,
если известны два независимых параметра.
p RT
k
h
p const
k 1
где k - показатель адиабаты
k
k 1,26...1,33
kпп 1,3
для оценочных расчетов можно принять
для сухого насыщеного пара
kвп 1,135
для перегретого водяного пара
для воздуха
kвозд 1,4
cp
c

21.

Уравнения состояния в виде формул используются для аналитического
описания процессов.
Для практических расчетов используются:
таблицы термодинамических свойств;
диаграммы, построенные на основании таблиц;
кДж
кг
3800
0,1
0, 02
1, 0
600
500
50
3400
400
300
3000
200
100
2600
x 1
0, 95
0,9
2200
0,85
0,8
0, 75
1800
0, 7
0, 65
5
6
7
8
9
кДж
кг К

22.

3800
600
500
3400
400
300
3000
200
100
2600
К
x 1
0,95
0,9
2200
0,85
изотерма.
0,8
0,75
1800
0,7
0,65
1400
1000
600
200
1
2
3
4
5
6
7
8
9

23.

электронные таблицы,
выполненные на основе аппроксимации
таблиц термодинамических свойств.
Изменение состояния происходит в результате совершения
термодинамического процесса.
Для нас важен адиабатный процесс – без подвода теплоты извне.
Идеальный адиабатный (изоэнтропийный) процесс описывается уравнением:
p t const
k

24.

2.1.2. Уравнение неразрывности
F0,p0,t0,
G0
F1,p1,t1,
G1
1
Определим объемный расход
[м3/с], проходящий через
сечение 0-0:
с1
V0 F0 c0 G0 0
1
м3
с
м
м
с
2
кг м3
с кг
f p0 , t0
G1
G0 G1
F1c1
1
F0c0 F1c1
0
1
G0
G F
c
F0c0
0
const

25.

1
а) Идеальное течение – без трения
F1c1t
G1t
1
1
1t f p1 , t1t p1, s0
с1t
при этом
с1ср
б) Действительное течение – с учетом сил
вязкости (трение)
G1д
c1
dF
1
( F1 )
1
1t
при этом
с1t
c1ср
c dF
1
F1
G1 F1
F1
c1
1
1
1
F1
c1ср
1ср
с1 F1 и 1 F1
1ср f p1 , t1
В общем случае:
Gi Fi
ci
i

26.

Уравнение неразрывности в дифференциальной форме
G F
c
const
Прологарифмируем формулу уравнения неразрывности
ln G ln F ln c ln
Продифференцируем это выражение (памятуя, что G = const)
dF dc d
0
F
c
dF d dc
F
c
dc d
, то dF 0
А) Если
c
Канал должен сужаться.
Б) Если
dc d
, то dF 0
c
Канал должен расширяться.

27.

2.1.3. Уравнение количества движения
А) Понятие количества движения и энергии в динамических системах
Второй закон Ньютона:
- для равноускоренного движения
R ma
где R - сила, н; m - масса, кг; a - ускорение, м/c2.
- для движения с переменным ускорением (дифференциальная
форма уравнения):
s
R m 2
2
где s - расстояние; τ - время.

28.

2s
d ds dc
2
d d d
ds
c - скорость, м/с.
d
dc
R m
d
разделим
переменные
Rd mdc
c
Rd mdc
0
c0
2 s dc ds ds dc dc
c
2
ds
d ds d ds
dc
R mc
ds
s
c
0
c0
Rds mcdc
2
2
0
mc mc
Rs
2
2
Уравнение
количества
0
движения Сила умноженная
Импульс силы равен изменению
на путь – механическая работа
количества движения
Изменение количества движения
происходит под действием импульса
силы
R mc mc
Rds mcdc
Кинетическая
энергия

29.

Б) Применение уравнения количества движения при движении жидкости (газа) в
канале.
I. Феноменологический подход
Если известен секундный расход массы G массы[кг/с] и скорости потока на входе с1 [м/с]
и выходе канала с2 [м/с], то можно определить силу R [н], которая заставила измениться
количеству движения
R G c2 c1
Т.к. по третьему закону Ньютона сила действия равна силе противодействия, то можно
определить силу, с которой поток действует на стенки канала
R R G c1 c2
II. Проблема определения действительной скорости

30.

p
dc
f 0 p0 f1 p0 dx dR dm
x
d
1
0
с0
p0
dR
с0+dc
p
p0 dx
x
dx
dR
f
0
1
0
где R
dR
dm
при dx 0 :
f
p
dc
dx dR dm
x
d
f1
f0 f1 f
: dm
p
dc
R
x
d
- сила сопротивления, отнесенная к 1кг массы протекающего газа.
Для установившегося режима
dp Rdx
dx
dc
d
dx
c
d
Интегрируя от 0-0 до 1-1
p dp
x dx
cdc dp Rdx
c12 c02
2
p0
x1
p1
x0
Уравнение изменения
количества движения в
одномерном потоке
dp Rdx
fdx

31.

c12 c02
2
c02
2
p0
p0
p1
p1
dp
x1
p1
x0
dp Rdx
R x 0
* Теоретический процесс расширения
c12t
p0
dp lтехн h0 h1t
c12t c02
h0 h1t
2
** Действительный процесс расширения
R f x
Известно, что
R f ( , Re (c, , d ), кривизны канала, …)
в частности, возможностью
отрыва пограничного слоя при
диффузорном характере
течения
В теории турбин уравнение количества движения для потока в канале при
действительном течении заменяется экспериментальными данными.

32.

2.1.4. Уравнение сохранения энергии
(для потока)
1
Подведенная энергия
Q
Gc02
Gh0 Q
2
0
Отведенная энергия
c0
1
L
0
G,p0,t0,
u0,υ0,h0
Частные случаи
а) q 0
c02
2
h0
c12
2
h1 l
G,p1,t1,
u1, υ 1,h1
Gc12
Gh1 L
2
c02
c12
h0 q h1 l
2
2
б) q 0, l 0
c02
c12
h0 h1
2
2

33.

q 0, l 0
Задано p0,t0,p1. Определить скорость на выходе из канала при
* Теоретический процесс расширения
p0
h0
c02
c12t
h0
h1t
2
2
t0
c12t c02
h0 h1t
2
c1t 2 h0 h1t c02
H0
h
Если h в кДж/кг
p1
h в Дж/кг
c1t 2000 h0 h1t c02
c02
c1t 44, 7 h0 h1t
2000
h1t
H 0 h0 h1t -располагаемый теплоперепд на канал
s
** Действительный процесс расширения
h0
p0
c02
c12
h0 h1
2
2
t0
H0
h
p1
h1
h1t
s
c02
c1 44, 7 h0 h1
2000
H i h0 h1 - действительный теплоперепд на канал

34.

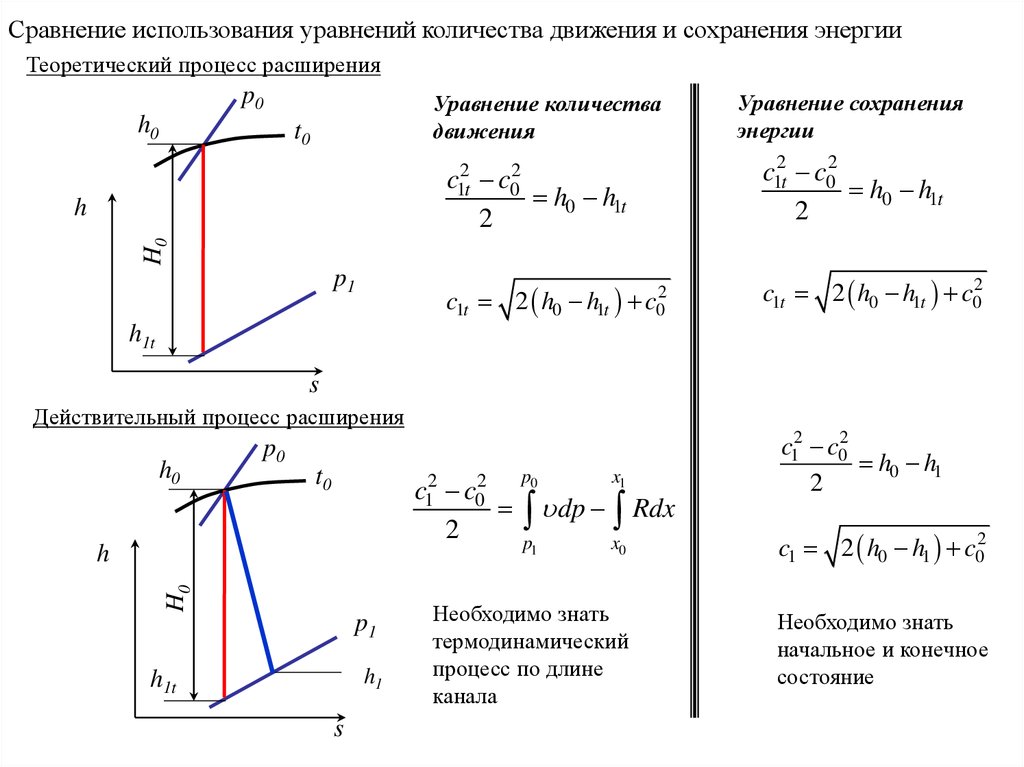
Сравнение использования уравнений количества движения и сохранения энергии
Теоретический процесс расширения
p0
h0
Уравнение количества
движения
t0
c12t
h
c02
c12t c02
h0 h1t
2
H0
2
h0 h1t
Уравнение сохранения
энергии
p1
c1t 2 h0 h1t c02
c1t 2 h0 h1t c02
h1t
s
Действительный процесс расширения
h0
p0
x1
c12 c02
h0 h1
2
p1
x0
c1 2 h0 h1 c02
Необходимо знать
термодинамический
процесс по длине
канала
Необходимо знать
начальное и конечное
состояние
p0
t0
c12 c02
2
H0
h
p1
h1
h1t
s
dp Rdx

35.

*** Ускорение потока
c12 c02
h0 h1
2
Если h1< h0 , то с1> с0 поток ускоряется (конфузорное течение)
Если h1> h0 , то с1< с0 поток замедляется (диффузорное течение)

36. 2.2. Характеристики потока при изоэнтропийном расширении газа в каналах

Канал, в котором поток плавно ускоряется, называется сопловым или просто
соплом.
Канал, в котором поток плавно замедляется, называется диффузорным или
просто диффузором.

37. 2.2.1. Ускорение потока в канале

Какую скорость будет иметь поток на выходе из
канала (в сечении 1)?
p0,t0
c1t?
p1
υ1t
c0
υ0
p0
h0
0
1h
c12t c02
h0 h1t
2
H 0 h0 h1t
t0
- располагаемый
теплоперепад на канал (по
статическим параметрам)
k
h
p const
k 1
υ0
H0
υ1t
p1
h1t
s
c12t
k
c02
p0 0 p1 1t
2 k 1
2

38.

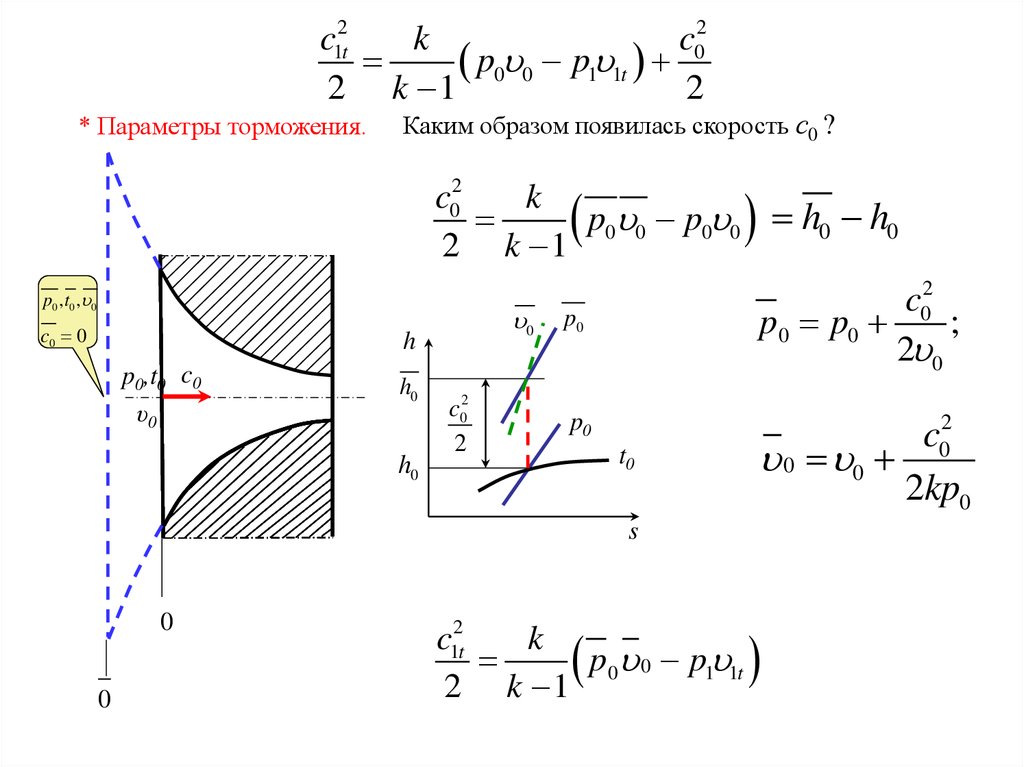
c12t
k
c02
p0 0 p1 1t
2 k 1
2
* Параметры торможения.
Каким образом появилась скорость с0 ?
c02
k
p0 0 p0 0 h0 h0
2 k 1
p0 , t0 , 0
c0 0
0
h
p0,t0 c0
υ0
h0
h0
c02
2
c02
p0 p0
;
2 0
p0
p0
t0
c02
0 0
2kp0
s
0
_
0
c12t
k
p0 0 p1 1t
2 k 1

39.

c12t
k
p0 0 p1 1t h0 h1t
2 k 1
H h
c
k
p1 1t
p 0 0 1
2 k 1
p
0
0
0
0
h1t - располагаемый теплоперепад на
канал (по параметрам торможения на
2
1t
p1 p0
p1 1t
p 0 p1
p0 0
1
k
а) По уравнению изоэнтропы
1
k
c02
H0 H0
2
k 1
k
p k const имеем
1t p 0
0 p1
k
p0 0 p1 1kt
б) Обозначим
входе)
p1
p0
1
k
отношение давлений на канал (сопло)
k 1
c12t
k
k
p 0 0 1
2 k 1