Similar presentations:
Распространение волн
1. Распространение волн
Часть 22. Дифракция Френеля
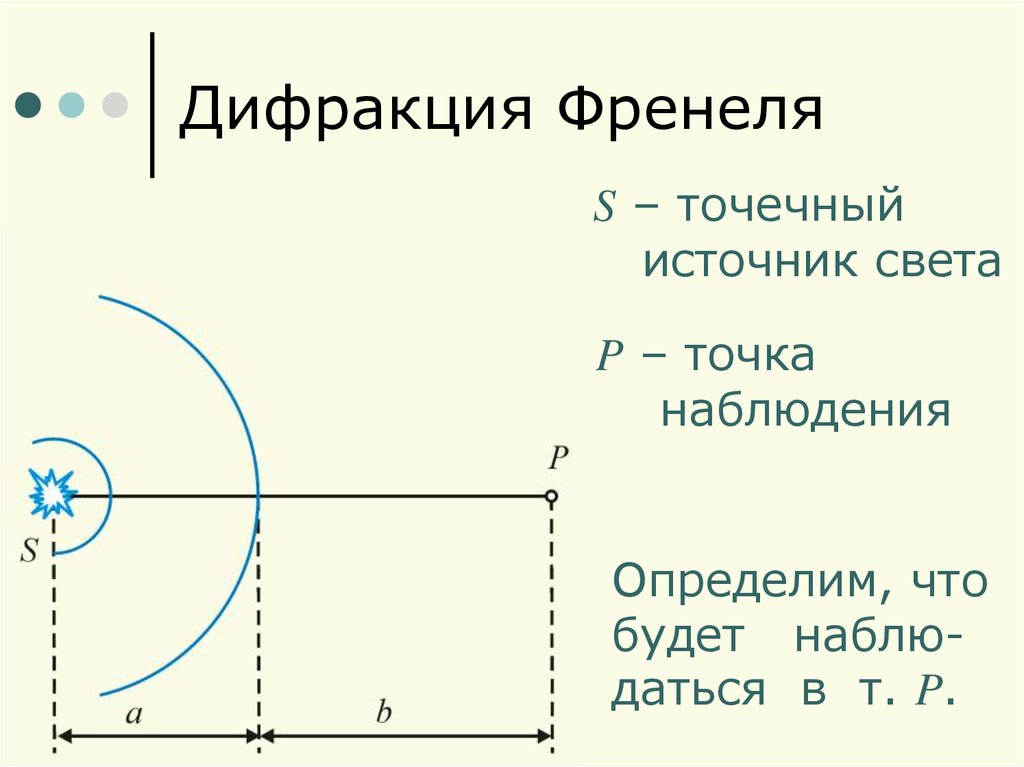
S – точечныйисточник света
P – точка
наблюдения
Определим, что
будет наблюдаться в т. P.
3.
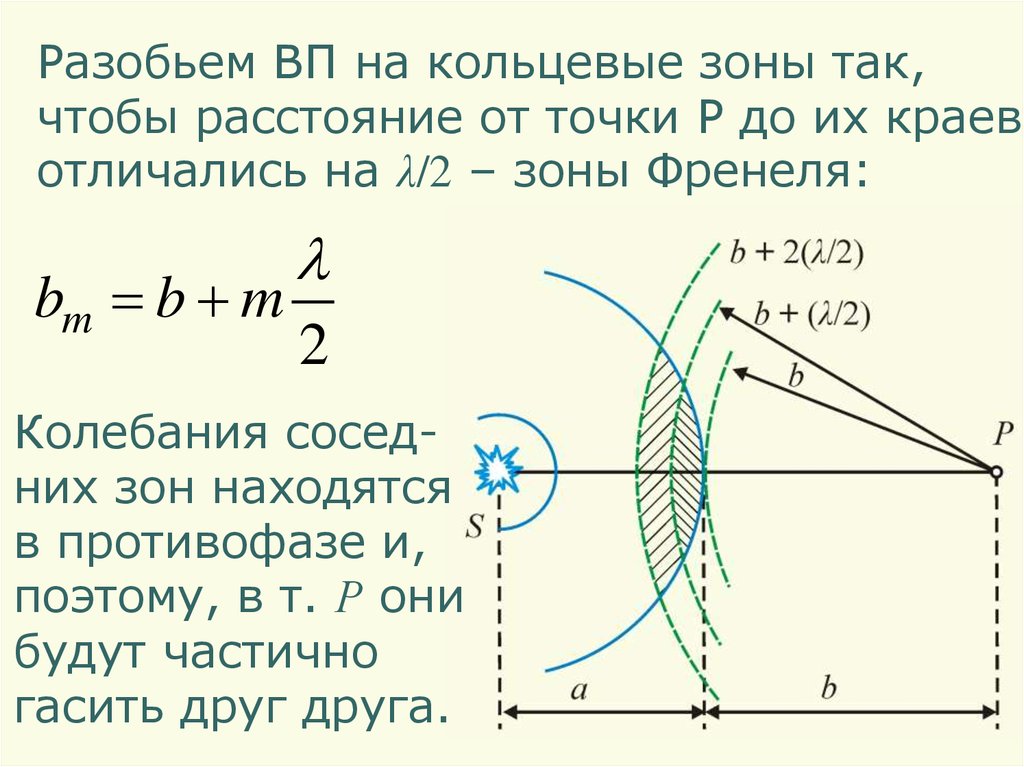
Разобьем ВП на кольцевые зоны так,чтобы расстояние от точки P до их краев
отличались на λ/2 – зоны Френеля:
bm b m
2
Колебания соседних зон находятся
в противофазе и,
поэтому, в т. Р они
будут частично
гасить друг друга.
4.
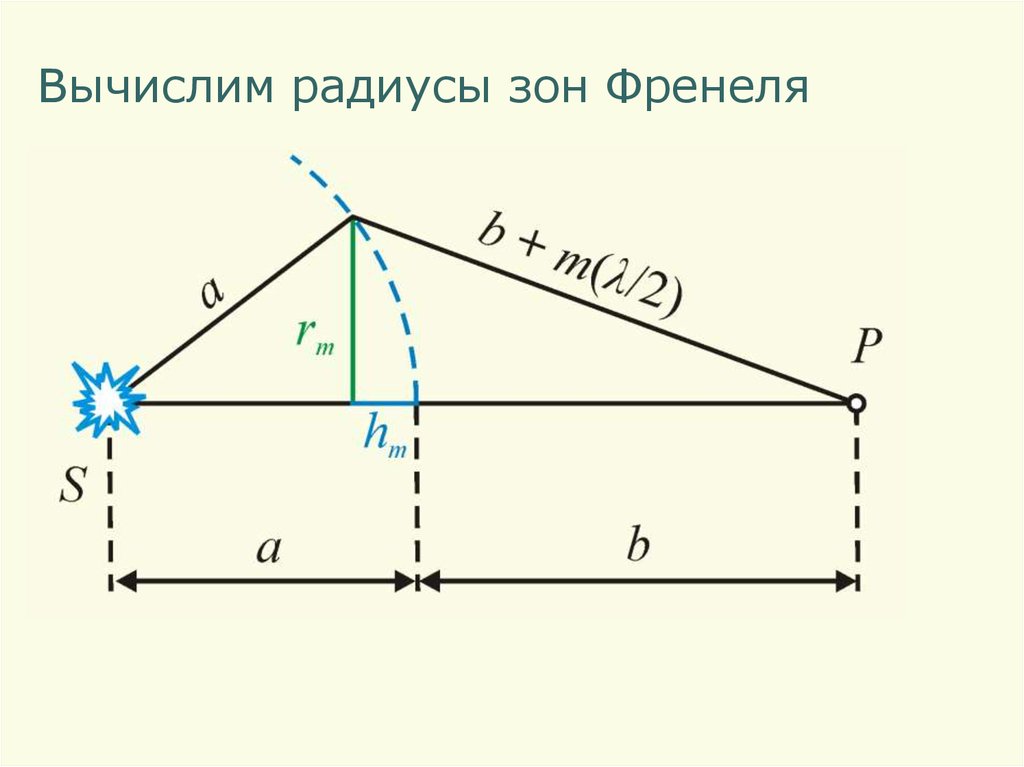
Вычислим радиусы зон Френеля5.
a (a hm )2
rm (b m ) 2 (b hm ) 2
2
2
rm
2
2
2ahm
2
rm 2bm 2bhm
2
2
rm
6.
hm
rm
bm
2( a b)
m
1 1
a b
– высота сферического
сегмента, занимаемого
зоной с номером m
– радиус m-ой зоны
Френеля
Площадь сферического
сегмента:
S 2 Rh 2 a hm
7.
Площадь m-ой зоны:S Sm Sm 1 2 a(hm hm 1 )
S
ab
a b
т.е. площади зон Френеля практически
одинаковы и энергия, переносимая
каждой зоной в отдельности,
почти одинакова
8.
Вычислим амплитуду в т.P, котораяполучается при сложении всех зон
и учтем, что зоны находятся в
противофазе:
Ap A1 A2 A3 A4 ...
A3 A3
A5
A1 A1
A2 A4 ...
2 2
2 2
2
A1
2
– действие всего фронта
9.
Например, радиус первой зоны приa =∞ (плоский в.ф.), b = 1 м получаем
r1 = 0.8 мм.
Следовательно, свет от ист. S к точке P
распространяется (как бы) в узком
канале, ограниченном первой зоной –
т.е. практически прямолинейно.
При открытии только первой зоны:
Ap A1 2 A, I p 4 I 0
Если отверстие в экране открывает и
вторую зону, то интенсивность в т.Р
падает практически до нуля.
10. Зонная пластинка
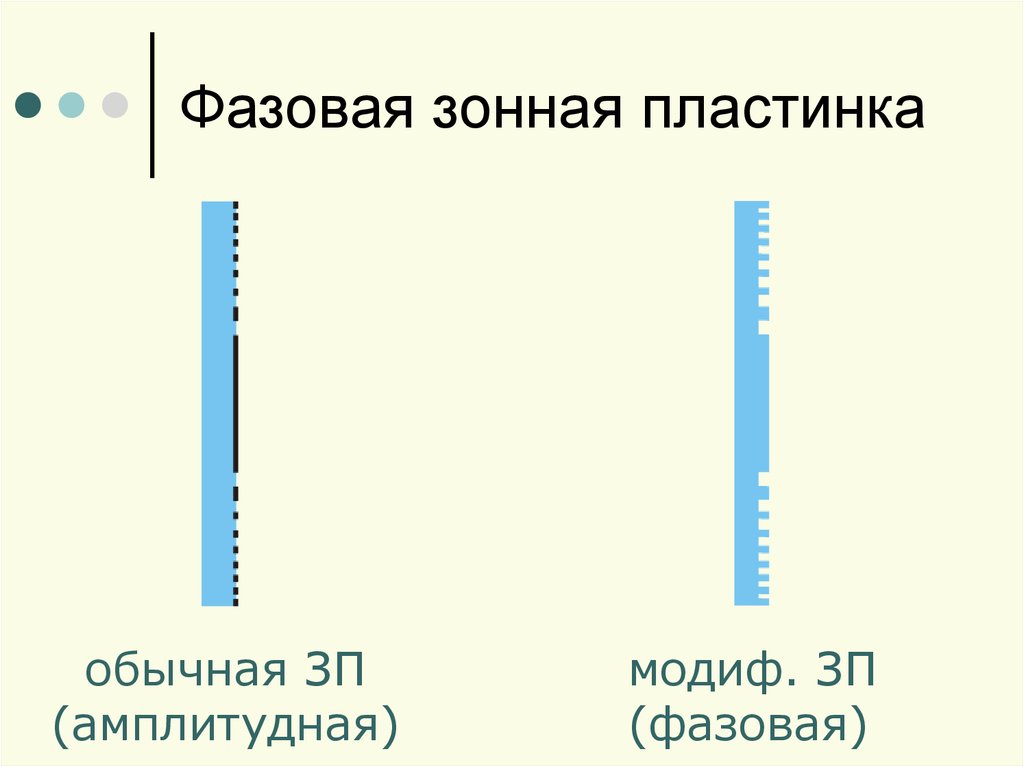
11. Фазовая зонная пластинка
обычная ЗП(амплитудная)
модиф. ЗП
(фазовая)
12. Дифракция рентгеновских лучей
Естественные 3х мерные периодическиеструктуры – кристаллы (d = 1–4 Å =
= 0.1–0.4 нм)
λвид ~ 500 нм
λрент ~0.01–100 нм
13.
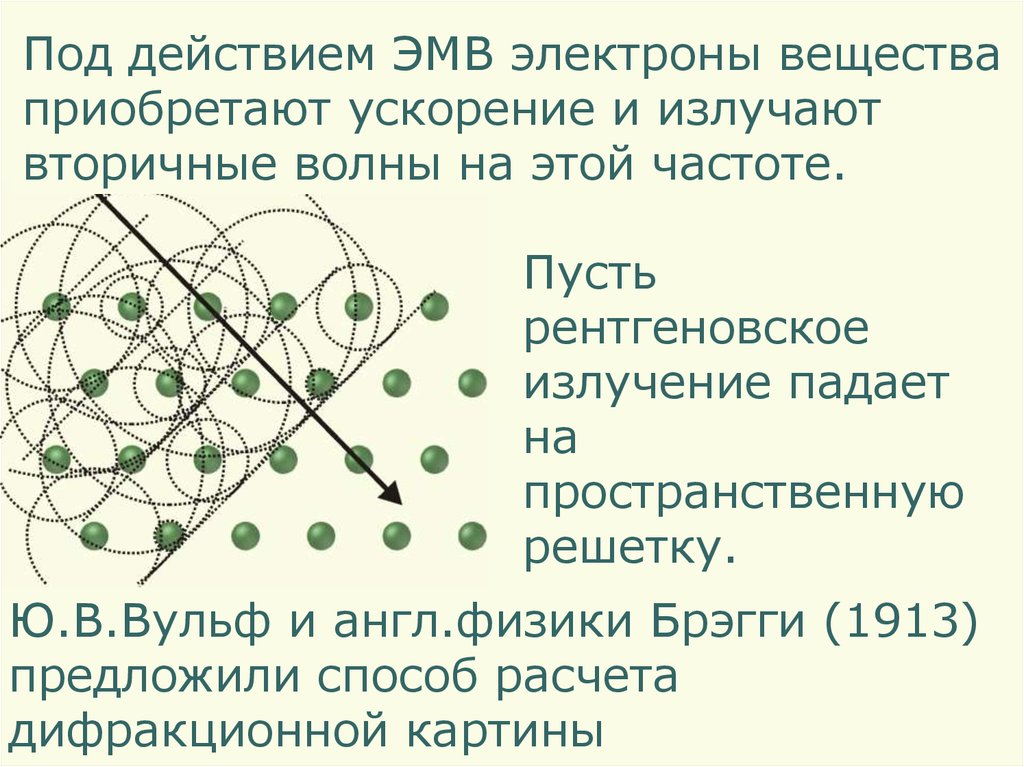
Под действием ЭМВ электроны веществаприобретают ускорение и излучают
вторичные волны на этой частоте.
Пусть
рентгеновское
излучение падает
на
пространственную
решетку.
Ю.В.Вульф и англ.физики Брэгги (1913)
предложили способ расчета
дифракционной картины
14.
Разобьем кристалл на ряд параллельныхплоскостей (одним из многих способов)
d – расстояние м/у атомными плоскостями
θ – угол скольжения, λ – длина волны
15.
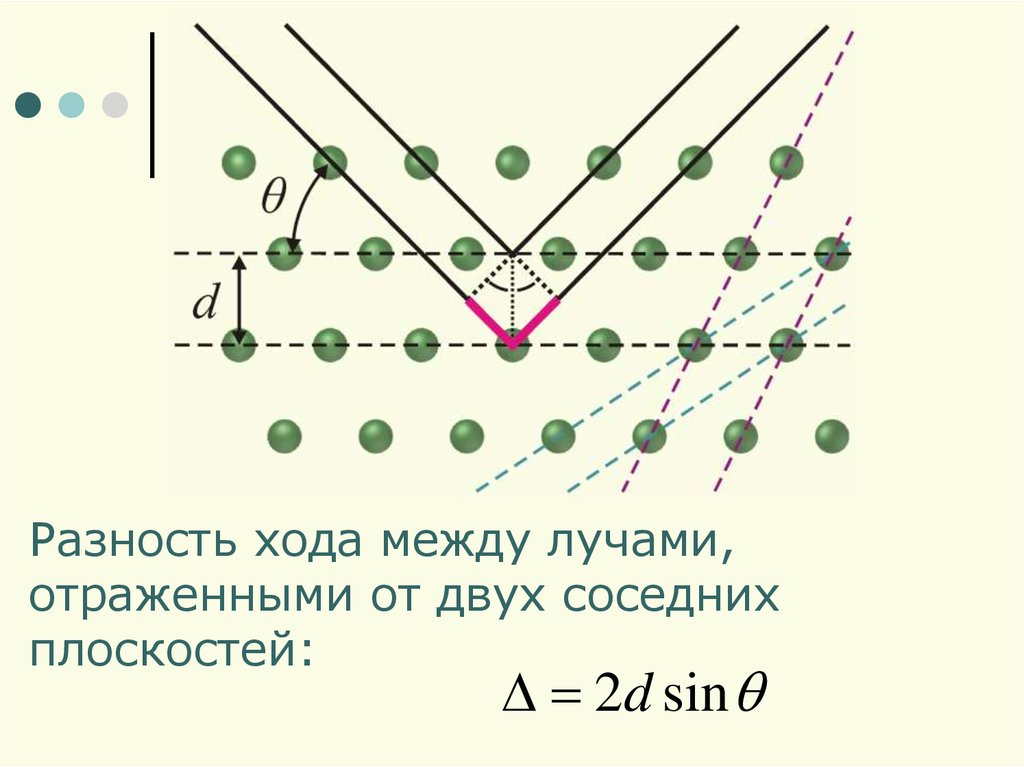
Разность хода между лучами,отраженными от двух соседних
плоскостей:
2d sin
16.
Условие наилучшего отражения:2d sin m
m 1,2,3...
– формула
Вульфа–Брэгга
17. Применение явления дифракции света на кристаллах
1) В рентгеновской спектроскопиидля исследования характеристик
излучения
2) В рентгеноструктурном анализе
для изучения внутренней структуры
кристаллов
18.
Если на одиночный кристалл направитьпучок монохроматического
рентгеновского излучения, то отражение
появится только при строго определенных
ориентировках кристалла
19. Метод порошков
Если взять поликристаллический образец(много кристалликов, спрессованных или
спеченных), то для любого направления
находится большое количество правильно
ориентированных атомных плоскостей.
20.
По порядку следования линий, углам иинтенсивности устанавливают тип и
параметры атомной решетки кристалла

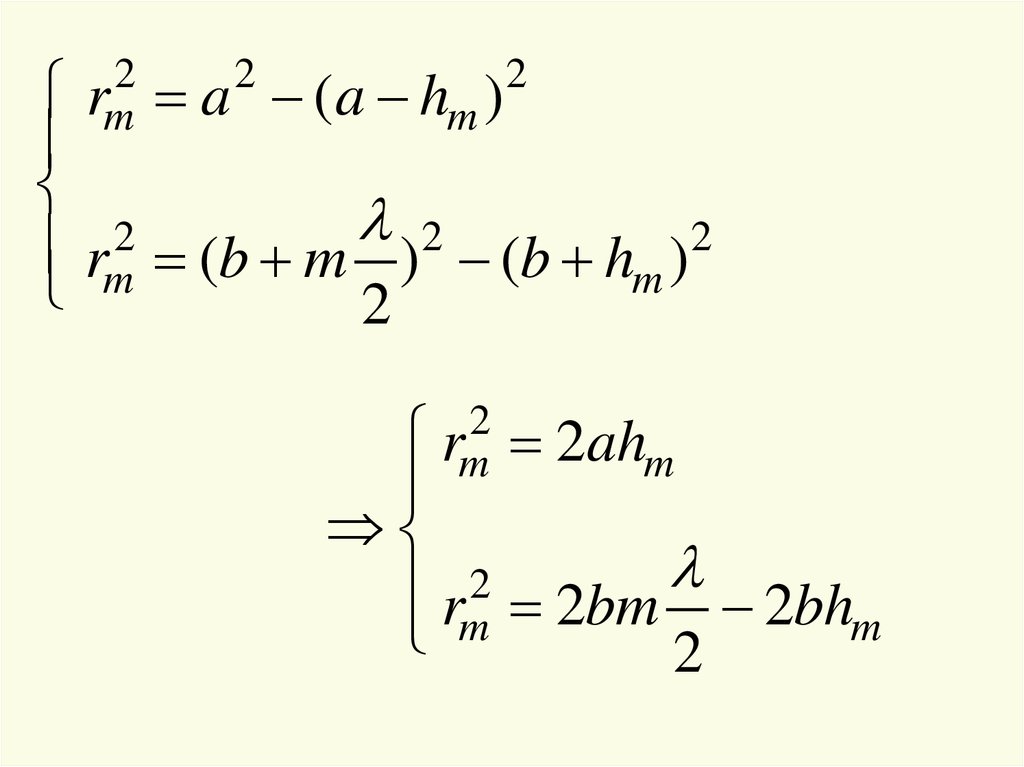












 physics
physics








