Similar presentations:
Дифракция света
1.
ДИФРАКЦИЯ СВЕТА2.
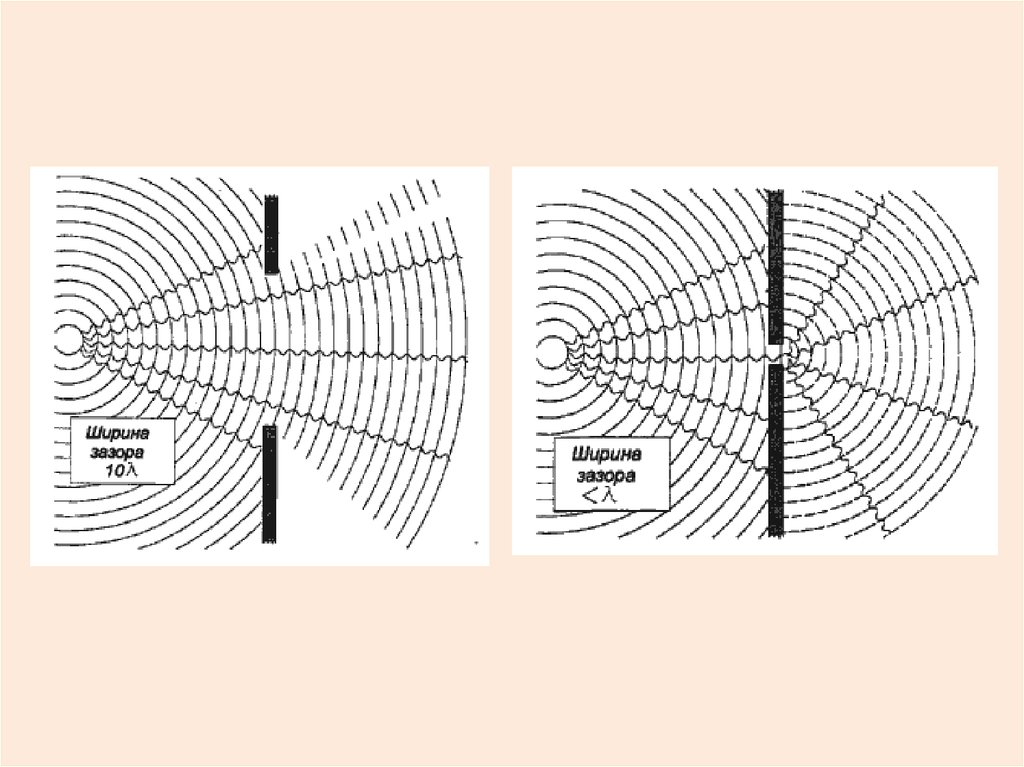
Дифракция - совокупность явлений,наблюдаемых при распространении
света в средах, включающих
неоднородности, из-за которых
наблюдается отклонение от законов
геометрической оптики. Проявление
дифракции - огибание светом
препятствий и проникновение в область
геометрической тени.
3.
4.
5.
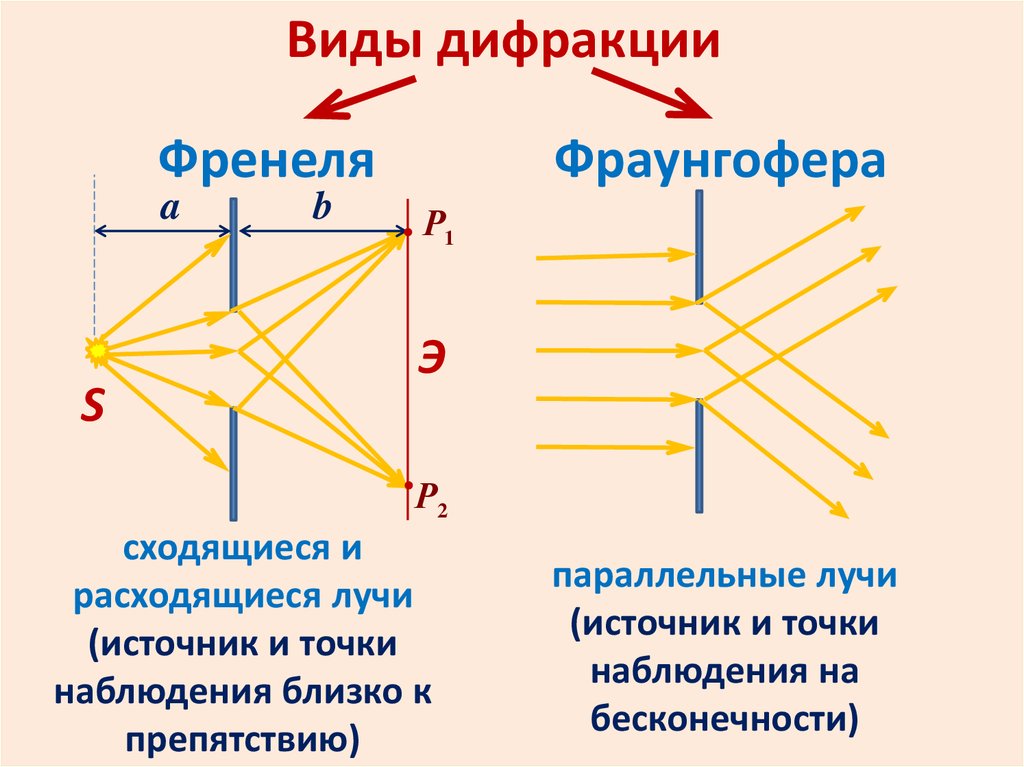
Виды дифракцииФренеля
a
S
b
Фраунгофера
Р1
Э
Р2
сходящиеся и
расходящиеся лучи
(источник и точки
наблюдения близко к
препятствию)
параллельные лучи
(источник и точки
наблюдения на
бесконечности)
6.
Френель Огюст Жан(1788 - 1827)
французский физик, член
Парижской академии наук.
Фраунгофер Йозеф
(1787- 1826)
немецкий физик,
профессор Мюнхенского
университета.
7.
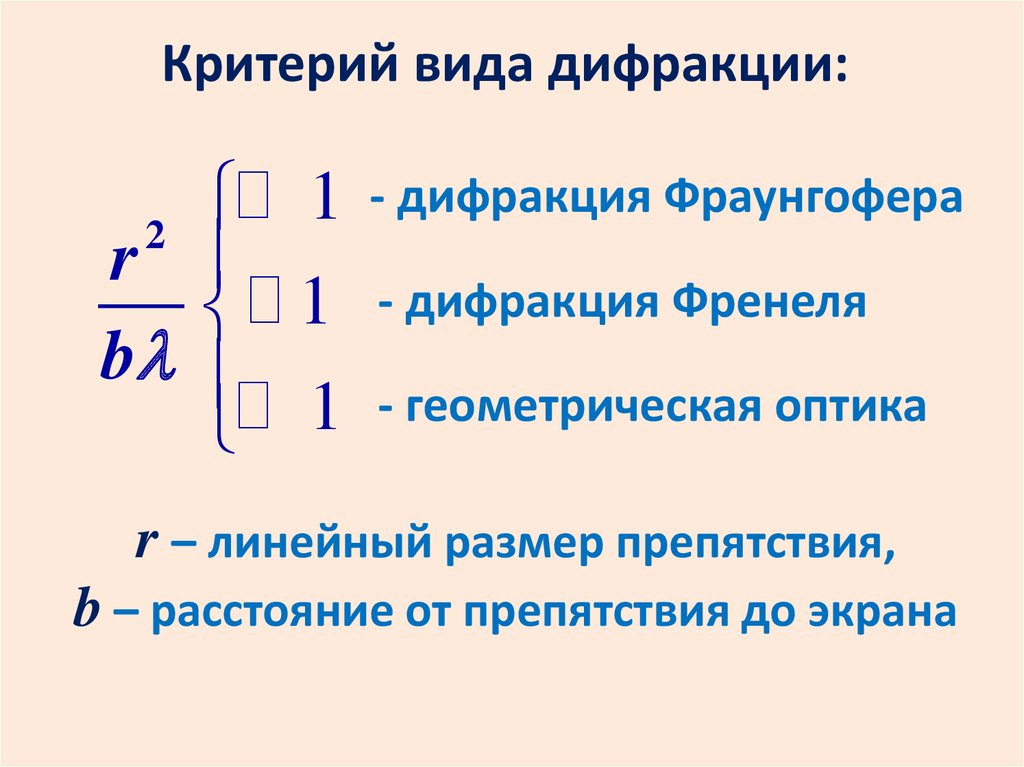
Критерий вида дифракции:1
2
r
1
b
1
- дифракция Фраунгофера
- дифракция Френеля
- геометрическая оптика
r – линейный размер препятствия,
b – расстояние от препятствия до экрана
8.
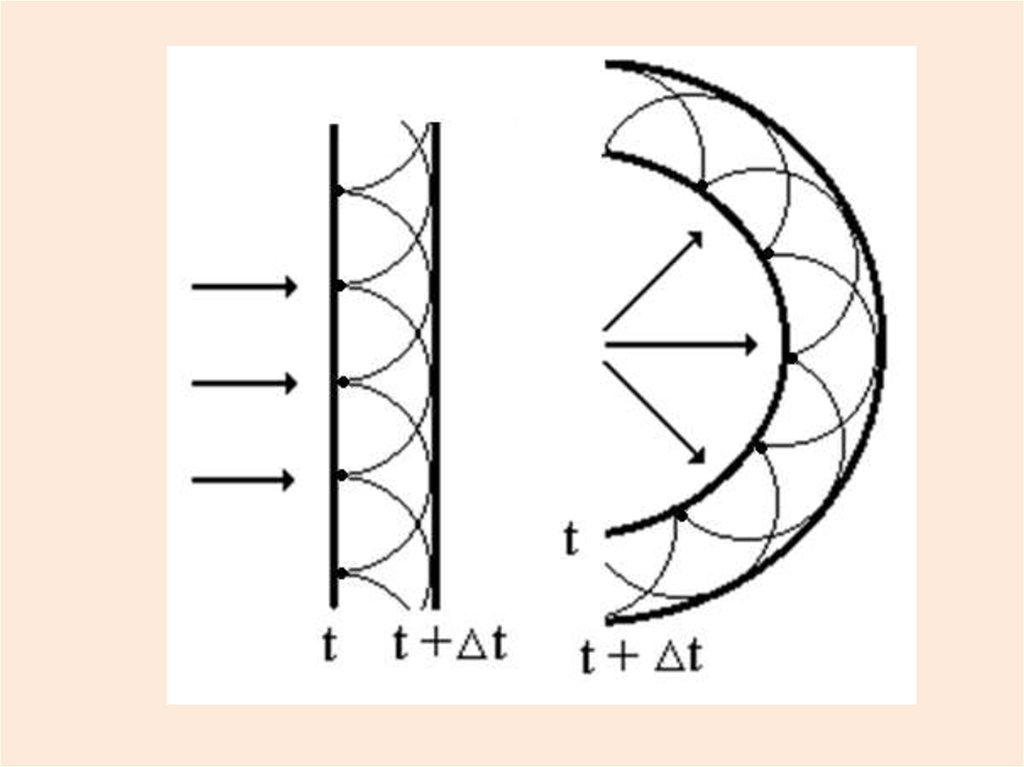
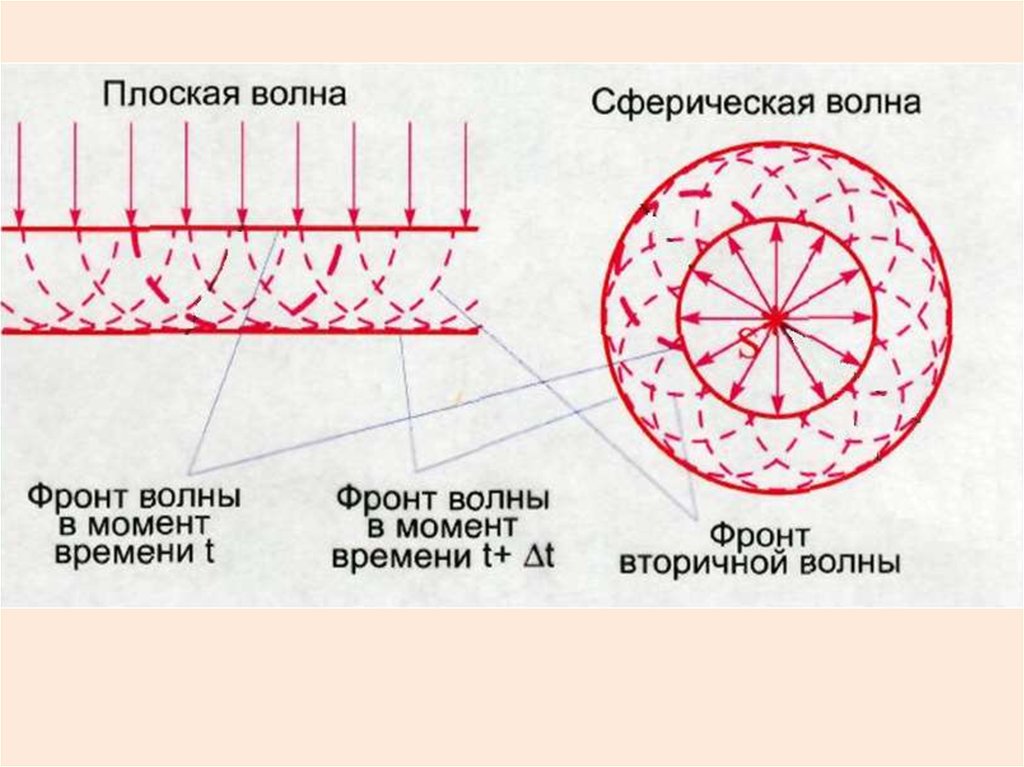
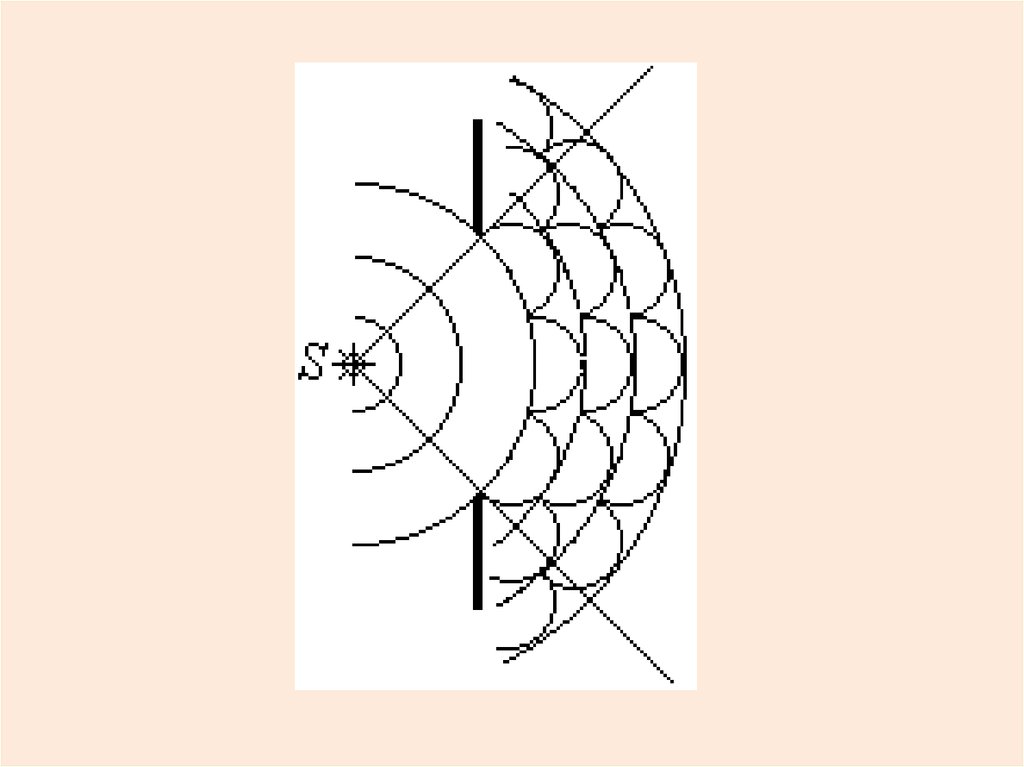
Принцип Гюйгенса(качественное объяснение дифракции)
Каждая точка фронта волны
является источником
вторичных волн, огибающая
которых образует новый
фронт волны.
9.
10.
11.
12.
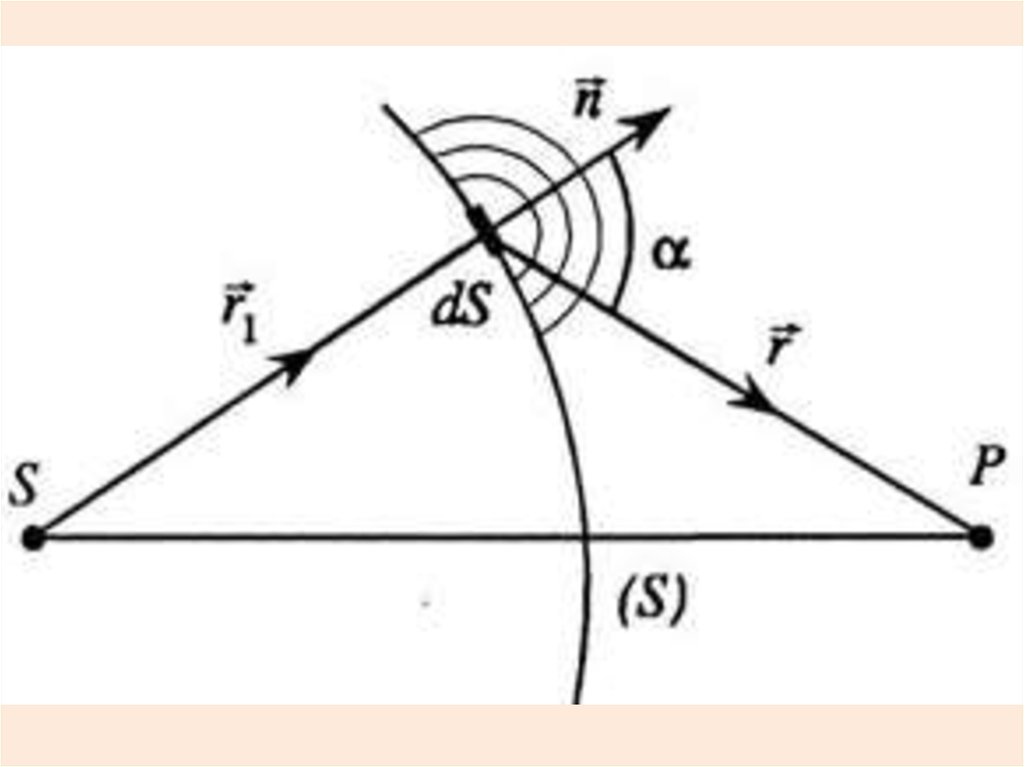
Метод зон ФренеляАмплитуда результирующей
волны в любой точке может быть
найдена как результат
интерференции всех вторичных
волн с учетом их фаз и амплитуд.
13.
14.
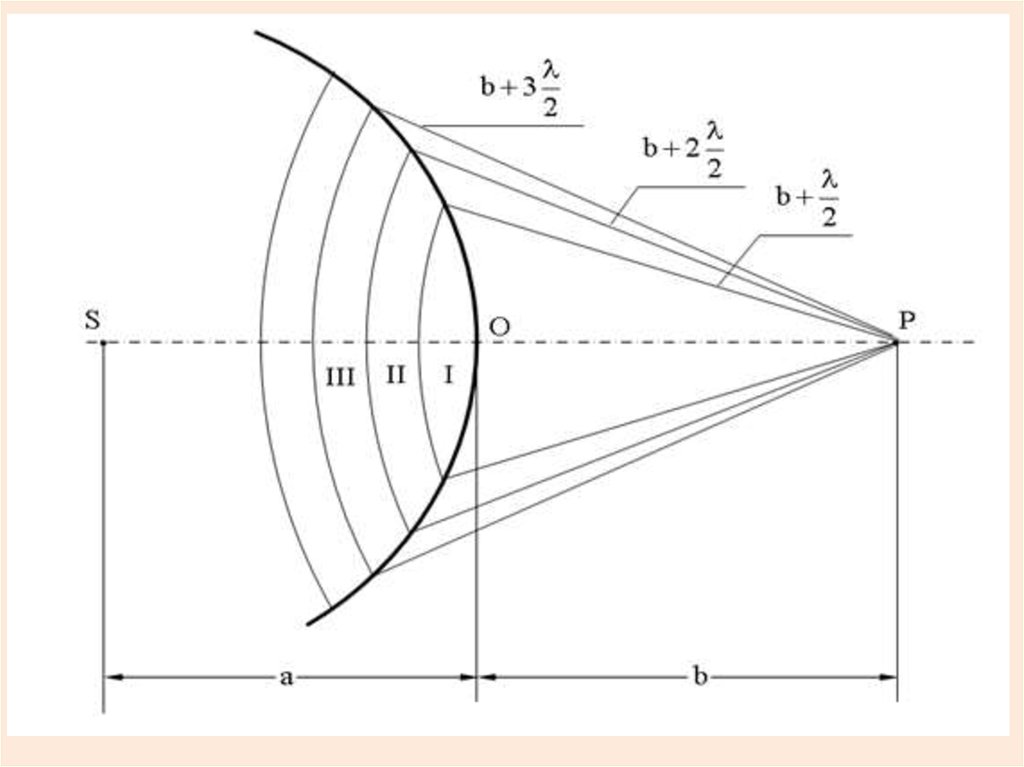
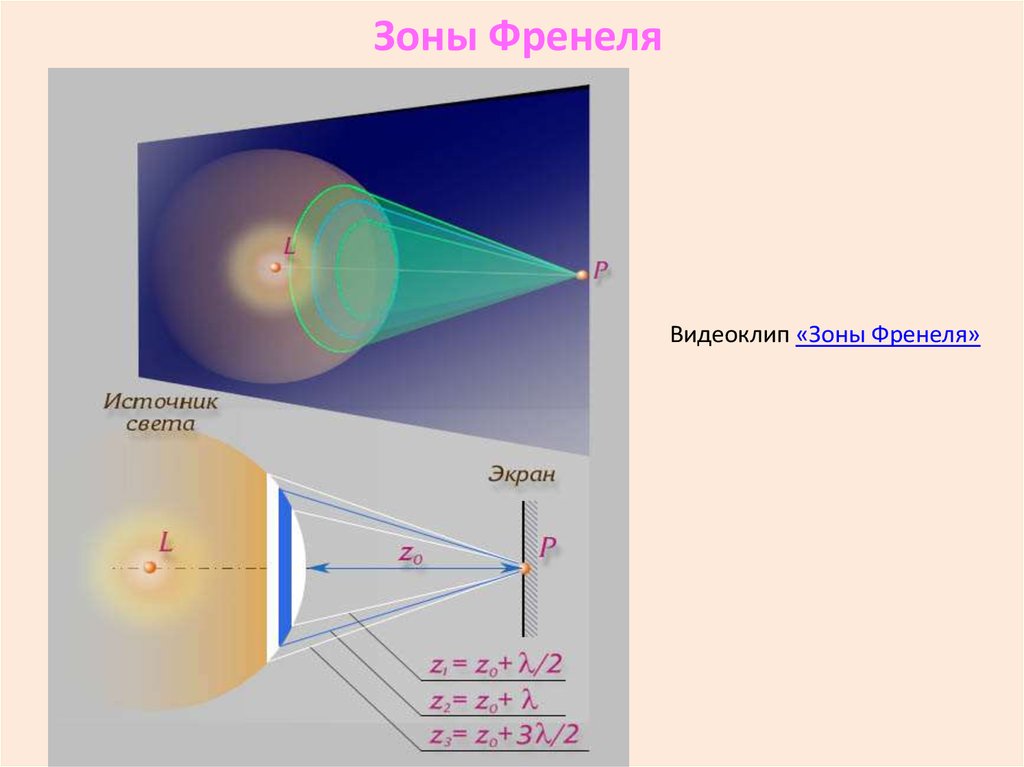
Пусть от источника света Sраспространяется монохроматическая
сферическая волна, P - точка
наблюдения. Разобьем сферическую
волновую поверхность на кольцевые
зоны I, II, III и т.д. так, чтобы
расстояния от краев зоны до точки P
отличались на λ/2.
14
15.
16.
Колебания, возбуждаемыев точке Р двумя соседними
зонами, противоположны
по фазе из-за разности хода
/2. Такие колебания гасят
друг друга.
17.
Гашение неполное, т.к. каждаяследующая зона создает в т. Р
колебания меньшей амплитуды,
чем предыдущая.
А1 A2 A3 ...
18.
Зоны ФренеляВидеоклип «Зоны Френеля»
Дифракция
18
19.
Метод векторных диаграммРазобьем каждую зону на много
узких кольцевых подзон. Изобразим
колебание, создаваемое каждой
подзоной в т. Р , в виде маленькой
стрелочки на векторной диаграмме.
Стрелочки повернуты друг
относительно друга на угол ,
соответствующий сдвигу фаз
колебаний.
20.
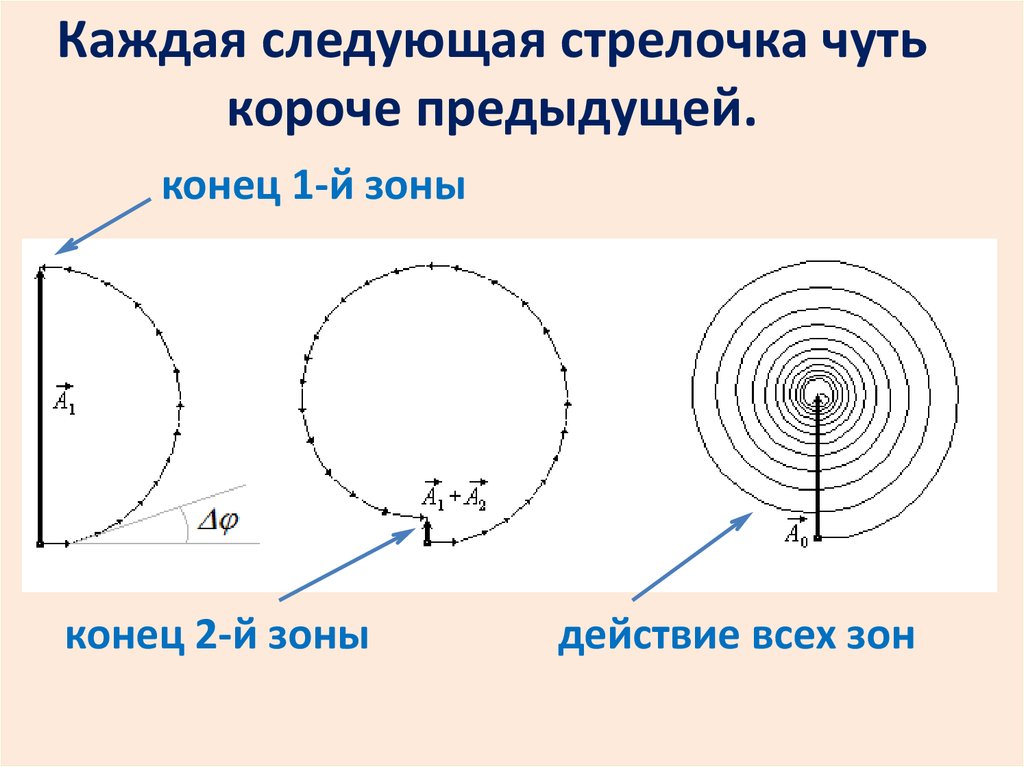
Каждая следующая стрелочка чутькороче предыдущей.
конец 1-й зоны
конец 2-й зоны
действие всех зон
21.
Как видно из рисунка,A1
I1
A0
, значит I 0
2
4
Весь фронт волны создает в т. Р
интенсивность в 4 раза меньшую,
чем одна только 1-я зона.
Волна сама себя частично гасит.
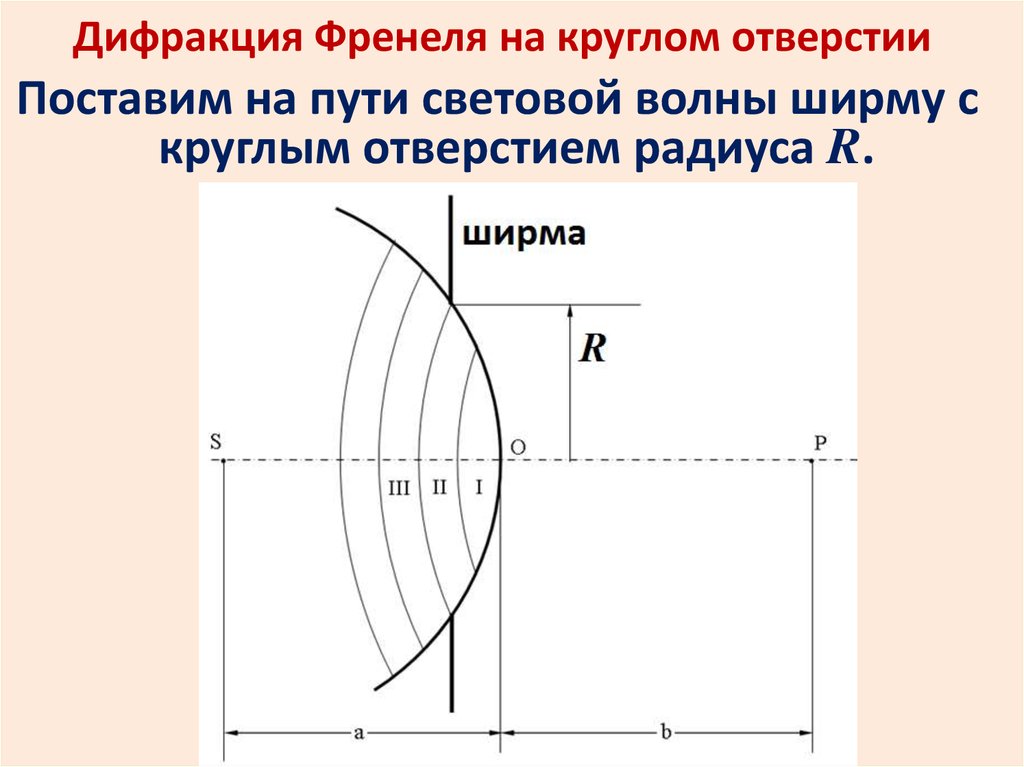
22. Дифракция Френеля на круглом отверстии
Поставим на пути световой волны ширму скруглым отверстием радиуса R.
23. Зоны Френеля в плоскости отверстия радиуса R.
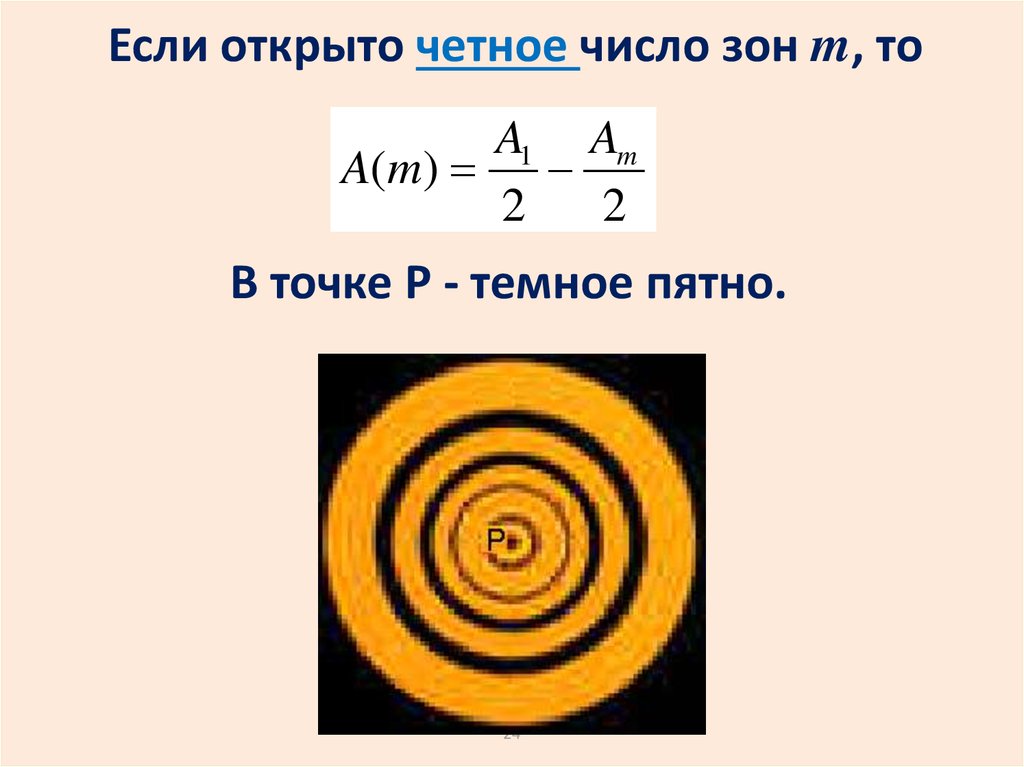
Если открыто четное число зон m, тоA1 Am
A(m)
2
2
В точке P - темное пятно.
24
24. Если открыто четное число зон m, то
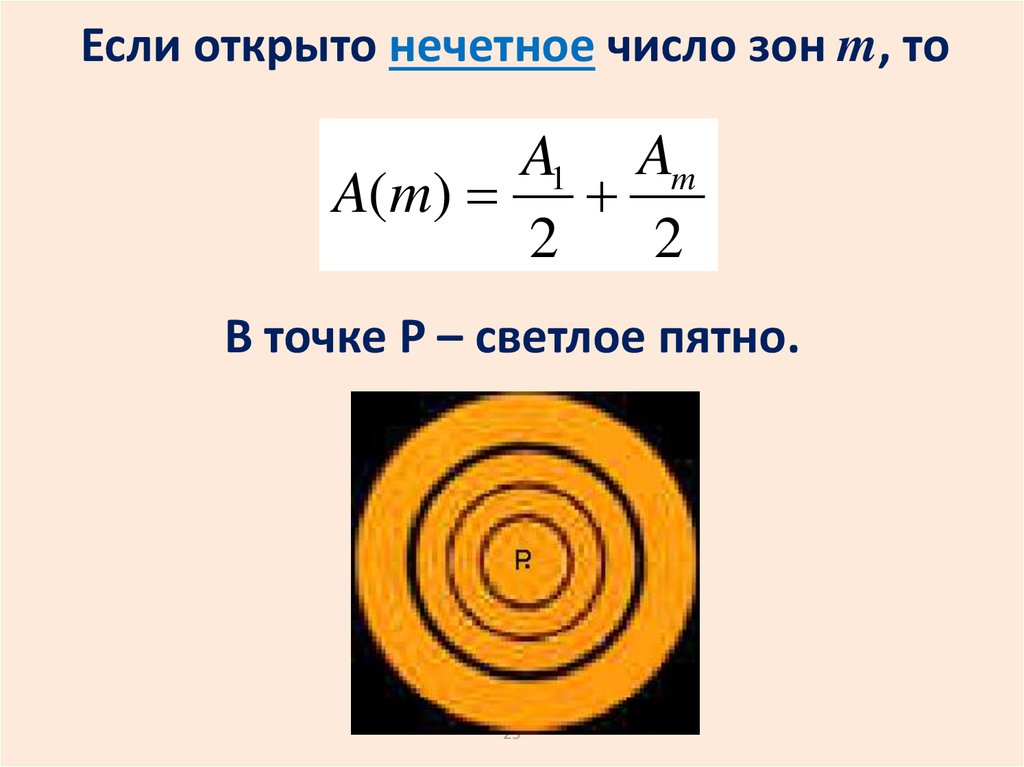
Если открыто нечетное число зон m, тоA1 Am
A(m)
2
2
В точке P – светлое пятно.
25
25. Если открыто нечетное число зон m, то
Дифракция на отверстииВидеоклип «Дифракция на круглом отверстии»
26. Дифракция на отверстии
Резюме:• Если отверстие открывает четное число зон
Френеля, то в точке P будет наблюдаться
минимум, так как все открытые зоны
можно объединить в соседние пары,
колебания которых в точке P
приблизительно гасят друг друга.
• При нечетном числе зон в точке P будет
максимум, так как колебания одной зоны
останутся непогашенными.
27. Резюме:
Зонные пластинкиЕсли на пути световых волн
поставить пластинку, которая
перекрывает все четные
зоны, то интенсивность света
в точке P резко возрастает.
Амплитуда в этой точке
равна сумме амплитуд от
нечетных зон: A=A1+A3+A5+...
Такая пластинка называется
зонной пластинкой
(видеоклип)
Она действует
подобно линзе.
28. Дифракция света на прямоугольном и круглом отверстиях.
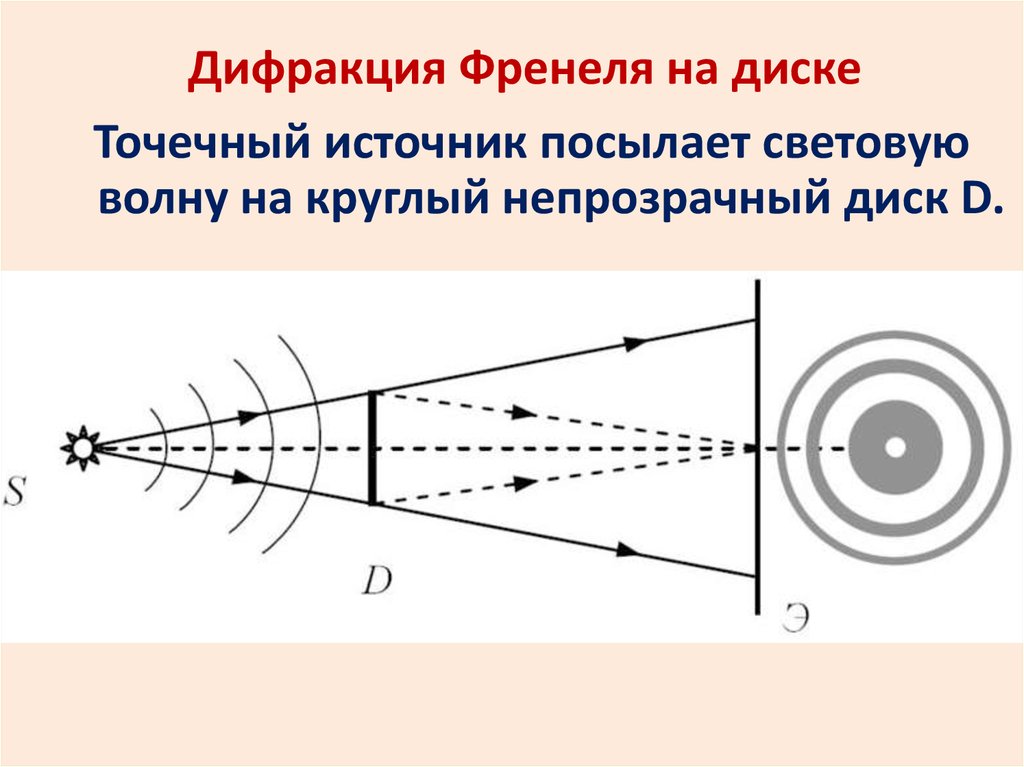
Дифракция Френеля на дискеТочечный источник посылает световую
волну на круглый непрозрачный диск D.
29. Если на пути световых волн поставить пластинку, которая перекрывает все четные зоны, то интенсивность света в точке P резко
Если закрыть m первых зон Френеля, тоAm 1
A
2
В центре экрана всегда будет светлое пятно от
m+1-й зоны.
Это пятно называют
пятном Пуассона.
30. Дифракция Френеля на диске
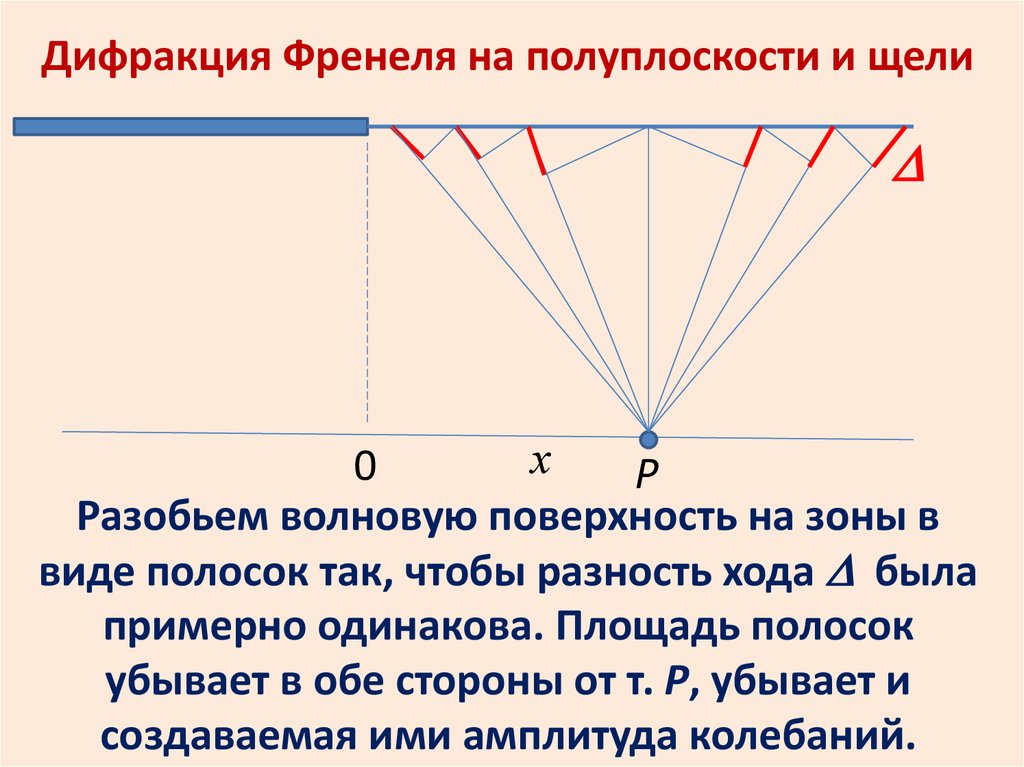
Дифракция Френеля на полуплоскости и щелих
0
Р
Разобьем волновую поверхность на зоны в
виде полосок так, чтобы разность хода была
примерно одинакова. Площадь полосок
убывает в обе стороны от т. Р, убывает и
создаваемая ими амплитуда колебаний.
31. Если закрыть m первых зон Френеля, то
Спираль КорнюA
Каждая стрелочка изображает колебание,
создаваемое одной полоской. Зеленая
стрела – результирующее колебание.
32.
33.
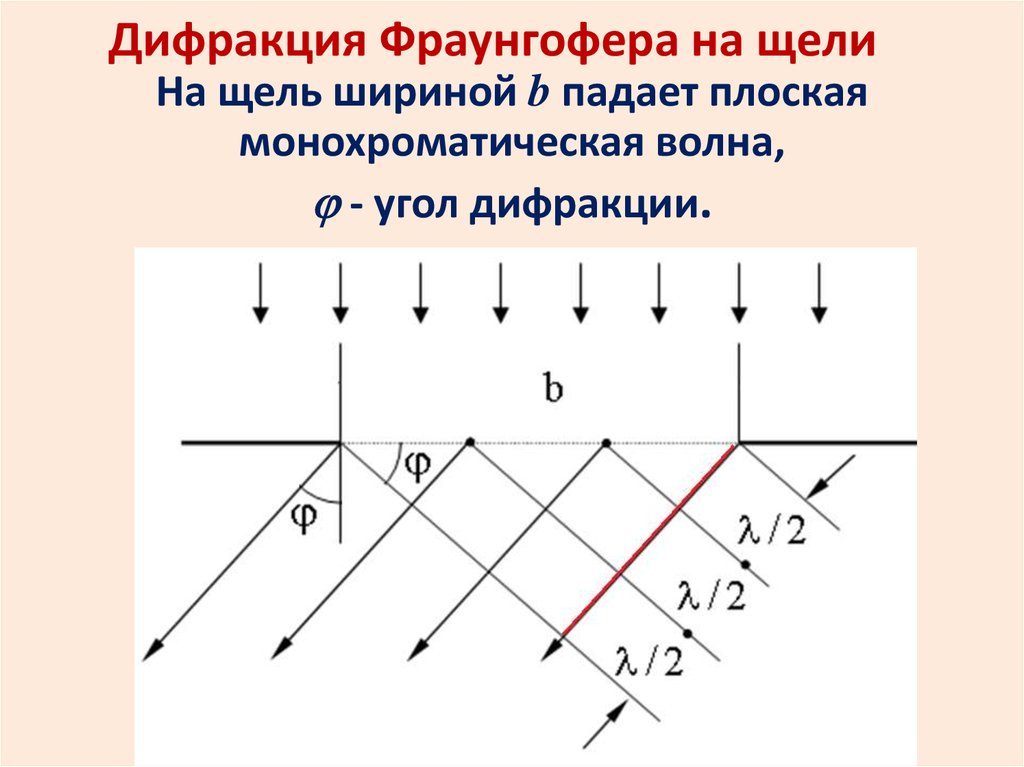
Дифракция Фраунгофера на щелиНа щель шириной b падает плоская
монохроматическая волна,
- угол дифракции.
34.
Применим метод Френеля.Разобьем щель на зоны (на рисунке
их три). Разность хода лучей,
идущих от краев каждой зоны
равна /2. Тогда на отрезке bsin
(красный) полволны уложится
столько раз k, сколько зон открыто.
b sin k
2
35. Дифракция Фраунгофера на щели
• При четном числе зон (k=2m)онипопарно гасят друг друга. Получим
условие минимума:
b sin m , m 1, 2, 3...
• При нечетном k = 2m + 1 колебания
одной из зон не будут погашены,
получим условие максимума:
b sin (2m 1)
2
, m 1, 2, 3...
36.
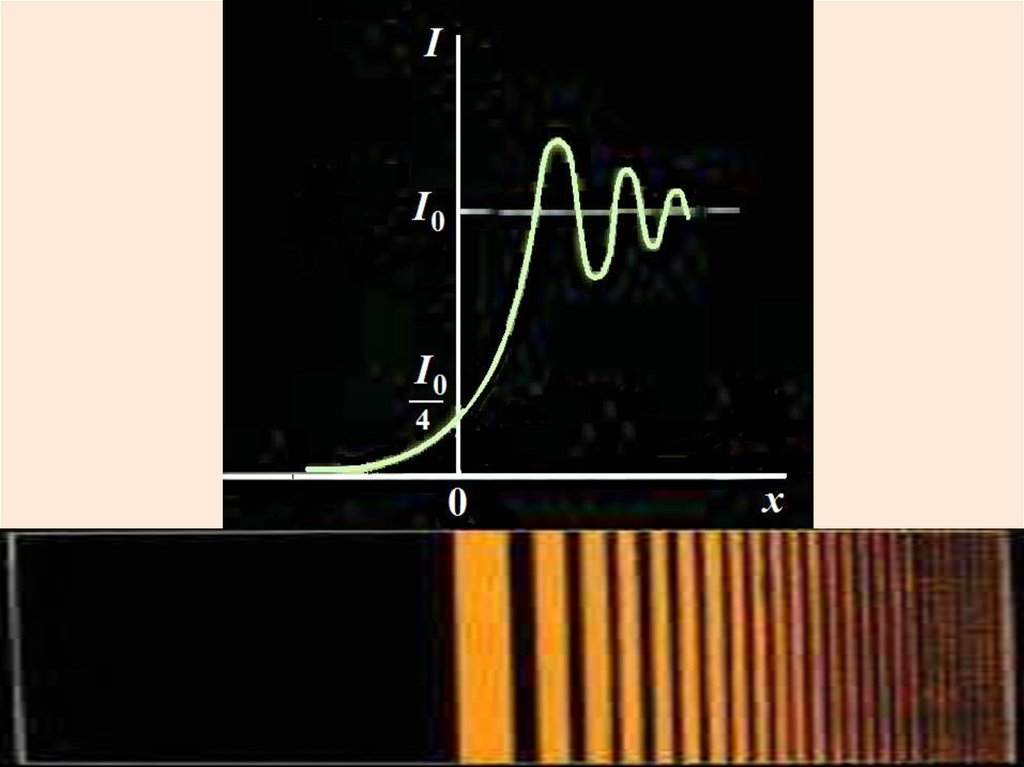
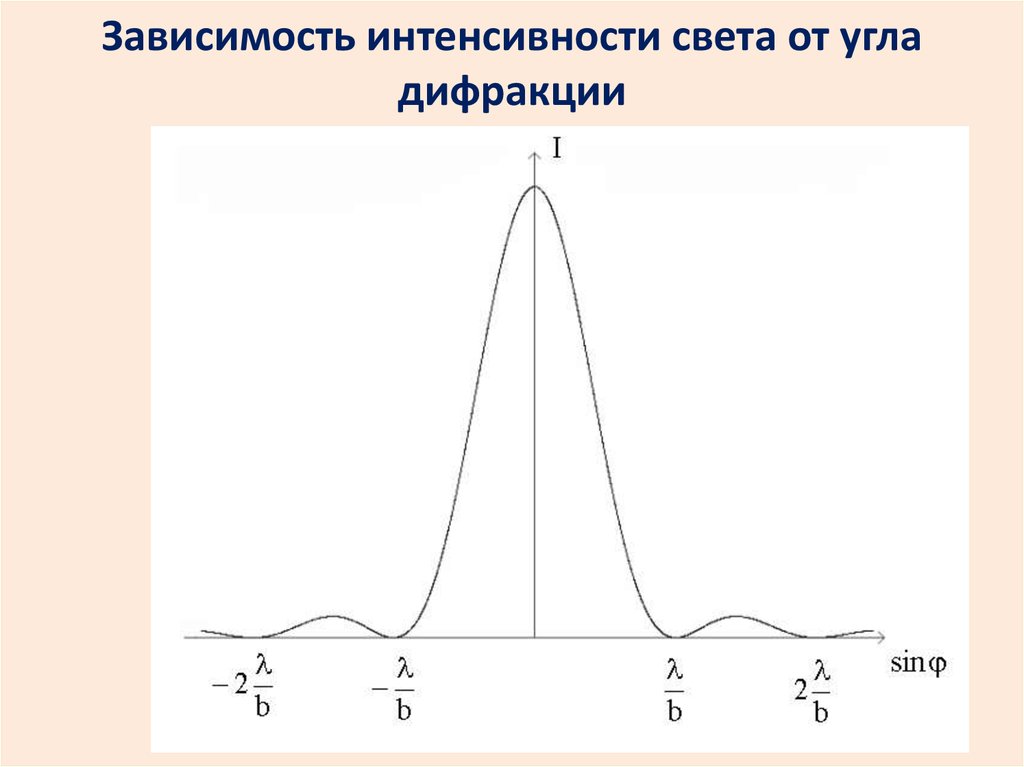
Зависимость интенсивности света от угладифракции
37.
Дифракция лазерного пучка от щели38. Зависимость интенсивности света от угла дифракции
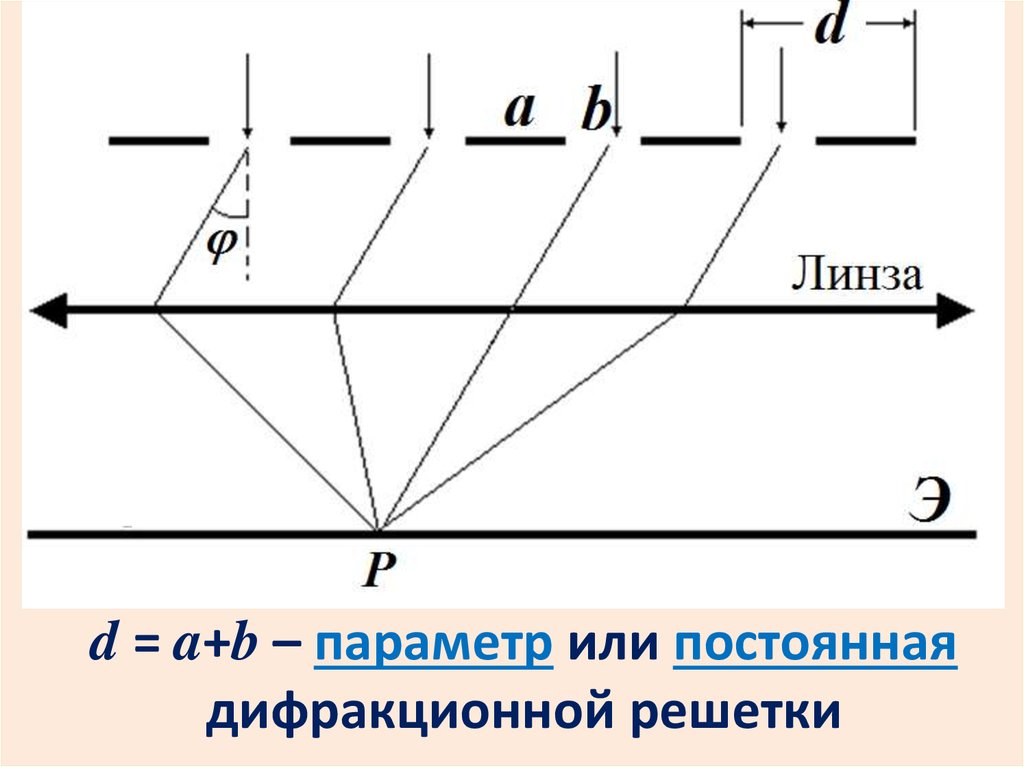
Дифракционная решеткаПравильная структура из большого числа
щелей называется дифракционной решеткой.
39. Дифракция лазерного пучка от щели
d = a+b – параметр или постояннаядифракционной решетки
40. Дифракционная решетка
Дифракция света на дифракционной решеткеВидеоклип «Дифракционная решетка»
Дифракция
42
41.
При дифракции на многихщелях имеет место наложение
лучей, идущих как от одной и
той же щели, так и от соседних
щелей. В одних направлениях
щели гасят друг друга, а в
других усиливают.
42. Дифракция света на дифракционной решетке
В спектре решетки есть три вида особых точек:1)Главные минимумы. Это “старые” минимумы.
Они получаются в тех же направлениях, что и
для одной щели. “Щель сама себя гасит”.
Условие: bsin = m (m=1,2,3…).
2)Главные максимумы. В этих направлениях
щели усиливают друг друга. Условие:
dsin = k (k=0,1,2,…).
3)Дополнительные минимумы. В них щели
гасят друг друга. Условие:
k
d sin ,( k 1, 2,...кроме 0, N , 2 N ...)
N
N – число щелей
43.
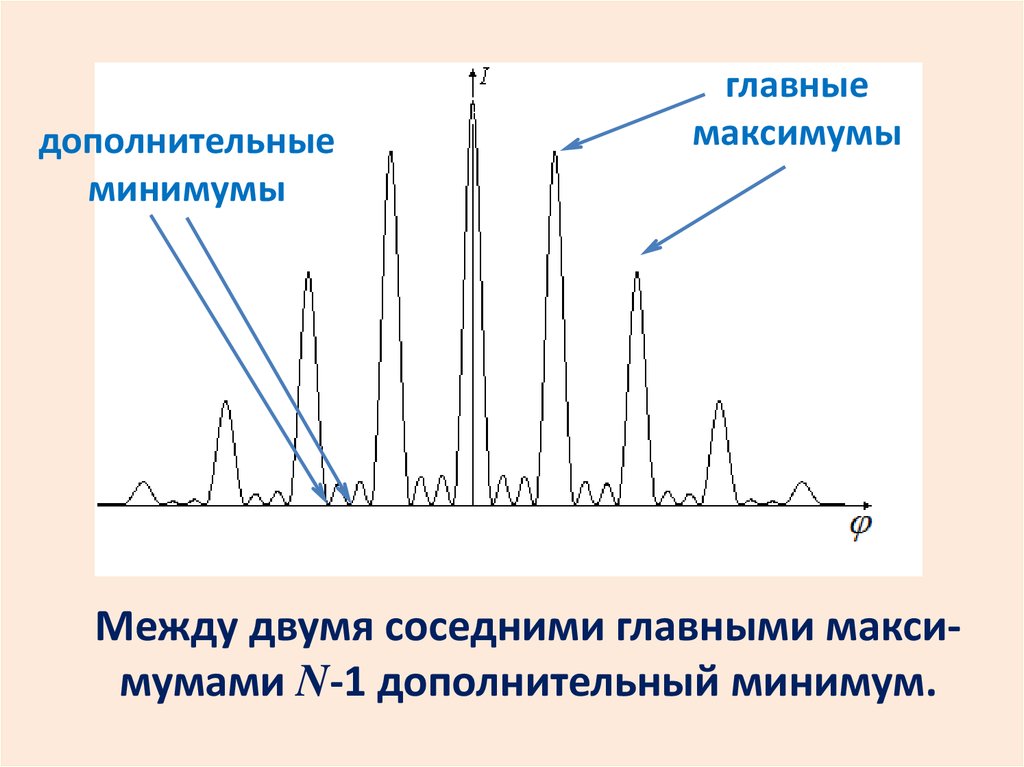
дополнительныеминимумы
главные
максимумы
Между двумя соседними главными максимумами N-1 дополнительный минимум.
44.
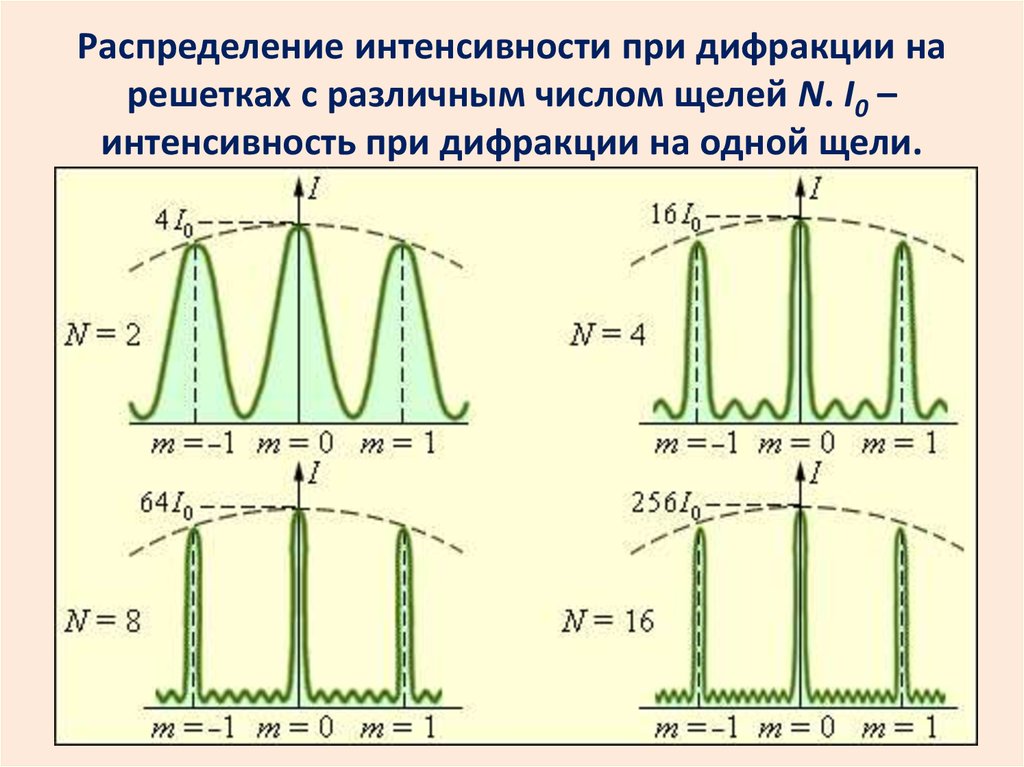
Распределение интенсивности при дифракции нарешетках с различным числом щелей N. I0 –
интенсивность при дифракции на одной щели.
45.
Число главных максимумовможно найти, зная , что sin 1.
d sin k
k
sin
1
d
d
k
46. Распределение интенсивности при дифракции на решетках с различным числом щелей N. I0 – интенсивность при дифракции на одной
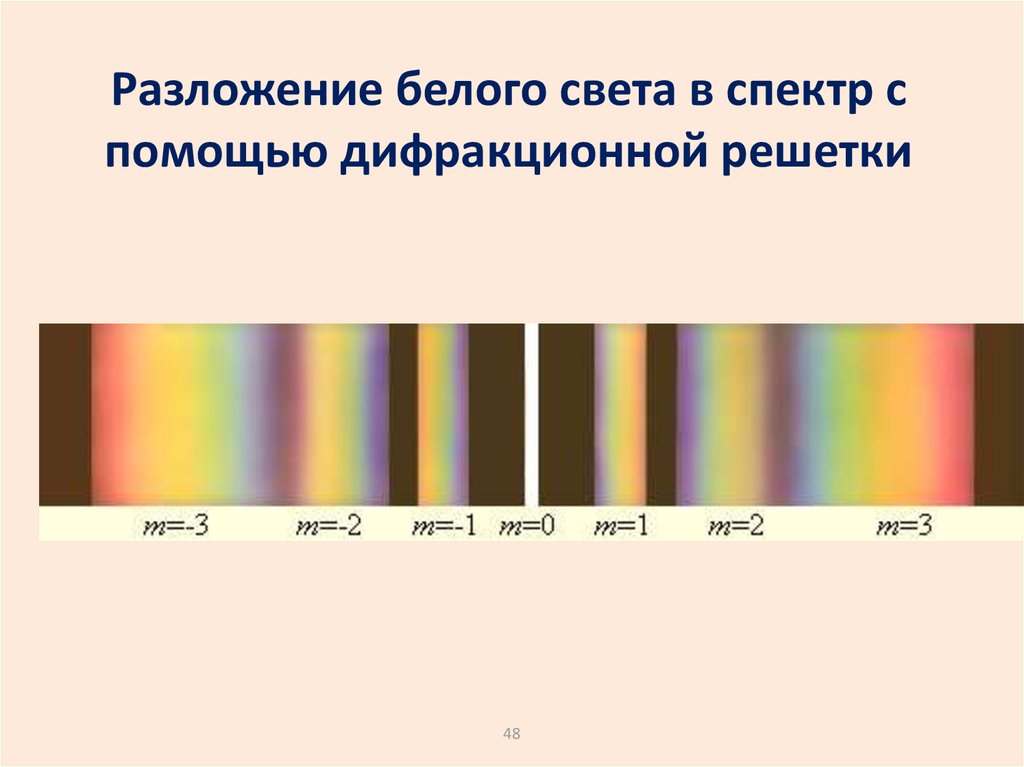
Разложение белого света в спектр спомощью дифракционной решетки
48
47.
Красный светФиолетовый свет
спектральные линии
48. Разложение белого света в спектр с помощью дифракционной решетки
Разрешающая способностьоптических приборов
R
- минимальная разность длин
волн соседних спектральных линий,
воспринимаемых раздельно
49. Красный свет
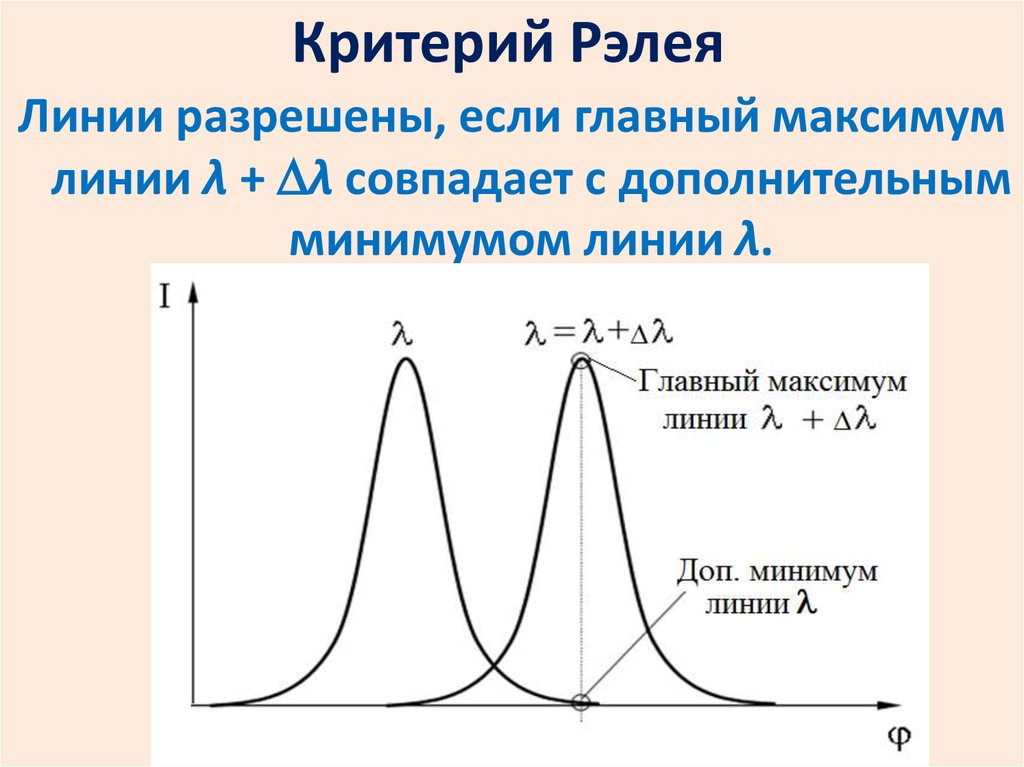
Критерий РэлеяЛинии разрешены, если главный максимум
линии λ + λ совпадает с дополнительным
минимумом линии λ.
50.
Предел разрешения по Релею – этоминимальное угловое расстояние между
максимумами, которые еще можно различить:
52
51.
Разрешающая способностьдифракционной решетки:
R mN
m порядок спектра
N число щелей
52. Предел разрешения по Релею – это минимальное угловое расстояние между максимумами, которые еще можно различить:
Разрешающая способностьобъектива:
R
1
min
D
1, 22
D диаметр объектива
min минимальное угловое
расстояние между двумя точками,
которые видны раздельно
53.
Глаз действует как объектив. Роль Dиграет диаметр зрачка глаза dзр.
Полагая dзр = 3 мм, λ = 550 нм, получим
предельное угловое разрешение глаза:
min 1, 22
d зр
47 1
"
'
54.
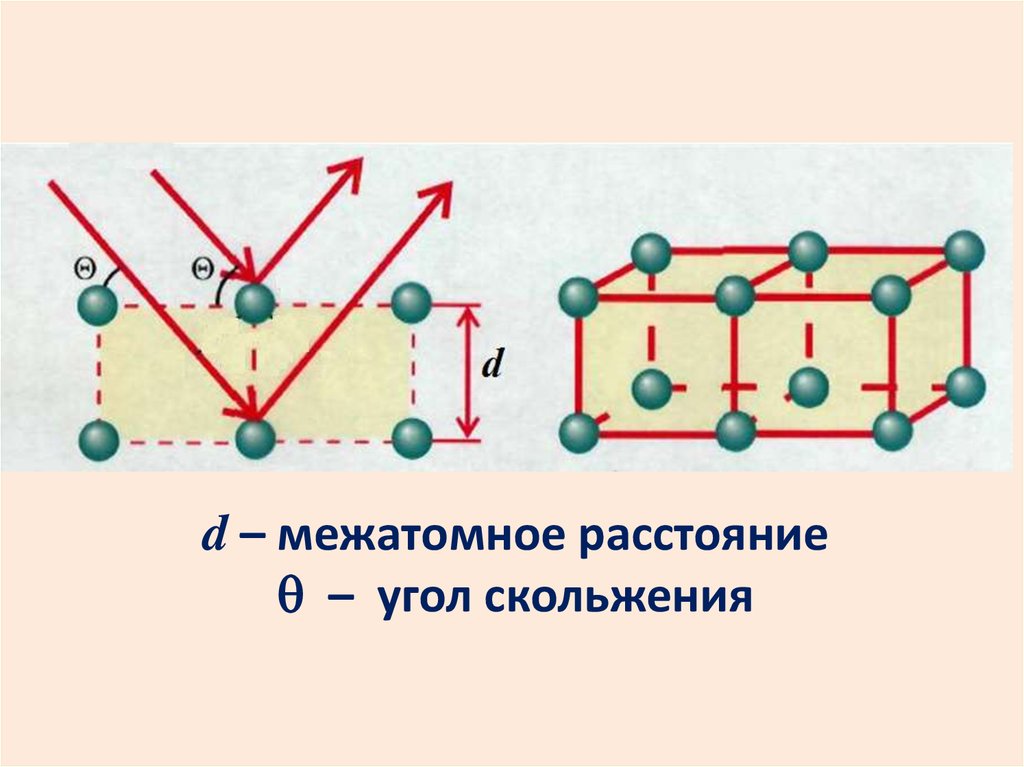
Дифракция на пространственнойрешетке
Роль дифракционной решетки
могут играть кристаллы.
Дифракцию на кристаллах
наблюдают в рентгеновских
лучах, т.к. нужна маленькая .
55. Глаз действует как объектив. Роль D играет диаметр зрачка глаза dзр. Полагая dзр = 3 мм, λ = 550 нм, получим предельное угловое
d – межатомное расстояние– угол скольжения
56.
Формула Вульфа-Брэгговдает условие дифракционных максимумов
2d sin m
m 1, 2, ...
57.
Применение рентгеновской дифракции:1)Рентгеноструктурный анализ.
По известным и находят межатомные
расстояния и определяют кристаллическую
структуру.
2)Рентгеновская спектроскопия.
По известным d и находят длину волны.
3)Электронография и нейтронография.
Последняя позволяет определить
магнитную структуру вещества.
4) Радиолокация
5) Дефектоскопия
58.
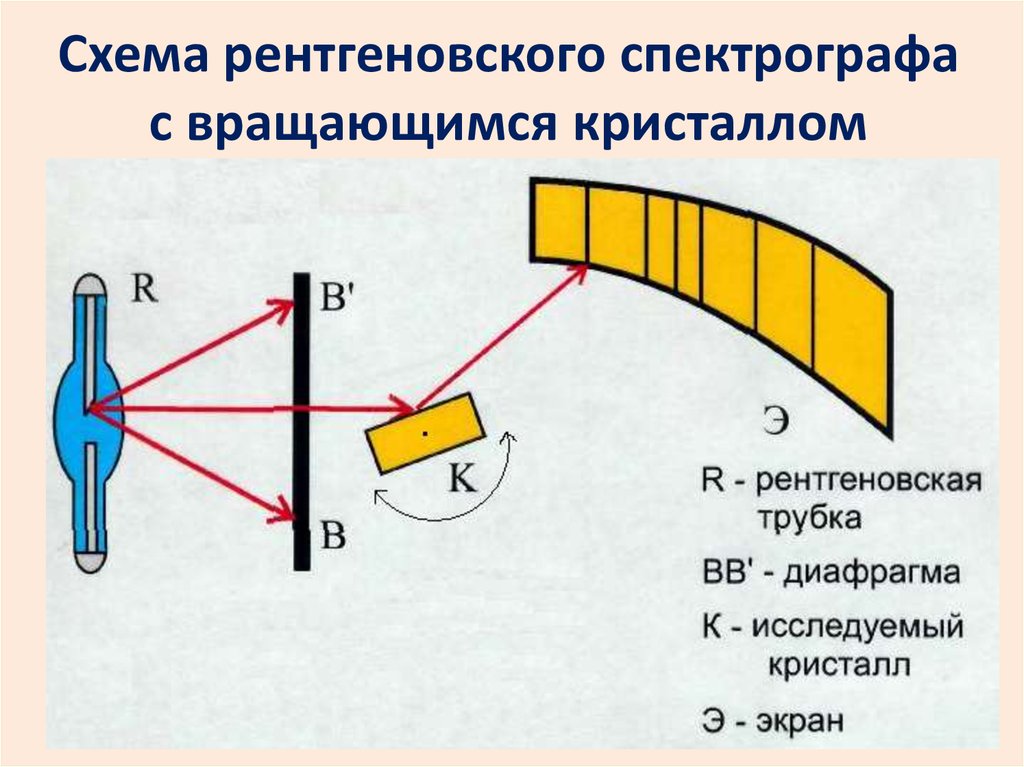
Схема рентгеновского спектрографас вращающимся кристаллом
Дифракция
60
59.
ГолографияПозволяет по дифракционной
картине полностью
восстановить объемное
изображение предмета.























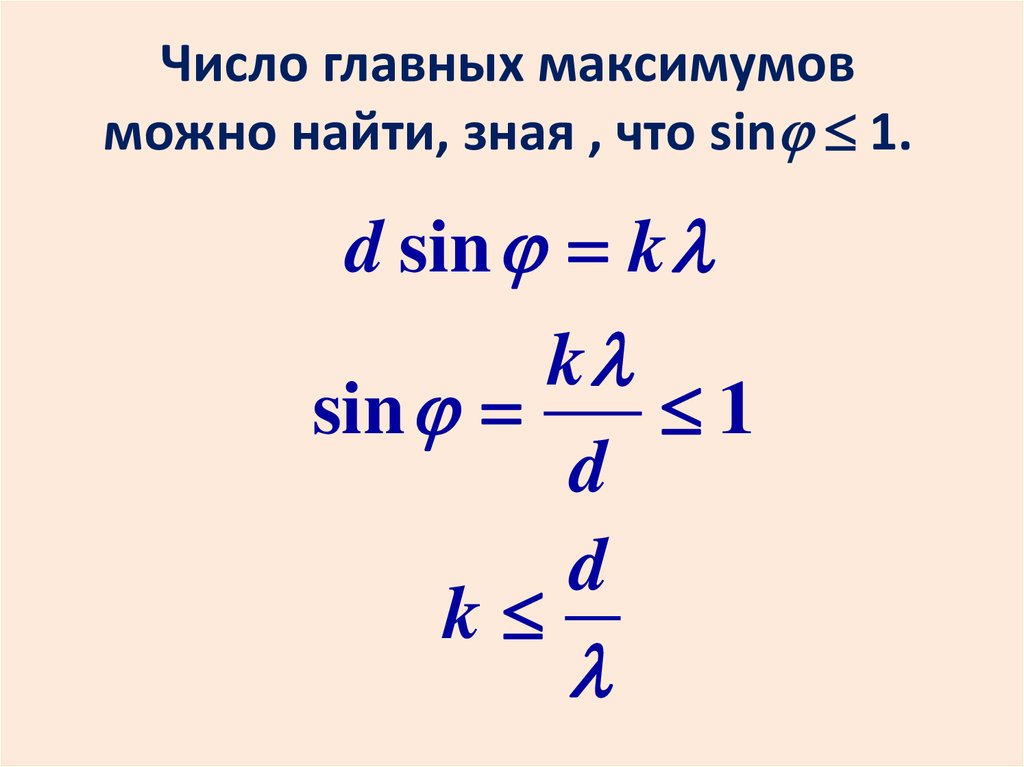










 physics
physics








