Множества. Числовые множества

1.

МНОЖЕСТВА

2.

Два множества А и В
называются равными, если
они состоят из одних и тех
же элементов, то есть
каждый элемент множества
А принадлежит множеству
В и наоборот – каждый
элемент множества В
принадлежит множеству А.

3.

Множество В
называется
подмножеством А,
если каждый
элемент множества
В является
элементом
множества А.

4.

Пересечением множества А
и В называют множество,
состоящее из всех
элементов, принадлежащих
и множетсву А, и множеству
В.
Объединением множества А
и В называют множество,
состоящее из всех
элементов, принадлежащих
хотя бы одному из этих
множеств: или множеству А,
или множеству В.

5.

ЧИСЛОВЫЕ
МНОЖЕСТВА

6.

N – множество натуральных чисел
Натуральные числа – это числа,
возникающие естественным образом при счете.
1,2,3,4,5,6,7,8,…
N={1,2,3,4,5,6,7,8,…}
Натуральные числа им противоположные и ноль– это
множество целых чисел
Z – множество целых чисел
Z={0,±1,±2,±3,±4,±5,±6,±7,…}
Целые и дробные (как положительные, так и
отрицательные) образуют множество рациональных чисел
Q – множество рациональных чисел

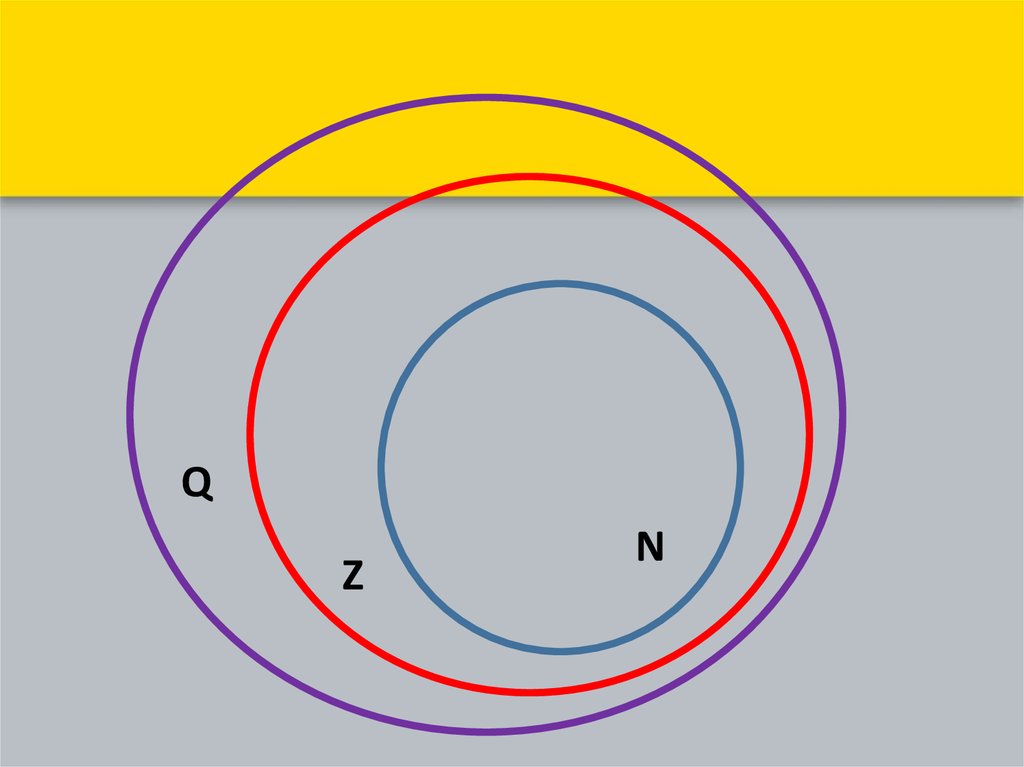
7.

Q
Z
N

8.

Не существует рационального числа,
квадрат которого равен 2
Эти числа являются примерами иррациональных
чисел
Иррациональные числа могут быть представлены в
виде бесконечных непериодических десятичных
дробей

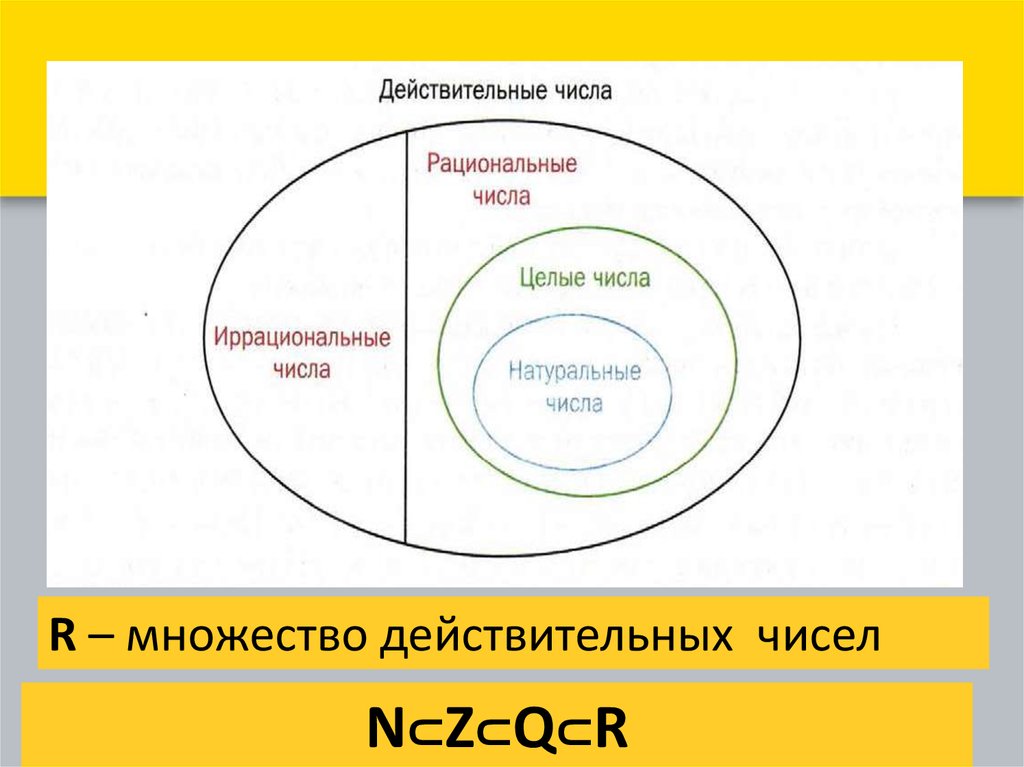
9.

R – множество действительных чисел
N⊂Z⊂Q⊂R

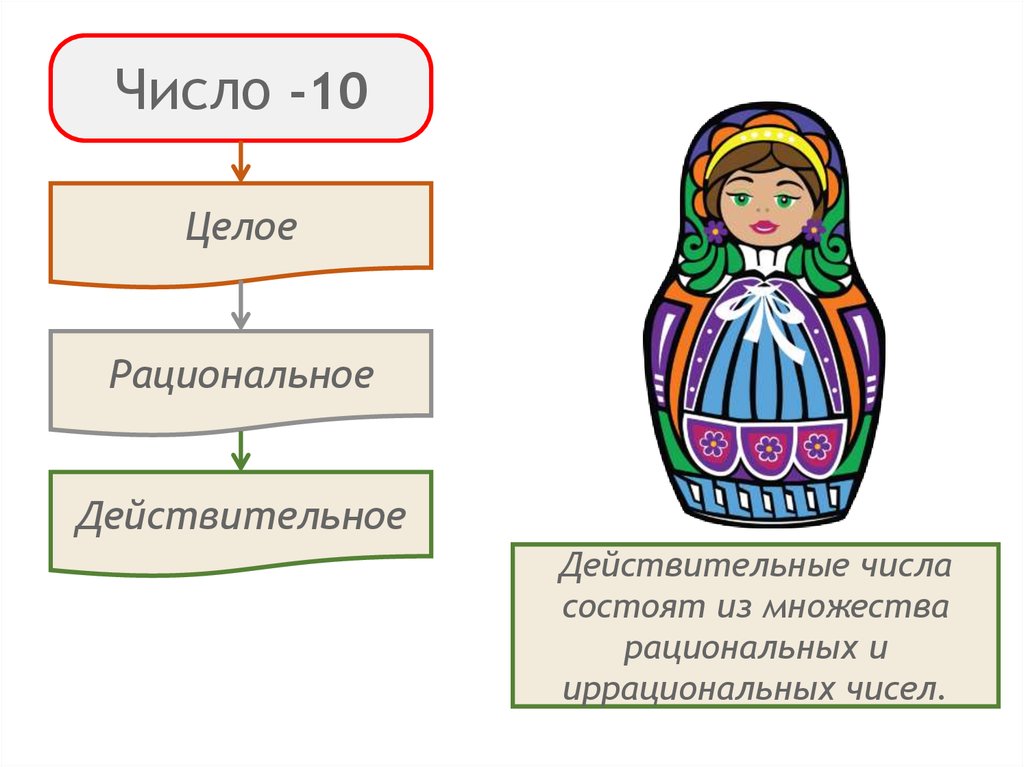
10.

Проверим себя в умении определять
принадлежность числа к определенному
числовому множеству.
Определите к каким числовым множествам будет
принадлежать данное число.
Множества нужно называть в порядке вложенности,
начиная с меньшего.

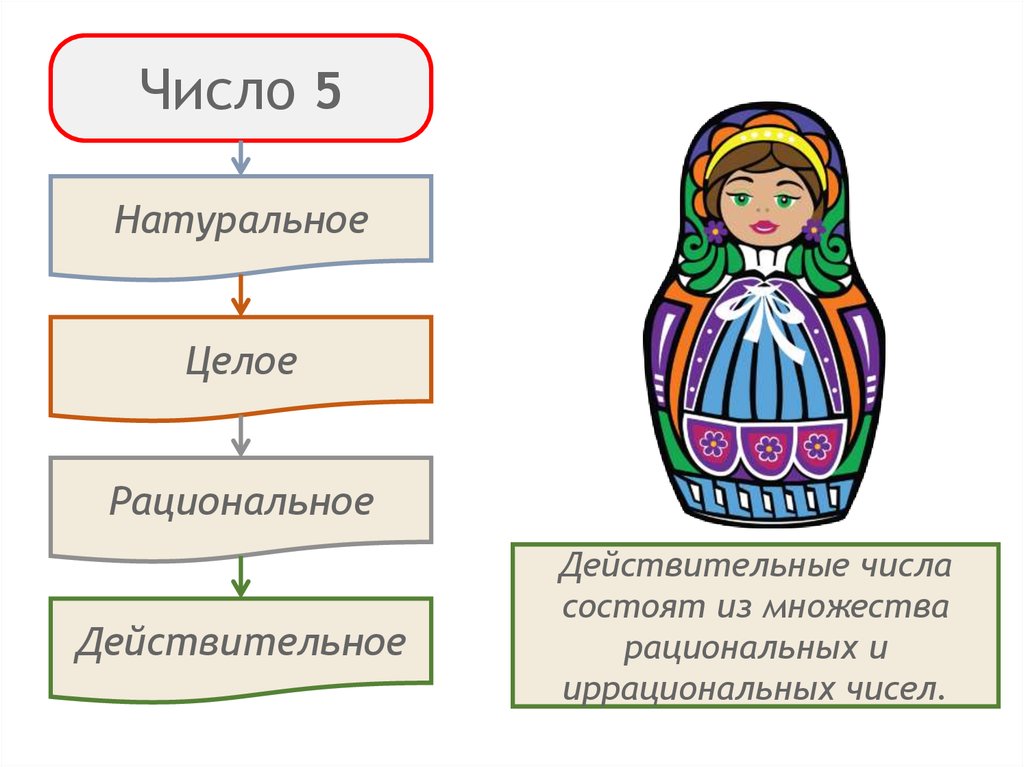
11.

Число 5
Натуральное
Целое
Рациональное
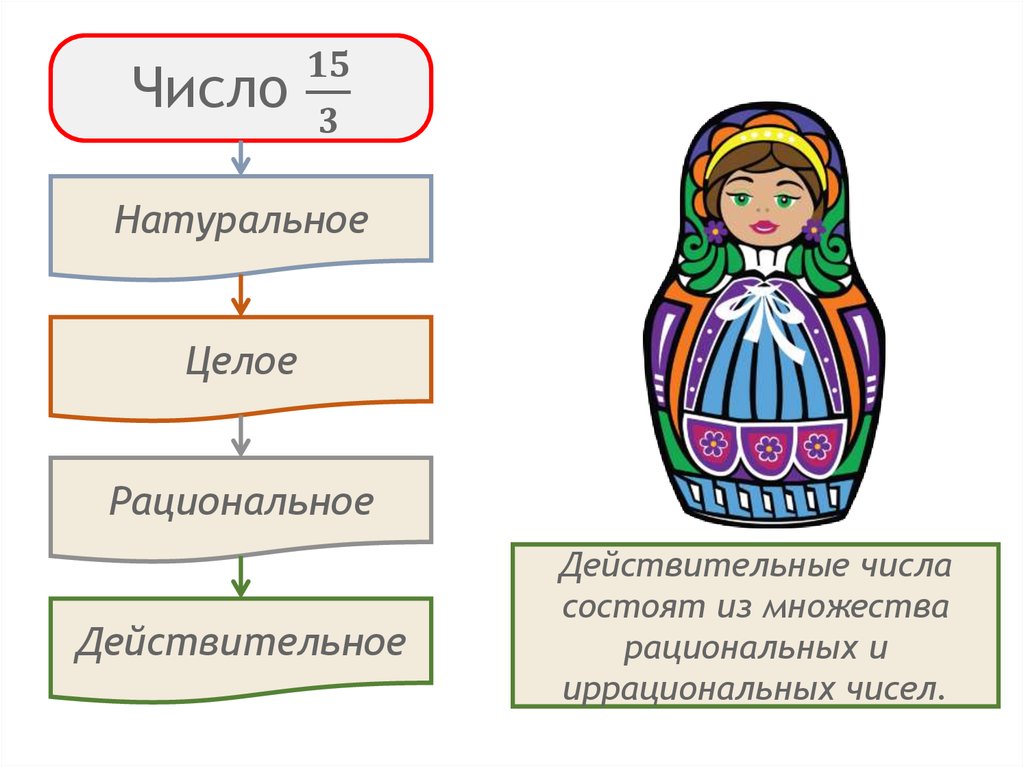
Действительное
Натуральные
Действительные
Целые числачисла
числа
– эточисла
–все
это –
Рациональные
числа
состоят
такие
натуральные,
числа,
из
множества
которые
это
числа,
которые
можно