Similar presentations:
Метод интерации
1.
2.
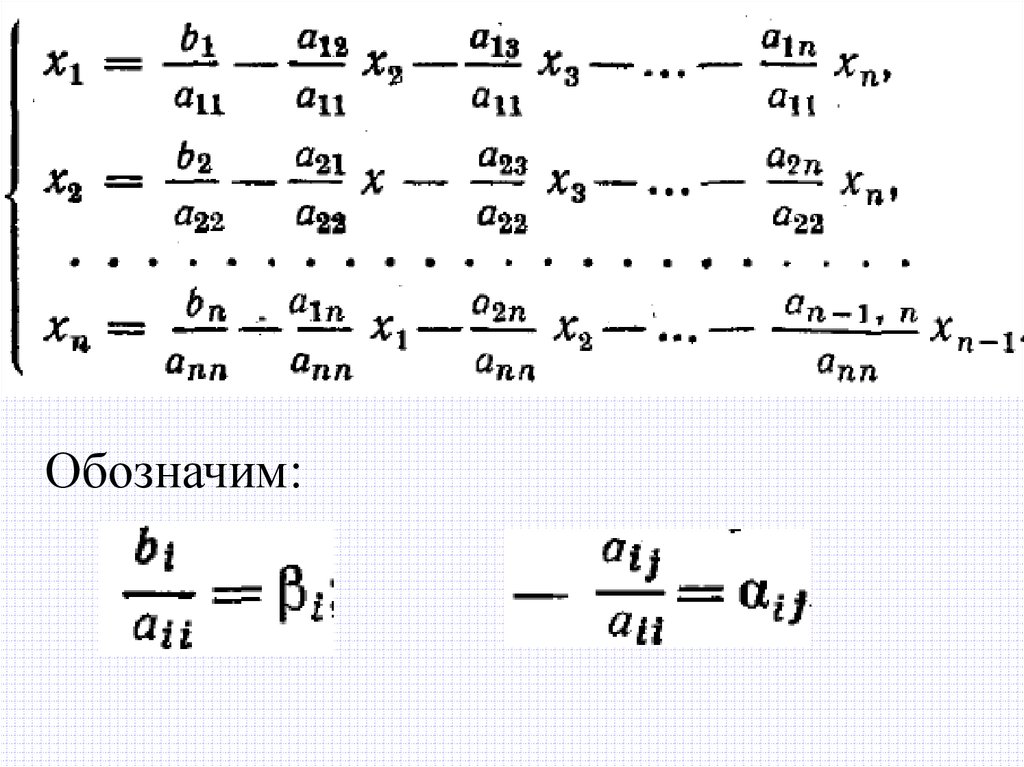
a11x1 + a12x2 + … + a1nxn = b1a21x1 + a22x2 + … + a2nxn = b2
…
am1x1 + am2x2 + … + amnxn = bm
3.
Обозначим:4.
x1 = α11x1 + α12x2 + … + α1nxn +x2 = α21x1 + α22x2 + … + α2nxn +
. . . . . . . . . . . . . . . . .
xn = αn1x1 + αn2x2 + … + αnnxn +
5.
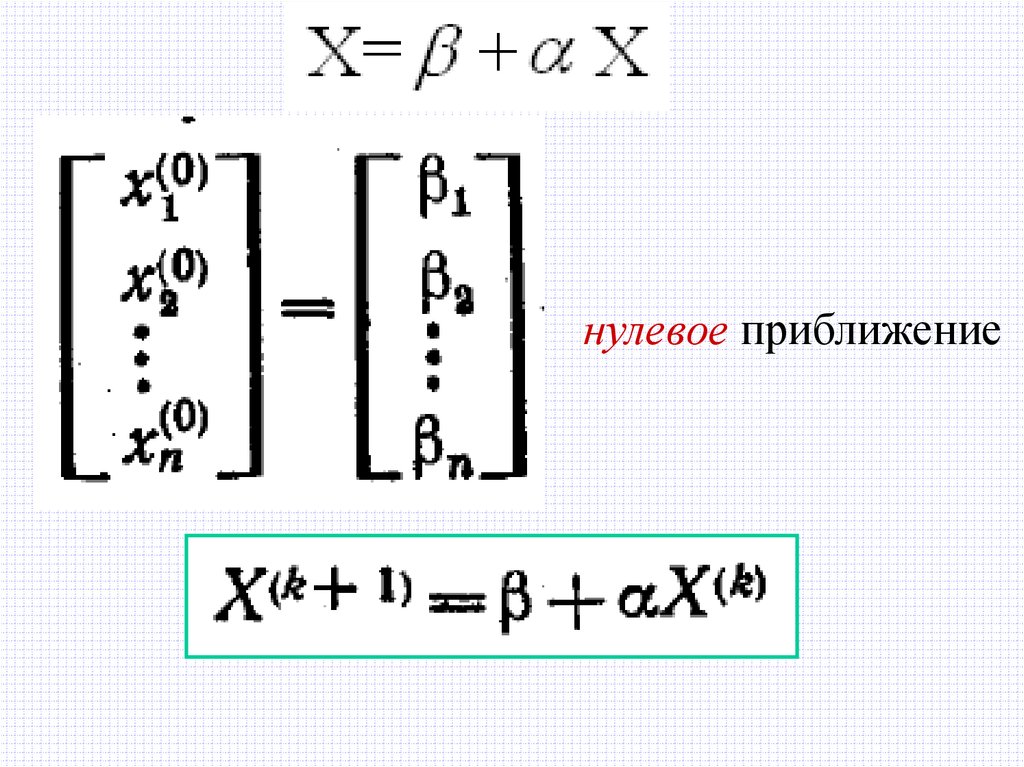
Обозначим:и
6.
нулевое приближение7.
Итерационная последовательность(0)
Х ,
(1)
Х ,
…,
(k)
Х
8.
Пример 1.Решить систему методом итерации
2 x1 x 2 x3 1,
3x1 4 x 2 x3 2,
x1 x 2 x3 3.
Решение
x1 3x1 x 2 x3 1
x 2 3x1 3x 2 x3 2
x3 x1 x 2 3
9.
x(0) (0;0;0) - нулевое приближение(1)
3* 0 0 0 1
x2
(1)
3* 0 3* 0 0 2
x3
(1)
0 0 3
x1
x(1) (-1;-2;-3) - первое приближение
10.
( 2)3 * ( 1) ( 2) ( 3) 1
x2
( 2)
3 * ( 1) 3 * ( 2) ( 3) 2
x3
( 2)
1 ( 2) 3
x1
x(2) (1;-2;-2) - второе приближение
11.
Условия сходимости итерационного процессаили
n
1
ij
J 1
n
1
ij
J 1
12.
Пример 2: Проверитьсходимость итерационного
процесса для системы.
Решение
=0+0,2+0,2=0,4<1
=0,125+0+0,2=0,325<1
=0,125+0,2+0=0,325<1
13.
14.
Матрица А=[aij] определяется тремя нормами:15.
Оценка погрешности приближенногопроцесса метода итерации
16.
Пример 3. Привести систему к нормальному виду7,6 х1 +0,5 х2 +2,4 х3 = 1,9
2,2 х1 +9,1 х2 +4,4 х3 = 9,7
-1,3 х1 + 0,2 х2 + 5,8 х3 = -1,4
Решение.
х1 +0,5
(10-2,4)
х2 +2,4 х3 = 1,9
2,2 х1 +(10-0,9) х2 +4,4 х3 = 9,7
-1,3 х1 + 0,2 х2 + (10-4,2) х3 = -1,4
10 х1 = 2,4 х1 -0,5 х2 -2,4 х3 + 1,9
10 х2 = -2,2 х1 +0,9 х2 -4,4 х3 + 9,7
10 х3 = 1,3 х1 - 0,2 х2 +4,2 х3 -1,4
х1 = 0,24 х1 -0,05 х2 -0,24 х3 + 0,19
х2 = -0,22 х1 +0,09 х2 -0,44 х3 + 0,97
х3 = 0,13 х1 – 0,02 х2 +0,42 х3 -0,14


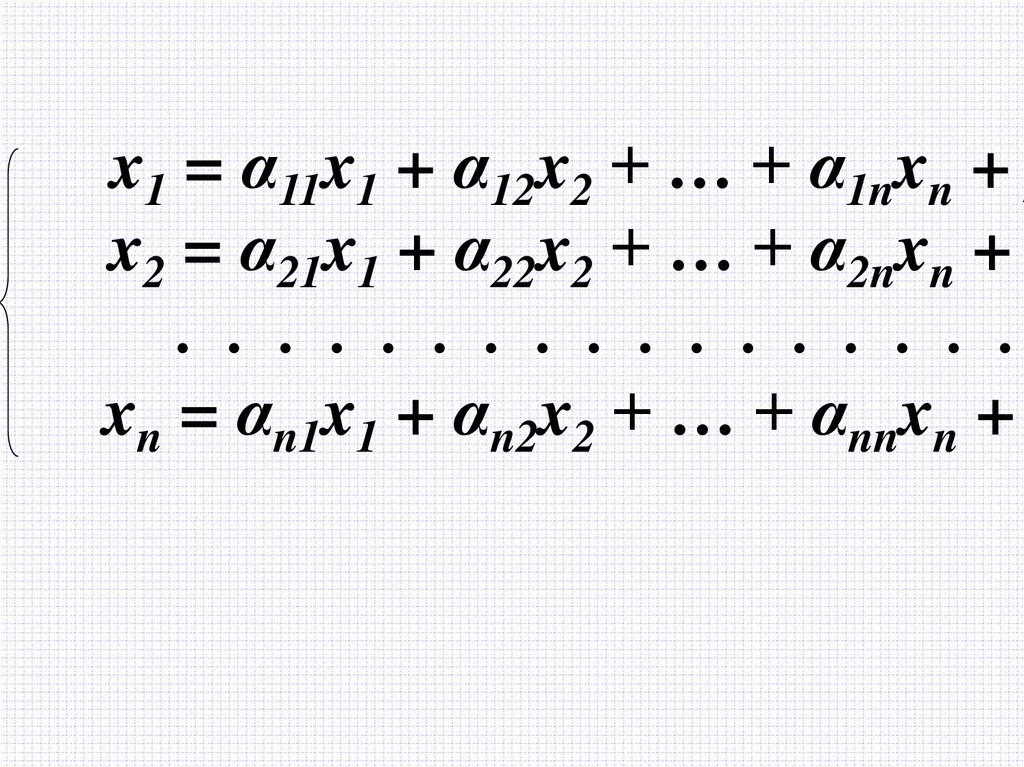







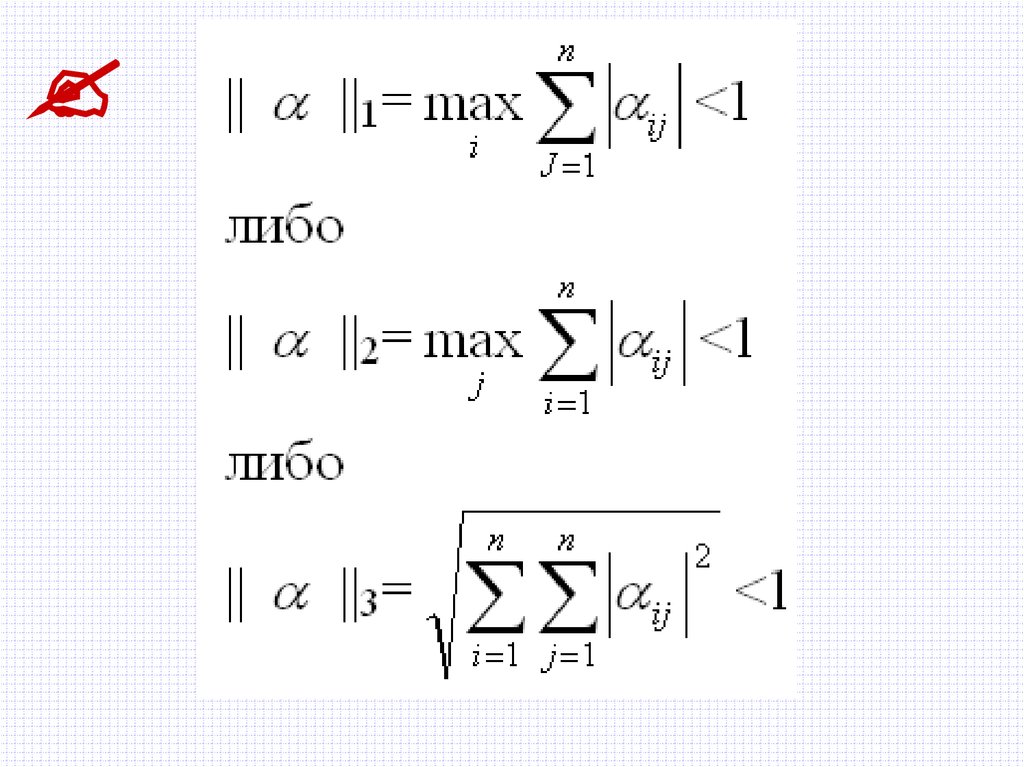



 mathematics
mathematics








