Построение графиков функций элементарными средствами

1. Построение графиков функций элементарными средствами

1

2.

Представим себе, что нам известен
график некоторой функции f(x),
который мы договоримся называть
Y
«старым» и будем обозначать Гf .
Поставим задачу построения графика
другой функции g(x), определённым
образом связанной со «старой»
o
функцией , используя
«старый»
X
график в качестве
исходного.
Искомый график назовём «новым» и
будем обозначать Гg .
2

3. Введение

Мы с вами научимся строить
Y
графики различных элементарных
функций без применения
производной. Такие методы
построения графиков мы и будем
o
X
называть элементарными.
3

4.

Y
Укажем правила построения Гg из Гf
в зависимости от того, каким образом
связаны f(x) и g(x) .
o
X
4

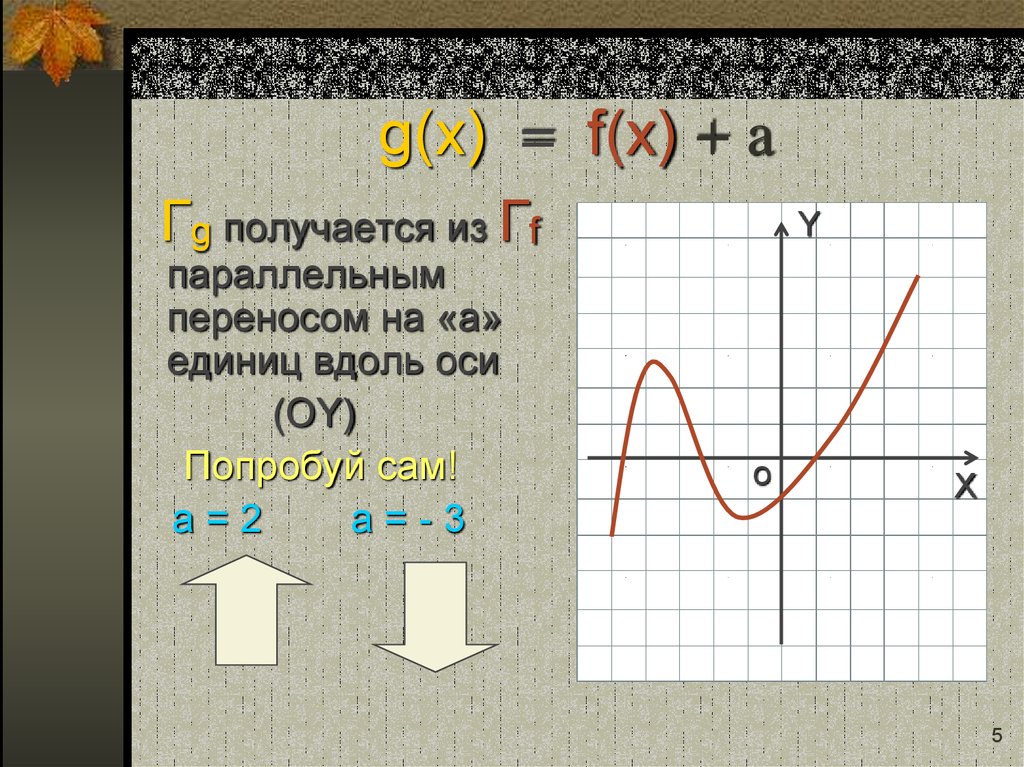
5. g(x) = f(x) + a

Гg получается из Гf
параллельным
переносом на «a»
единиц вдоль оси
(OY)
Попробуй сам!
a=2
a=-3
Y
o
X
5

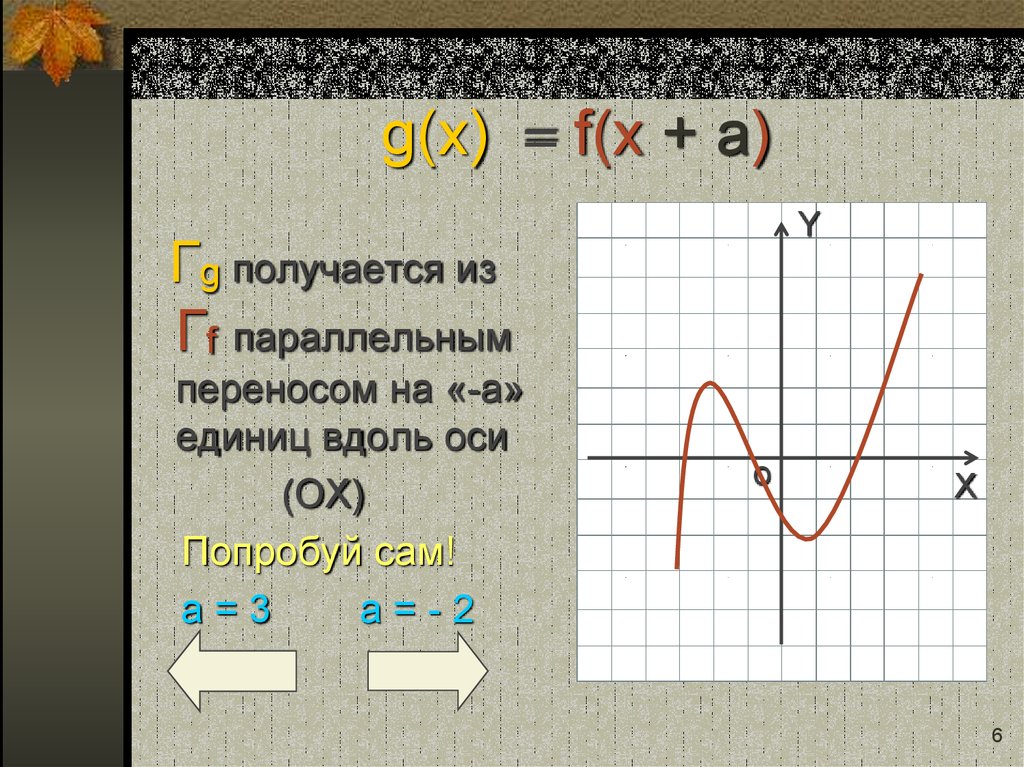
6. g(x) = f(x + a)

Y
Гg получается из
Гf параллельным
переносом на «-a»
единиц вдоль оси
(ОХ)
Попробуй сам!
a=3
a=-2
o
X
6

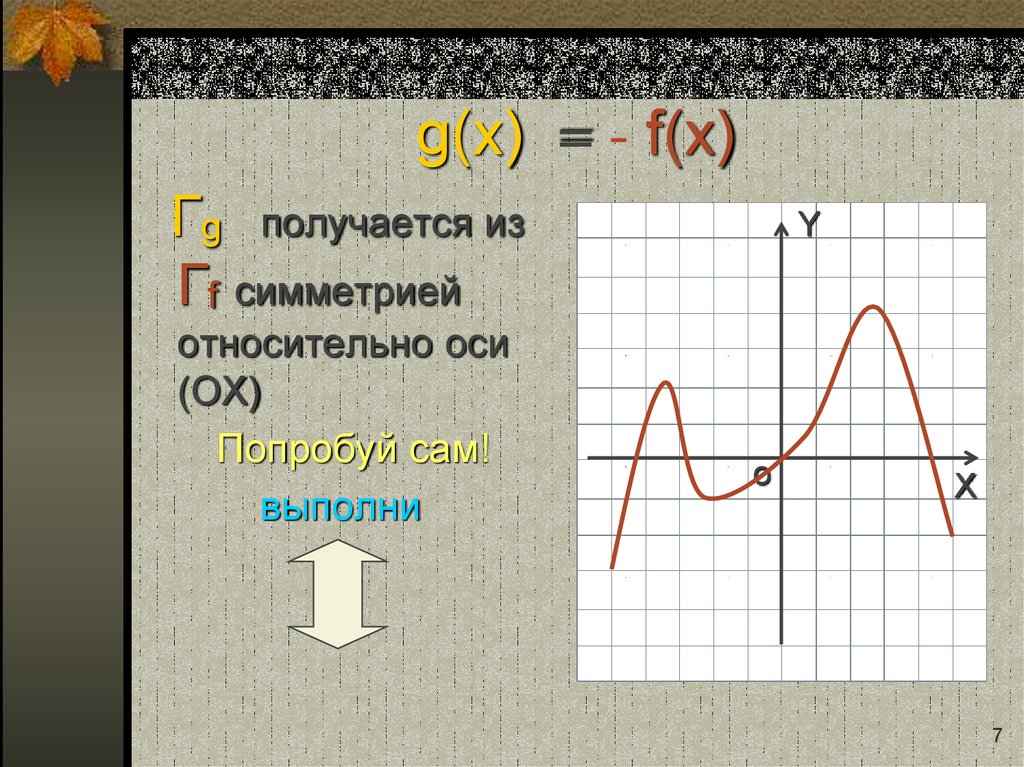
7. g(x) = - f(x)

Гg получается из
Гf симметрией
относительно оси
(ОХ)
Попробуй сам!
выполни
Y
o
X
7

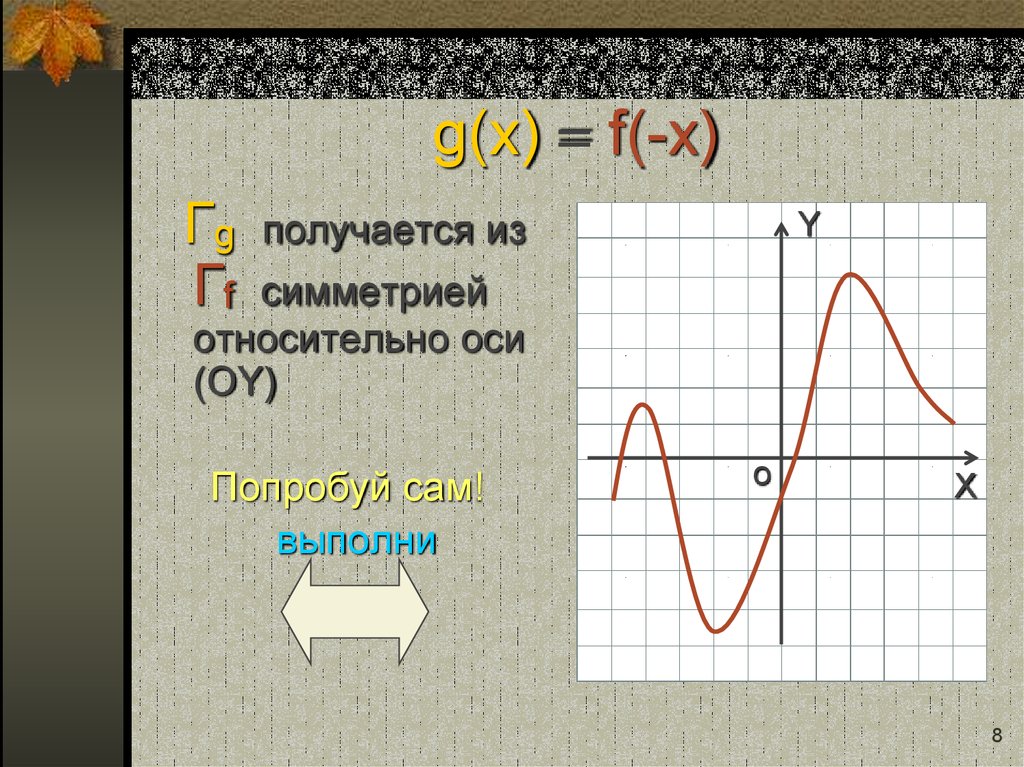
8. g(x) = f(-x)

Гg
Гf
получается из
Y
симметрией
относительно оси
(OY)
Попробуй сам!
выполни
o
X
8

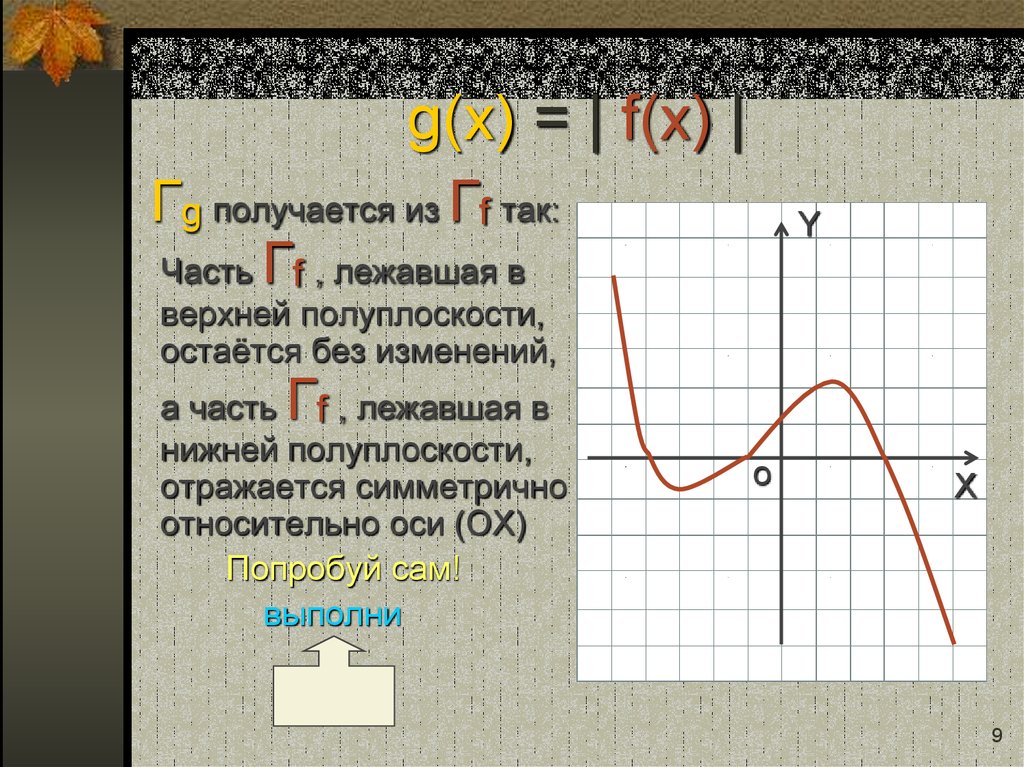
9. g(x) = | f(x) |

Гg получается из Гf так:
Часть Гf , лежавшая в
Y
верхней полуплоскости,
остаётся без изменений,
Г
а часть f , лежавшая в
нижней полуплоскости,
отражается симметрично
относительно оси (ОХ)
Попробуй сам!
выполни
o
X
9

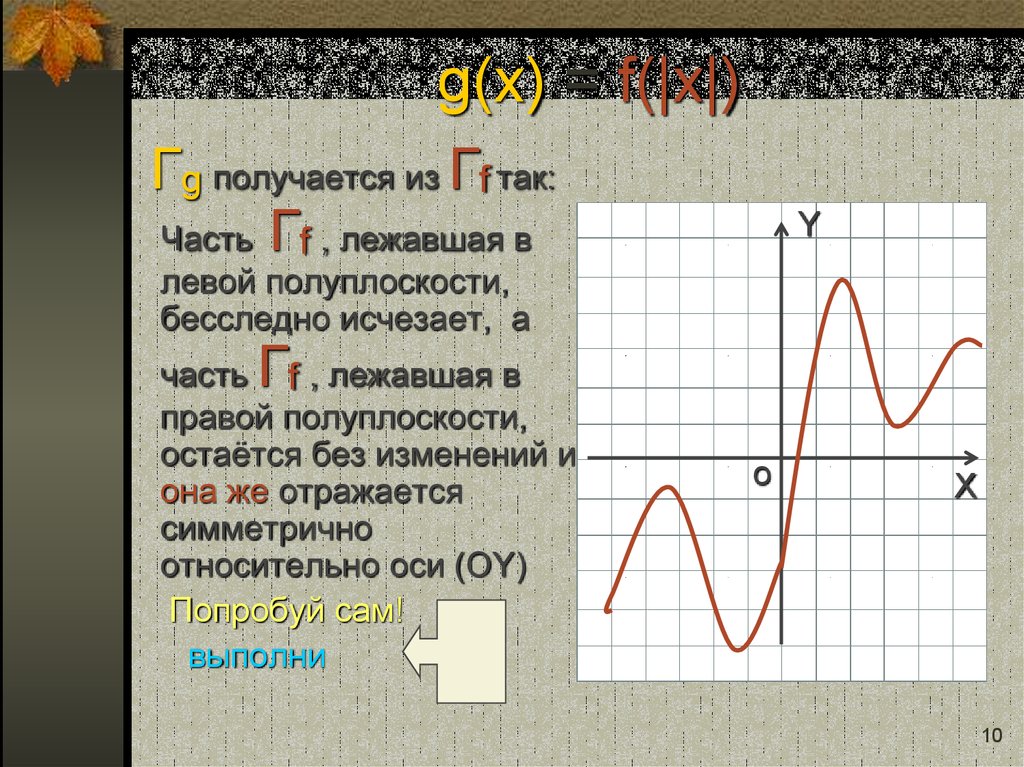
10. g(x) = f(|x|)

Гg получается из Гf так:
Часть Гf , лежавшая в
Y
левой полуплоскости,
бесследно исчезает, а
Г
часть f , лежавшая в
правой полуплоскости,
остаётся без изменений и
она же отражается
симметрично
относительно оси (ОY)
Попробуй сам!
выполни
o
X
10

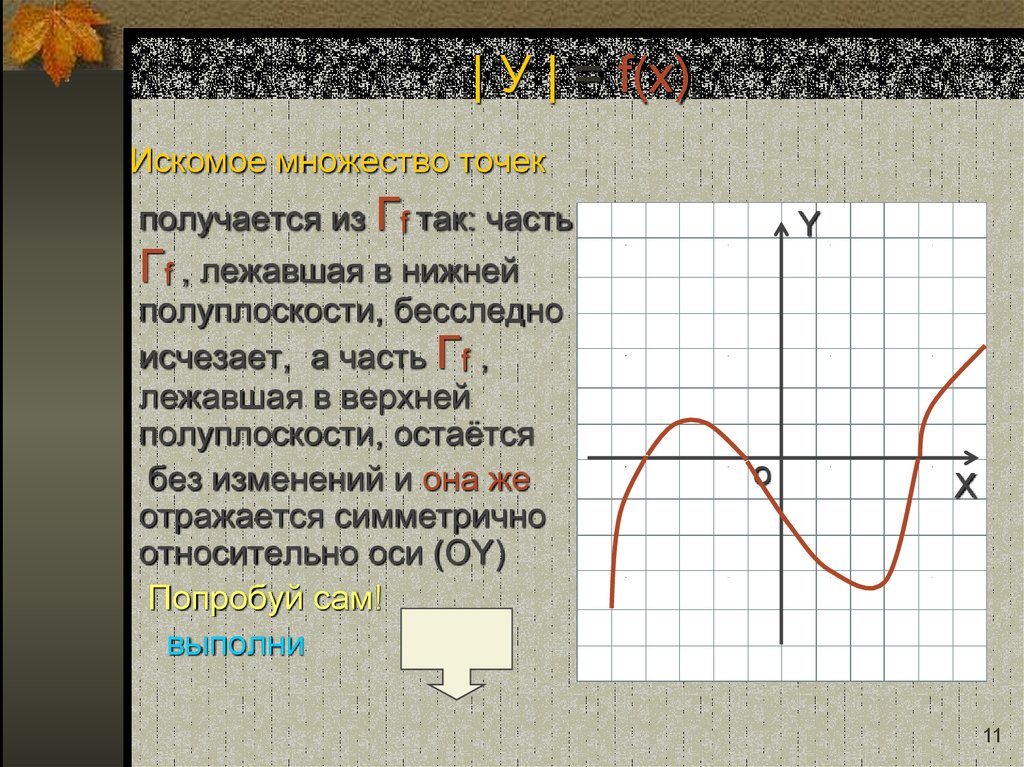
11. | У | = f(x)

Искомое множество точек
получается из Гf так: часть
Y
Гf , лежавшая в нижней
полуплоскости, бесследно
исчезает, а часть Гf ,
лежавшая в верхней
полуплоскости, остаётся
без изменений и она же
отражается симметрично
относительно оси (ОY)
Попробуй сам!
выполни
o
X
11

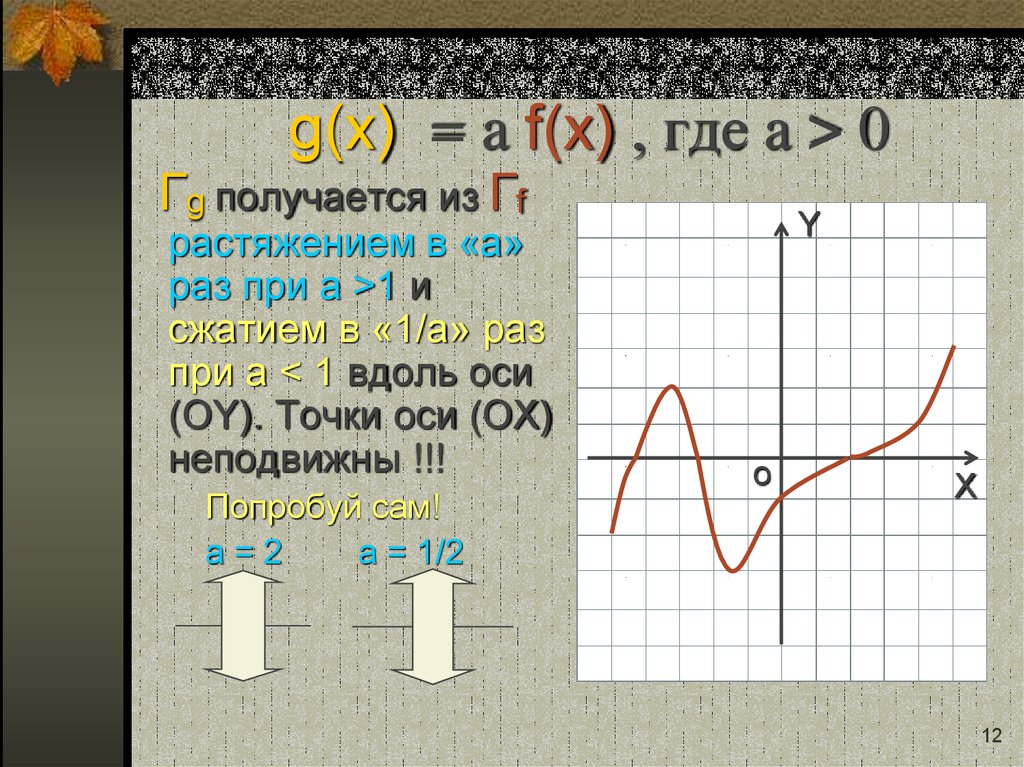
12. g(x) = a f(x) , где a > 0

g(x) = a f(x) , где a > 0
Гg получается из Гf
растяжением в «a»
раз при a >1 и
сжатием в «1/a» раз
при a < 1 вдоль оси
(OY). Точки оси (ОХ)
неподвижны !!!
Попробуй сам!
a=2
a = 1/2
Y
o
X
12

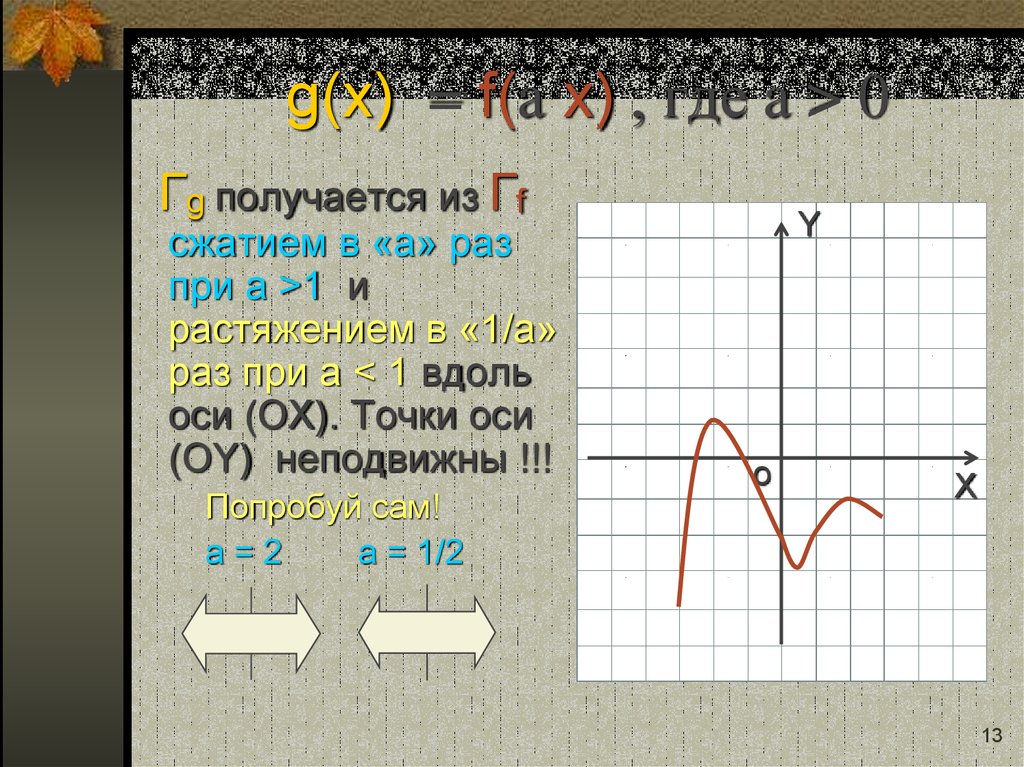
13. g(x) = f(a x) , где a > 0

g(x) = f(a x) , где a > 0
Гg получается из Гf
сжатием в «a» раз
при a >1 и
растяжением в «1/a»
раз при a < 1 вдоль
оси (OХ). Точки оси
(OY) неподвижны !!!
Попробуй сам!
a=2
a = 1/2
Y
o
X
13

14. Счастливо упражняться !!!

Y
o
X
14

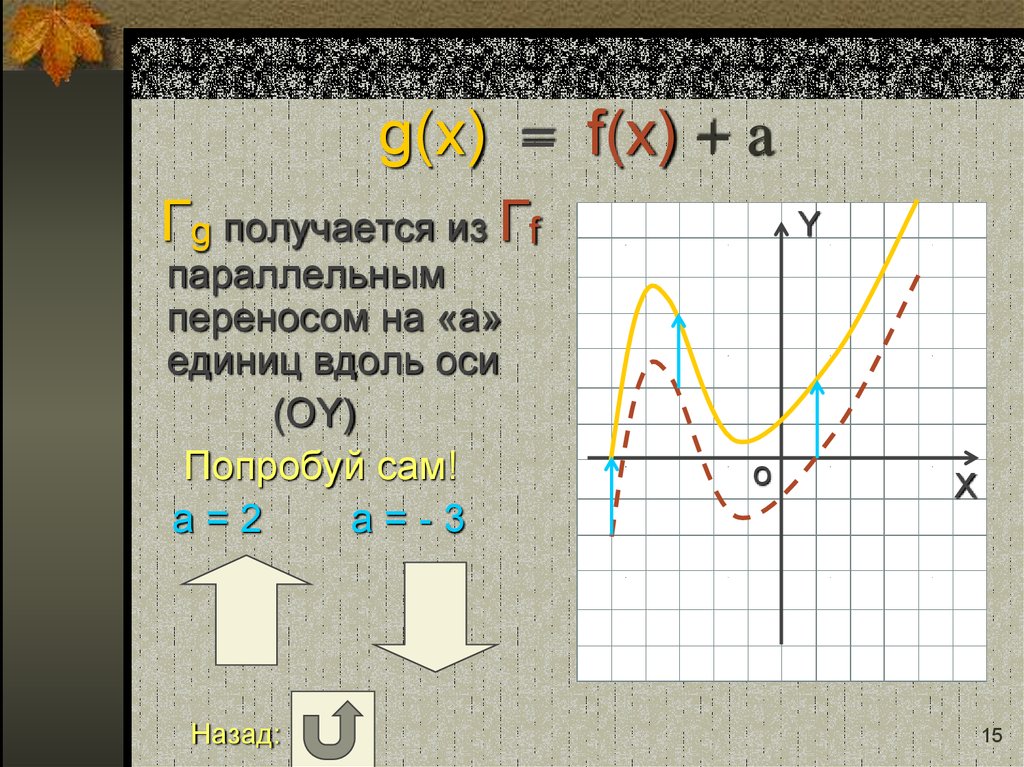
15. g(x) = f(x) + a

Гg получается из Гf
параллельным
переносом на «a»
единиц вдоль оси
(OY)
Попробуй сам!
a=2
a=-3
Назад:
Y
o
X
15

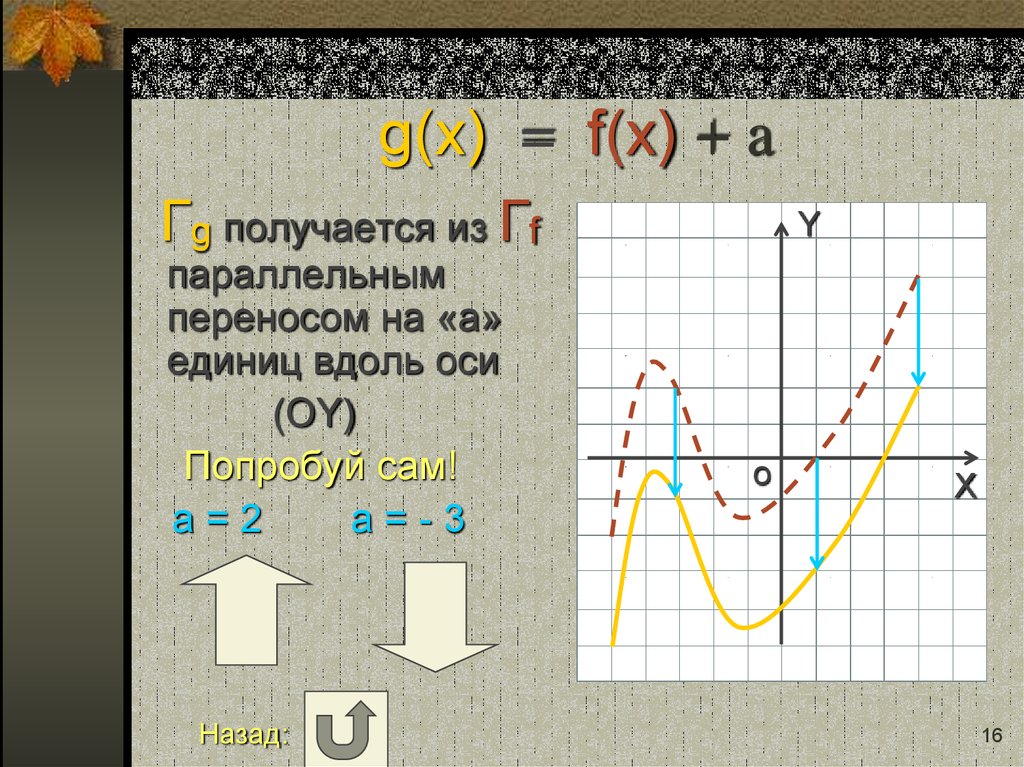
16. g(x) = f(x) + a

Гg получается из Гf
параллельным
переносом на «a»
единиц вдоль оси
(OY)
Попробуй сам!
a=2
a=-3
Назад:
Y
o
X
16

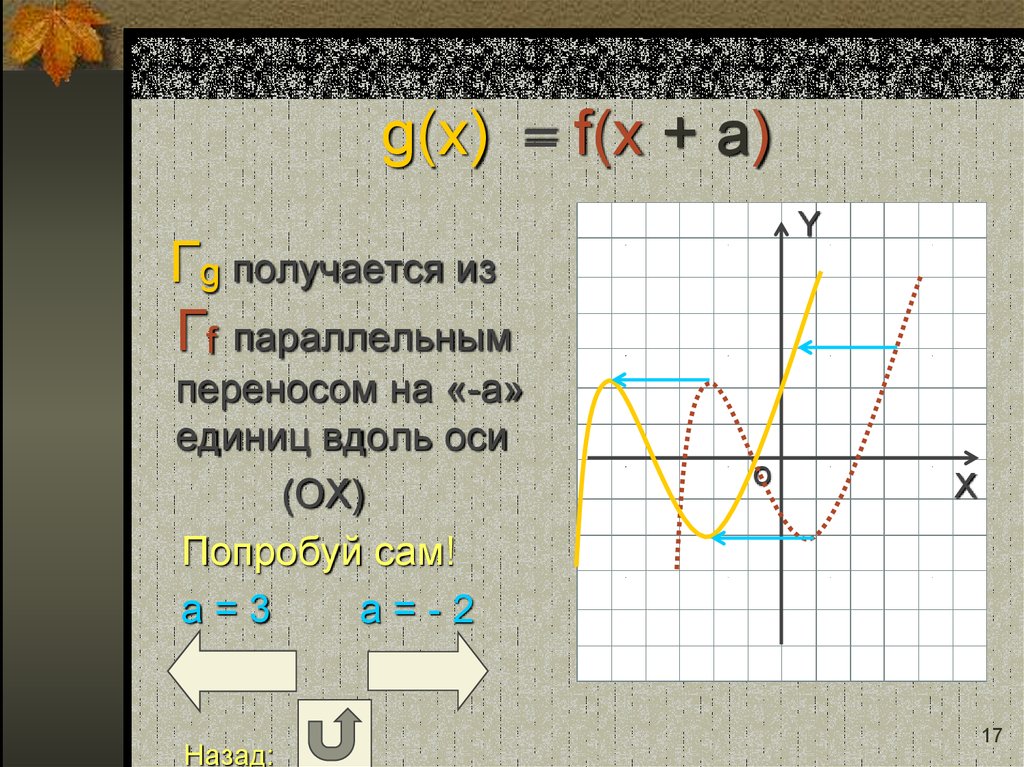
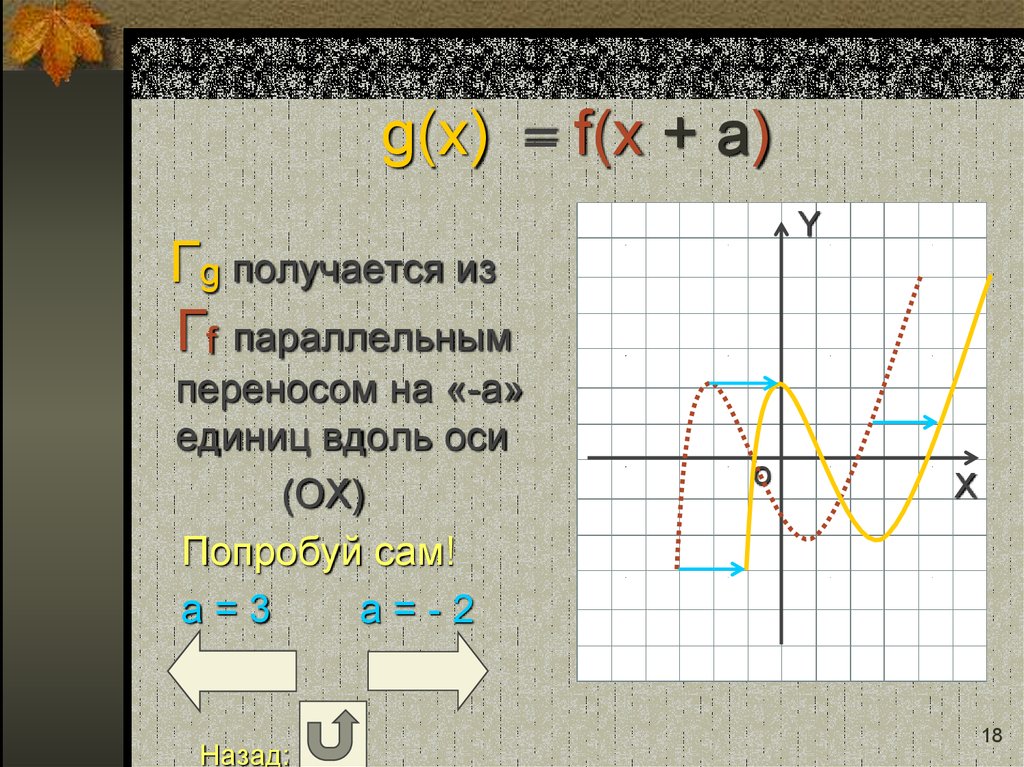
17. g(x) = f(x + a)

Y
Гg получается из
Гf параллельным
переносом на «-a»
единиц вдоль оси
(ОХ)
Попробуй сам!
a=3
a=-2
Назад:
o
X
17

18. g(x) = f(x + a)

Y
Гg получается из
Гf параллельным
переносом на «-a»
единиц вдоль оси
(ОХ)
Попробуй сам!
a=3
a=-2
Назад:
o
X
18

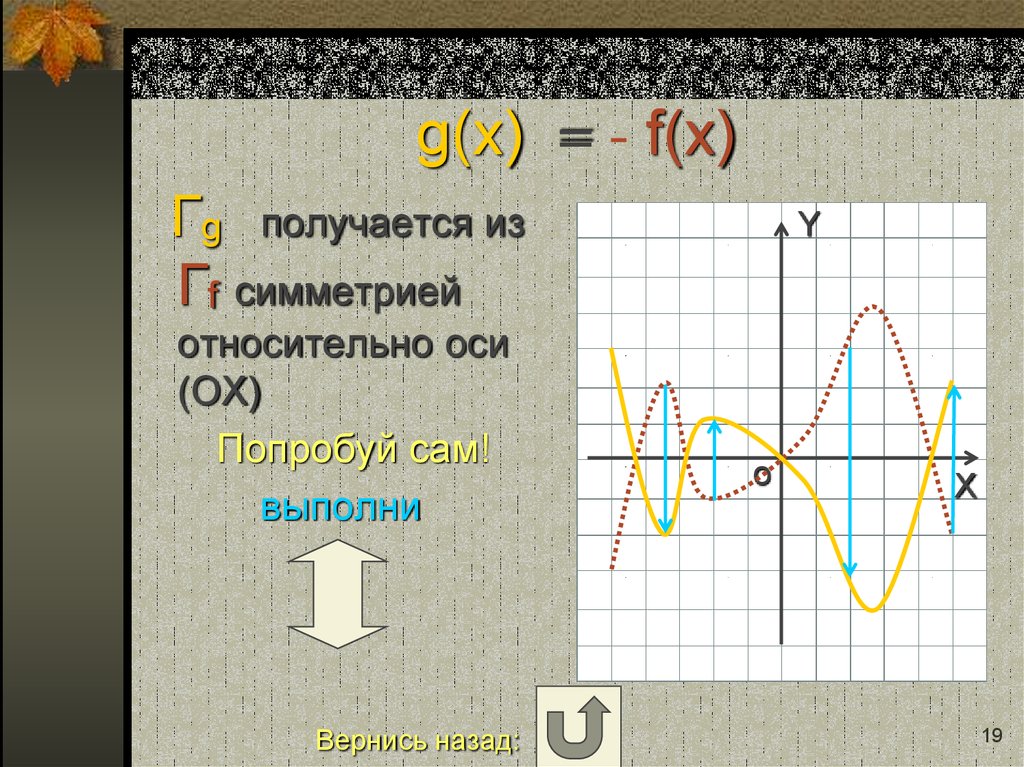
19. g(x) = - f(x)

Гg получается из
Гf симметрией
относительно оси
(ОХ)
Попробуй сам!
выполни
Вернись назад:
Y
o
X
19

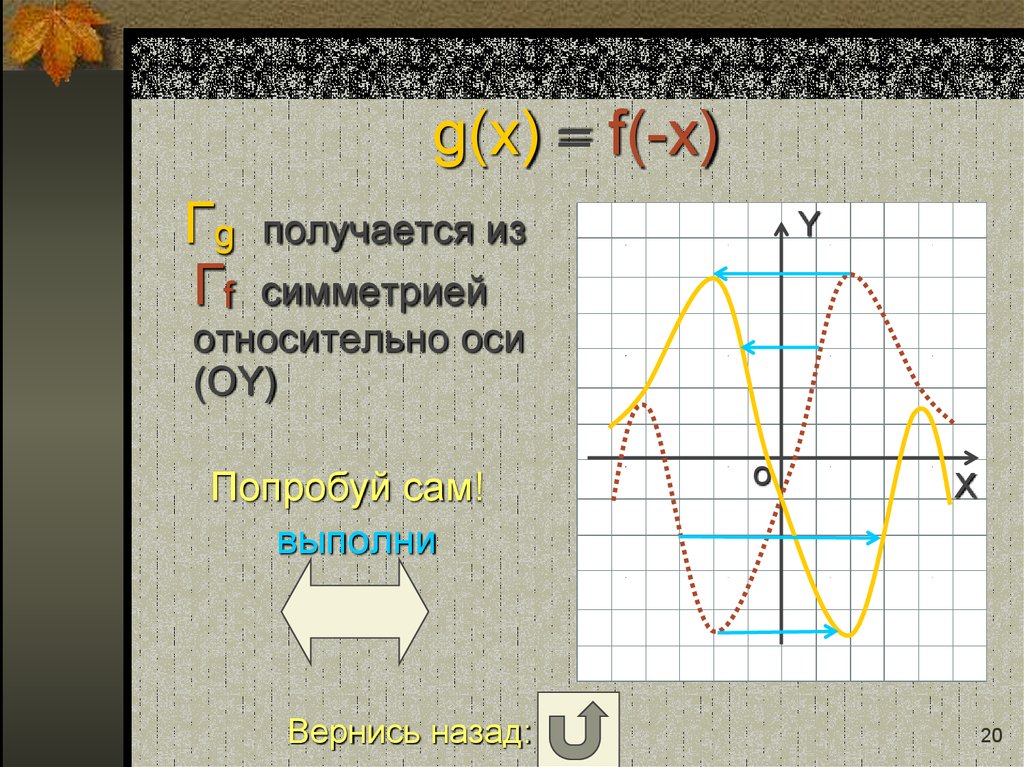
20. g(x) = f(-x)

Гg
Гf
получается из
Y
симметрией
относительно оси
(OY)
Попробуй сам!
выполни
Вернись назад:
o
X
20

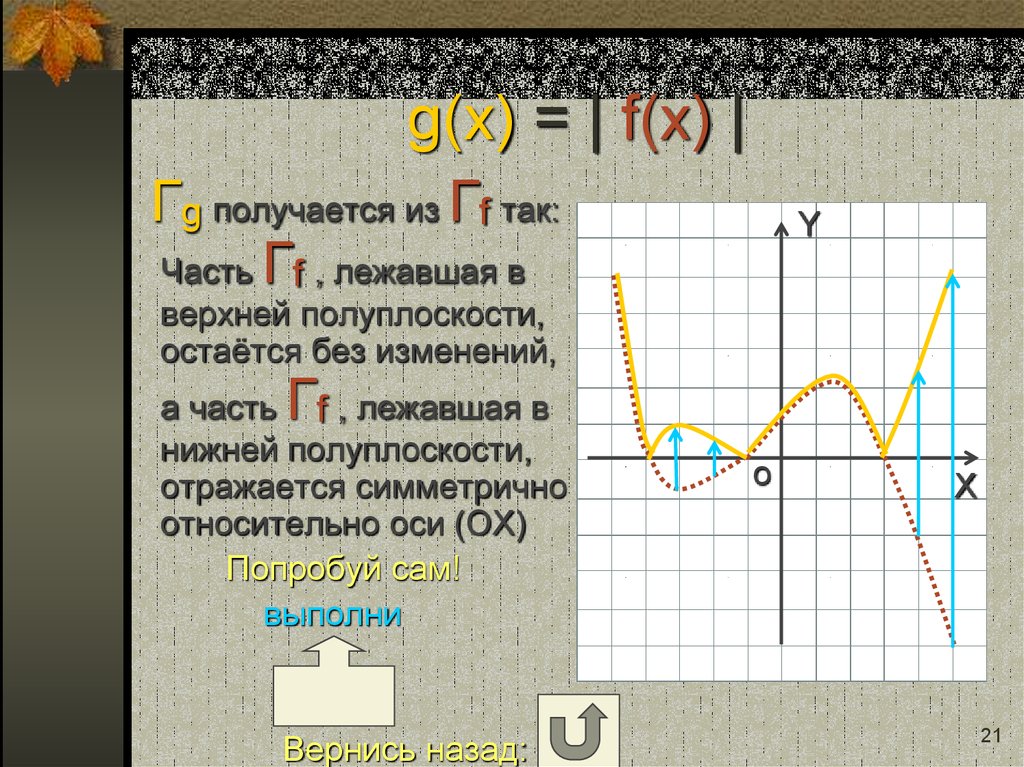
21. g(x) = | f(x) |

Гg получается из Гf так:
Часть Гf , лежавшая в
Y
верхней полуплоскости,
остаётся без изменений,
Г
а часть f , лежавшая в
нижней полуплоскости,
отражается симметрично
относительно оси (ОХ)
Попробуй сам!
выполни
Вернись назад:
o
X
21

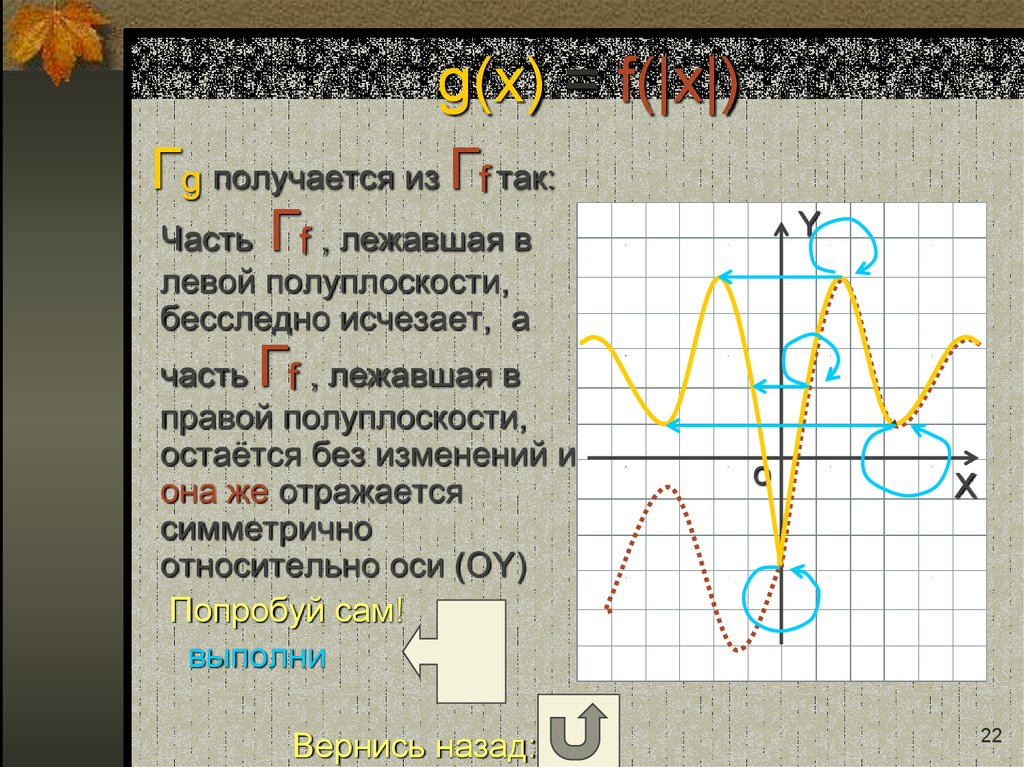
22. g(x) = f(|x|)

Гg получается из Гf так:
Часть Гf , лежавшая в
Y
левой полуплоскости,
бесследно исчезает, а
Г
часть f , лежавшая в
правой полуплоскости,
остаётся без изменений и
она же отражается
симметрично
относительно оси (ОY)
Попробуй сам!
выполни
Вернись назад:
o
X
22

23. | У | = f(x)

Искомое множество точек
получается из Гf так: часть
Y
Гf , лежавшая в нижней
полуплоскости, бесследно
исчезает, а часть Гf ,
лежавшая в верхней
полуплоскости, остаётся
без изменений и она же
отражается симметрично
относительно оси (ОY)
Попробуй сам!
выполни
Вернись назад:
o
X
23

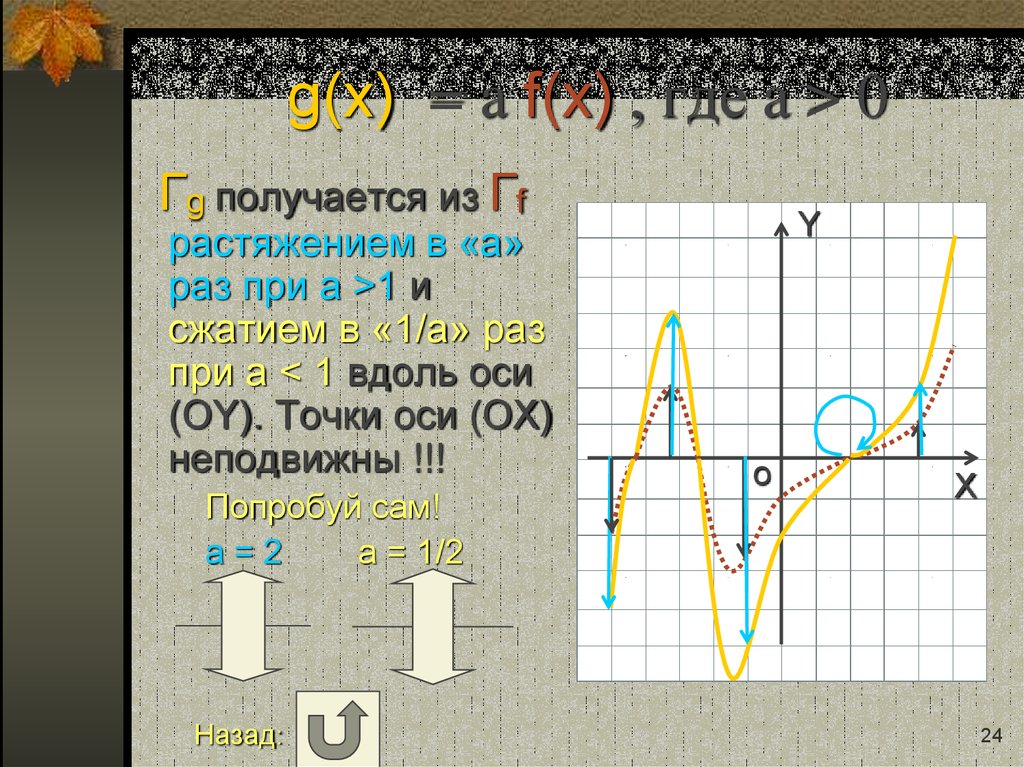
24. g(x) = a f(x) , где a > 0

g(x) = a f(x) , где a > 0
Гg получается из Гf
растяжением в «a»
раз при a >1 и
сжатием в «1/a» раз
при a < 1 вдоль оси
(OY). Точки оси (ОХ)
неподвижны !!!
Попробуй сам!
a=2
a = 1/2
Назад:
Y
o
X
24

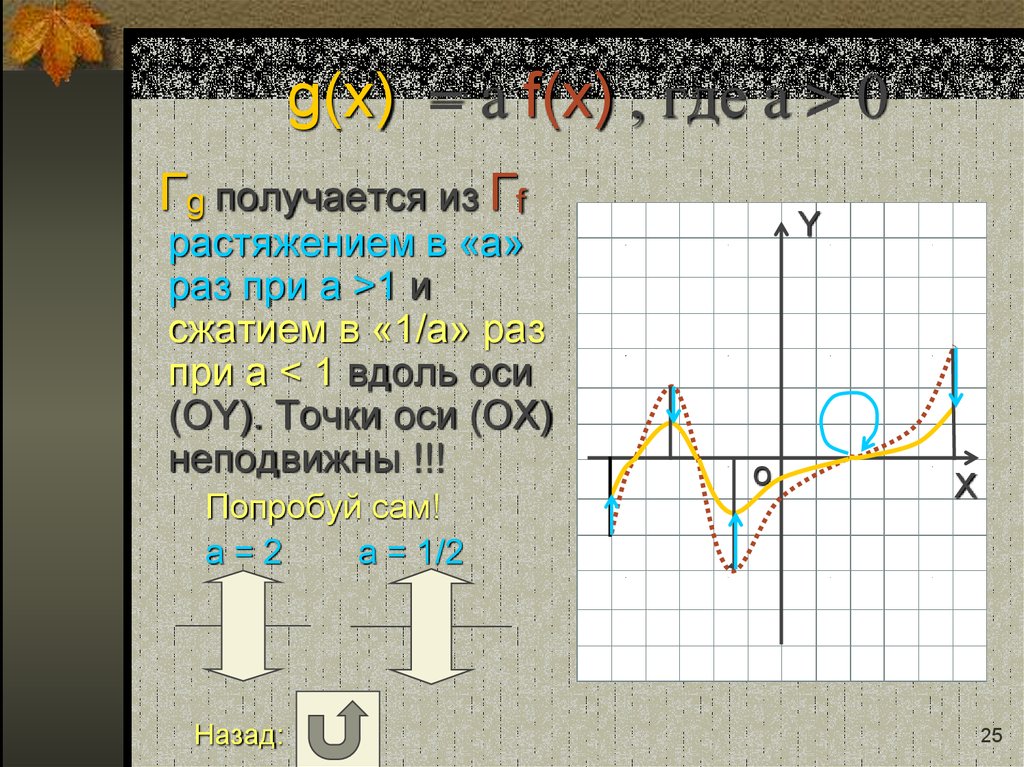
25. g(x) = a f(x) , где a > 0

g(x) = a f(x) , где a > 0
Гg получается из Гf
растяжением в «a»
раз при a >1 и
сжатием в «1/a» раз
при a < 1 вдоль оси
(OY). Точки оси (ОХ)
неподвижны !!!
Попробуй сам!
a=2
a = 1/2
Назад:
Y
o
X
25

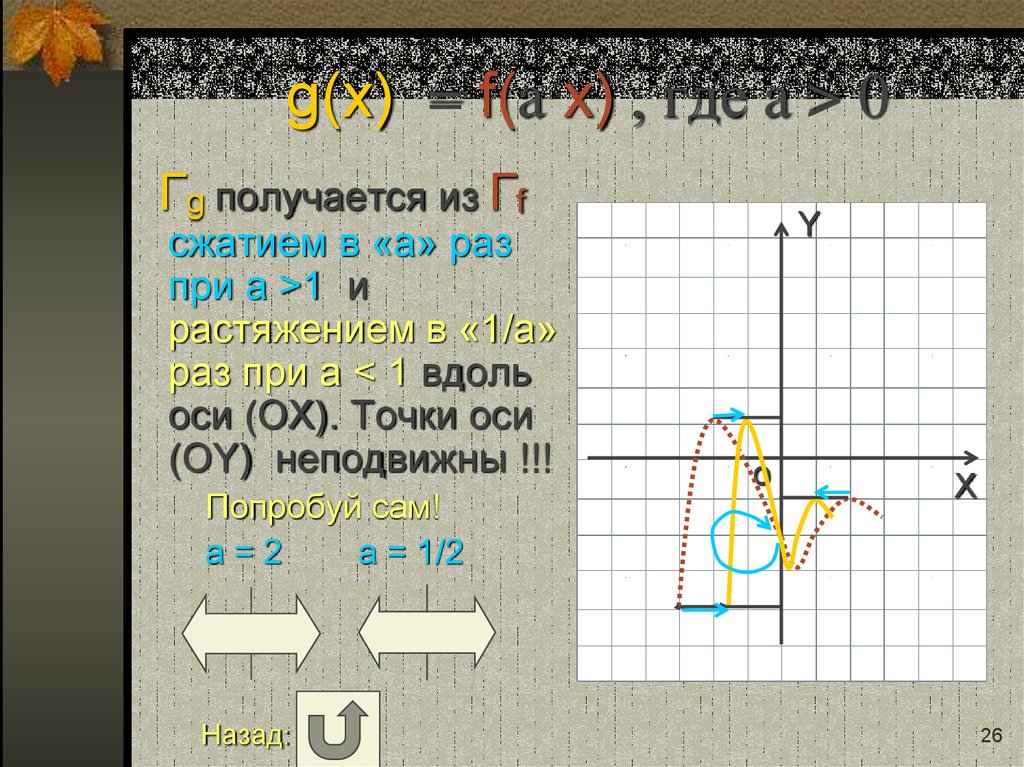
26. g(x) = f(a x) , где a > 0

g(x) = f(a x) , где a > 0
Гg получается из Гf
сжатием в «a» раз
при a >1 и
растяжением в «1/a»
раз при a < 1 вдоль
оси (OХ). Точки оси
(OY) неподвижны !!!
Попробуй сам!
a=2
a = 1/2
Назад:
Y
o
X
26

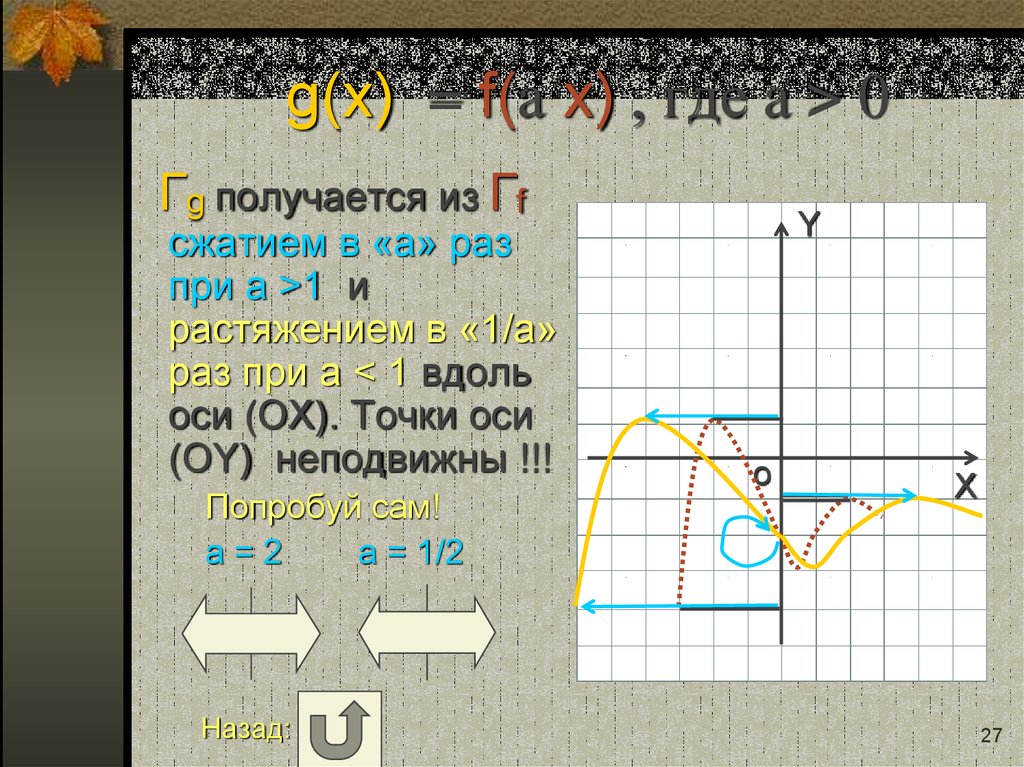
27. g(x) = f(a x) , где a > 0

g(x) = f(a x) , где a > 0
Гg получается из Гf
сжатием в «a» раз
при a >1 и
растяжением в «1/a»
раз при a < 1 вдоль
оси (OХ). Точки оси
(OY) неподвижны !!!
Попробуй сам!
a=2
a = 1/2
Назад:
Y
o
X
27