Многомерный регрессионный анализ. Использование для решения задачи однооткликового метода наименьших квадратов

1. 4. Многомерный регрессионный анализ

Использование для решения задачи однооткликового
метода наименьших квадратов:
В моделях - объясняющих переменных xi несколько,
результирующая переменная (отклик) y, одна – множественная
(многофакторная) регрессия (с 1-откликом).
Общий вид
M ( y | x1 , x2 ,..., xn ) f ( x1 , x2 ,..., xn )
Линейная форма (модель)
y y v a1 x1 a1 x1 ... ak
Неизвестных v и ai больше числа уравнений – надо
дополнительная информация, например на поправки v.
Требование: найти такие ai чтобы Ф = [v2] = vTv была
минимальной для всех наборов ai – метод наименьших квадратов
(МНК)
1

2. 4. Многомерный регрессионный анализ

Общая (теоретическая) последовательность решения
для получения коэффициентов и оценки точности для
множественной 1-откликовой регрессии – сведения
процесса поиска коэффициентов к задаче поиска
экстремума целевой функции (функции качества).
Алгебраический и матричный подход. Шаги:
1. Из линейной модели
y y v a1 x1 a1 x1 ... ak
выражаем поправки v
v y y a1x1 a1x1 ... ak y
2

3. 4. Многомерный регрессионный анализ

2. Запишем целевую функцию Ф
2
2
2
Ô [v ] [( y y ) ] a1 x1 a1 x1 ... ak y
которую надо минимизировать в точке ai
3. От функции Ф возьмем производные по а1, а2 , …,аk и
полученные выражения приравняем к нулю
Ô
a 2 a1 x1 a1 x1 ... ak y x1 0
1
Ô
2 a1 x1 a1 x1 ... ak y x2 0
a2
Ô
a 2 a1 x1 a1 x1 ... ak y 1 0
k
3

4. 4. Многомерный регрессионный анализ

4. Систему делим на
группировкой и имеем
2,
раскрываем
сумму
с
[ x12 ]a1 [ x1 x2 ]a2 ... [ x1 xn ]ak [ x1 y ] N11a1 N12 a2 ... N1n ak b1
N a N a ... N a b
2
[
x
x
]
a
[
x
]
a
...
[
x
x
]
a
[
x
y
]
2 1 1
21 1
22 2
2n k
2
2
2
2 n
k
2
N k1a1 N k 2 a2 ... N kk ak bk
[ xn x1 ]a1 [ xn x2 ]a2 ... nak [ y ]
совместную систему нормальных уравнений (?). Размер
по числу определяемых коэффициентов ai. Решение –
необходимые коэффициенты ai.
Алгебраический вид: не совсем удобен для выводов,
может быть удобен для анализа.
4

5. 4. Многомерный регрессионный анализ

Минимизация целевой функции в матричном виде по
шагам:
1. Линейная модель y y v a1 x1 a1 x1 ... ak
в
матричном виде
v X a y
-система уравнений поправок с матрицей плана Х и
вектором свободных членов у
x11 x12 ... x1( k 1) 1
y1
x
x22 ... x2( k 1) 1
y2
21
y
X
... ... ...
... 1 ,
...
x
x
...
x
n1
n ( k 1) 1
yn
n1
5

6. 4. Многомерный регрессионный анализ

Условие МНК – Ф = vTv = [v2] =min, v X a y
Минимизация в матричном виде сразу по всему вектору а
Ô Ô v
2vT X 0
a v a
Откуда лемма Гаусса
XT v 0
Подставив вид v - совместная система нормальных уравнений
X
T
X a y 0
X TX a X Ty
N a b
6

7. 4. Многомерный регрессионный анализ

Из вида уравнений поправок
v X a y
-левая трансформация Гаусса
XT v XT X a XT y
0 N a b
- та же совместная система нормальных уравнений. Решение –
через обратную матрицу N 1 Q
a Q b
7

8. 4. Многомерный регрессионный анализ

Практическая реализация по шагам:
1. Составляется
модель
(например
многофакторная с 1-откликом)
y y v a1 x1 a1 x1 ... ak
линейная
2. Строится матрица плана Х их коэффициентов при
определяемых величинах в модели и вектор
свободных членов из элементов моделируемого ряда у
x11
x
21
X
...
xn1
x12
x22
...
xn1
x1( k 1) 1
... x2( k 1) 1
...
... 1
... xn ( k 1) 1
...
y1
y
y 2
...
yn
8

9. 4. Многомерный регрессионный анализ

3. Для системы нормальных уравнений N a b
строится матрица нормальных уравнений N и вектор свободных
членов системы нормальных уравнений b
N XT X
b XT y
4. Решаем систему с полученными матрицами методом
обращения
N 1 Q
5. Модельные значения
a Q b
y y v X a
Шаги универсальны для любых моделей линейного
(полиномиального) или линеаризованного вида.
9

10. 4. Многомерный регрессионный анализ

Графическая трактовка метода наименьших
квадратов
Модель в векторах - y +v X a. Тогда имеем
Гиперплоскость – матрица плана Х, вектор моделируемых
величин - у
Разложение у на
ортогональные составляющие
y
Xa
X
v
y X a v
y P y P y, P P E
P X Q X T
P X Q X T E
X a P y X Q X T y a Q X T y
v P y X Q X T E y y y
10

11. 4. Многомерный регрессионный анализ

Оценка точности: модель, коэффициенты модели ai,
смоделированные величины y и поправки v. Основа – формула
погрешности Бесселя и теорема переноса ошибок.
- для оценки модели надо v y y и тогда по Бесселю
v 2
vT v
Ô
0
n k
n k
t
Вычисления поправок v
v X a y y y ( XQX T E ) y
и целевой функции Ф
v v y ( E XQX ) y
T
T
T
11

12. 4. Многомерный регрессионный анализ

- для оценки точности вектора коэффициентов регрессии а:
Выражаем коэффициенты линейно через измерения у с известной
ковариационной матрицей Ку
a = (Q·XT)·y
По теореме переноса ошибок
Ka F K y F T , F Q X T
Окончательно
Ka F K y F T QX T K y XQ 02 Q
2
так как у – вектор, и K y 0
Эта оценка через ковариационную матрицу. Извлечь корень.
12

13. 4. Многомерный регрессионный анализ

Оценка через матрицу обратных весов Q (матрицу кофакторов)
Ka 02 Q,
a 0 Qii
y
i
Оценка смоделированных значений
. Линейное выражение
y X a (X Q X T ) y
По теореме переноса ошибок
K y F K y F T 02 ( X Q X T ) ( X Q X T )
02 ( X Q X T ) 02 Qy
Оценка через матрицу обратных весов Q (матрицу кофакторов
K y 02 Qy ,
y 0 Qy
i
ii
13

14. 3. Многомерный регрессионный анализ

Использование для решения задачи
многооткликовой регрессии метода наименьших
квадратов
Основные виды:
-Матричный метод наименьших квадратов
-Метод «растяжения».
Основная модель для обоих методов: из k рядов k1 –
факторные X, k2 - отклик Y
y , y ,..., y f x , x ,..., x Y f ( X )
1
2
k2
1
2
k1
14

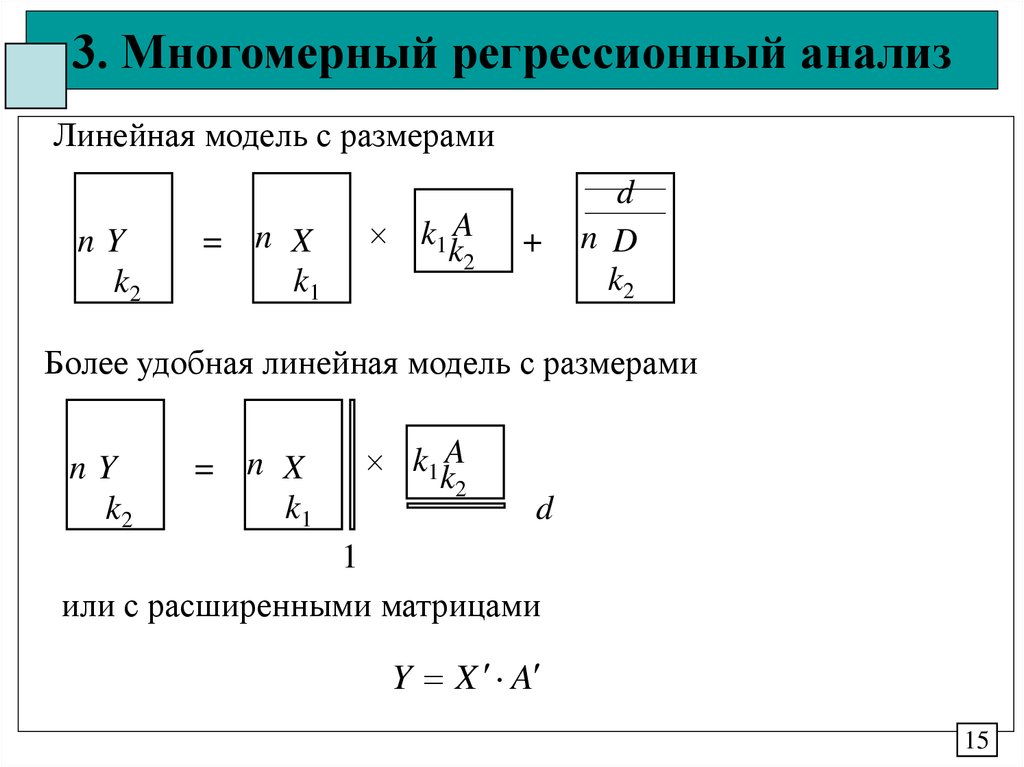
15. 3. Многомерный регрессионный анализ

Линейная модель с размерами
nY
k2
= n X
k1
k1kA
2
+
d
n D
k2
Более удобная линейная модель с размерами
nY
k2
= n X
k1
k1kA
2
d
1
или с расширенными матрицами
Y X A
15

16. 3. Многомерный регрессионный анализ

Не дает естественную алгебраическую запись- транспонирование
k2 YT
n
T
= k2 A k1 XT
k1
n
d
1
или с расширенными матрицами
Y T A T X T
Реальная модель с матрицей поправок V
Y T V T A T X T
Решается под матричным условием МНК с V vec(V T )
V T V Trace(V T V )
16

17. 3. Многомерный регрессионный анализ

Минимизация целевой функции Ф с
V T A T X T Y T
k1 n
k1 k2 1
k2 1 n
k1 n
совместная система нормальных уравнений через
правую трансформацию Гаусса (домножение на Х')
Y T X 0 M X T X Y T X M N b
М N = b.
Решение через обращение
1
,
N Q
M b Q
17

18. 3. Многомерный регрессионный анализ

Оценка точности производится по обычной схеме:
– погрешность модели
vT v
ˆ 0
n0 k
п0 – число всех измерений, k – число необходимых
измерений.
Матричная
операции
vec(X),
для
растягивания по столбцам матрицы Х в вектор-столбец
чтобы получить вектор поправок v из матрицы поправок
V
T
v vec V
Квадратичную форму Ф = vTv, можно определить на
основе известной формулы
Ô Y XQX T E Y T Y P Y T
18

19. 3. Многомерный регрессионный анализ

– погрешности определения коэффициентов через
ковариационную матрицу
K M ˆ 0 Q
где матрица кофакторов
определена как
оцененных
параметров
Q E X X E Q
T
1
Здесь Е – единичная матрица размера (k2 + 1) (k2 + 1),
- символ произведения Кронекера.
Упрощения из-за дублирования – вычисляют 1 блок, все
остальные эквивалентны.
19

20. 3. Многомерный регрессионный анализ

Метод растяжения
Основная матричная модель
nY
k2
k1kA
2
= n X
k1
d
1
С расширенными матрицами
Y X A
Переписывается так, чтобы матрица неизвестных А
стала вектором неизвестных а. модификация X и Yсведение к обычному векторному МНК с стандартной
схемой и оценкой точности.
20