Точка рівновіддалена від сторін многокутника

1. Геометричні місця точок

Властивість точки,
рівновіддаленої від сторін
многокутника
Творчий проект Новоренської Мар’яни

2.

Геометричне місце точок площини, що лежать усередині кута й
рівновіддалені від його сторін, є бісектриса цього кута
A
К
B
C

3.

Геометричне місце точок площини, кожна з яких рівновіддалена
від сторін трикутника АВС, є точка О – точка перетину бісектрис цього
трикутника, яка є центром вписаного в трикутник кола.
B
O
C
A

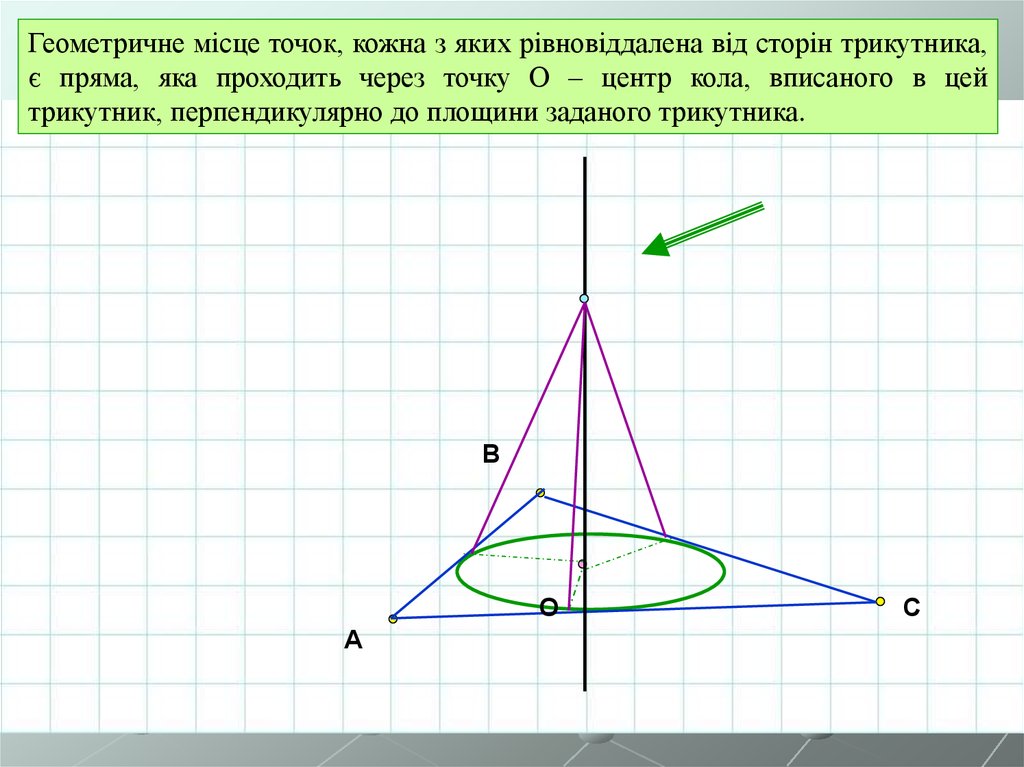
4.

Геометричне місце точок, кожна з яких рівновіддалена від сторін трикутника,
є пряма, яка проходить через точку О – центр кола, вписаного в цей
трикутник, перпендикулярно до площини заданого трикутника.
B
O
A
C

5.

Опорна задача (про точку, рівновіддалену від усіх сторін многокутника) Якщо
точка поза площиною многокутника рівновіддалена від усіх його сторін, то
основою перпендикуляра, проведеного з даної точки до площини
многокутника, є центр кола, вписаного в многокутник.
Опустимо з точки Р перпендикуляр РО до площини АВС.
Проведемо перпендикуляри PK, PM i PN до сторін АВ, ВС і АС відповідно.
За умовою PK=PM=PN.
Відрізки ОK, ОM, ОN проекції
рівних похилих, тому ОK=ОM=ОN.
За теоремою про три перпендикуляри
ці проекції перпендикулярні
до сторін : точка О
площини АВС рівновіддалена
від сторін трикутника
K
(многокутника),
тобто є центром
вписаного у нього
A
кола, що й треба
було довести
Р
B
M
O
C
N

6.

Обернена задача Якщо через центр кола, вписаного в многокутник, проведено
пряму, перпендикулярну до площини многокутника, то точки даної прямої
рівновіддалені від усіх сторін многокутника.
Проведемо через точку О перпендикуляр РО до площини АВС.
Проведемо перпендикуляри ОK, ОM iОN до сторін АВ, ВС і АС відповідно.
За умовою рівності проекцій ОK=ОM=ОN
Отримаємо рівні похилі: PK=PM=PN.
За теоремою про три перпендикуляри
ці похилі перпендикулярні
до сторін : будь-яка точка РО
рівновіддалена
від сторін трикутника
B
(многокутника),
K
що й треба
було довести
A
Р
M
O
C
N

7.

Задача 1. Катети прямокутного трикутника дорівнюють 12 см і 16см. Точка,
рівновіддалена від усіх сторін трикутника, розміщена на відстані 3 см від
площини трикутника. Знайдіть відстань від даної точки до сторін трикутника.
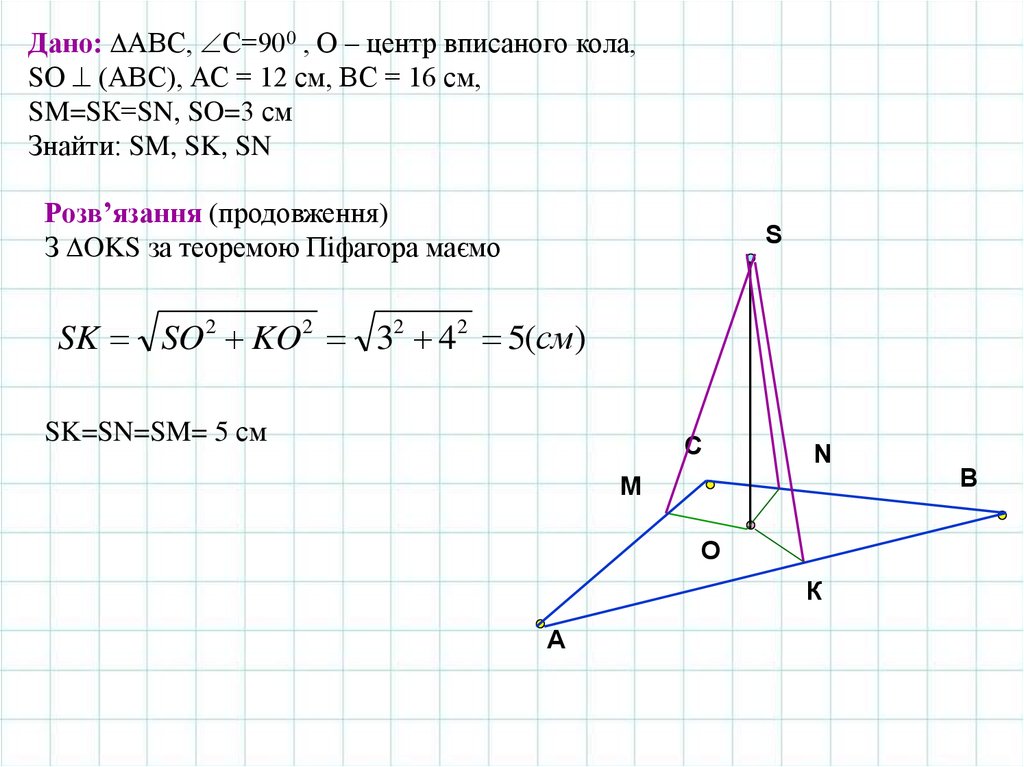
Дано: АВС, С=900 , О – центр вписаного кола,
SО (АВС), АС = 12 см, ВС = 16 см,
SM=SК=SN, SO=3 см
Знайти: SM, SK, SN
Розв’язання
Перпендикуляр SО до площини АВС
проектується в центр вписаного кола.
З АВС за теоремою Піфагора маємо
S
C
N
AB AC 2 BC 2 122 162 20(cм) M
Для прямокутного трикутника АВС радіус
вписаного кола можна
обчислити за формулою
a b c 12 16 20
r
4(см)
2
2
A
B
O
К

8.

Дано: АВС, С=900 , О – центр вписаного кола,
SО (АВС), АС = 12 см, ВС = 16 см,
SM=SК=SN, SO=3 см
Знайти: SM, SK, SN
Розв’язання (продовження)
З OKS за теоремою Піфагора маємо
S
SK SO 2 KO2 32 42 5(cм)
SK=SN=SM= 5 см
C
N
B
M
O
К
A

9.

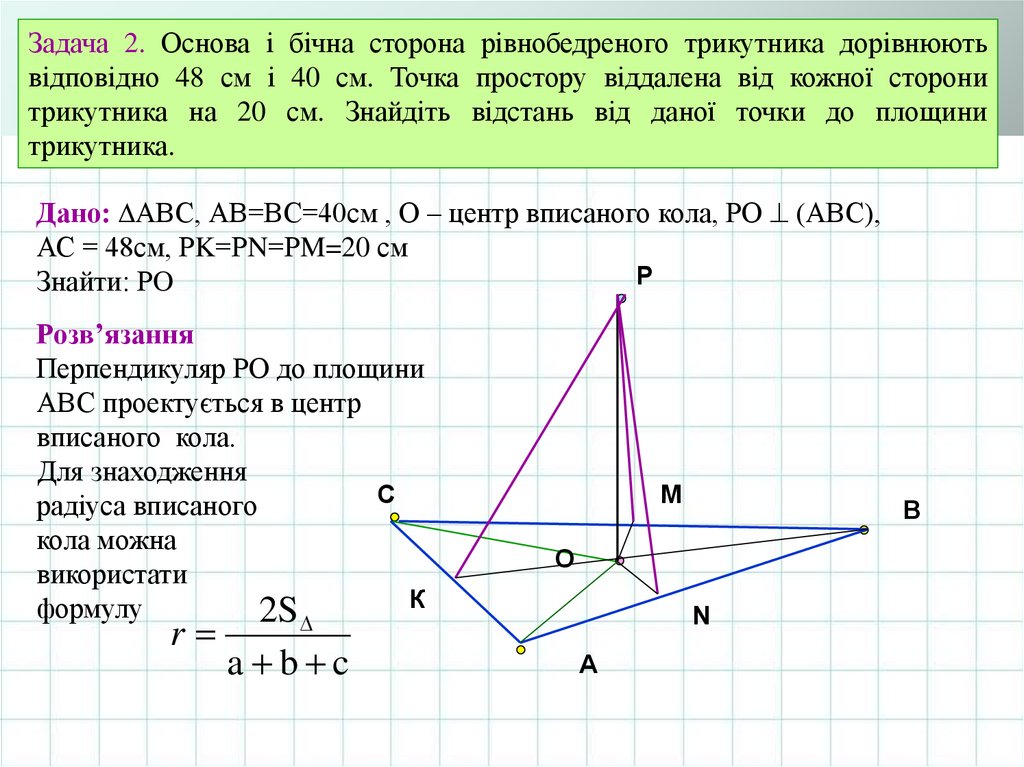
Задача 2. Основа і бічна сторона рівнобедреного трикутника дорівнюють
відповідно 48 см і 40 см. Точка простору віддалена від кожної сторони
трикутника на 20 см. Знайдіть відстань від даної точки до площини
трикутника.
Дано: АВС, АВ=ВС=40см , О – центр вписаного кола, РО (АВС),
АС = 48см, РK=РN=РM=20 см
Р
Знайти: РO
Розв’язання
Перпендикуляр РО до площини
АВС проектується в центр
вписаного кола.
Для знаходження
C
радіуса вписаного
кола можна
використати
К
формулу
2S
r
a b c
M
B
O
N
A

10.

Дано: АВС, АВ=ВС=40см , О – центр вписаного кола, РО (АВС),
АС = 48см, РK=РN=РM=20 см
Знайти: РO
Розв’язання (продовження)
Площу трикутника легко обчислити за формулою Герона,
враховуючи, що a=c=40 см, b= 48см
Р
р=(40+40+48): 2= 64 (см)
Тому знаходимо
S 64 24 24 16 768(см 2 )
r
2S
2 768
12(см)
a b c 40 40 48
C
M
B
O
З КРО за наслідком
з теореми Піфагора
К
N
A
PO PK 2 KO2 202 122 16(см)