Similar presentations:
Правильні многокутники. (9 клас)
1. Правильні многокутники
2.
AF
E
В
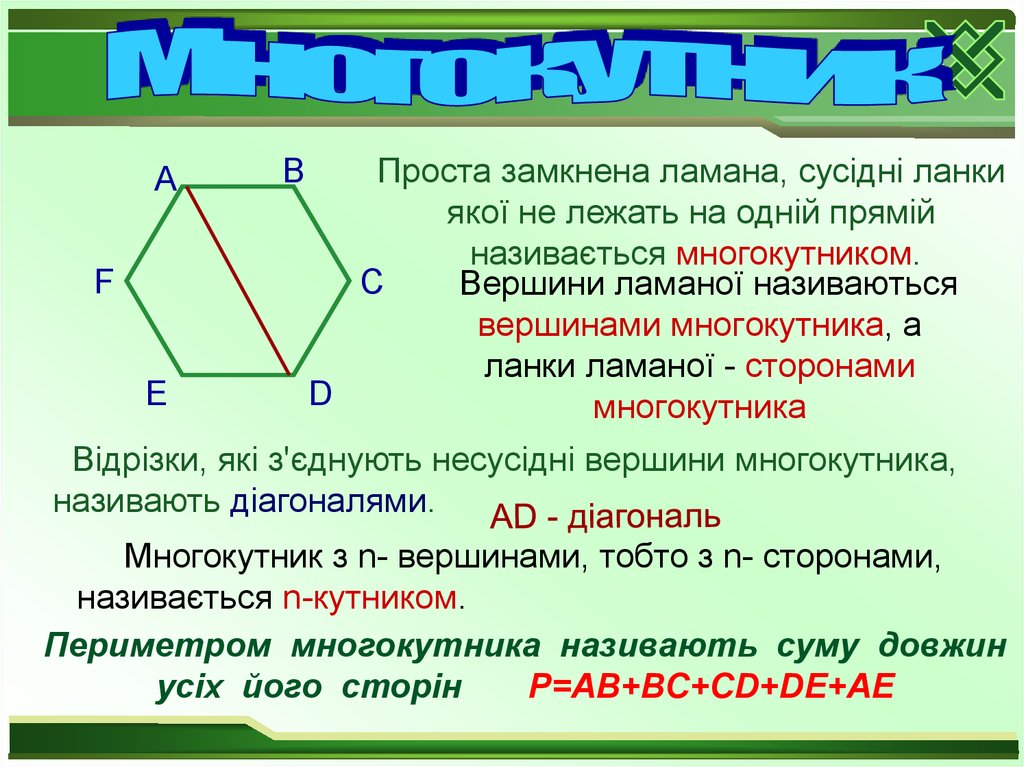
Проста замкнена ламана, сусідні ланки
якої не лежать на одній прямій
називається многокутником.
С
Вершини ламаної називаються
вершинами многокутника, а
ланки ламаної - сторонами
D
многокутника
Відрізки, які з'єднують несусідні вершини многокутника,
називають діагоналями.
Многокутник з n- вершинами, тобто з n- сторонами,
називається n-кутником.
Периметром многокутника називають суму довжин
усіх його сторін
P=AB+BC+CD+DE+AE
3.
4.
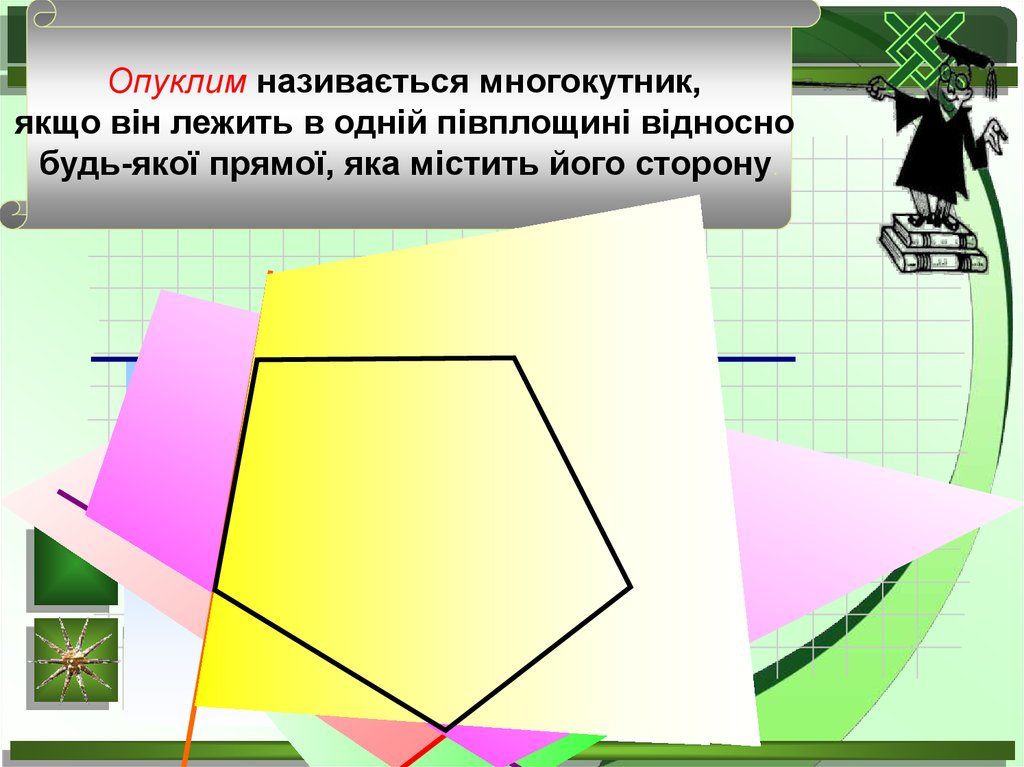
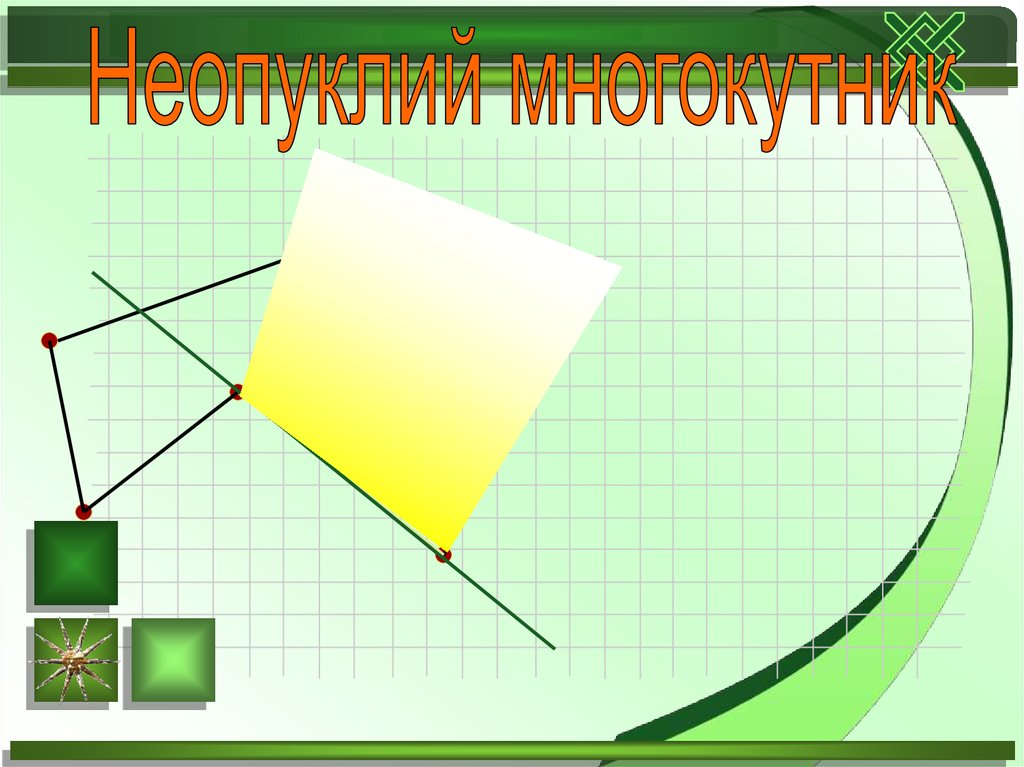
Опуклим називається многокутник,якщо він лежить в одній півплощині відносно
будь-якої прямої, яка містить його сторону.
5.
6. Правильні многокутники
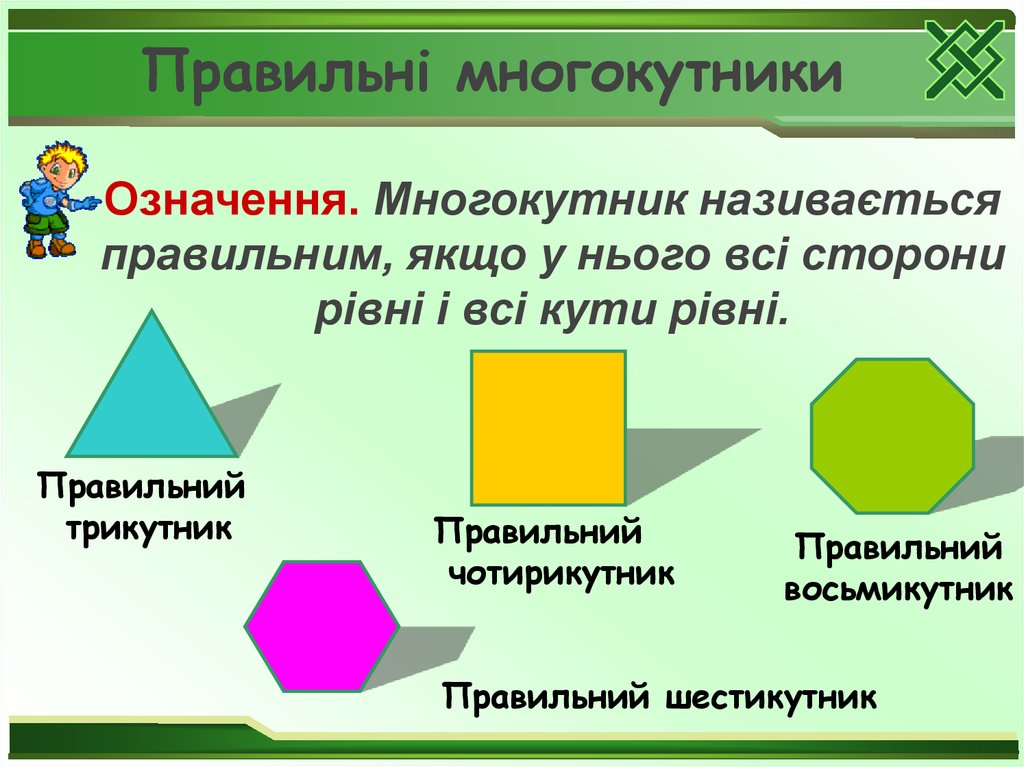
Означення. Многокутник називаєтьсяправильним, якщо у нього всі сторони
рівні і всі кути рівні.
Правильний
трикутник
Правильний
чотирикутник
Правильний
восьмикутник
Правильний шестикутник
7.
1. З кожної вершини можна провестиn-3 діагоналі.
2. Кількість усіх діагоналей дорівнює
n(n 3)
;
2
3. Для будь-якої сторони a справедливо, що a<P
(P – периметр n-кутника).
4. Периметр правильного n-кутник P=an
(P – периметр, a – сторона)
8.
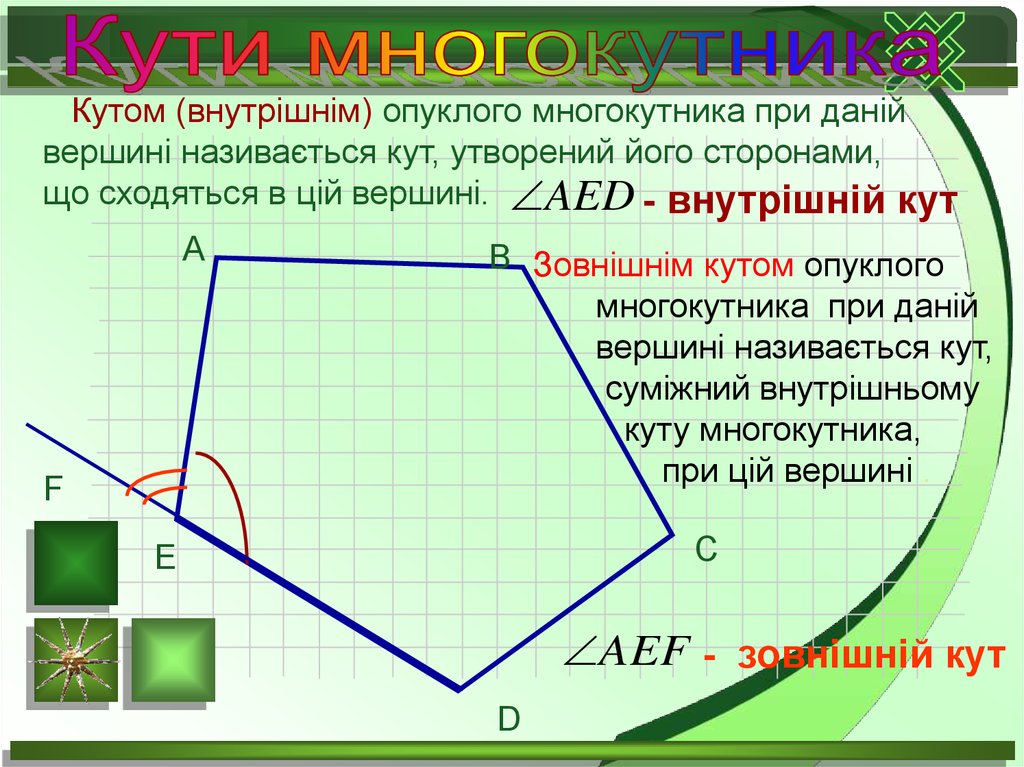
Кутом (внутрішнім) опуклого многокутника при данійвершині називається кут, утворений його сторонами,
що сходяться в цій вершині. AED - внутрішній кут
A
F
B Зовнішнім кутом опуклого
многокутника при даній
вершині називається кут,
суміжний внутрішньому
куту многокутника,
при цій вершині .
C
E
AEF - зовнішній кут
D
9. Сума кутів опуклого n – кутника дорівнює 180°·(n-2)
10. Сума зовнішніх кутів опуклого многокутника дорівнює 360°
°°
°
11.
Кути правильногоn-кутника
180 (n 2)
1. Внутрішній кут:
;
n
360
2. Зовнішній кут:
;
n
3. Центральний кут:
360
;
n
12. Вписані і описані правильні многокутники
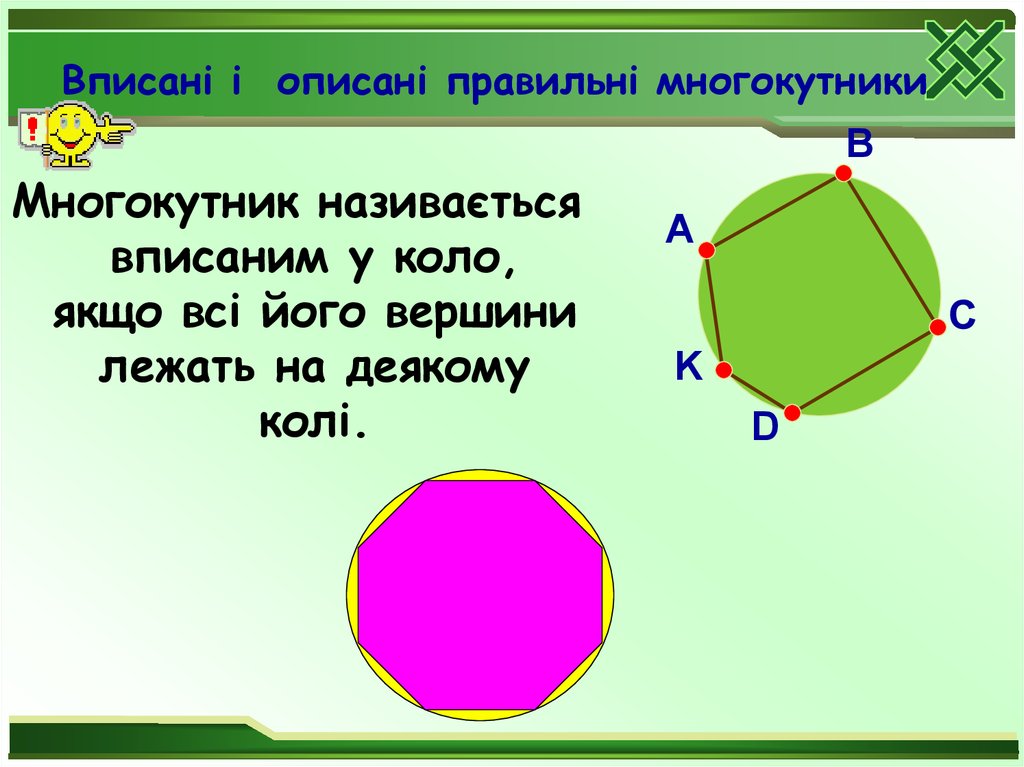
BМногокутник називається
вписаним у коло,
якщо всі його вершини
лежать на деякому
колі.
A
K
D
13.
14. Вписані і описані правильні многокутники
Многокутник називаєтьсяописаним навколо кола, якщо
всі його сторони дотикаються
до деякого кола.
S
K
R
Р
T
15.
16. Вписані і описані правильні многокутники
rО
R
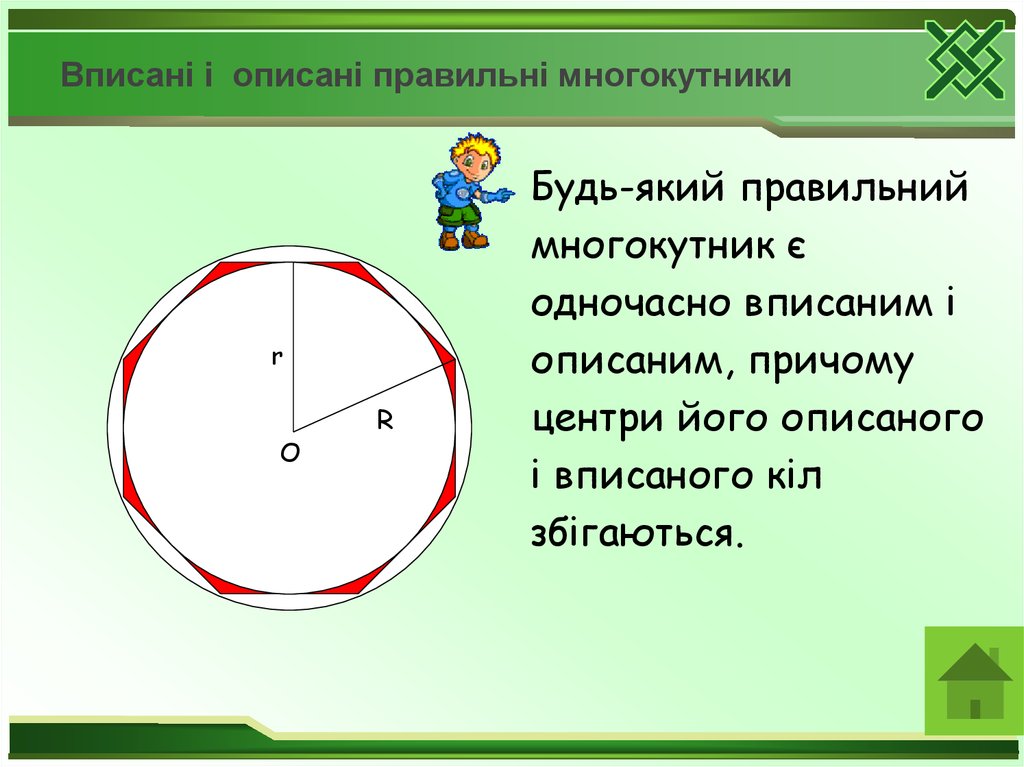
Будь-який правильний
многокутник є
одночасно вписаним і
описаним, причому
центри його описаного
і вписаного кіл
збігаються.
17.
Дудник Н.М.18.
Сторона многокутникаі радіус вписаного кола
Е
D
ОА – радіус описаного
кола ( R )
О
F
С
ОН – радіус вписаного
кола ( r )
В
Н
А
АВ – сторона правильного п-кутника
( ап )
19.
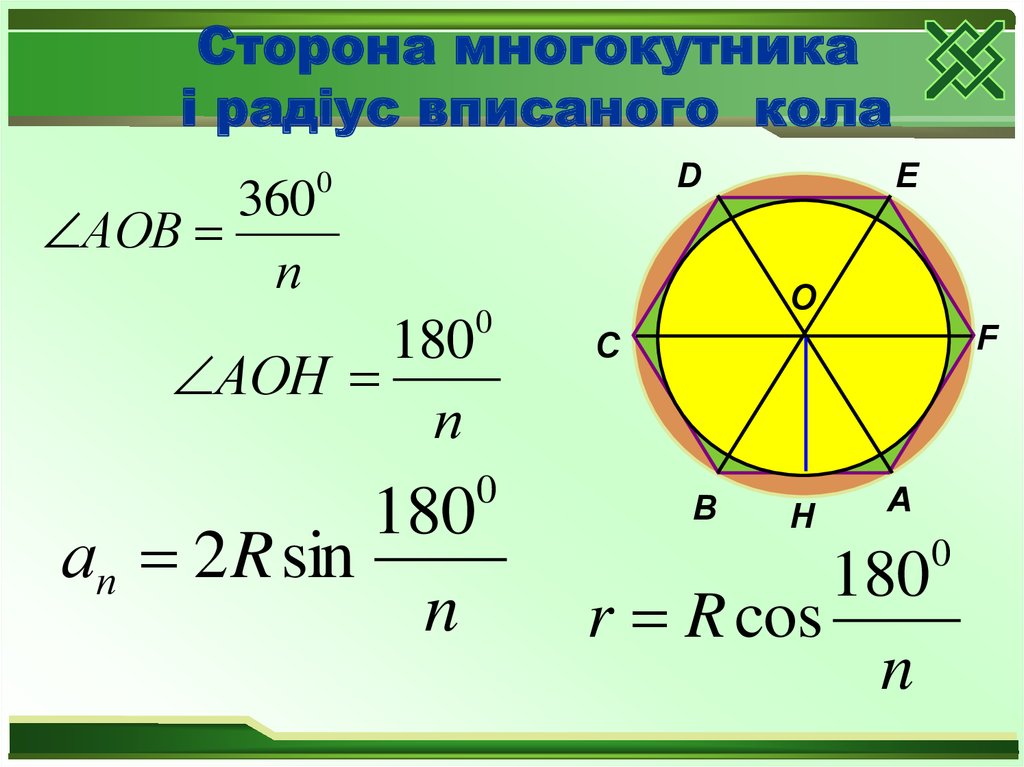
Сторона многокутникаі радіус вписаного кола
360
АОВ
п
Е
D
0
180
АОН
п
0
180
ап 2 R sin
n
0
О
F
С
В
Н
А
180
r R cos
n
0
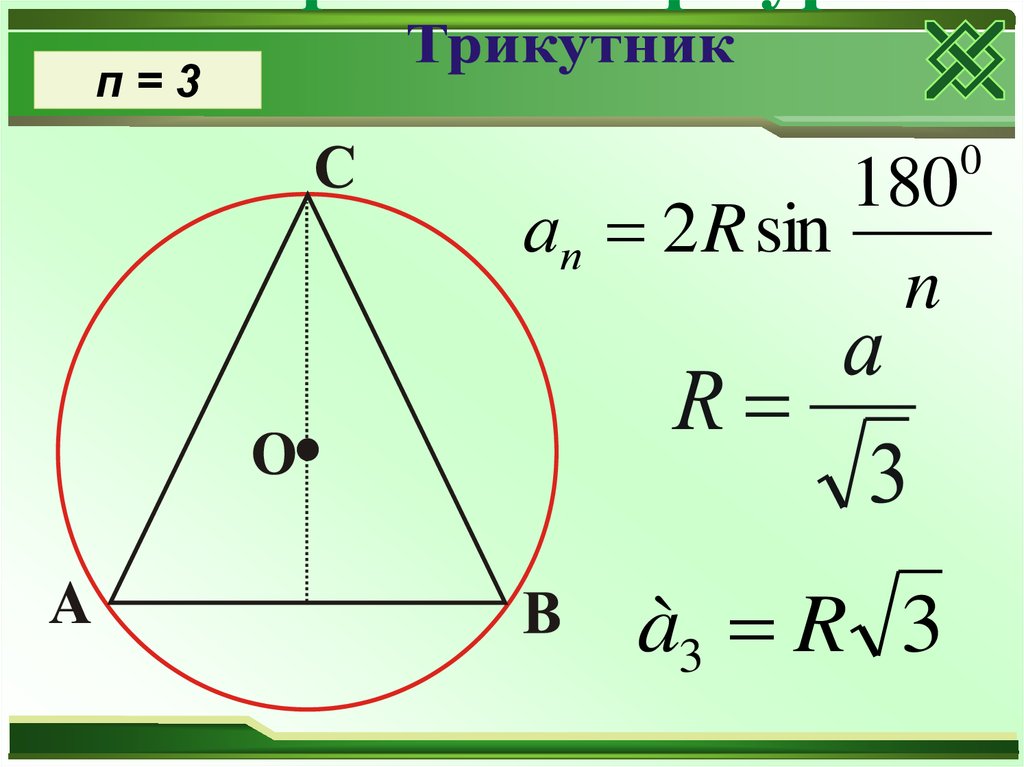
20.
п=3180
ап 2 R sin
n
à3 R 3
0
21.
22.
п=4180
ап 2 R sin
n
0
à4 R 2
23.
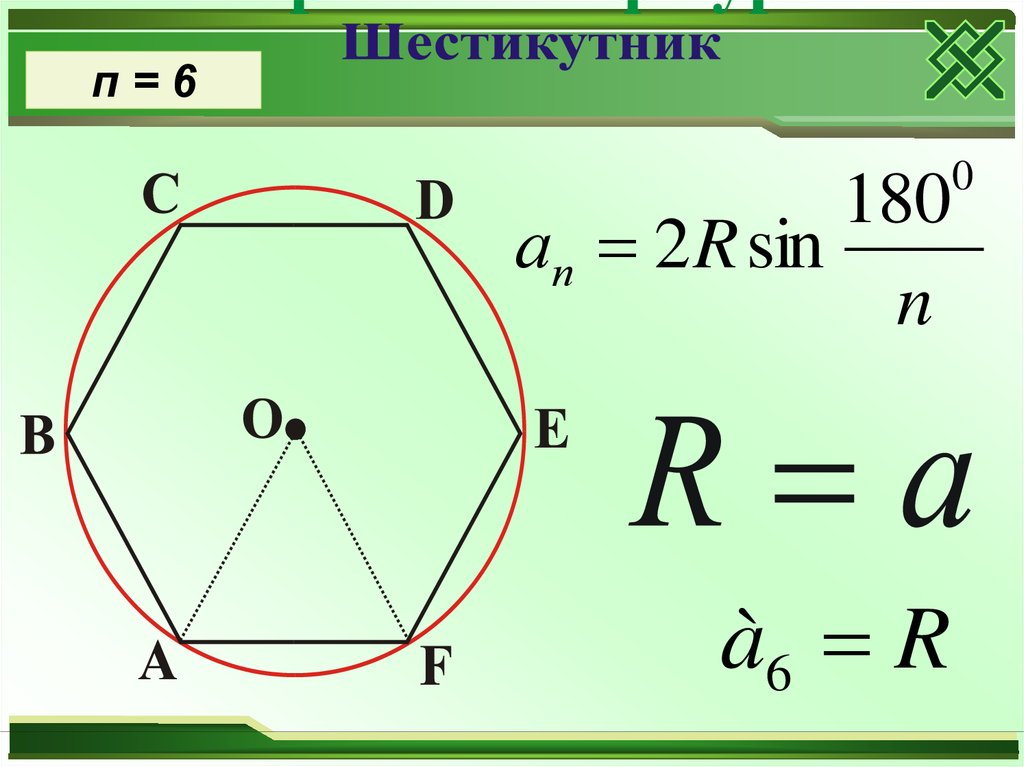
24.
п=6180
ап 2 R sin
n
à6 R
0
25.
26. Формули для радіусів вписаних і описаних кіл правильних многокутників
Кількістьсторін
n 3
n 4
n 6
Радіус
R
r
an
o
180
2 sin n
an
180o
2tg n
R
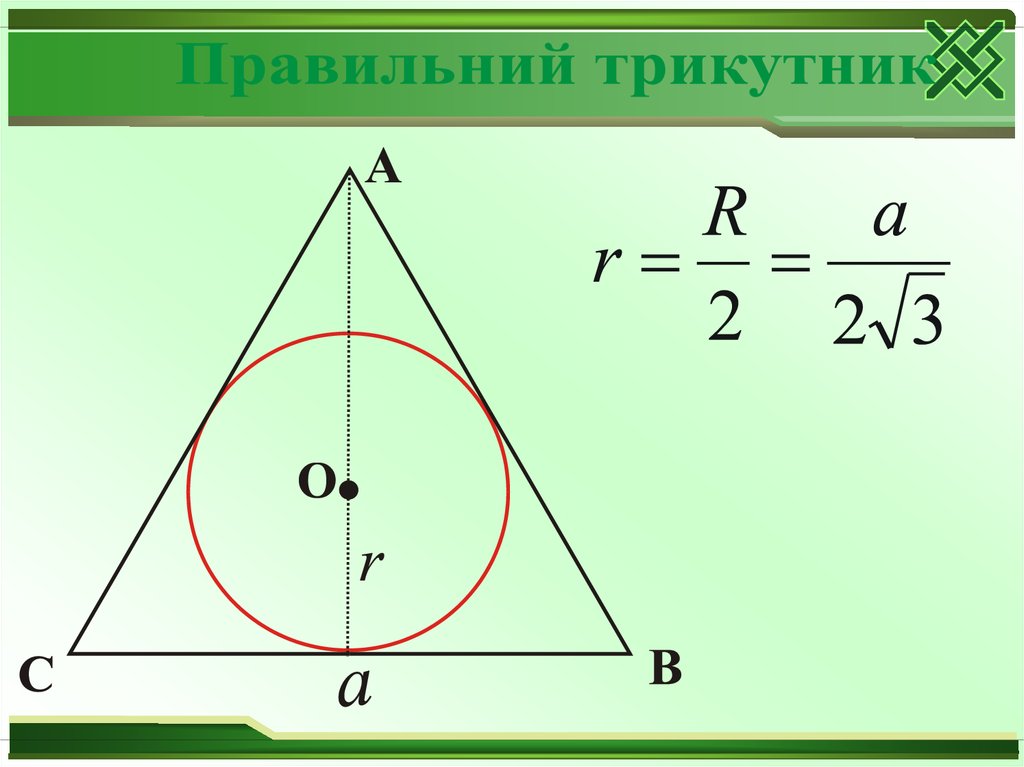
a3 3
3
a3 3
r
6
а4 2
R
2
R a6
а4
r
2
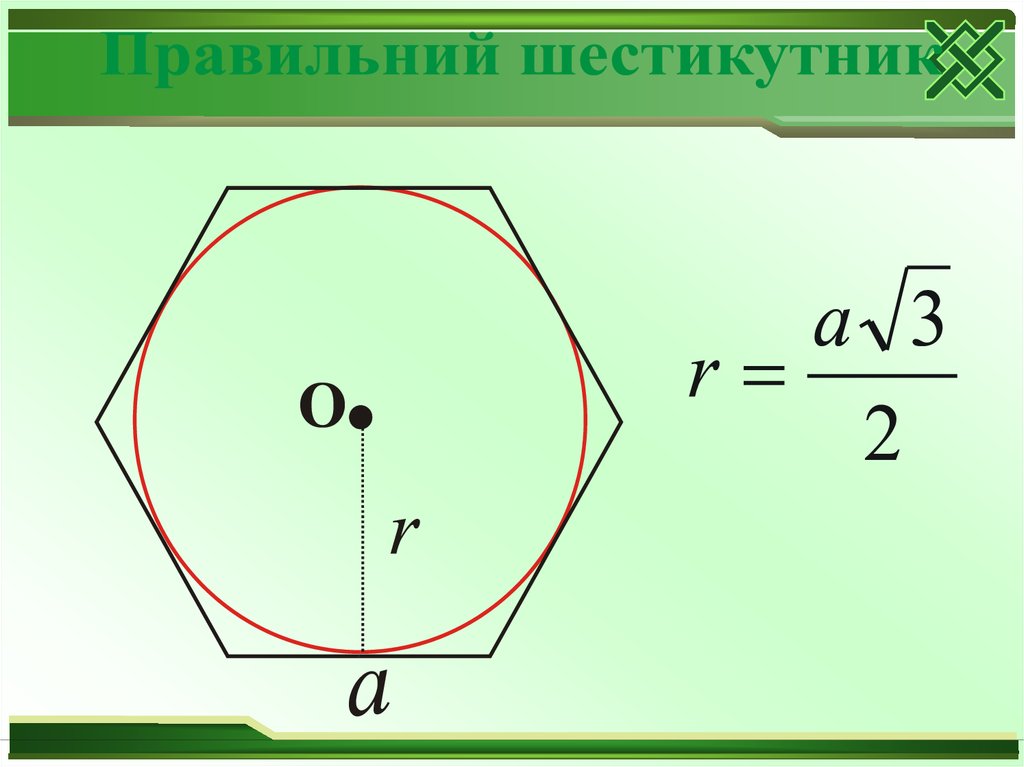
a6 3
r
2
27.
R, ran
an
a3
R
R
180
2 R sin
n
a6
180
2rtg
n
o
R 3
a4
r
r
2r 3
2r
R 2
R
o
2
3
3
r
28.
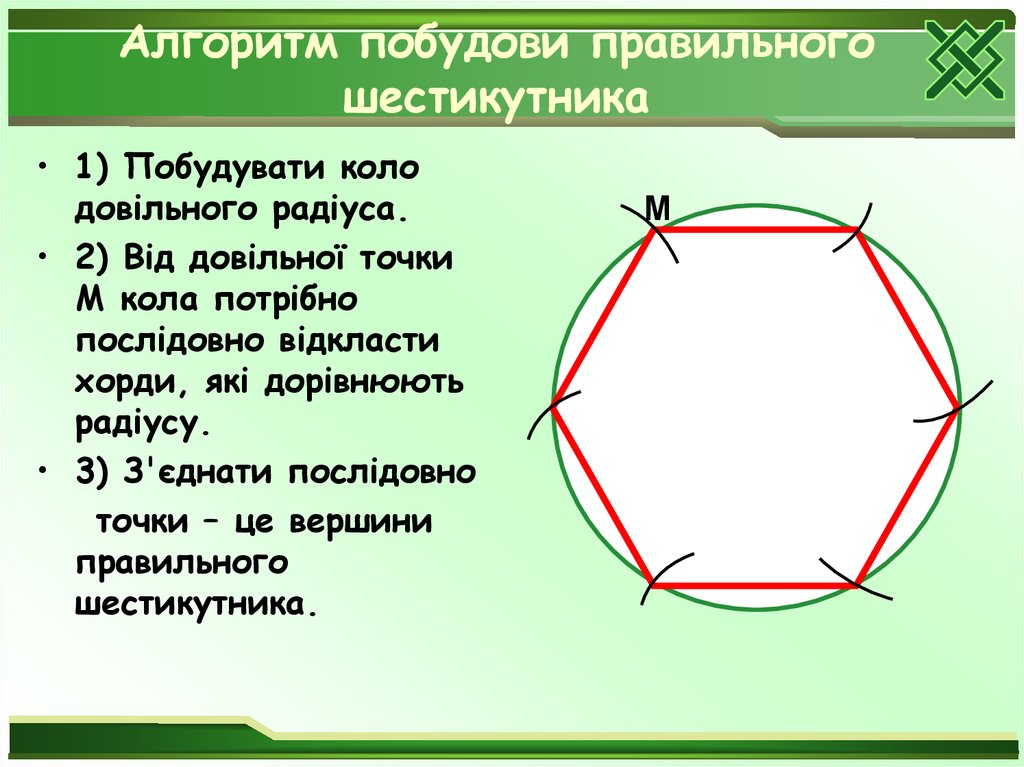
Дудник Н.М.29. Алгоритм побудови правильного шестикутника
• 1) Побудувати колодовільного радіуса.
• 2) Від довільної точки
М кола потрібно
послідовно відкласти
хорди, які дорівнюють
радіусу.
• 3) З'єднати послідовно
точки – це вершини
правильного
шестикутника.
М
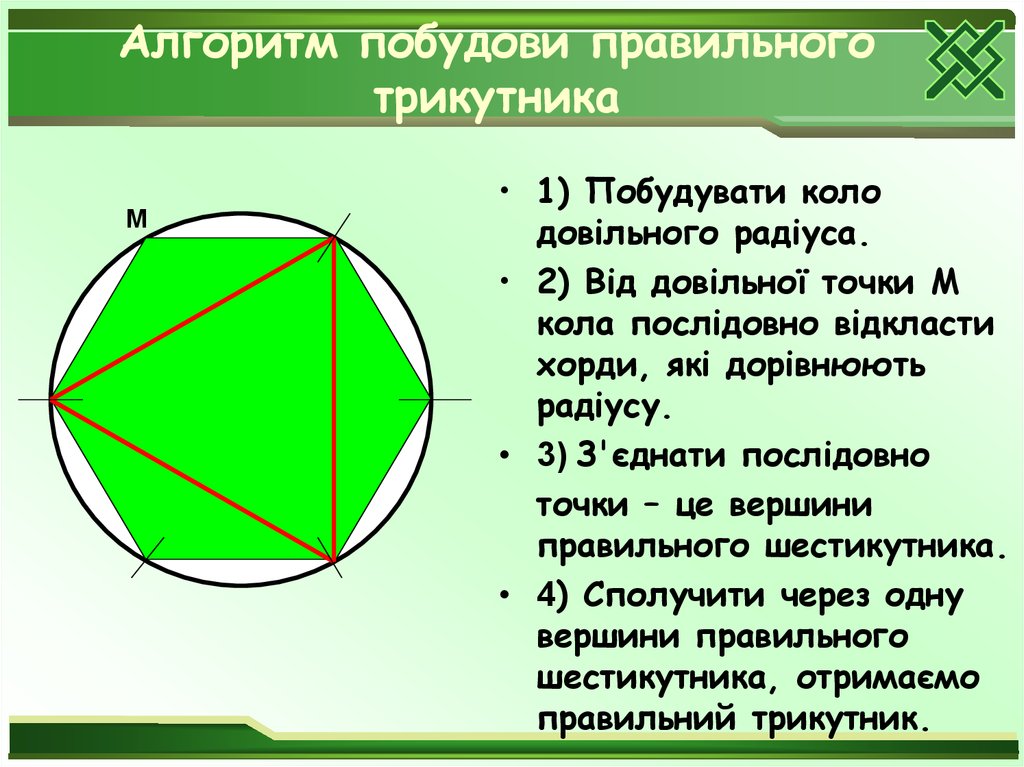
30. Алгоритм побудови правильного трикутника
М• 1) Побудувати коло
довільного радіуса.
• 2) Від довільної точки М
кола послідовно відкласти
хорди, які дорівнюють
радіусу.
• 3) З'єднати послідовно
точки – це вершини
правильного шестикутника.
• 4) Сполучити через одну
вершини правильного
шестикутника, отримаємо
правильний трикутник.
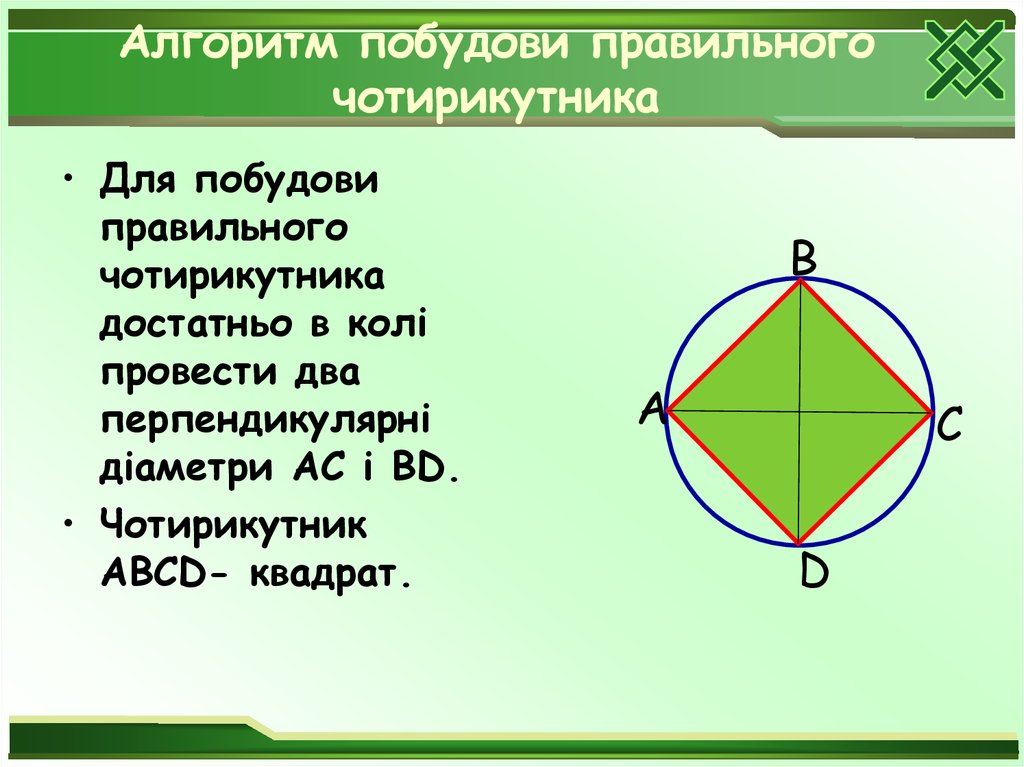
31. Алгоритм побудови правильного чотирикутника
• Для побудовиправильного
чотирикутника
достатньо в колі
провести два
перпендикулярні
діаметри АС і ВD.
• Чотирикутник
АВСD- квадрат.
B
A
C
D
32.
Дудник Н.М.33.
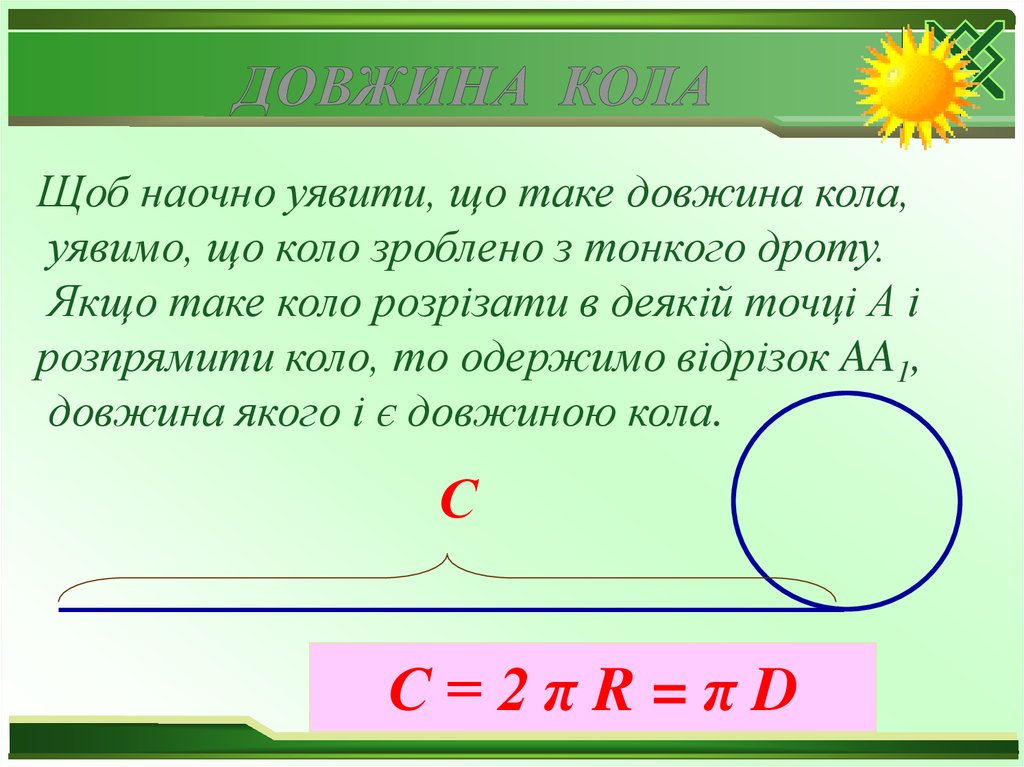
Щоб наочно уявити, що таке довжина кола,уявимо, що коло зроблено з тонкого дроту.
Якщо таке коло розрізати в деякій точці А і
розпрямити коло, то одержимо відрізок AA1,
довжина якого і є довжиною кола.
С
С=2πR=πD
34.
35.
36.
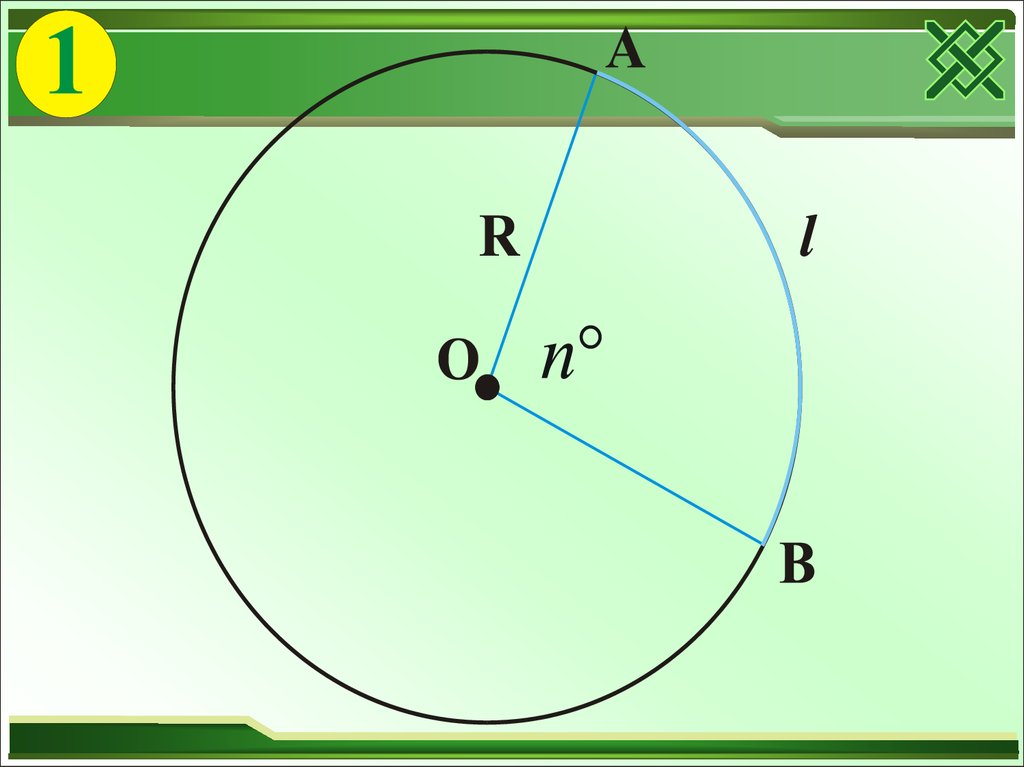
Довжина кола. Довжина дугиНазва формули
Формула
Довжина кола
С=2 R
C= D
О
Довжина дуги
О
n°
l
Rn
180
Позначення
C - довжина кола
R – радіус кола
D - діаметр
- довжина дуги
R- радіус кола
n° - градусна
міра відповідного
центрального
кута
l
37.
Дудник Н.М.38.
Частина площини,обмежена колом.
S =
2
πR
39.
Сектор 1.А
С
D
О
Круговим сектором
називається частина
круга, обмежена дугою і
двома радіусами, що
з’єднують кінці дуги з
центром круга.
В
Сектор 2.
Дуга АВС – дуга кругового сектора 1.
Дуга АDВ – дуга кругового сектора 2.
40.
21) Площа
круга?
S = πR
10
S
R
S1
0
0
360
360
2
2) Площа кругового сектора,
обмеженого дугою в 10?
R
S
0
360
2
3) Площа кругового сектора,
обмеженого дугою в α0?
41.
42.
43.
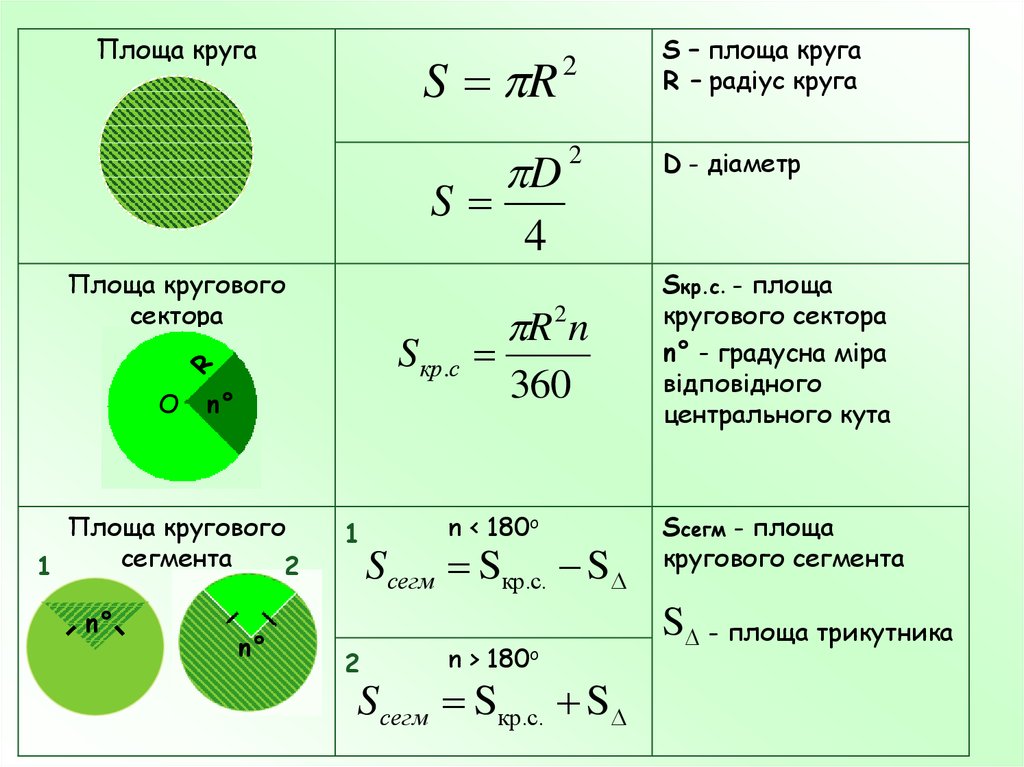
Площа кругаS R
2
S – площа круга
R – радіус круга
D
2
D - діаметр
S
Площа кругового
сектора
О
n°
Площа кругового
сегмента
1
2
n°
Sкр .с
n°
1
2
4
R 2 n
360
n < 180o
Sсегм Sкр.с. S
n > 180o
Sсегм Sкр.с. S
Sкр.с. - площа
кругового сектора
n° - градусна міра
відповідного
центрального кута
Sсегм - площа
кругового сегмента
S - площа трикутника
44.
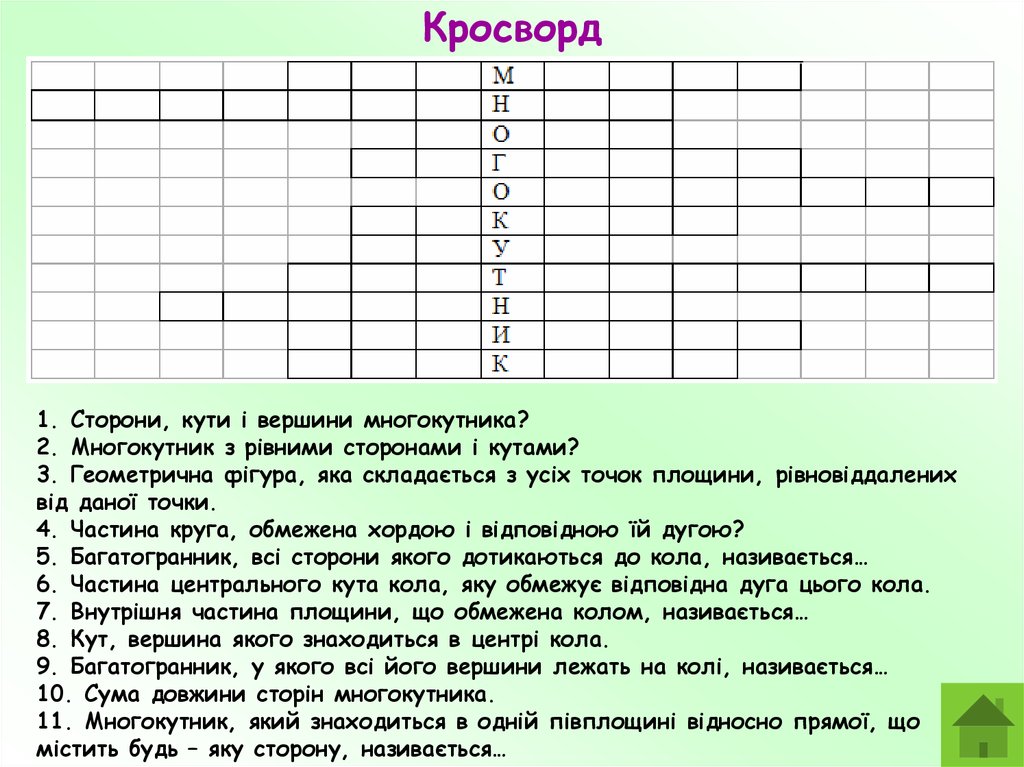
Кросворд1. Сторони, кути і вершини многокутника?
2. Многокутник з рівними сторонами і кутами?
3. Геометрична фігура, яка складається з усіх точок площини, рівновіддалених
від даної точки.
4. Частина круга, обмежена хордою і відповідною їй дугою?
5. Багатогранник, всі сторони якого дотикаються до кола, називається…
6. Частина центрального кута кола, яку обмежує відповідна дуга цього кола.
7. Внутрішня частина площини, що обмежена колом, називається…
8. Кут, вершина якого знаходиться в центрі кола.
9. Багатогранник, у якого всі його вершини лежать на колі, називається…
10. Сума довжини сторін многокутника.
11. Многокутник, який знаходиться в одній півплощині відносно прямої, що
містить будь – яку сторону, називається…

























 mathematics
mathematics








