Расчет динамических характеристик объекта с сосредоточенными координатами

1.

Лабораторная работа 2
Расчет динамических характеристик объекта
с сосредоточенными координатами

2.

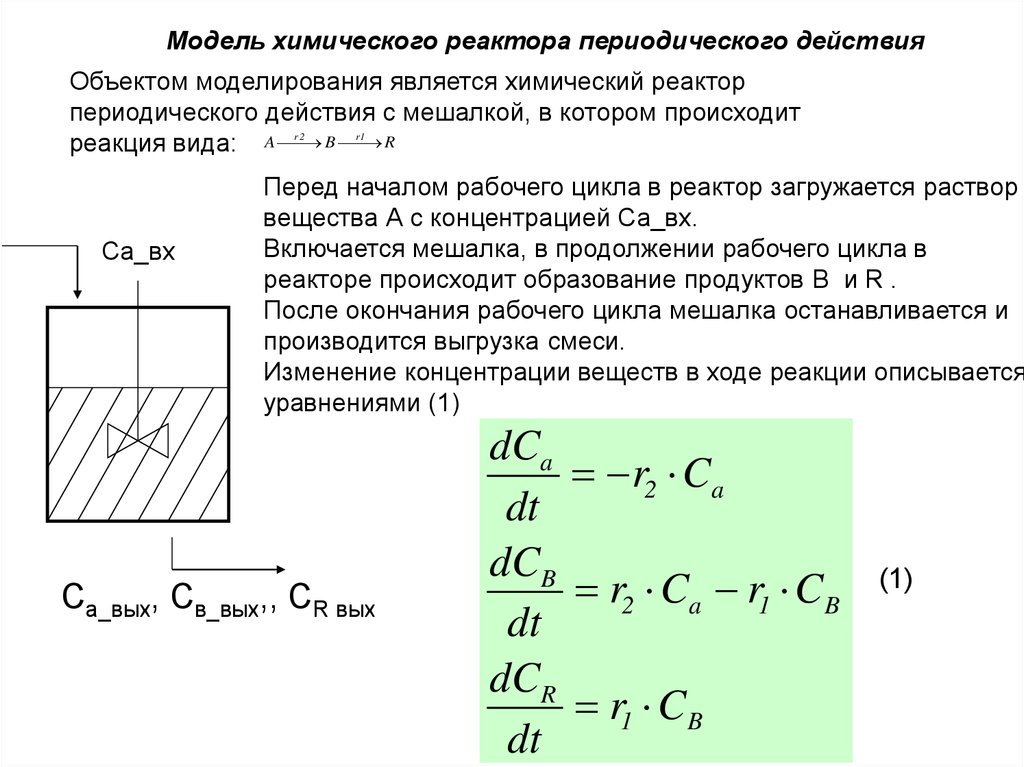
Модель химического реактора периодического действия
Объектом моделирования является химический реактор
периодического действия с мешалкой, в котором происходит
реакция вида: A B R
r2
Са_вх
r1
Перед началом рабочего цикла в реактор загружается раствор
вещества А с концентрацией Са_вх.
Включается мешалка, в продолжении рабочего цикла в
реакторе происходит образование продуктов B и R .
После окончания рабочего цикла мешалка останавливается и
производится выгрузка смеси.
Изменение концентрации веществ в ходе реакции описывается
уравнениями (1)
Са_вых, Св_вых,, СR вых
dCa
r2 Ca
dt
dCB
r2 Ca r1 CB
dt
dCR
r1 CB
dt
(1)

3.

В течение рабочего цикла в реакторе происходит образование
полезного (В) и побочного (R) продуктов.
Изменение концентраций веществ в течение рабочего цикла можно
оценить по графикам динамических характеристик этого объекта.
На рисунке приведен один из вариантов таких характеристик.
На основе этих графиков
можно оценить
- необходимое время
рабочего цикла (Т)
- максимальную
концентрацию полезного
продукта (Cb_max)
График динамических
характеристик получают
путем решения уравнений
модели (1).
Для этого используют численные методы решения систем
дифференциальных уравнений

4.

Решение систем дифференциальных уравнений.
Система дифференциальных уравнений должна быть представлена в форме
Коши:
dy
(2)
dt
F ( y, t )
Исходные данные для решения системы (2):
- начальные условия y0
- интервал решения t0 <= t <= tfinal
Для решения систем вида (2) используются различные методы. Их реализации
в МатЛаб названы решателями ОДУ (solver).
решатели
Тип задачи
ode45
ode23
Не жесткая
Не жесткая
ode113
Не жесткая
ode23tb
жесткая
Степень
точности
средняя
низкая
Область применения
В большинстве случаев
При
допустимости
грубой
погрешности или при решении
умеренно жестких задач
От низкой до При высокой точности решения или
высокой
при
решении
сложны
в
вычислительном отношении задач
низкая
При уравнениях, заданных в неявной
форме Коши.

5.

Решение систем дифференциальных уравнений
Правую часть системы уравнений (2) оформляют в виде отдельного файлафункции, так называемого ODE файла
function dydt = vdp101(t,y)
% лаб. Раб. 2….
dydt = [правая часть 1-го уравнения системы (1);
правая часть 2-го уравнения системы (1);
И т.д. все уравнения в системе……];
В командном окне выполняется обращение к соответствующей функции
МатЛаб с использованием пользовательской функции в качестве
параметра:
[T,Y]=solver(‘F’,[t0 tfinal],y0)
Параметры функции:
Solver – имя решателя
‘F’ - имя ODE-файла, в котором описывается правая часть исходной системы.
[t0 tfinal] – интервал решения
y0 – вектор начальных условий

6.

Пример ODE-файла с описанием правой части системы уравнений (3),
определяющей модель объекта в форме Коши:
function dydt = vdp101(t,y)
dy1
a1 y1
dt
dy 2
a2 y1 a1 y2
dt
(3)
a1=10;
a2=38;
dydt = [a1*y(1);
a2*y(1)-a1*y(2)];
Сохраняем функцию vdp101(t,y) в файле
vdp101.m.
В командном окне обращаемся к решателю
ODE45 и получаем решение:
>> [T,Y]=ode45(@vdp101,[0,4],[25,0]);
>> plot(T,Y)
>>
Размерность вектора нач. условий
равна числу уравнений в системе

7.

ЗАДАНИЕ на лабораторную работу 2
1. Рассчитать динамические характеристики реактора периодического
действия
2. В качестве исходных данных использовать значения из таблицы
вариантов на следующем слайде.
3. Построить графики динамических характеристик
4. Определить время выгрузки (время рабочего цикла) для получения
максимального выхода полезного продукта В
5. Исследовать влияние изменения состава исходного раствора на:
а) выход полезного продукта (концентрация полезного продукта в
момент окончания рабочего цикла)
Св_вых = F(Са_вх),
СR вых= F(Са_вх)
Изменять аргумент в диапазоне: -50% Са_вх _баз< Са_вх < +50% Са_вх _баз
б) время рабочего цикла
Т_кон = F(Са_вх) при полезном продукте В
Т_кон = F(Са_вх) при полезном продукте R

8.

ВАРИАНТЫ
ЗАДАНИЯ
на лабораторную
работу 2
N
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
r1
1
1,2
1,4
1,9
0,3
0,5
9
1,2
1,1
1
1,2
1,4
1,9
0,3
0,5
9
1,2
1,1
r2
2
3
4
5
1
2
11
2
2
3
4
2
4
1
1
11
2
2
Ca_vx
23
25
26
27
30
32
34
38
41
44
39
43
47
43
48
48
44,2
49,4

9.

ВАРИАНТЫ
ЗАДАНИЯ
на лабораторную
работу 2
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
2
3
4
5
1
1,6
1,8
1,4
1
1,2
1,4
1,9
0,3
0,5
9
1,2
1,1
2
3
4
3
4
6
7
2
2
2
3
2
5
2
3
1
2
11
5
1
1,6
1,8
1,4
49,9
44,5
49,9
58,9
45,7
51
59,9
46,9
52,4
61,8
47,2
52,9
70,8
48,4
54
72,8
51,4
58
77,8
52,4

10.

Порядок выполнения лабораторной работы 2
1. Создать файл-функцию с описанием правой части системы дифференциальных
уравнений
2. Создать файл сценарий :
- с расчетом динамических характеристик объекта Са(t), Cb(t), Cr(t)
- оценкой времени рабочего цикла (Т) и оценкой концентраций полезного и
побочного продуктов в момент окончания рабочего цикла Cb(Т), Cr(Т).
- с расчетом графика изменения этих характеристик (Т, Cb(Т), Cr(Т)) при изменении
состава исходного раствора (получить 10 точек).
3. Построить графики динамических характеристик Са(t), Cb(t), Cr(t) при заданном
значении Са_вх (исходные данные из таблицы).
4. Построить графики
Св_вых = F(Са_вх),
СR вых= F(Са_вх), Т = F(Са_вх)

11.

Лабораторная работа 2
Расчет динамических характеристик объекта
с сосредоточенными координатами
Содержание отчета
1. Объект моделирования (схема, уравнения модели)
2. Текст программы (файл-функция с расчетом вектора dY/dt и файлсценарий с описанием обращения к решателю и циклом по Са_вх)
3. Графики динамических характеристик Са(t), Cb(t), Cr(t)
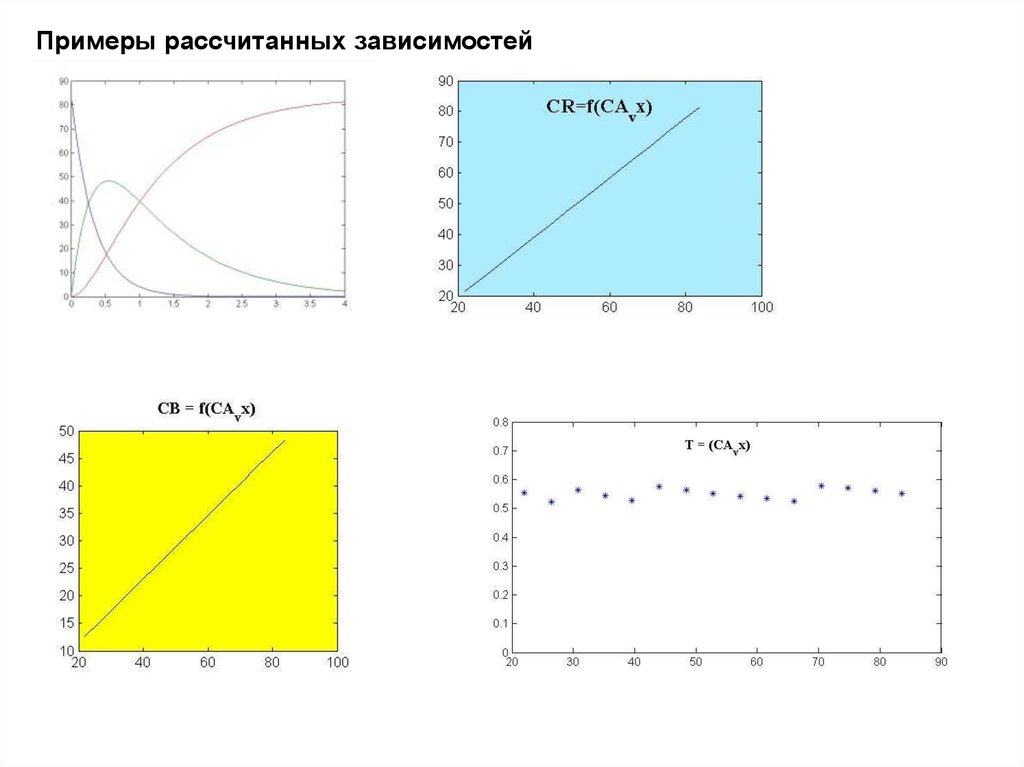
4. Графики зависимостей:
Св_вых = F(Са_вх),
СR вых= F(Са_вх),
Т = F(Са_вх)

12.

Примеры рассчитанных зависимостей