Similar presentations:
Обучение младших школьников решению логических задач
1. ОБУЧЕНИЕ МЛАДШИХ ШКОЛЬНИКОВ РЕШЕНИЮ ЛОГИЧЕСКИХ ЗАДАЧ
Проф. МГПУ Л. П. Стойлова2. Рекомендуемая литература
1. Никольская И. Л., Тигранова Л. И.Гимнастика для ума: Книга для
учащихся. – М.: Просвещение, 1997
2. Лихтарников Л. М. Занимательные
логические задачи: Для учащихся
начальной школы. – СПб: Лань, МИК,
1996
3. Останина Е. Е. Обучение младших
школьников решению нестандартных
арифметических задач // Начальная
школа. – 2004, № 7
3.
Логические задачи – это задачи,при решении которых поиск ответа
на вопрос осуществляется на
основе рассуждений.
Вычисления при решении
логических задач играют
вспомогательную роль, а иногда
совсем не нужны.
4. Существуют различные подходы и классификации логических задач.
В данном курсе будут рассмотреныследующие виды логических задач:
с истинными и ложными высказываниями;
на установление соответствия между
множествами;
на упорядочивание множества;
на доказательство, основанное на выявлении
худшего случая и с использованием принципа
Дирихле;
на планирование действий (взвешивания,
переливания, переправы и др.)
5. Задачи с истинными и ложными высказываниями
Задача 1. На необитаемом островерастут три дерева – дуб, береза и
сосна. Под одним из них пираты зарыли
клад, а на деревья повесили таблички.
На дуб: клад зарыт под сосной; на
березу: клад зарыт не здесь; на сосну:
клад зарыт под березой. Узнайте, под
каким деревом зарыт пиратский клад,
если из трех надписей две истинные, а
одна ложная.
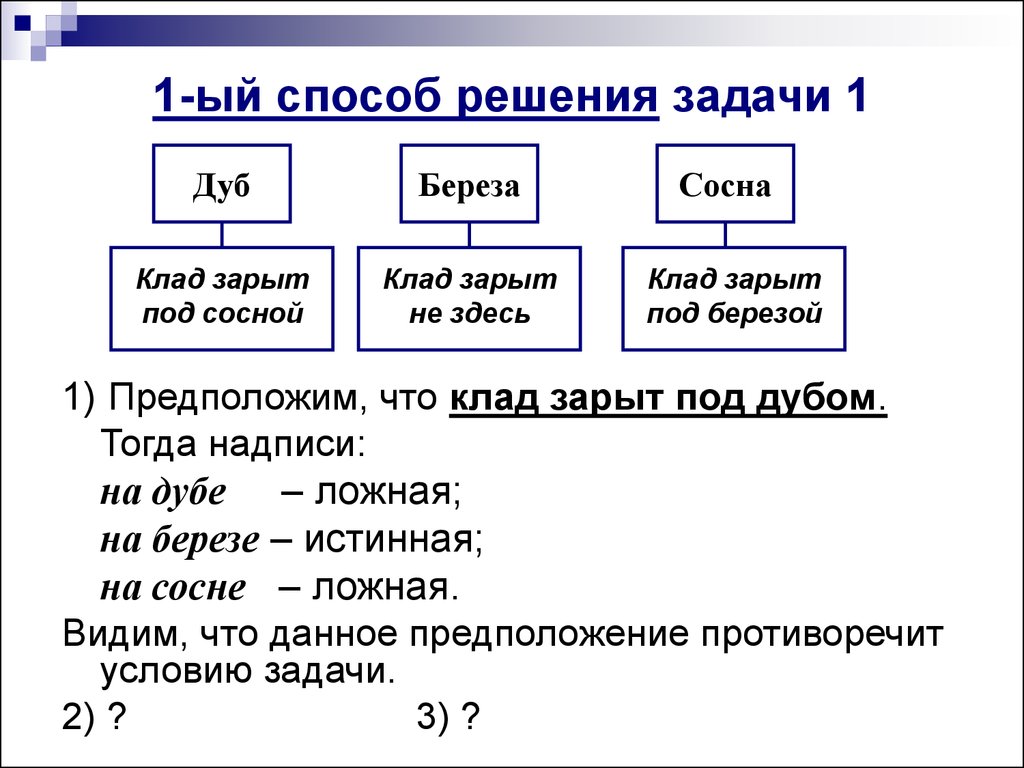
6. 1-ый способ решения задачи 1
ДубБереза
Клад зарыт
под сосной
Клад зарыт
не здесь
Сосна
Клад зарыт
под березой
1) Предположим, что клад зарыт под дубом.
Тогда надписи:
на дубе – ложная;
на березе – истинная;
на сосне – ложная.
Видим, что данное предположение противоречит
условию задачи.
2) ?
3) ?
7. 2-ой способ решения задачи 1
Надписи на березе и сосне противоречатдруг другу, поэтому одна из них истинная, а
другая ложная. Но так как по условию задачи из
трех надписей две должны быть истинными, то
надпись на дубе истинная, и, следовательно,
клад зарыт под сосной.
Задача 2. В лесу проводились соревнования по
бегу. Когда у волка спросили, как
распределились места между победителями, он
ответил, что первое место занял медведь или
лиса, второе место занял заяц, а третье место –
медведь. Но оказалось, что все эти утверждения
ложные. Какое место заняли медведь, лиса и
заяц?
8. Задачи на соответствие между множествами
Задача 3. Три друга – Алеша, Боря и Витяучатся в одном классе. Один из них ездит
домой из школы на автобусе, один на трамвае,
один – на троллейбусе. Однажды после уроков
Алеша пошел проводить своего друга до
остановки автобуса. Когда мимо них проходил
троллейбус, третий друг крикнул из окна:
«Боря, ты забыл в школе тетрадку!» Кто из
друзей на чем ездит домой?
Решение. В задаче рассматривается два
множества: множество учащихся и множество
видов транспорта. Между этими множествами
требуется установить взаимно-однозначное
соответствие. Удобно делать это с помощью
таблицы.
9.
АвтобусТроллейбу
с
Трамвай
Алеша
Боря
Витя
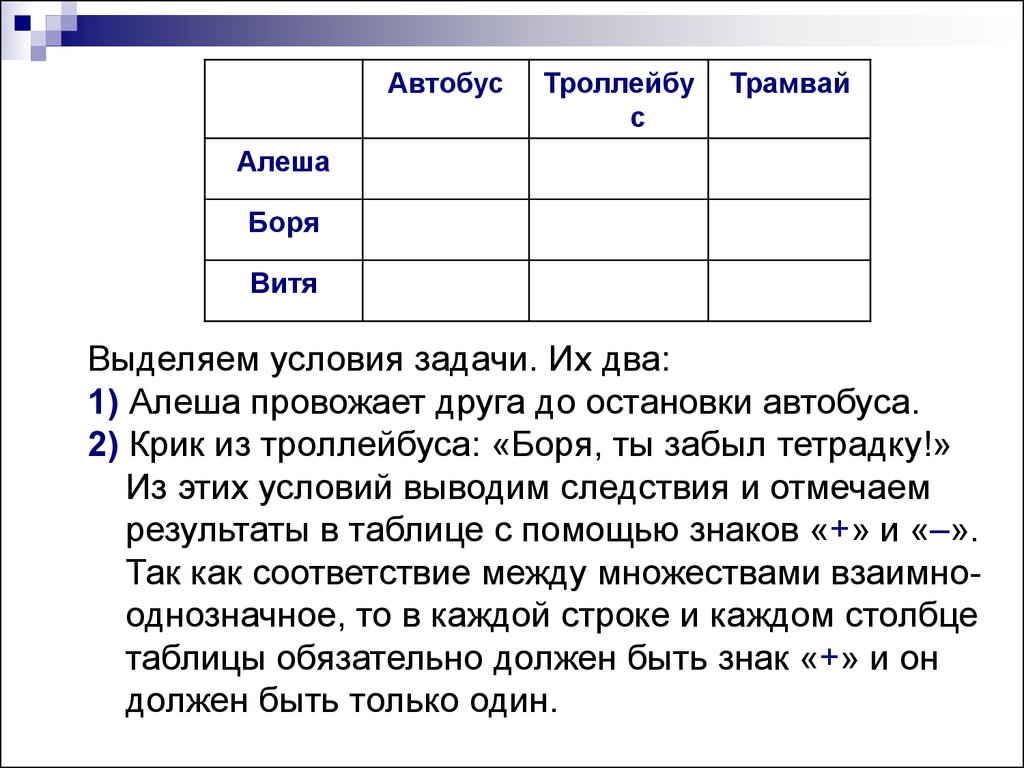
Выделяем условия задачи. Их два:
1) Алеша провожает друга до остановки автобуса.
2) Крик из троллейбуса: «Боря, ты забыл тетрадку!»
Из этих условий выводим следствия и отмечаем
результаты в таблице с помощью знаков «+» и «–».
Так как соответствие между множествами взаимнооднозначное, то в каждой строке и каждом столбце
таблицы обязательно должен быть знак «+» и он
должен быть только один.
10.
Задача 4. В трех мешках находится рис,мука и сахар. На первом мешке написано
«рис», на втором – «мука». На третьем –
«в первом мешке мука». Все надписи
неверные. Что находится в каждом
мешке?
1) Какие множества рассматриваются в
задаче?
2) Какое соответствие установлено между
ними?
3) Каковы условия задачи?
4) Какие следствия можно вывести из этих
условий?
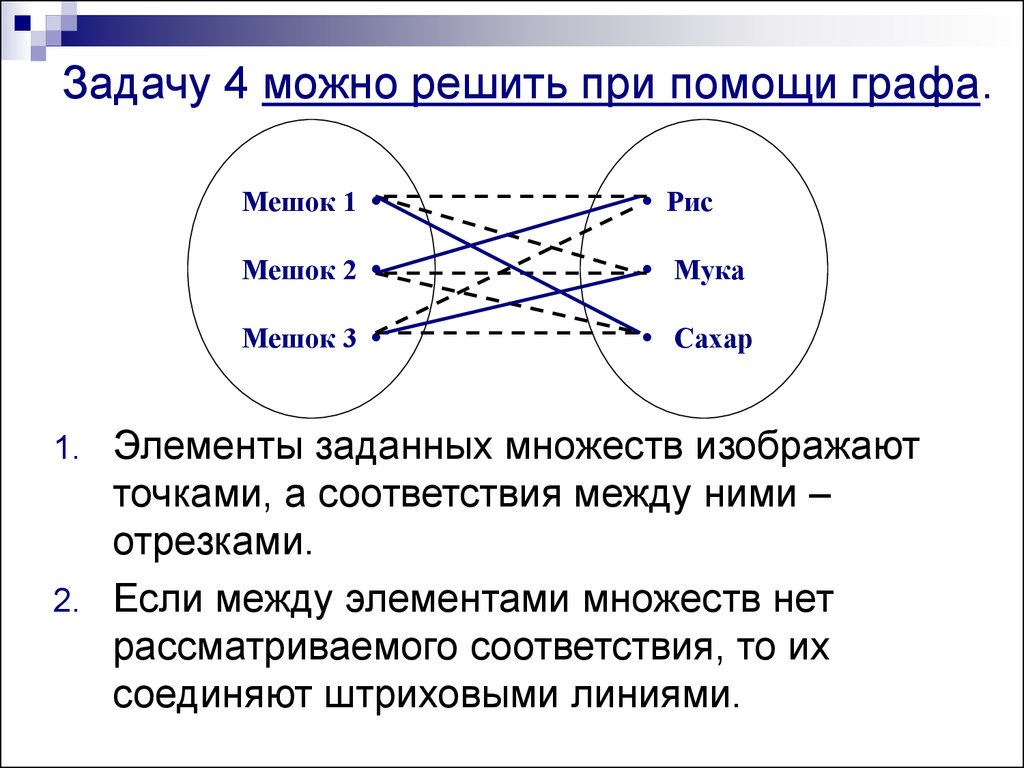
11. Задачу 4 можно решить при помощи графа.
Мешок 1• Рис
Мешок 2
• Мука
Мешок 3
• Сахар
1. Элементы заданных множеств изображают
точками, а соответствия между ними –
отрезками.
2. Если между элементами множеств нет
рассматриваемого соответствия, то их
соединяют штриховыми линиями.
12.
Задача 5. Встретились три подруги: Белова,Розова и Краснова. На одной из них было красное
платье, на другой – розовое, на третьей – белое.
Девочка в белом платье говорит Красновой: «Нам
надо поменяться платьями, а то цвет наших
платьев не соответствует фамилиям». Кто в какое
платье был одет?
Задача 6. Миша, Сережа и Яша участвовали в
шахматном турнире. Один из них учится во 2 «А»,
другой – во 2 «Б», третий – во 2 «В». Первую
партию играли Миша и ученик 2 «А». Вторую –
Сережа с учеником 2 «В», а Миша отдыхал. В
каком классе учится каждый из мальчиков?
13.
Задача 7. Три клоуна - Бим, Бом и Бам вышлина арену в красной, зеленой и синей рубашках.
Их туфли были тех же цветов. У Бима цвета
рубашки и туфель совпадали. У Бома ни туфли,
ни рубашка не были красными. Бам был в
зеленых туфлях, но в рубашке другого цвета.
Как были одеты клоуны?
Задача 8. У трех подружек – Ксюши, Насти и
Оли – новогодние карнавальные костюмы
белого, синего и розового цветов, и шапочки тех
же цветов. У Насти цвет костюма и шапочки
совпал, у Ксюши ни костюм, ни шапочка не были
розового цвета, а Оля была в белой шапочке, но
цвет костюма у нее не был белым. Как были
одеты девочки?
14. Задачи на упорядочивание множеств
Если на множестве М задано бинарноеотношение порядка, то , говорят, что множество
М упорядочено с помощью этого отношения.
Задача 9. Наташа старше Светы. Ира младше
Ани, но старше Наташи. Кто самый старший?
Задача 10. Лягушка встречала гостей. Лиса
пришла раньше медведя, волк – позже зайца,
медведь – раньше зайца, сорока – позже волка.
В каком порядке приходили гости?
Задача 11. В семье четверо детей. Им 5, 8, 13 и
15 лет. Детей зовут Аня, Боря, Вера и Галя.
Сколько лет каждому ребенку, если одна девочка
ходит в детский сад, Аня старше Бори, а сумма
лет Ани и Веры делится на 3?











 pedagogy
pedagogy








