Векторная алгебра

1. Векторная алгебра

Определение вектора, единичного вектора, орта
вектора, коллинеарных / компланарных векторов
Проекция вектора на координатные оси
Линейные операции над векторами
Определение линейно зависимых/независимых
векторов
Теорема о разложении вектора на плоскости и в
пространстве

2. Векторная алгебра

Вектором называется направленный отрезок
Обозначение вектора:
АВ , a
АВ, a
- длина вектора
Вектор, длина которого равна единице
называется единичным вектором

3. Векторная алгебра

Единичный вектор, направление которого
совпадает с направлением вектора a называется
ортом вектора a и обозначается a 0
a a a
0
Три вектора в пространстве называются
комплонарными, если они лежат в одной плоскости
или в параллельных плоскостях
коллинеарных векторов
a // b 0 : a b

4. Векторная алгебра

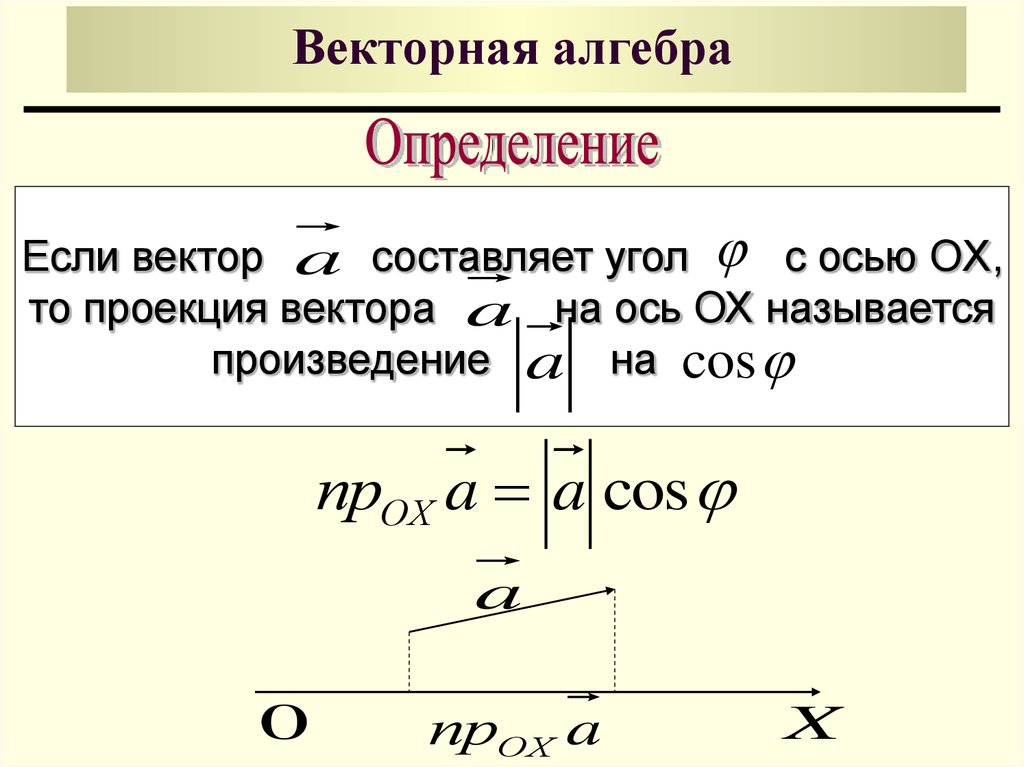
Если вектор a составляет угол с осью OX,
то проекция вектора a на ось ОХ называется
произведение a на cos
прОХ a a cos
a
0
прОХ a
X

5. Векторная алгебра

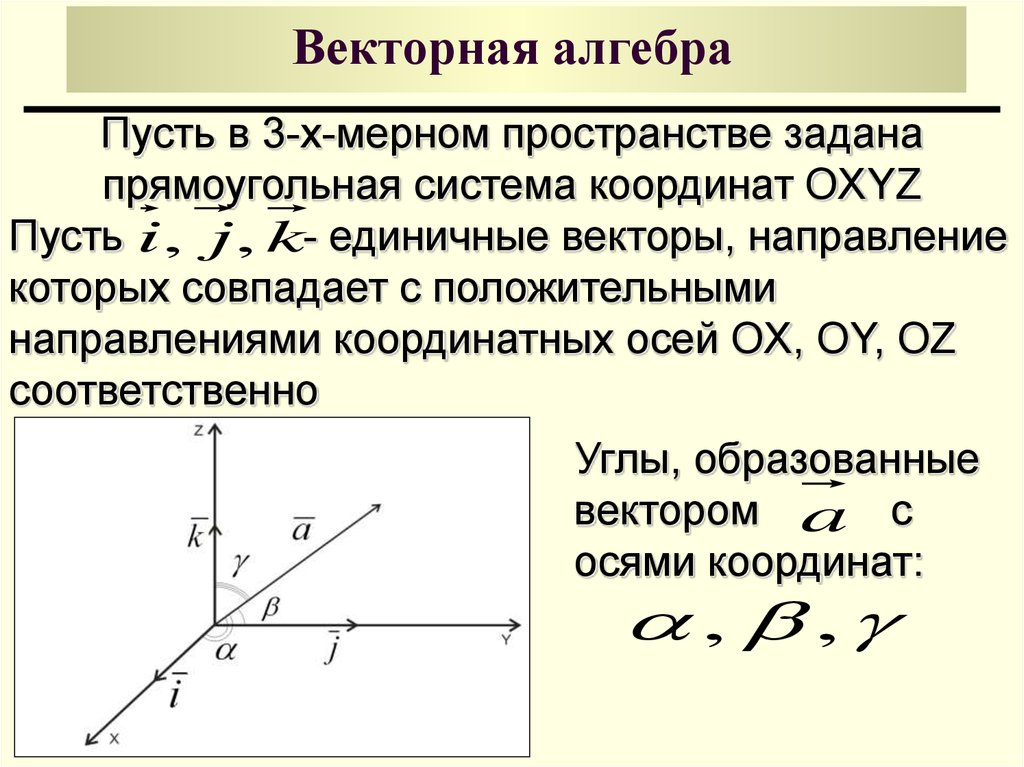
Пусть в 3-х-мерном пространстве задана
прямоугольная система координат OXYZ
Пусть i, j , k- единичные векторы, направление
которых совпадает с положительными
направлениями координатных осей OX, OY, OZ
соответственно
Углы, образованные
вектором a с
осями координат:
, ,

6. Векторная алгебра

Проекция вектора a на оси координат
x a cos y a cos z a cos
Вектор a имеет координаты x, y, z, то есть
a( x, y, z ) в прямоугольной системе
координат ОXYZ или a xi y j z k , где
i, j, k - единичные векторы координатных осей
a x y z - длина вектора a
cos , cos , cos - направляющие косинусы
вектора a : cos 2 cos 2 cos 2 1
2
2
2

7. Векторная алгебра

Действия сложения векторов a b
и
умножения вектора на число a называются
линейными операциями над векторами
Пусть a1 , a2 ,..., ak - векторы, заданные на
плоскости R2 или в пространстве R3
Выражение вида 1 a1 2 a2 ... k ak
k
a ,
i 1
i
i
где i , i 1, k -произвольные действительные числа
называется линейной комбинацией векторов

8. Векторная алгебра

Векторы a1 , a2 ,..., ak называются линейно
зависимыми, если существуют такие
действительные числа i R, i 1, k одновременно
k
не обращающиеся в ноль i 0 , что линейная
i 1
комбинация векторов с этими числами равна
нулевому вектору
1 a1 2 a2 ... k ak 0 (1)
Если равенство (1) выполняется только в случае,
когда 1 2 ... k 0 , то вектора a1 , a2 ,...
..., ak называются линейно независимыми

9. Пример

Рассмотрим на плоскости два неколлинеарных
вектора e1 и e2
Покажем, что эти векторы линейно независимы
(метод от противного)
Предположим, что вектора e1 , e2 линейно
зависимы. По определению линейно зависимых
векторов 1 , 2 R,
2
i 1
i
0 : 1 e1 2 e2 0
1 0 , тогда
2
2
e1
e2 Таким образом, : e1 e2
1
1
Для определенности предположим
e1 // e2 Противоречие! Предположение не верно

10. Пример

Проверим, являются ли линейно зависимыми
вектора
e1 (1, 1,0); e2 (1,2,3); e3 (0,1, 1)
По определению линейно (не)зависимых векторов
1 , 2 , 3 R : 1 e1 2 e2 3 e3 0
Запишем это равенство для координат векторов
1 e1 2 e2 3 e3 0
1 (1, 1,0) 2 (1,2,3) 3 (0,1, 1) (0,0,0)
( 1 2 , 1 2 2 3 ,3 2 3 ) (0,0,0)

11. Пример

1 2 0
1 2 2 3 0
3 2 3 0
Получена система линейных однородных
уравнений относительно неизвестных 1 , 2 , 3.
Если ранг матрицы системы меньше 3, то
система имеет ненулевое решение вектора
e1 , e2 , e3 линейно зависимы
Если ранг равен 3, то система имеет только
тривиальное решение вектора
e , e , e линейно независимы
1
2
3

12. Пример

1
1
0
1
2
1 6 0 r ( A) 3
0
3
1
Вектора e1 , e2 , e3
линейно независимые

13. Векторная алгебра

(о разложении вектора на плоскости)
Пусть e1 , e2 - неколлинеарные векторы на
плоскости, тогда всякий комплонарный им вектор
a можно представить и притом единственным
образом в виде линейной комбинации векторов
e1 и e2 , то есть , R , что
1
2
a 1 e1 2 e2
(2)

14. Векторная алгебра

1) Покажем существование разложения
По условию векторы e1 , e2- неколлинеарные
векторы эти векторы не нулевые.
В случае, если а // e1 R : a e1 ,
тогда разложение (2) справедливо при
1 , 2 0
a 1 e1 2 e2

15. Векторная алгебра

В случае, если а // e2 R : a e2 ,
тогда разложение (2) справедливо при
1 0, 2
a 1 e1 2 e2
Одновременное выполнение
а // e1 , а // e2
не может быть

16. Векторная алгебра

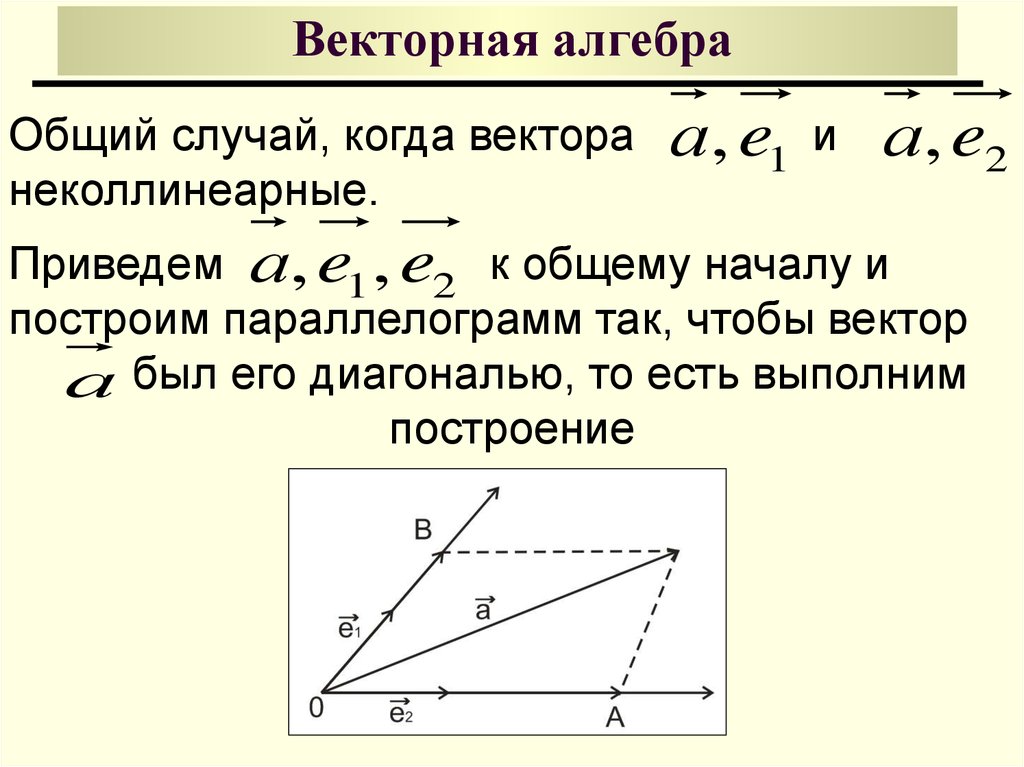
Общий случай, когда вектора
неколлинеарные.
а, e1
и
а, e2
Приведем а, e1 , e2 к общему началу и
построим параллелограмм так, чтобы вектор
а был его диагональю, то есть выполним
построение

17. Векторная алгебра

По правилу сложению векторов
а ОА ОВ
ОА // e2 2 R : ОА 2 e2
ОВ // e1 1 R : ОВ 1 e1
а 1 e1 2 e2
Таким образом, разложение (2) существует

18. Векторная алгебра

1) Докажем единственность разложения (2)
Предположим противное, что разложение (2)
не единственно, то есть
2
1 , 2 R : i 0 a 1 e1 2 e2 (3)
i 1
Вычтем из (2) разложение (3)
0 ( 1 1 )e1 ( 2 2 )e2
2 2
e1
e2 при 1 1 (*)
1 1

19. Векторная алгебра

Таким образом, существует такое число
2 2
1 1
что выполняется (*) вектора e1 , e2 .
коллинеарные, что противоречит условию
теоремы Разложение (2) единственно
Ч.Т.Д.

20. Векторная алгебра

(о разложении вектора в пространстве )
Пусть e1 , e2 , e3- некомпланарные векторы в
пространстве R3, тогда любой вектор a R3
единственным образом разлагается в их
линейную комбинацию, то есть
1 , 2 , 3 R
a 1 e1 2 e2 3 e3
(4)