Классическая задача оценивания

1. Обработка многократно измеренных величин

Избыточные (п–1) измерения:
-контроль;
-неоднозначничть.
Задача оценивания:
-оценка количественной стороны (оценка
математического ожидания);
-оценка качественной стороны (оценка меры
разброса).
Оценки точечные, предпочтительнее интервальные.
Большая зависимость от точности знания закона
распределения погрешностей измерений и числа
измерений.
1

2. Обработка многократно измеренных величин

Основные подходы:
-Классический случай;
-Анализируемый классический случай;
-Не классические методы оценивания:
-обобщенный метод наименьших квадратов
(ОМНК),
-робастные (помехоустойчивые) оценки,
-параметрические неклассические оценки,
- не параметрические неклассические оценки,
-адаптивные (индикаторные) оценки.
2

3. Обработка многократно измеренных величин

Классическая задача оценивания.
Условия.
N ( ; 2 , x ), cov( i , j ) 0, D( i ) 2
Оценка МО – СА, оценка стандарта – СКП (Гаусс,
Бессель). Хьюбер. ЦФ для МНК – квадратичная.
2
v
1
2
(v) Ф(v) x xˆ
min
2
2
Ф Ф dv
1
2 x xˆ ( 1) 0
xˆ
v dxˆ
2
T
T
ˆ
x
n
x
e
x
(
e
e) xˆ 0
T
x
e x xˆ x
n eT e
3

4. Обработка многократно измеренных величин

Оценки качества:
x
0
0
0
k – ч.с.с.
2 k
Если необходимо – устранение смещения:
Для формулы Бесселя
n
e e
T
n 1
n 1 2
kn
2
n
Задачи:
2
1
9
2
kn 1
1
2
4
n
32
n
8n 1
Известно МО – задача эталонирования,
Неизвестно МО – задача оценивания.
4

5. Обработка многократно измеренных величин

Интервальные оценки основных характеристик:
2
1. Cтандарт известен, M ( x ) D( x )
n
x
нормально распределена, вероятность
z
/ n
x
P 1 ( z )
P
n z P ( z )
P zP
x zP
( z )
n
n
P x zP
x zP
( z )
n
n
2. Стандарт не известен – все тоже, но s → , величина
x
t
имеет
распределение
Стьюдента.
s/ n
5

6. Обработка многократно измеренных величин

Построение доверительного интервала для дисперсии 2
по выборочной дисперсии s2, полученной по n
измерениям с НЗР погрешностей.
(n s2) / 2 имеет распределение 2 с k = n –1 степенями
свободы.
2 n m
2
P 1
2 1 q
2
2
n m2
22
2
n m2
12
n 1
n 1
; m
m 1; m 2
m
2
2
2
1
6

7. Обработка многократно измеренных величин

Последовательность обработки – точечная, интервальная
Задача эталонирования:
- определение погрешности;
-выявление мешающих параметров.
2
n
правило 3 – «трех сигм»
Значимая систематика:
n
2
n
n
t 0
t M ( ) t
t
7

8. Обработка многократно измеренных величин

Неравноточный случай обработки.
Вес как степень доверия и мера разности условий
измерений. (Р. Коутс, 1700 г).
p1
Произвол k.
k
2
1
,
k
,
2
1
mi ti m1
pn
k
n2
12
p1 1, p2 2 ,
2
1
p1 1, p2 2 ,
t2
Погрешность единицы веса: p ,
1
2
0
2
1
12
, pn 2
n
1
, pn 2
tn
, pn
2
0
2
n
8

9. Обработка многократно измеренных величин

Вычисление при неизвестном стандарте – искаженность
Пример:
n
1
n
02 n
pn 2
0 1
pn n
k
pn k n
2
0
2
1
Не более 2 значащих цифр: 1.5, 0.27.
9

10. Обработка многократно измеренных величин

Приведение не равноточных измерений к
равноточным – домножить на pi : i i pi
Погрешность через вес:
i
0
pi
0
1
0 qi
pi
10

11. Обработка многократно измеренных величин

Учет разности условий многократно измеренной
величины – среднее весовое.
Получение на основе принципа Лагранжа:
xˆ k1 x1 k2 x2
kn xn
Условие: одинаковы x, одинаковы k
k k
2
xˆ
2
1
2
1
Функция Лагранжа:
2
2
2
2
[k] = 1.
k
2
n
2
n
Ф 2 k 1 min
2
xˆ
11

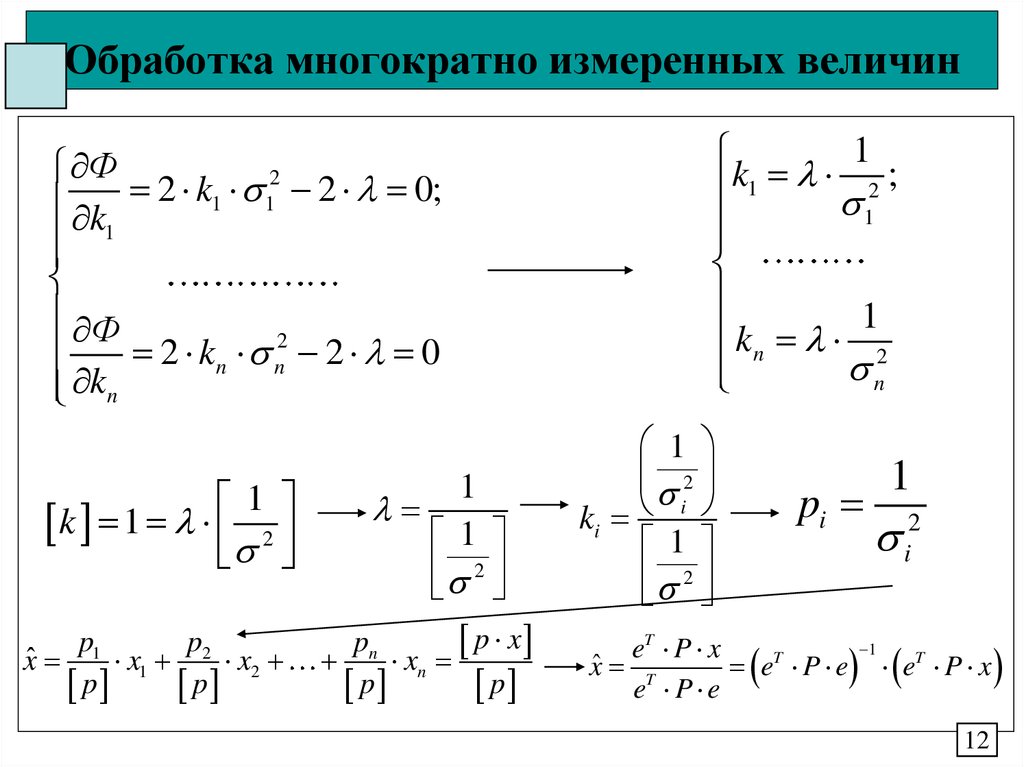
12. Обработка многократно измеренных величин

Ф
2
2
k
1
1 2 0;
k
1
Ф
2 kn n2 2 0
kn
1
k 1 2
p
p
xˆ 1 x1 2 x2
p
p
1
1
2
p x
pn
xn
p
p
1
k1 2 ;
1
1
kn 2
n
1
2
i
ki
1
2
pi
1
i2
1
eT P x
T
xˆ T
e P e eT P x
e P e
12

13. Обработка многократно измеренных величин

Стандартное отклонение (СО) среднего взвешенного
2
p1
2
2
x
1
p
2
2
pn
2
0 p1
n
2
p
p
02 pn
p
2
02 p
p
2
02
p
2
2
2
2
2
0
pi2 i2
i
0
0 pi
2
i
2
0
2
i
M 2 x2 02 eT P e
1
Вес СО ср. взвешенного
→ x
02
[ P]
02
eT P e
x2 1
1
q
; px p
2
0 px
p
x
Те же свойства что и для среднего.
13

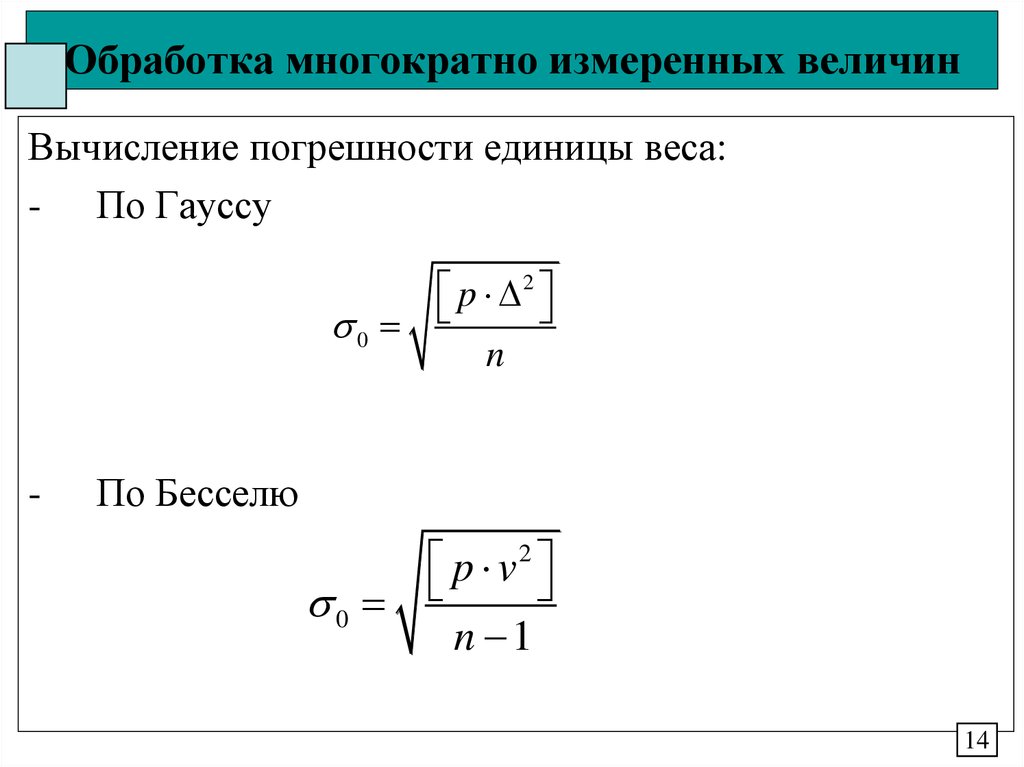
14. Обработка многократно измеренных величин

Вычисление погрешности единицы веса:
- По Гауссу
p 2
0
n
-
По Бесселю
p v 2
0
n 1
14