Обработка многократно измеренных величин. Анализируемый случай

1. Обработка многократно измеренных величин

Анализируемый случай:
1. Закон распределения погрешностей известен, или
неизвестен. Параметрический – непараметрический подход
2. Случайность – отсутствие ярко выраженной
закономерности (для геодезии значимые систематич.
влияния)
3. Однородность – в выборке нет грубых измерений и
все части выборки имеют примерно одинаковую
оценку сдвига и масштаба
4. Независимость – элементы в ряде достаточно
независимы (не коррелированы) между собой
1

2. Обработка многократно измеренных величин

Исследование на нормальность:
1. Предварительные исследования (грубость,
систематика – условия Ляпунова – основн. мат.
условия)
2.
Графические
исследования
–
гистограмма,
вероятностная бумага
3. Приближенные исследования (форма –ассиметрия,
эксцесс – важно для тестирования)
4. Основные критерии на основе проверки гипотез
- критерий 2-Пирсона
- критерий Мизеса–Крамера– Смирнова
2

3. Обработка многократно измеренных величин

Суть критерия Пирсона:
Подсчет разности практических и теоретических
относительный частот, попавших в соответствующий
интервал. Вывод по степени различия
n
2
n
j
n pj
2
t2 ( p, k )
n pj
Суть критерия Мизеса-Крамера-Смирнова:
Подсчет взвешенной разности практических и
теоретических накопленных частот. Вывод по степени
различия
n
1
2
2
n
P( x) W ( x) t2
12n i 1
i 1
3

4. Обработка многократно измеренных величин

Случайность – параметрический подход
Неслучайность -линейный тренд - систематика.
Критерий коэффициентов регрессии. Модель
( ym )i yi vi a i b
Суть – значимость а. Выявление по МНК.
Функция качества (целевая функция) Ф
2
Ф v a i b yi
2
Для нахождения а и b – производные от Ф и к нулю
Ф
2
2
a
i
b
y
i
i
a i b y i 0
a
Ф 2 a i b y 1 i a n b y 0
b
4

5. Обработка многократно измеренных величин

Решить нормальные уравнения относительно а и b
i 2 a i b x i 0 n11a n12b c1
n21a n22b c2
i a n b x 0
В матричном виде
i 2
N k c
i
i
a x i
x
b
n
Лучшая вычислительная схема:
- Составляем матрицу планы А из
коэффициентов при неизвестных а и b
( ym )i yi vi a i 1 b
1 1
2 1
A
...1
n 1
5

6. Обработка многократно измеренных величин

- Составляем матрицу нормальных уравнений N и
вектор с для системы нормальных уравнений N k c
N AT A, c AT y
- Решаем систему обращением матрицы
k N 1 c Q c
- Выявление значимости отличия от нуля а на основе
t- критерия Стьюдента
t
a
a
, tкр. t(1 p )/2, ( n 2)
t tкр.
Если неравенство выполняется – ряд достаточно
случаен.
6

7. Обработка многократно измеренных величин

Случайность – непараметрический подход – мало
измерений, неизвестен закон распределения измерений
Лучший критерий – критерий инверсий. Инверсия ряда
ki - число элементов, которые меньше предыдущего
элемента. Коэффициент критерия – сумма инверсий I
Суть критерия – если все последующие элементы ряда
меньше предыдущего, максимум инверсий – ряд полностью
убывающий и наоборот (0 инверсий). В середине - ряд
случаен – отличие числа инверсий от среднего значения.
Нормировка
| I *|
| I M (I ) |
u1 p
D( I )
2
где М(I) и D(I) – известные мат. ожидание и дисперсия I
7

8. Обработка многократно измеренных величин

Проверка однородности результатов измерений.
Общий случай - сравнение законов распределений
между собой - трудоёмко и часто невозможно. Сводят к
сравнению главных характеристик распределения:
сдвига, масштаба и наличия грубых измерений.
В геодезии для практики проверка однородности:
– проверить ряд на наличие грубых измерений;
– проверить на степень однородности дисперсии частей
ряда измерений (проверка на гетероскедастичность);
– проверить на степень однородности сдвига некоторых
частей ряда измерений (проверка на сдвиг центра).
8

9. Обработка многократно измеренных величин

Параметрические
и
непараметрические
методы.
Основой проверки на грубые измерения нормальная
метка (z-метка) вида
x MO( x)
z ( x)
D( x)
Параметрический критерий Смирнова-Греббса.
Статистика
z
xэкст. х
xmax. x
x xmin.
; zmin.
zmax.
Если z z ,n то с P = 1 – α выброс.
Не устойчив. Лучшие оценки параметров
9

10. Обработка многократно измеренных величин

Критерий Романовского – вычисление
характеристик без подозреваемых:
x( n ) x
tq
m
Неравенство выполняется – крайние грубые.
Критерий Ирвина по соседним в вариационном
ряду:
x(2) x(1)
x( n ) x( n 1)
x x(1)
tq
m
m
Если P - крайние грубые.
m
10

11. Обработка многократно измеренных величин

Непараметрические
методы
оценивания
грубых
погрешностей – устойчивые оценки сдвига и масштаба –
робастные метки.
Основной - критерий Хоглина-Иглевича (у нас правило
Хэмпэла).
В нормальной метке – сдвиг-медиана, масштаб абсолютное медианное отклонение (АМО, англ. MAD)
| x med ( x) |
| x med ( x) |
z R ( x)
med (| x med ( x)) |
АМО( x)
Чтобы определить ЗР метки - переводят АМО(х) в
стандартное отклонение теоретическим коэффициентом
11

12. Обработка многократно измеренных величин

1
c 1
1.4826
F (0.75)
F-1(р) - квантиль нормального закона распределения для
вероятности р. Взяв вероятность 0.999 - предельный
коэффициент 3.5
| x med ( x) | 3.5 1.4826 AMO( x) 5.2 AMO( x)
Устойчив, эффективен. Другой вид через границы
med ( x) 5.2 AMO( x);
med ( x) 5.2 AMO( x)
Все что выходит за границы – грубое. Другие
параметризации характеристик сдвига и масштаба.
12

13. Обработка многократно измеренных величин

Проверка ряда измерений на однородность по главным
характеристикам.
Делят на 2 или более части, используют
параметрические и непараметрические критерии.
В параметрических критериях предполагается НЗР.
Тогда
- для однородности масштаба используют обычный
критерий
отношений
дисперсий
(квадратов
стандартного отклонения ,или F-критерий Фишера,
- для однородности сдвигов (степень отличия центров
распределения) t-критерий Стьюдента.
13

14. Обработка многократно измеренных величин

Неравноточность дисперсий по критерию Фишера
разбиением выборки на 2 подвыборки.
2
Статистика
F 12
2
Если F < Fэт(p, f1, f2) ряд равноточен с вероятностью р.
Неоднородность средних по критерию Стьюдента с тем
же разбиением. Статистика
t
x1 x2
cp
Если t < tэт((p+1)/2, f1) ряд однороден по сдвигу
(положению) с вероятностью р
14

15. Обработка многократно измеренных величин

Непараметрические критерии - закон распределения не
известен, мало измерений.
Основной - критерий ранговой корреляции Спирмена
(гетероскедастичность, неравноточность) элементов
ряда.
Суть критерия – оценка меры рассеивания результатов
измерений в виде остатков от модели (среднего). Есть
выраженная неравноточность – есть постоянное
увеличение (уменьшение) остатков с увеличением
номера измерения i. Степень связанности номера и
остатка - коэффициент корреляции. Нет неравенства
дисперсий измерений – нет корреляции.
15

16. Обработка многократно измеренных величин

Для устойчивости - ранговый коэффициент корреляции
Спирмена.
Реализация критерия:
- получаем оценки рассеивания измерений в виде
остатков vi
vi xi x
- находим ранги ряда остатков
Ранг элемента – его номер в вариационном ряде.
- находим разность рангов di = i – ni и вычисляем
коэффициент ранговой корреляции Спирмена
d 2
ri ,v 1 6
n(n2 1)
.
16

17. Обработка многократно измеренных величин

Окончание критерия - оценка отличия от нуля
коэффициента корреляции между номером элемента в
ряде и остатком. Используют t-критерий Стьюдента:
практика
ri ,v n 2
t
теория (эталон)
1 ri 2,v
tэт((1 + р)/2, п -2 ).
Если t < tэт нулевая гипотеза об отсутствии
гетероскедастичности
(неравенства
дисперсий
измерений в ряде) не отвергается с вероятностью р.
17

18. Обработка многократно измеренных величин

Исследование на независимость элементов в ряде
измерений.
Предполагает отсутствие значимой связи между
элементами ряда с каким либо сдвигом (лагом).
Определяется автокорреляцией лага 1.
Самый известный и используемый тест - критерий
Дарбина-Уотсона.
Суть – установить значимость тесноты связи между
рядом стоящими элементами ряда измерений.
Для вычисления критерия Дарбина-Уотсона выполняют
следующие шаги:
18

19. Обработка многократно измеренных величин

– используя любой способ строят линейную модель для
ряда измерений, чаще вида (yi)мод = a ∙ i + b и находят
величины остатков vi = (yi)мод – yi;
– по величинам остатков vi вычисляют статистику DW
критерия Дарбина-Уотсона как характеристику тесноты
связи между рядом стоящими элементами ряда
n
измерений yi
(v v ) 2
DW
i 2
i 1
i
n
2
v
i
2(1 ri ,i 1 )
i 1
откуда для коэффициента корреляции имеем
rvi ,vi 1
DW
1
2
.
19

20. Обработка многократно измеренных величин

Анализ результатов тестирования (см. формулы выше):
0 DW 4
если rv ,v 0 (отсутствие автокорреляции), то DW 2,
если rv ,v 1 (положительнаяr автокорреляция), то DW 0,
если rv ,v –1 (отрицательная автокорреляция), то DW 4.
Есть таблицы. Вычисления сложны.
i 1
i
i
i
i 1
vi ,vi 1
i 1
Можно считать (но грубо), что если 1.5 < DW < 2.5, то
автокорреляция отсутствует.
20

21. Обработка многократно измеренных величин

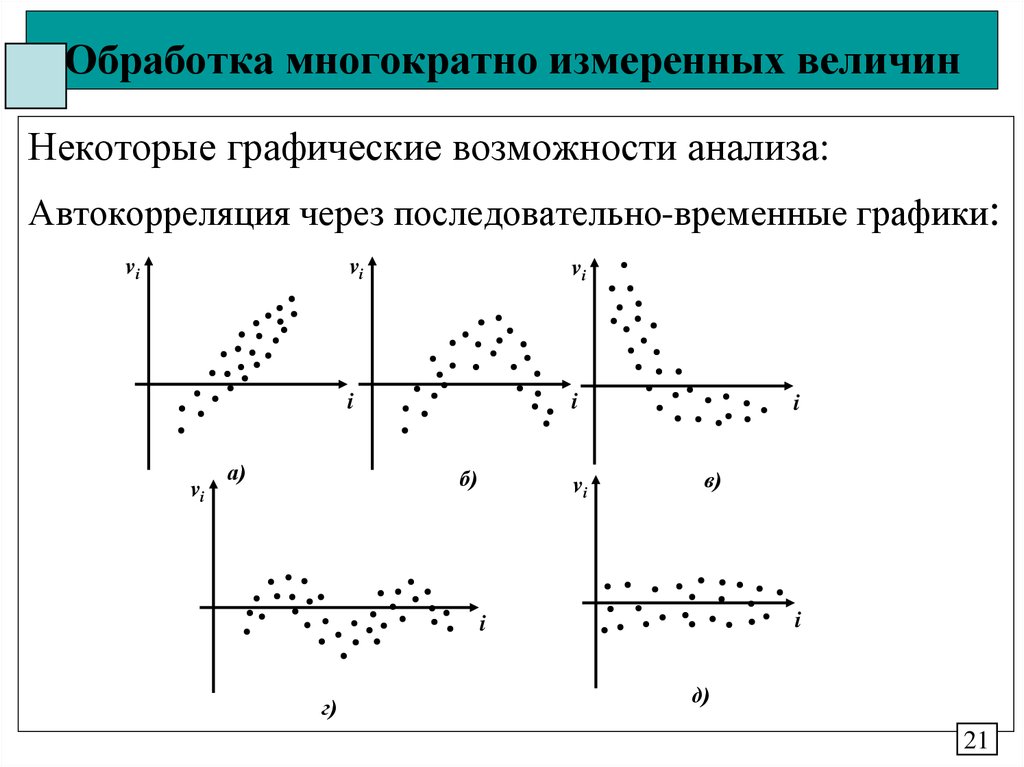
Некоторые графические возможности анализа:
Автокорреляция через последовательно-временные графики:
vi
vi
а)
vi
vi
i
i
б)
vi
i
в)
i
i
г)
д)
21

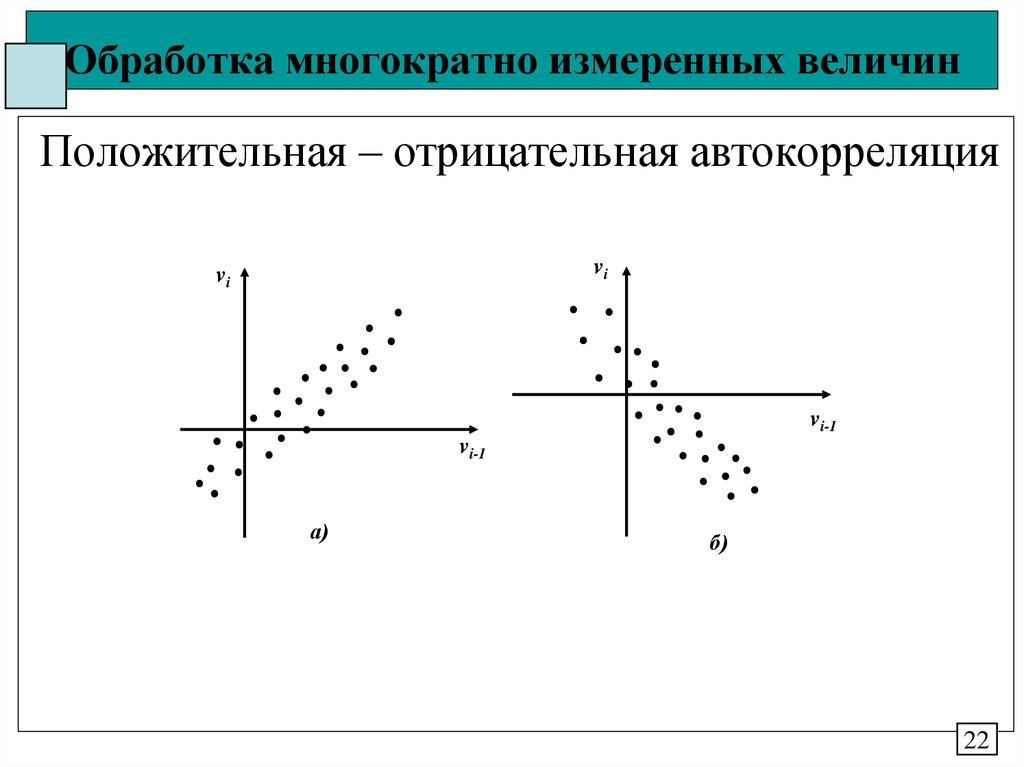
22. Обработка многократно измеренных величин

Положительная – отрицательная автокорреляция
vi
vi
vi-1
vi-1
а)
б)
22

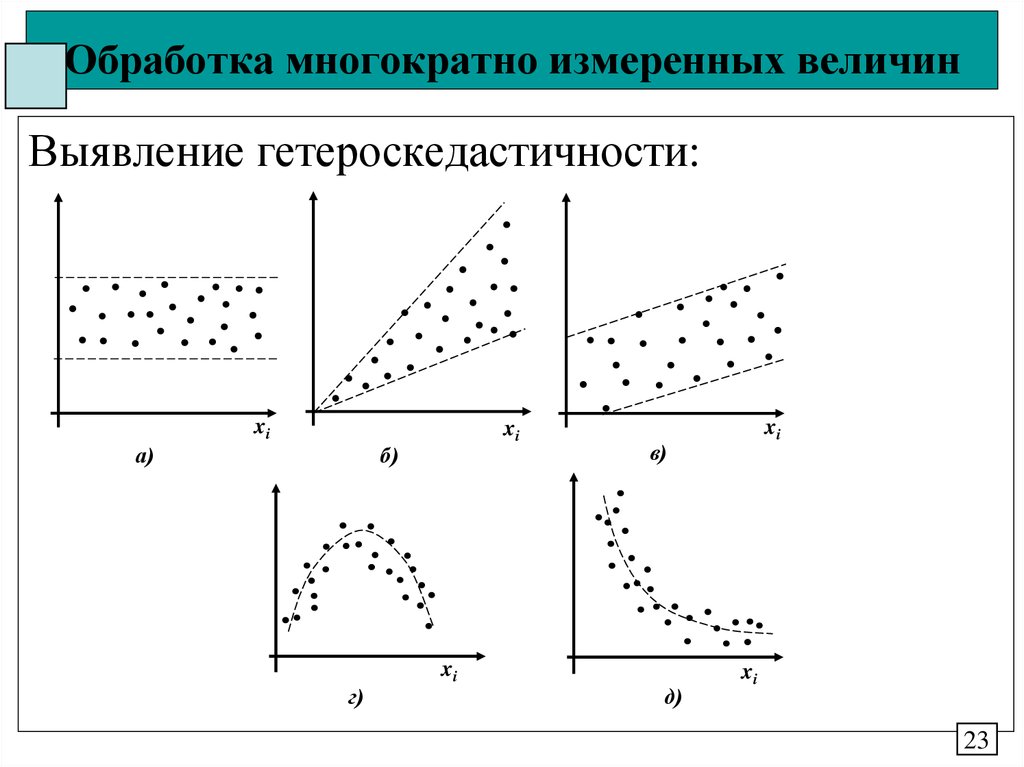
23. Обработка многократно измеренных величин

Выявление гетероскедастичности:
xi
а)
xi
б)
г)
xi
xi
в)
д)
xi
23