Модели межотраслевого баланса. (Лекция 2)

1. Лекция 2. Модели межотраслевого баланса

Содержание лекции:
1.
2.
3.
Схема межотраслевого баланса по В. Леонтьеву
Анализ экономических показателей при помощи
межотраслевого баланса
Теорема о балансовой системе
Модели межотраслевого баланса
(с) Н.М. Светлов, 2007
1/11

2. Литература

Экономико-математические методы и прикладные
модели: Учеб. пособие для вузов / Под ред. В.В.
Федосеева. — 2-е изд. М.: ЮНИТИ-ДАНА, 2005. —
глава 6.
Коссов В.В. Межотраслевые модели (теория и
практика использования). М.: Экономика, 1973.
Светлов Н.М. На пути к новой концепции
стоимости. М.: Изд-во МСХА, 2002.
Модели межотраслевого баланса
(с) Н.М. Светлов, 2007
2/11

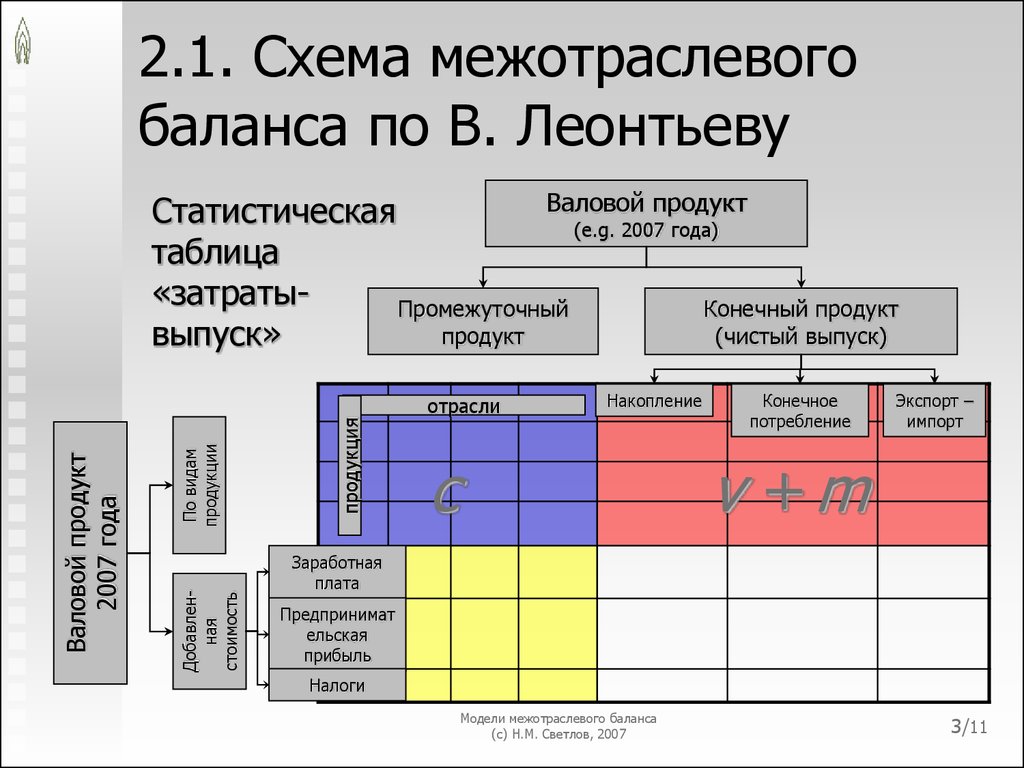
3. 2.1. Схема межотраслевого баланса по В. Леонтьеву

продукция
По видам
продукции
Добавленная
стоимость
Валовой продукт
2007 года
Валовой продукт
Статистическая
(e.g. 2007 года)
таблица
«затратыПромежуточный
Конечный продукт
продукт
(чистый выпуск)
выпуск»
отрасли
Накопление
c
Конечное
потребление
Экспорт –
импорт
v +m
Заработная
плата
Предпринимат
ельская
прибыль
Налоги
Модели межотраслевого баланса
(с) Н.М. Светлов, 2007
3/11

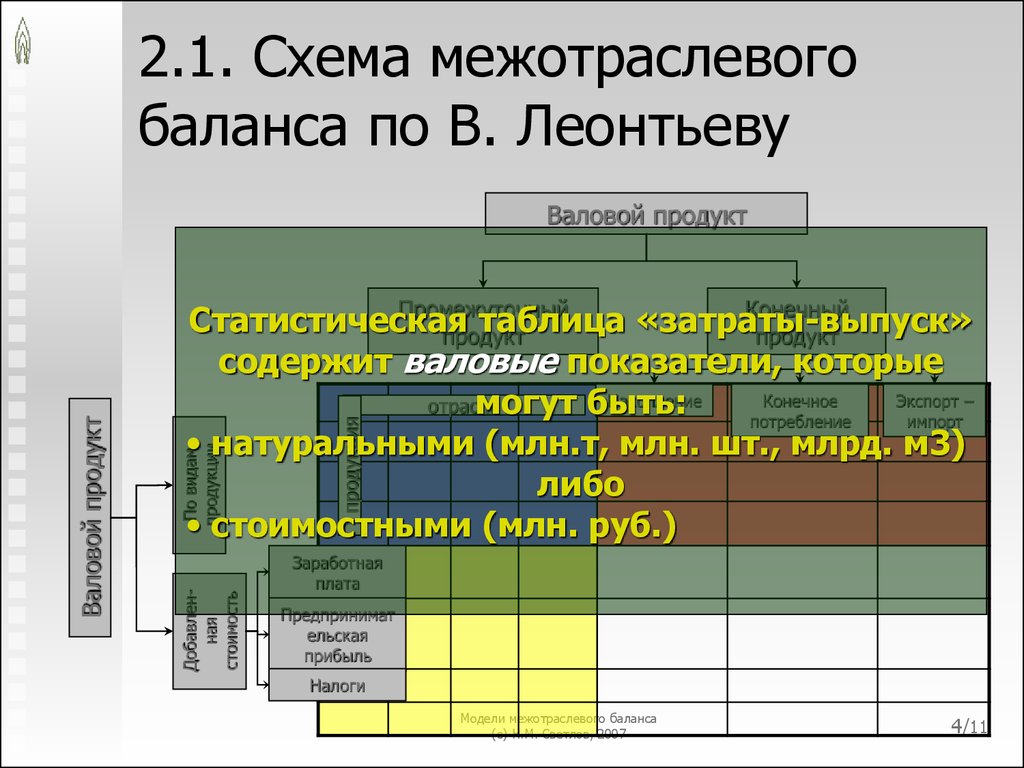
4. 2.1. Схема межотраслевого баланса по В. Леонтьеву

продукция
По видам
продукции
Промежуточный
Конечный
Статистическая
таблица
«затраты-выпуск»
продукт
продукт
содержит валовые показатели, которые
Накопление
Конечное
Экспорт –
отрасли
могут быть:
потребление
импорт
• натуральными (млн.т, млн. шт., млрд. м3)
либо
• стоимостными (млн. руб.)
Добавленная
стоимость
Валовой продукт
Валовой продукт
Заработная
плата
Предпринимат
ельская
прибыль
Налоги
Модели межотраслевого баланса
(с) Н.М. Светлов, 2007
4/11

5. 2.1.

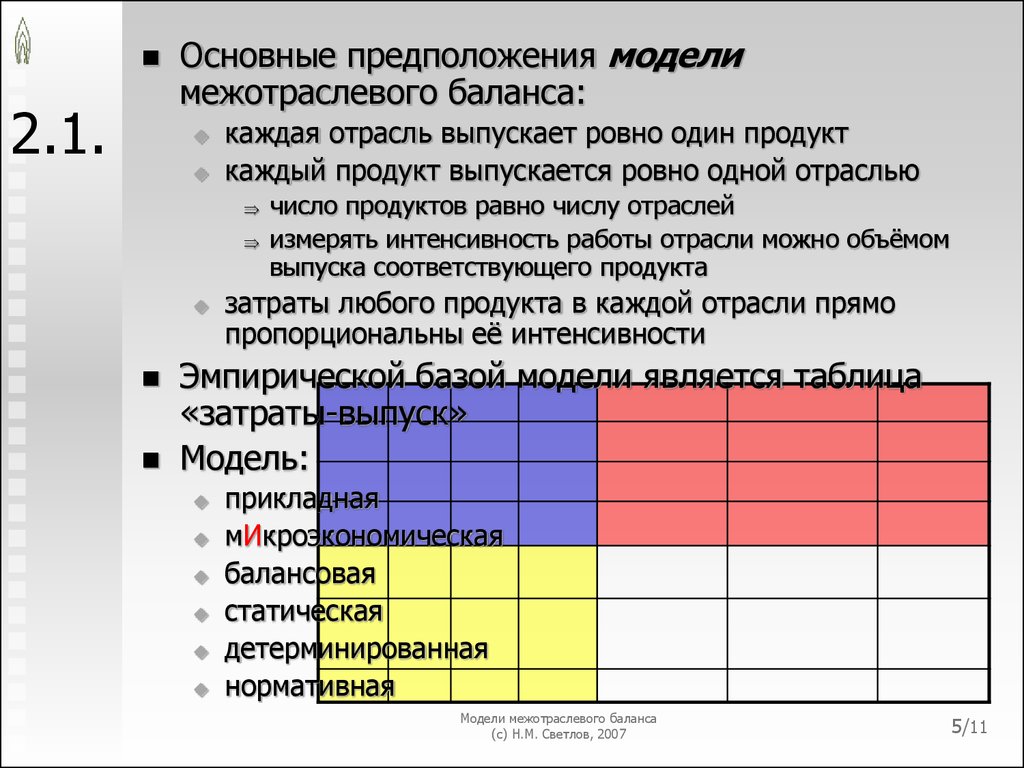
Основные предположения модели
межотраслевого баланса:
каждая отрасль выпускает ровно один продукт
каждый продукт выпускается ровно одной отраслью
число продуктов равно числу отраслей
измерять интенсивность работы отрасли можно объёмом
выпуска соответствующего продукта
затраты любого продукта в каждой отрасли прямо
пропорциональны её интенсивности
Эмпирической базой модели является таблица
«затраты-выпуск»
Модель:
прикладная
мИкроэкономическая
балансовая
статическая
детерминированная
нормативная
Модели межотраслевого баланса
(с) Н.М. Светлов, 2007
5/11

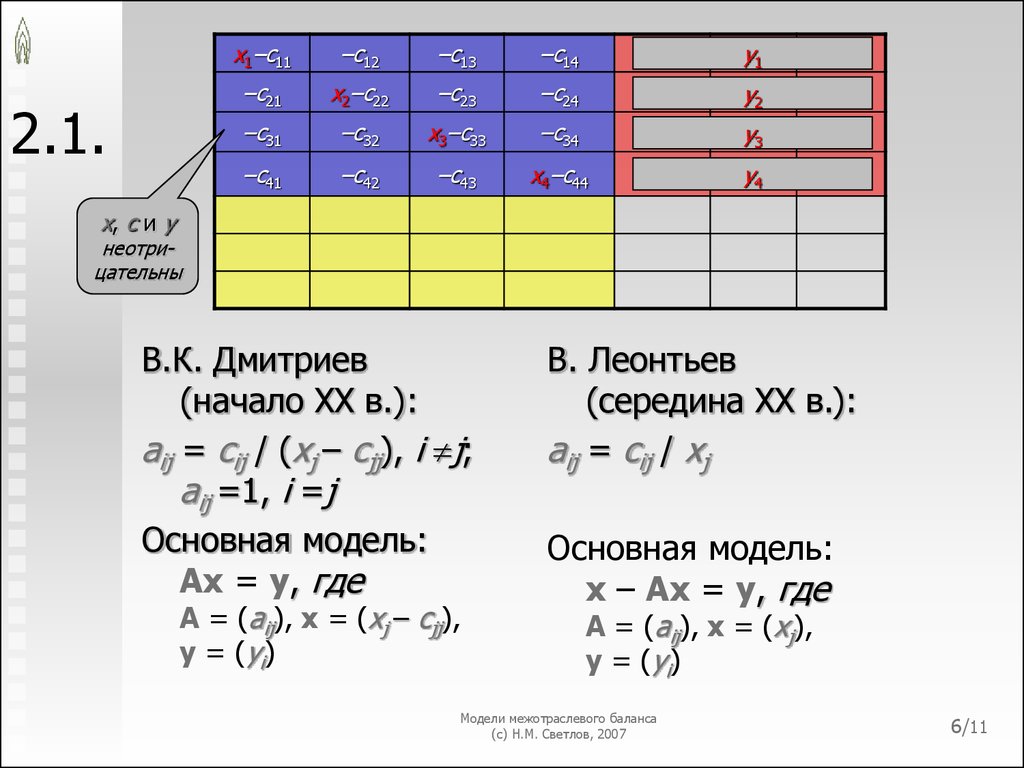
6. 2.1.

x1–c11
–c12
–c13
–c14
y1
–c21
x2–c22
–c23
–c24
y2
–c31
–c32
x3–c33
–c34
y3
–c41
–c42
–c43
x4–c44
y4
x, c и y
неотрицательны
В.К. Дмитриев
(начало XX в.):
aij = cij / (xj – cjj), i j;
aij =1, i =j
Основная модель:
Ax = y, где
A = (aij), x = (xj – cjj),
y = (yi)
В. Леонтьев
(середина XX в.):
aij = cij / xj
Основная модель:
x – Ax = y, где
A = (aij), x = (xj),
y = (yi)
Модели межотраслевого баланса
(с) Н.М. Светлов, 2007
6/11

7. 2.2. Анализ экономических показателей при помощи межотраслевого баланса

x – Ax = y
(I – A)x = y, где
I = (iab):
iab = 0, если a b;
iab = 1, если a = b
–1
Пусть B = (I – A)
Тогда
(I – A)Bx = By , то
есть x = By
Чтобы определить,
каковы должны быть
производственные
мощности отраслей
экономики для
производства
конечного продукта в
размере y, достаточно
умножить его (слева)
на матрицу B,
называемую матрицей
полных затрат.
Модели межотраслевого баланса
(с) Н.М. Светлов, 2007
7/11

8. 2.2.

Пусть p – вектор цен
продукции каждой
отрасли, c – вектор
добавленной
стоимости в единице
продукции каждой
отрасли. Тогда
p – pA = c
p(I – A) = c
Отсюда
p(I – A)B = cB , то есть
p = cB
Чтобы определить,
каковы должны быть
цены для создания
добавленной
стоимости в размере
c, достаточно
умножить c (справа)
на матрицу B.
Модели межотраслевого баланса
(с) Н.М. Светлов, 2007
8/11

9. 2.2.

Рассмотрим компоненты матрицы B = (bji).
Величина bji показывает, на сколько единиц нужно
увеличить объём производства в отрасли j, чтобы
увеличить чистый выпуск блага i на единицу.
Она отражает полные затраты продукции отрасли j на
производство всех других видов продукции,
необходимых для единичного выпуска блага i, во
всех производственных циклах:
Можно доказать, что I + A + A2 + A3 + … = B (при
стандартных условиях модели межотраслевого баланса и
неотрицательности элементов главной диагонали матрицы
(I – A)).
Её единица измерения – единиц блага j на единицу
блага i.
Модели межотраслевого баланса
(с) Н.М. Светлов, 2007
9/11

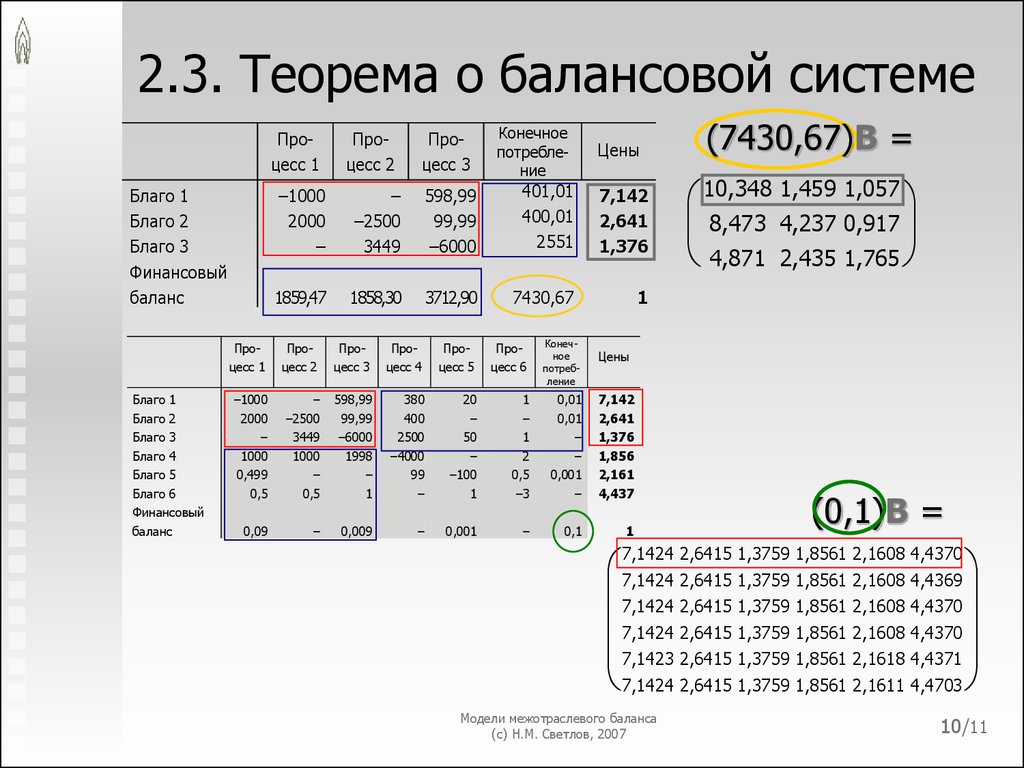
10. 2.3. Теорема о балансовой системе

Про-
Про-
Про-
цесс 1
цесс 2
цесс 3
7,142
–6000
2551
1,376
3712,90
7430,67
–1000
–
598,99
Благо 2
2000
–2500
99,99
–
3449
1859,47
1858,30
Процесс 1
Цены
401,01
400,01
Благо 1
Благо 3
Финансовый
баланс
Конечное
потребление
Процесс 2
Процесс 3
Процесс 4
Процесс 5
Процесс 6
Конечное
потребление
2,641
10,348 1,459 1,057
8,473 4,237 0,917
4,871 2,435 1,765
1
Цены
Благо 1
–1000
–
598,99
380
20
1
0,01
7,142
Благо 2
Благо 3
Благо 4
Благо 5
Благо 6
Финансовый
2000
–
1000
0,499
0,5
–2500
3449
1000
–
0,5
99,99
–6000
1998
–
1
400
2500
–4000
99
–
–
50
–
–100
1
–
1
2
0,5
–3
0,01
–
–
0,001
–
2,641
1,376
1,856
2,161
4,437
0,09
–
0,009
–
0,001
–
0,1
1
баланс
(7430,67)B =
(0,1)B =
7,1424 2,6415 1,3759 1,8561 2,1608 4,4370
7,1424 2,6415 1,3759 1,8561 2,1608 4,4369
7,1424 2,6415 1,3759 1,8561 2,1608 4,4370
7,1424 2,6415 1,3759 1,8561 2,1608 4,4370
7,1423 2,6415 1,3759 1,8561 2,1618 4,4371
7,1424 2,6415 1,3759 1,8561 2,1611 4,4703
Модели межотраслевого баланса
(с) Н.М. Светлов, 2007
10/11

11. 2.3.

Теорема.
2.3.
Пусть V — произвольная невырожденная матрица порядка
–1
n n, wij — (i, j)-компонент матрицы W = V , wj = (wij), матрица Y порядка n n
имеет ранг n – 1, вектор p* — любое нетривиальное решение системы уравнений
Yp = 0, pi — i-й компонент вектора p. Тогда если j-я строка матрицы Y представляет
w j cp *.
собой линейную комбинацию каких-либо других строк Y, то Vlim
Y
Теорема о балансовой системе утверждает:
чем меньшую часть ВВП мы рассматриваем в качестве
конечного результата функционирования экономики,
тем точнее соответствие между коэффициентами любой
строки матрицы B и стоимостными (ценовыми)
пропорциями, обеспечивающими необходимый и
достаточный объём финансовых ресурсов каждой
отрасли.
Следовательно, полные затраты любого блага на производство
любого другого блага объясняют пропорции цен,
складывающихся в экономике, если в качестве конечного
продукта признаётся очень малая часть ВВП.
Модели межотраслевого баланса
(с) Н.М. Светлов, 2007
11/11