Балансовые модели

1. Раздел № 4 Сетевые, имитационные и балансовые модели

Тема №3
Балансовые модели

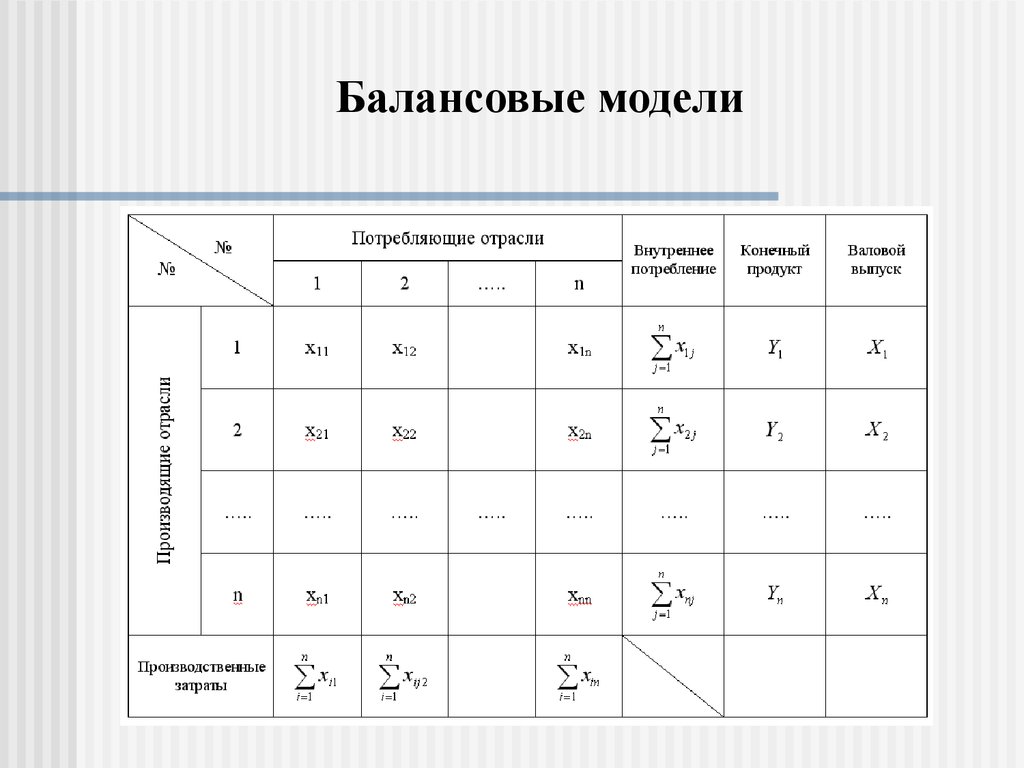
2. Балансовые модели

экономикоматематическая модель, построенная в виде
системы
уравнений,
представляющих
балансовые соотношения и характеризующих
равенство произведенного (поступившего) и
потребленного (распределенного) продукта.
БАЛАНСОВАЯ
МОДЕЛЬ
-

3. Балансовые модели

Рассматривается
экономическая
система,
состоящая
из
n
взаимосвязанных
отраслей
производства. Продукция каждой отрасли частично
идет на внешнее потребление (конечный продукт), а
частично используется в других отраслях, в том числе
и в данной. Потребление этой части продукции
называют производственным потреблением. Поэтому
каждая из рассматриваемых отраслей выступает и как
производитель продукции и как ее потребитель.
Для упрощения будем считать, что баланс
составляется не в натуральном, а в стоимостном
разрезе

4. Балансовые модели

5. Балансовые модели

Обозначим через Xi валовой выпуск продукции iой отрасли за планируемый период, а через Yi –
конечный продукт i-ой отрасли, идущий на внешнее
для рассматриваемой системы потребление.
Таким образом, разность Xi - Yi составляет часть
продукции i-ой отрасли, предназначенную для
внутрипроизводственного потребления.
Обозначим через xij
часть продукции i-ой
отрасли, которая потребляется j-ой отраслью, для
обеспечения выпуска ее продукции в размере Xj .

6. Балансовые модели

Величины, расположенные в строках таблицы
связаны следующими балансовыми равенствами:
X 1 ( x11 x12 ... x1n ) Y1
X 2 ( x21 x22 ... x2 n ) Y2
.............................................
X n ( xn1 xn 2 ... xnn ) Yn

7. Балансовые модели

Одна из задач балансовых исследований
заключается в том, чтобы на базе данных об
исполнение баланса за предшествующий период
определить исходные данные на планируемый
период.
Будем снабжать штрихом данные,
относящиеся к истекшему периоду, а теми же
буквами, но без штриха – аналогичные данные,
связанные с планируемым периодом. Балансовые
равенства должны выполняться как в истекшем, так
и в планируемом периоде.

8. Балансовые модели

Совокупность значений Y1, Y2, …, Yn, характеризующих выпуск конечного продукта, называется
ассортиментным вектором:
Y (Y1 , Y2 ,..., Yn )
Совокупность значений X1, X2, …, Xn, определяющих валовой выпуск всех отраслей – векторпланом:
X ( X 1 , X 2 ,..., X n )

9. Балансовые модели

Зависимость между двумя этими векторами
определяется балансовыми равенствами. Однако они
не дают возможности определить по заданным
значениям, например, вектор Y необходимый для его
обеспечения вектор-плана X, т.к. кроме искомых
неизвестных Xj, содержат n2 неизвестных xij, которые в
свою очередь зависят от Xj.
Преобразуем эти равенства, рассчитав величины aik
из соотношений:
aij
xij
Xj

10. Балансовые модели

Величины aij называются коэффициентами прямых
затрат или технологическими коэффициентами. Они
определяют затраты продукции i-ой отрасли,
используемые j-ой отраслью на изготовление единицы
ее продукции. С некоторым приближением можно
полагать, что коэффициенты aij постоянны в
некотором промежутке времени, охватывающим как
истекший, так и планируемый период, т.е.:
xij
xij
aij const
X j X j

11. Балансовые модели

Поскольку,
xij
, то xij aij * X j
aij
Xj
То есть затраты i-ой отрасли в j-ую отрасль
пропорциональны ее валовому выпуску, или, другими
словами, зависят линейно от валового выпуска Xj.
Поэтому последнее равенство называют условием
линейности прямых затрат.

12. Балансовые модели

Рассчитав коэффициенты прямых затрат
используя
данные
об
исполнении
баланса
предшествующий период, получим матрицу:
a11
a12
aij,
за
... a1n
a21 a22 ... a2 n
A
... ... ... ...
an1 an 2 ... ann
Эту матрицу называют матрицей затрат. В этой
матрице отражены все внутренние взаимосвязи между
производством и потреблением. Все элементы этой
матрицы неотрицательны.

13. Балансовые модели

Подставив значения xij = aij * Xj во все уравнения
системы, получим линейную балансовую модель,
характеризующую баланс затрат - выпуска продукции:
X 1 (a11 X 1 a12 X 2 ... a1n X n ) Y1
X 2 (a21 X 2 a22 X 2 ... a2 n X n ) Y2
............................................................
X n (an1 X n an 2 X n ... ann X n ) Yn
Теперь, исходя из заданного ассортиментного вектора
можно определить необходимый для его производства
вектор-план.

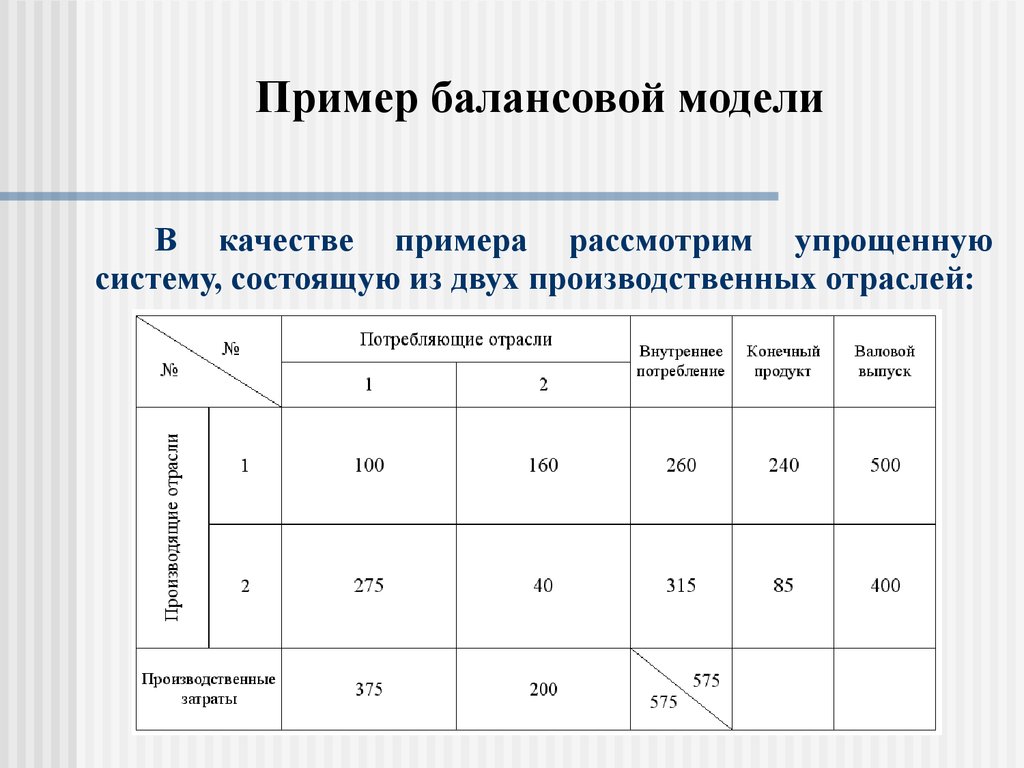
14. Пример балансовой модели

В качестве примера рассмотрим упрощенную
систему, состоящую из двух производственных отраслей:

15. Пример балансовой модели

Пусть исполнение баланса за предшествующий
период характеризуется данными, помещенными в
приведенной выше таблице
Тогда коэффициенты прямых затрат равны:
100
160
275
40
a11
0.2; a12
; a 21
; a 22
500
400
500
400
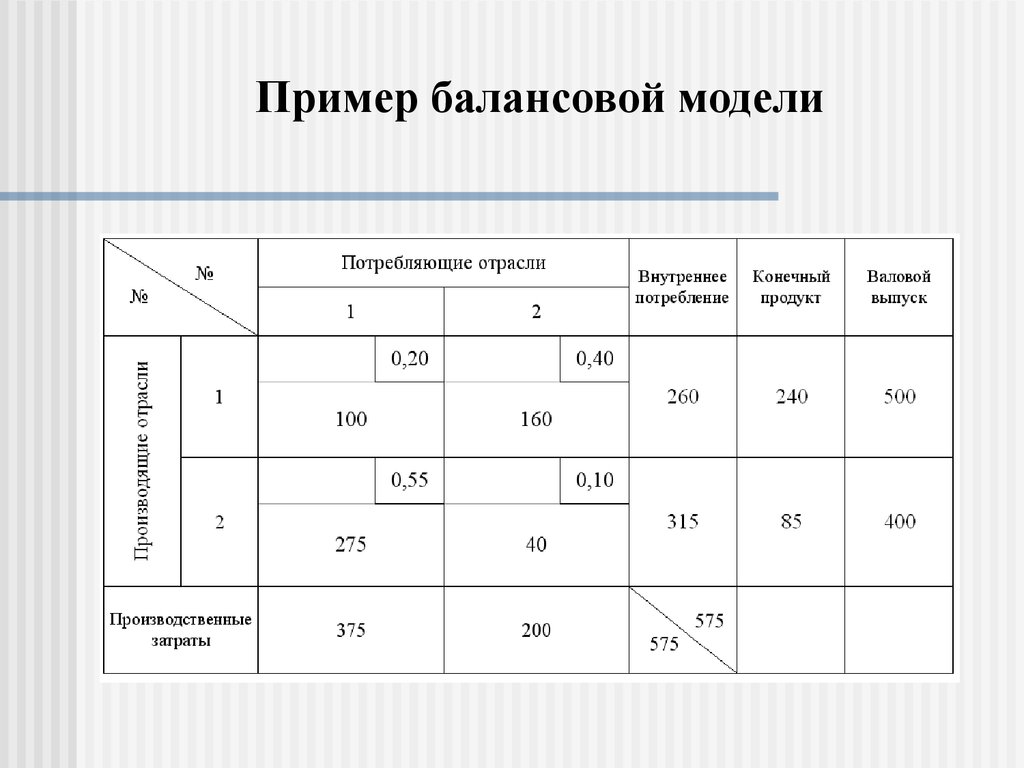
Эти
коэффициенты
записываются
соответствующих клеток исходной таблицы.
в
углах

16. Пример балансовой модели

17. Пример балансовой модели

Балансовая модель, соответствующая исходным
данным примера:
Х1 - 0.20Х1 - 0.40Х2 = Y1
X2 - 0.55X1 - 0.10X2 = Y2
Эта система двух уравнений может быть
использована для определения X1 и X2 при заданных
значениях Y1 и Y2, для определения влияния на валовой
выпуск каких-либо изменений в ассортименте конечного
продукта и т.д.
Так, например, задавшись Y1 =240 и Y2 =85,
получим X1=500 и X2 =400, задавшись Y1 =480 и Y2 =170,
получим X1=1000 и X2 =800 и т.д.