Механическое движение

1. Механика для описания движения тел в зависимости от условий конкретных задач использует разные физические модели.

Механическое движение
Механика для описания движения тел в зависимости от условий
конкретных задач использует разные физические модели.
Материальная точка (МТ)
- тело, размерами которого
можно пренебречь по
сравнению с расстояниями
до других тел.
Абсолютно твердое тело (АТТ) –
тело, деформациями
которого в условиях данной
задачи можно пренебречь.
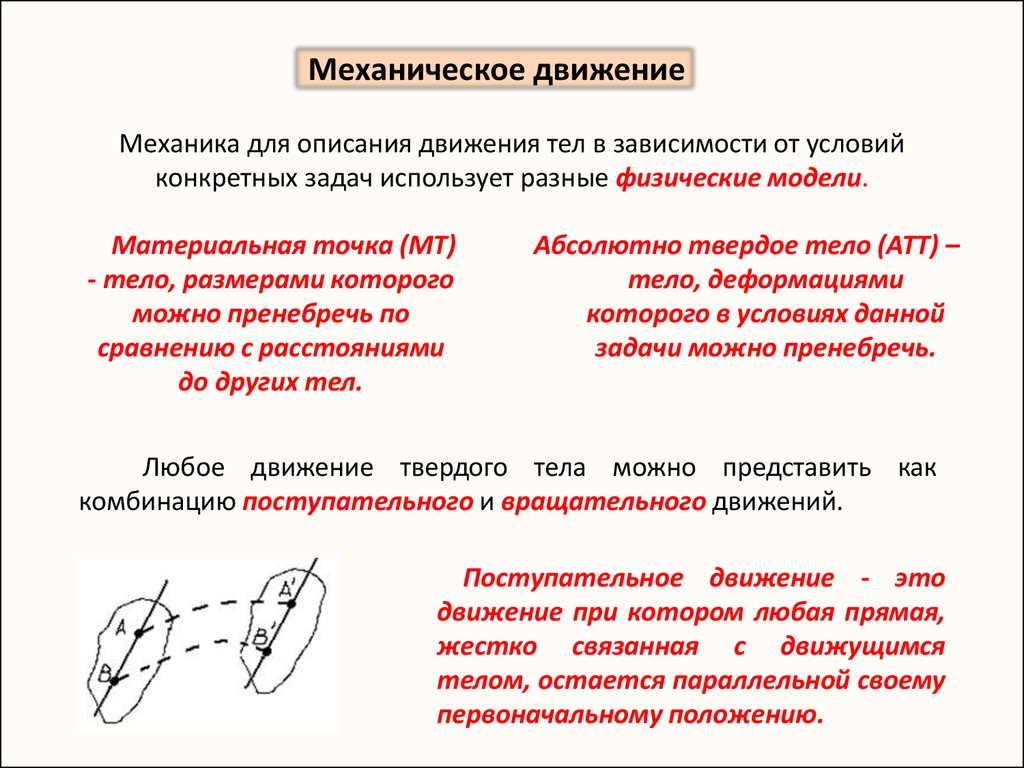
Любое движение твердого тела можно представить как
комбинацию поступательного и вращательного движений.
Поступательное движение - это
движение при котором любая прямая,
жестко связанная с движущимся
телом, остается параллельной своему
первоначальному положению.

2.

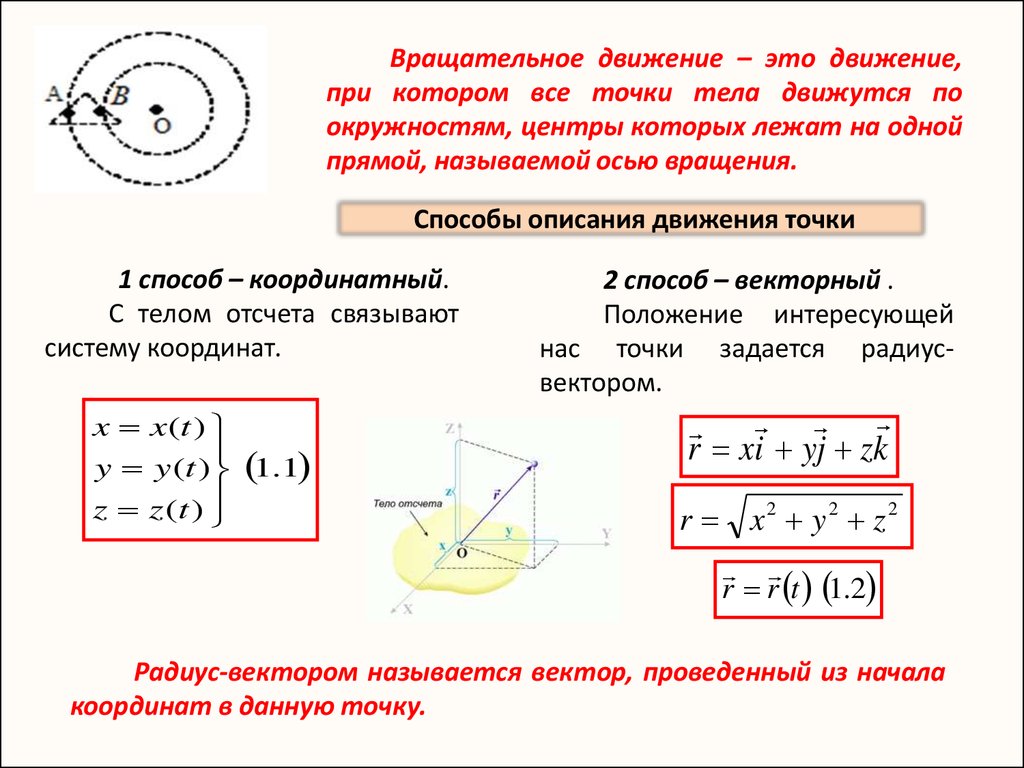
Вращательное движение – это движение,
при котором все точки тела движутся по
окружностям, центры которых лежат на одной
прямой, называемой осью вращения.
Способы описания движения точки
1 способ – координатный.
С телом отсчета связывают
систему координат.
x x(t )
y y (t ) 1.1
z z (t )
2 способ – векторный .
Положение интересующей
нас точки задается радиусвектором.
r xi yj zk
r x2 y2 z 2
r r t 1.2
Радиус-вектором называется вектор, проведенный из начала
координат в данную точку.

3.

Основные характеристики механического движения
1. Длина пути или путь - ∆S.
Длина участка траектории, пройденного материальной точкой
называется длинной пути.
Си: [∆S]=[м]
2. Перемещение – вектор, проведенный из начального положения
движущейся точки в положение ее в данный момент времени.
Си : r м
3. Скорость.
Характеризует быстроту движения материальной точки по
траектории, а так же направление, в котором точка движется в
данный момент времени.
В зависимости от скорости движение может быть равномерным и
неравномерным.

4.

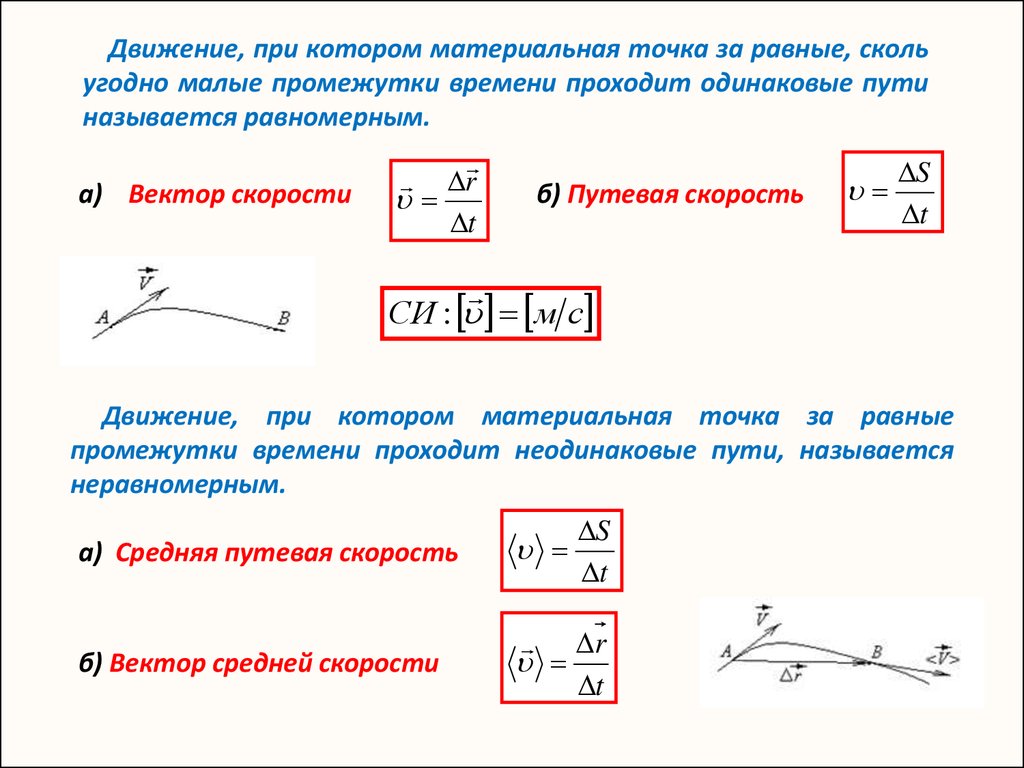
Движение, при котором материальная точка за равные, сколь
угодно малые промежутки времени проходит одинаковые пути
называется равномерным.
а) Вектор скорости
r
t
б) Путевая скорость
S
t
СИ : м с
Движение, при котором материальная точка за равные
промежутки времени проходит неодинаковые пути, называется
неравномерным.
а) Средняя путевая скорость
S
t
б) Вектор средней скорости
r
t

5.

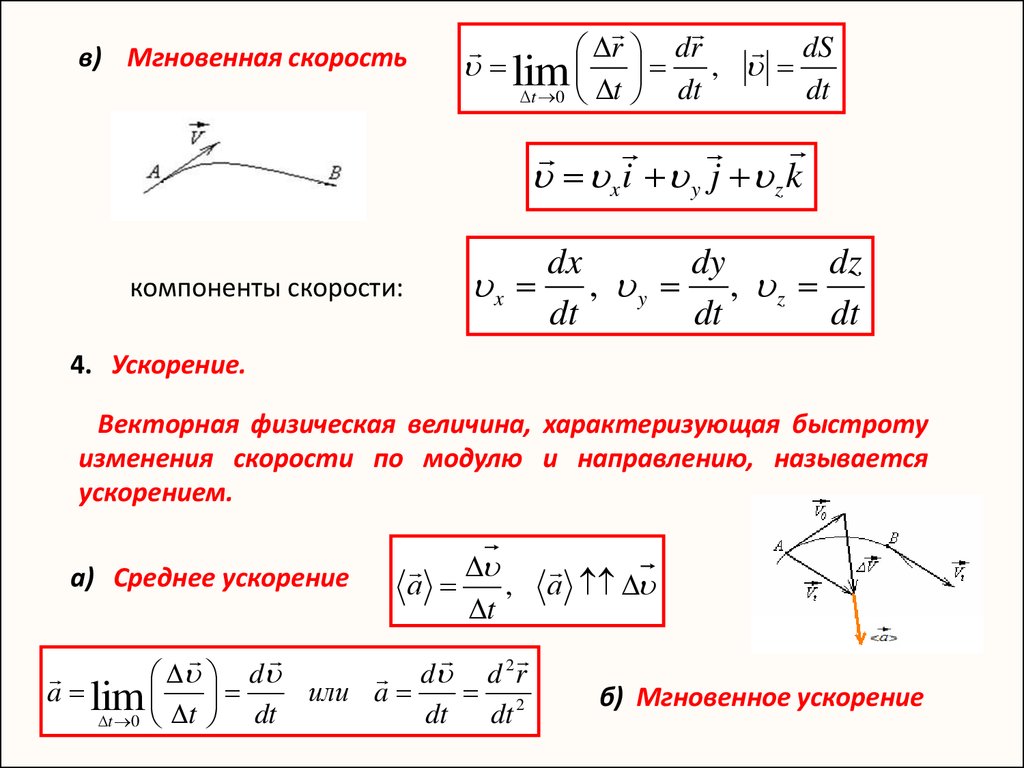
в) Мгновенная скорость
dS
r
d
r
lim ,
dt
dt
t 0 t
xi y j z k
компоненты скорости:
dx
dy
dz
x , y , z
dt
dt
dt
4. Ускорение.
Векторная физическая величина, характеризующая быстроту
изменения скорости по модулю и направлению, называется
ускорением.
а) Среднее ускорение
а
,
t
2
d d r
d
a lim
или a
2
dt
dt
dt
t 0 t
а
б) Мгновенное ускорение

6.

a ax i a y j az k
СИ : а м с 2
d y d 2 y
d x d 2 x
d z d 2 z
ax
2 , ay
2 , az
2
dt
dt
dt
dt
dt
dt
Компоненты ускорения равны вторым производным
соответствующих координат по времени.
В общем случае ускорение направлено под
некоторым углом к вектору скорости.
a
- тангенциальная составляющая ускорения
или касательное ускорение.
- характеризует изменение скорости по модулю физический смысл.
d
d
a
, a
dt
dt
Тангенциальная составляющая вектора
ускорения равна первой производной по
времени от модуля скорости.
- единичный вектор,
направленный по касательной.
a если движение " "
a если движение " "

7.

an
- нормальная составляющая ускорения или
центростремительное ускорение .
- характеризует изменение скорости по
направлению физический смысл.
2
2
a n n , an ,
R
R
an
Нормальная составляющая вектора ускорения равна отношению
квадрата модуля мгновенной скорости к радиусу кривизны
траектории.
n - единичный вектор, направленный по нормали к траектории к центру
ее кривизны.
Полное ускорение можно представить в виде векторной суммы двух
ускорений:
a a an , a a 2 an2

8.

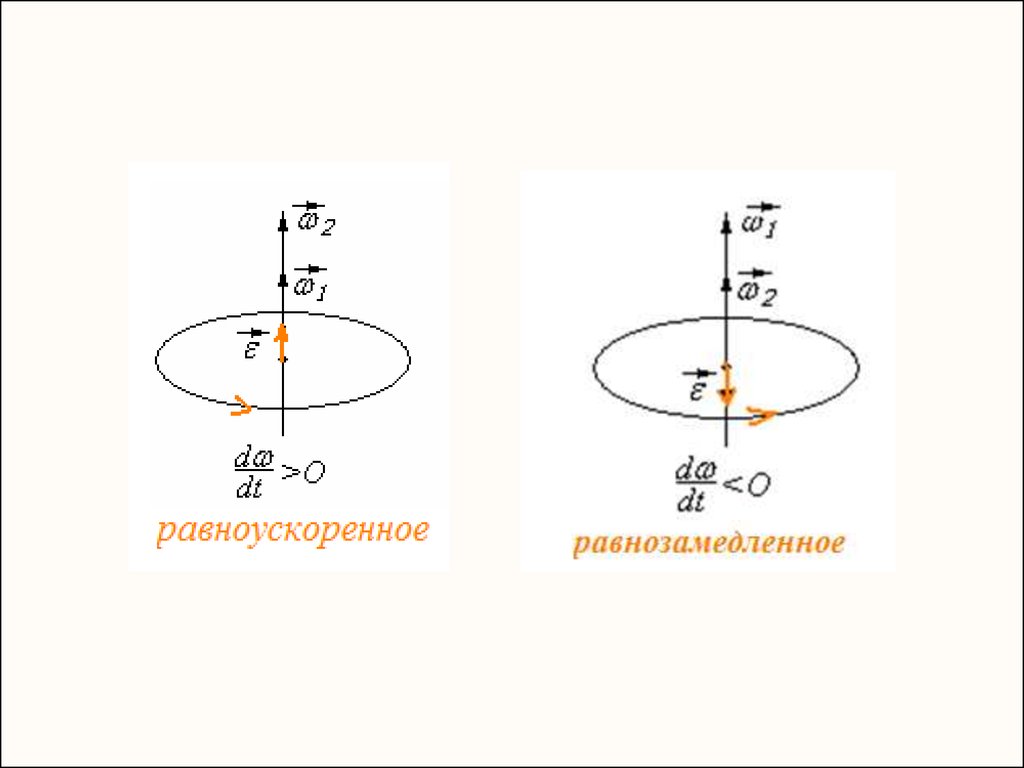
Вращение ТТ может быть равномерным и неравномерным.
.
. а)
Вращение называется равномерным, если за любые равные,
сколь угодно малые промежутки времени тело поворачивается
на одинаковые углы.
Характеристики равномерного вращения:
1)
Величина равная отношению угла поворота в единицу
времени называется модулем угловой скорости.
t
, СИ : рад / c
2) Период вращения – это время, за которое тело совершает один
оборот вокруг оси , т.е. поворачивается на угол =2 .
Т
t
, CИ : Т с
N
если =2 , а t=T, то
2
2
T
t
T

9.

3) Частотой вращения называется число полных оборотов тела
в единицу времени.
1
, СИ : с 1 или Гц
T 2
б) Вращение ТТ, при котором за равные промежутки времени
тело поворачивается
на разные углы называется
неравномерным.
Если угол - мал, его характеризуют вектором d ,
модуль которого равен углу поворота, а
направление определяют по правилу правого
винта.
1) Вектор средней угловой скорости
/ t, ,
t
Если направление вектора определяют по правилу правого винта это псевдовектор. Его откладывают из любой точки оси вращения.

10.

2) Вектором мгновенной угловой скорости
называется в.ф.в., равная первой производной
угла поворота по времени:
lim
t 0
d
, d ,
t
dt
d
dt
3) Вектором среднего углового ускорения называется изменение
вектора угловой скорости со временем.
, ,
t
, СИ : рад с 2
t
4) Вектором мгновенного углового ускорения в момент времени t
является предел приращения вектора угловой
приращению времени, за которое оно произошло:
lim
t 0
d
,
t
dt
d d 2
2
dt
dt
скорости
к

11.

12.

Связь между линейными и угловыми характеристиками движения.
линейные
характеристики
угловые
характеристики
связь между ними
S
S R
dr
r
dt
d
dt
R, r
d
a
dt
d
a
dt
an
2
R
d
dt
a R, a R
2
an R, an Rn
2

13.

Система уравнений, описывающих равномерное движение:
const
поступательное
a 0
const
вращательное
0
Система уравнений, описывающих равнопеременное движение:
0 at
at 2
поступательное S 0t
,
2
a const
0 t
t 2
вращательное 0t
2
const
2
формулы связи
2 N

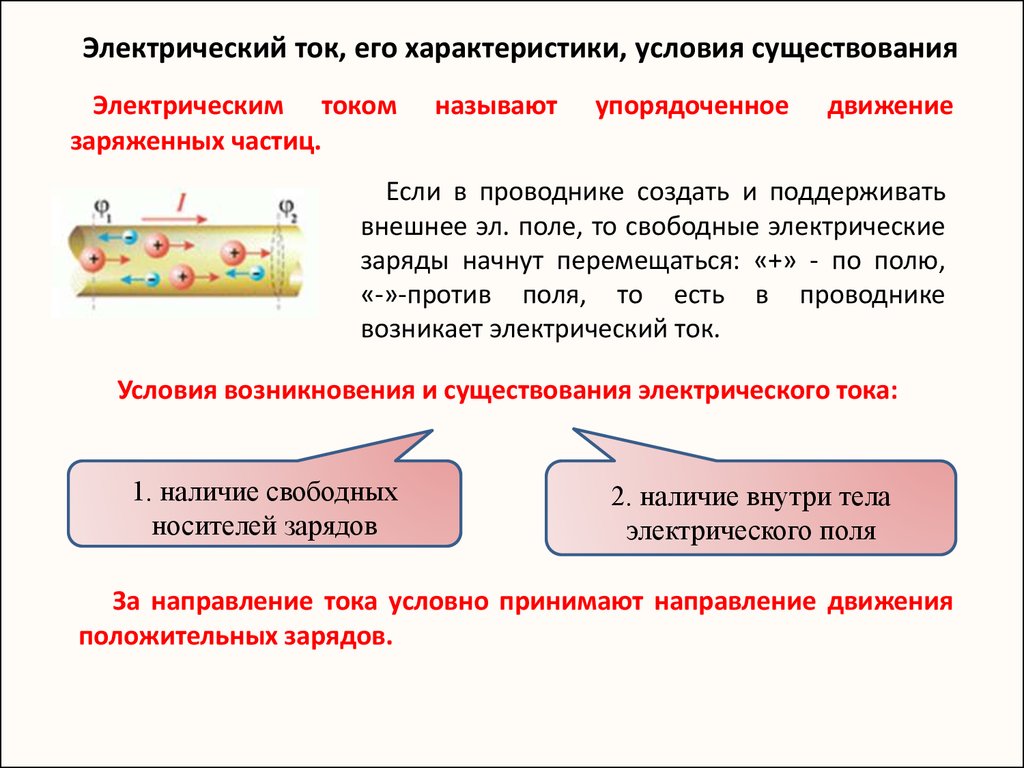
14. Электрический ток, его характеристики, условия существования

Электрическим током
заряженных частиц.
называют
упорядоченное
движение
Если в проводнике создать и поддерживать
внешнее эл. поле, то свободные электрические
заряды начнут перемещаться: «+» - по полю,
«-»-против поля, то есть в проводнике
возникает электрический ток.
Условия возникновения и существования электрического тока:
1. наличие свободных
носителей зарядов
2. наличие внутри тела
электрического поля
За направление тока условно принимают направление движения
положительных зарядов.

15.

Характеристики эл. тока:
1.
Сила
тока
–
с.ф.в.
определяемая электрическим
зарядом, проходящим через
поперечное сечение проводника
в единицу времени.
Ток, сила и направление
которого не изменяются со
временем, наз. постоянным
током.
q
I , СИ : I A
t
dq
I
dt
2. Физическая величина, определяемая силой тока, проходящего
через единицу площади поперечного сечения проводника,
перпендикулярного направлению тока, называется плотностью
тока.
dI
A
j
, СИ: j 2
dS
м
j ne
dI
j
I j dS , где dS ndS
dS
S
Сила тока это поток
вектора плотности тока через
поверхность dS.

16. Сторонние силы. Электродвижущая сила и напряжение

Два разноименно заряженных проводника
А и В, ( 2> 1) соединяют проводником С.
Сторонние силы, перемещая электрические заряды, совершают работу.
Физическая величина, определяемая работой, совершаемой
сторонними силами при перемещении положительного единичного
заряда, называется электродвижущей силой ЭДС.
Aq , СИ: В
ст
Aст q Eст dl
Aст
q
q Eст dl
q
В общем случае в цепи на заряд q действуют
электростатического поля и сторонние силы, следовательно:
А12 Аэл Аст ,
2
A12 q Eэл dl q Eст dl ,
2
1
1
Eст dl
силы
А12 q( 1 2 ) q
12

17.

Напряжением U на участке 1-2 называется с.ф.в., определяемая
работой, совершаемой суммарным полем электростатических
(кулоновских) и сторонних сил при перемещении единичного
положительного заряда на данном участке цепи.
A12 Aэл Aст
U
q
q
А12 q( 1 2 ) q
Участок цепи, на котором не
действуют сторонние силы,
называют однородным.
Участок цепи, на котором
на носители тока действуют
сторонние силы, называют
неоднородным.
Для замкнутой цепи:
12
U ( 1 2 ) 12
U12 1 2
U12
( )
12
U 12
1
2

18. Закон Ома. Электрическое сопротивление проводника

Немецкий физик Г.Ом экспериментально установил: I U
R
Для цилиндрического
проводника:
- удельное сопротивление
проводника (зависит от
материала проводника и от
температуры)
СИ: = Ом м
R
S
СИ : [R] Oм
Сопротивление
проводника
зависит от :
размера
формы
материала
Закон Ома в дифференциальной форме:
j E или j E
- удельная электрическая проводимость
вещества проводника. СИ: [σ]= См/м .
Для неоднородного участка цепи:
j ( Eэл Eст )

19. Закон Ома.

Для однородного участка цепи:
Для неоднородного участка цепи:
U ( 1 2 ), 12 0
U ( 1 2 ) 12
U ( )
I 1 2
R
R
j E
( 1 2 ) 12
I
R r
j ( EЭЛ EСТ )
Если цепь замкнута:
1 2
I
R r
Если цепь разомкнута:
I 0
12 1 2

20. Правила Кирхгофа для разветвленных цепей.

1.
Первое
правило
Кирхгофа:
алгебраическая сумма токов,
сходящихся в узле, равна нулю.
n
Ii 0
i 1
Пример: I1+I2 - I3-I4+I5=0.
Любая точка разветвленной цепи, в которой сходится не менее
трех проводников с током, называется узлом.
Ток, входящий в узел, считается «+», выходящий из узла – «-».
Первое правило Кирхгофа
электрического заряда.
вытекает
из
закона
2. Второе правило Кирхгофа: алгебраическая сумма
произведений сил токов в отдельных участках
произвольного
замкнутого
контура
на
их
сопротивления равна алгебраической сумме ЭДС,
действующих в этом контуре.
сохранения
n
I R k
i 1
i
i
k

21.

Контур – любой замкнутый путь, который
можно обойти перемещаясь по любым ветвям
цепи.
Ветвью электрической цепи – называется
участок цепи вдоль которого проходит один и тот
же ток.
Второе правило Кирхгофа является следствием
закона Ома для неоднородного участка цепи.