Моделирование траектории самолёта

1.

Моделирование траектории 
самолёта
лабораторная работа

2.

Системы координат

3.

Углы ориентации

4.

Параметр
\
Этап
крен
Отрыв
T1 = 2 Lр/Vотр
T2 = 2 Hбез/(Vотрsin отр)
0---------------------0
0---------------------0
тангаж
курс
0---------------------0
0------------------- отр
0------------------ 0 0------------------ 0
VN V
d скорость
,
dT R N H
VE
d0------------------V
dH
V ---------------V
отр
без
, отр
VU ,
dT RE H cos
dT
V N V cos 0 cos ,
(0) 0 ,
RE
Разбег
VE V sin 0 cos ,
( 0) 0 ,
A
1 e 2 sin 2
,
H ( 0) H 0 ,
RN
A 1 e2
VU V sin ,
1 e 2 sin 2
3
.

5.

Расчёт летных характеристик 
самолёта
f = 0.2
Xa = Ya /10
Cya отр = 1.5
= 1.2 кг/м3

6.

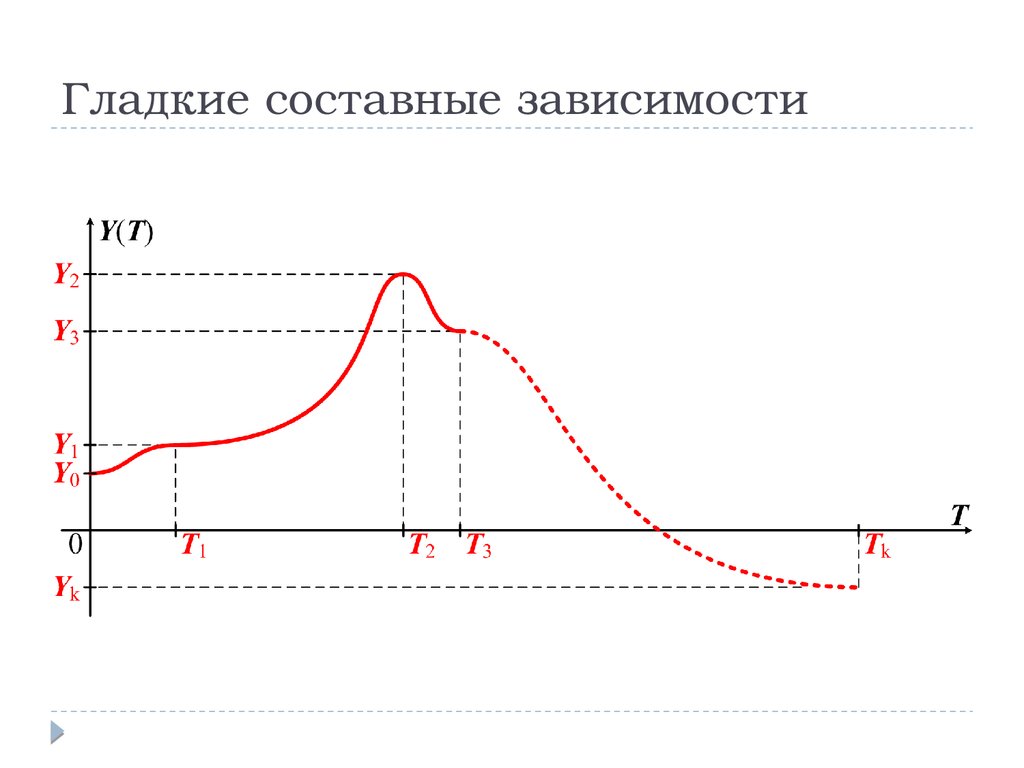
Гладкие составные зависимости

7.

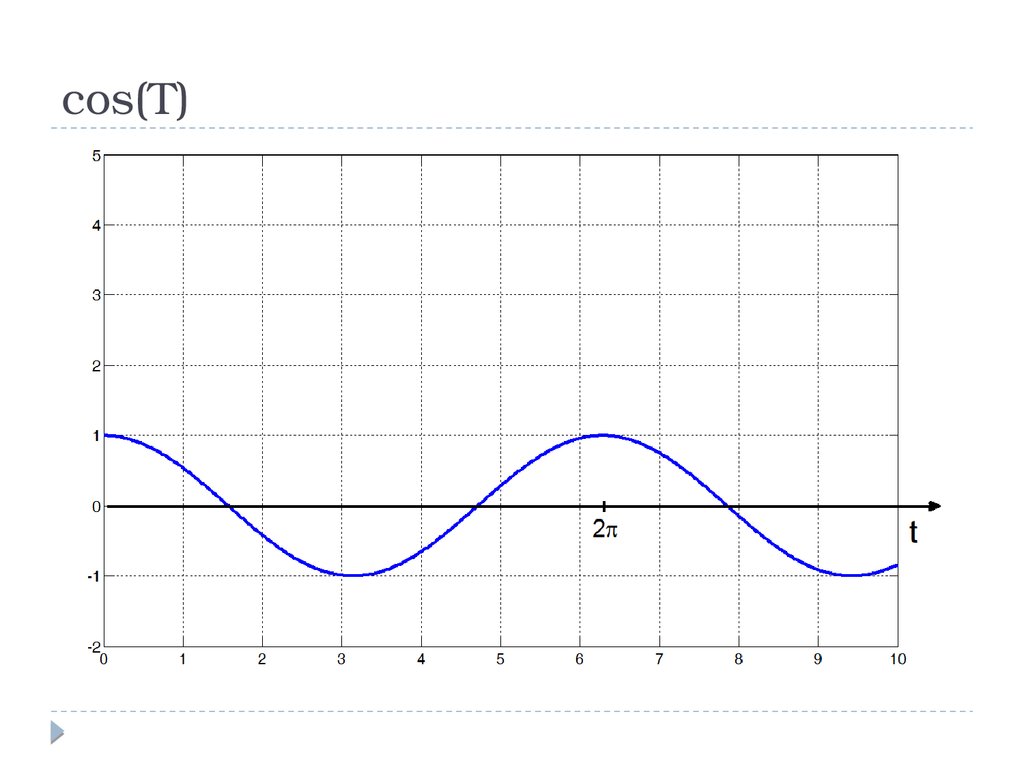
cos(T)

8.

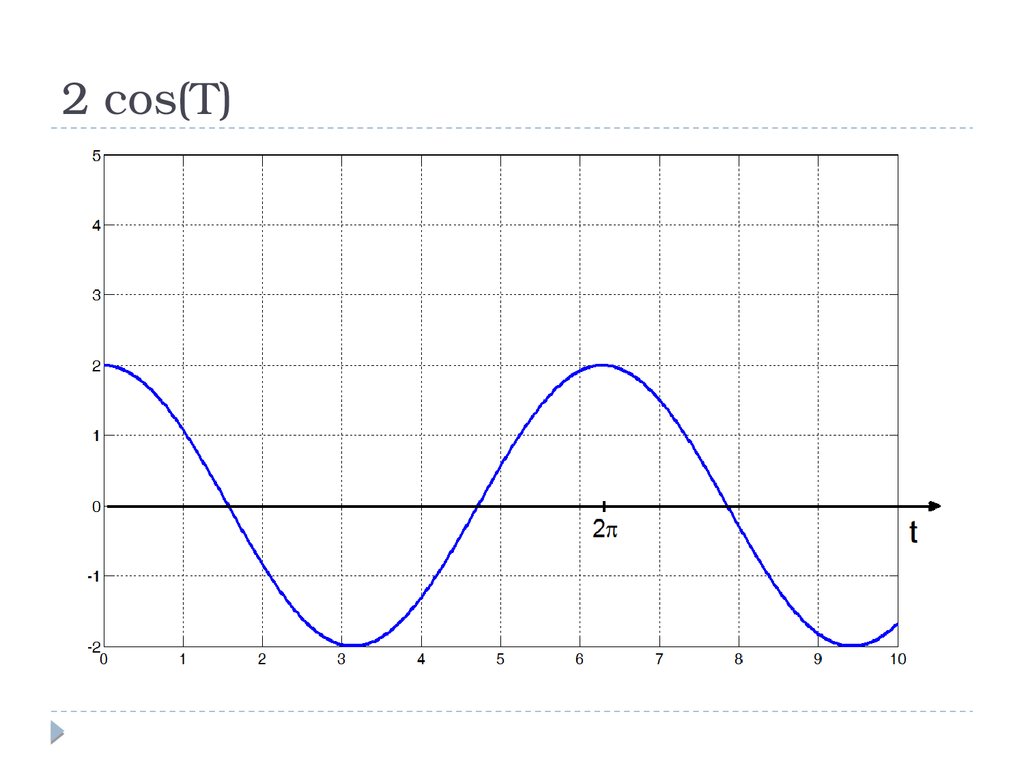
2 cos(T)

9.

2 cos(T) + 1

10.

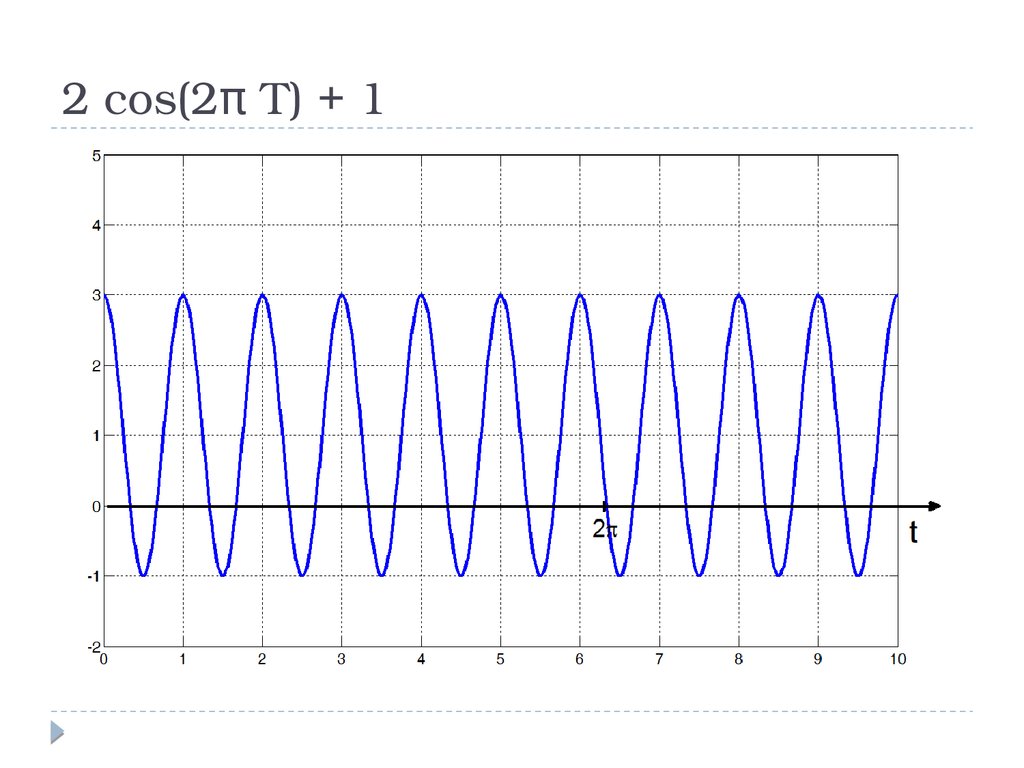
2 cos(2π T) + 1

11.

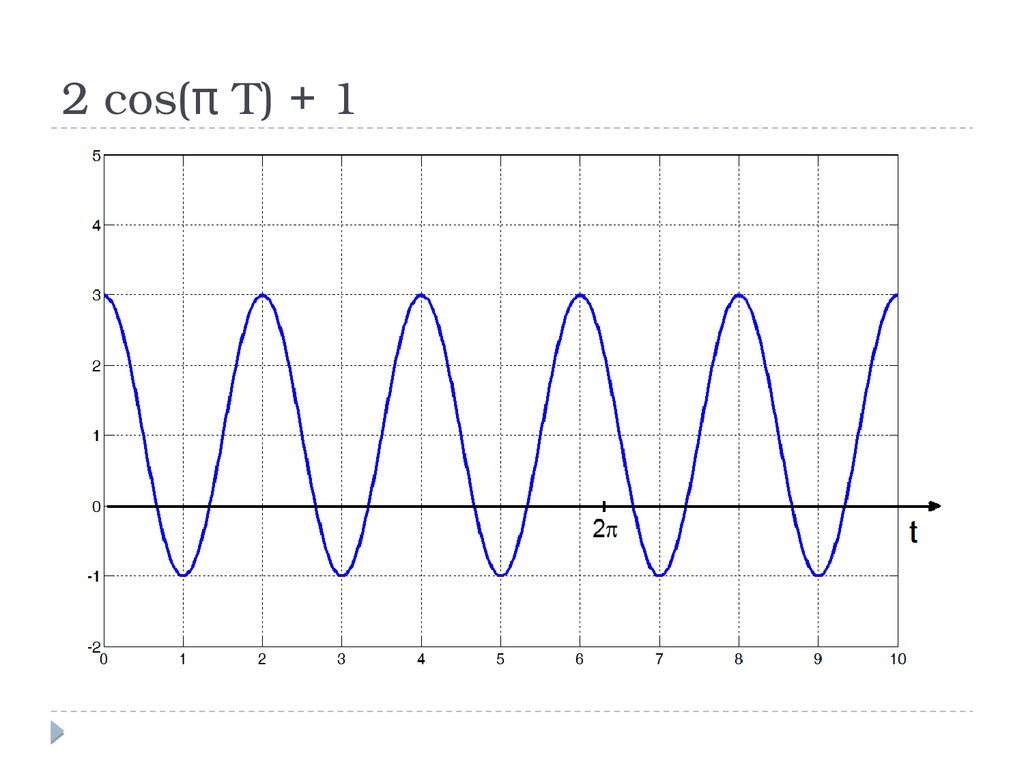
2 cos(π T) + 1

12.

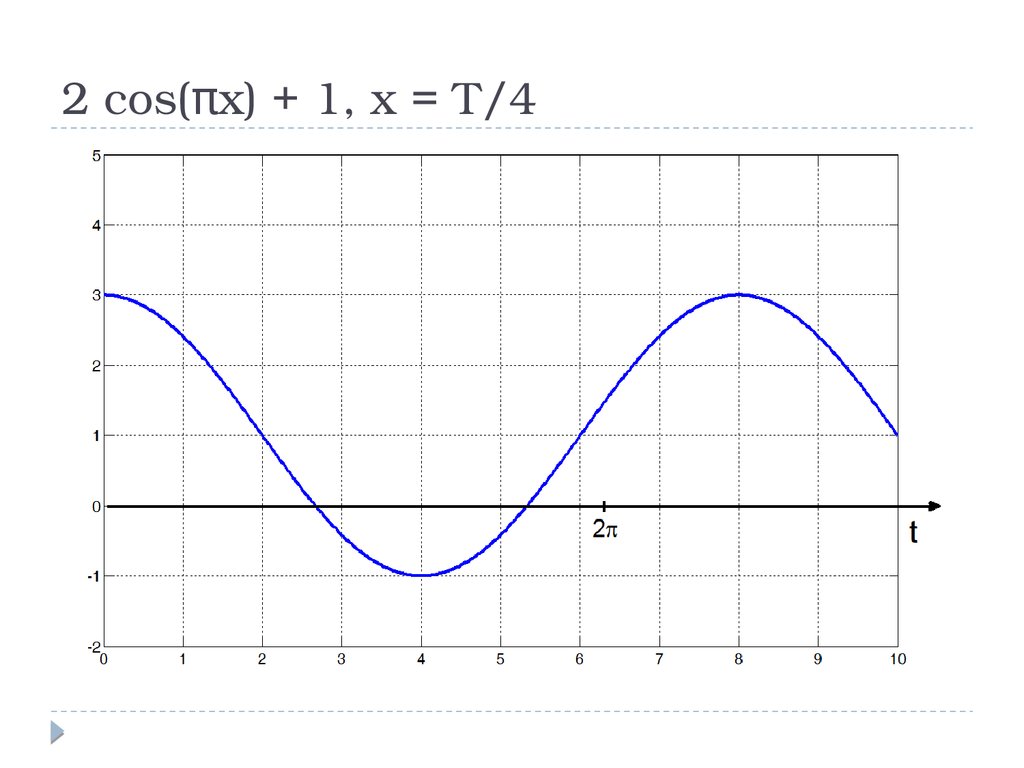
2 cos(πx) + 1, x = T/4

13.

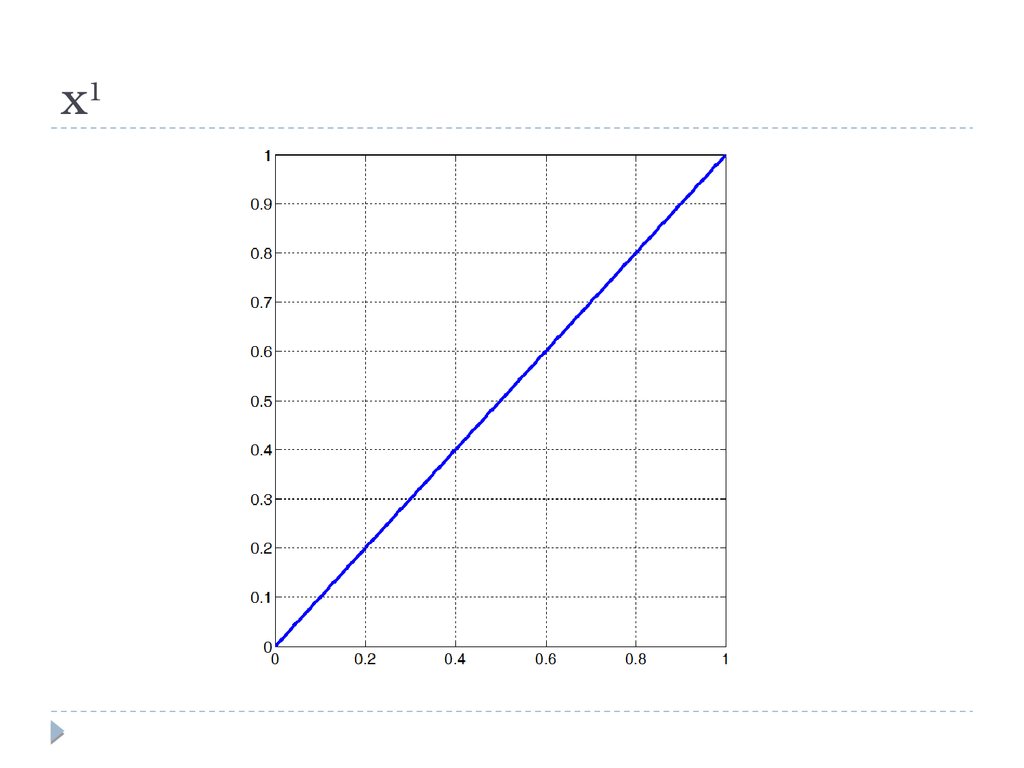
x1

14.

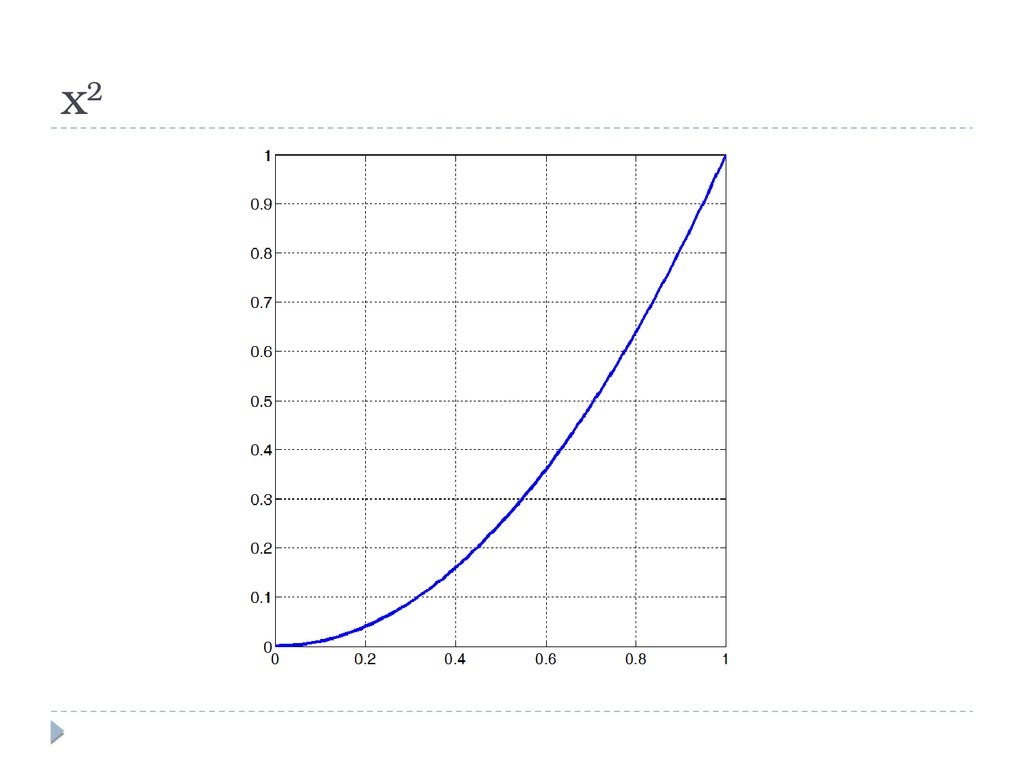
x2

15.

x3

16.

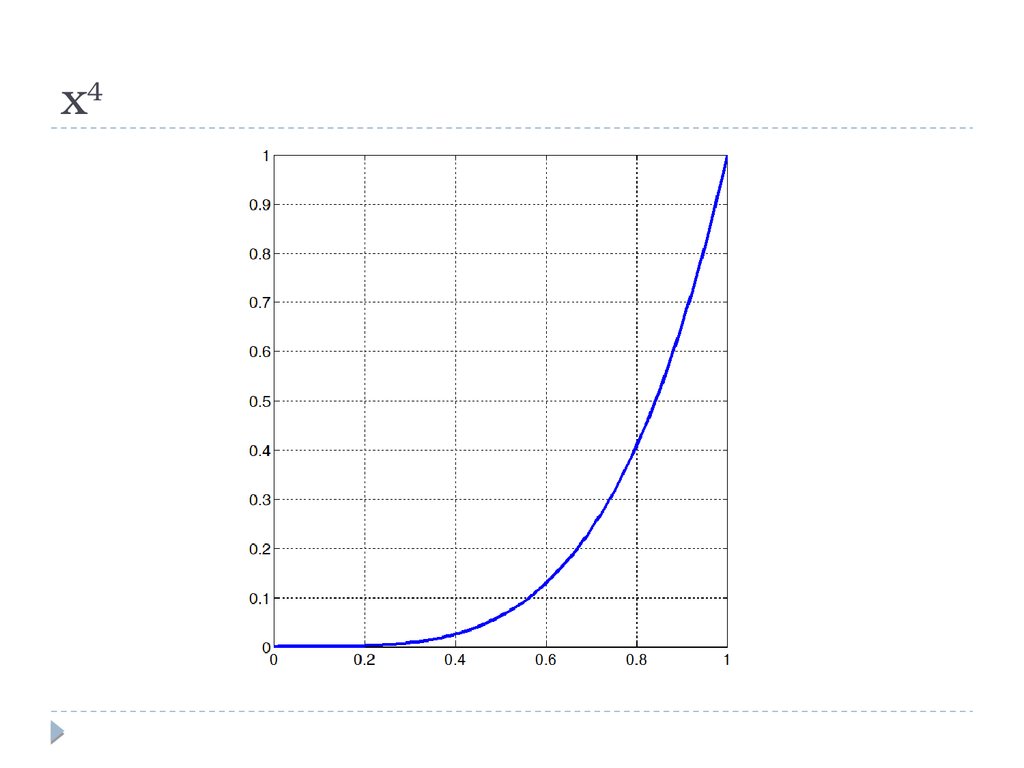
x4

17.

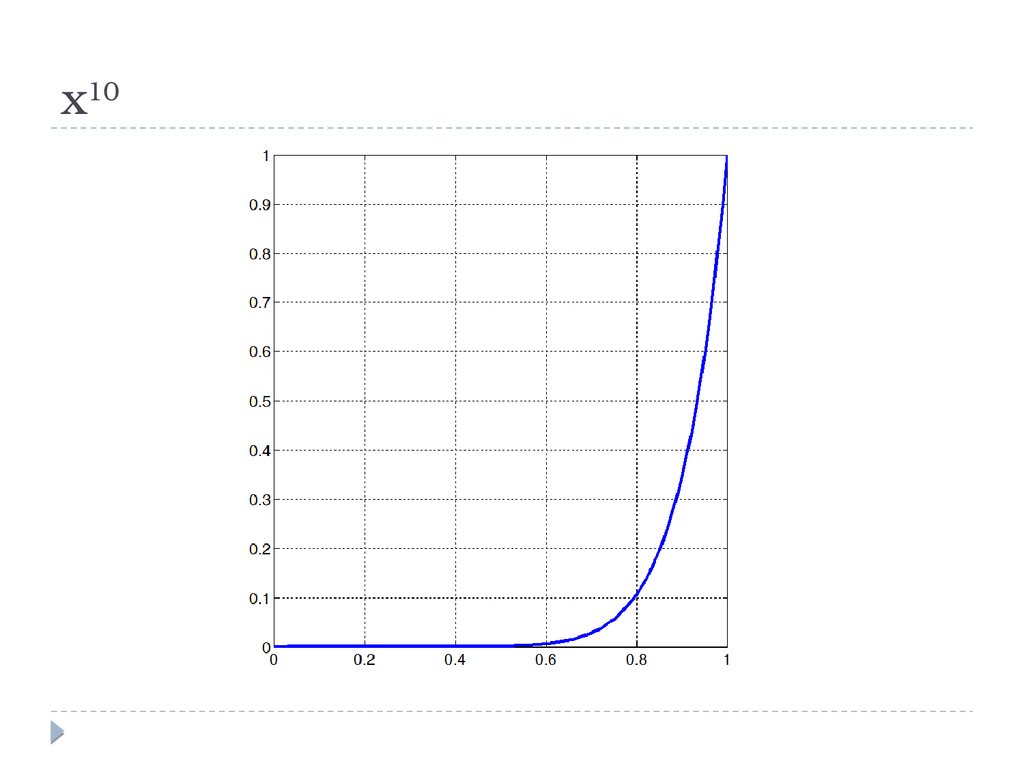
x10

18.

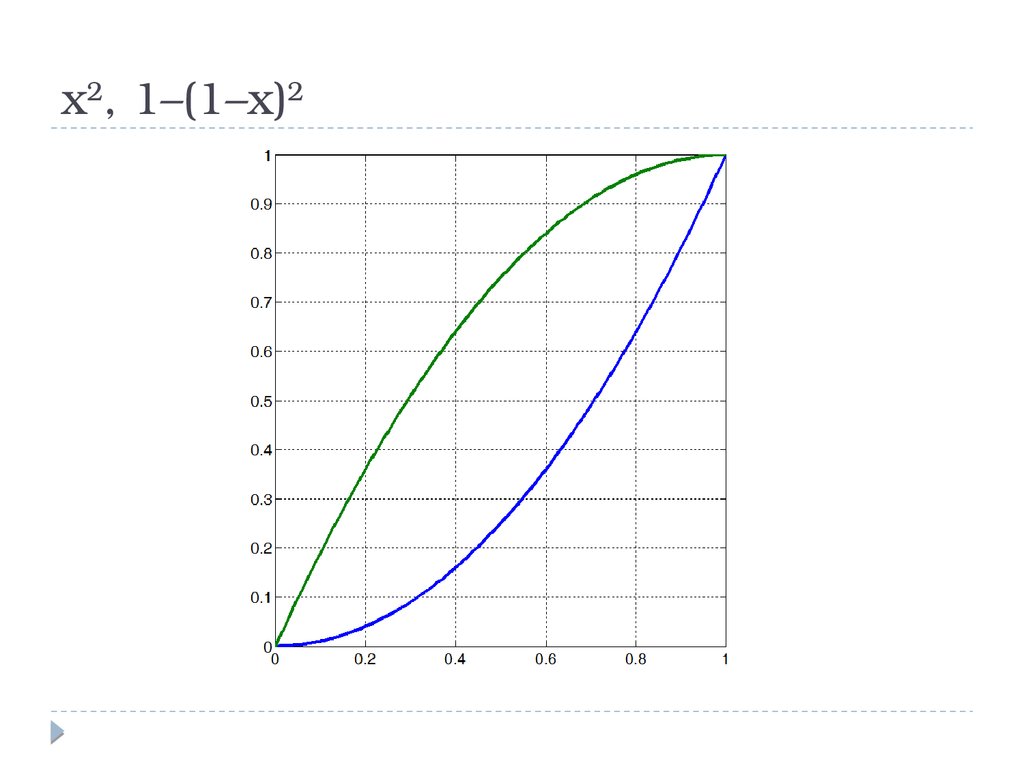
x2, 1–(1–x)2

19.

x10, 1–(1–x)10

20.

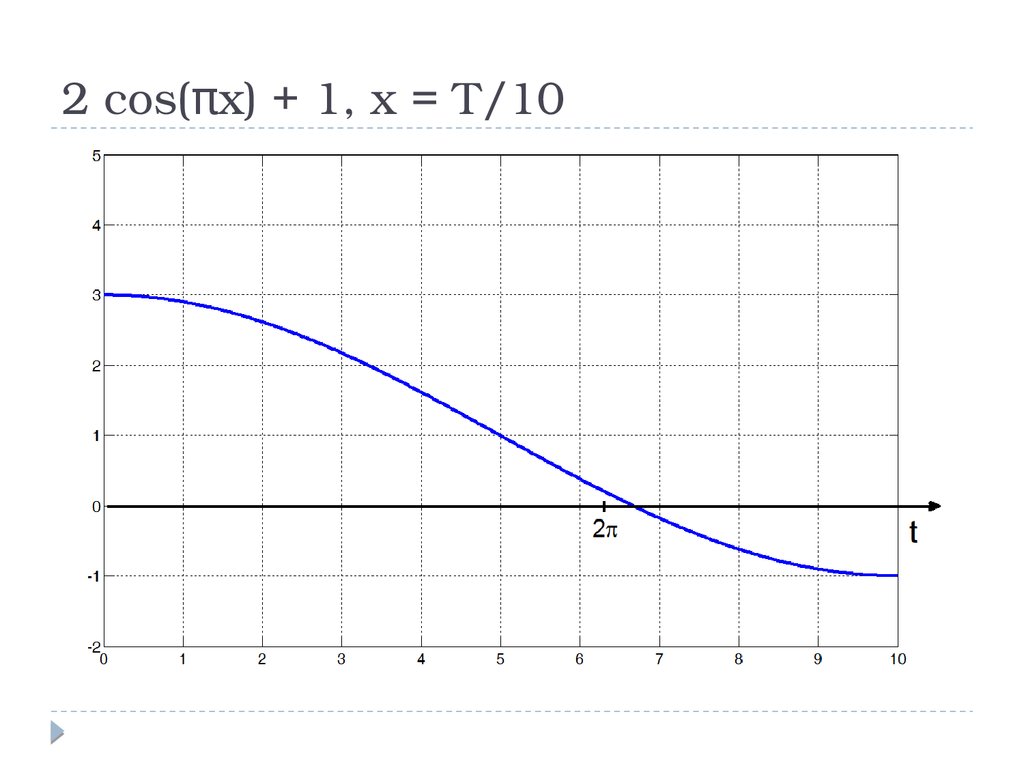
2 cos(πx) + 1, x = T/10

21.

2 cos(π x) + 1, 
x = (T/10)2, x = 1–(1–T/10)2

22.

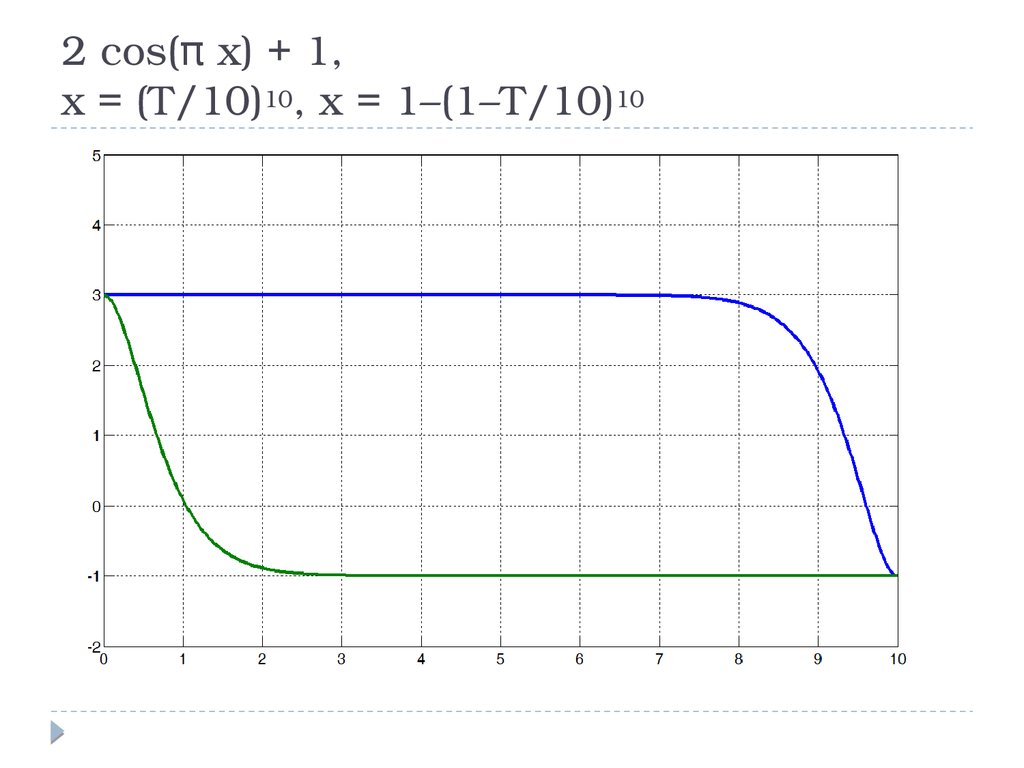
2 cos(π x) + 1, 
x = (T/10)10, x = 1–(1–T/10)10

23.

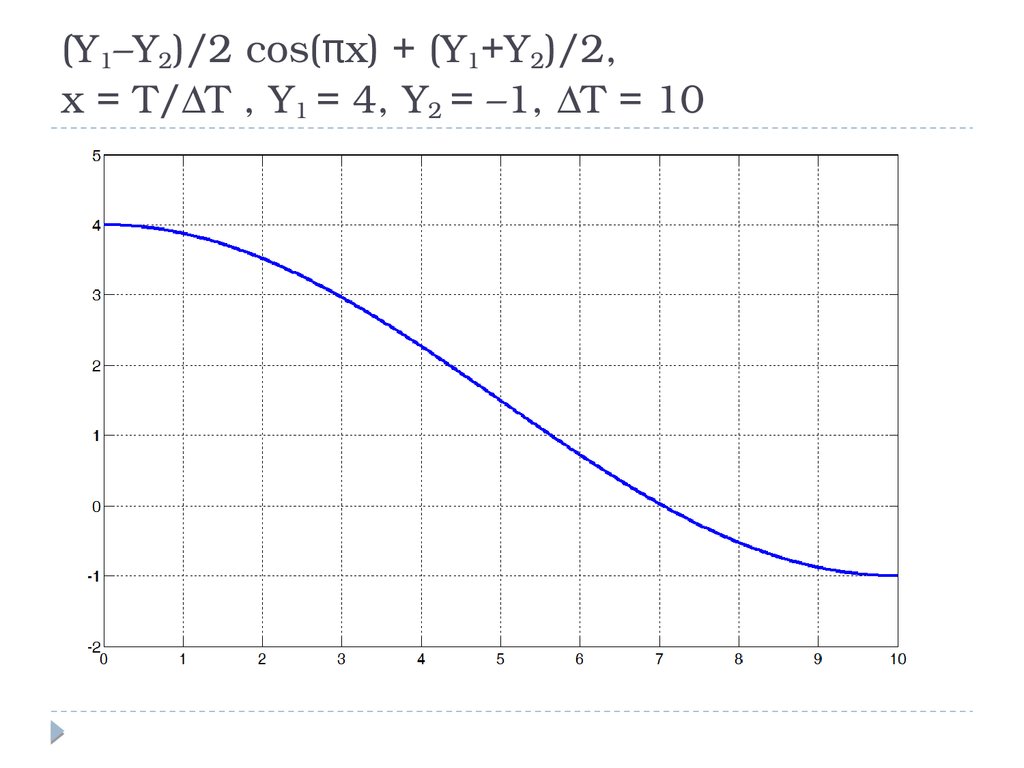
(Y1–Y2)/2 cos(πx) + (Y1+Y2)/2,
x = T/∆T , Y1 = 4, Y2 = –1, ∆T = 10

24.

(Y1–Y2)/2 cos(πx) + (Y1+Y2)/2,
x = (T/∆T)k , Y1 = 4, Y2 = –1, ∆T = 10, k = 2

25.

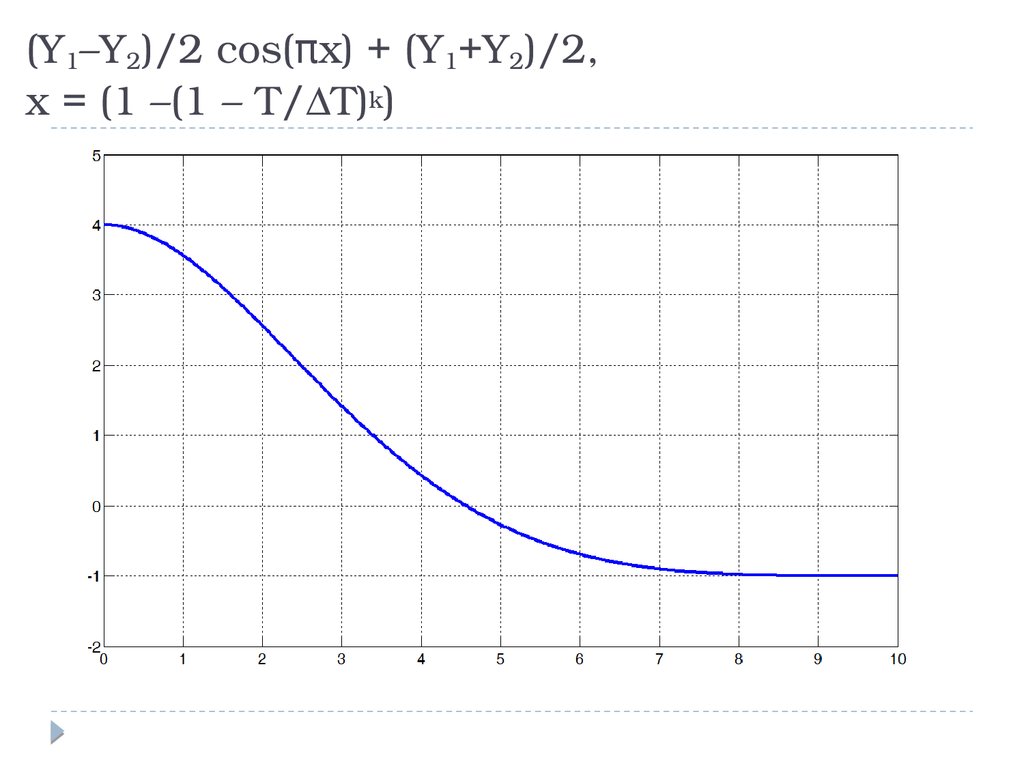
(Y1–Y2)/2 cos(πx) + (Y1+Y2)/2,
x = (1 –(1 – T/∆T)k)

26.

k = 10

27.

Построение участка кривой
1)
Ti 1 ,
Ti ,
3)
Yi ,
k
T Ti 1
,
Ti Ti 1
2)
Yi 1 ,
x
k
T Ti 1
1 1 T T , k 0
i
i 1
Y Y
Y Y
Y i 1 i cos x i 1 i
2
2
k 0
k

28.

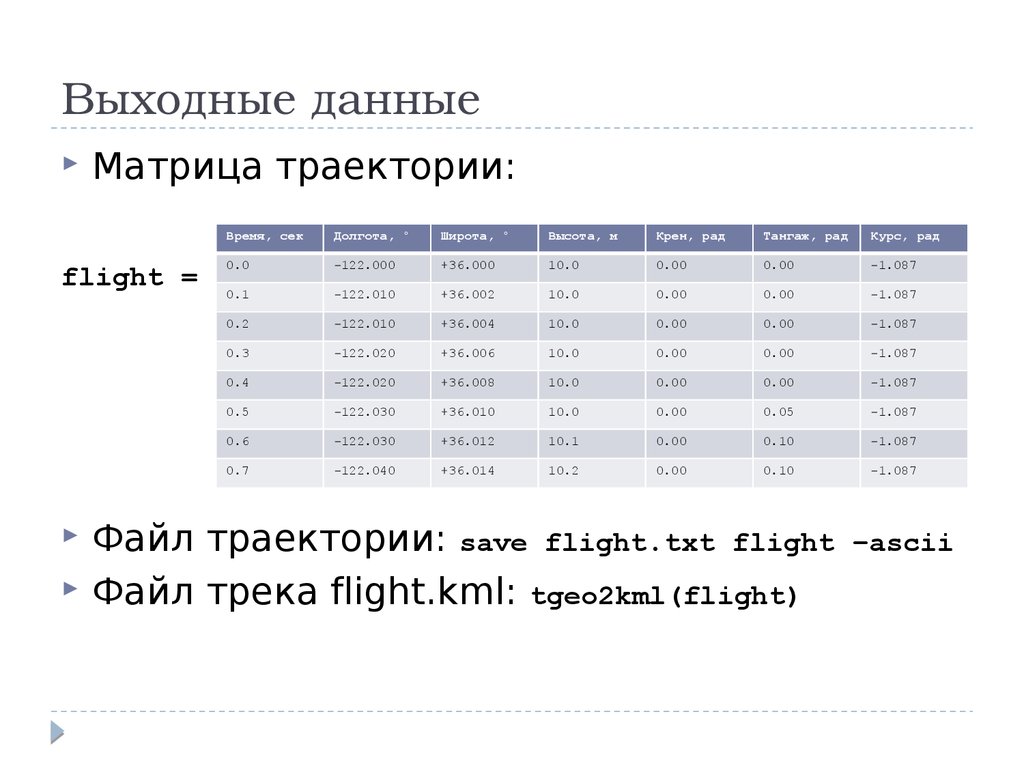
Выходные данные
Матрица траектории:
flight =
Время, сек
Долгота, °
Широта, °
Высота, м
Крен, рад
Тангаж, рад
Курс, рад
0.0
-122.000
+36.000
10.0
0.00
0.00
-1.087
0.1
-122.010
+36.002
10.0
0.00
0.00
-1.087
0.2
-122.010
+36.004
10.0
0.00
0.00
-1.087
0.3
-122.020
+36.006
10.0
0.00
0.00
-1.087
0.4
-122.020
+36.008
10.0
0.00
0.00
-1.087
0.5
-122.030
+36.010
10.0
0.00
0.05
-1.087
0.6
-122.030
+36.012
10.1
0.00
0.10
-1.087
0.7
-122.040
+36.014
10.2
0.00
0.10
-1.087
Файл траектории: save flight.txt flight
Файл трека flight.kml: tgeo2kml(flight)
–ascii