Similar presentations:
Распределения Максвелла и Больцмана
1. Распреде-ления Максвелла и Больцмана
РАСПРЕДЕЛЕНИЯМАКСВЕЛЛА
И
БОЛЬЦМАНА
2.
3.
a 12a 22
U 0 1CV T
2CV T
,
V1
V1
a( 1 2 ) 2
U ( 1 2 )CV T
U0
V1 V2
( 1 2 ) 2 12 22
T T
2CV ( 1 2 ) V1 V2
V1 V2 1
1
2
a
a
T
2CV
2
4
(
V
V
)
1 1
a 4VV
1 2
1
2
T
2CV VV
V1 V2 V1 V2
1 2 (V1 V2 )
(V1 V2 ) 2 ,
a
T
2CV V1V2 (V1 V2 )
2 RT
p
V1 V2 2b
4.
5.
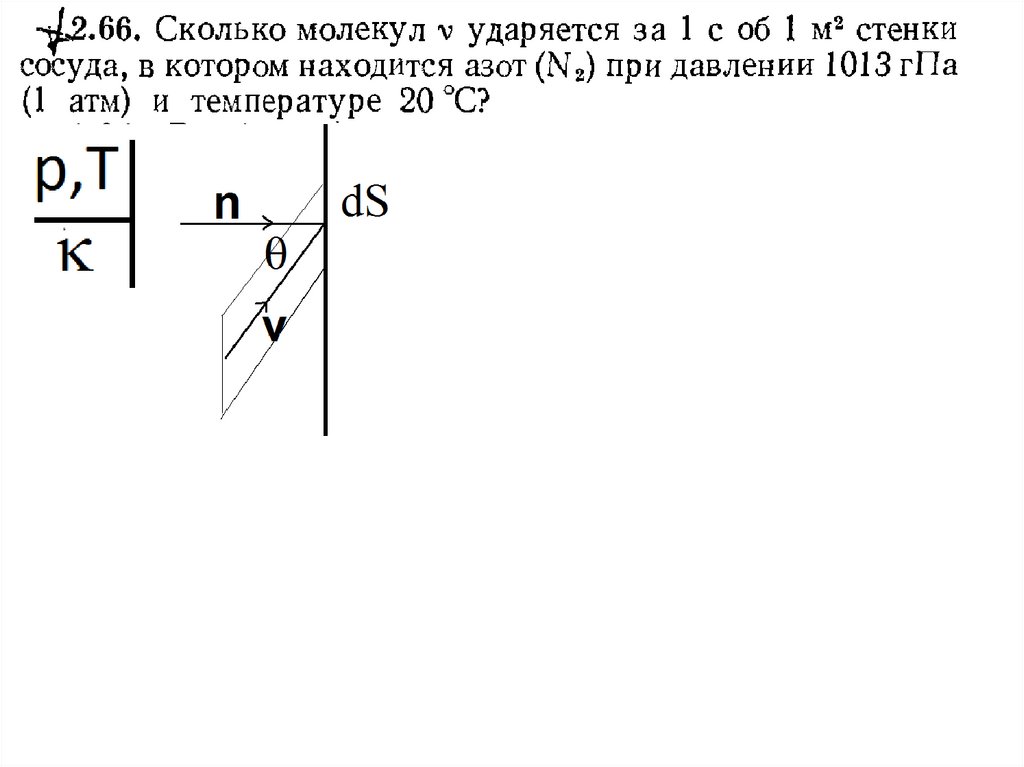
d1
dv
nv dV
dtdS
2
d 2 sin d 2 d cos , dV dSvdt cos
/ 2
cos d cos vn dv
v
0
0
n v
4
,
1
v
n
vn dv
v
0
6.
7.
1d
1
d
dv
nv dV
dv
nv dV
dtdS
2
2 dtdS
2
d 2 sin d 2 d cos , dV dSvdt cos
/ 2
cos d cos vn dv
v
0
0
n v
4
,
1
v
n
vn dv
v
0
8. Следствия изотропности простраства
f ( v) x (vx ) y (v y ) z (vz )f ( v) (v) (vx ) (v y ) (vz )
v v v v
2
x
2
y
2
z
ln (v) ln (vx ) ln (v y ) ln (vz )
vx
(v) v (v) vx (vx )
(v) vx (v) v (vx )
9. Распределение по одной проекции
(vx ) 1 (v) 1(vx ) vx (v ) v
(vx )
2
vx (v) A exp v
(v x )
m
A
exp
v
dx
1
A
2
kT
m
mv 2
kT
2
2 A exp v dx 2 2kT
2
10. Подробности взятия интегралов
A exp v dx A 12
2
exp x dx
2
2
v
exp
v
dv
1
1 2
2
2
v exp v exp v dv
2
2
m
kT
A
4
2
m
,
2kT
m
A
2 kT
11. Распределение Максвелла
mf ( v ) (v )
2 kT
3/ 2
mv
exp
2kT
2
x
3/ 2
2
mv y2
mvz m
mv 2
exp
exp
exp
2kT
2kT
2kT 2 kT
m
F (v) 4 v (v) 4 v
2 kT
2
2
3/ 2
mv 2
exp
2kT
12. О нормировке и размерностях
1(v)dv 1, (v) v .
f ( v)dv
f ( v)dvx dv y dvz 1,
1
f ( v ) (v ) 3 .
v
0
1
F (v)dv 1, F (v) .
v
13. Характерные скорости
ХАРАКТЕРНЫЕ СКОРОСТИ2kT
vв : F (vв ) 0 vв
m
8kT
v vF (v)dv
m
0
vкв
v
2
3kT
0 v F (v)dv m
2
14. Безразмерный вид
mvm
F (v) dv 4 v
dv
exp
2 kT
2kT
2
2
4 2
4 v
v
2
u
exp(
u
)du,
3/ 2 3 exp 2 dv
vв
vв
3/ 2
2
2
m
v
u v
2kT vв
mv 2
m
1
2
(v) dv
exp
dv
exp
u
du
2 kT
2kT
15.
16.
1,01vвF (v)dv
0,99 vв
4
4
1,01
u 2 exp( u 2 )du
0,99
0, 08
0, 02 u exp( u )
u 1
e
2
2
17.
Найти среднее значение модуля скороcтимолекул газа, находящегося в равновесном
состоянии при температуре T. Масса молекулы
равна m.
18.
Найти среднее значение модуля скороcтимолекул газа, находящегося в равновесном
состоянии при температуре T. Масса молекулы
равна m.
vF (v)dv
0
4vв
u
0
3
exp( u ) du
2
2vв
u exp( u )
2
2
0
exp( u )
2kT
da u exp( u ) du, a
vв
2
m
2
b u ,
db 2udu
4vв
2vв
8kT
2
u exp( u ) du
m
0
2
2
19. Найти среднюю квадратичную скорость молекул газа, находящегося в равновесном состоянии при температуре T. Масса молекулы равна
m.vкв
v2
0
F (v)v 2 dv
20. Найти среднюю квадратичную скорость молекул газа, находящегося в равновесном состоянии при температуре T. Масса молекулы равна
m.vкв
v2
F (v)v 2 dv
0
2
кв
mv
iпост
3
3kT
kT kT vкв
2
2
2
m
21.
22.
(v) dv1
exp u du
vx
2kT
vв
m
2
2
v (v)dv
2kT
2
m
2kT
m
exp( u
2
2
u exp( u )du
2
0
)
2kT
m
0
23. Распределение Больцмана
pS p
p dN F nSdzF
nF
z
z dz
z
z
z
z
p nF n U
kT n n U
p nkT
n
U
U
ln n
n
kT
kT
U
n n0 exp
kt
U
mgh
p p0 exp p0 exp
kt
kt
24.
25.
ma m 2r Fц , Fц U ,m 2 r 2
U
2
2
m( r )
U
p p0 exp p0 exp
kT
kT
26.
27.
N E N0 exp E / kT ,N1 N0 exp E1 / kT ,
N2 N0 exp E2 / kT ,
N1 N2 N0 exp E1 / kT N0 exp E2 / kT N ,
N
N0
,
exp E1 / kT exp E2 / kT
N1
N exp E1 / kT
exp E1 / kT N 0 xp E2 / kT
N2
N exp E2 / kT
,
exp E1 / kT N 0 xp E2 / kT


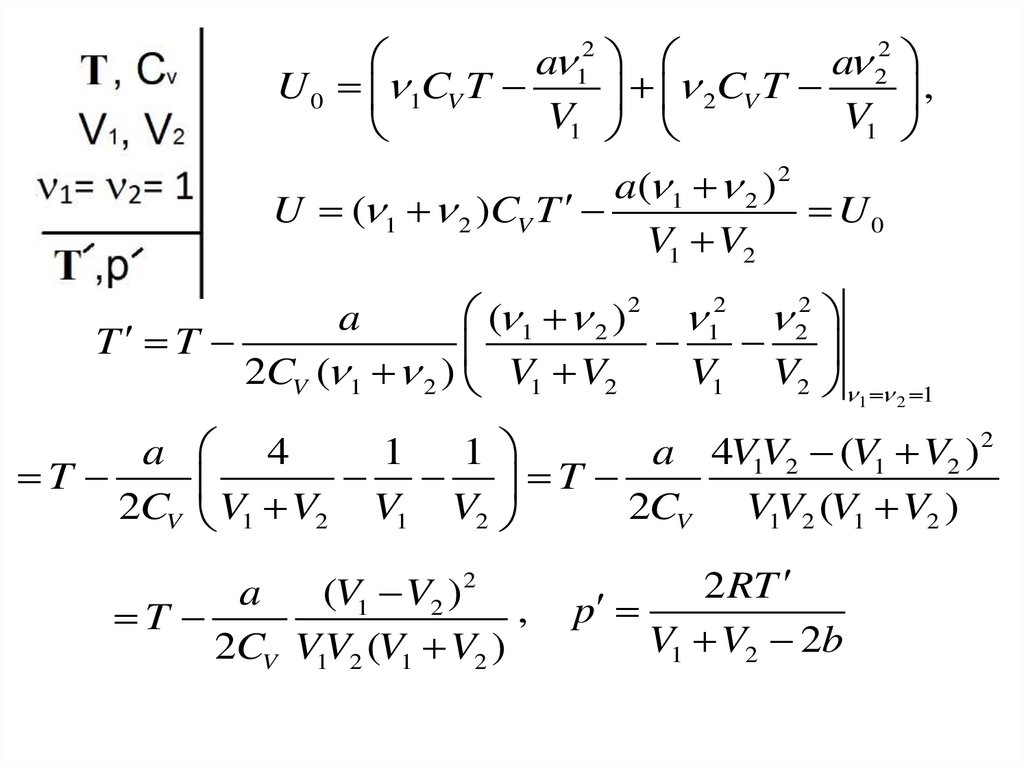






















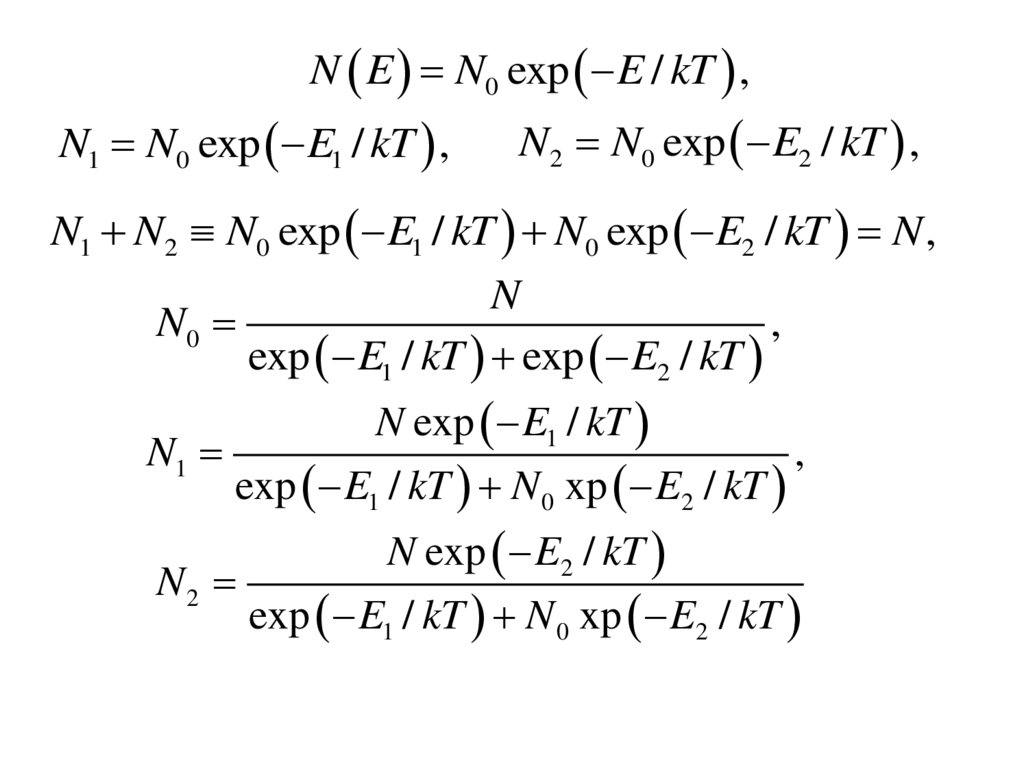
 physics
physics