Модели полос поглощения

1. Модели полос поглощения

Будак Владимир Павлович,
Национальный исследовательский
университет «МЭИ»
кафедра светотехники
Richard M. Goody Walter M. Elsasser
: +7 (495) 763-5239
BudakVP@mpei.ru

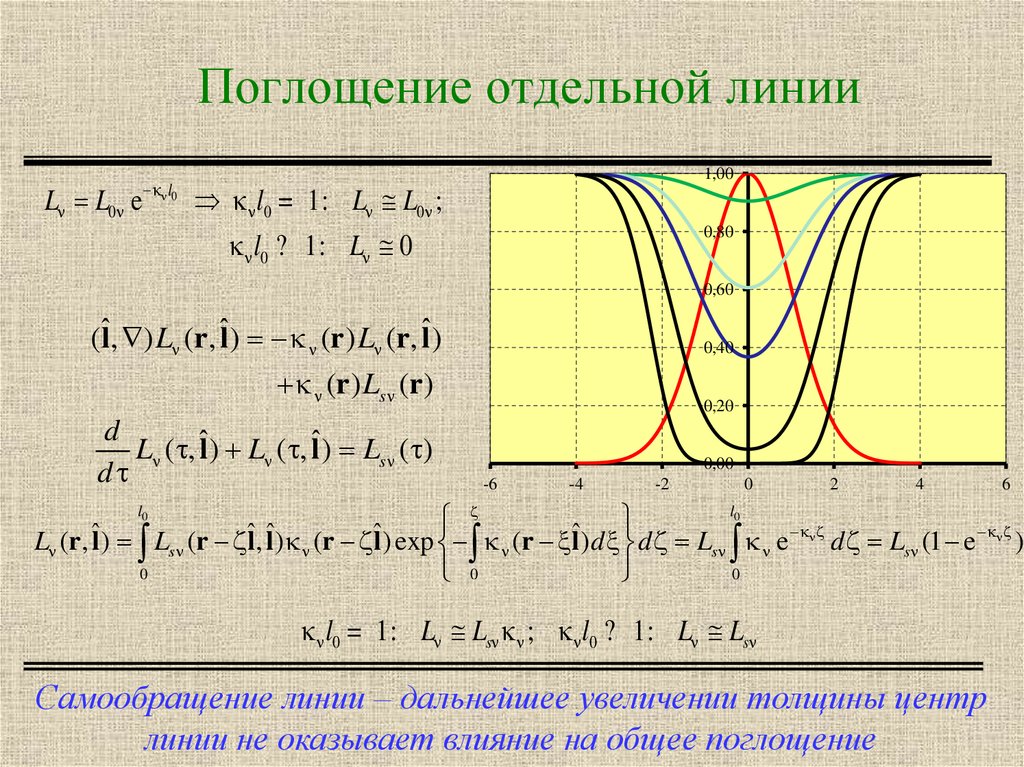
2. Поглощение отдельной линии

L L0 e
l0
1,00
l0 = 1: L L0 ;
0,80
l0 ? 1: L 0
0,60
(ˆl , ) L (r, ˆl ) (r ) L (r, ˆl )
0,40
(r ) Ls (r )
d
L ( , ˆl ) L ( , ˆl ) Ls ( )
d
0,20
0,00
-6
-4
-2
0
2
4
6
l0
L (r, ˆl ) Ls (r ˆl , ˆl ) (r ˆl ) exp (r ˆl ) d d Ls e d Ls (1 e )
0
0
0
l0
l0 = 1: L Ls ; l0 ? 1: L Ls
Самообращение линии – дальнейшее увеличении толщины центр
линии не оказывает влияние на общее поглощение

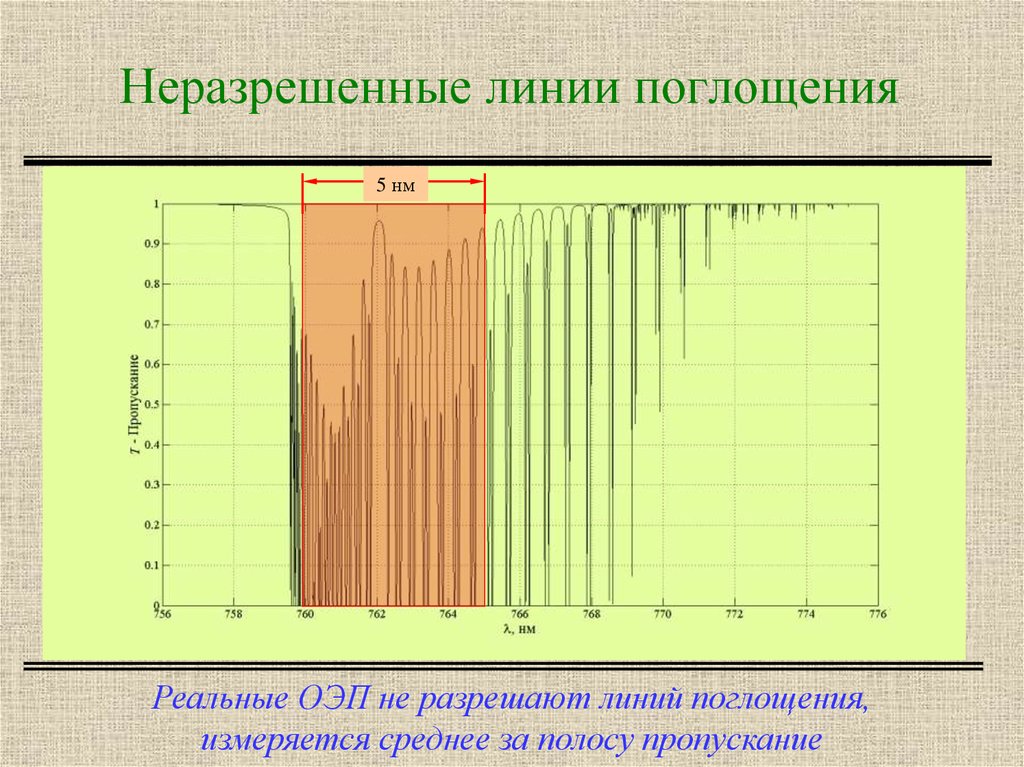
3. Неразрешенные линии поглощения

5 нм
Реальные ОЭП не разрешают линий поглощения,
измеряется среднее за полосу пропускание

4. Интегральное пропускание и поглощение

2
T
L ( ) d
1
2
L ( ) d
2
2
1
l
e
d ;
1
L ( ) L ( ) d
0
A
1
2
L ( ) d
0
1
1 2
l
1
e
d
1
0
L( ) L0 ( ) e
l
1
,
A 1 T
S L l
1
Sl
y2
y2
2u 2
Лоренцевский контур линии: l
2
2
2
2
L ( 0 )
L x y
x y2
x ( 0 ) / ,
y L / , u Sl / (2 L ),
y
1, x 1
y 2
AL 1 exp 2u 2
dx
2
x y
В общем случае не интегрируется, рассмотрим частные случаи
слабого и сильного поглощения

5. Частные случаи:

1. поглощение слабой линией:
y2
y2
y2
u 1: 1 exp 2u 2
1 1 2u 2
2u 2
2
2
2
x
y
x
y
x
y
2
y
dt
1/ y
AL 2u 2
dx
2
uy
2
uy
arctg
t
2 uy
2
2
1/ y
x y
1 t
2. поглощение сильной линией u>>1 и x>>y:
y 2
AL 1 exp 2u 2 dx
x
y2
y
2
2 u 2 , x 2 u , dx
x
y 2u
2u
u 1 e 2 du 2 e 2 d
2
1
e
y
2
u
d
1
dv
v
2
ΔλD =0.1Ả
y
2
d
2 e
1 e
2
2
d
2
d 2 y 2 u

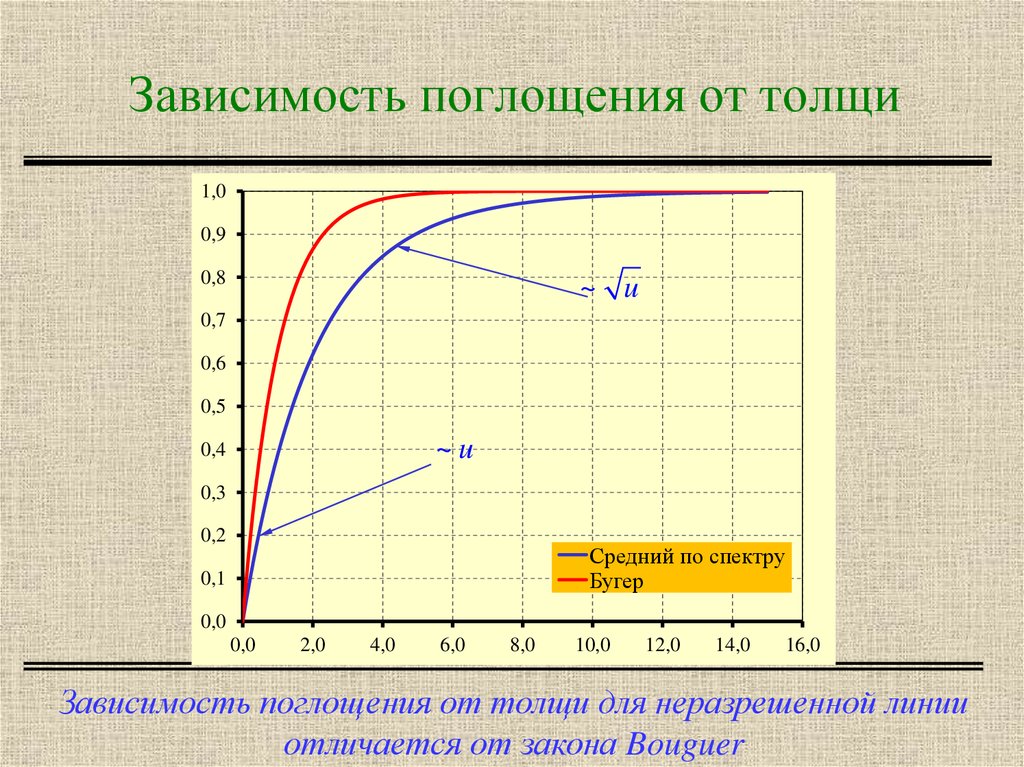
6. Зависимость поглощения от толщи

1,0
0,9
0,8
~ u
0,7
0,6
0,5
~u
0,4
0,3
0,2
Средний по спектру
Бугер
0,1
0,0
0,0
2,0
4,0
6,0
8,0
10,0
12,0
14,0
16,0
Зависимость поглощения от толщи для неразрешенной линии
отличается от закона Bouguer

7. Line-by-line (полинейный) метод

Наиболее строгий путь – непосредственное вычисление коэффициентов
поглощения и пропускания по трассе:
1 2
T
exp
l
S
f
(
)
d
i i
1
i
Для этого необходимо:
• иметь базу данных по силам линии
• иметь базу данных по уширениям
• концентрациям и составу атмосферы
• уметь быстро вычислять контур Voigt линии
Такой подход получил название LBLRTM – line by line radiative transfer model
Основные базы данных:
• HITRAN – high-resolution transmission molecular absorption database
• GEISA – Gestion et Etude des Informations Spectroscopiques
Atmosphériques: Management and Study of Atmospheric Spectroscopic
Information
GOSAT (Greenhouse gases Observing SATellite, IBUKI) :
http://www.gosat.nies.go.jp/index_e.html - 18500 линий

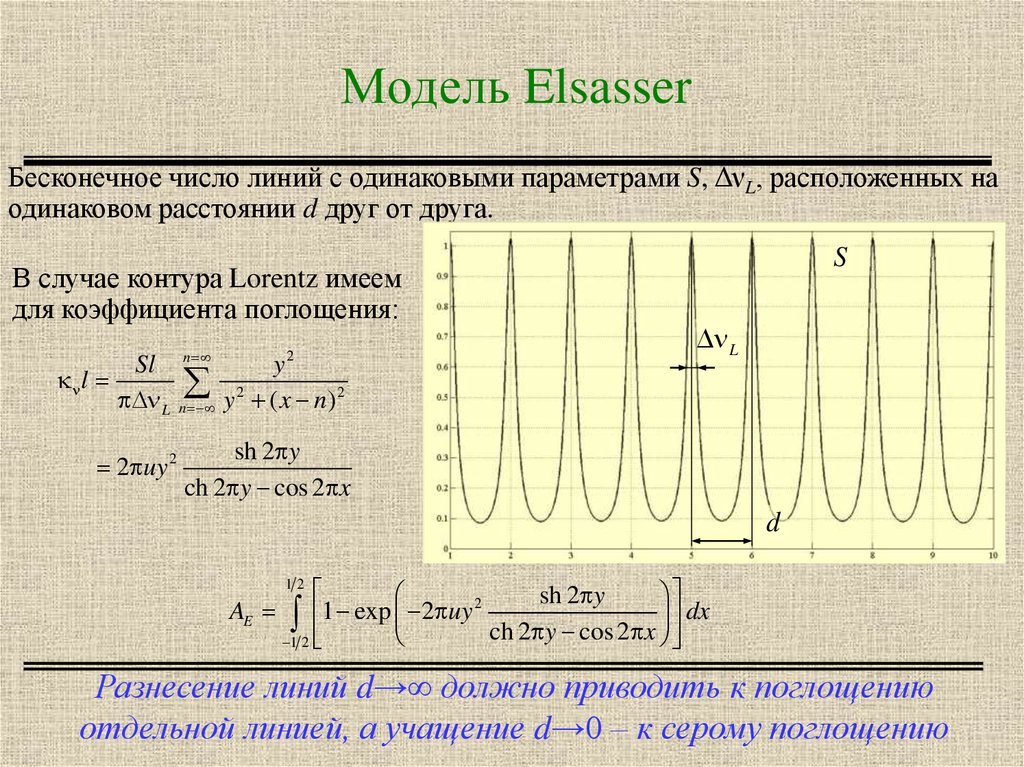
8. Модель Elsasser

Бесконечное число линий с одинаковыми параметрами S, ΔνL, расположенных на
одинаковом расстоянии d друг от друга.
В случае контура Lorentz имеем
для коэффициента поглощения:
l
Sl
L
2 uy 2
n
n
2
y
y 2 ( x n) 2
S
L
sh 2 y
ch 2 y cos 2 x
d
sh 2 y
2
1
exp
2
uy
dx
1 2
ch 2 y cos 2 x
12
AE
Разнесение линий d→∞ должно приводить к поглощению
отдельной линией, а учащение d→0 – к серому поглощению

9. Частные случаи:

Случай редко расположенных линий:
sh 2 y 2 y, ch 2 y 1 (2 y ) 2 2, cos 2 x 1 (2 x) 2 2
12
2
2
y
1
2
AE 1 exp 2 uy 2
dx
1
exp
2
uy
dx AL
2
2
2
2
(2
y
)
(2
x
)
y
x
1 2
1 2
12
Случай часто расположенных линий:
y
12
AE
1 2
1, sh 2 y
ch 2 y
cos 2 x 1
1 exp 2 uy 2 dx 1 exp 2 uy 2
Модель Elsasser соответствует колебательному спектру,
который в атмосфере характерен для паров воды

10. Случайная модель Goody

Пусть n линий располагаются на интервале шириной nd равновероятно. Тогда
вероятность данной реализации спектра имеет вид
n
dw( , S )
TG
0 nd
0
1
TG
nd
1
nd
d
i 1
(nd ) n
n
p ( S , S0 )dS
i 1
d i
p ( S , S 0 )dS
nd
0 nd n
Sl
Sl
L
p( S , S0 )
L
exp
dw
(
,
S
)
exp
dSd i
2
2
2
2
(
)
nd
L
i
L ( i )
0 0 i 1
Sl L
0 p(S , S0 ) nd 2 exp 2L x 2 dxdS
nd 2
nd 2
p( S , S )
0
0
i
nd 2
dxdS 1
1
TG 1
nd
n
Sl L
0 p(S , S0 ) nd 2 1 exp 2L x 2 dxdS
nd 2
Допустим, что число линий в полосе очень велико: n→∞.
n

11. Бесконечное число линий в модели Goody

n
Второй замечательный предел:
1
TG 1
nd
a
lim 1 e a
n
n
n
Sl L
n
0 p(S , S0 ) nd 2 1 exp 2L x 2 dxdS
nd 2
1
Sl L
exp p ( S , S0 ) 1 exp
dxdS
2
2
d
x
L
0
1)
p ( S , S0 ) ( S S0 ) линии одинаковой интенсивности
1
Sl L
TG exp 1 exp
dx exp AL
2
2
L x
d
2)
p ( S , S0 ) exp( S / S0 ) S0 пуассоновское распределение
1. внутри групп линий по Elsasser, а группы случайно;
2.спектр разбивается на интервалы, внутри линии по Goody.

12. Неоднородные трассы. Модель Curtis-Godson

однородные трассы – изометрические и изобарическим
неоднородная трасса заменяется эффективной однородной
в случаях слабого и сильного поглощений совпадает с точными формулами
на примере поглощения с линией Lorentz:
l
Sn ( z )
n ( z )
1
1 exp
A
dz d
2
2
( )
0 n ( n ) n ( z )
l
S n n
1
A
) 1 exp n ( )2
(
n
n
Случай слабого поглощения
d
2
Sn ( z )
n ( z )
1
A
) 0 n ( )2 ( z ) 2 dzd
(
n
n
l
n ( z )
1
Sn ( z )
d dz S n ( z )dz
2
2
( ) ( n ) n ( z )
0 n
0 n
l
l
Аналогично распишем для выражения через эффективные
A l S n
параметры:
n

13. Случай сильного поглощения

Сравнивая оба выражения получим:
l
Sn
1
S n ( z )dz
l0
При сильной линии поглощение происходит “крыльями” линии и можно
допустить, что ( n ) 2 2n ( z ) :
l
1
1
1
A
S ( z ) n ( z )dz d
1 exp
2 n
( )
n ( n ) 0
1
1
1
A
) 1 exp n ( n )2 Sn n l d
(
Сравнивая выражения
n
1
S l
l
Sn ( z ) n ( z )dz
0
l
S
n
( z ) n ( z ) dz
0
l
S
n
( z )dz
0
Неоднородные трассы с неразрешенными линиями поглощения
считаются с помощью таблиц