Similar presentations:
Математика 6 класс. Обыкновенные дроби
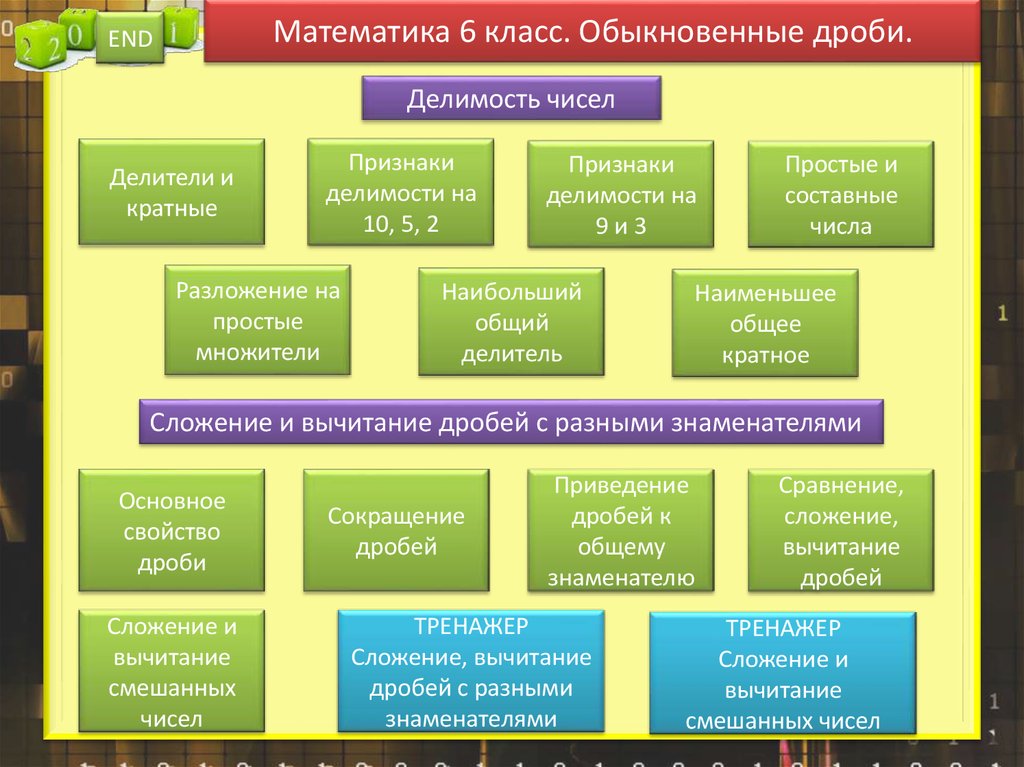
1. Математика 6 класс. Обыкновенные дроби.
ENDДелимость чисел
Делители и
кратные
Признаки
делимости на
10, 5, 2
Разложение на
простые
множители
Признаки
делимости на
9и3
Наибольший
общий
делитель
Простые и
составные
числа
Наименьшее
общее
кратное
Сложение и вычитание дробей с разными знаменателями
Основное
свойство
дроби
Сложение и
вычитание
смешанных
чисел
Сокращение
дробей
Приведение
дробей к
общему
знаменателю
ТРЕНАЖЕР
Сложение, вычитание
дробей с разными
знаменателями
Сравнение,
сложение,
вычитание
дробей
ТРЕНАЖЕР
Сложение и
вычитание
смешанных чисел
2.
Делителем натурального числа а называютнатуральное число, на которое а делится без
остатка.
Пример:
Д(18): 1, 2, 3, 6, 9, 18
Д(37): 1, 37
Д(25): 1, 5, 25
Д(6): 1, 2, 3, 6
Д(19): 1, 19
КОНЕЧНОЕ КОЛИЧЕСТВО
3.
Кратным натурального числа а называютнатуральное число, которое без остатка
делится на а.
Пример:
К(8): 8, 16, 24, 32 …
К(11): 11, 22, 33, 44 …
К(48): 48, 96 …
К(99): 99, 198, 297 …
БЕСКОНЕЧНОЕ КОЛИЧЕСТВО
4. Пример: 1. Доказать, что число 70525 кратно числу 217.
70525 : 217= 32570525 217
651
____
325
- 542
434
____
5
- 108
1085
____
0
Делится нацело,
значит 70525 кратно 217.
5. Пример: 2. Доказать, что число 729 делитель числа 225261.
225261 : 729 = 309729
- 225261
2187
____
309
1
656
- ____
6561
0
Делится нацело,
значит 729 делитель
числа 225261.
6. На 10: число оканчивается цифрой 0.
Примеры: 10 10; 100 10; 251 107. На 5: число оканчивается цифрами 0 и 5.
Примеры: 10 5; 255 5; 161 58. На 2: число должно быть четным (оканчивается на цифры 0, 2, 4, 6, 8).
Примеры: 32 2; 68 2; 51 2Нечетные числа оканчиваются
цифрами 1, 3, 5, 7, 9.
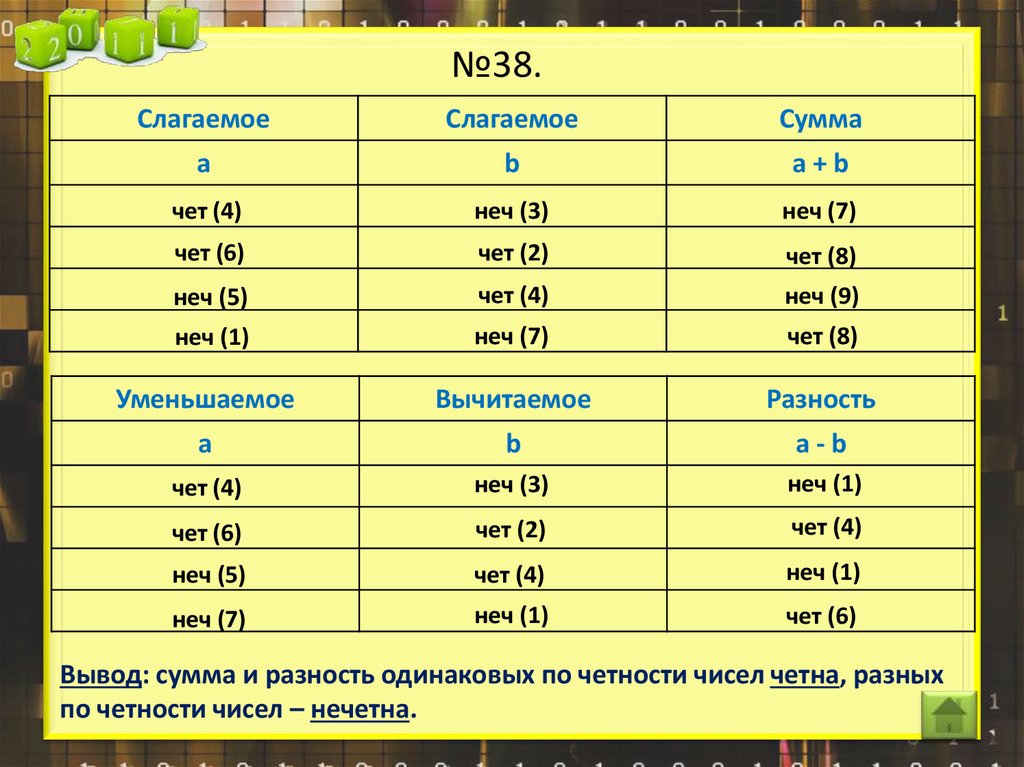
9. №38.
СлагаемоеСлагаемое
Сумма
а
b
а+b
чет (4)
неч (3)
неч (7)
чет (6)
чет (2)
чет (8)
неч (5)
чет (4)
неч (9)
неч (1)
неч (7)
чет (8)
Уменьшаемое
Вычитаемое
Разность
а
b
а-b
чет (4)
неч (3)
неч (1)
чет (6)
чет (2)
чет (4)
неч (5)
чет (4)
неч (1)
неч (7)
неч (1)
чет (6)
Вывод: сумма и разность одинаковых по четности чисел четна, разных
по четности чисел – нечетна.
10. Простые числа имеют только 2 делителя (1 и само число). (см. таблицу на форзаце учебника)
Составные числа имеют более 2делителей.
Число 1 не является ни простым,
ни составным.
11.
Примеры:Простые: 2, 3, 5, 7,…
Составные: 4, 6, 8, 9,…
12. На 9: если сумма цифр числа делится на 9, то и число делится на 9.
На 3: если сумма цифр числа делитсяна 3, то и число делится на 3.
13.
Примеры: 1) 75432 3 ( 9 ), т.к.7+5+4+3+2=21, 21 3, 21 9.
2) 2772825 3 ( 9), т.к.
2+7+7+2+8+2+5=33, 33 3, 33 9.
3)5402070 3 ( 9), т.к.
5+4+2+7=18, 18 3, 18 9.
14. Любое число можно разложить на простые множители.
15.
Примеры: 216 = 2 2 2 3 3 3 23 33216
108
54
27
9
3
1
2
2
2
3
3
3
16.
2Примеры: 60 = 2 2 3 5 2 3 5
60
30
15
5
1
2
2
3
5
17.
НОД (х, у) – это наибольшее натуральноечисло, на которое числа х и у делятся без
остатка.
Пример:
Д(6): 1, 2, 3, 6
Д(12): 1, 2, 3, 4, 6, 12
НОД(6, 12) = 6
18. План нахождения НОД:
1. Разложить числа на простые множители.2. Обвести в кружок одинаковые множители.
3. Найти их произведение – это и есть НОД.
19.
Примеры: НОД(12; 18) = 2 3 612
6
3
1
2
2
3
18 2
9 3
3 3
1
20.
Примеры: НОД(675; 825) = 5 5 3 75675
135
27
9
3
1
5
5
3
3
3
825
165
33
11
1
5
5
3
11
21.
Примеры: НОД(24; 35) = 124
12
6
2
1
2
2
3
2
35 5
7 7
1
Нет общих
делителей, кроме
1.
Если у чисел нет общих множителей, кроме 1, то
они называются взаимно простые (НОД(х, у)=1).
22.
НОК (х, у)– наименьшее натуральное
число, которое кратно и х, и у.
23. План нахождения НОК:
1. Разложить числа на простые множители.2. В НОК выписать наибольшее число.
3. Домножить выписанное число на
недостающие множители из другого
разложения.
4. Найти произведение.
24.
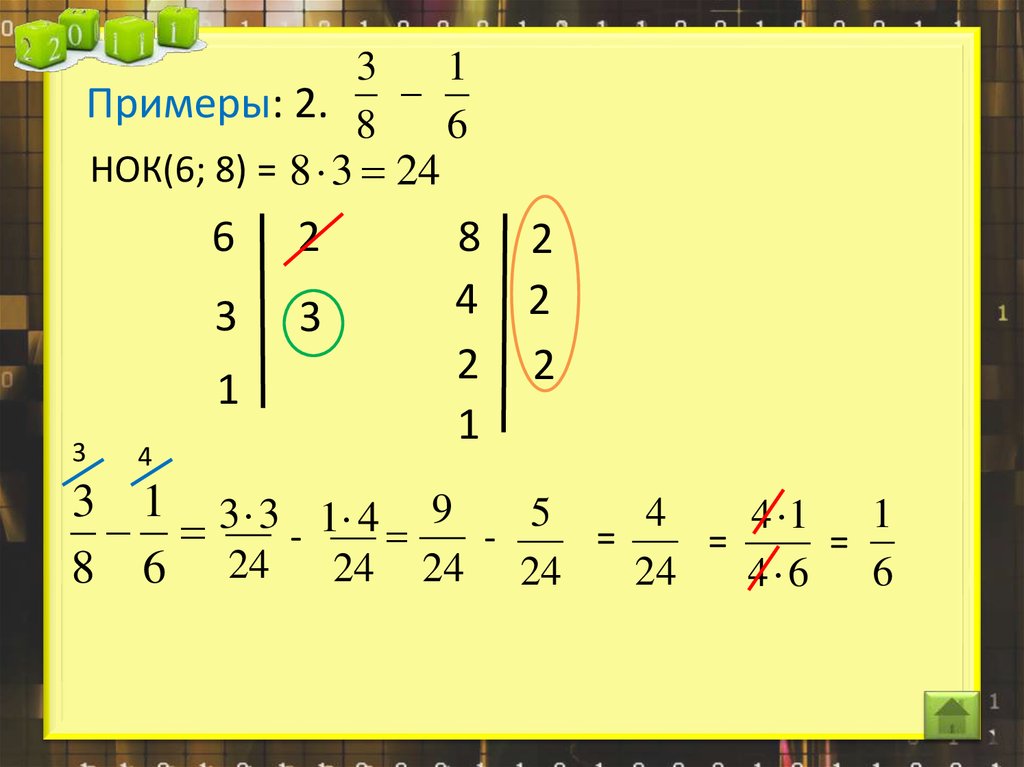
Примеры: НОК(6; 8) = 8 3 248 2
6 2
4 2
3 3
2
Недостающий 2
1 множитель
1
выписали
25.
НОК(72; 99) = 99 2 2 2 99 8 79272
36
12
4
2
1
2
3
3
2
2
99 3
33 3
11 11
1
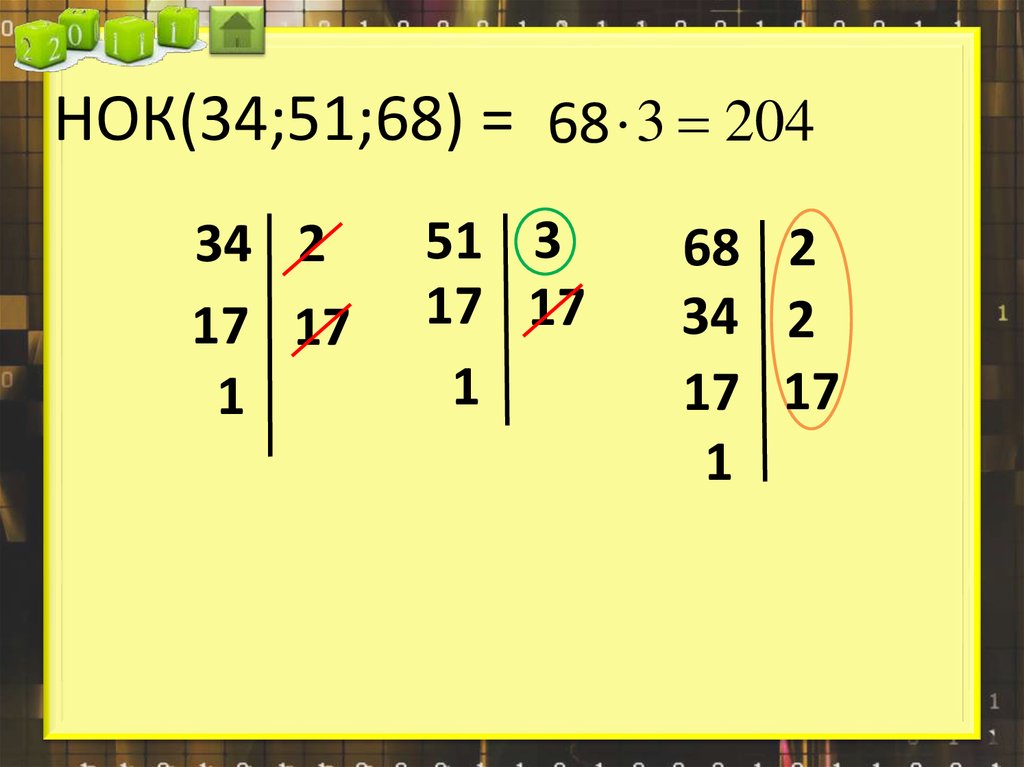
26.
НОК(34;51;68) = 68 3 20434 2
17 17
1
51 3
17 17
1
68 2
34 2
17 17
1
27.
a 2 2 3 5 5b 2 2 3 3 3 5
НОК(a, b) = 2 2 3 3 3 5 5 =2700
28.
Если числитель и знаменатель дробиумножить или разделить на одно и то же
натуральное число, то получится равная ей
дробь.
29. Примеры:
1) 2 2 2 43
3 2
2 2 3 6
3 3 3 9
6
8
2 2 4
3 3 4 12
2 4 6
8 10
3 6 9 12 15
2) 20 20 : 2 10
24
24 : 2
20 10 5
24 12 6
12
20 20 : 4 5
24 24 : 4 6
30.
НОД используется присокращении дробей
31.
Примеры:198
Сократить дробь:
66 3
3
1452 66 2 11 22
198
99
33
11
1
2 1452 2
3 726 2
3 363 3
11 121 11
11 11
1
НОД(198,1452)= 2 3 11 66 , значит числитель и
знаменатель можно сократить на 66
32.
Примеры:56
Сократить дробь:
196
56
28
14
7
1
2
2
2
7
196
98
49
7
1
28 2 2
28 7 7
2
2
7
7
НОД(56, 196)= 2 2 7 28 , значит числитель и
знаменатель можно сократить на 28
33.
Примеры:Сократить дробь:
15 3 5 3
25 5 5 5
2 2 1 1
6 2 3 3
34.
Любые две дроби можнопривести к одному и тому же
знаменателю.
Наименьший общий
знаменатель (НОЗ) равен НОК
знаменателей дробей.
35. План приведения к НОЗ:
1. Найти НОК знаменателей дробей – этоНОЗ.
2. Расставить дополнительные множители
для всех дробей (НОЗ делим на
знаменатели дробей).
3. Умножить числители дробей на
дополнительный множитель.
36.
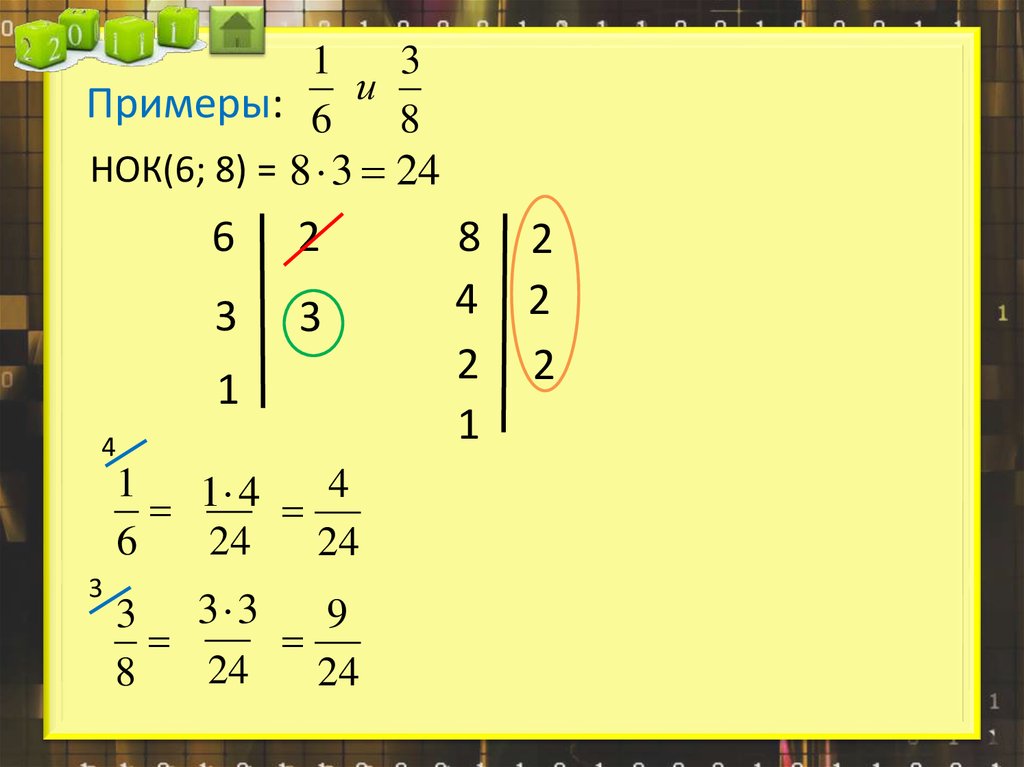
13
Примеры: 6 и 8
НОК(6; 8) = 8 3 24
6
2
3
3
1
4
1
4
1
4
6
24
24
3
3 3 3
9
24
8
24
8
4
2
1
2
2
2
37.
47
Примеры: 9 и 15
НОК(9; 15) = 15 3 45
9
3
3
3
1
5
4 5 4 20
9
45
45
3
7 7 3 21
45
15
45
15 5
3 3
1
38. План:
1. Привести дроби к НОЗ.2. Сравнить (сложить, вычесть) полученные
дроби.
39.
13
Примеры: 1. Сравнить и
6
8
НОК(6; 8) = 8 3 24
6
2
3
3
1
4
1
4
1
4
6
24
24
3
3 3 3
9
24
8
24
8
4
2
1
2
2
2
4
9
24 24
1 3
6 8
40.
31
Примеры: 2. 6 8
НОК(6; 8) = 8 3 24
6
2
3
3
1
4
3
8
4
2
1
2
2
2
1 3 1 4 3 3 4
9
13
+
+
=
6 8 24 24 24 24
24
41.
13
Примеры: 2. 8 6
НОК(6; 8) = 8 3 24
6
2
3
3
1
3
4
8
4
2
1
2
2
2
3 1 3 3 1 4 9
5
4
1
4 1
=
=
=
8 6 24 24 24 24
24
6
4 6
42. План сложения:
1. Привести дробные части чисел к НОЗ.2. Отдельно выполнить сложение целых и
дробных частей.
3. Если нужно – сократить дробь.
4. Если при сложении дробных частей
получилась неправильная дробь, выделить целую часть и прибавить к
полученной целой части.
43. План вычитания:
1. Привести дробные части чисел к НОЗ.2. Если дробная часть уменьшаемого
меньше дробной части вычитаемого,
превратить ее в неправильную дробь,
уменьшив на 1 целую часть.
3. Отдельно выполнить вычитание целых и
дробных частей.
44.
Примеры:2
3
2
3
7
7 1
1
4
5
8
3 5
3
8
8
14
7
14
14
7 2
2
14
3
2
7
5
31
31
21
10
5 2
5
+2
7 7
=
8
12
24
24
24
24
7
7
7 1 8
24
24
2
2
7 4 11
9
9
3
3
1
5 2
2
10
1
9
8
8
8
8
8
5 15
5 3
3
15 15
15
45.
Примеры:3 4 3 1
1
4 4 4 4
7
8
7
1
7 1 6 1 5
8
8
8
8
3
3
8 4 4
11
11
3
4
7
3
19
9
28
5
5
5
15 20
60 60
60
7
9
1
9
12
6
21
9
7
10 4 10 4 9 4 5 5
14
2
14
14
7
14
14
14
3
4
7
5
2
8
15
7 3 7
-3 4
36
36
36
12
9













































 mathematics
mathematics








