Similar presentations:
Математические методы в экономике
1. МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ЭКОНОМИКЕ
К.э.н., доценти.о. зав. каф. ЭЭММИ
Бурцева Татьяна Александровна
2. БАЗОВЫЙ УЧЕБНИК
3. История вопроса
4. История вопроса
5. История вопроса
6. Понятие о модели и моделировании
7. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
8. Математическая модель
9.
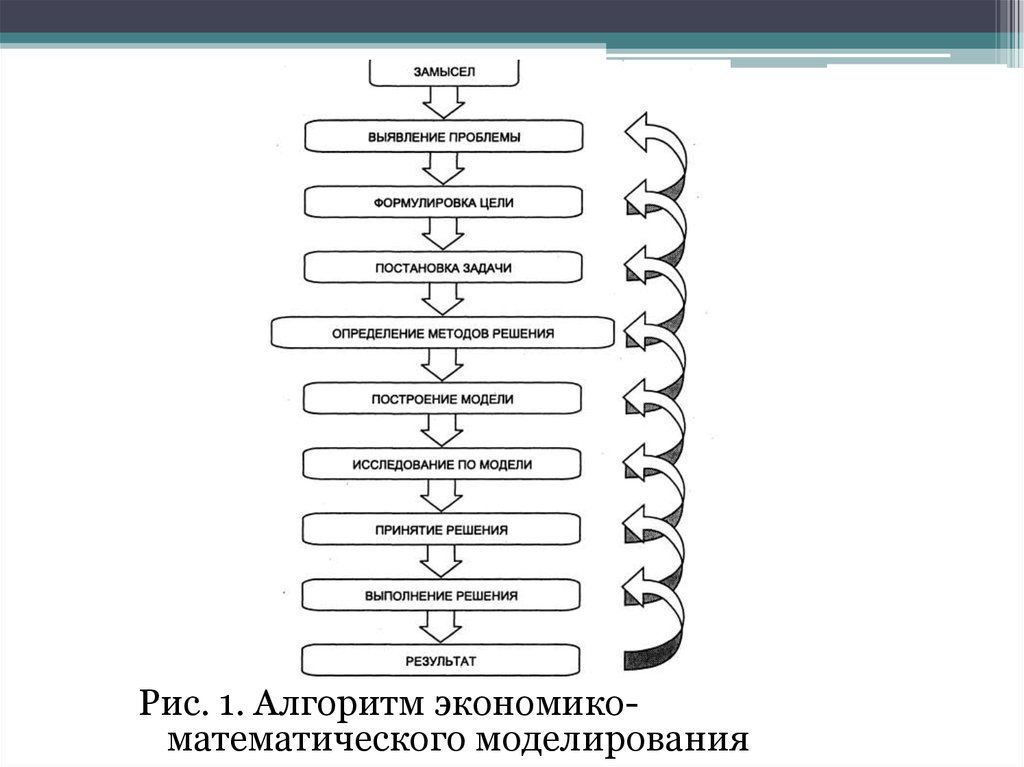
Рис. 1. Алгоритм экономикоматематического моделирования10.
11. продолжение
12. Цель и критерии моделирования
13. Пример модели
14. Пример модели
15. Пример модели
16. Специальная модель - производственная функция
Специальная модель производственная функция17. Производственная функция Кобба-Дугласа
Производственная функция КоббаДугласа18.
19. Специальная модель - функция потребления
20.
21.
22.
23. Математическое моделирование задач экономической (коммерческой) деятельности
Особенности данной деятельностиопределяющие необходимость применения
математического моделирования
• Системность
• Многофакторность
• Многовариантность
• Необходимость обеспечения оптимальности
при принятии решений
24.
25. ПОНЯТИЕ ЦЕЛЕВОЙ ФУНКЦИИ
26.
27. Общая постановка задачи принятия решения включает:
• Задание цели;• Средств достижения цели;
• Оценка результата
28. Математическая модель принятия решения
• Формализованное описание цели, средств,результатов и способа связи между
средствами и результатами.
29. Если множества альтернатив и состояний конечны: то целевую функцию F можно представить в матричном виде
30. Целевая функция в виде матрицы
31. РЕШЕНИЕ ЗАДАЧИ ПРИНЯТИЯ РЕШЕНИЯ В УСЛОВИЯХ ОПРЕДЕЛЕННОСТИ
• Существует детерминированная связь междупринятием решения и результатом, поэтому
задачи называются детерминированными
• Существует единственное оптимальное
решение и оно может быть определено с
помощью нахождения экстремума целевой
функции
32. Пример: решение задачи распределения коммерсантов по операциям (дан хронометраж по затратам времени на операцию)
33. Критерий эффективности: общее число человеко-часов на все операции (Т)
34.
35. Если увеличивается число вариантов принятия решения (число стратегий, то есть растет n!), то уже нужно применять сложные
методы, в данномслучае методы линейного
программирования
36.
37. РЕШЕНИЕ ЗАДАЧИ ПРИНЯТИЯ РЕШЕНИЯ ПРИ ЗАДАНИИ ОТНОШЕНИЙ ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ
• Вводят количественный критерий,позволяющий задать отношения
предпочтения (прибыль, издержки, доход и
т.п.)
38.
39.
40.
41.
42.
43.
44.
45.
46.
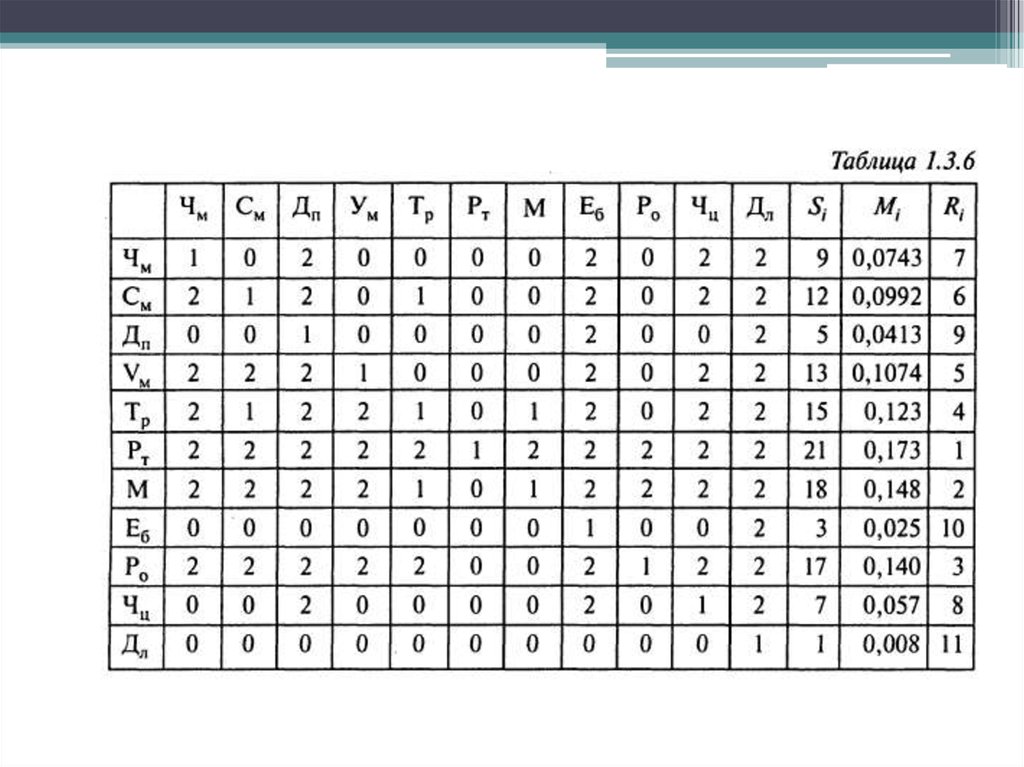
47. Расчет интегральных оценок
• F(2105)=0,0743*1+0,0992*1+0,413*1+0,1074*2+0,123*
2+0,173*1+0,148*1+0,025*
2+0,14*2+0,057*1+0,08*2=1,4754
• F(2106)
=0,0743*1+0,0992*2+0,413*1+0,1074*1+0,123*
1+0,173*2+0,148*1+0,025*
1+0,14*1+0,057*1+0,08*1=1,2722
• Так как лучшему меньший ранг, то 2106
лучше
48. ПРИМЕР ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ОЦЕНОК
48ПРИМЕР ПОСТРОЕНИЯ
ИНТЕГРАЛЬНЫХ ОЦЕНОК
Проект
NPV,
тыс. руб.
PI
IRR, %
PBP, лет
А
900
1,1
25
2
В
800
1,15
40
1,5
С
1000
1,2
30
1,8
D
1010
1,25
20
1,0
Е
300
1,4
15
1,2
49. Таблица рангов проектов
49Таблица рангов проектов
Ранг
NPV
PI
IRR
PBP
Сумма
А
3
1
3
1
8
В
2
2
5
3
12
С
4
3
4
2
13
D
5
4
2
5
16
Е
1
5
1
4
11
Наилучшими при выборе является проект D,
набравший максимальное количество баллов
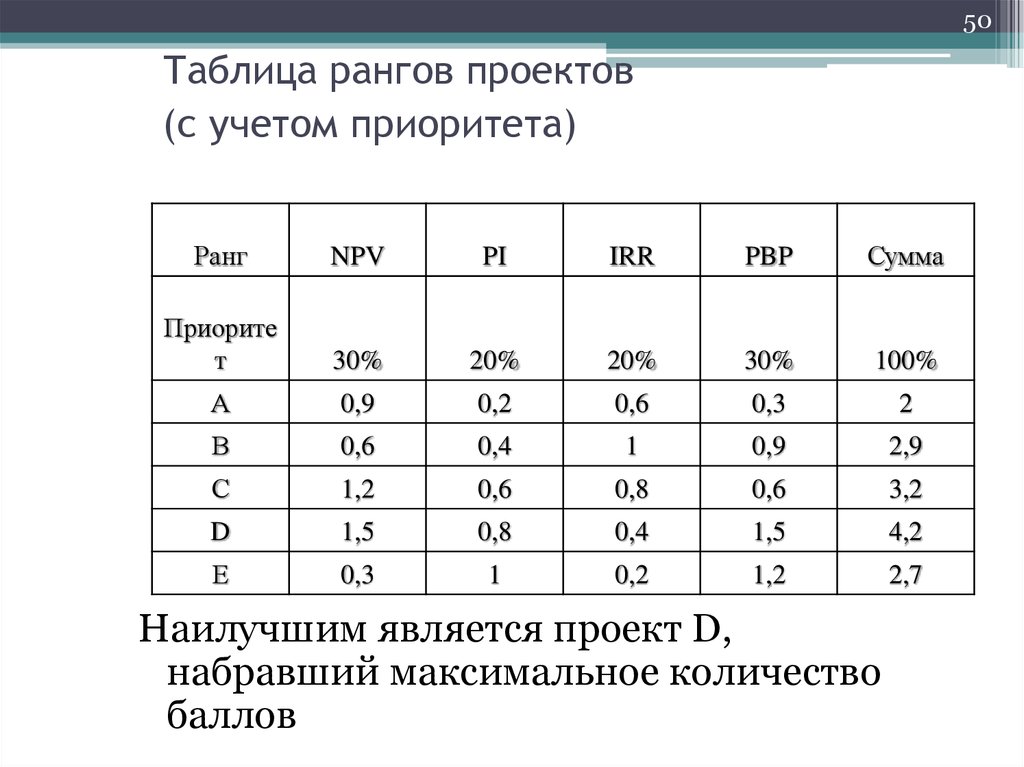
50. Таблица рангов проектов (с учетом приоритета)
50Таблица рангов проектов
(с учетом приоритета)
Ранг
NPV
PI
IRR
PBP
Сумма
Приорите
т
30%
20%
20%
30%
100%
А
0,9
0,2
0,6
0,3
2
В
0,6
0,4
1
0,9
2,9
С
1,2
0,6
0,8
0,6
3,2
D
1,5
0,8
0,4
1,5
4,2
Е
0,3
1
0,2
1,2
2,7
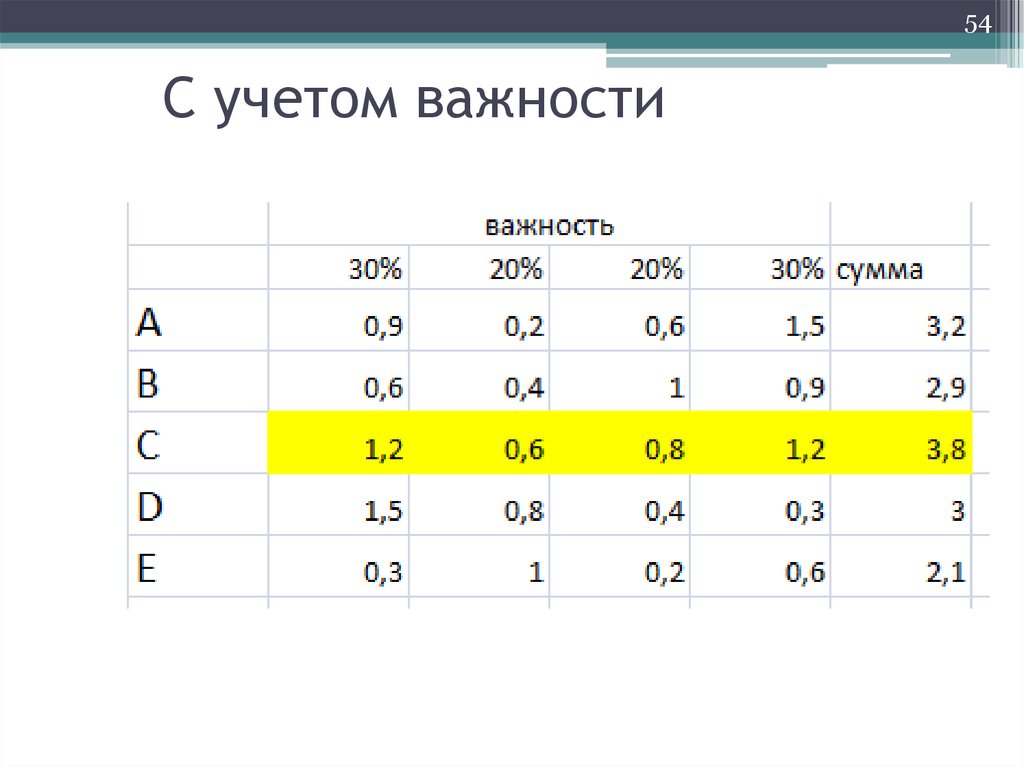
Наилучшим является проект D,
набравший максимальное количество
баллов
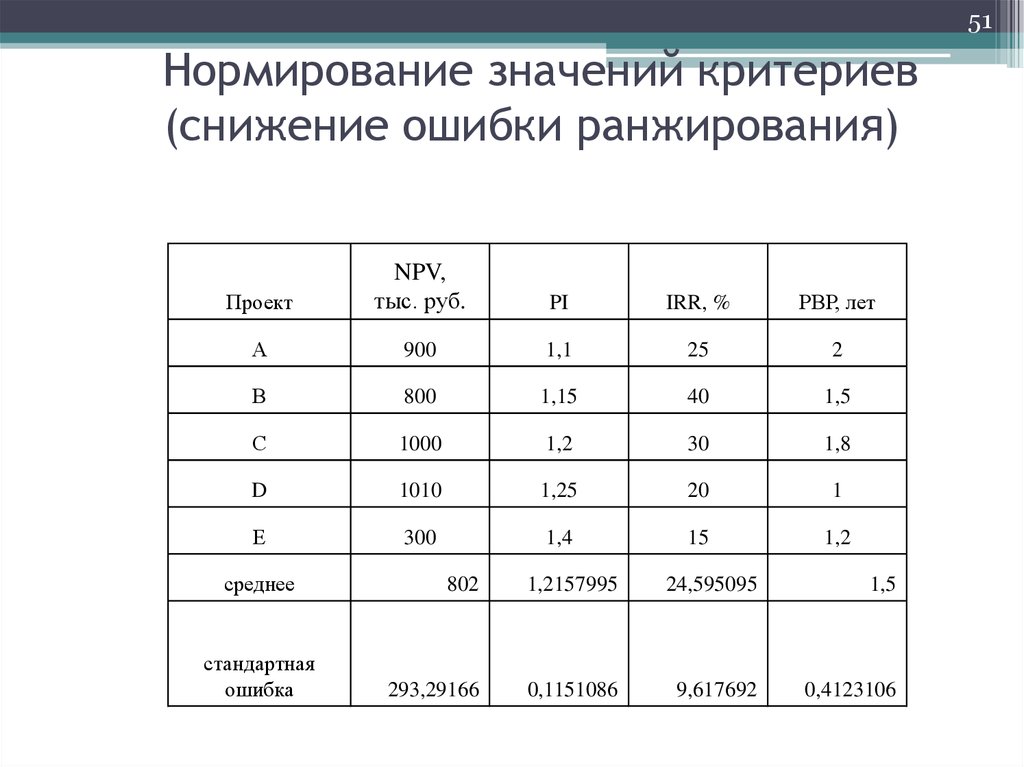
51. Нормирование значений критериев (снижение ошибки ранжирования)
51Нормирование значений критериев
(снижение ошибки ранжирования)
Проект
NPV,
тыс. руб.
PI
IRR, %
PBP, лет
А
900
1,1
25
2
В
800
1,15
40
1,5
С
1000
1,2
30
1,8
D
1010
1,25
20
1
Е
300
1,4
15
1,2
среднее
стандартная
ошибка
802
1,2157995
24,595095
1,5
293,29166
0,1151086
9,617692
0,4123106
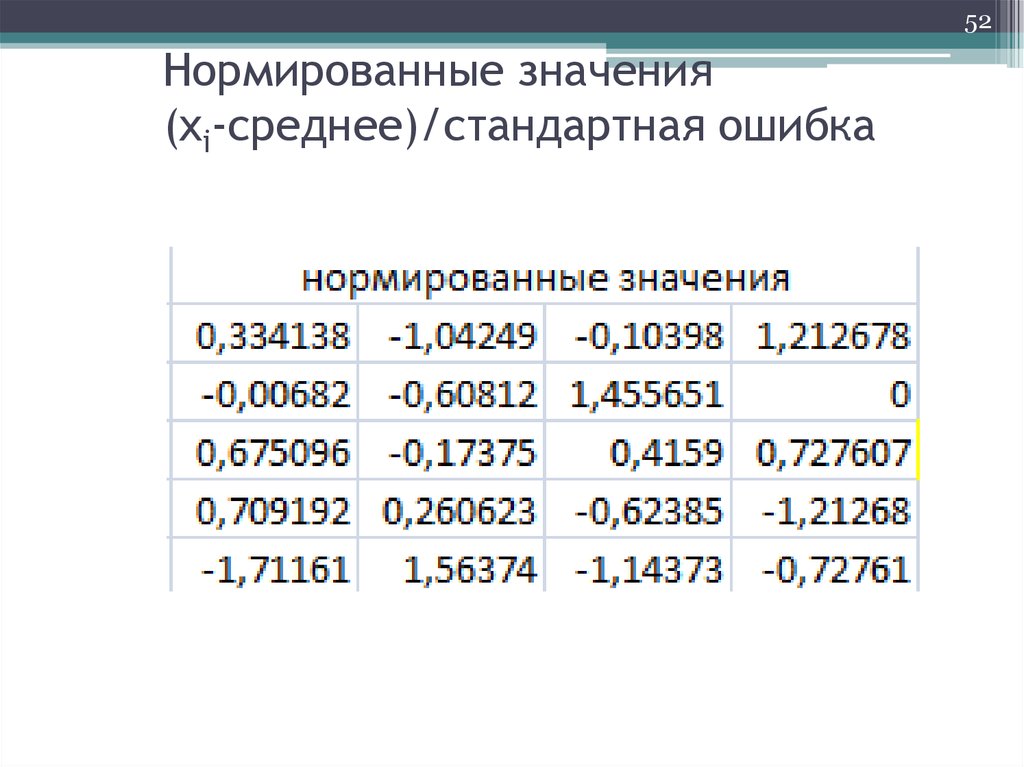
52. Нормированные значения (xi-среднее)/стандартная ошибка
52Нормированные значения
(xi-среднее)/стандартная ошибка
53. РАНГИ НОРМИРОВАННЫХ ПОКАЗАТЕЛЕЙ
53РАНГИ НОРМИРОВАННЫХ
ПОКАЗАТЕЛЕЙ
54. С учетом важности
54С учетом важности













































 economics
economics








