Similar presentations:
Статическая детерминированная модель с дефицитом
1. Статическая детерминированная модель с дефицитом
2. Статическая детерминированная модель с дефицитом
Рассмотрим случай, который отличается от предыдущеготолько тем, что превышение спроса над запасами
допускается, т.е. штраф за дефицит конечный.
• Дефицит ресурса - термин, означающий, что при
отсутствии запасаемого продукта спрос сохраняется с
той же интенсивностью, потребляется запас, создание
или хранение которого требует больших затрат.
Эта разница в затратах составляет штраф за дефицит.
Штраф за дефицит может также быть связан с тем, что
клиент временно уходит к другому поставщику, а мы
недополучаем прибыль от реализации продукции.
Такая модель носит название статической
детерминированной модели с дефицитом.
3. Статическая детерминированная модель с дефицитом
Статическая детерминированная модель сдефицитом - задача управления запасами,
которая сводится к отысканию такого
оптимального объема партии и уровня
запаса, при которых суммарные затраты на
хранение, доставку и уплату штрафа за
дефицит были бы минимальными.
Будем называть ее модель II.
4. Статическая детерминированная модель с дефицитом
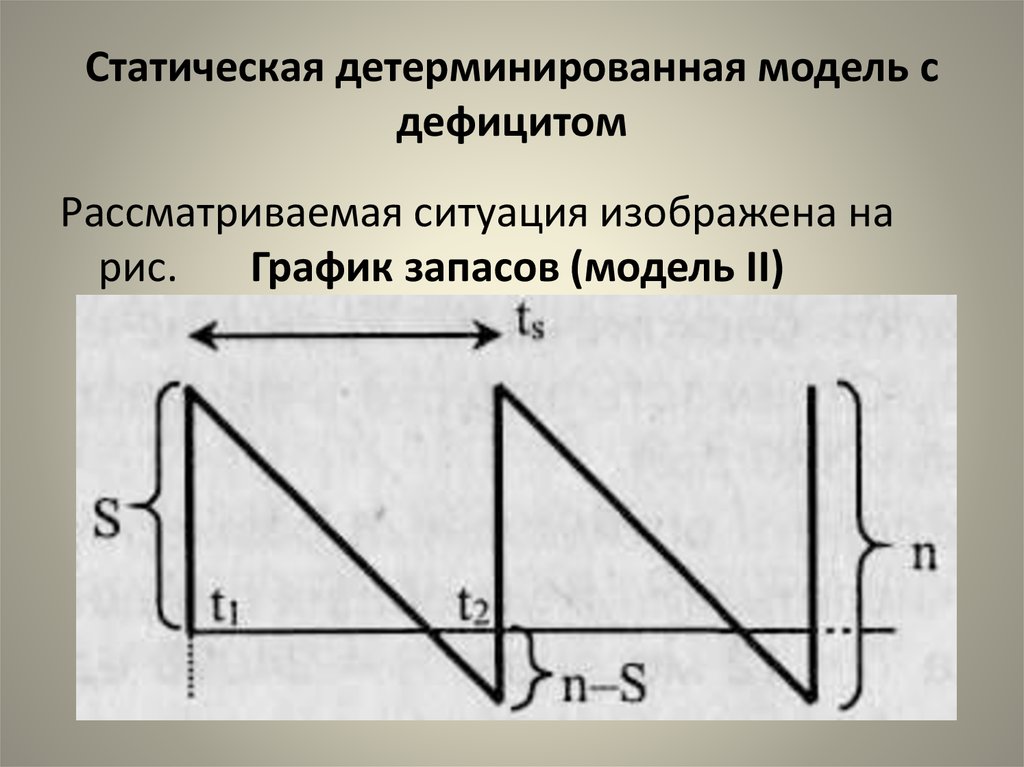
Рассматриваемая ситуация изображена нарис.
График запасов (модель II)
5. Статическая детерминированная модель с дефицитом
В начале каждого интервала имеется уровеньзапасов.
Из подобия треугольников находим:
6. Статическая детерминированная модель с дефицитом
Средний запас в течение t, равен . Поэтомузатраты на хранение за все время t1
S
составляют — C1 t1 .
2
Средняя нехватка (превышение спроса над
уровнем запасов) за время t2 равна (n-S)/2,
и штраф за время t2 составляет n S
2
Ct
2
2
7. Статическая детерминированная модель с дефицитом
Таким образом, ожидаемые суммарныерасходы за все время Т определяются
выражением
8. Статическая детерминированная модель с дефицитом
Подставляя сюда найденные выше выражениядля t1 и t2 и учитывая полученное в
предыдущем разделе выражение для ts,
имеем
(5)
9. Статическая детерминированная модель с дефицитом
уравнения (5) можно найти оптимальныезначения для n и S.
Получаем:
(6)
(7)
10. Статическая детерминированная модель с дефицитом
Этим значениям соответствуют:t so 2
Q
0
T Cs
R C1
2 RT C1 C s
C C
C
1
2
(8)
2
C
2
C1 C 2
(9)









 mathematics
mathematics economics
economics








