Линейное программирование

1. Линейное программирование

LOGO

2. Примеры задач линейного программирования

LOGO

3.

Задача о распределении ресурсов
Для изготовления двух видов продукции
А и В используют три вида ресурсов:

4.

Задача о распределении ресурсов
Изучение рынка сбыта показало, что объем выпуска
изделий А не должен превышать объема изделий В
более, чем на три единицы
Необходимо составить такой план производства
продукции, при котором выручка от ее реализации
будет максимальной

5.

Задача о распределении ресурсов
Решение
Введем переменные
х1 – число единиц продукции А, запланированных к
производству
х2 – число единиц продукции В, запланированных к
производству
Выручка:
F 2 x1 3x2
Цель:
F max

6.

Задача о распределении ресурсов
Решение
Ограничения
1) Условие неотрицательности:
x1 0, x2 0
3x1 3x2 15
3) На запас сырья 2: 2 x1 6 x2 18
4) На запас сырья 3:
4 x1 16
5) Соотношение между 1 и 2: x1 x2 3
2) На запас сырья 1:

7.

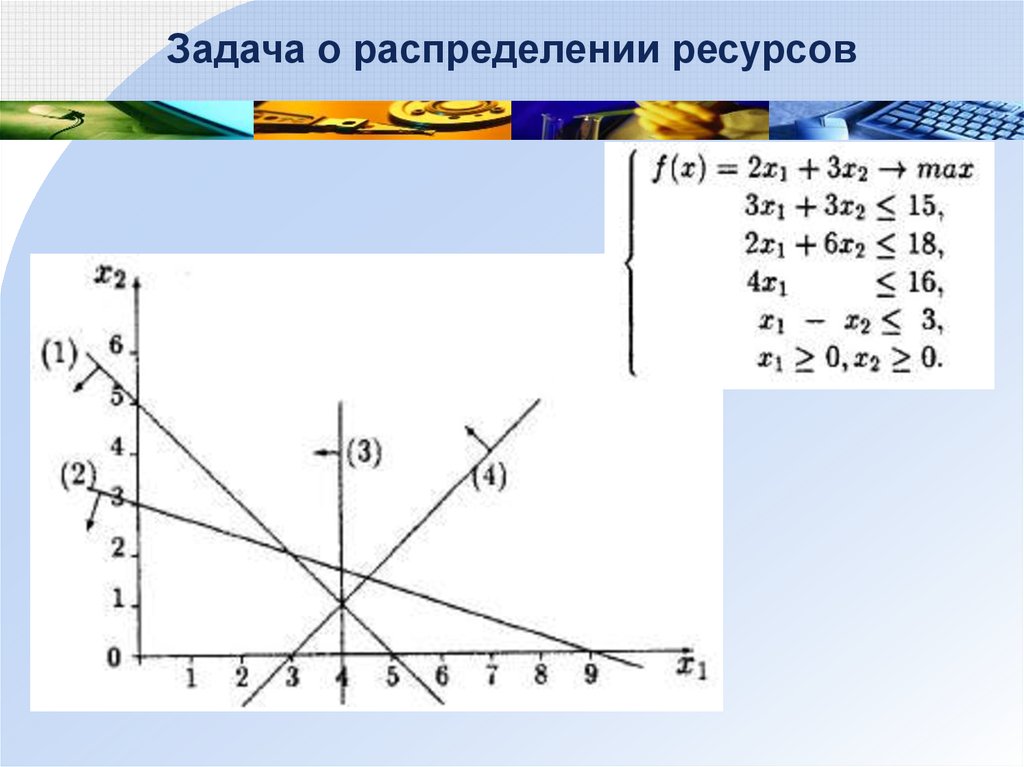
Задача о распределении ресурсов
Математическая модель

8.

Задача о рационе (о диете)
В дневной рацион питания цыплят включают два
продукта П1 и П2. Причем продукта П1 должно
войти в дневной рацион не более 200 ед.
Стоимость 1 ед. продукта П1 составляет 2 ден.
ед., а продукта П2 – 4 ден. ед.
Определить оптимальный рацион питания,
стоимость которого будет наименьшей

9.

Задача о рационе (о диете)
Решение
Введем переменные
х1 – число единиц продукта П1, входящего в дневной
рацион
х2 – число единиц продукта П2, входящего в дневной
рацион
Стоимость дневного рациона :
Цель:
F 2 x1 4 x2
F min

10.

Задача о рационе (о диете)
Решение
Ограничения
1) Условие неотрицательности:
x1 0, x2 0
2) Ограничение на максимальное содержание
продукта П1: x1 200
3) Ограничения на минимальное содержание
питательных веществ:
0,2 x1 0,2 x2 120 0,4 x1 0,2 x2 160

11.

Задача о рационе (о диете)
Математическая модель

12. Основные понятия

LOGO

13.

Терминология
Термин линейное программирование
линейное означает: ищется экстремальное значение
(min или max) линейной целевой функции при
линейных ограничениях (линейных уравнениях или
неравенствах)
Линейное программирование (ЛП) — это метод
оптимизации моделей, в которых целевые функции
и ограничения линейны

14.

Общая задача линейного
программирования
Задача линейного программирования в общем виде
(ЗЛП) – это задача о нахождении экстремума
линейной функции на множестве, заданном
линейными уравнениями и неравенствами
Допустимый план – любой элемент допустимого
множества
Оптимальный план – допустимый план, являющийся
решением ЗЛП

15.

Каноническая задача линейного
программирования

16.

Каноническая задача линейного
программирования
В канонической задаче ЛП (КЗЛП):
1) находится максимум целевой функции
2) все ограничения имеют вид уравнений
3) все переменные неотрицательны

17.

Сведение общей ЗЛП к канонической
В канонической задаче:
1) целевая функция → max
2) все ограничения - уравнения
3) все переменные неотрицательны
Целевая функция F min
Решение. Переходим к (-F) max (переходим к
противоположной функции)

18.

Сведение общей ЗЛП к канонической
В канонической задаче:
1) целевая функция → max
2) все ограничения - уравнения
3) все переменные неотрицательны
В ограничениях есть неравенство
a1x1+a2x2 b
Решение. Вводим новую переменную х3 0:
a1x1+a2x2 - х3 = b

19.

Сведение общей ЗЛП к канонической
В канонической задаче:
1) целевая функция → max
2) все ограничения - уравнения
3) все переменные неотрицательны
Есть не положительные переменные
Решение.
xi 0 ti xi 0
не известен знак xi
вводим xk 0, xl 0 : xi xk xl

20.

Сведение общей ЗЛП к канонической
В канонической задаче:
1) целевая функция → max
2) все ограничения - уравнения
3) все переменные неотрицательны
Вывод
Каждую задачу линейного программирования можно
привести к канонической форме

21.

Теоретическое обоснование
Теорема
Если целевая функция принимает максимальное
значение в некоторой точке допустимого множества, то
она принимает это значение и некоторой вершине
этого множества
Вывод
Оптимальное решение следует искать в вершинах
допустимого множества

22.

Варианты решения ЗЛП F max
Решение
достигается в
вершине
Целевая
функция не
ограничена
Бесконечное
множество
решений
f (x)
x2
x2
x2
f (x)
D
f (x)
D
D
x1
x1
x1

23. Графический метод решения

LOGO

24.

Графическое решение
f (x) c1x1 c2 x2 max
x2
f ( x) f ( x)
f ( x)
,
(c1 , c2 )
x2
x1
x*
D
f ( x) xConst3
1
f ( x) Const1
f ( x) Const2

25.

Графическое решение
Алгоритм решения
Построить на плоскости допустимое множество
Найти градиент целевой функции
Построить прямую – линию уровня целевой функции
Найти оптимальный план
x*

26.

Задача о распределении ресурсов

27.

Задача о распределении ресурсов
С – оптимальный план

28.

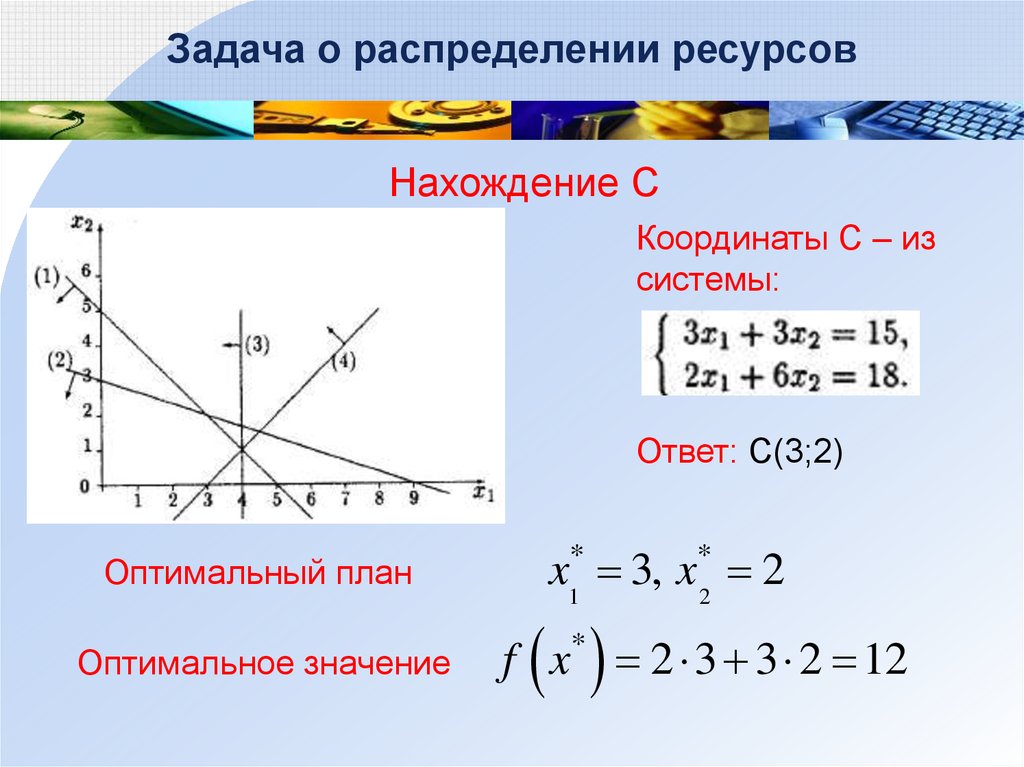
Задача о распределении ресурсов
Нахождение С
Координаты С – из
системы:
Ответ: С(3;2)
Оптимальный план
Оптимальное значение
x1* 3, x*2 2
f x 2 3 3 2 12
*

29. Симплекс-метод

LOGO

30.

Основные теоретические сведения
Система линейных уравнений ─ система с базисом,
если в каждом уравнении есть базисная переменная
Базисная переменная уравнения: входит в уравнение с
коэффициентом +1 и отсутствует x1 3 x3 x4 1,
в остальных уравнениях системы
Остальные переменные свободные x2 4 x3 x5 3
Специальная задача ЛП ─ каноническая задача ЛП, в
которой:
f x3 x4 max
• все правые части
x 3x x 1,
уравнений неотрицательны; 1
3
4
• система уравнений ─
x2 4 x3 x4 3,
система с базисом;
x1 0, x2 0, x3 0, x4 0
• в целевой функции
нет базисных переменных

31.

Основные теоретические сведения
Базисное решение ─ решение системы,
соответствующее нулевым значениям свободных
переменных.
x 3 x x 1,
3
4
(1;3;0;0) 1
x2 4 x3 x4 3
Опорный план ─ базисное решение, удовлетворяющее
условию неотрицательности.
Опорный план (решение) ─ вершина допустимого
множества.

32.

Основная теорема ЛП
Если каноническая задача линейного
программирования разрешима, то её оптимальный
план содержится среди конечного числа её опорных
планов.
Симплекс-метод ─ метод перебора опорных
решений.

33.

Пример
x1 x2 150
x1 3 x2 300
x1 0, x2 0
f x1 2 x2 max
Каноническая форма задачи: x1 x2 x3 150
Она же ─ специальная!
x1 3 x2 x4 300
x1 0, x2 0, x3 0, x4 0
f x1 2 x2 max

34.

Пример
Опорный план:
x3 150 x1 x2
(0;0;150;300)
x4 300 x1 3 x2
Значение целевой функции
f (0;0;150;300) 0
f x1 2 x2
План не оптимальный!
Увеличиваем x2
x1 0 x2 100 (второе уравнение!)
x2 100 f (0;100;50;0) 200

35.

Пример
Проверка оптимальности
Приведение задачи к специальному виду:
1
1
x2 100 3 x1 3 x4 ,
x3 50 2 x1 1 x4
3
3
Выражение целевой функции через свободные
переменные
1
2
f x1 2 x2 200 x1 x4
3
3
План не оптимальный!

36.

Пример
1
2
Увеличиваем x1 f 200 x1 x4
3
3
1
1
x2 100 3 x1 3 x4 ,
x4 0 x1 75
x3 50 2 x1 1 x4
3
3
Опорный план: (75;75;0;0)
Соответствует базисным переменным x1 и x2
Значение целевой функции
f (75;75;0;0) 225 f x1 2 x2

37.

Пример
Проверка оптимальности
Приведение задачи к специальному виду:
3
1
x1 75 2 x3 2 x4 ,
x2 75 1 x3 1 x4
2
2
Выражение целевой функции через свободные
переменные
1
1
f x1 2 x2 225 x3 x4
2
2
(75;75;0;0) оптимальный план

38.

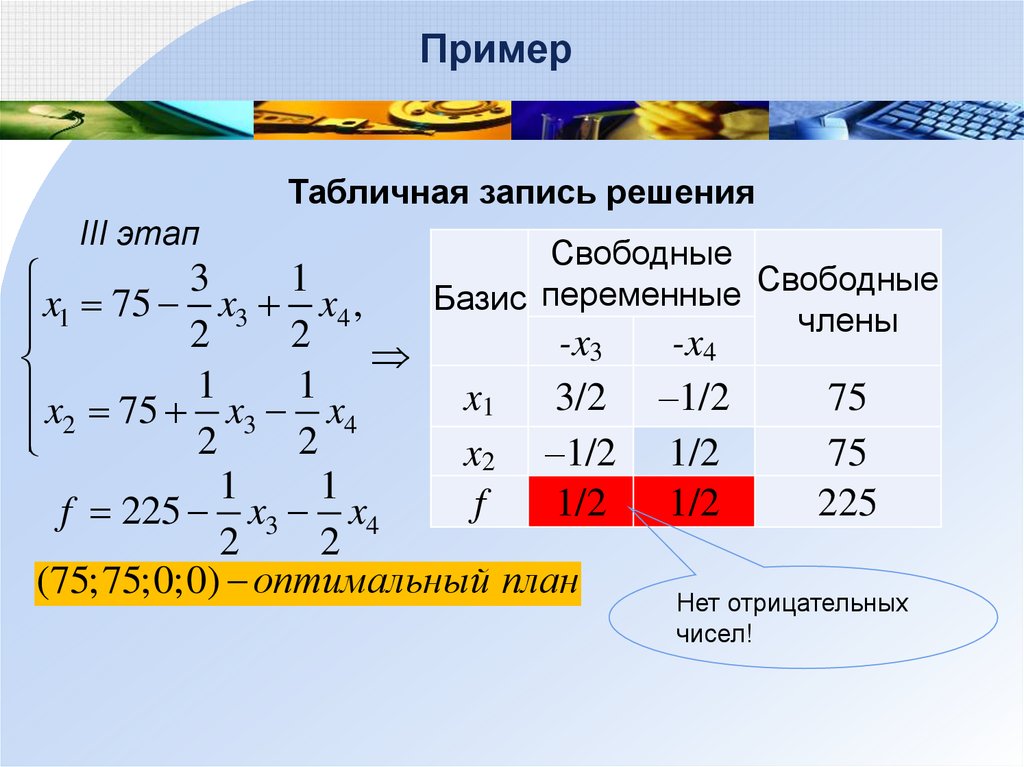
Пример
Табличная запись решения
I этап
x3 150 x1 x2
x4 300 x1 3 x2
Свободные
Свободные
Базис переменные
члены
f x1 2 x2
f (0;0;150;300) 0
1. Самое маленькое
отрицательное число в
последней строке
x3
x4
f
-x1
1
1
–1
-x2
1
3
–2
150
300
0
2. Самое маленькое
отношение свободного
члена к
положительному числу
в столбце

39.

Пример
Табличная запись решения
II этап
1
1
x2 100 3 x1 3 x4 ,
x3 50 2 x1 1 x4
3
3
1
2
f 200 x1 x4
3
3
f (0;100;50;0) 200
1. Самое маленькое
отрицательное число в
последней строке
Свободные
Свободные
Базис переменные
члены
x2
x3
f
-x1
1/3
2/3
–1/3
-x4
1/3
–1/3
2/3
100
50
200
2. Самое маленькое
отношение свободного
члена к
положительному числу
в столбце

40.

Пример
Табличная запись решения
III этап
Свободные
Свободные
Базис переменные
члены
3
1
x1 75 2 x3 2 x4 ,
-x3
x1
3/2
x2 75 1 x3 1 x4
2
2
x2 –1/2
1
1
f
1/2
f 225 x3 x4
2
2
(75;75;0;0) оптимальный план
-x4
–1/2
1/2
1/2
75
75
225
Нет отрицательных
чисел!

41.

Специальная задача ЛП
xn 1 a11 x1 a12 x2 ... a1n xn b1 ,
xn 2 a21 x1 a22 x2 ... a2 n xn b2 ,
...
xn m am1 x1 am 2 x2 ... amn xn bm .
Базисные
переменные
Свободные
переменные
f c c1 x1 c2 x2 ... cn xn max
Все xi 0 (i 1,2, , n m)
Все b j 0 (i 1,2, , m)

42.

Симплексная таблица
Базисные Свободные переменные Свободные
переменные -x1 . . . -xs . . . -xn
члены
xn+1
...
xn+r
...
xn+m
f
a11
...
ar1
...
am1
-c1
. . . a1s
... ...
. . . ars
... ...
. . . ams
. . . -cs
Опорное решение (0,0,
n
...
...
...
...
...
...
0, b1, b2 ,
a1n
...
arn
...
amn
-cn
, bn m )
b1
...
br
...
bm
c

43.

Алгоритм симплекс-метода
x1 x2 150
Подготовительный этап
x1 3 x2 300
1. Приведение к каноническому виду
2. Приведение к специальному виду x1 0, x2 0
3. Составление симплексной таблицыf x 2 x max
1
2
Свободные
Свободные
Базис переменные
члены
x3
x4
f
-x1
1
1
–1
-x2
1
3
–2
150
300
0
x3 x1 x2 +150,
x4 x1 3 x2 +300
x1 0, x2 0, x3 0, x4 0
f ( x1 ) 2( x2 ) max

44.

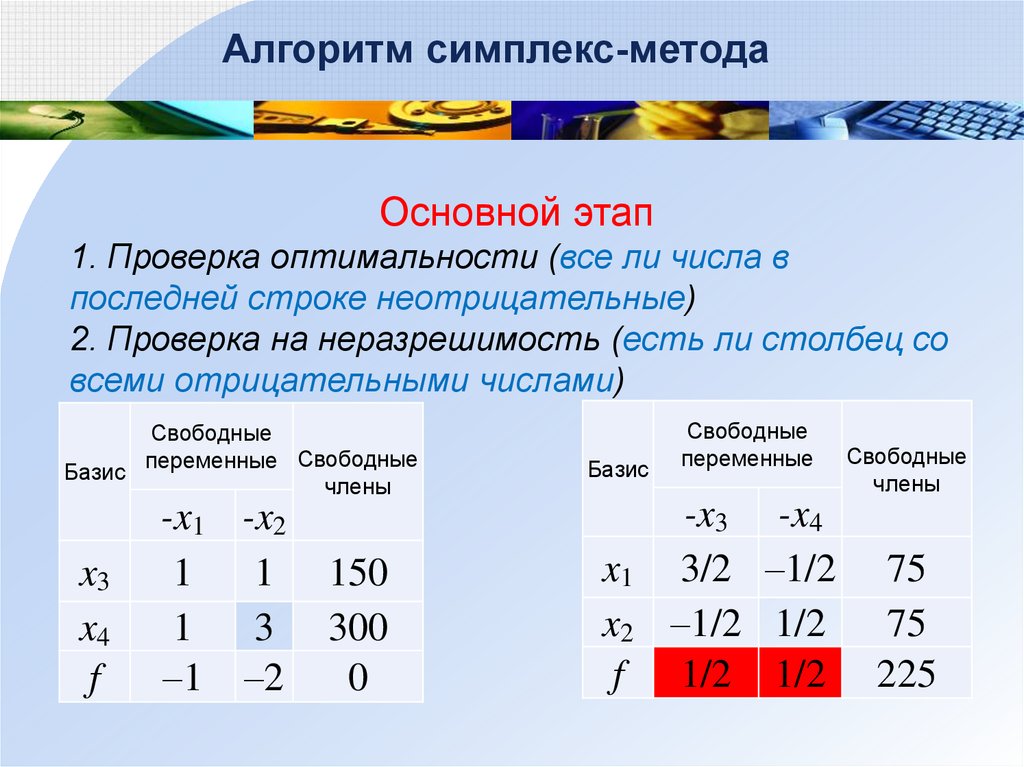
Алгоритм симплекс-метода
Основной этап
1. Проверка оптимальности (все ли числа в
последней строке неотрицательные)
2. Проверка на неразрешимость (есть ли столбец со
всеми отрицательными числами)
Свободные
переменные Свободные
Базис
члены
x3
x4
f
-x1 -x2
1
1
1
3
–1 –2
150
300
0
Базис
x1
x2
f
Свободные
переменные
-x3
3/2
–1/2
1/2
-x4
–1/2
1/2
1/2
Свободные
члены
75
75
225

45.

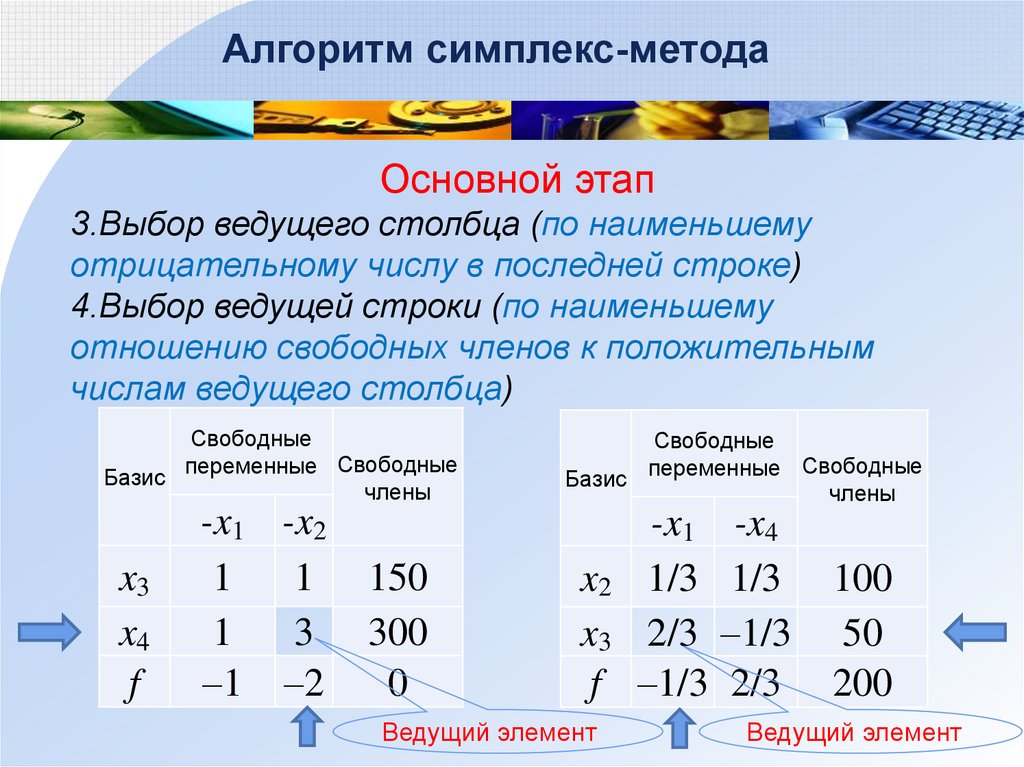
Алгоритм симплекс-метода
Основной этап
3.Выбор ведущего столбца (по наименьшему
отрицательному числу в последней строке)
4.Выбор ведущей строки (по наименьшему
отношению свободных членов к положительным
числам ведущего столбца)
Свободные
переменные Свободные
Базис
члены
x3
x4
f
-x1 -x2
1
1
1
3
–1 –2
150
300
0
Свободные
Свободные
Базис переменные
члены
-x1 -x4
x2 1/3 1/3
x3 2/3 –1/3
f –1/3 2/3
Ведущий элемент
100
50
200
Ведущий элемент

46.

Алгоритм симплекс-метода
Основной этап
5. Замена базисной переменной: переменная
ведущего столбца становится базисной, ведущей
строки ─ свободной
6. Преобразование ведущего элемента: вместо него
записывается его обратная величина
Свободные
переменные Свободные
Базис
члены
x3
x4
f
-x1 -x2
1
1
1
3
–1 –2
Свободные
Свободные
Базис переменные
члены
-x1 -x4
150
300
0
x3
x2
f
1/3

47.

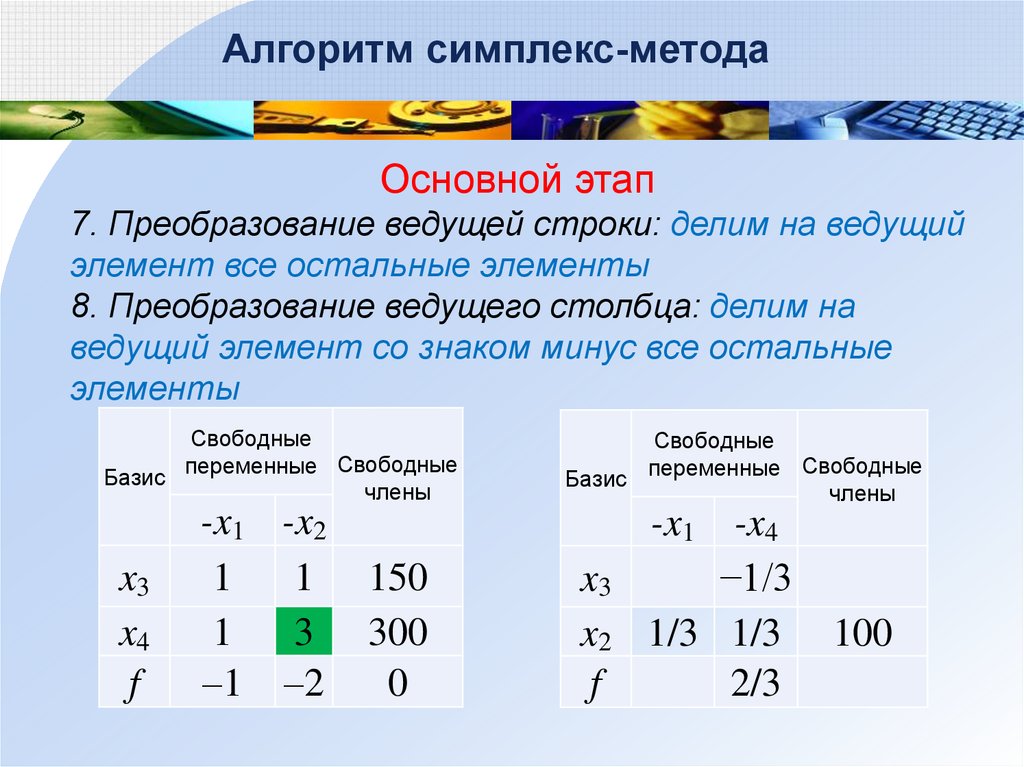
Алгоритм симплекс-метода
Основной этап
7. Преобразование ведущей строки: делим на ведущий
элемент все остальные элементы
8. Преобразование ведущего столбца: делим на
ведущий элемент со знаком минус все остальные
элементы
Свободные
переменные Свободные
Базис
члены
x3
x4
f
-x1 -x2
1
1
1
3
–1 –2
150
300
0
Свободные
Свободные
Базис переменные
члены
x3
x2
f
-x1 -x4
−1/3
1/3 1/3 100
2/3

48.

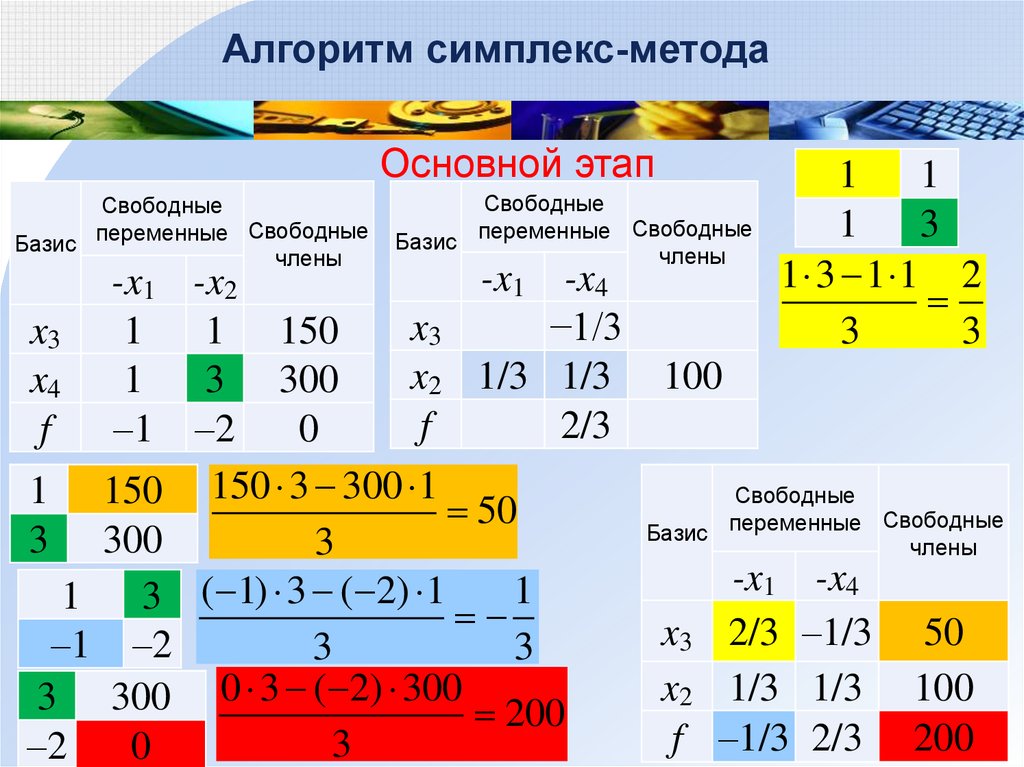
Алгоритм симплекс-метода
Основной этап
8. Преобразование остальных элементов таблицы по
правилу прямоугольника
Исходный элемент
a
Значение c в ведущей
строке и в том же столбце
Новое значение
Значение d в ведущем
столбце и той же строке
Ведущий элемент b
ab cd
a
b

49.

Алгоритм симплекс-метода
Основной этап
Свободные
Свободные
Базис переменные
члены
Свободные
Свободные
Базис переменные
члены
1
1
1
3
1 3 1 1 2
3
3
-x1 -x4
-x1 -x2
x3
−1/3
x3
1
1 150
x2 1/3 1/3 100
x4
1
3 300
f
2/3
f
–1 –2
0
Свободные
1 150 150 3 300 1 50
переменные Свободные
Базис
3 300
3
члены
-x1 -x4
1
3 ( 1) 3 ( 2) 1 1
x3 2/3 –1/3 50
–1 –2
3
3
x2 1/3 1/3 100
3 300 0 3 ( 2) 300 200
f –1/3 2/3 200
3
–2
0

50.

Пример (распределении ресурсов)
Исходная модель
Каноническая форма
задачи:
3 x1 3 x2 15
2 x 6 x 18
1
2
4 x1 16,
x1 x2 3
x1 0, x2 0
3 x1 3 x2 x3 15
2 x 6 x x 18,
1
2
4
4 x1 x5 =16,
x1 x2 x6 =3
xi 0 (i 1,2, ,6)
f 2 x1 3 x2 max
f 2 x1 3 x2 max
Она же ─ специальная!

51.

Пример (распределении ресурсов)
Симплекс-таблица
Свободные
переменные Свободные
Базис
члены
x3
x4
x5
x6
f
-x1 -x2
3
3
2
6
4
0
1 –1
–2 –3
План не
оптимальный
15
18
16
3
0
3 x1 3 x2 x3 15
2 x 6 x x 18,
1
2
4
4 x1 x5 =16,
x1 x2 x6 =3
xi 0 (i 1,2, ,6)
f 2 x1 3 x2 max
Задача разрешима

52.

Пример (распределении ресурсов)
Симплекс-таблица
Преобразованная таблица
Свободные
переменные Свободные
Базис
члены
x3
x4
x5
x6
f
-x1 -x2
3
3
2
6
4
0
1 –1
–2 –3
Ведущий элемент
15
18
16
3
0
Базис
x3
x2
x5
x6
f
План не
оптимальный
Свободные
переменные
-x1 -x4
2 –1/2
1/3 1/6
4
0
4/3 1/6
–1 1/2
Свободные
члены
6
3
16
6
9
Задача разрешима

53.

Пример (распределении ресурсов)
Симплекс-таблица
Базис
x3
x2
x5
x6
f
Свободные
переменные
-x1 -x4
2 –1/2
1/3 1/6
4
0
4/3 1/6
–1 1/2
Преобразованная таблица
Свободные
члены
6
3
16
6
9
Базис
x1
x2
x5
x6
f
Свободные
переменные
-x3
1/2
−1/6
−2
−2/3
1/2
-x4
–1/4
1/4
1
1/2
1/4
Ведущий элемент
3
2
4
2
12
x1 3, x 2 2
*
План
оптимальный!
Свободные
члены
*
f ( x* ) 12