Similar presentations:
Система m линейных уравнений с n неизвестными
1. Система m линейных уравнений с n неизвестными
2.
Система m линейных уравнений с nпеременными имеет вид
a11 x1 a12 x2 a1n xn b1 ,
a x a x a x b ,
21 1 22 2
2n n
2
,
.............................................
am1 x1 am 2 x2 amn xn bm
3.
В задачах линейного программированияпредставляют интерес системы, в
которых ранг матрицы r системы A=(aij),
i=1,2…m, j=1,2…n, или, что то же самое,
максимальное число независимых
уравнений меньше числа переменных
4.
Любые m переменных системы mлинейных уравнений с n переменными
(m<n) называются основными (или
базисными), если определитель
матрицы коэффициентов при них
отличен от нуля.
Тогда остальные n - m переменных
называются неосновными ( или
свободными)
5.
Базисным решением системы m линейныхуравнений с n переменными называется
решение, в котором все n-m неосновных
переменных равны нулю.
В задачах линейного программирования
особый интерес представляют допустимые
базисные решения (опорные планы).
Число базисных решений является
конечным.
Базисное решение, в котором хотя бы одна
из основных переменных равна нулю,
называется вырожденным.
6.
Основными могут быть разные группы изn переменных. Максимальное число
групп основных переменных
C
m
n
7.
Пример. Найти все возможные группыосновных переменных в системе
x1 x2 2 x3 x4 0
2 x1 x2 2 x3 x4 2
8.
Решение системы называетсядопустимым, если оно содержит только
неотрицательные компоненты, в
противном случае – решение
допустимое.
9.
Базисным решением системы m линейныхуравнений с n переменными называется
решение, в котором все n-m
неосновных переменных равны нулю
10.
Пример. Найти все базисные решениясистемы
x1 x2 2 x3 x4 0
2 x1 x2 2 x3 x4 2
11. Симплексный метод решения задач линейного программирования
12.
Решение любой задачи линейногопрограммирования можно найти
симплексным методом.
Симплексный метод решения задачи
линейного программирования основан
на переходе от одного опорного плана к
другому, при котором значение целевой
функции возрастает ( убывает) (при
условии, что данная задача имеет
оптимальный план).
13.
Оптимальный план - совокупностьзначений переменных, при которых
достигается наибольшее или
наименьшее значение целевой
функции, любая другая совокупность
значений, удовлетворяющая
ограничениям, определяет опорный
(базисный) план.
14.
Для реализации симплексного методанеобходимо освоить три основных элемента:
Способ определения какого-либо
первоначального допустимого базисного
решения задачи (опорного плана)
Правило перехода к лучшему (не худшему)
решению
Критерий проверки оптимальности найденного
решения.
15.
Пусть требуется найти максимальное(минимальное) значение функции
F с1 x1 с2 x2 ... сn xn max(min)
16.
при условияха11 x1 а12 x2 ... а1п хn b1
a x a x ... a x b
21 1
22 2
2n n
2
..........
..........
..........
..........
........
am1 х1 am 2 x2 ... amn xn bm
17.
x1 0..........
x
n 0
18.
Алгоритм решения задачи симплекснымметодом:
привести задачу линейного
программирования к стандартному виду.
найти начальное базисное решение
(опорный план). Если базисное решение
отсутствует, задача не имеет решения в виду
несовместности системы ограничений
проверить полученное базисное решение на
оптимальность с помощью критерия
оптимальности
19.
если выполняется критерий оптимальностирешения, то решение задачи заканчивается
если выполняется условие существования
множества оптимальных решений, то путем
простого перебора найти все оптимальные
решения
если имеют место условия неограниченности
целевой функции, то задача не имеет решения
если пункты 4 - 6 алгоритма не выполняются,
найти новое опорное решение и перейти к
пункту 3
20.
Для нахождения первоначальногобазисного плана все переменные
разбиваются на две группы:
основные(базисные) и неосновные.
Положив неосновные переменные
равными нулю, получаем базисное
решение.
21.
Критерий оптимальности решенияпри отыскании
максимума(минимума) линейной
функции:
Если в выражении линейной функции
через неосновные переменные
отсутствуют положительные
(отрицательные) коэффициенты при
неосновных переменных, то решение
оптимально.
22.
Если система ограниченийнепротиворечива, то
выполнение конечного числа
последовательных шагов
симплексного метода приводит
к нахождению оптимального
решения задачи.
23.
Алгоритм решения задачилинейного
программирования
построением симплексной
таблицы
24.
Алгоритм:1. Систему линейных неравенств
записываем в каноническом виде. Для
этого в каждое неравенство добавляем
дополнительную переменную со знаком
«+», если неравенство имеет знак
меньше или равно и со знаком «-» в
противном случае
25.
После введения добавочных переменныхсистему уравнений и линейную
функцию записываем в виде:
26.
а11 x1 а12 x2 ... а1п хn хn 1 b1a x a x ... a x x b
21 1
22 2
2n n
n 2
2
................................................
a х a x ... a x x
m1 1
m2 2
mn n
n m bm
F c1 x1 c2 x2 ... cn xn 0
27.
2.Исходную расширенную систему
заносим в первую симплексную таблицу.
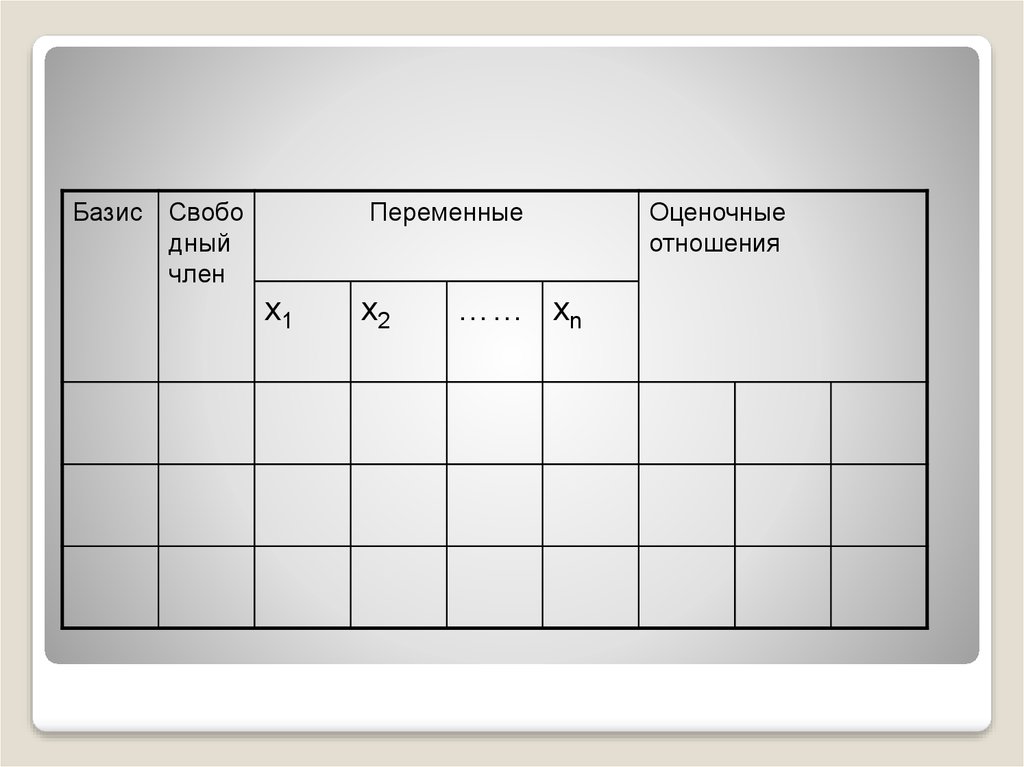
28.
БазисСвобо
дный
член
Переменные
х1
х2
…… хn
Оценочные
отношения
29.
3. Проверяем выполнение критерияоптимальности при решении задач на
максимум- наличие в последней
строке отрицательных коэффициентов.
Если таковых нет, то полученное
решение оптимально.
30.
4 Если критерий оптимальности невыполнен, то наибольший по модулю
отрицательный элемент в последней
строке определяет разрешающий
столбец s
31.
Составляем оценочные отношения каждойстроки по правилам:
1) ∞, если bi и ais имеют разные знаки;
2) ∞, если bi=0 и ais <0
3) ∞, если ais =0
4)
, если bi и ais имеют одинаковые
bi
ais
знаки
32.
Определяемbi
min
i
ais
.
33.
Если конечного минимума нет, тозадача не имеет конечного оптимума
(Fmax=∞)
Если минимум конечен, то выбираем
строку, в которой он достигается и
называем ее разрешающей строкой
q.
На пересечении разрешающей строки
и разрешающего столбца находится
разрешающий элемент аqs
34.
5. Переходим к следующей таблице поправилам:
в левом столбце записываем новый
базис: вместо основной переменной хqпеременную xs
в столбцах, соответствующим основным
переменным проставляем нули и
единицы: 1 – против «своей» основной
переменной 0- против «чужой»
основной переменной. 0 в последней
строке для всех основных переменных.
35.
новую строку с номером q получаем изстарой строки делением на
разрешающий элемент aqs
все остальные элементы получаем по
правилу прямоугольника:
a aij
/
ij
b bi
/
i
ais aqj
aqs
aisbq
aqs
36.
Пример. Решим задачу об использованииресурсов
37.
x1 3 x2 182 x x 16
1
2
x2 5
3 x1 21
x 0
1
x2 0
38.
F 2x1 3x2 max39.
1. Шагx1 3 x2 х3 18
2 x x х 16
2
4
1
x2 х5 5
3 x х 21
6
1
F 2 x1 3 x2 0
40.
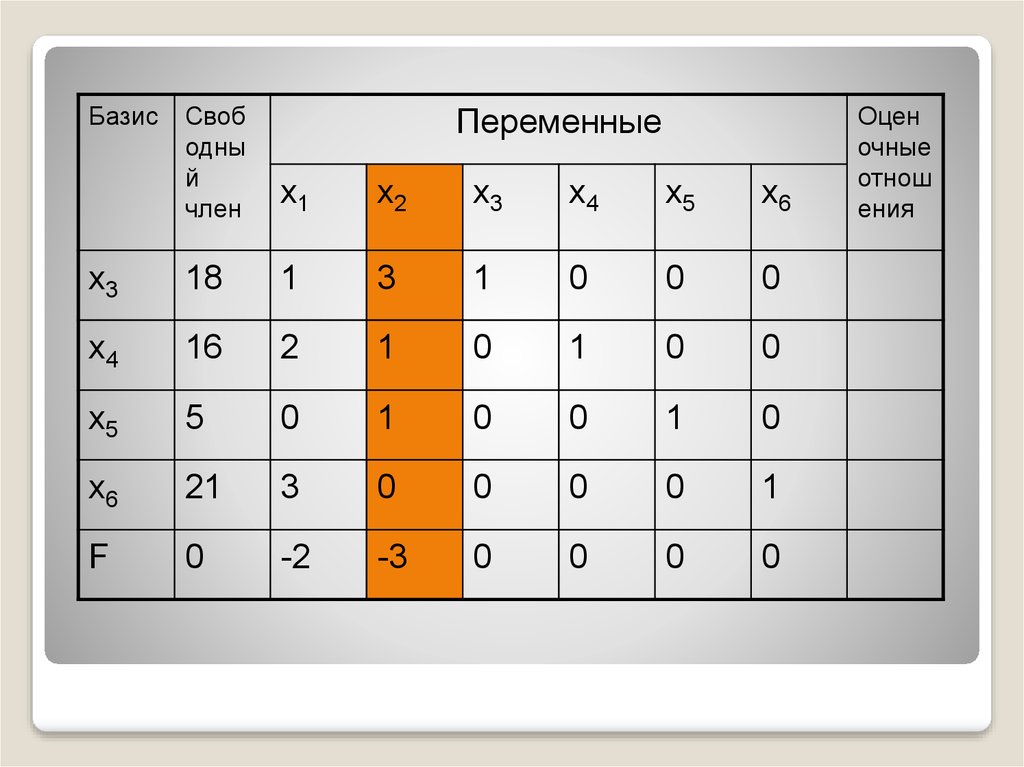
Заполняем первую симплексную таблицу,в которой переменные х3,х4,х5,х6 основные
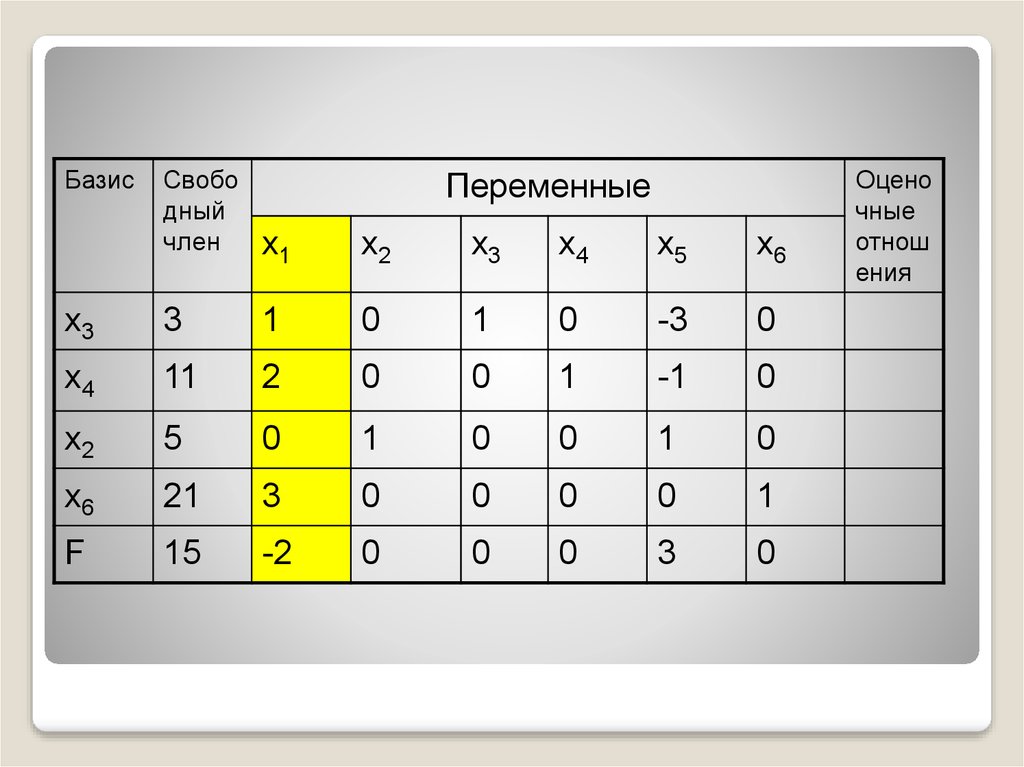
41.
БазисСвоб
одны
й
член
х1
х2
х3
х4
х5
х6
х3
18
1
3
1
0
0
0
х4
16
2
1
0
1
0
0
х5
5
0
1
0
0
1
0
х6
21
3
0
0
0
0
1
F
0
-2
-3
0
0
0
0
Переменные
Оцен
очные
отнош
ения
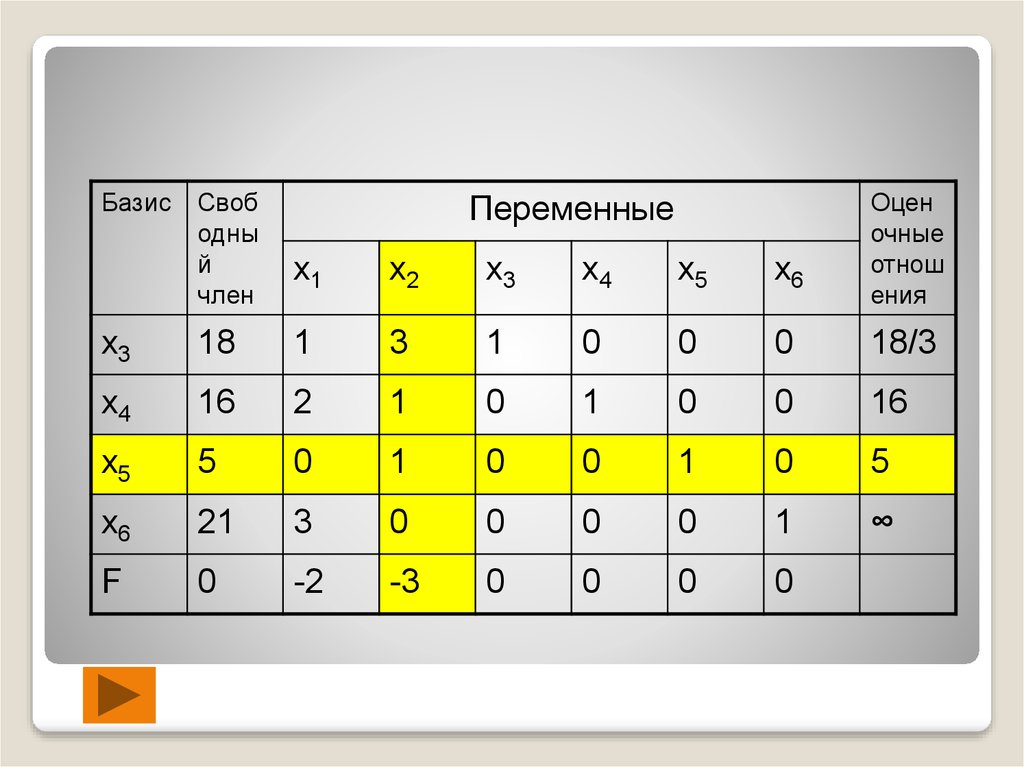
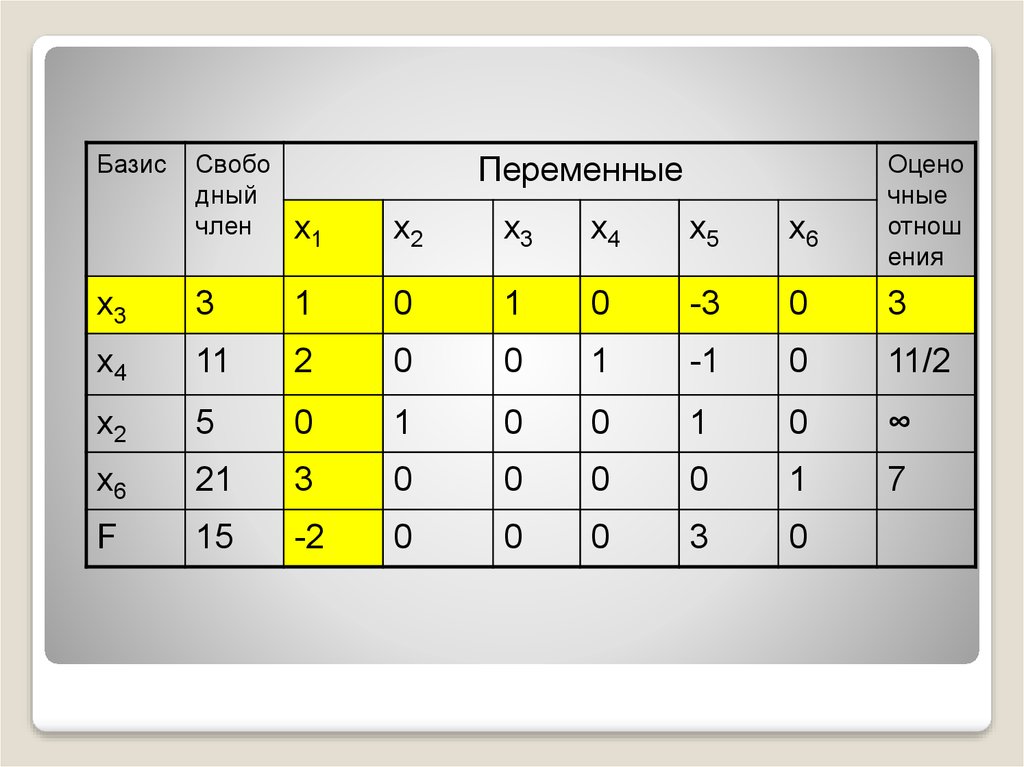
42.
БазисСвоб
одны
й
член
Переменные
х1
х2
х3
х4
х5
х6
Оцен
очные
отнош
ения
х3
18
1
3
1
0
0
0
18/3
х4
16
2
1
0
1
0
0
16
х5
5
0
1
0
0
1
0
5
х6
21
3
0
0
0
0
1
∞
F
0
-2
-3
0
0
0
0
43.
Базисх3
х4
х2
х6
F
Своб
одны
й
член
Переменные
х1
х2
х3
х4
х5
х6
Оцен
очные
отнош
ения
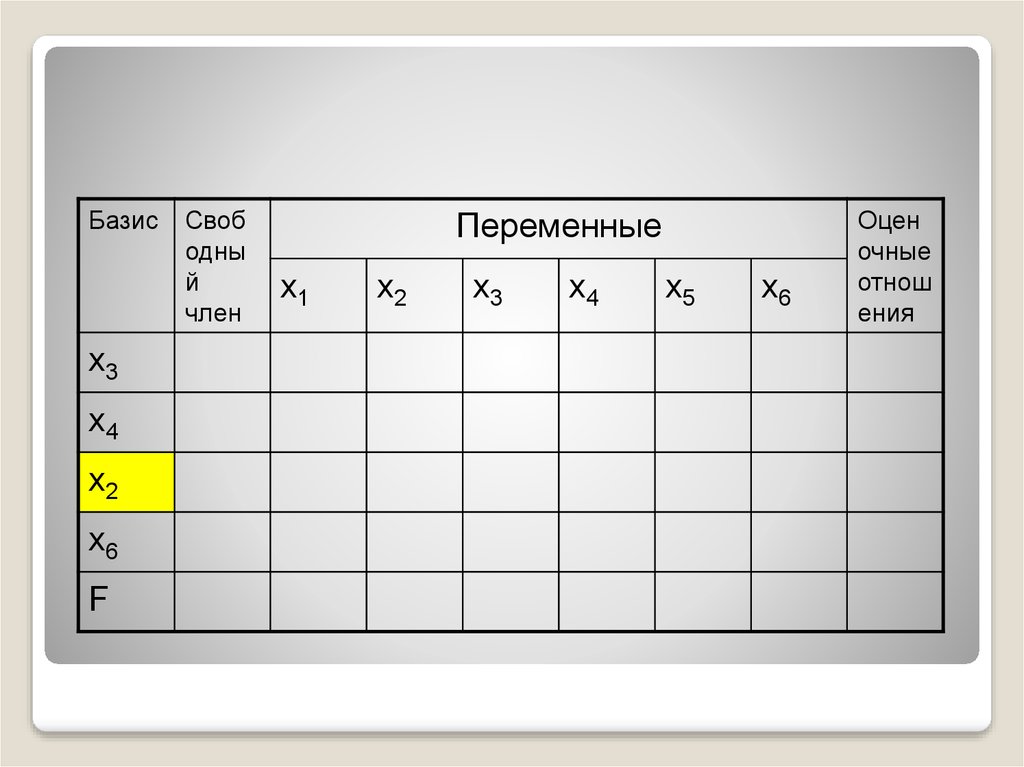
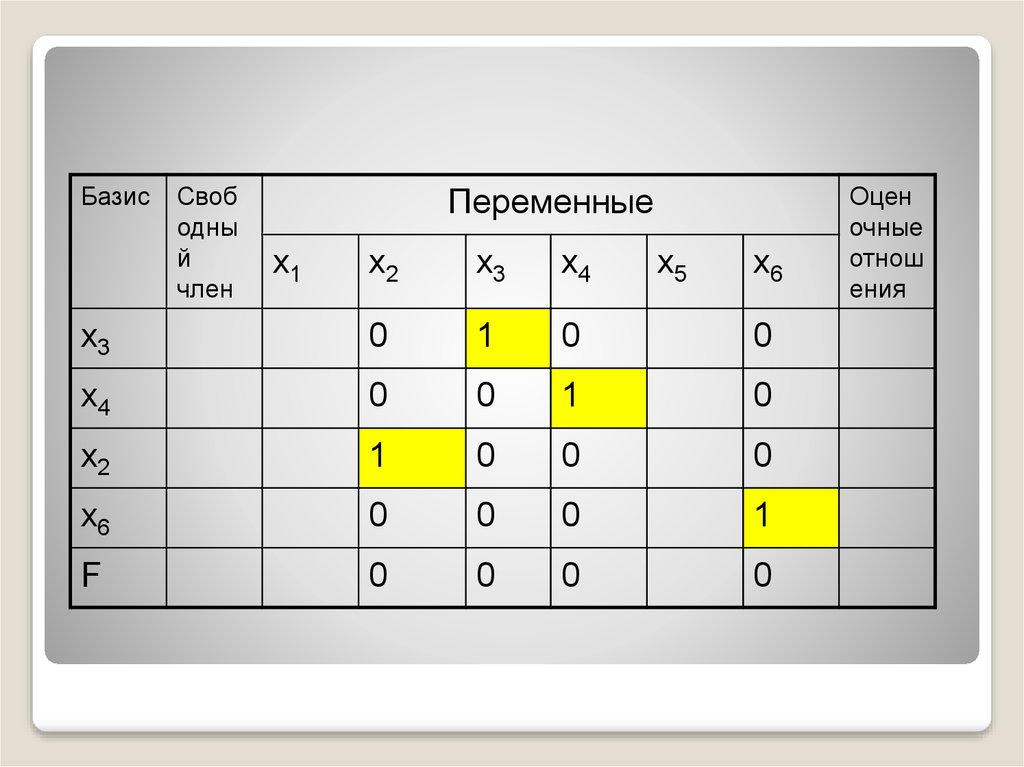
44.
БазисСвоб
одны
й
член
Переменные
х1
х2
х3
х4
х5
х6
х3
0
1
0
0
х4
0
0
1
0
х2
1
0
0
0
х6
0
0
0
1
F
0
0
0
0
Оцен
очные
отнош
ения
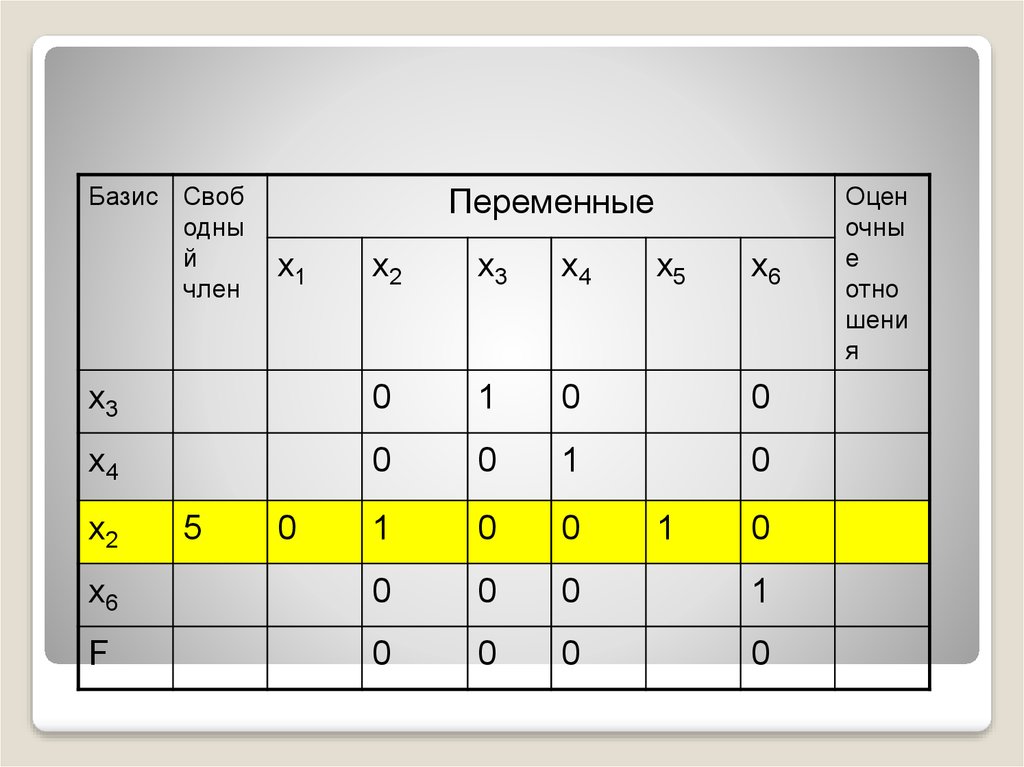
45.
Базис Свободны
й
член
Переменные
х2
х3
х4
х3
0
1
0
0
х4
0
0
1
0
1
0
0
х6
0
0
0
1
F
0
0
0
0
х2
5
х1
0
х5
1
х6
0
Оцен
очны
е
отно
шени
я
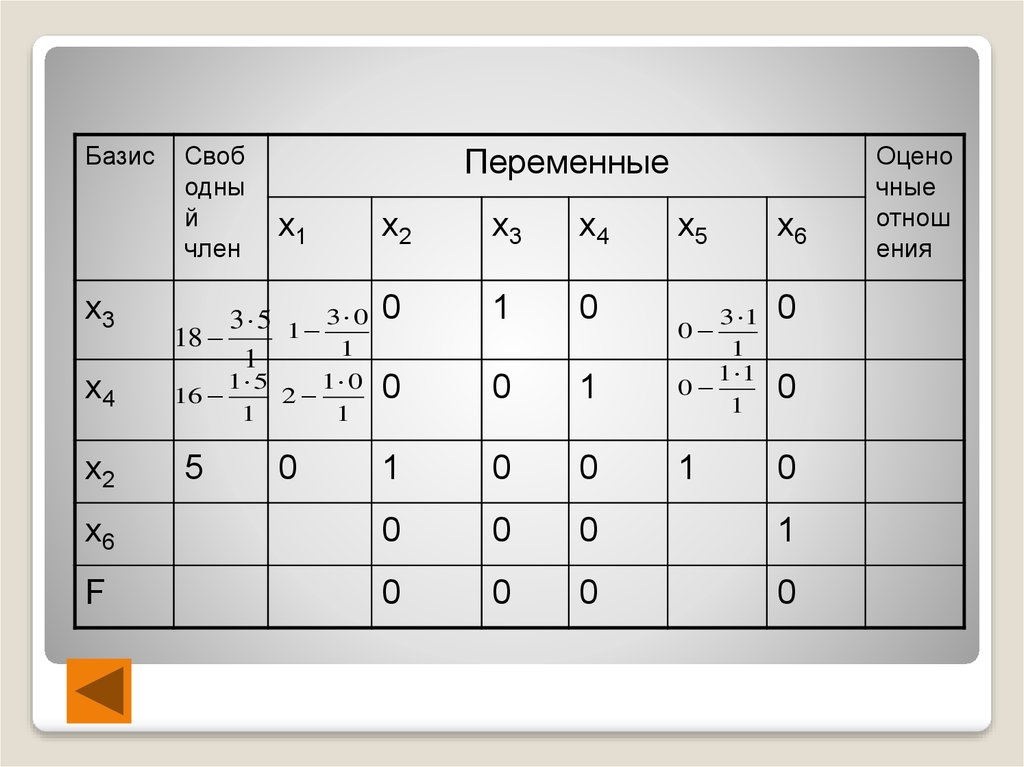
46.
БазисСвоб
одны
й
член
Переменные
х2
х3
х4
0
1
0
х4
3 5 1 3 0
18
1
1
16
0
0
1
х2
5
1
0
0
х6
0
0
0
1
F
0
0
0
0
х3
х1
1 5
1 0
2
1
1
0
х5
х6
3 1
1
1 1
0
1
0
1
0
0
0
Оцено
чные
отнош
ения
47.
БазисСвобо
дный
член
х1
х2
х3
х4
х5
х6
х3
3
1
0
1
0
-3
0
х4
11
2
0
0
1
-1
0
х2
5
0
1
0
0
1
0
х6
21
3
0
0
0
0
1
F
15
-2
0
0
0
3
0
Переменные
Оцено
чные
отнош
ения
48.
БазисСвобо
дный
член
х1
х2
х3
х4
х5
х6
х3
3
1
0
1
0
-3
0
3
х4
11
2
0
0
1
-1
0
11/2
х2
5
0
1
0
0
1
0
∞
х6
21
3
0
0
0
0
1
7
F
15
-2
0
0
0
3
0
Переменные
Оцено
чные
отнош
ения
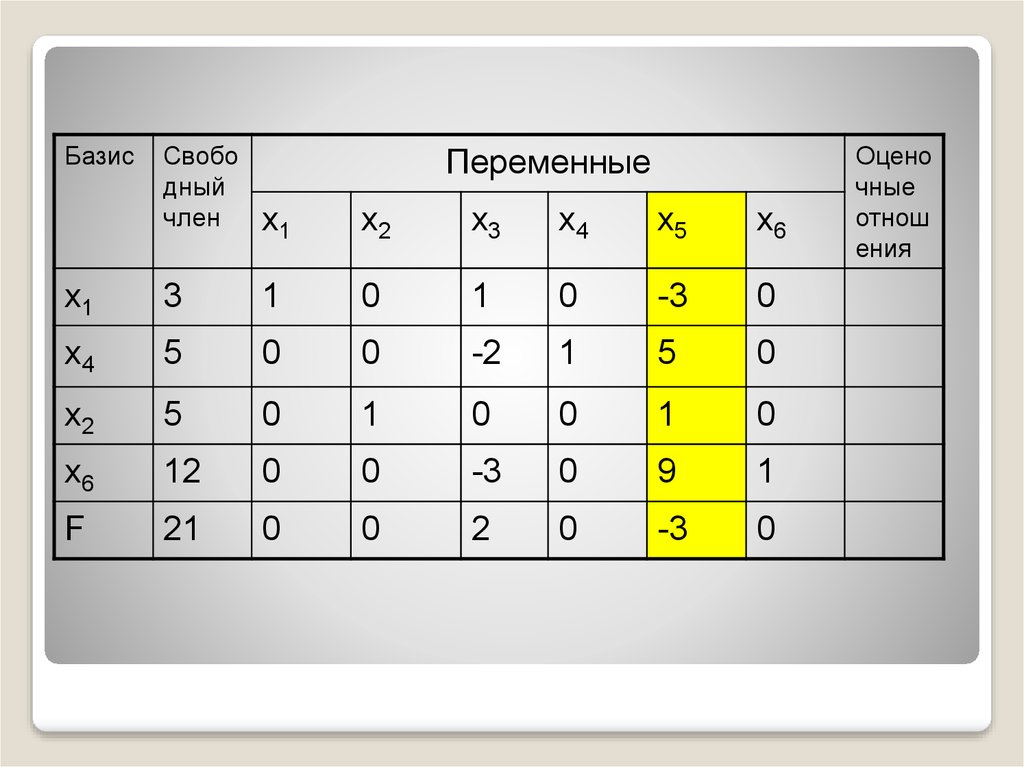
49.
БазисСвобо
дный
член
х1
х2
х3
х4
х5
х6
х1
3
1
0
1
0
-3
0
х4
5
0
0
-2
1
5
0
х2
5
0
1
0
0
1
0
х6
12
0
0
-3
0
9
1
F
21
0
0
2
0
-3
0
Переменные
Оцено
чные
отнош
ения
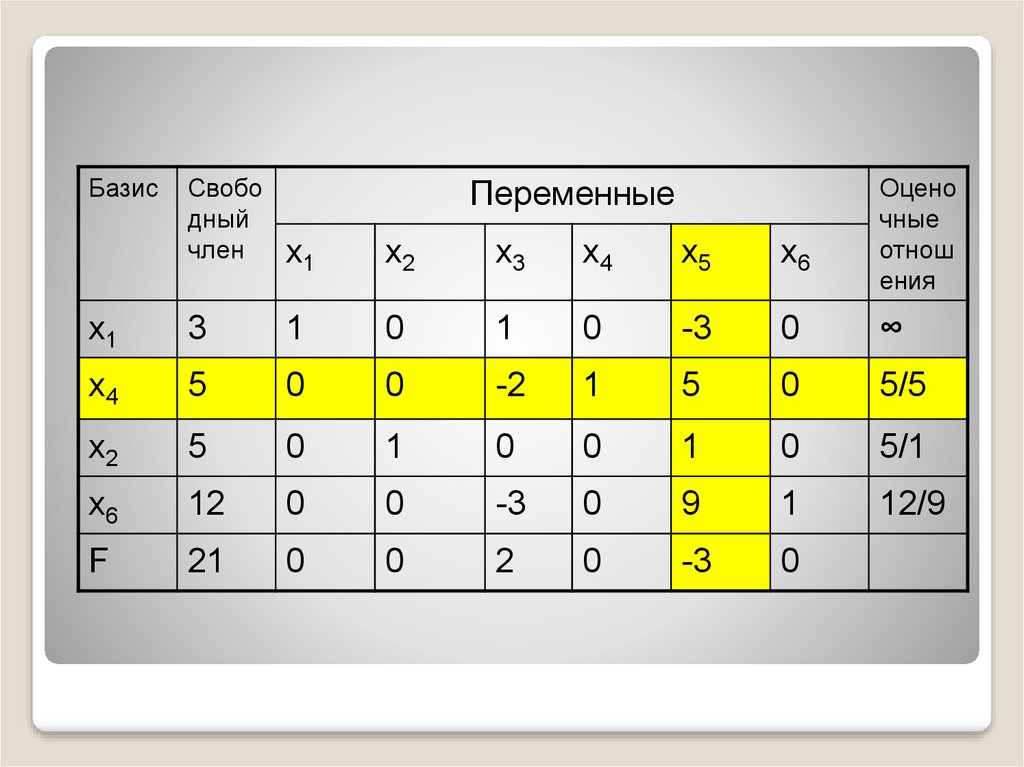
50.
БазисСвобо
дный
член
х1
х2
х3
х4
х5
х6
х1
3
1
0
1
0
-3
0
∞
х4
5
0
0
-2
1
5
0
5/5
х2
5
0
1
0
0
1
0
5/1
х6
12
0
0
-3
0
9
1
12/9
F
21
0
0
2
0
-3
0
Переменные
Оцено
чные
отнош
ения
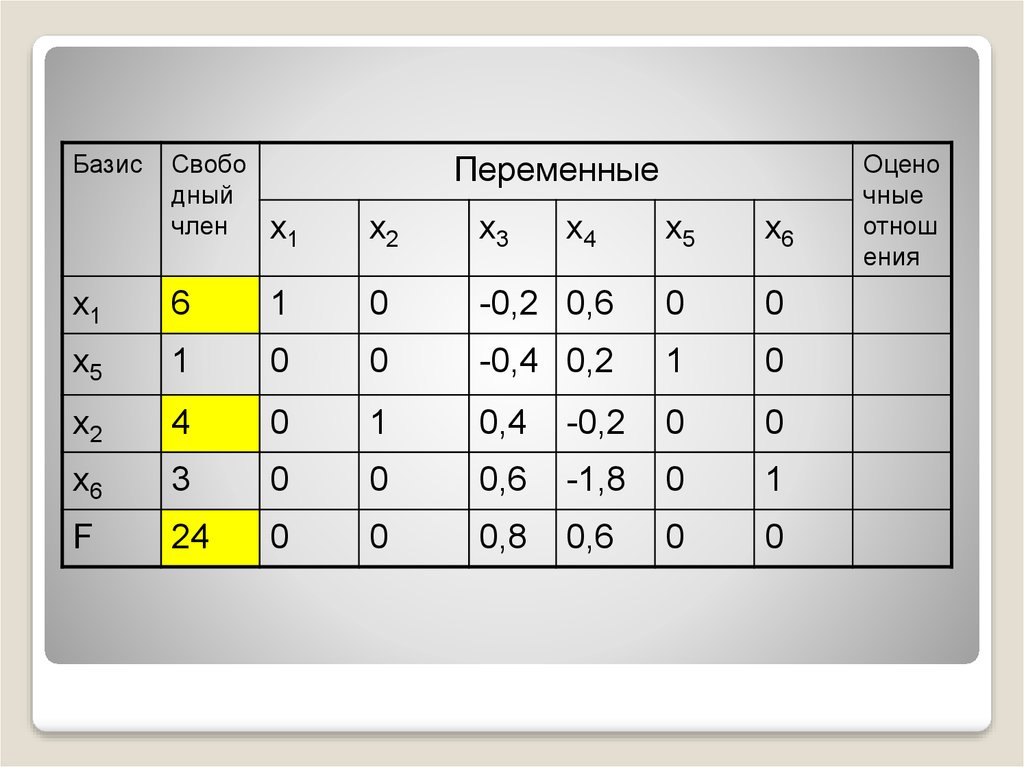
51.
БазисСвобо
дный
член
х1
х2
х3
х1
6
1
0
х5
1
0
х2
4
х6
F
Переменные
х4
х5
х6
-0,2 0,6
0
0
0
-0,4 0,2
1
0
0
1
0,4
-0,2
0
0
3
0
0
0,6
-1,8
0
1
24
0
0
0,8
0,6
0
0
Оцено
чные
отнош
ения
















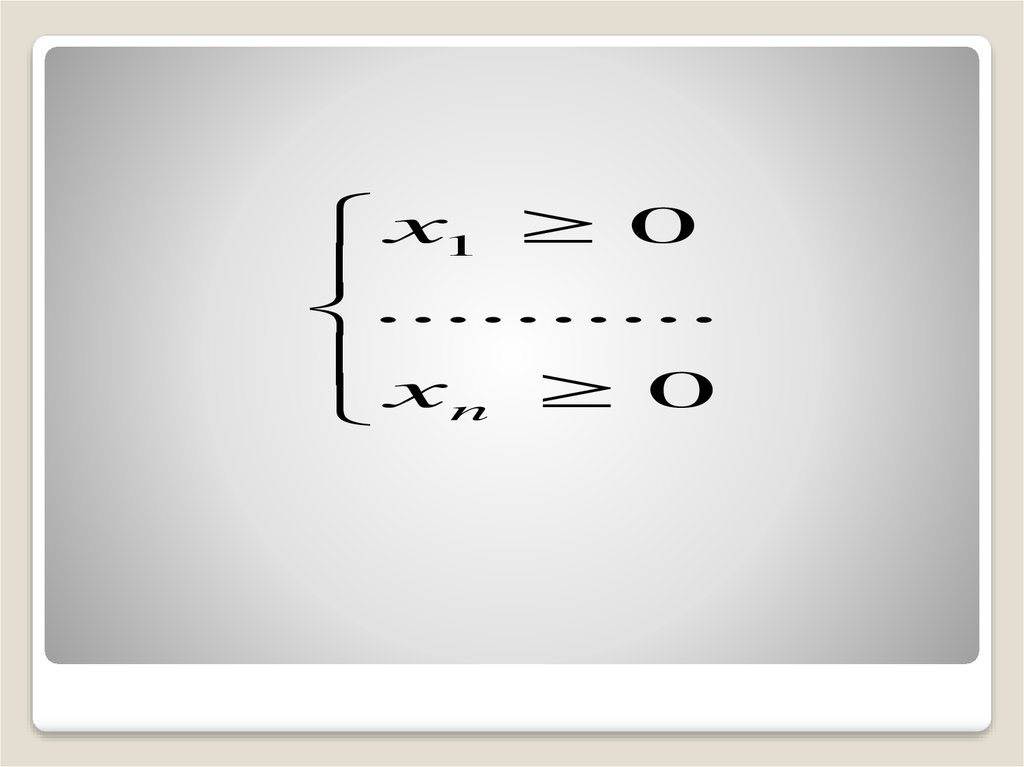








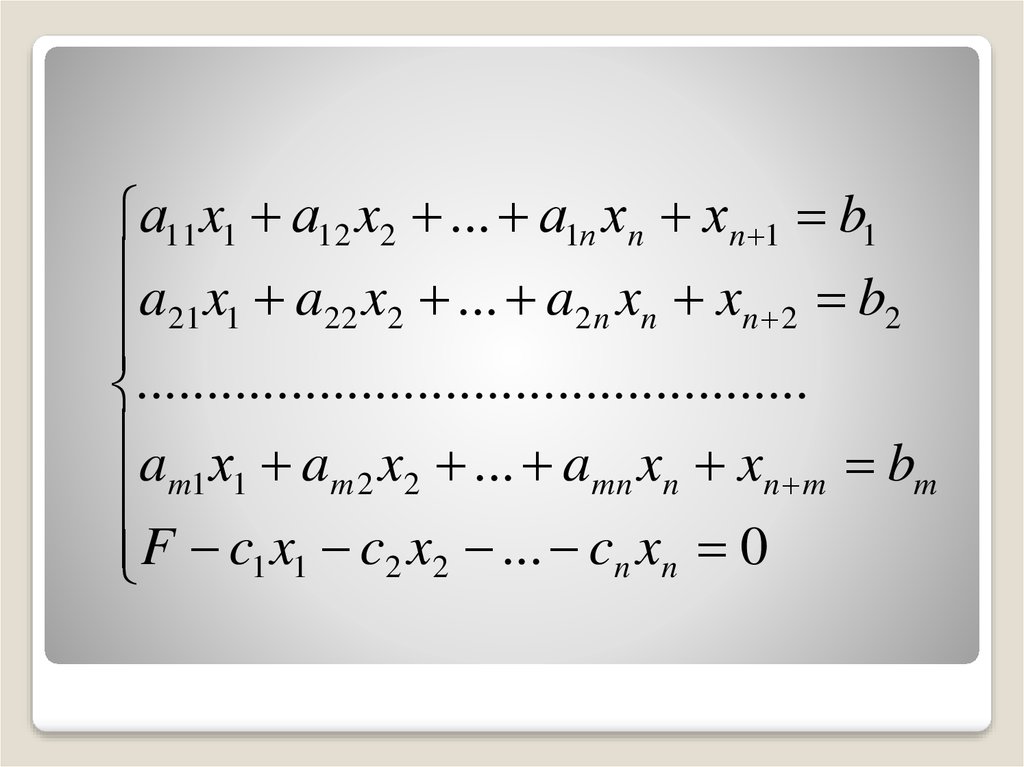









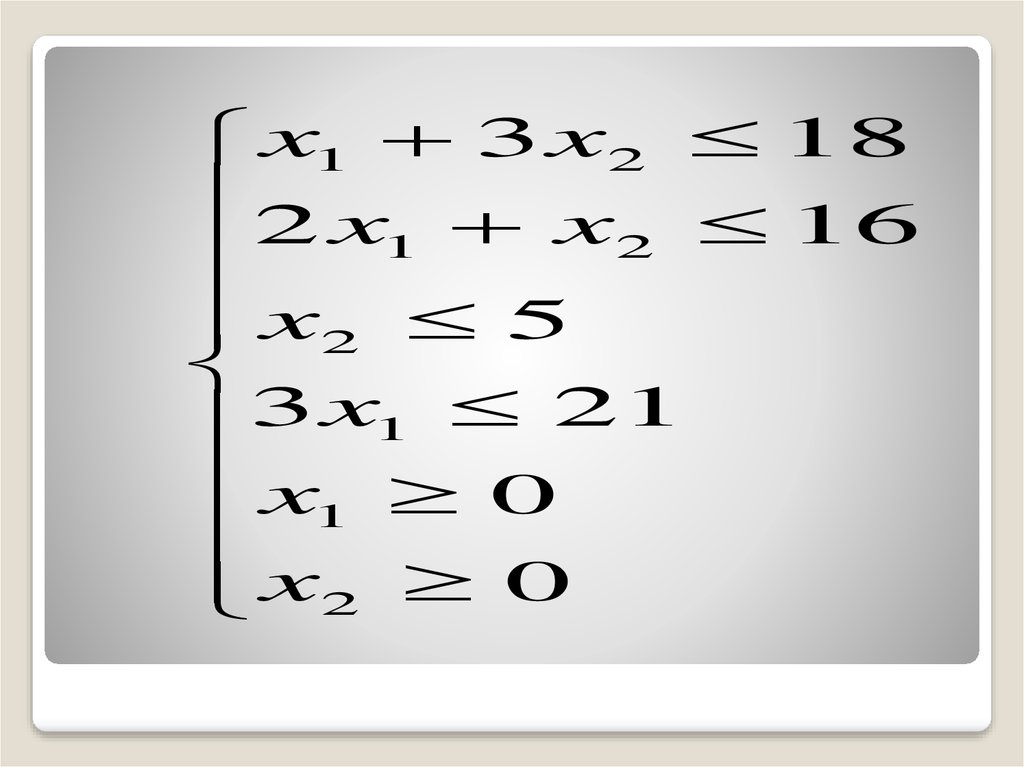
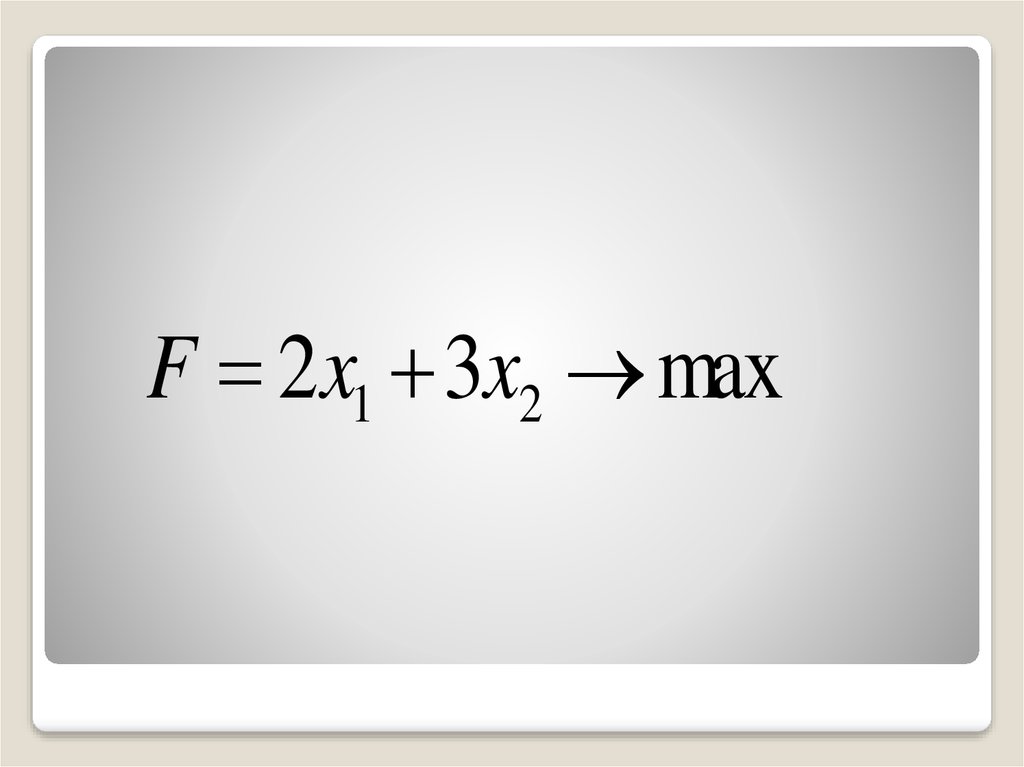
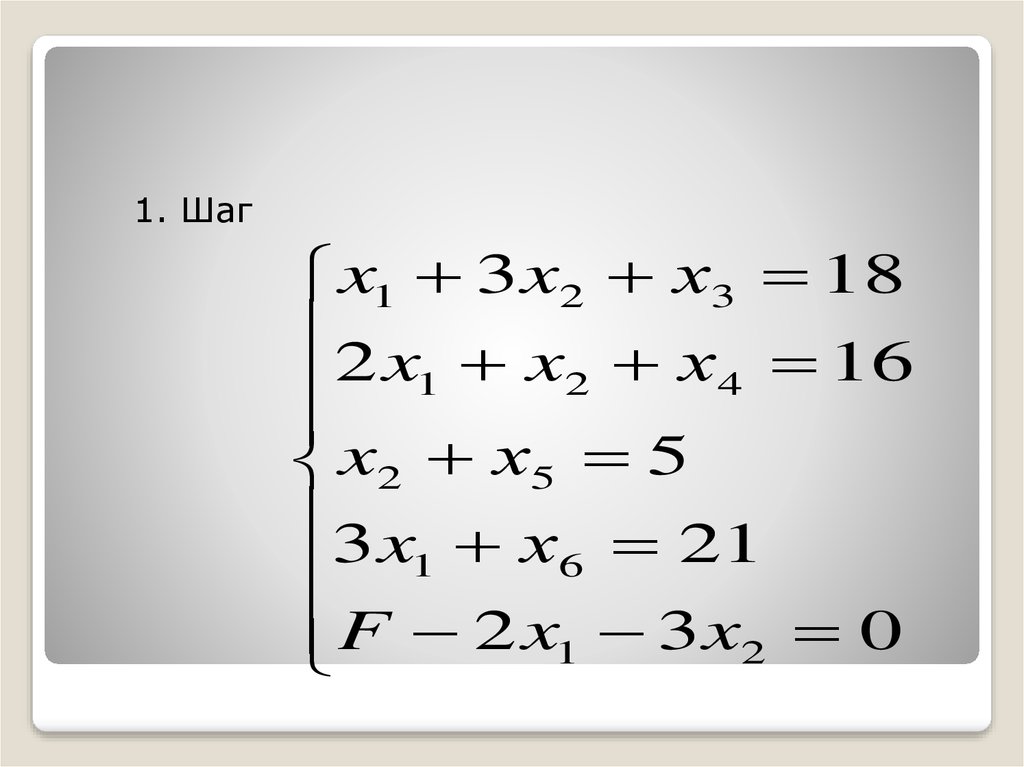

 mathematics
mathematics








