Similar presentations:
Типы условий оптимизации развития ЭЭС. Критерии принятия решений в условиях неопределенности
1. 3. Типы условий оптимизации развития ЭЭС. Критерии принятия решений в условиях неопределенности
2.
Условия оптимизации развития ЭЭСОптимальное планирование — способ получения оптимального
плана развития системы.
Критерий
—
показатель,
устанавливающий
соответствие
полученного решения поставленной цели, и осуществляющий
сравнительную оценку качества различных планов.
Целевой функционал — математическое выражение критерия.
Критерий оптимальности — глобальный экстремум целевого
функционала.
Многоцелевая оптимизация — оптимизация, преследующая
несколько не сводимых одна с другой целей.
Управление — это совокупность воздействий на систему с целью
достижения заранее поставленной цели.
Математическая модель системы — математическое
описание основных свойств системы-оригинала.
f j xit 0, j 1,2,...J ; t 1,2,....T ; i 1,2,...n.
2
3.
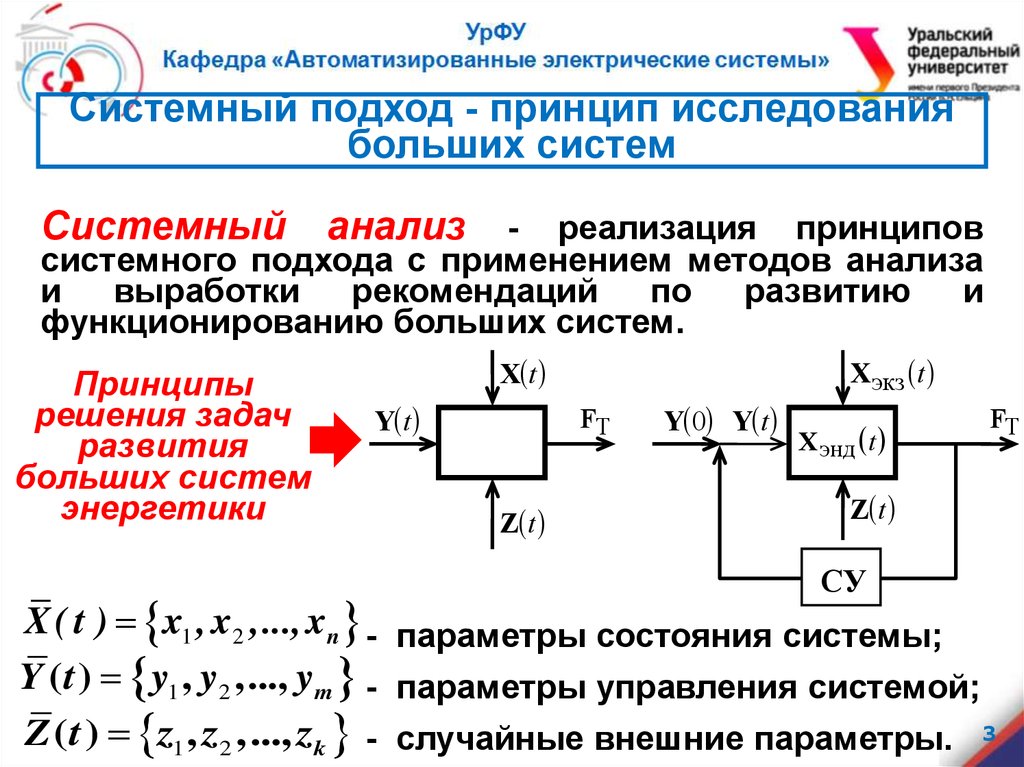
Системный подход - принцип исследованиябольших систем
Системный
анализ
- реализация принципов
системного подхода с применением методов анализа
и
выработки
рекомендаций
по
развитию
и
функционированию больших систем.
X экз t
X t
Принципы
решения задач
FT
FT
Y 0 Y t
Y t
X энд t
развития
больших систем
Z t
энергетики
Z t
СУ
X ( t ) x1 , x2 ,..., xn - параметры состояния системы;
Y ( t ) y1 , y2 ,..., ym - параметры управления системой;
Z ( t ) z1 , z2 ,..., zk - случайные внешние параметры. 3
4.
Условия оптимизации развития ЭЭСВ задачах развития энергосистем решения приходится
принимать в условиях многокритериальности.
Исследователь всегда стремится упростить постановку задачи,
сводя ее к однокритериальной.
Результат решения зависит от свойств исходной информации о
внешних условиях развития ЭЭС.
Вид информации определяет условия оптимизации.
Виды информации
1. Детерминированная полная
2. Детерминированная частично
неопределенная
3. Вероятностная полная
4. Вероятностная частично
неопределенная
Условия оптимизации
1. Детерминированные
2. Вероятностные
3. Неопределенные
4
5.
Условия оптимизации развития ЭЭСДетерминированные условия оптимизации
оптимизируемая функция цели , оптимальное
F X ,Y -решение
соответствует экстремуму целевого
функционала, например
Y - параметр управления;
X - параметр внешних условий,
имеет фиксированное значение
и не влияет на результаты
оптимизации
Решение единственно!
F Y min ;
F
Fmin
Yопт
Y
5
6.
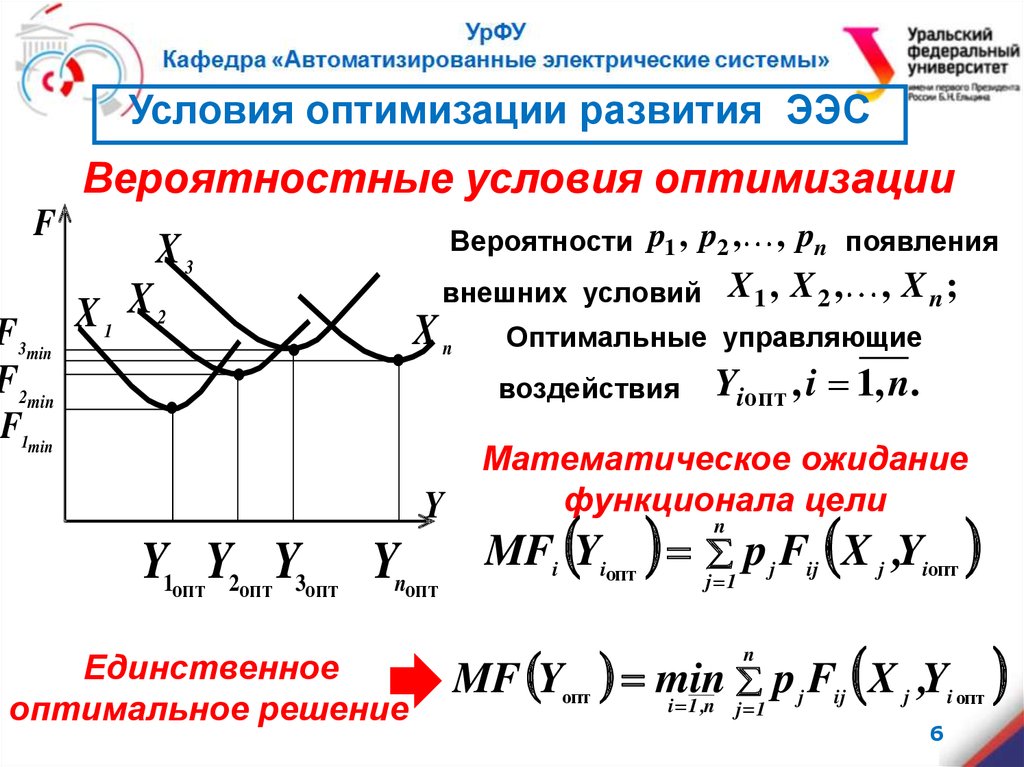
Условия оптимизации развития ЭЭСВероятностные условия оптимизации
F
F3min
F2min
F1min
X3
X1 X2
Вероятности p1 , p2 ,
Y
, X n;
Оптимальные управляющие
воздействия
Yiопт , i 1, n.
Математическое ожидание
функционала цели
Y1оптY2оптY3опт Ynопт MF Y
i
Единственное
оптимальное решение
X1 , X 2 ,
внешних условий
Xn
, pn появления
iопт
p F X
n
j
j 1
ij
j
,Yiопт
MF Yопт min
p j Fij X j ,Yi опт
i 1 ,n
n
j 1
6
7.
Условия оптимизации развития ЭЭСВероятностные условия оптимизации
Вероятности
p1 , p2 ,
, pn появления условий X 1 , X 2 ,
Затруднено получение оптимального управления,
Дискретное изменение управляющего параметра,
, Xn.
Yiопт , i 1, n.
Yi , i 1, m .
Прямая оптимизация для всех допустимых значений Y.
Математическое ожидание функционала цели
n
MF Yопт min p j Fij X j ,Yi
i 1,m j 1
Единственное оптимальное решение
7
8.
Вероятностные условия оптимизацииX1
X2
...
Xj
...
Xn
p1
p2
...
pj
...
pn
Y1
F11
F12
...
F1j
...
F1n
...
...
...
...
...
...
...
Y
MF
n
MFi = p j Fij
...
j=1
n
Yi
Fi1
Fi2
...
Fij
...
Fin
MF1 = p j F1j
j=1
...
...
...
...
...
...
...
...
n
Ym
Fm1
Fm2
...
Fmj
...
Fmn
MFm = p j Fmj
j=1
Критерий оптимальности
min MFi
i=1,m
8
9.
Вероятностные условия оптимизацииЗадача 1. Капиталовложения в угольную КЭС
имеют диапазон неопределенности 7250 – 7650 млн.
руб., а годовые издержки на топливо 1810 – 1890
млн. руб. Для газовой КЭС эти показатели равны
соответственно 5900 – 6300 и 2050 – 2250 млн. руб.
Полагая,
что
сочетание
минимальных
капиталовложений и издержек на топливо имеет
вероятность 0,15, максимальных – 0,25, а
минимальных
капиталовложений
при
максимальных издержках и наоборот – по 0,3,
определить лучший вариант. Использовать метод
годовых приведенных затрат при Ен=0,2 и αам=0,08.
Решение. Годовые приведенные затраты
З Ен К И = Ен К ам К + И топл
10.
Расчет приведенных затрат в угольную станциюПри максимальных капиталовложениях и максимальных
издержках на топливо
З=0,28 К+ И топл 0,28 7650+1890 = 4032 млн.руб.
При максимальных капиталовложениях и минимальных
издержках на топливо
З=0,28 К+ И топл 0,28 7650 + 1810 = 3952 млн.руб.
При минимальных капиталовложениях и максимальных
издержках на топливо
З=0,28 К+ И топл 0,28 7250 + 1890 = 3920 млн.руб.
При минимальных капиталовложениях и минимальных
издержках на топливо 8.
З=0,28 К+ И топл 0,28 7250 + 1810 = 3840 млн.руб.
11.
Расчет приведенных затрат в станцию на газеПри максимальных капиталовложениях и максимальных
издержках на топливо
З=0,28 К+ И топл 0,28 6300 + 2250 = 4014 млн.руб.
При максимальных капиталовложениях и минимальных
издержках на топливо
З=0,28 К+ И топл 0,28 6300 + 2050 = 3814 млн.руб.
При минимальных капиталовложениях и максимальных
издержках на топливо
З=0,28 К+ И топл 0,28 5900 + 2250 = 3902 млн.руб.
При минимальных капиталовложениях и минимальных
издержках на топливо 8.
З=0,28 К+ И топл 0,28 5900 + 2050 = 3702 млн.руб.
12.
Вероятностные условия оптимизацииn
MF Yопт min p j Fij X j ,Yi
i 1,m j 1
Вероятные приведенные затраты в станцию на угле
n
MF Yопт p j Fij 0,25 4932+ 0,3 3952+
j 1
+ 0,3 3920+ 0,15 3840 4170 , 6 млн.руб .
Вероятные приведенные затраты в станцию на газе
n
MF Yопт p j Fij 0,25 4014+ 0,3 3814+
j 1
+ 0,3 3902+ 0,15 3702 3887 ,1 млн.руб .
13.
Оптимизация в вероятностных условияхПлатежная матрица, млн.руб
Вероятность
события
Внешние
условия
Вероятностные
условия
Кмах , Имах К , И
Кмин , Имах Кмин , Имин оптимимах
мин
зации
p = 0,25 p = 0,3 p = 0,3 p = 0,15
Угольная
КЭС
4932
3952
3920
3840
4170,6
Газовая
КЭС
4014
3814
3902
3702
3887,1
Рекомендация
по критерию
n
MF Yопт p j Fij
j 1
КЭС
на газе
14.
Условия оптимизации развития ЭЭСНеопределенные условия оптимизации
Наиболее распространенным в практике случаем являются
условия неопределенности. Например, удается дать прогноз
диапазона
перспективных
нагрузок
энергосистемы,
но
неизвестны вероятности наступления каждого значения нагрузки
из этого диапазона.
Значения
функционала
цели
F
,
сопоставляемых вариантов (альтернатив)
внешних условиях
получаемые
Y
для
при различных
X , образуют платежную матрицу.
14
15.
Условия оптимизации развития ЭЭСНеопределенные условия оптимизации
Платежная матрица
Выбор стратегии выполняется по критериям
принятия в условиях неопределенности.
15
16.
Условия оптимизации развития ЭЭСНеопределенные условия оптимизации
Рекомендации или правила выбора наилучшего решения в
такой ситуации даются теорией принятия решений в условиях
неопределенности.
Теория не позволяет дать однозначный ответ по выбору
наилучшего решения, но позволяет выстроить несколько цепей
логических рассуждений по обоснованию выбора по нескольким
критериям, заимствованным из теории игр.
Критерии теории игр
1. Критерий минимаксных затрат (критерий Вальда).
2. Критерий недостаточного основания (критерий Лапласа).
3. Критерий минимаксного риска (критерий Севиджа).
4. Критерий Гурвица.
16
17.
Условия оптимизации развития ЭЭСНеопределенные условия оптимизации
Критерий Вальда - критерий минимакса
Принцип принятия решения по критерию основан на ориентации,
из осторожности, на наиболее
неблагоприятные
внешние
X 1 , X 2 ...X j ...X n
условия
при
реализации каждой
альтернативы (варианта решения) Y1 ,Y2 ...Yi ...Ym .
Решение принимается на базе платежной матрицы в которой
определяются значения критерия
для каждой альтернативы
максимальные max Fij (при стремлении к минимизации критерия),
затем выбирается альтернатива с минимальным значением
критерия оптимальности (минимальное из максимальных).
F min max Fij
i 1 , m j 1 , n
17
18.
Условия оптимизации развития ЭЭСНеопределенные условия оптимизации
Критерий Вальда - критерий минимакса
F min max Fij
i 1 , m j 1 , n
max Fij
max F1 j
max Fij
max Fmj
18
19.
Условия оптимизации развития ЭЭСНеопределенные условия оптимизации
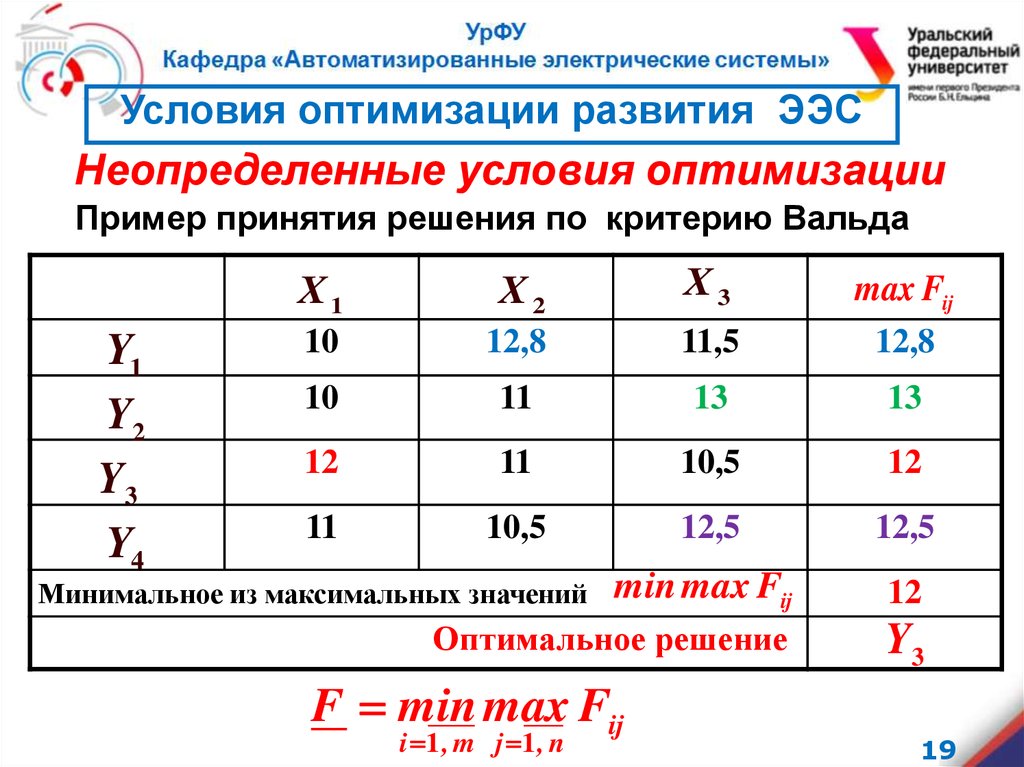
Пример принятия решения по критерию Вальда
Y1
Y2
Y3
Y4
X1
X2
X3
max Fij
10
12,8
11,5
12,8
10
11
13
13
12
11
10,5
12
11
10,5
12,5
12,5
min max Fij
12
Оптимальное решение
Y3
Минимальное из максимальных значений
F min max Fij
i 1 , m j 1 , n
19
20.
Критерий Вальда - критерийминимакса
Недостатком критерия минимакса является его ориентация на
учет только самой неблагоприятной ситуации. Такой критерий
имеет безусловное преимущество, если выбор стратегии
приходится делать в условиях, когда кто-то (противник) стремится
создать неблагоприятные внешние условия при реализации всех
альтернатив. Такие ситуации могут возникать в антагонистических
играх двух лиц Y и X (теория игр).
В задачах развития энергетики нельзя представить внешние
условия – сторону X сознательно стремящимися создать при
развитии энергетики наиболее неблагоприятную обстановку.
Значения X есть результат нашего недостаточного знания
закономерностей природы, а природа может ставить перед нами
сложные задачи, но она не злонамеренна. Поэтому при выборе
стратегии развития энергетики логично учитывать не только
наиболее неблагоприятные условия, но и любые другие.
20
21.
Условия оптимизации развития ЭЭСНеопределенные условия оптимизации
Критерий Лапласа - критерий недостаточного
основания
Принятие решения по критерию основано на ориентации на
равные вероятности наступления разных внешних X
условий,
ибо нет основания отдать преимущество какому-либо конкретному.
При этом в платежной матрице определяются средние значения
критерия для каждой альтернативы Y
и затем выбирается
альтернатива с минимальным значением критерия оптимальности
(минимальное из средних).
n
F min 1
i 1 , m
n
j 1
Fij
21
22.
Условия оптимизации развития ЭЭСНеопределенные условия оптимизации
Критерий Лапласа - критерий недостаточного
основания
1
1
F min 1
i 1 , m
n
F
j 1 ij
Fij
n j 1
F1 j
n
Fmj
1
n
n j 1
n
n
n
j 1
22
23.
Условия оптимизации развития ЭЭСНеопределенные условия оптимизации
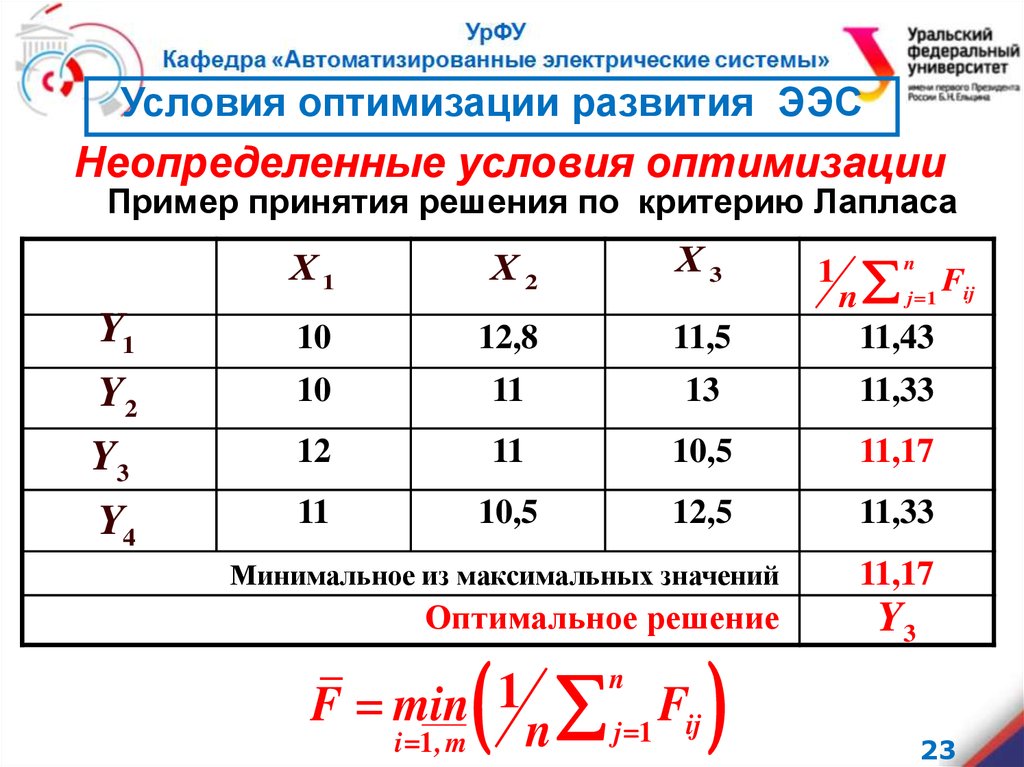
Пример принятия решения по критерию Лапласа
X1
X2
X3
Y1
10
12,8
11,5
11,43
Y2
10
11
13
11,33
Y3
12
11
10,5
11,17
Y4
11
10,5
12,5
11,33
Минимальное из максимальных значений
Оптимальное решение
F min 1
i 1 , m
n
n
F
j 1 ij
1
n j 1
n
Fij
11,17
Y3
23
24.
Условия оптимизации развития ЭЭСНеопределенные условия оптимизации
Критерий Севиджа - критерий минимаксного риска
Принцип принятия решения по критерию основан на
преобразовании платежной матрицы в матрицу риска и
последующем применении к ней минимаксного критерия.
R
Получение матрицы риска
основано на определении
перерасхода ресурса в каждой альтернативе Y по сравнению с
лучшей для каждого из вариантов внешних условий X .
Элементы матрицы риска
R ji F ji Fmin i
.
24
25.
Условия оптимизации развития ЭЭСНеопределенные условия оптимизации
Критерий Севиджа - критерий минимаксного риска
Построение матрицы риска
Элементы матрицы риска
R ji F ji Fmin i .
Платежная матрица
X1
Y1
Y2
Y3
Y4
10
X2
X3
12,8 11,5
10
11
13
12
11
10,5
11
10,5 12,5
Матрица риска
X1
0
Y1
0
Y2
Y3 12 - 10 = 2
Y4 11 - 10 = 1
R
X2
X3
12,8–10,5=2,3
1
11 – 10,5 =0,5
2,5
11 – 10,5 =0,5
0
0
2
25
26.
Условия оптимизации развития ЭЭСНеопределенные условия оптимизации
Пример принятия решения по критерию Севиджа
X1
Y1
Y2
Y3
Y4
X2
X3
max Rij
0
2,3
1
2, 3
0
0,5
2,5
2,5
2
0,5
0
2
1
0
2
2
Минимальный риск максимальных значений
Оптимальное решение
F min max Rij
i 1 , m j 1 , n
Y3
2
,
Y4
26
27.
Условия оптимизации развития ЭЭСНеопределенные условия оптимизации
Критерий Гурвица - взвешенный
критерий
Принцип принятия решения по критерию основан на том, что в
задачах развития энергетики ситуации внешних условий
складываются стихийно. Это приводит к критерию оптимальности,
взвешенно учитывающему как наиболее благоприятные, так и
наиболее неблагоприятные внешние условия X при реализации
каждой альтернативы (варианта решения) Y .
В платежной матрице определяются значения критерия Fi для
каждой альтернативы
на основе выбранных значений
коэффициентов «пессимизма - » и
«оптимизма 1 ».
В качестве критерия оптимальности выбирается минимальное из
значения критерия для всех альтернатив
F min max Fij 1 min Fij
i 1, m j 1, n
j 1, n
27
28.
Условия оптимизации развития ЭЭСНеопределенные условия оптимизации
Критерий Гурвица - взвешенный
критерий
В качестве критерия оптимальности выбирается минимальное из
значения критерия для всех альтернатив
F min max Fij 1 min Fij
i 1, m j 1, n
j 1, n
Наиболее трудным является выбор величины
.
С учетом больших экономических потерь от неверных решений
по развитию систем энергетики и высокую инерционность
инвестиционного комплекса энергетики, рекомендуется выбирать
значение коэффициента пессимизма в диапазоне 0 , 5 1 .
28
29.
Условия оптимизации развития ЭЭСНеопределенные условия оптимизации
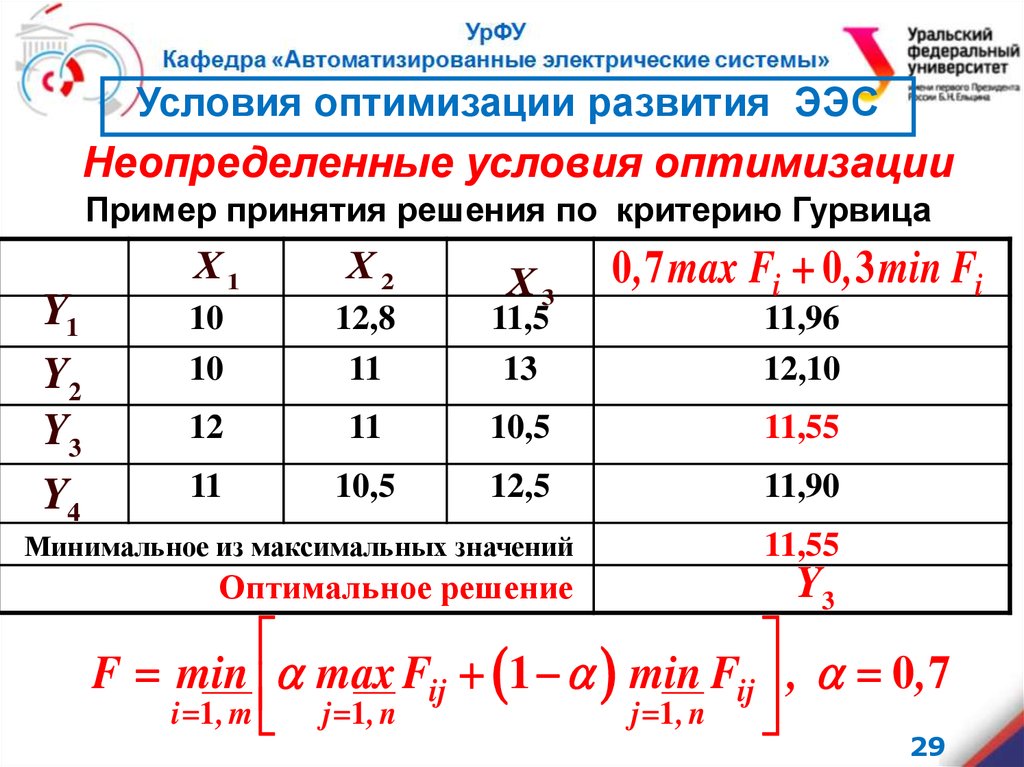
Пример принятия решения по критерию Гурвица
Y1
Y2
Y3
Y4
X1
X2
X3
0 , 7 max Fi 0 , 3 min Fi
10
10
12,8
11
11,5
13
11,96
12,10
12
11
10,5
11,55
11
10,5
12,5
11,90
Минимальное из максимальных значений
11,55
Оптимальное решение
Y3
F min max Fij 1 min Fij , 0 , 7
i 1 , m j 1 , n
j 1 , n
29
30.
Неопределенные условия оптимизацииЗадача 2. Капиталовложения в угольную КЭС
имеют диапазон неопределенности 7250 – 7650 млн.
руб., а годовые издержки на топливо 1810 – 1890
млн. руб. Для газовой КЭС эти показатели равны
соответственно 5900 – 6300 и 2050 – 2250 млн. руб.
Рассмотрев ситуации взаимно независимых
колебаний
капиталовложений
и
издержек,
одинаковые для обеих станций, дать рекомендацию
по варианту проекта, используя метод годовых
приведенных затрат с Ен=0,12 при годовых
амортизационных отчисленных 0,08.
Решение. Годовые приведенные затраты
З Ен К И = Ен К ам К + И топл
31.
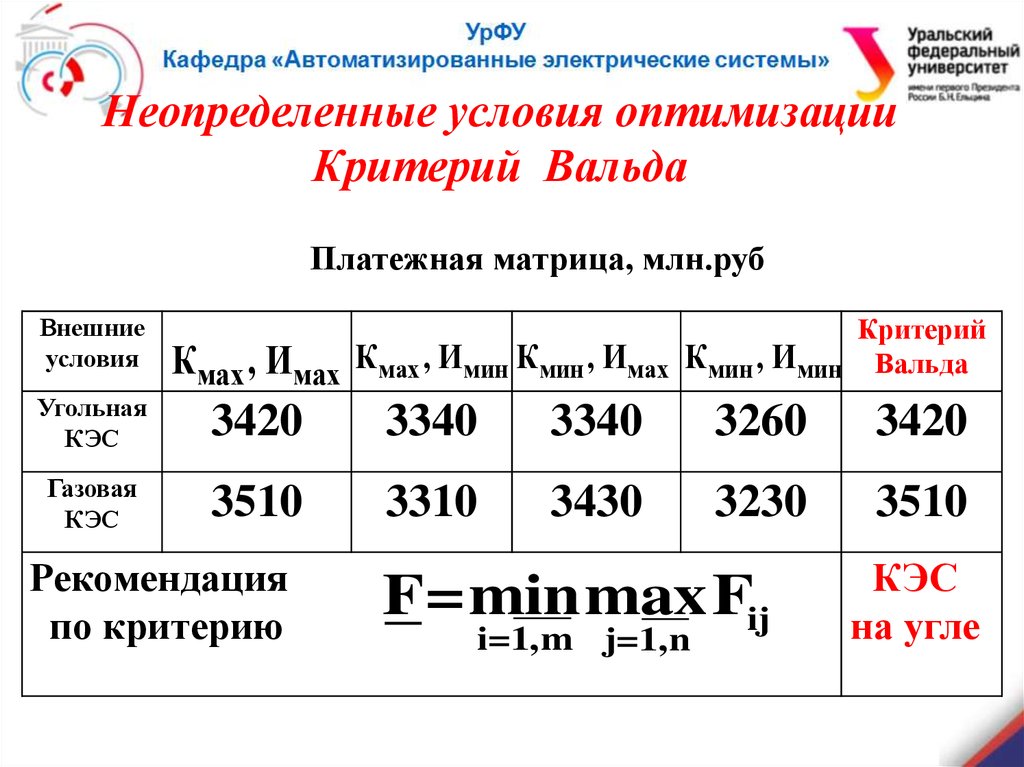
Неопределенные условия оптимизацииКритерий Вальда
Платежная матрица, млн.руб
Внешние
условия
Критерий
Кмах , Имах Кмах , Имин Кмин , Имах Кмин , Имин Вальда
Угольная
КЭС
3420
3340
3340
3260
3420
Газовая
КЭС
3510
3310
3430
3230
3510
Рекомендация
по критерию
F=minmaxFij
i=1,m j=1,n
КЭС
на угле
32.
Неопределенные условия оптимизацииКритерий Лапласа
Платежная матрица, млн.руб
Внешние
условия
Критерий
Кмах , Имах Кмах , Имин Кмин , Имах Кмин , Имин Лапласа
Угольная
КЭС
3420
3340
3340
3260
3340
Газовая
КЭС
3510
3310
3430
3230
3370
Рекомендация
по критерию
1 n
F= min Fij
i=1,m
n j=1
КЭС
на угле
33.
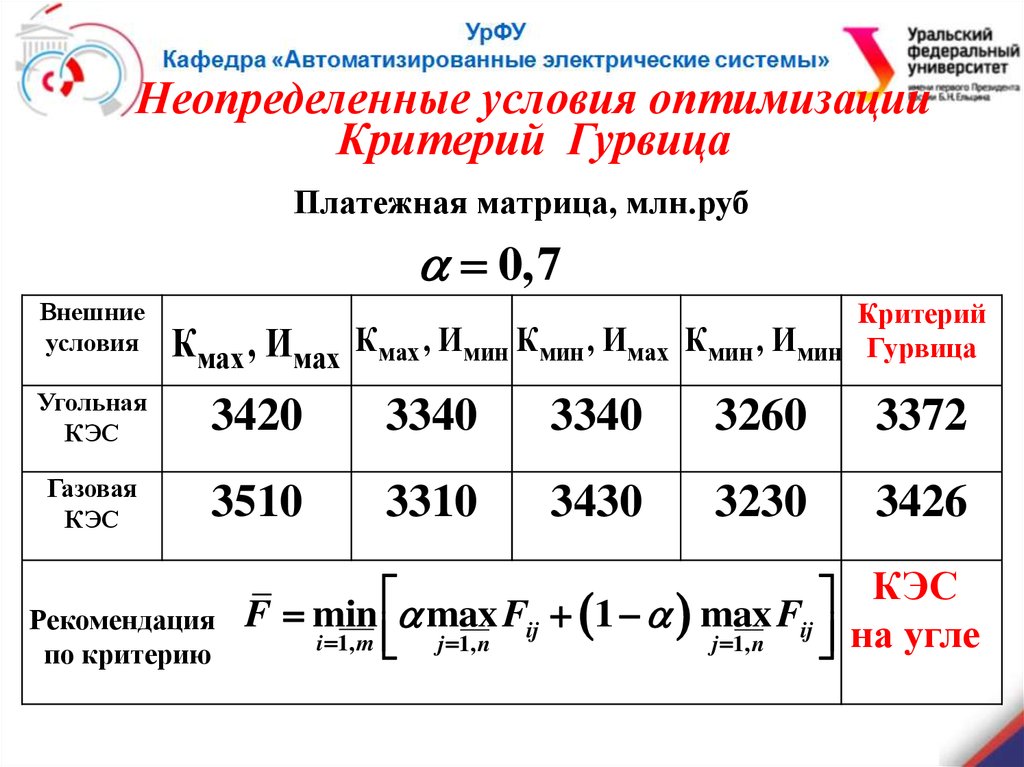
Неопределенные условия оптимизацииКритерий Гурвица
Платежная матрица, млн.руб
0,7
Внешние
условия
Критерий
Кмах , Имах Кмах , Имин Кмин , Имах Кмин , Имин Гурвица
Угольная
КЭС
3420
3340
3340
3260
3372
Газовая
КЭС
3510
3310
3430
3230
3426
Рекомендация
по критерию
КЭС
F min max Fij 1 max Fij
на угле
i 1, m
j 1, n
j 1, n
34.
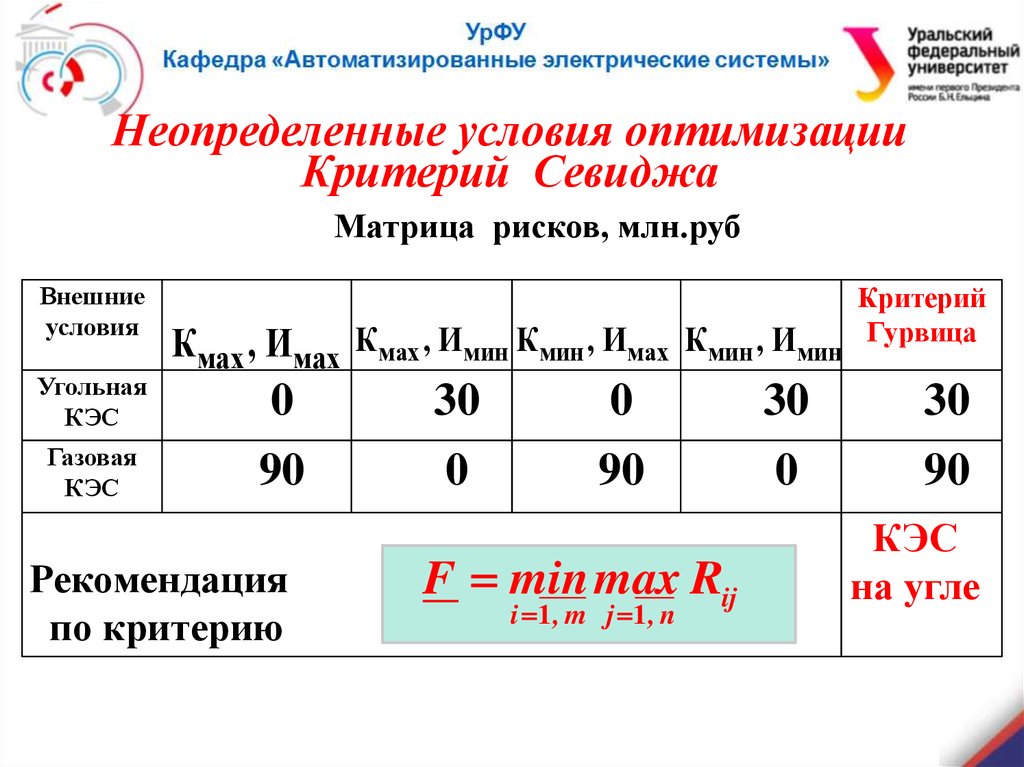
Неопределенные условия оптимизацииКритерий Севиджа
Матрица рисков, млн.руб
Внешние
условия
Угольная
КЭС
Газовая
КЭС
Кмах , Имах Кмах , Имин Кмин , Имах Кмин , Имин
Критерий
Гурвица
0
30
0
30
30
90
0
90
0
90
Рекомендация
по критерию
min max R
Rijij
RF minmax
i 1 , m j 1 , n
i 1, m j 1, n
КЭС
на угле



























 economics
economics








