Similar presentations:
ГИА – 2013 г. Модуль «Алгебра». № 6
1. ГИА – 2013 г. Модуль «Алгебра». № 6
ГИА – 2013 г.Модуль «Алгебра».
№6
Автор презентации:
Гладунец Ирина Владимировна
учитель математики МБОУ гимназии №1
г. Лебедянь Липецкой области
2. ГИА – 2013 г.
Модуль«Алгебра»
№6
«ГИА-2013. Математика:
типовые экзаменационные варианты: 30 вариантов»
под редакцией А. Л. Семенова, И. В. Ященко.
М.: Изд. «Национальное образование», 2013.
3. Арифметическая прогрессия
Какая последовательность называетсяарифметической прогрессией?
Какой формулой можно записать
арифметическую прогрессию?
Как найти разность арифметической
прогрессии?
Какой формулой выражается n-ый член
арифметической прогрессии?
Как можно вычислить сумму n
первых членов арифметической
прогрессии?
4. Повторение
Арифметическая прогрессия –последовательность, каждый член которой
больше предыдущего на одно и то же число.
an 1 an d
d an 1 an
an a1 d (n 1)
a1 an
2a1 d (n 1)
Sn
n, S n
n
2
2
4
5. Модуль «Алгебра»
№6Модуль «Алгебра»
Ответ: ⎕⎕⎕⎕
6. Модуль «Алгебра»
№6Модуль «Алгебра»
51=270-3n
3n=270-51
n=255:3
n=85
n∊N
15=270-3n
3n=270-15
n=219:3
n=73
n∊N
151=270-3n
3n=270-151
n=119:3
n=39,66…
n∉N
Ответ: ⎕ ⎕ ⎕ ⎕
123=270-3n
3n=270-123
n=147:3
n=49
n∊N
7. Модуль «Алгебра»
№6Модуль «Алгебра»
Ответ: 24
8. Модуль «Алгебра»
№6Модуль «Алгебра»
Ответ: 5
9. Модуль «Алгебра»
№6Модуль «Алгебра»
Дана арифметическая прогрессия: -4; -1; 2; … . Найдите
сумму первых шести её членов.
Ответ: 21
10. Модуль «Алгебра»
№6Модуль «Алгебра»
Ответ: 20
11. Геометрическая прогрессия
Какая последовательность называетсягеометрической прогрессией?
Какой формулой можно записать
геометрическую прогрессию?
Как найти знаменатель геометрической
прогрессии?
Какой формулой выражается n-ый член
геометрической прогрессии?
Как можно вычислить сумму n
первых членов геометрической
прогрессии?
12. Повторение
Геометрическая прогрессия –последовательность, каждый член которой
больше предыдущего в одно и то же число.
bn 1 bn q
q bn 1 : bn
bn b1 q
n 1
b1 (q n 1)
Sn
q 1
12
13. Модуль «Алгебра»
№6Модуль «Алгебра»
Геометрическая прогрессия (an) задана формулой an 3 2 n.
Какоe из следующих чисел не является членом прогрессии:
1) 24
2) 72
3) 192
4) 384 ?
Дано: (an), an 3 2 n
Решение: подставим поочередно данные числа в формулу
n-го члена прогрессии и найдем n (порядковый номер). Если n
– натуральное, то число является членом данной прогрессии.
3∙2ⁿ=24
2ⁿ=8
n=3 N
3∙2ⁿ=72
2ⁿ=24
n N
3∙2ⁿ=192
2ⁿ= 64
n =6 N
Ответ: ⎕ ⎕ ⎕ ⎕
3∙2ⁿ=384
2ⁿ=138
n=7 N
14. Модуль «Алгебра»
№6Модуль «Алгебра»
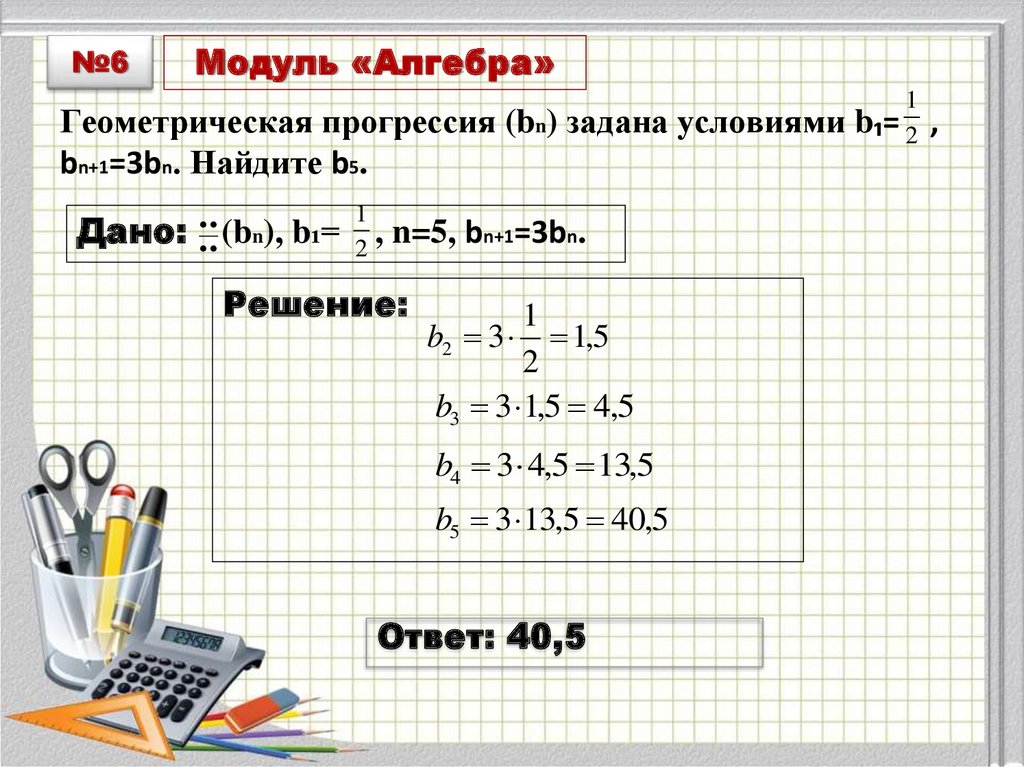
Геометрическая прогрессия (bn) задана условиями
bn+1=3bn. Найдите b5.
Дано:
(bn), b₁=
1
,
2
n=5, bn+1=3bn.
Решение:
1
b2 3 1,5
2
b3 3 1,5 4,5
b4 3 4,5 13,5
b5 3 13,5 40,5
Ответ: 40,5
1
b₁= 2
,
15. Модуль «Алгебра»
№6Модуль «Алгебра»
(an) - геометрическая прогрессия: b4= -1, b7=27. Найдите
знаменатель этой прогрессии.
Дано:
(an), b4= -1, b7=27.
Решение: bn b1 q n 1
b1 q 3 1
1 27
3
q 3
q
27
⇒
⇒
⇒
3
6
q
q
b1 q 6 27
Ответ: -3
16. Модуль «Алгебра»
№6Модуль «Алгебра»
1
Дана геометрическая прогрессия: , 1, 4. Найдите
4
произведение первых пяти ее членов.
Дано:
(bn):
1
4
, 1, 4.
1
Решение: q bn 1 : bn ⇒ q b2 : b1 1 : 4
4
bn 1 bn q
b4 b3 q 4 4 16
b5 b4 q 16 4 64
1
b1b2b3b4b5 1 4 16 64 1024
4
Ответ: 1024.
17. Модуль «Алгебра»
№6Модуль «Алгебра»
(bn) – геометрическая прогрессия, знаменатель которой
равен 3, b₁= 1 . Найдите сумму первых пяти её членов.
9
1
Дано: (bn), q=3, b₁= 9 , n=5.
Решение:
b1 (q n 1)
Sn
q 1
1 5
(3 1)
242 121
4
S5 9
13
3 1
9 2
9
9
4
Ответ: 13
9
















 mathematics
mathematics








