Similar presentations:
Электрическое поле в веществе
1.
Лекция 2Электрическое поле в веществе
Содержание
Проводник в электрическом поле
Распределение зарядов на проводнике
Электрическое поле внутри и вне проводника
Электростатическая защита
Электрическая емкость
Конденсаторы
Энергия электрического поля
1
2.
Проводники в электростатическом полеВ металлах имеется огромное число свободных электронов,
которые могут перемещаться по всему объему металла.
Если поместить металлический проводник во внешнее
электростатическое поле, то свободные электроны будут
смещаться против поля до тех пор, пока
не установится такое
распределение зарядов, при котором E =0.
2
3.
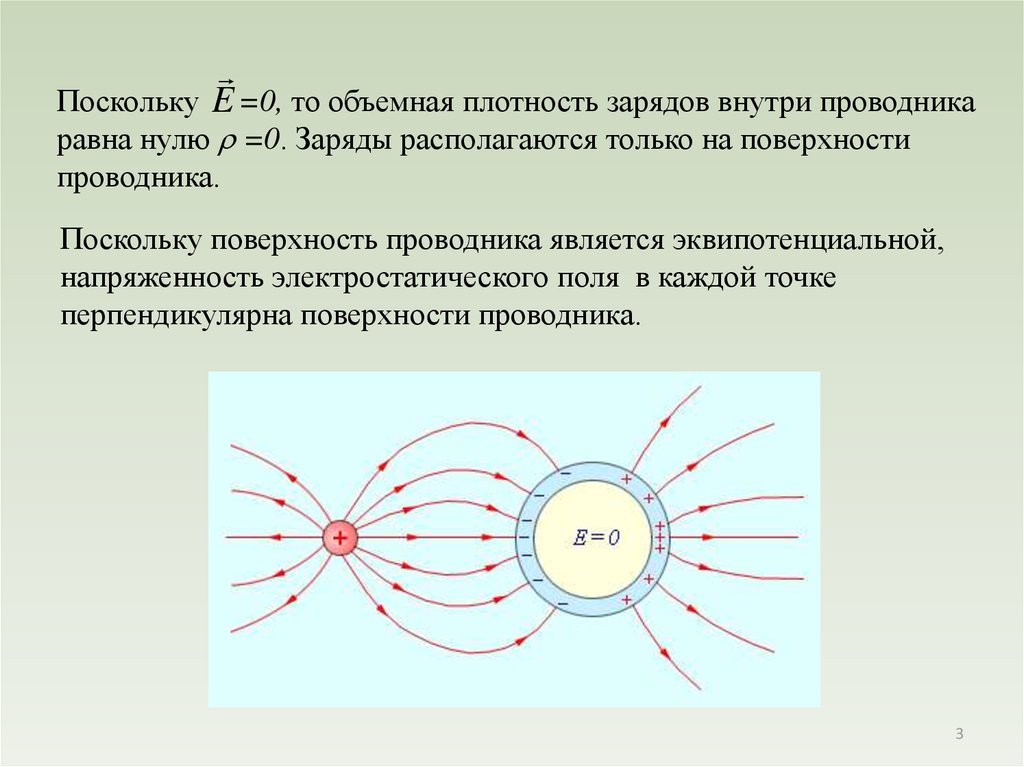
Поскольку E =0, то объемная плотность зарядов внутри проводникаравна нулю =0. Заряды располагаются только на поверхности
проводника.
Поскольку поверхность проводника является эквипотенциальной,
напряженность электростатического поля в каждой точке
перпендикулярна поверхности проводника.
3
4.
Напряженность электростатического поля вблизи поверхностиметалла можно найти с помощью теоремы Гаусса:
q
EdS
0
Рассмотрим малую область пространства вблизи произвольной точки
на поверхности металла. Окружим ее замкнутой поверхностью в виде
малого цилиндра площадью основания S и высотой h.
4
5.
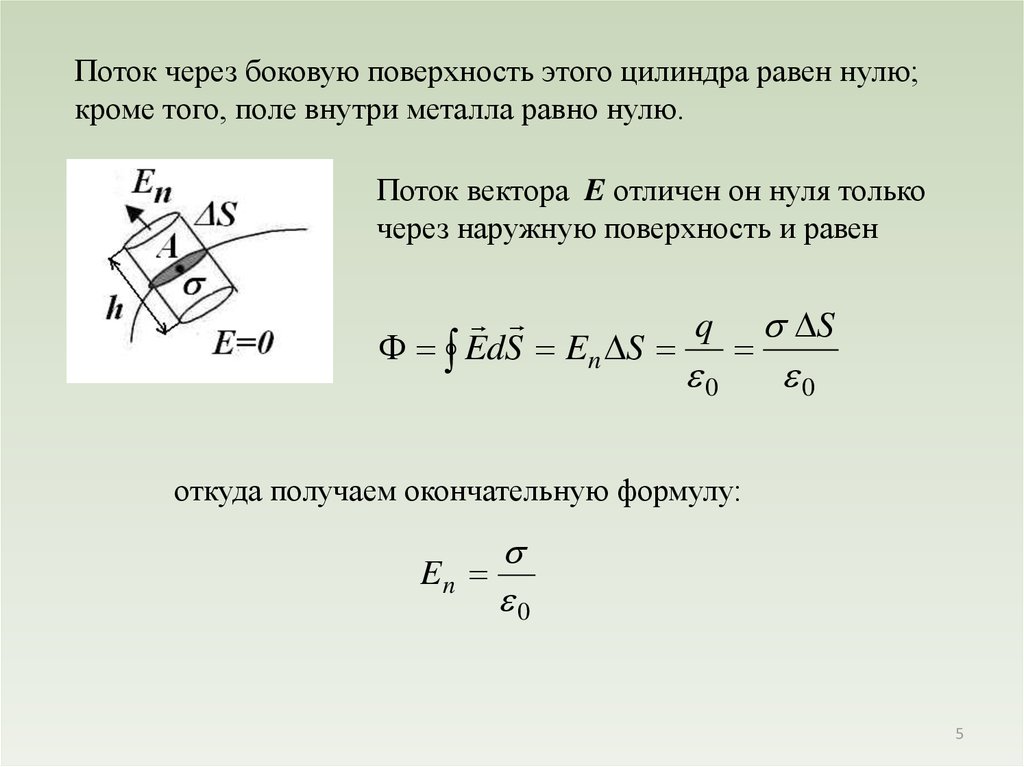
Поток через боковую поверхность этого цилиндра равен нулю;кроме того, поле внутри металла равно нулю.
Поток вектора E отличен он нуля только
через наружную поверхность и равен
q S
EdS En S
0
0
откуда получаем окончательную формулу:
En
0
5
6.
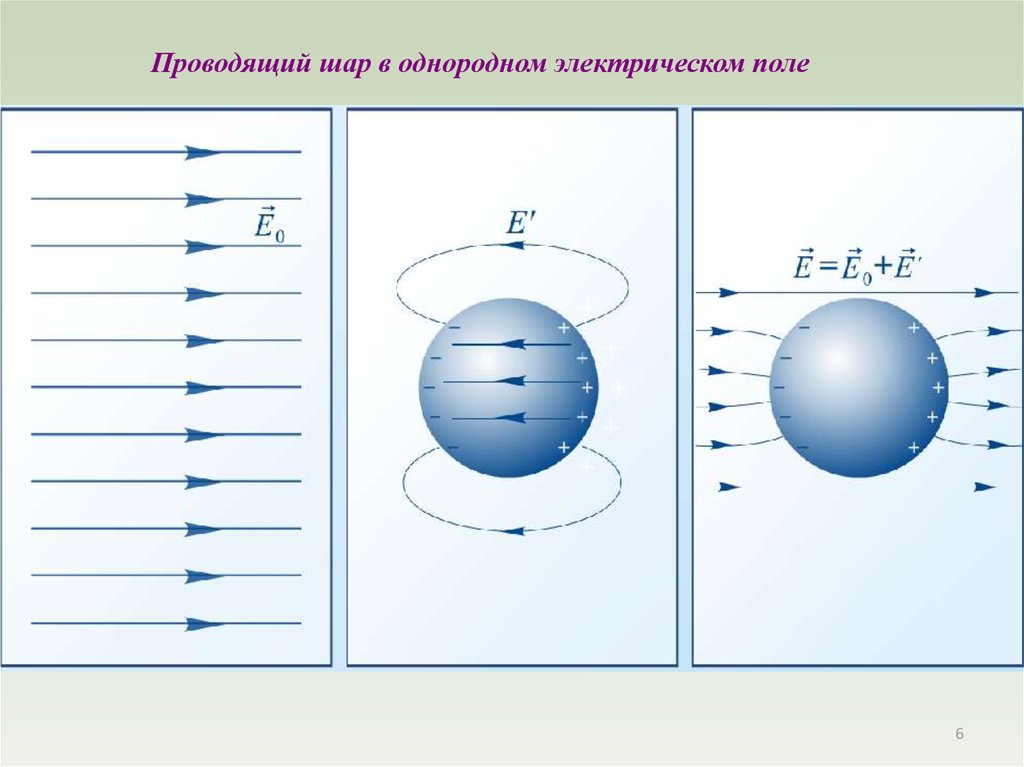
Проводящий шар в однородном электрическом поле6
7.
Электроемкость уединенного проводника и конденсатораВеличину
C
q
(3.1)
называют электроемкостью уединенного проводника.
Электроемкость зависит от размеров и формы проводника.
Единица электроемкости в системе СИ: фарад (Ф)
1Кл
C
1Ф
1В
Пример. Найдем электроемкость уединенного проводника,
имеющего форму шара радиуса R .
Для этого зарядим проводник зарядом q и вычислим его
потенциал :
Edr
R
1
qdr
4 0 R r 2
1
q
.
4 0 R
7
8.
Тогдаq 4 0 R
C
4 0 R . (3.2)
q
q
• Электроемкость сферы размерами с
Землю равна всего 709 мкФ.
• Электроемкость сферы равна 1 Ф,
если радиус сферы в 1400 раз больше
радиуса Земли, т.е. R = 9⋅1012 м.
Конденсаторы — это устройства, которые состоят из двух или более
проводников, разделенных тонким слоем диэлектрика.
Проводники, из которых состоит конденсатор, называются обкладками.
Электроемкостью конденсатора называют
отношение заряда на положительно заряженной
обкладке к разности потенциалов между
обкладками (эту разность потенциалов называют
напряжением):
q
q
C
.
1 2 U
8
9.
Соединения конденсаторовДля получения необходимой емкости конденсаторы соединяют между
собой в батареи, применяя при этом параллельное, последовательное и
смешанное соединения.
• Параллельное
соединение
Общий заряд равен
алгебраической сумме зарядов
каждой из обкладок отдельных
конденсаторов:
q q1 q2 qn .
Т.к. соединенные обкладки представляют собой один проводник, то потенциалы
всех соединенных в один узел обкладок одинаковы и разность потенциалов
между обкладками всех конденсаторов одинакова: U1 U 2 U 3 U .
Т.к. q = CU , q1 = C1U , q2 = C2U , q3 = C3U , то
n
Cпар. С1 С2 Сn Ci
i 1
9
10.
• Последовательноесоединение
q q1 q2 qn ,
U U1 U 2 U n .
q
q
q
q
Т.к. U , U1 =
, U2 =
, Un =
, то
C
C1
C2
Cn
1
Cпосл.
n 1
1
1
1
C1 C2
Cn i 1Ci
10
11.
Емкость плоского конденсатораПлоский конденсатор состоит из
двух параллельных пластин,
разделенных зазором шириной d .
Если заряд конденсатора q , то
напряженность поля, создаваемого
каждой из пластин равна по модулю:
(по теореме Гаусса),
E1
2 0
результирующая напряженность поля между обкладками:
E
, где
0
q S.
11
12.
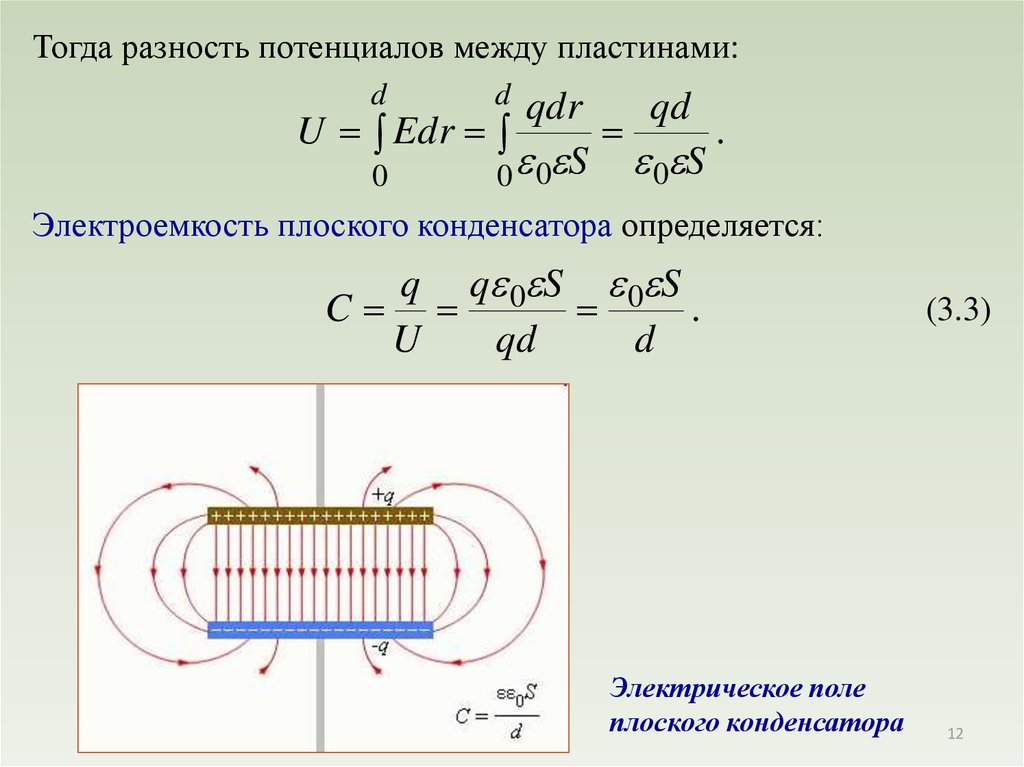
Тогда разность потенциалов между пластинами:d
d
qdr
qd
U Edr
.
0
0 0 S 0 S
Электроемкость плоского конденсатора определяется:
q q 0 S 0 S
C
.
U
qd
d
Электрическое поле
плоского конденсатора
(3.3)
12
13.
Емкость сферического конденсатора:R1R2
C 4 0
.
R2 R1
(3.4)
Емкость цилиндрического конденсатора:
2 0 l
C
,
ln R2 R1
(3.5)
где l - длина конденсатора, R1 и R2 - радиусы внутренней и
наружной обкладок цилиндрических обкладок.
Т.о., электроемкость конденсатора зависит от размеров и формы
обкладок, от зазора между ними и от заполняющей конденсатор среды.
13
14.
Энергия заряженного конденсатораПусть имеется конденсатор емкости C , заряженный до
напряжения U . Для того, чтобы перенести на него добавочный
заряд dQ требуется совершить работу dA UdQ ; но в
конденсаторе заряд и напряжение связаны соотношением
Q CU , дифференцируя которое, получим dQ CdU . Тогда
dA CUdU, и полная работа, которую надо совершить для
заряда конденсатора:
CU 2 Q 2 QU
A CUdU
.
2
2C
2
0
U
Эта работа идет на создании энергии электрического поля
конденсатора:
CU 2
(3.6)
W
.
2
14
15.
Учтем, что объем конденсатора V Sd , тогда можноW
ввести величину плотность энергии: w
V
.
Подставим в формулу (3.6) выражение для емкости
плоского конденсатора и учтем, что U Ed , C
0 S
d
и находим:
W
0
2d
SE d
2 2
0
2
2
E V ;
w
0 E 2
2
.
,
(3.7)
15
16.
Применение конденсаторовКонденсаторы находят широкое применение во многих областях радиои электротехники.
• При быстром разряде конденсатора можно получить импульс большой
мощности, например, в фотовспышках, электромагнитных ускорителях,
импульсных лазерах и т. п.
• Так как конденсатор способен длительное время сохранять заряд, то
его можно использовать в качестве элемента памяти или устройства
хранения электрической энергии.
• Емкость конденсатора заметно изменяется при малейших изменениях
параметра конденсатора. Так малое изменение расстояния между
обкладками учитывается в измерителях малых перемещений, изменение
состава диэлектрика при изменении влажности фиксируется в
измерителях влажности, учет изменения высоты диэлектрика между
обкладками конденсатора позволяет измерять уровень жидкости и т.п.
• Конденсаторы (совместно с катушками индуктивности и/или
резисторами) используются для построения различных цепей с
частотно-зависимыми свойствами, в частности, фильтров, цепей
16
обратной связи, колебательных контуров и т. п.












 physics
physics