Similar presentations:
Простые и составные числа
1. Простые и составные числа
2.
У879.1
2
3
4
5
6
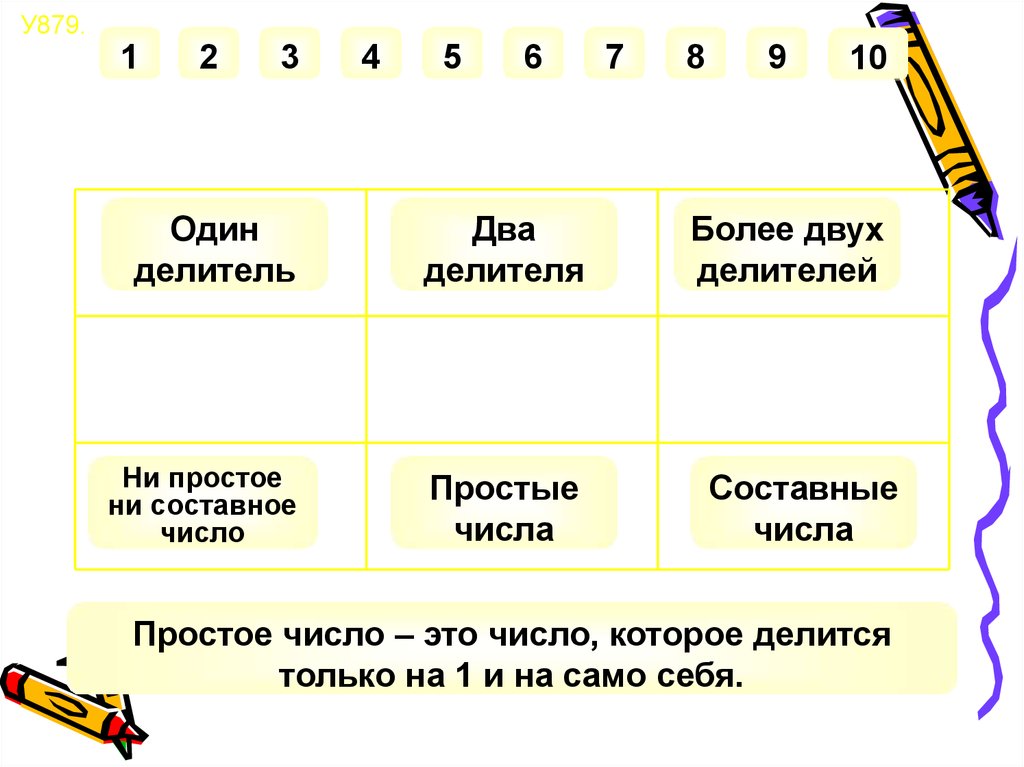
Один
делитель
Два
делителя
Ни простое
ни составное
число
Простые
числа
7
8
9
10
Более двух
делителей
Составные
числа
Простое число – это число, которое делится
только на 1 и на само себя.
3. определения
-Натуральные числа, имеющие толькодва делителя называют простыми.
-Натуральные числа, имеющие более
двух делителей называют
составными.
-Число 1 не относится ни к простым, ни
к составным.
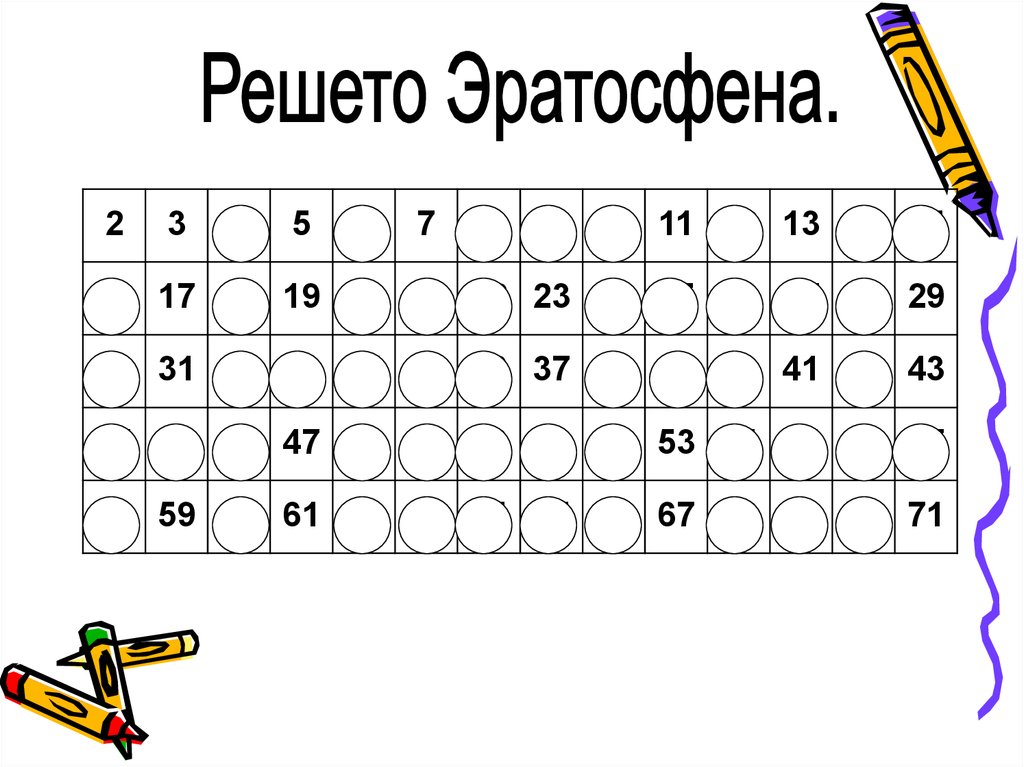
4. Древнегреческий ученый Эратосфен (276г.до н.э. – 194г. до н.э.) предложил свой способ для составления таблицы простых чисел
5.
23
4
5
6
7
8
9 10 11 12 13 14 15
16 17 18 19 20 21 22 23 24 25 26 27 28 29
30 31 32 33 34 35 36 37 38 39 40 41 42 43
44 45 46 47 48 49 50 51 52 53 54 55 56 57
58 59 60 61 62 63 64 65 66 67 68 69 70 71
6.
Даны числа14,17,27,29,33,37,41,43,45.
Укажите, какие из них являются
а) простыми; б) составными.
7. В III веке до н.э. Евклид доказал, что простых чисел бесконечно много, что наибольшего простого числа не существует.
8. Простые числа, между которыми в натуральном ряду чисел находится только одно число, называют числами-близнецами.
Простые числа, междукоторыми в натуральном
ряду чисел находится
только одно число,
называют числами-
близнецами.
9. Изучением свойств простых чисел занимался русский математик Пафнутий Львович Чебышев. Он доказал, что между любым натуральным числом, бол
Изучением свойств простыхчисел занимался русский
математик Пафнутий
Львович Чебышев. Он
доказал, что между любым
натуральным числом,
большим 1 и числом, вдвое
больше данного, всегда
имеется не менее одного
простого числа.
10. Пифагор (Vl в.до н.э.) и его ученики изучали вопрос о делимости чисел. Есть такие числа, которые равны сумме всех его делителей (без самого числ
Пифагор (Vl в.до н.э.) и егоученики изучали вопрос о
делимости чисел. Есть такие
числа, которые равны сумме
всех его делителей (без
самого числа). Их назвали
совершенными числа.
Например 6=1+2+3,
28=1+2+4+7+14.
11.
Следующие совершенные числа 496,8128, 33550336. Пифагорейцы
знали только первые три
совершенные числа. Четвертое –
8128-стало известно в I в.н.э. Пятое
– 33550336- было найдено в XV в. К
1983 г. было известно уже 27
совершенных чисел. Но до сих пор
ученые не знают, есть ли нечетные
совершенные числа, есть ли самое
большое совершенное число.
12.
Задача 1Эратосфен родился примерно в
276г. до н.э. и умер примерно
в 194г. до н.э.
Какие года, выраженные
простыми числами,
приходятся на период жизни
Эратосфена?
13. Задача 2
Посмотрев внимательно таблицупростых чисел, можно увидеть
симметричные пары
«ПЕРЕВЕРТЫШИ». Например:
13-31; 107-701. Найдите остальные
пары.
14. Задача 3
В таблице имеются стайки«жар-птиц»-простых чисел с
«пером» 13 в хвостике
(оканчивающихся на 13):
13,113,313... стайки простых
чисел с «пером» 31 в хвостике.
Какие еще можно найти стайки?
15. Рефлексия
1. Какие натуральные числаназываются простыми?
2. Какие натуральные числа
называются составными?
3. Почему число 1 не является ни
простым, ни составным?
4. Верно ли, что все четные числа
являются составными?
16. Домашнее задание:
Стр.191 (выучить определения)Найти числа «перевертыши».
Найти «стайки» жар-птиц















 mathematics
mathematics








