Дифференциальные уравнения

1.

Дифференциальные уравнения
G(t , y, y ,..., y ( n ) ) 0
y ( n ) F (t , y, y ,..., y ( n 1) )
y y (t )
(1)
(2)

2.

dy
1 sin 2t
dt
1
y t cos 2t C
2

3.

Описание линейных динамических систем дифференциальными уравнениями
n
ai y
i 0
где
(i)
m
b j x( j) ,
j 0
i
j
d
y
d
x
(i)
(i)
y i , x j , an 1, m n
dt
dt

4. Преобразование Лапласа

L f t F p f t e dt
0
f (t) - оригинал
F (p) - изображение
f(t) F(p)
pt

5. Преобразование Лапласа

Если f(t) F(p)
то
f'(t) pF(p) – f(0)
f''(t) p2 F(p) - pf(0) - f'(0)
здесь f(0), f'(0)- нач.условия

6.

Найти изображения следующих
оригиналов:
• E(t)
• sin( t)
• cos( t)

7. Решение линейных дифференциальных уравнений с помощью преобразования Лапласа

x 3 x 2 x 0
x(0) 0, x (0) 1

8. Найти передаточные функции по следующей системе уравнений

d 2 y
dy
dz
a2
a3 z a4 x(t )
2 a1
dt
dt
dt
dz dy b z b x(t )
1
2
dt dt

9. Определение процесса регулирования

10
W
2
0.1 p p 10
g(t)=E(t)

10. Определение процесса регулирования

X(p)=W(p)G(p)
10
100
X ( p)
2
2
p(0.1 p p 10) p( p 10 p 100)

11. Определение процесса регулирования

A
Bp C
X ( p) 2
p p 10 p 100

12. Определение процесса регулирования

1
p
10
X ( p) 2
2
p p 10 p 100 p 10 p 100

13. Определение процесса регулирования

p 10 p 100 ( p 5) 75
2
2

14. Преобразование Лапласа

Пример 5. Найти выходную величин y(t) системы,
описываемой уравнением
dy (t )
T
y (t ) g (t )
dt
если g(t)=Gм*sin( t)
y(0)=y0

15. Численные методы решения дифференциальных уравненрий

16. Численные методы решения ДУ

y f (t , y )
y (t0 ) y0

17. Численные методы решения ДУ

(tm , ym )
y f (tm , ym )
'
m
t m 1 t m h

18. Численные методы решения ДУ

y ym y (t t m )
'
m
y m' f (t m , ym ), t m 1 t m h
ym 1 ym h f (tm , ym ) (1)

19. Численные методы решения ДУ

t m , ym
t m h, ym h y
'
m
1
F1 (t m , y m , h) [ f ( xm , y m ) f ( xm h, y m h y m' ), a y m' f ( xm , y m )
2
y ym h F1 (tm , ym , h)
ym 1 ym h F1 (t m , ym , h)
(2)

20. Численные методы решения ДУ

h
h '
'
F2 (t m , y m , h) f ( xm , y m y m ), a y m f ( xm , y m )
2
2
ym 1 ym h F2 (tm , ym , h) (3)

21. Численные методы решения ДУ

y m 1
h
y m ( k1 2 k 2 2 k 3 k 4 )
6
где
k1 f ( x m , y m )
h k1
h
k 2 f ( xm , y m
)
2
2
h k2
h
k 3 f ( xm , y m
)
2
2
k 4 f ( x m h, y m h k 3 )

22. Численные методы решения ДУ

y y,
'
y ( 0 ) 1.
Ðåøåíèå :
y (t ) c et .
Ïðè çàäàííîì
y (t ) e .
t
íà÷àëüíîì
óñëîâèè :

23. Численные методы решения ДУ

y ' y,
Численные методы решения ДУ
y ( 0 ) 1.
ym 1 ym h f (tm , ym ) (1)
[0,2]; h=0.5
t
exp(t)
0,0
1,00
0,5
1,65
1,0
2,72
1,5
4,48
2,0
7,39
Eiler
1,00

24. Численные методы решения ДУ

8,00
7,00
6,00
5,00
4,00
3,00
2,00
1,00
0,00
1
2
3
4
5

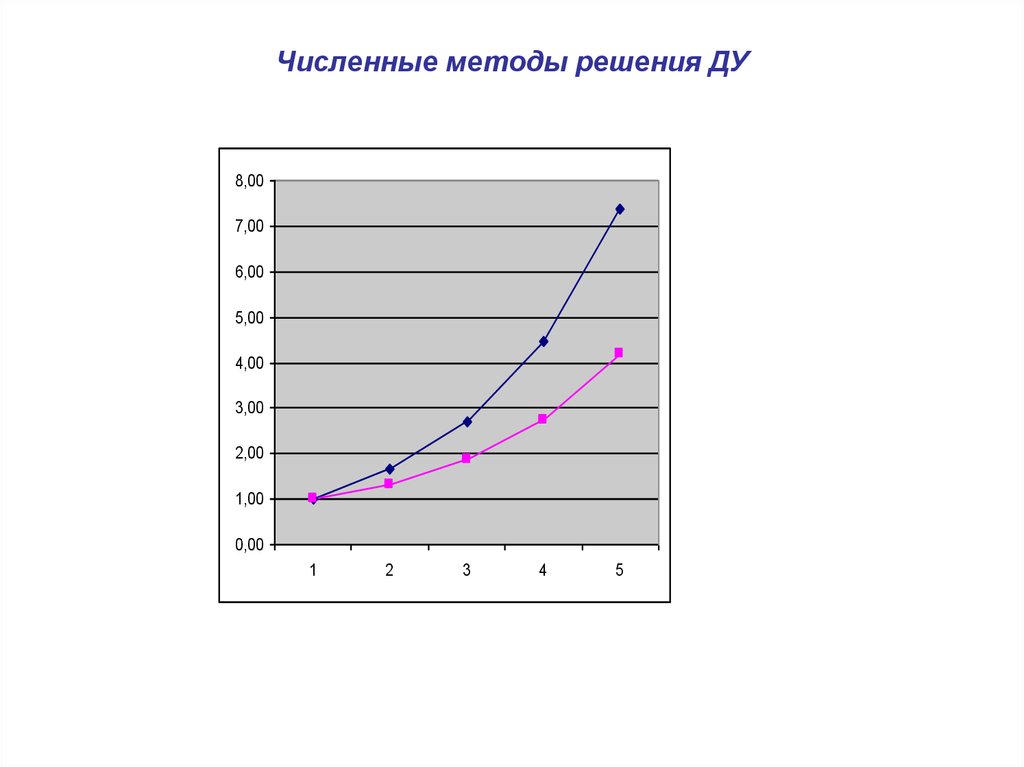
25. Численные методы решения ДУ

k1 y m
h
k 2 ym ym
2
h
h
k 3 y m ( y m y m )
2
2
h
h
k 4 y m h [ y m ( y m y m )]
2
2
h2 h3 h4
y m 1 y m (1 h )
2 6 24

26.

Ðåøèòü çàäàííîå äèô . óðàâíåíèå :
1) àíàëèòè÷åñ êè
2) ìåòîäîìÝéë
3) ìåòîäîì
åðà
Ðóíãå Êóòòà
íà èíòåðâàëå [0,2] ñ øàãîì 0,1.
Îòðàçèòü âñåòðè ðåøåíèÿ íà îäíîì
Îöåíèòü îøèáêó
y y 2,
'
y (0) 0.
ãðàôèêå .