Математические основы психологии

1. Математические основы психологии

Автор:
к.пс.н., доцент Дорофеев В.А.
1

2. Общая схема математического анализа эмпирических данных в психологии

Тип решаемой
задачи
Определение
значимости
различий на
уровне
исследуемого
признака
Определение
значимости
различий на
уровне
исследуемого
признака
Шкала
измерений
Выборки
Характер
распределения
признака
Статистическая
операция
номинативная
две
не определяется
интервальная
две
не отличается от
нормального
интервальная
две
отличается от
нормального
непараметрический
U-критерий Манна-Уитни
интервальная
три и более
не определяется
непараметрический
Н-критерий КрускалаУоллиса
интервальная
две
не определяется
Непараметрический
Т-критерий Вилкоксона
интервальная
три и более
не определяется
Непараметрический
L-критерий Пейджа
Непараметрический
2- критерий
Параметрический
t-критерий Стьюдента
2

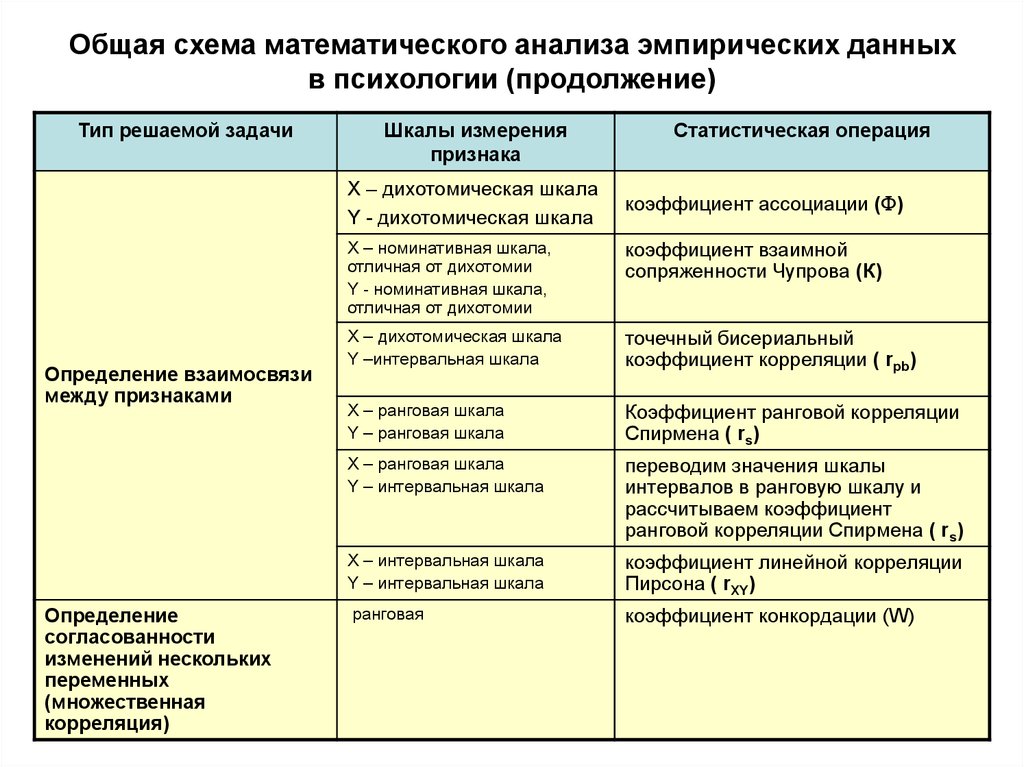
3. Общая схема математического анализа эмпирических данных в психологии (продолжение)

Тип решаемой задачи
Шкалы измерения
признака
X – дихотомическая шкала
Y - дихотомическая шкала
Определение взаимосвязи
между признаками
Определение
согласованности
изменений нескольких
переменных
(множественная
корреляция)
Статистическая операция
коэффициент ассоциации ( )
X – номинативная шкала,
отличная от дихотомии
Y - номинативная шкала,
отличная от дихотомии
коэффициент взаимной
сопряженности Чупрова (К)
X – дихотомическая шкала
Y –интервальная шкала
точечный бисериальный
коэффициент корреляции ( rpb)
X – ранговая шкала
Y – ранговая шкала
Коэффициент ранговой корреляции
Спирмена ( rs)
X – ранговая шкала
Y – интервальная шкала
переводим значения шкалы
интервалов в ранговую шкалу и
рассчитываем коэффициент
ранговой корреляции Спирмена ( rs)
X – интервальная шкала
Y – интервальная шкала
коэффициент линейной корреляции
Пирсона ( rXY)
ранговая
коэффициент конкордации (W)
3

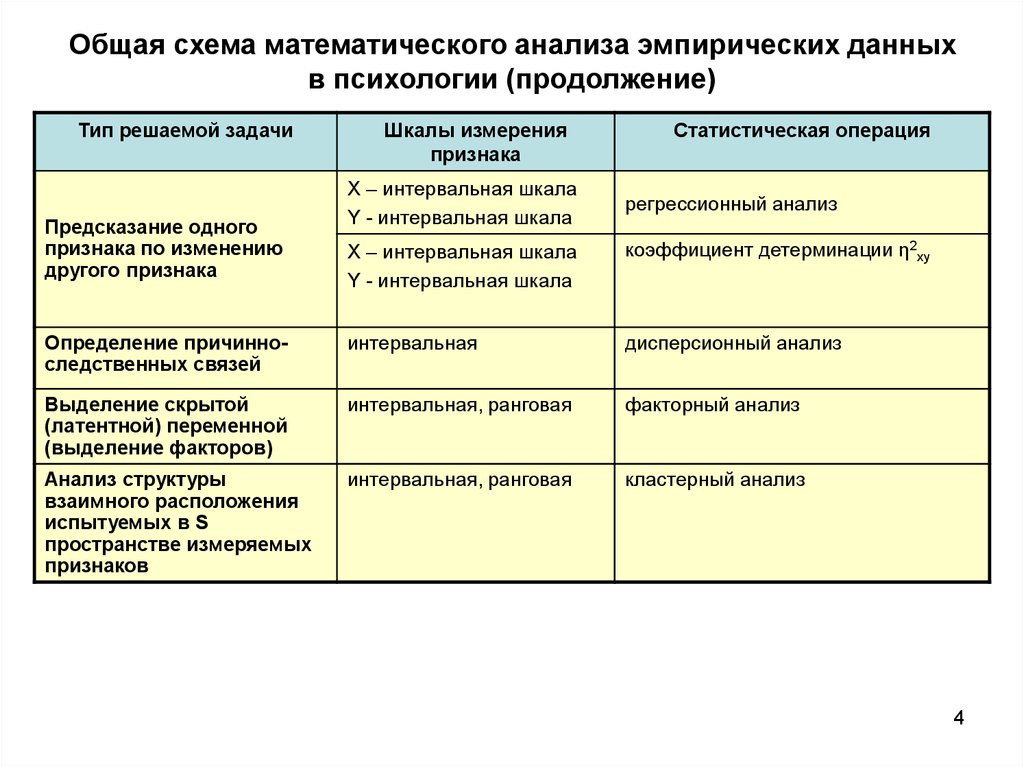
4. Общая схема математического анализа эмпирических данных в психологии (продолжение)

Тип решаемой задачи
Предсказание одного
признака по изменению
другого признака
Шкалы измерения
признака
X – интервальная шкала
Y - интервальная шкала
Статистическая операция
регрессионный анализ
X – интервальная шкала
Y - интервальная шкала
коэффициент детерминации η2xy
Определение причинноследственных связей
интервальная
дисперсионный анализ
Выделение скрытой
(латентной) переменной
(выделение факторов)
интервальная, ранговая
факторный анализ
Анализ структуры
взаимного расположения
испытуемых в S
пространстве измеряемых
признаков
интервальная, ранговая
кластерный анализ
4

5. Понятие о кривой и законе распределения

Кривая распределения – это предел, к которому стремится полигон частот при
неограниченном увеличении объема статистической совокупности и
уменьшении интервалов измерения (увеличение точности измерения, переход
от дискретной величины к непрерывной).
Закон распределения – математическое соотношение, устанавливающее
связь между возможными значениями варианты и соответствующими им
вероятностями.
Закон распределения может быть задан:
а) рядом распределения, в котором каждому значению xi поставлена в
соответствие его вероятность pi;
б) полигоном частот;
в) функцией распределения – аналитическим выражением (формулой), по
которому может быть установлена вероятность каждого текущего значения
случайной величины
5

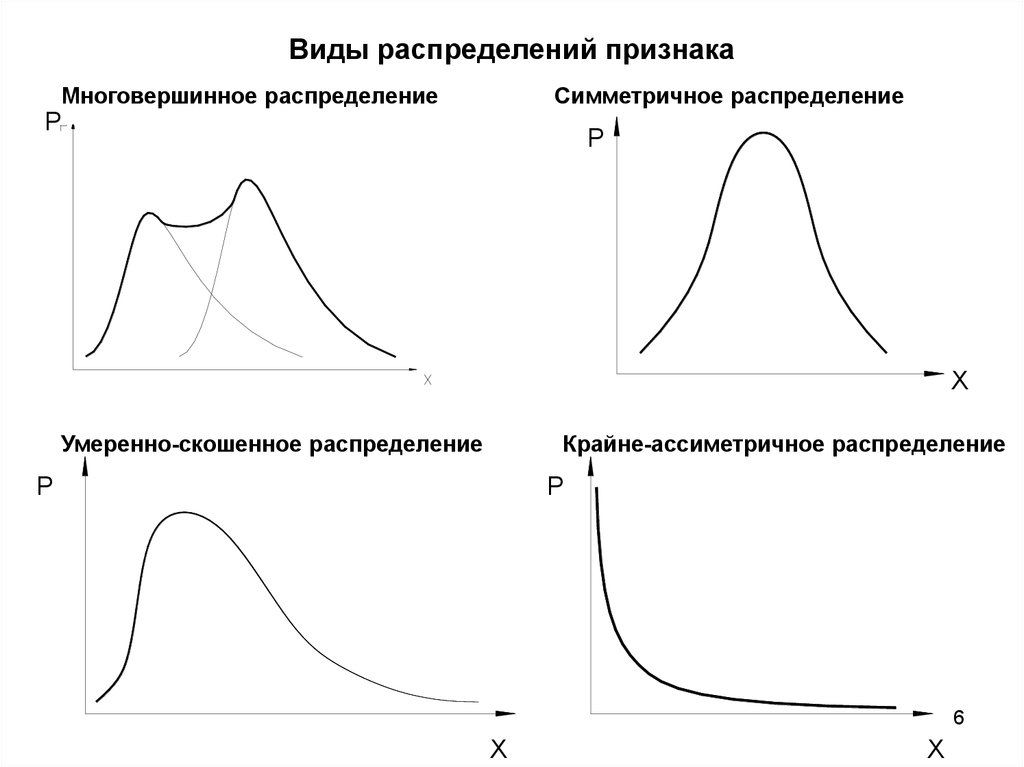
6. Виды распределений признака

Многовершинное распределение
Симметричное распределение
P
Р
Х
Умеренно-скошенное распределение
Крайне-ассиметричное распределение
Р
Р
6
Х
Х

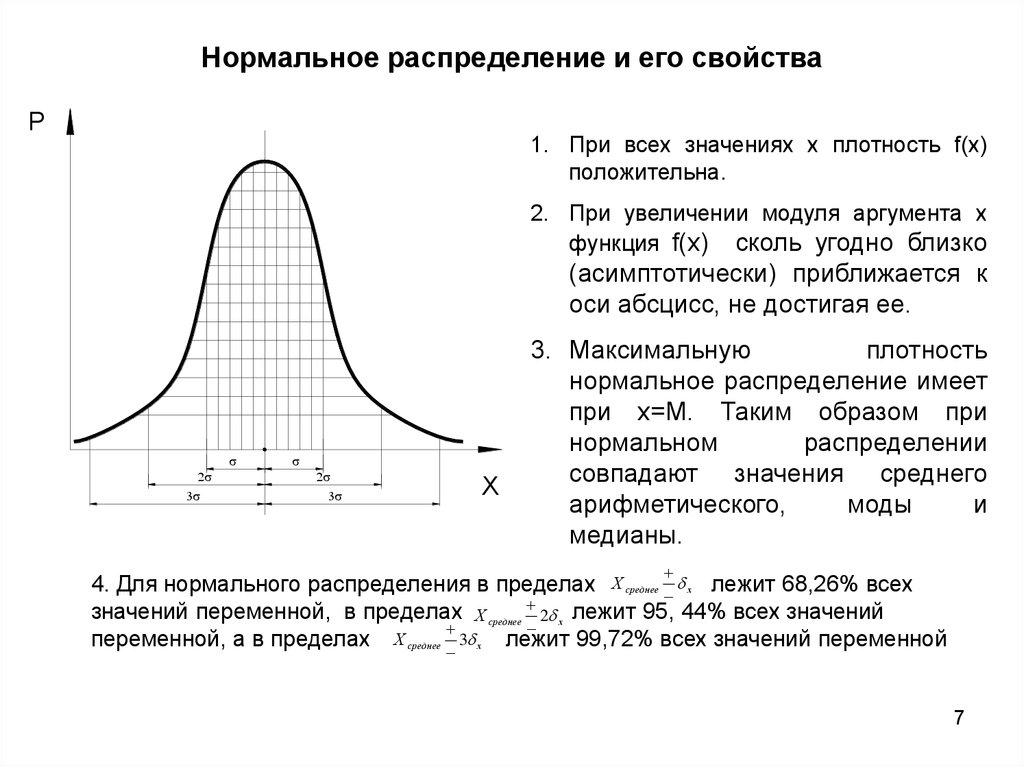
7. Нормальное распределение и его свойства

Р
1. При всех значениях х плотность f(x)
положительна.
2. При увеличении модуля аргумента х
функция f(x) сколь угодно близко
(асимптотически) приближается к
оси абсцисс, не достигая ее.
Х
3. Максимальную
плотность
нормальное распределение имеет
при х=М. Таким образом при
нормальном
распределении
совпадают значения среднего
арифметического,
моды
и
медианы.
4. Для нормального распределения в пределах Х среднее х лежит 68,26% всех
значений переменной, в пределах Х среднее 2 х лежит 95, 44% всех значений
переменной, а в пределах Х среднее 3 х лежит 99,72% всех значений переменной
7

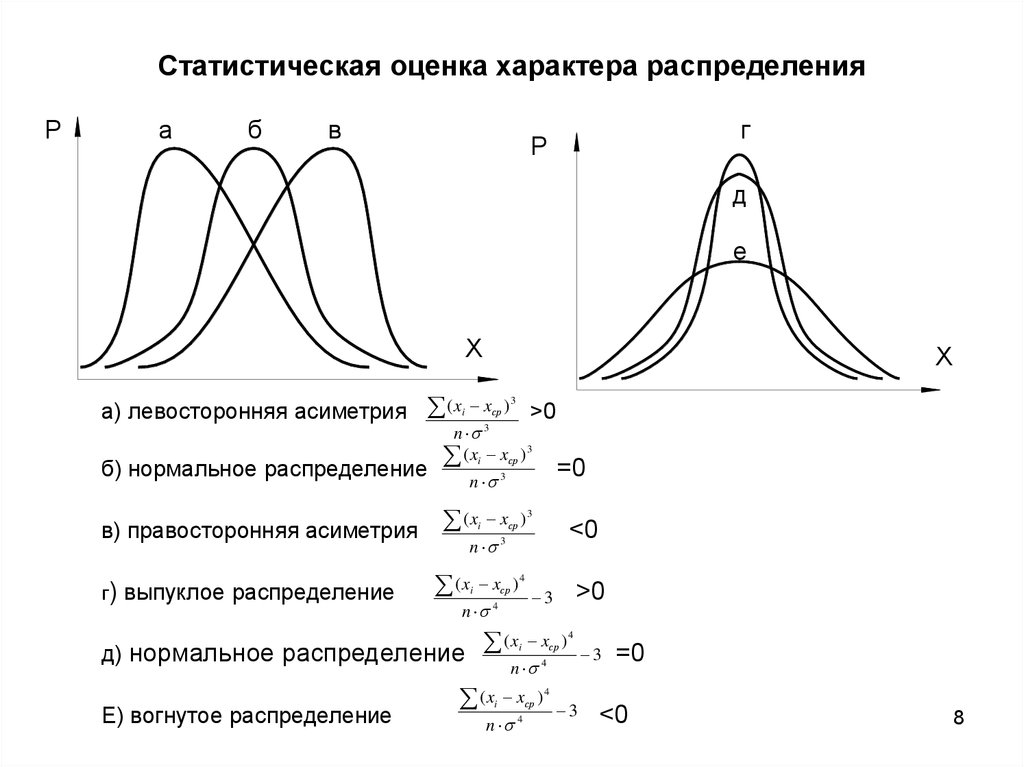
8. Статистическая оценка характера распределения

Р
а
б
в
г
Р
д
е
Х
Х
а) левосторонняя асиметрия ( xi xср ) >0
3
б) нормальное распределение
n 3
( xi xср ) 3
=0
n 3
(x
в) правосторонняя асиметрия
i
xср ) 3
<0
n 3
г) выпуклое распределение
(x
i
xср ) 4
n 4
>0
3
(x x
д) нормальное распределение
n
i
ср
)4
4
Е) вогнутое распределение
(x
i
xср ) 4
n 4
3
3
=0
<0
8

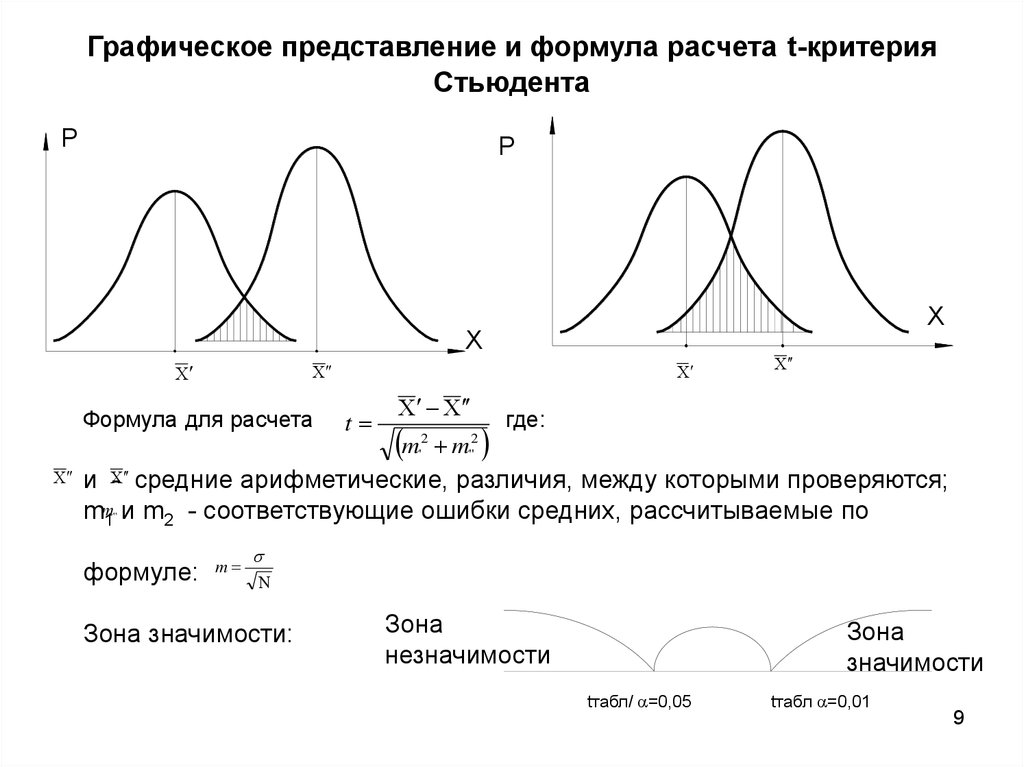
9. Графическое представление и формула расчета t-критерия Стьюдента

Р
Р
Х
Х
Формула для расчета
t
m
2
'
m
2
''
где:
и - средние арифметические, различия, между которыми проверяются;
mm1 и m2 - соответствующие ошибки средних, рассчитываемые по
''
формуле:
m
Зона значимости:
Зона
незначимости
Зона
значимости
tтабл/ =0,05
tтабл =0,01
9

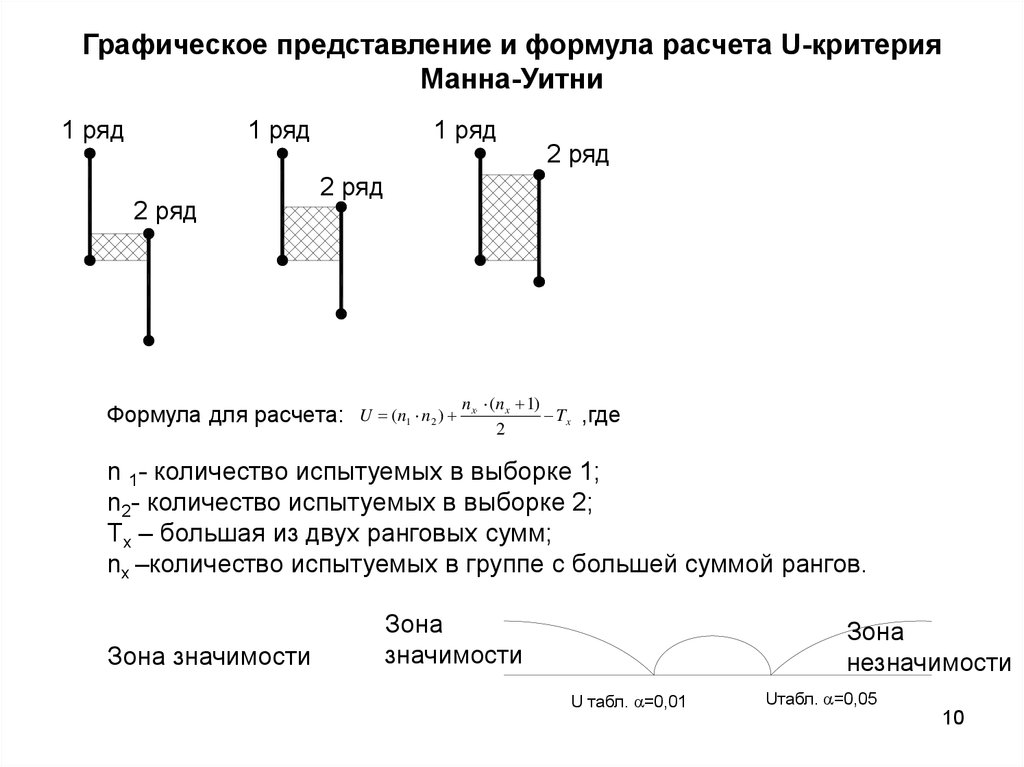
10. Графическое представление и формула расчета U-критерия Манна-Уитни

1 ряд
1 ряд
2 ряд
1 ряд
2 ряд
2 ряд
Формула для расчета:
U (n1 n2 )
n x (n x 1)
Tx
2
,где
n 1- количество испытуемых в выборке 1;
n2- количество испытуемых в выборке 2;
Тx – большая из двух ранговых сумм;
nx –количество испытуемых в группе с большей суммой рангов.
Зона значимости
Зона
значимости
Зона
незначимости
U табл. =0,01
Uтабл. =0,05
10

11. Графическое представление и формула расчета Н-критерия Крускала-Уоллиса

1 ряд
1 ряд
2 ряд
3 ряд
2 ряд
3 ряд
Формула для расчета
2
12
Tj
Н
n
N N 1
3 N 1
, где
N – общее количество испытуемых в объединенной выборке;
n – количество испытуемых в каждой выборке;
Т – суммы рангов по каждой группе
Зона
незначимости
Зона значимости:
Нтабл =0,01
Зона
значимости
Нтабл/ =0,05
11

12. Графическое представление и формула расчета Т-критерия Вилкоксона

б
а
а) «светлый фон» преобладает над «желтым фоном» по
количеству сдвигов, и по их интенсивности
б) «светлый фон» преобладает над «желтым фоном»
только по интенсивности сдвигов, а по количеству
сдвигов они равны
в
в) «светлый фон» уступает «желтому фону» по
количеству сдвигов, но самые интенсивные сдвиги
принадлежат «светлому фону»
Для оценки статистической значимости сдвига подсчитывает сумму рангов в нетипичном
направлении и сравниваем с Ттабл. =0,01 и Ттабл. =0,05
Зона значимости:
Зона
значимости
Зона
незначимости
12

13. Корреляция и ее свойства

Корреляция – статистическая зависимость между случайными величинами, не
имеющими строго функционального характера, при котором изменение одной
из случайных величин приводит к изменению математического ожидания
другой.
Сопряженность
–
стохастическая
(вероятностная)
связь
между
классифицированными событиями
Свойства корреляции.
Направленность корреляции – свойство корреляции, характеризующее
одностороннюю обусловленность изменения одной из случайных величин
изменениями значений другой случайной величины (отрицательные значения
коэффициента корреляции
характеризуют обратную направленность, а
положительные значения коэффициента корреляции характеризуют прямую
направленность)
Теснота (сила) корреляции – свойство корреляции, характеризующее степень
обусловленности изменений одной из случайных величин изменениями
значений другой случайной величины (теснота выражается числовым
значением коэффициента корреляции в диапазоне от -1 до +1)
13

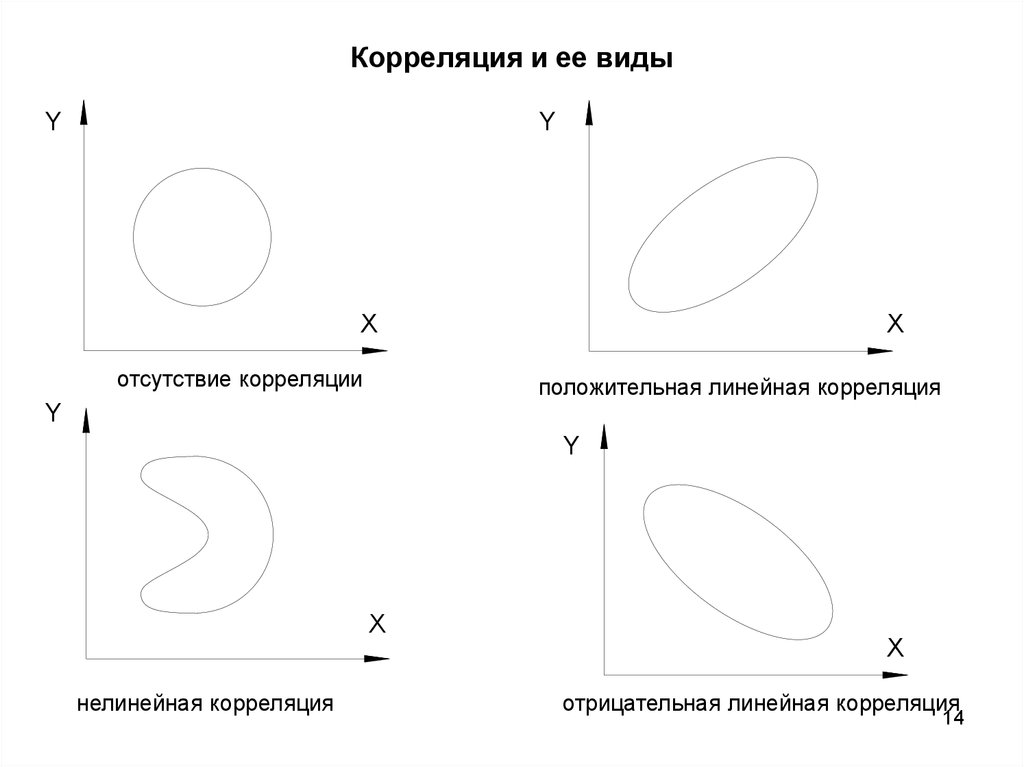
14. Корреляция и ее виды

Y
Y
Х
отсутствие корреляции
Х
положительная линейная корреляция
Y
Y
Х
нелинейная корреляция
Х
отрицательная линейная корреляция
14

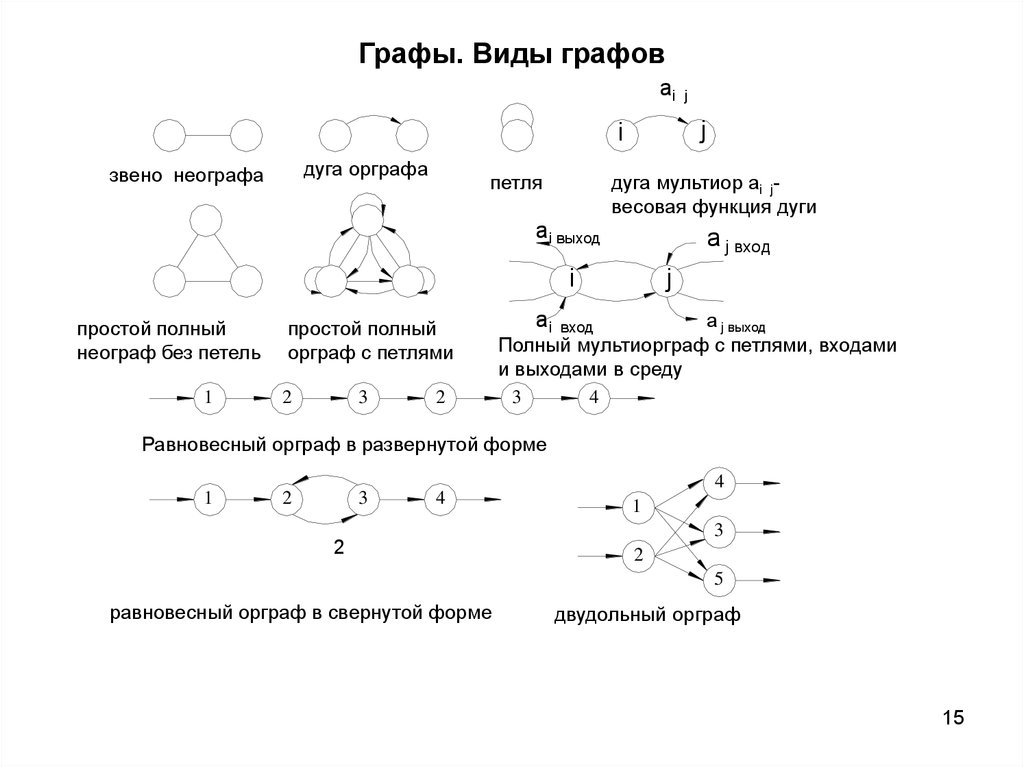
15. Графы. Виды графов

ai
j
i
дуга орграфа
звено неографа
петля
аi выход
дуга мультиор аi jвесовая функция дуги
a j вход
i
простой полный
неограф без петель
1
простой полный
орграф с петлями
2
3
2
аi
j
j
a j выход
Полный мультиорграф с петлями, входами
и выходами в среду
3
вход
4
Равновесный орграф в развернутой форме
1
2
3
4
2
4
1
3
2
5
равновесный орграф в свернутой форме
двудольный орграф
15

16. Операции над графами

1
2
A
3
сверстка графа в вершину
2
1
4
5
5
сверстка подграфа в линию
3
1
1
1
1
5
2
4
4
2
3
объединение графов
1
1
4
2
1
3
пересечение графов
1
1
1
4
2
4
3
4
2
2
1
2
3
2
2
3
Обобщение графов
16