Similar presentations:
Виды деформации, растяжение и сжатие
1. Растяжение и сжатие
2.
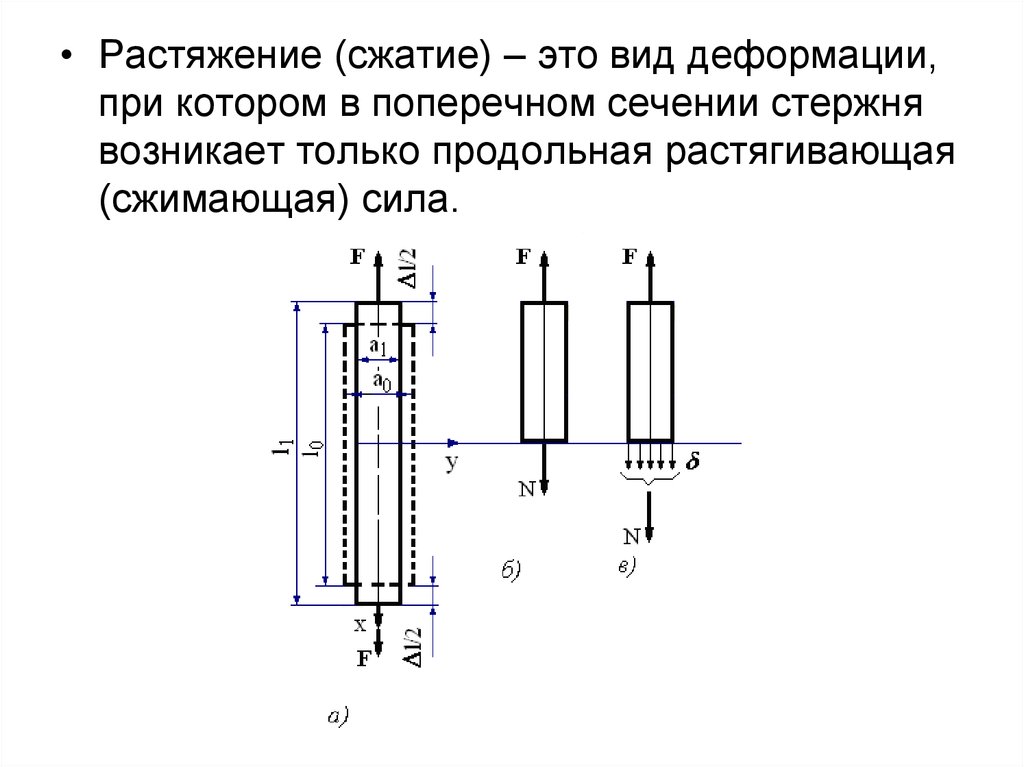
• Растяжение (сжатие) – это вид деформации,при котором в поперечном сечении стержня
возникает только продольная растягивающая
(сжимающая) сила.
3.
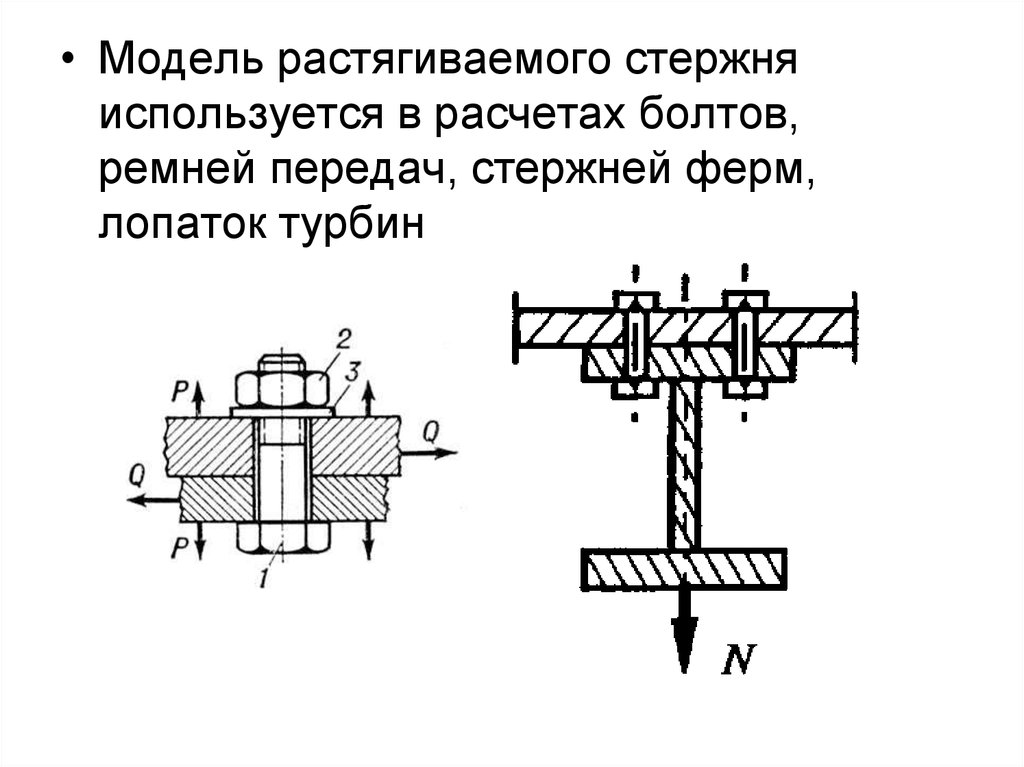
• Модель растягиваемого стержняиспользуется в расчетах болтов,
ремней передач, стержней ферм,
лопаток турбин
4.
5.
• При осевом растяжении и сжатиивнутренние силы в поперечном сечении
могут быть заменены одной силой,
направленной вдоль оси стержня—
продольной силой N.
• В случае когда сила направлена к
отброшенной части наружу, имеет
место растяжение
• Если сила направлена от отброшенной
части внутрь имеет место сжатие.
6.
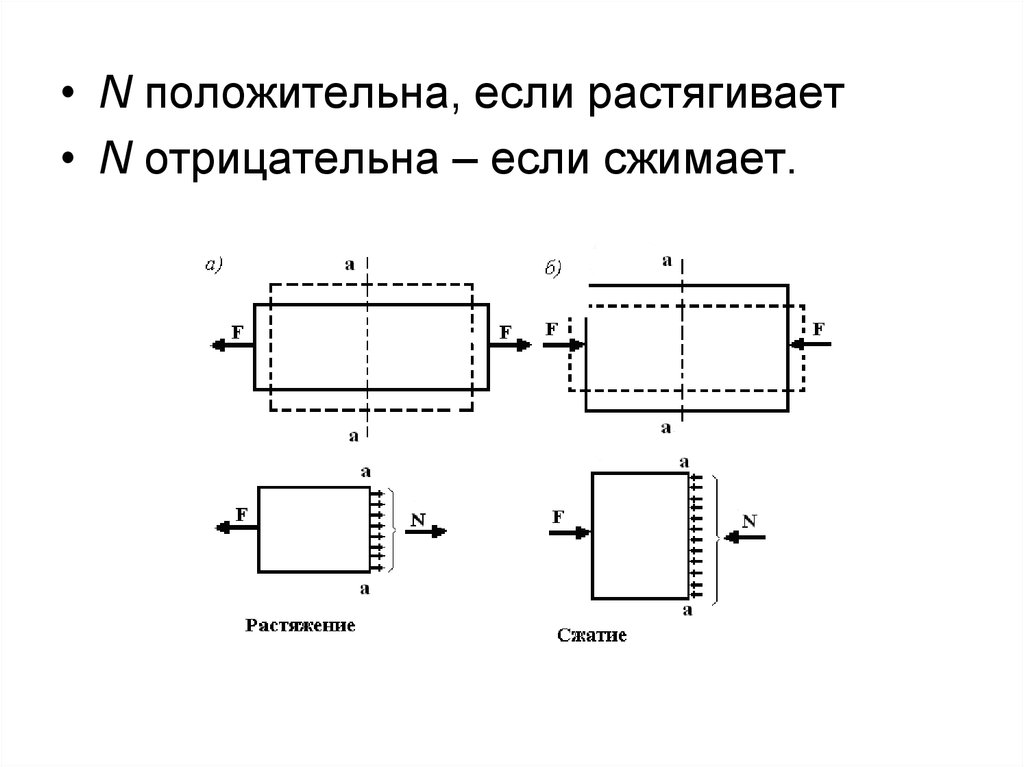
• N положительна, если растягивает• N отрицательна – если сжимает.
7.
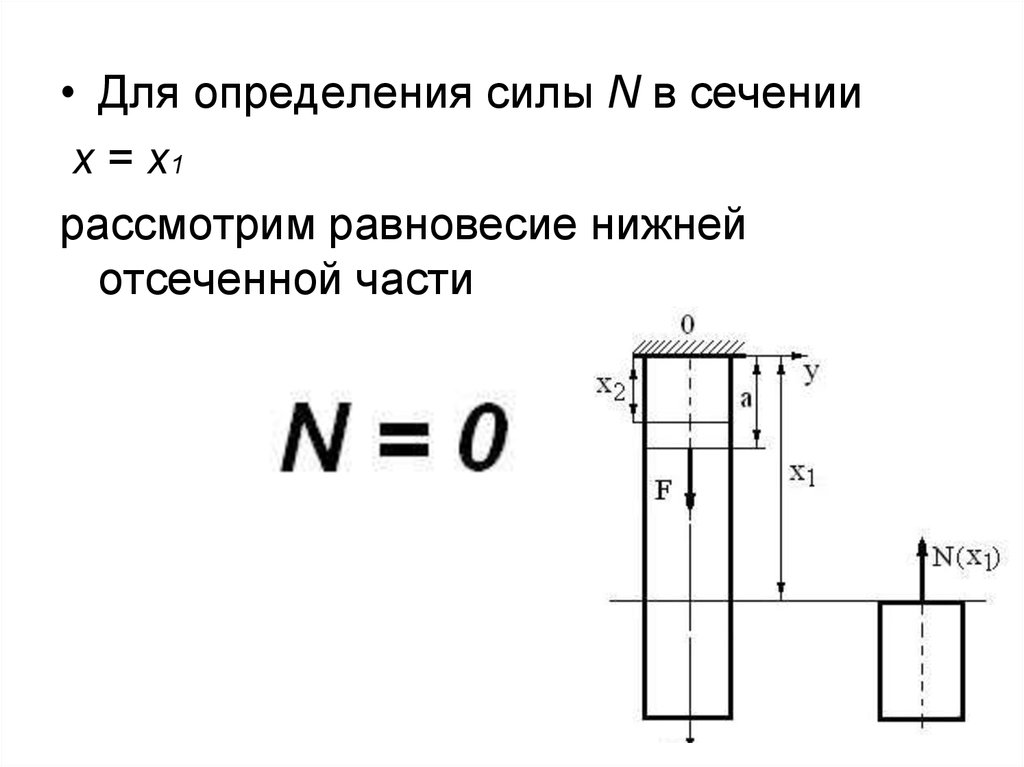
• Для определения силы N в сеченииx = х1
рассмотрим равновесие нижней
отсеченной части
8.
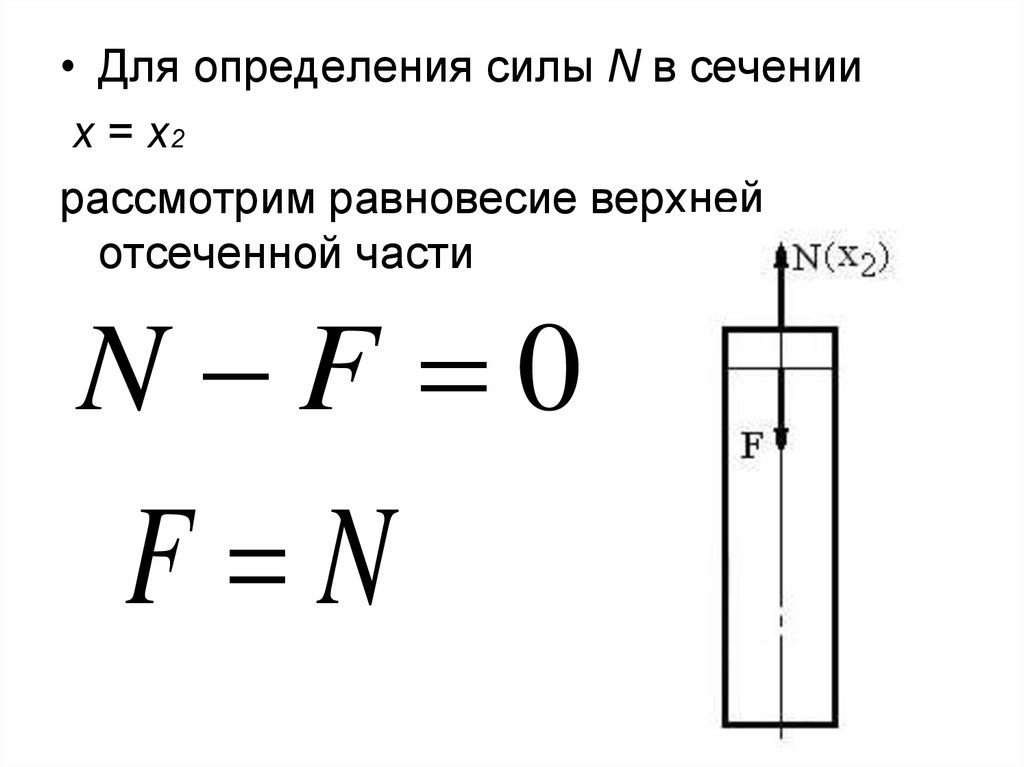
• Для определения силы N в сеченииx = х2
рассмотрим равновесие верхней
отсеченной части
N F 0
F N
9.
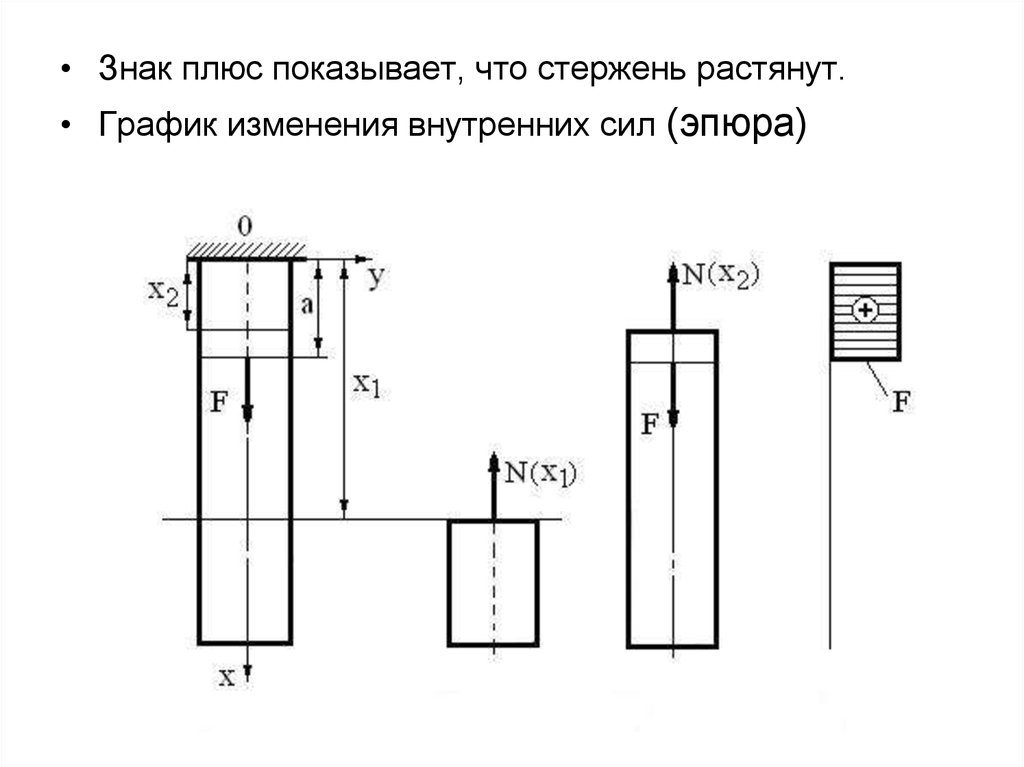
• Знак плюс показывает, что стержень растянут.• График изменения внутренних сил (эпюра)
10.
• Нормальное напряжение в поперечномсечении стержня при растяжении
равно поделенной на площадь сечения
продольной силе в этом сечении
N
A
11.
• Под действием осевых растягивающих силстержень постоянного сечения площадью
удлиняется на величину
• l 1, l 0 − длины стержня в деформированном и
недеформированном состоянии, ∆l −
абсолютное (полное) удлинение при
растяжении (в случае сжатия данная
величина называется абсолютным
(полным) укорочением)
l l1 l0
12.
• Наиболее удобной мерой деформацииявляется относительное удлинение
– удлинение, отнесенное к
первоначальной длине стержня
l l1 l0
l0
l0
13.
• Если первоначальная ширина стержняa0, то под действием сил F она
уменьшится на величину
а а1 а0
• Относительная поперечная
деформация будет определяться
выражением
а
п
а0
14.
• Отношение поперечной деформации кпродольной при растяжении (сжатии),
взятое по абсолютной величине,
называют коэффициентом Пуассона
п
15.
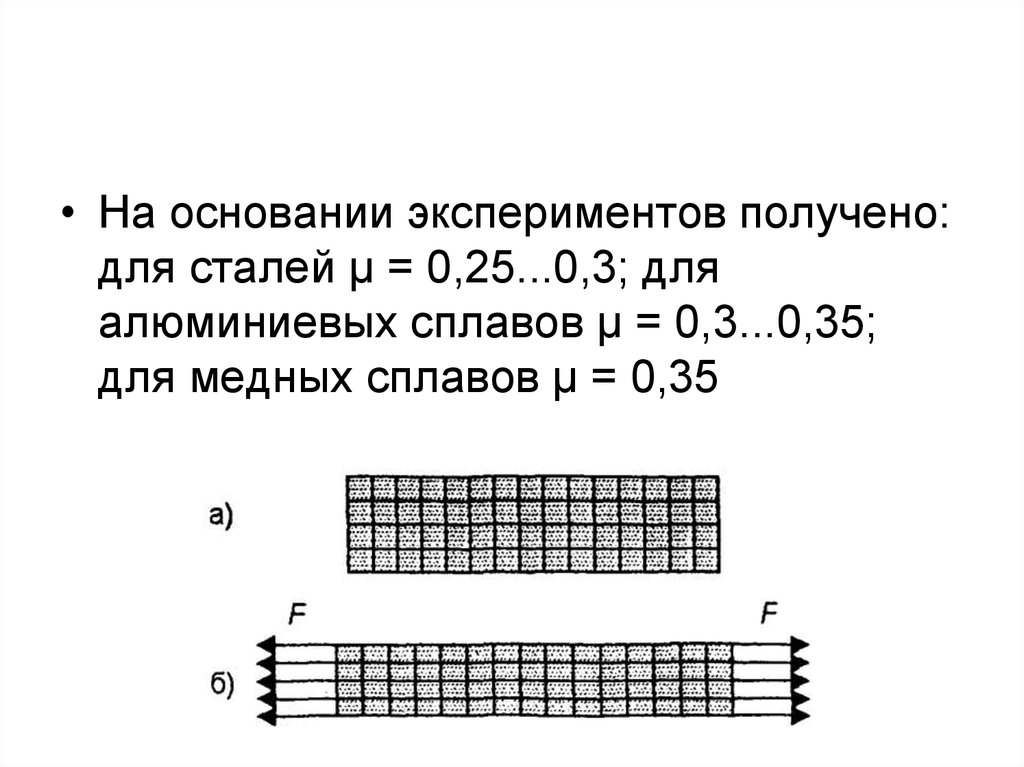
• На основании экспериментов получено:для сталей μ = 0,25...0,3; для
алюминиевых сплавов μ = 0,3...0,35;
для медных сплавов μ = 0,35
16.
• Между напряжениями и малымидеформациями существует линейная
зависимость, называемая законом
Гука. Для центрального растяжения
(сжатия) она имеет вид:
E
17.
• где E – коэффициент пропорциональности,именуемый модулем упругости (модулем
Юнга).
• По физическому смыслу модуль упругости –
напряжение, которое вызывает деформацию
ε = 1 (удлинение стержня, равное
первоначальной длине).
18.
• По данным экспериментов:• E = (2...2,2)∙105 МПа – для сталей;
E = 1,1∙105 МПа – для титановых
сплавов;
• E = 0,7∙105 МПа – для алюминиевых
сплавов.
19.
• закон Гука для растянутого (сжатого)стержня можно записать в виде
F l
l
F,
E A
20.
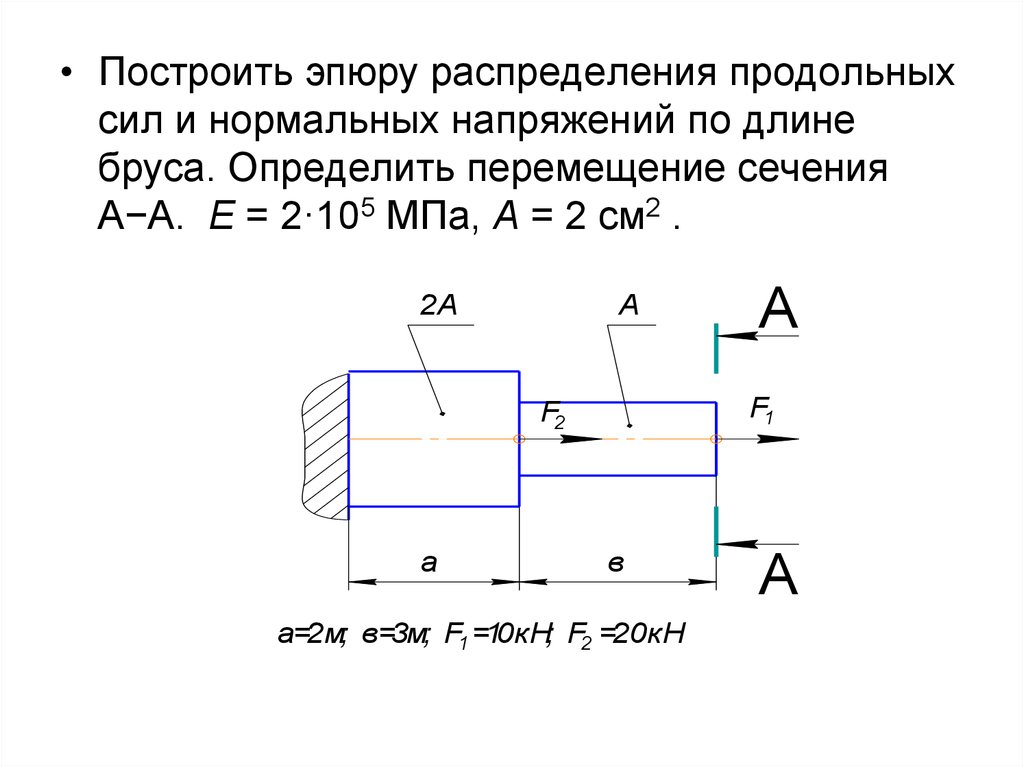
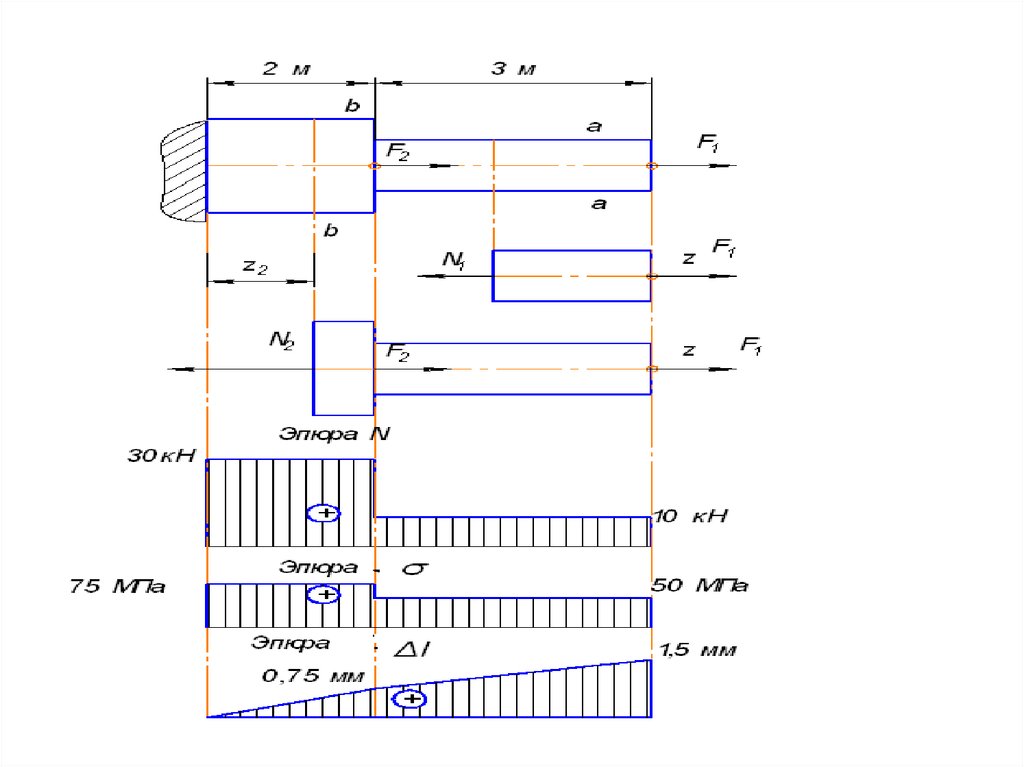
• Построить эпюру распределения продольныхсил и нормальных напряжений по длине
бруса. Определить перемещение сечения
А−А. Е = 2·105 МПа, А = 2 см2 .
2А
А
F1
F2
а
А
в
а=2м; в=3м; F1 =10кН; F2 =20кН
А
21.
22.
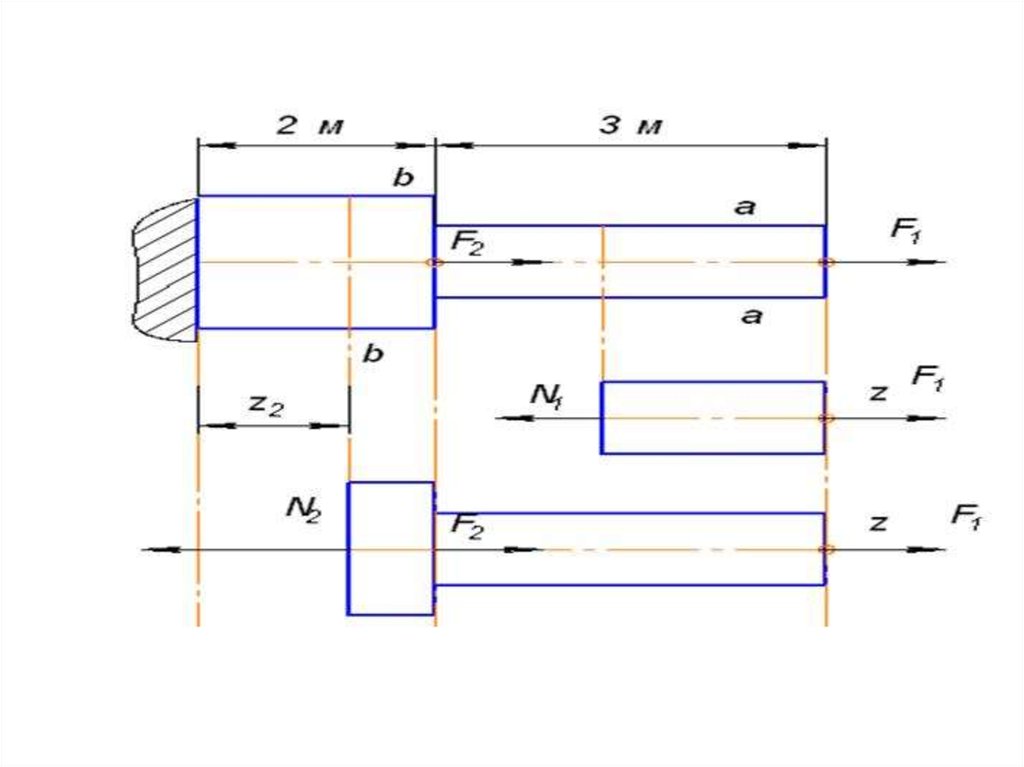
• Построим график (эпюру)показывающую как изменяется N по
длине бруса. В пределах одного участка
продольная сила не меняется, поэтому
эпюра N ограничена линией
параллельной оси.
• Эпюру нормальных напряжений
получим, разделив значения N на
соответствующие площади поперечных
сечений.
23.
N 1 10 10 3Н
σ
50
50МПа;
2
2
A1 2 10
мм
N 2 30 10
Н
75
75
МПа
;
2
2
A2
4 10
мм
3
24.
25.
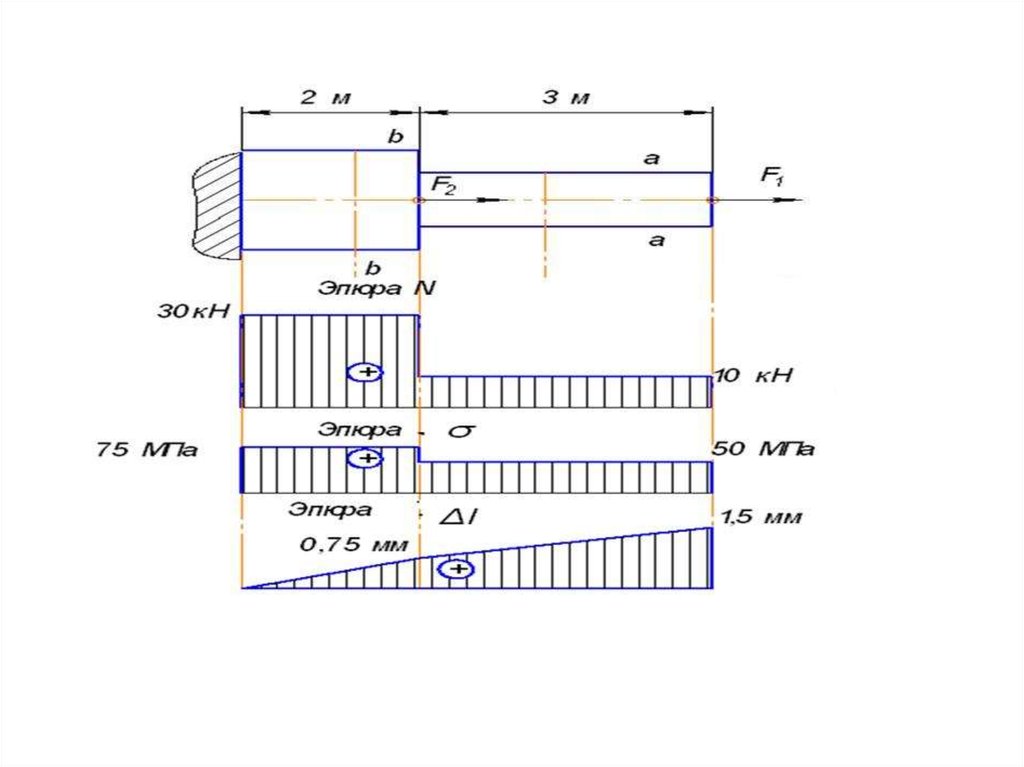
• Эпюрой перемещений называетсяграфик, показывающий закон
изменения величин перемещений
поперечных сечений бруса по его
длине.
• Эпюру перемещений строят, начиная с
защемленного конца.
• Перемещение произвольного сечения b
− b бруса на участке 2 равно удлинению
части бруса длиной z2.
• На конце второго участка z2 = 2 м.












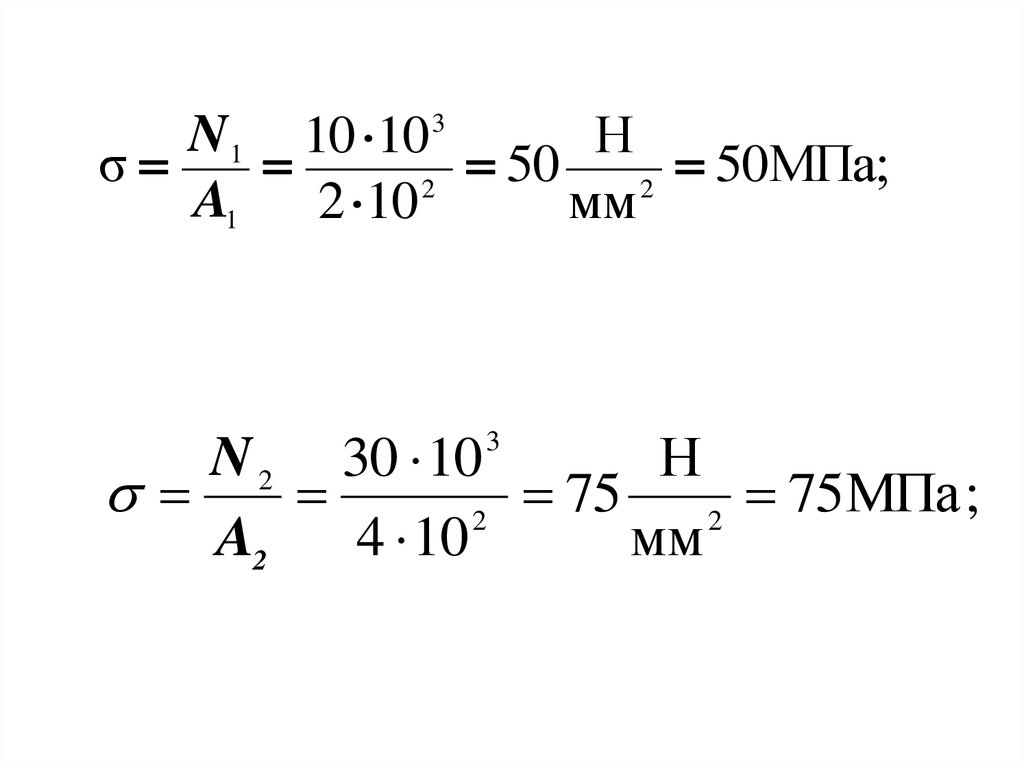

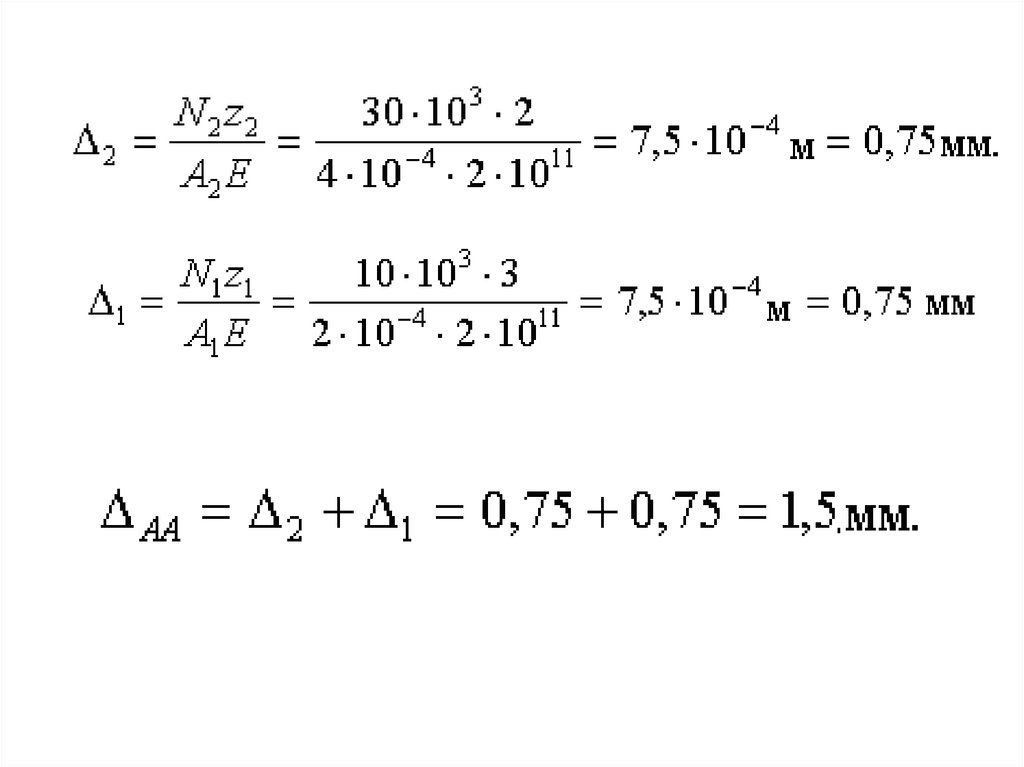
 physics
physics








