Обработка экспериментальных данных. Часть 1

1.

А.В.Богомолов
НИИЯФ МГУ

2. О чем этот доклад:

• Прежде всего, это помощь в анализе результатов,
полученных в процессе запуска аппаратов CanSat.
• Будут рассмотрены примеры типичных ошибок,
встречающихся на защитах проектных работ, особенно
при построении графиков .
• Поскольку все мы учимся проводить космические
эксперименты, я буду рассказывать не только о CanSat, но и
о работе с данными реальных экспериментов на спутниках.
• Если останется время, я расскажу о современных
математических методах анализа данных.

3. Я ориентируюсь на следующую аудиторию:

• Большинство слушателей изучали квадратные уравнения
и тригонометрию, но не изучали логарифмов, производных
и интегралов.
• Среди слушателей имеются те, кто серьёзно
занимается программированием, но большинство все-таки
предпочитает использовать для обработки данных
прикладные пакеты программ (например, MS Excel)
• Большинство
слушателей
знакомы
с
теорией
вероятностей в объёме решения соответствующих задач
ГИА и ОГЭ. Но очень немногие изучали математическую
статистику, про оценку точности измерений, дисперсию
и метод наименьших квадратов информации нет.
•Некоторая часть слушателей уже обрабатывала данные
своих предыдущих полётов. Но это не все слушатели.

4. Вопросы, которые должны быть заданы ещё ДО запуска:

• Какой объём данных Вы рассчитываете получить в
своём эксперименте?
• В каком виде эти данные попадут к вам для обработки?
• Какие результаты Вы ожидаете получить?
• Насколько эти результаты будут достоверны?
• Какова точность Ваших измерений?
• Как Вы планируете представить свои результаты в
наглядном виде? Какие графики планируете построить?

5. Ещё вопросы...

• Измеренные Вами температура и давление – внутри
«спутника» или снаружи? А сильно или нет они
отличаются?
• Во время эксперимента «спутник» нагреется?
• Если Вы повторите эксперимент ещё раз, результаты
будут сильно различаться?
• От метеорологичеких
зависит?
условий
Ваш
эксперимент
• А если бы «спутник» висел в одной и той же точке,
насколько велик был бы разброс в показаниях?
• Вы получите уникальные данные или всего лишь
повторите уже известные опыты?

6.

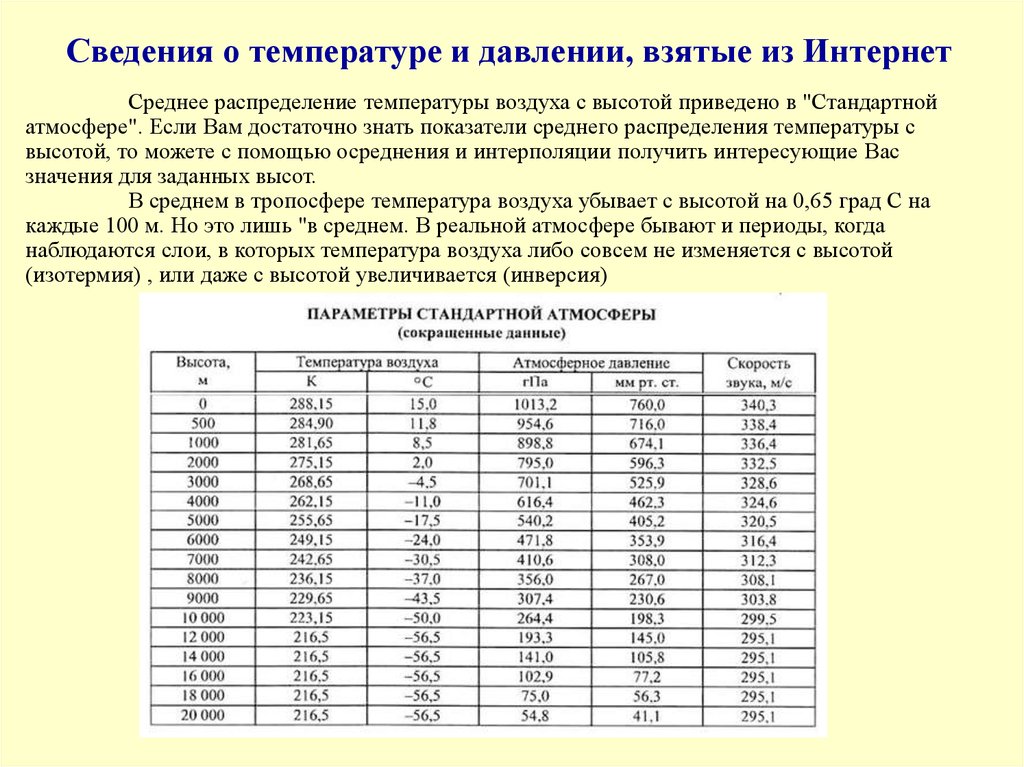
Сведения о температуре и давлении, взятые из Интернет
Среднее распределение температуры воздуха с высотой приведено в "Стандартной
атмосфере". Если Вам достаточно знать показатели среднего распределения температуры с
высотой, то можете с помощью осреднения и интерполяции получить интересующие Вас
значения для заданных высот.
В среднем в тропосфере температура воздуха убывает с высотой на 0,65 град С на
каждые 100 м. Но это лишь "в среднем. В реальной атмосфере бывают и периоды, когда
наблюдаются слои, в которых температура воздуха либо совсем не изменяется с высотой
(изотермия) , или даже с высотой увеличивается (инверсия)

7.

Что можно использовать для компьютерной обработки
данных? (красным цветом выделены основные средства, которые
используют команды проекта CanSat)
Табличные процессоры (Excel)
Математичесие пакеты (MathCad)
Программирование на алгоритмических языках (C, Delphi, Basic,
Fortran …)
Специализированные языки для работы с данными, например,
IDL (Interactive Data Language)
Библиотеки приложений, как правило, написанные на языках
программирования и включаемые в программы (GEANT и т.п.)
Статистические пакеты общего назначения (Statistica, SPSS,
StatGraphics)
Специализированные пакеты (под определенный круг задач,
например, анализ временных рядов (Эвриста) или нейронные сети

8.

Форматы файлов
Файлы, с которыми придется иметь дело, могут быть следующих
типов:
1. Текстовые файлы. Каждый байт – это код символа, который
воспроизводится на экране. Каждая цифра, составляющая число,
занимает 1 байт. То, что при этом отобразится на экране,
интерпретирует драйвер.
2. Бинарные файлы. Каждый байт – это числовое значение параметра
(или его части). На экране такой файл просматривать неудобно. При
проведении измерений в космических или ускорительных
экспериментах мы чаще всего имеем дело с бинарными файлами. Для
перевода его в более привычный текстовый формат программисты
пишут программы.
3. Файлы, в которых используется стандарт определенного пакета
программ. Как правило, такие файлы обрабатываются только этим
пакетом. Типичный пример – Microsoft Excel. В любом пакете имеется
возможность загрузить текстовый файл данных.

9.

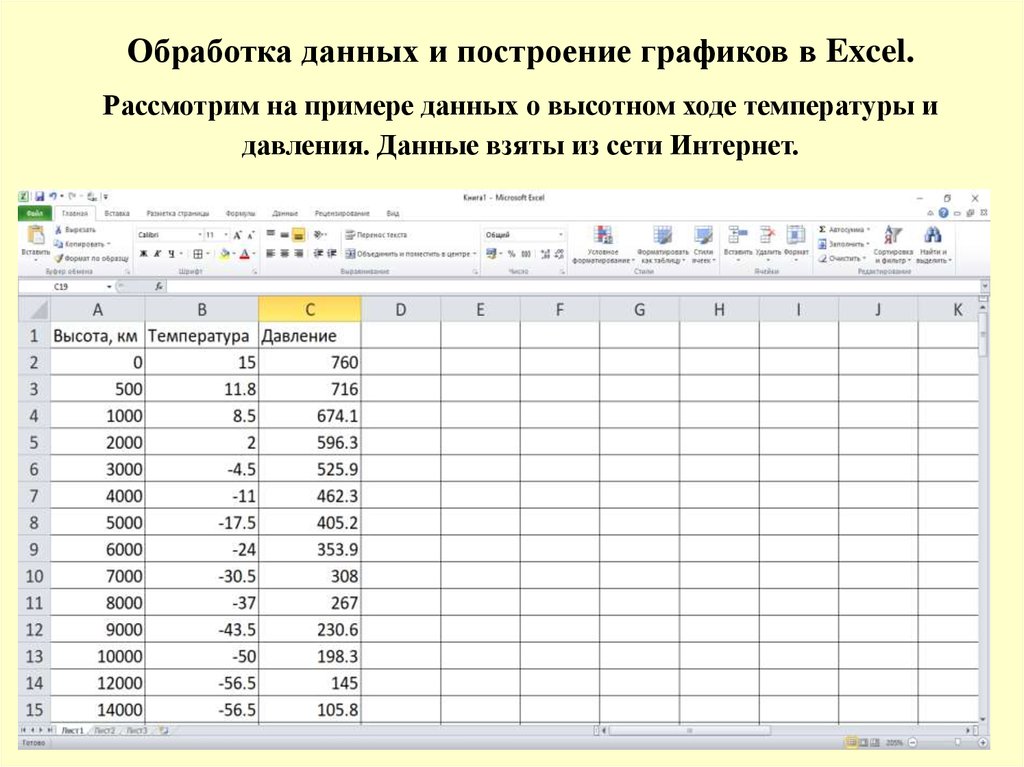
Обработка данных и построение графиков в Excel.
Рассмотрим на примере данных о высотном ходе температуры и
давления. Данные взяты из сети Интернет.
Скорее всего, в Excel данные нужно будет загрузить из
текстового файла (тип .txt).С данными, записанными в
бинарном формате, Excel не работает.

10.

Обработка данных и построение графиков в Excel.
Рассмотрим на примере данных о высотном ходе температуры и
давления. Данные взяты из сети Интернет.

11.

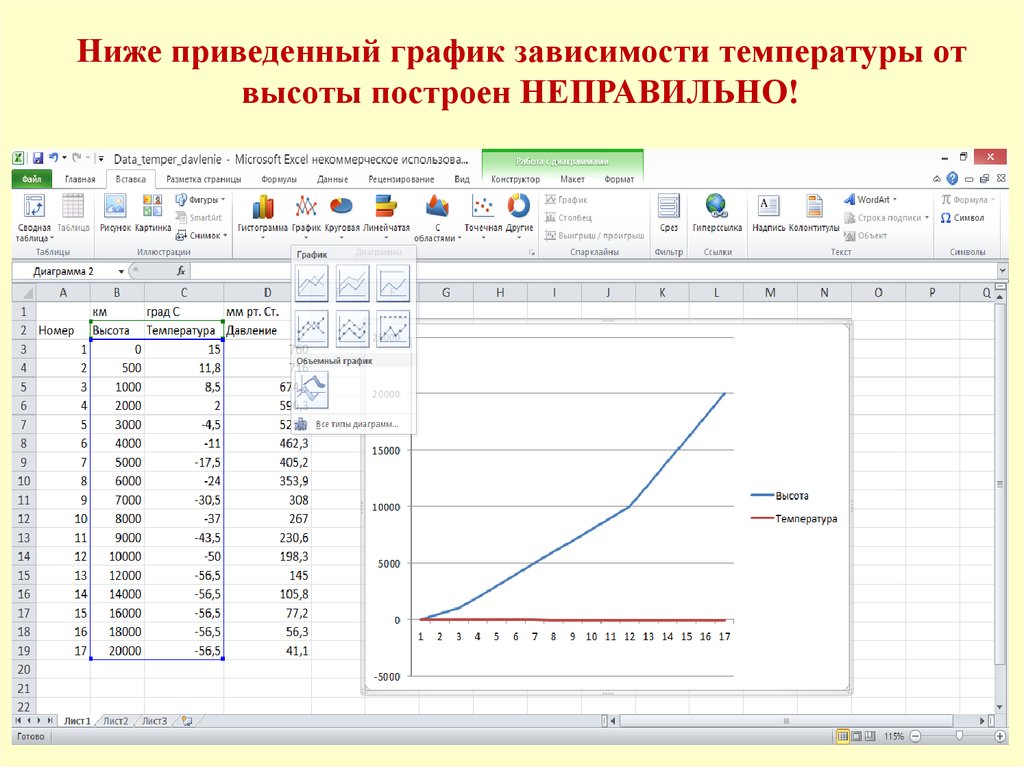
Ниже приведенный график зависимости температуры от
высоты построен НЕПРАВИЛЬНО!

12.

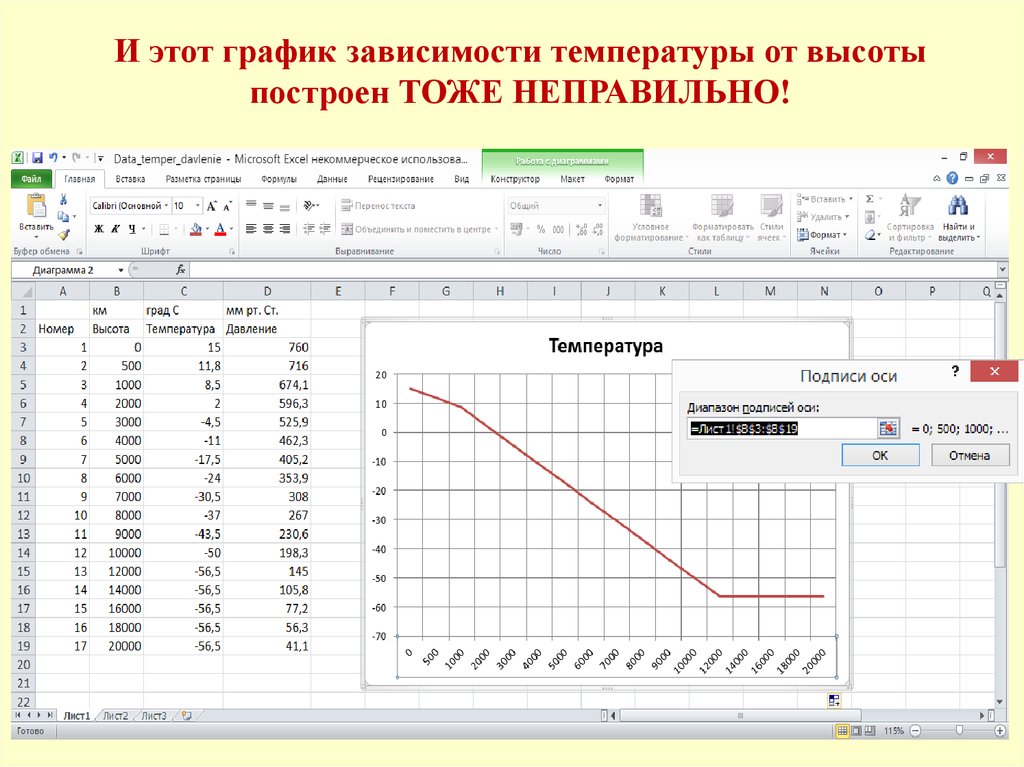
И этот график зависимости температуры от высоты
построен ТОЖЕ НЕПРАВИЛЬНО!

13.

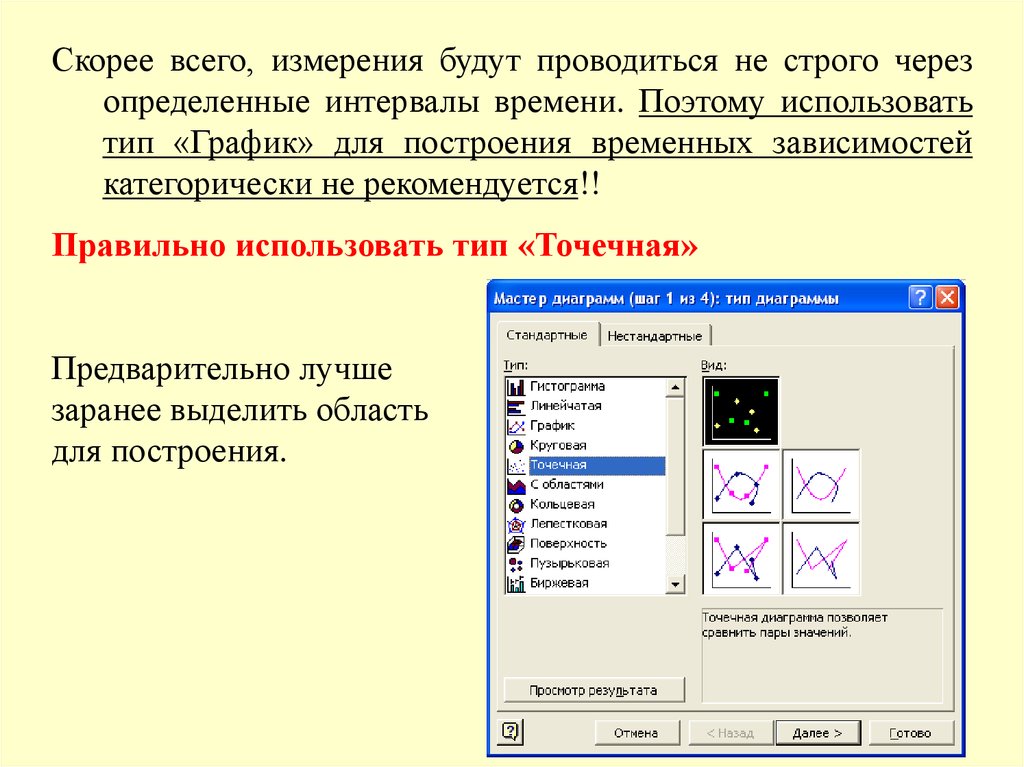
Скорее всего, измерения будут проводиться не строго через
определенные интервалы времени. Поэтому использовать
тип «График» для построения временных зависимостей
категорически не рекомендуется!!
Правильно использовать тип «Точечная»
Предварительно лучше
заранее выделить область
для построения.

14.

Графики выглядят примерно так (построены зависимость P и T от высоты):
Если потребуется изменить параметры оси
(например, минимальное и максимальное
значения диапазона) , кликните дважды в
подпись под осью.
Откроется контекстное меню.
Пункт «шкала» как раз даёт
возможность изменить диапазон.

15.

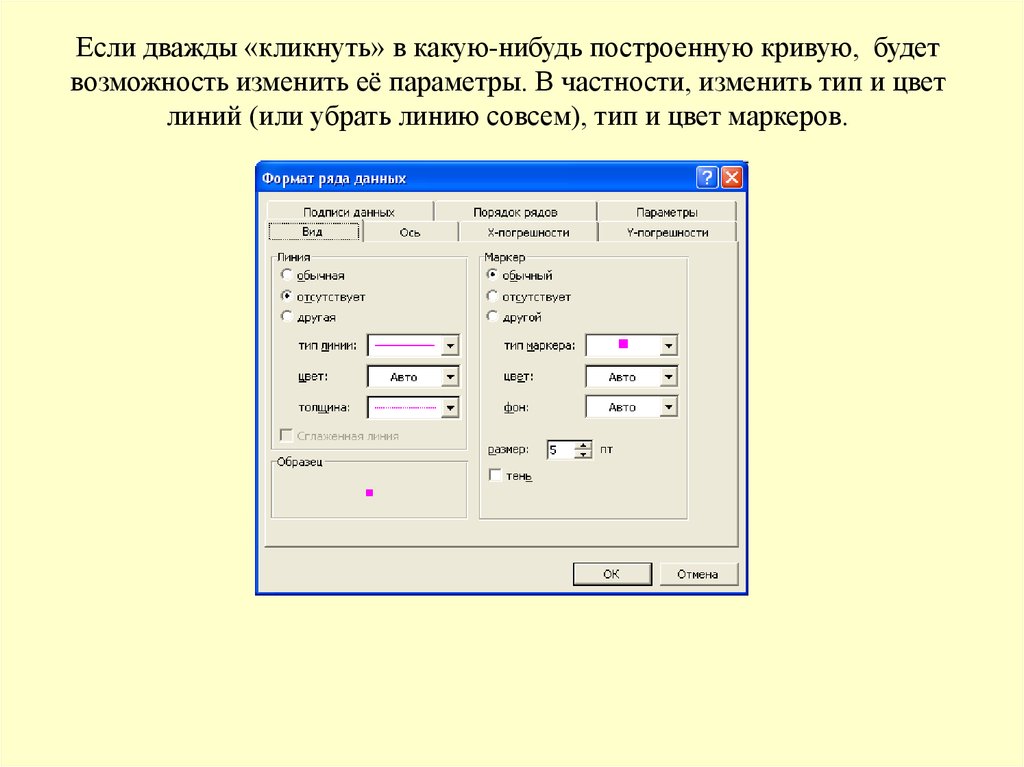
Если дважды «кликнуть» в какую-нибудь построенную кривую, будет
возможность изменить её параметры. В частности, изменить тип и цвет
линий (или убрать линию совсем), тип и цвет маркеров.

16. Значения, полученные в нескольких измерениях, могут различаться между собой по следующим причинам:

• Это проявление того явления, которое Вы изучаете.
• На показание приборов также может повлиять другое
явление, которое для вас будет считаться фоновым, его
надо будет исключать.
•Точность приборов не бесконечна. Например, цена деления
прибора может оказаться достаточно грубой.
•Наконец, множество мелких факторов, которые вы учесть
не можете, (а часто и не знаете их), обеспечивают
статистический разброс.

17.

Точность измерений и вычислений.
Любые измерения в естественных науках производятся с
некоторой точностью. Так, используя различные методы
измерений, расстояние 1км можно определить с точностью до
10м, до 1м, до 10см... В любом случае точность не будет
абсолютной. Представляя результат, принято указывать не
только саму величину, но и погрешность, с которой она
получена: S=1км 10м. или S=1000 10 м.
Кроме абсолютной погрешности, которую обычно
обозначают х, часто используется относительная погрешность
х= х/х. В приведенном выше примере относительная
погрешность равна 10м / 1000м = 0.01 = 1%. Отметим, что
относительная погрешности – безразмерная величина. Вместо
слова «погрешность» часто используется термин «ошибка».
Наличие «ошибок» не указывает на промахи экспериментатора, а
лишь свидетельствует о конечной точности эксперимента.

18.

Ошибки в случае сложных измерений.
Для доказательства удобно считать, что величина ошибки
х означает, что максимальное возможное значение измеряемой
величины будет равно х+ х, а минимальное возможное значение
равно х- х .
Погрешность суммы и разности.
Если есть две измеренные величины x х и y y , то
максимально возможное значение их суммы z=x+y равно
zmax=x+y+ х+ y, минимальное значение zmin= x+y- х- y .
Значит, погрешность величины суммы равна z= х+ y.
Поскольку для величины разности z=x-y максимальное
значение достигается в случае наибольшего уменьшаемого и
наименьшего вычитаемого, значит, как и для суммы,
zmax=x+y+ х+ y. Аналогично, zmin= x+y- х- y. Поэтому
погрешность разности равна сумме погрешностей:
z= х+ y.

19.

Ошибки в случае сложных измерений.
Погрешность произведения.
Для рассмотрения погрешности произведения z=xy
заметим, что максимальное значение произведения (если
сомножители неотрицательны) равно zmax=(x+ х)(y+ y).
Каждый из сомножителей в скобках представим в виде
xmax=x+ х=x(1+ x/x)=x(1+ x)
ymax=y+ y=y(1+ y/y)=y(1+ y)
Тогда, раскрывая скобки, получим:
zmax=xy(1+ x) (1+ y)=xy(1+ x+ x+ x y) xy(1+ x+ y)
(Мы воспользовались тем, что в случае малых
относительных ошибок их произведение x y значительно
меньше каждой из них). Сравнивая записи для xmax и zmax ,
приходим к выводу, что в случае произведения относительные
погрешности складываются. z= x+ y. Аналогично можно
доказать справедливость этой же формулы и для частного
z=x/y.

20.

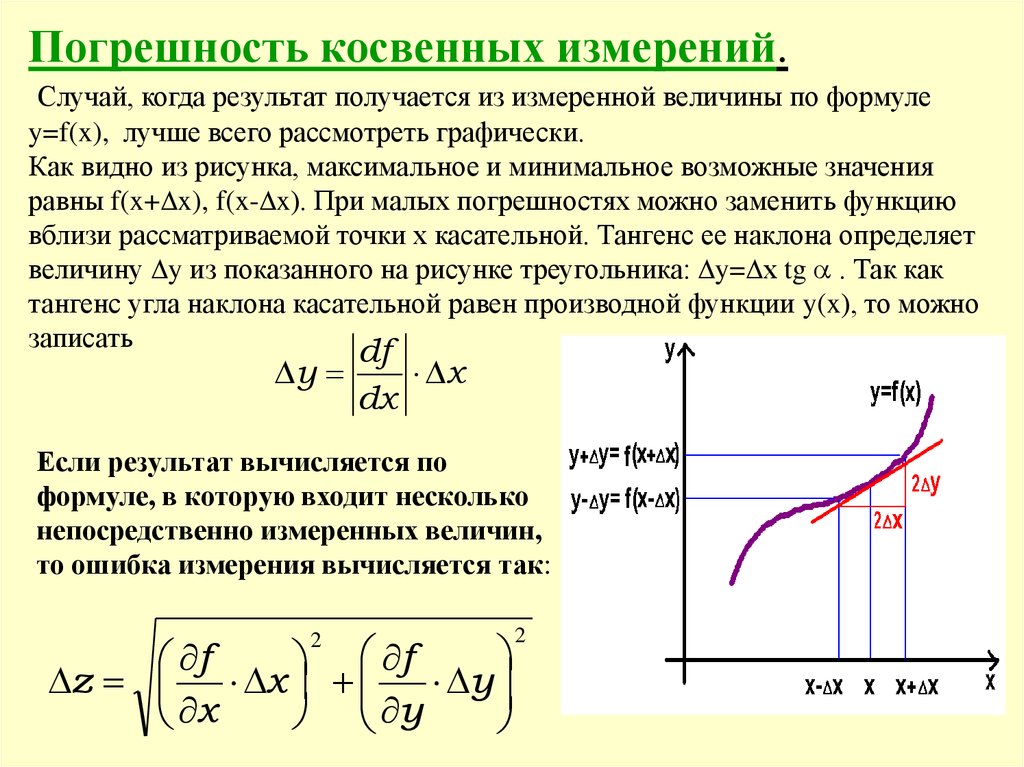
Погрешность косвенных измерений.
Случай, когда результат получается из измеренной величины по формуле
y=f(x), лучше всего рассмотреть графически.
Как видно из рисунка, максимальное и минимальное возможные значения
равны f(x+ x), f(x- x). При малых погрешностях можно заменить функцию
вблизи рассматриваемой точки х касательной. Тангенс ее наклона определяет
величину y из показанного на рисунке треугольника: y= х tg . Так как
тангенс угла наклона касательной равен производной функции y(x), то можно
записать
df
y
x
dx
Если результат вычисляется по
формуле, в которую входит несколько
непосредственно измеренных величин,
то ошибка измерения вычисляется так:
f
f
z
x
y
x
y
2
2

21.

Случайные и систематические ошибки.
Ошибка измерения отдельного параметра, как правило,
состоит из двух частей:
1)Точность измерительных приборов, например, ограничения
цены деления, точность метода и т. п. называется
систематической ошибкой эксперимента.
2)На результат эксперимента влияет большое количество
мелких факторов, которые мы не учитываем хотя бы потому, что
не измеряем их непосредственно, а часто и не знаем о них. Тем
не менее, в совокупности эти факторы приводят к разбросу
измеряемых значений относительно средних показателей, и этот
разброс часто превышает точность приборов. Такую случайную
ошибку оценивают после проведения нескольких одинаковых
измерений.

22.

Как оценить разброс значений.
Среднее арифметическое значение:
x
X x
i
n
Для оценки разброса значений пользуются стандартным
отклонением:
1 n
2
(
x
x
)
i
n 1 i 1
Смысл: примерно 2/3 всех измеренных значений отличаются от
среднего не более, чем на Х .
При проведении n измерений точность результата улучшается в
число раз, равное квадратному корню из числа измерений.
Стандартная ошибка среднего значения равна
x
x
n

23.

Пункты «X-погрешности» и «Y-погрешности» позволяют нанести на
графике ошибки измерений. Для этого нужно предварительно создать
отдельный столбец с величинами ошибок.
Для примера построим зависимость температуры от высоты. В
качестве ошибок создадим столбец D, значения которого вычислим как
стандартное отклонение по трем соседним значениям. Стандартное
отклонение в Excel можно найти с помощью функции СТАНДОТКЛОН.

24.

Аппроксимация методом наименьших
квадратов.
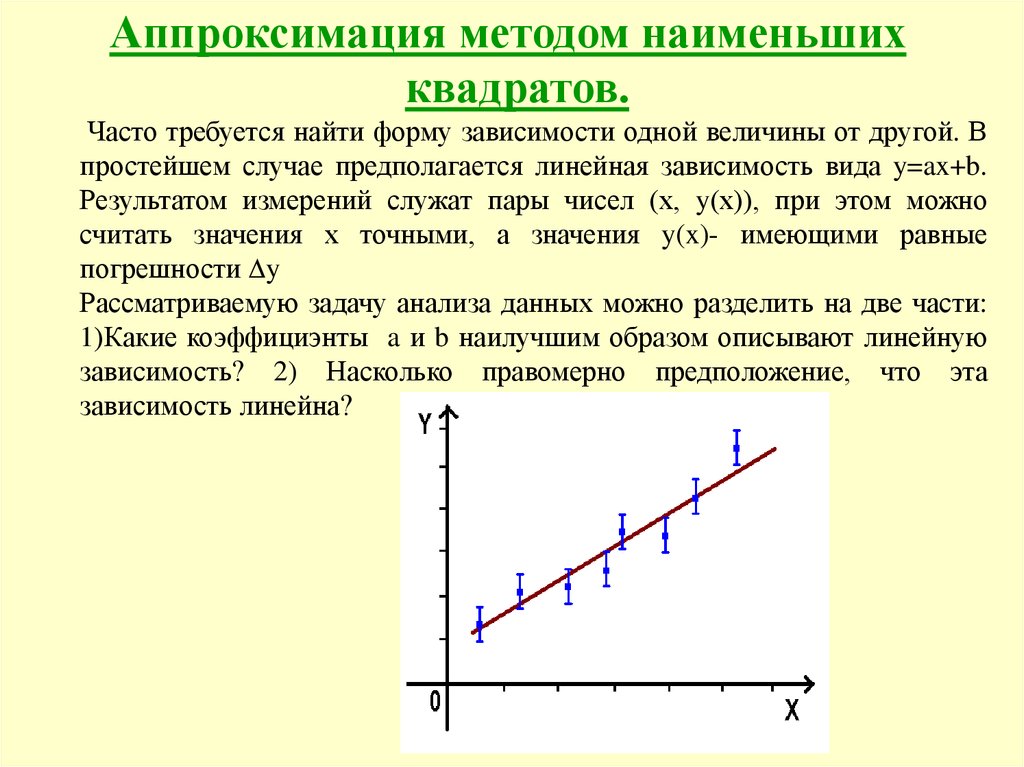
Часто требуется найти форму зависимости одной величины от другой. В
простейшем случае предполагается линейная зависимость вида y=ax+b.
Результатом измерений служат пары чисел (х, y(х)), при этом можно
считать значения х точными, а значения y(x)- имеющими равные
погрешности y
Рассматриваемую задачу анализа данных можно разделить на две части:
1)Какие коэффициэнты a и b наилучшим образом описывают линейную
зависимость? 2) Насколько правомерно предположение, что эта
зависимость линейна?

25.

Аппроксимация методом наименьших
квадратов.
Коэффициенты a и b выбираются такими, чтобы
вероятность получить измеренные значения при данных
коэффициентах была максимальна.
Максимальная вероятность достигается в том случае,
когда сумма квадратов отклонений измеренных значений от
вычисленных по предполагаемой формуле минимальна.

26.

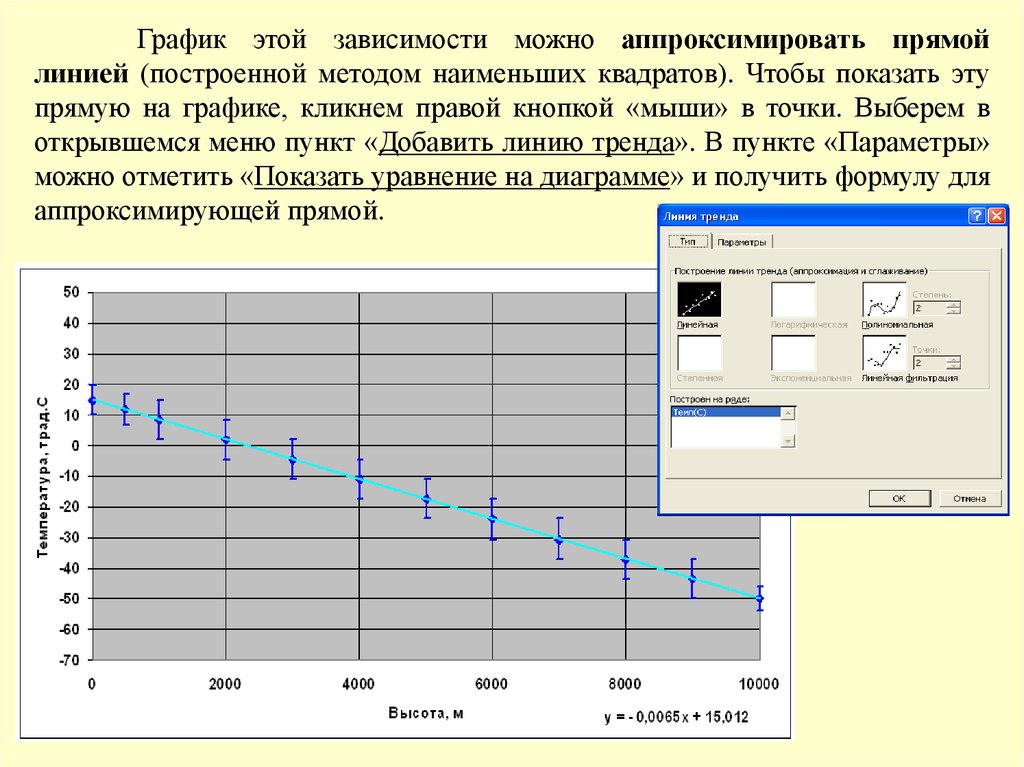
График этой зависимости можно аппроксимировать прямой
линией (построенной методом наименьших квадратов). Чтобы показать эту
прямую на графике, кликнем правой кнопкой «мыши» в точки. Выберем в
открывшемся меню пункт «Добавить линию тренда». В пункте «Параметры»
можно отметить «Показать уравнение на диаграмме» и получить формулу для
аппроксимирующей прямой.

27.

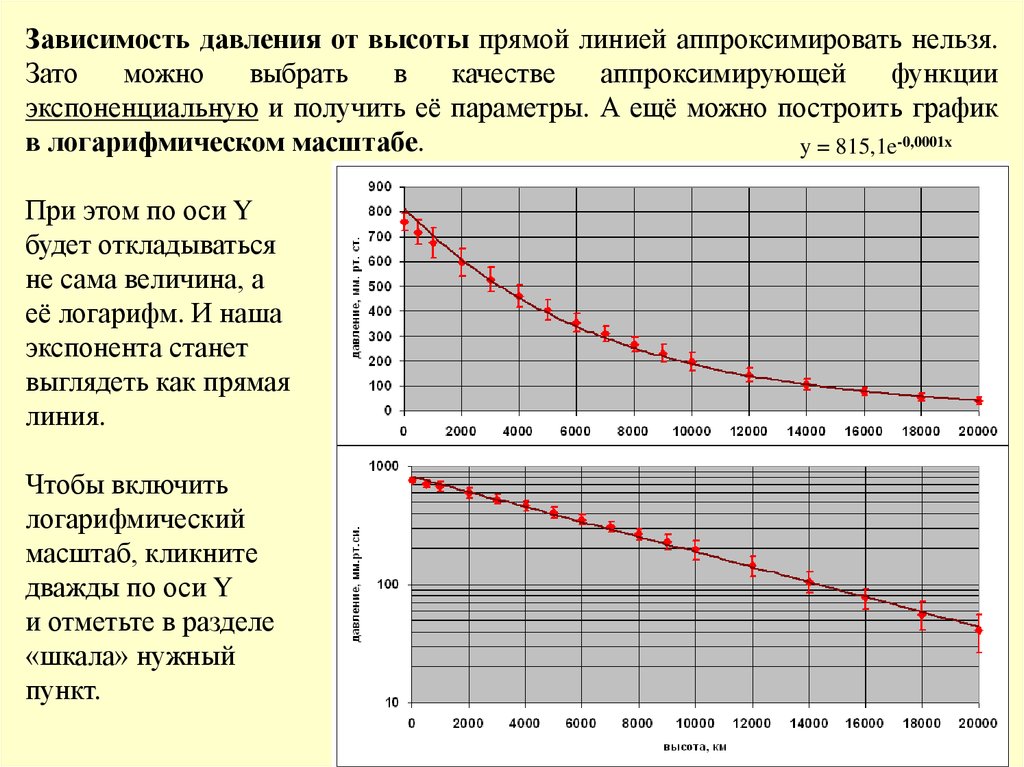
Зависимость давления от высоты прямой линией аппроксимировать нельзя.
Зато
можно
выбрать
в
качестве
аппроксимирующей
функции
экспоненциальную и получить её параметры. А ещё можно построить график
в логарифмическом масштабе.
y = 815,1e-0,0001x
При этом по оси Y
будет откладываться
не сама величина, а
её логарифм. И наша
экспонента станет
выглядеть как прямая
линия.
Чтобы включить
логарифмический
масштаб, кликните
дважды по оси Y
и отметьте в разделе
«шкала» нужный
пункт.

28.

Как, скорее всего, будут выглядеть данные космического
эксперимента для компьютерной обработки?
1. Данные будут записаны в один или несколько файлов. Структура
всех файлов (если их несколько) будет однотипная. Как правило, в
каждой строке файла буду содержаться результаты измерения
нескольких параметров в определенный момент времени. (в
эксперименте CanSat файл, скорее всего, будет один).
2. Этот момент времени (если он важен для обработки) также будет
записан в файл по некоторому стандарту. Для космических и
геофизических экспериментов используется мировое время (UT), а
также местное (локальное) время. Чтобы обеспечить непрерывность
временного ряда, часто время переводят в количество секунд (минут,
часов) от определенного момента (например, число дней с 1 января
2001 г.) (А какое время будет записано у вас?)
3. Каждый столбец отводится под значение определенного параметра
(число событий, поток, скорость, энергия и т.п. ).
4. Строки еще называют наблюдениями, кадрами или записями.
Столбцы называют полями, переменными.

29.

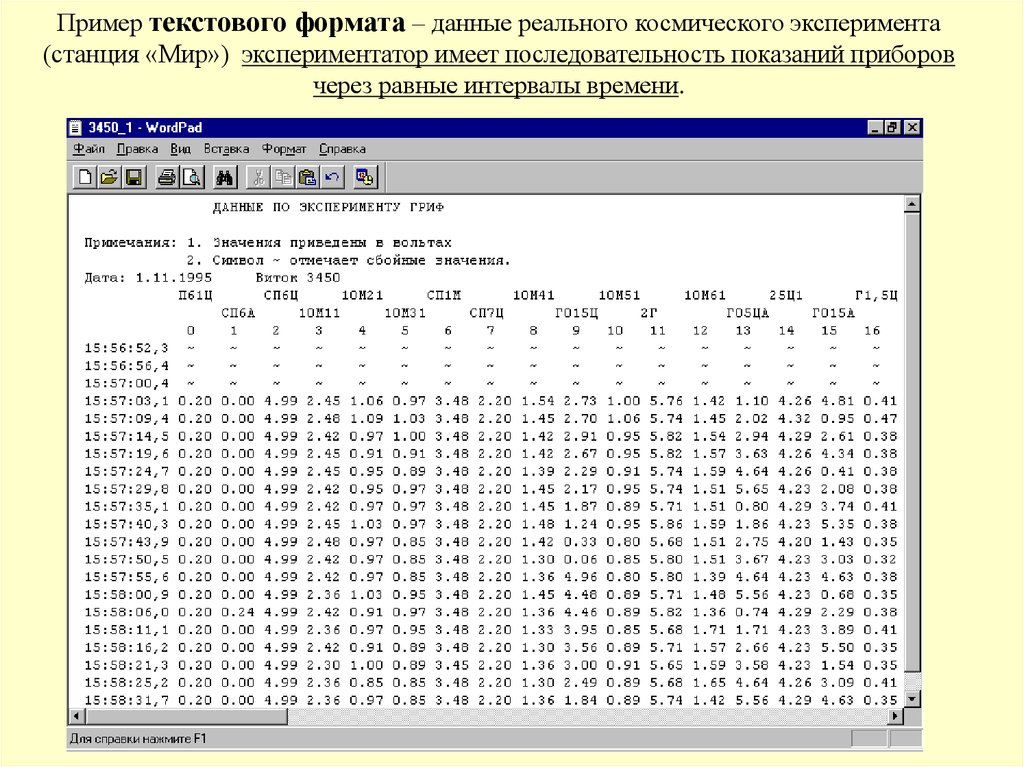
Пример текстового формата – данные реального космического эксперимента
(станция «Мир») экспериментатор имеет последовательность показаний приборов
через равные интервалы времени.

30. Как выглядят массивы данных, переданные с использованием бортового процессора?

01000
01010
01020
01030
01040
01050
01070
01080
01090
010A0
010B0
010C0
010D0
010E0
010F0
01100
01110
01120
01130
01140
01150
7C
5A
D1
36
81
46
76
A0
27
25
70
04
19
20
03
21
FE
01
42
28
98
6E
50
07
8C
CB
00
06
24
E0
70
03
1F
20
02
14
A0
59
A7
06
1D
02
A1
01
84
F6
58
1E
E9
28
11
04
1F
80
05
21
A0
01
21
C5
DD
11
58
2C
70
1E
66
09
8C
0F
70
01
25
F0
02
1E
80
00
45
70
43
0D
50
01
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
03
27
78
27
D4
F9
08
7C
5A
00
02
22
B0
02
1E
A0
28
74
78
01
09
6F
E0
02
34
07
88
00
6E
50
02
20
90
03
1C
50
3B
3B
BB
00
A1
06
40
11
B4
69
5B
7F
1F
A1
01
2E
A0
03
25
50
08
28
91
DA
16
C8
AA
5E
50
01
70
1E
61
82
2C
25
00
06
22
80
04
19
70
01
08
7C
3D
0E
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
FE
01
83
27
2E
F4
2E
03
B0
07
22
A0
02
16
60
7C
5A
DF
70
61
B3
59
C7
07
EF
02
2E
82
25
05
20
E0
04
1B
90
03
6E
50
06
79
AC
00
20
87
DE
51
B6
18
43
41
2C
C0
04
1D
90
00
1E
A1
01
DB
24
7C
15
70
51
13
50
01
70
5D
DE
C0
02
22
C0
05
1A
F0
2C
70
1B
59
08
75
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
¦
28
44
A5
01
57
27
60
FE
07
26
D0
04
1B
50
04
03
28
10
38
59
78
0D
D7
00
C4
07
FE
28
C1
28
30
06
1B
80
03
1B
DD
0D
02
23
06
70
D1
41
21
1D
BF
91
EA
6B
80
02
21
C0
06
1D
60
41
D1
73
BE
32
59
01
09
8F
4F
10
50
FB
70
04
1A
A0
02
18
C0
04
5E
50
01
70
18
53
Скорее всего, именно в таком, БИНАРНОМ виде информацию со своих
«спутников» получите и Вы.

31. Проверка качества информации

В серьезных космических экспериментах приходится иметь дело со сбоями при
записи и передаче данных. А у вас подобная проблема может возникнуть?
Проверка качества информации
Сбои при передаче
информации
Уточнение режима
работы прибора
Проверка контрольных сумм позволяет
выявить информацию, которая может
оказаться сбойной. В кадре ставится признак
сбоя. Эти кадры при обработке скорее всего
придется исключать.
Если часть параметров имеют нулевые
значения или не изменяются, то
возможно, что-то в приборе вышло из
строя и следует отключить эту часть
прибора по команде с Земли.
Сбои
датчика
времени
(в
кадре
неправильное время) в редких случаях, когда
все кадры идут подряд через равные
промежутки, можно учесть с помощью
интерполяции данных о соседних кадров.
Если какие-либо параметры показывают
практически нулевой уровень или
зашкаливают, имеет смысл изменить
усиление, время набора событий или
предварительный пересчет по команде с
Земли.
Сбои, не отслеженные контрольными
суммами, выглядят как нелогичные значения
(как правило, единичные). Могут быть
исключены автоматически по характерным
признакам (например, очень резкое отличие
от соседних значений, сравнение с другими
параметрами и т.п.)
Если в Вашем приборе имеется бортовой
процессор
и
несколько
типов
информации, возможно, Вы захотите
перераспределить квоты, чтобы с прибора
поступало больше массивов, которые с
научной точки зрения Вам ценнее.

32.

Некоторые функции исследователя
(первичный анализ):
Непосредственное (прямое) экспериментальное измерение
физической величины прибором. Ошибки измерения вызваны
точностью приборов и, возможно, опытом экспериментатора.
Получение значения физической величины путем измерения других
величин с расчетом по формулам. Случай похож на предыдущий..
Измерение параметров процессов, носящих статистический характер.
Ошибки измерения, в основном, статистические. Набор статистики
приводит к большим массивам (тысячи значений). Точность прямого
измерения – стандартное отклонение:
(x x)
i
i
N 1
2
x1 x2 ... xn
x
n

33.

Некоторые функции исследователя
(анализ данных):
Проверка того, нет ли между факторами связи. Анализ возможных
причин этой связи.
Получение формул, описывающих связь между параметрами.
Аппроксимация в область, где измерения не проводились.
Классификация объектов (событий). Поиск объектов с близкими
характеристиками.
Поиск закономерностей в измеряемых параметрах и выявление
«скрытых» факторов. Иными словами – поиск причин явлений по их
проявлениям. Пример задачи – по потокам различных видов
излучения на орбите Земли определить параметры области ускорения
частиц в источнике излучения (солнечные вспышки и т.п.).
Поиск периодических процессов. Определение времен запаздывания.
Прогнозирование.

34.

Корреляционный анализ
Коэффициент линейной корреляции Пирсона определяет силу
связи между двумя параметрами. Он вычисляется по формуле:
R
(x y ) N x y
i
i
i
N Sx S y
Если рост первого параметра происходит одновременно с ростом
второго, то коэффициент корреляции близок к 1.
Если рост 1-го параметра происходит одновременно с убыванием 2го параметра, то коэффициент корреляции близок к –1.
Если параметры независимы, то коэффициент корреляции близок к
0.

35.

Матрица корреляций для оценки связи параметров солнечной активности и
околоземного пространства (обработка проводилась в SPSS):
Correlations
LP_10
LP_100
LE50_175
L_FL
L_SXR
L_V
L_MC
L_EC
Pears on Correlation
Sig. (2-tailed)
N
Pears on Correlation
Sig. (2-tailed)
N
Pears on Correlation
Sig. (2-tailed)
N
Pears on Correlation
Sig. (2-tailed)
N
Pears on Correlation
Sig. (2-tailed)
N
Pears on Correlation
Sig. (2-tailed)
N
Pears on Correlation
Sig. (2-tailed)
N
Pears on Correlation
Sig. (2-tailed)
N
LP_10
LP_100
LE50_175
1,000
,797**
,750**
,
,000
,000
34
25
32
,797**
1,000
,642**
,000
,
,001
25
25
24
,750**
,642**
1,000
,000
,001
,
32
24
50
,831**
,631
,502*
,000
,050
,024
13
10
20
,451**
,518**
,325*
,009
,009
,022
33
24
49
,649**
,222
,497**
,000
,334
,001
29
21
45
,710**
,572*
,385*
,000
,026
,023
22
15
35
,769**
,599*
,453**
,000
,018
,006
22
15
35
**. Correlation is s ignificant at the 0.01 level (2-tailed).
*. Correlation is s ignificant at the 0.05 level (2-tailed).
L_FL
,831**
,000
13
,631
,050
10
,502*
,024
20
1,000
,
32
,608**
,000
31
,608**
,000
32
,532**
,006
25
,600**
,002
25
L_SXR
,451**
,009
33
,518**
,009
24
,325*
,022
49
,608**
,000
31
1,000
,
92
,464**
,000
71
,458**
,000
56
,419**
,001
56
L_V
,649**
,000
29
,222
,334
21
,497**
,001
45
,608**
,000
32
,464**
,000
71
1,000
,
72
,626**
,000
56
,826**
,000
56
L_MC
,710**
,000
22
,572*
,026
15
,385*
,023
35
,532**
,006
25
,458**
,000
56
,626**
,000
56
1,000
,
57
,872**
,000
57
L_EC
,769**
,000
22
,599*
,018
15
,453**
,006
35
,600**
,002
25
,419**
,001
56
,826**
,000
56
,872**
,000
57
1,000
,
57

36.

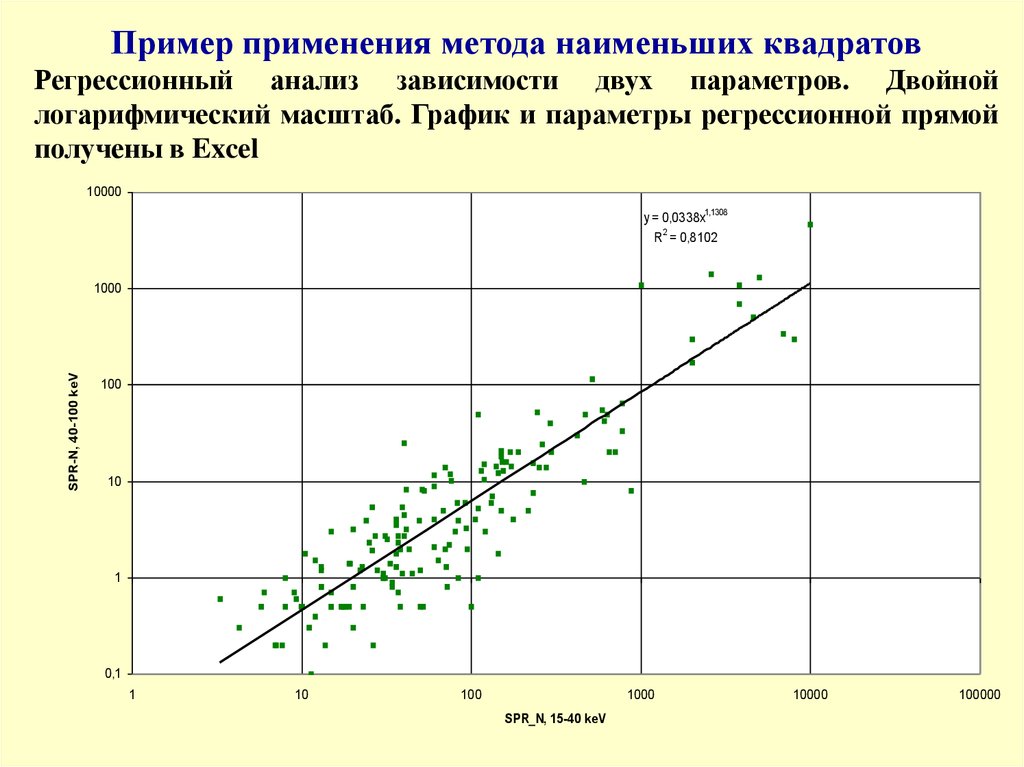
Пример применения метода наименьших квадратов
Регрессионный анализ зависимости двух параметров. Двойной
логарифмический масштаб. График и параметры регрессионной прямой
получены в Excel
10000
y = 0,0338x1,1308
R2 = 0,8102
SPR-N, 40-100 keV
1000
100
10
1
0,1
1
10
100
1000
SPR_N, 15-40 keV
10000
100000

37.

Факторный анализ
Факторный анализ – это совокупность методов выделения скрытых
закономерностей по измеренным параметрам. Предполагается, что
измеренные параметры являются вторичными проявлениями
нескольких «скрытых» факторов. Например, потоки излучения
различных типов и энергий могут определяться параметрами области
рождения этих частиц (температура, плотность, концентрация
определенных элементов и т.п.). Задача факторного анализа –
выявление скрытых факторов и их интерпретация.

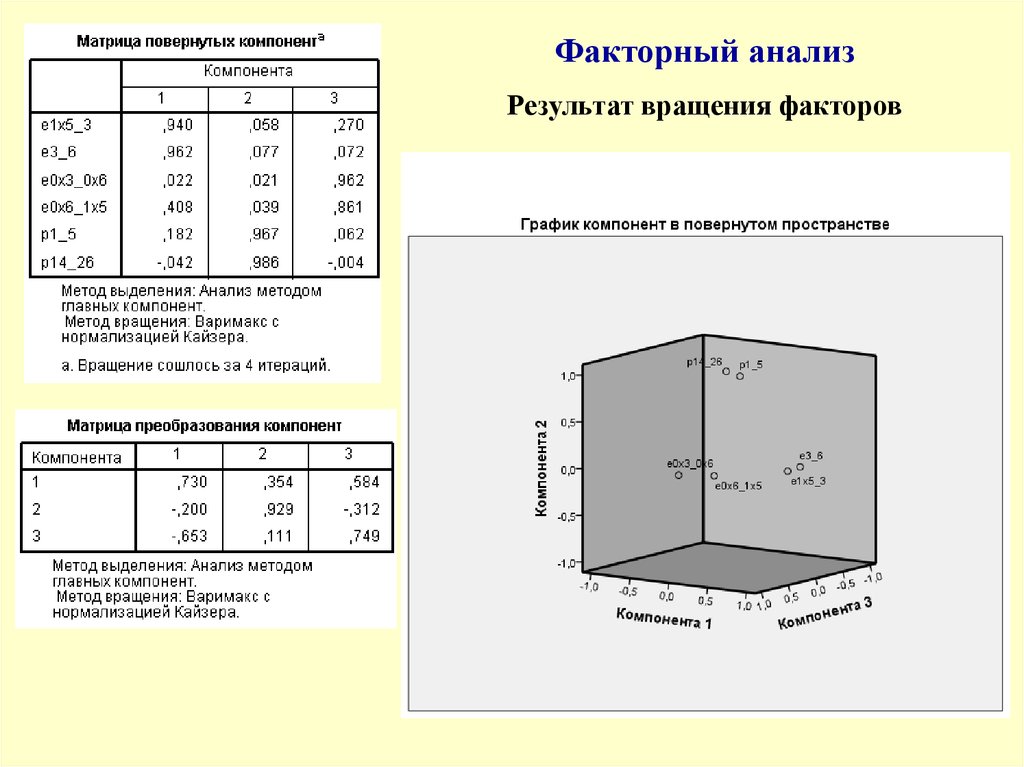
38.

Факторный анализ
Результат вращения факторов

39.

Кластерный анализ
Пример – классификация солнечных вспышек. Параметры –
длительность, время нарастания и спада, поток в мягком
рентгеновском излучении, жесткость спектра, положение области.
Задача – определить группы вспышек с близкими характеристиками.

40.

Евклидово расстояние
В качестве меры близости объектов кластеризации чаще всего
используют Евклидово расстояние. Оно вычисляется по формуле:
Чтобы все параметры входили в формулу для расстояния с равным
весом, их нормируют: из каждого значения вычитают среднее значение
параметра, и эту разность делят на стандартное отклонение.
Для определения расстояние между группами из нескольких объектов
можно использовать :
Среднее арифметическое всех расстояний между объектами
разных групп,
Минимальное расстояние между объектами разных групп,
Максимальное расстояние между объектами разных групп.

41.

Иерархический метод кластеризации:
1.
Вычисляем расстояния между всеми N объектами. Находим
минимальное расстояние. Эти два объекта объединяем в одну
группу.
2.
Вычисляем средние характеристики этой группы. Включаем эту
группу как новый единый объект. Имеем N-1 объект.
3.
Ищем минимальное расстояние в новом списке из объектов.
Объединяем и эти объекты. Получаем N-2 объекта.
4.
И так до тех пор, пока не будут объединены все объекты.
5.
Закономерности ищем, анализируя моменты, на которых
расстояния начинают резко увеличиваться, а также изучая то,
какие объекты оказались близки, и почему.

42.

43.

Метод К-средних:
1.
Должно быть заранее задано число кластеров (обозначим К).
2.
Компьютер выбирает в качестве центров кластеризации первые К
наблюдений.
3.
Просматривая каждое следующее наблюдение, компьютер решает,
не заменить ли один из имеющихся центров на это наблюдение.
Для этого он вычисляет матрицу расстояний между К+1
объектами - этим наблюдением и всеми центрами. В результате
остаются К максимально удаленных друг от друга наблюдений.
4.
И так до тех пор, пока не будет просмотрены все объекты.
5.
Затем компьютер просматривает выборку еще раз и приписывает
каждый объект к тому центру, до которого от него ближе
расстояние.
6.
Разбив объекты на группы, компьютер вычисляет средние
характеристики этих групп (т.е. координаты центров) и еще раз
просматривает данные – может быть, какой-то объект надо будет
отнести к другому кластеру, и т.д.

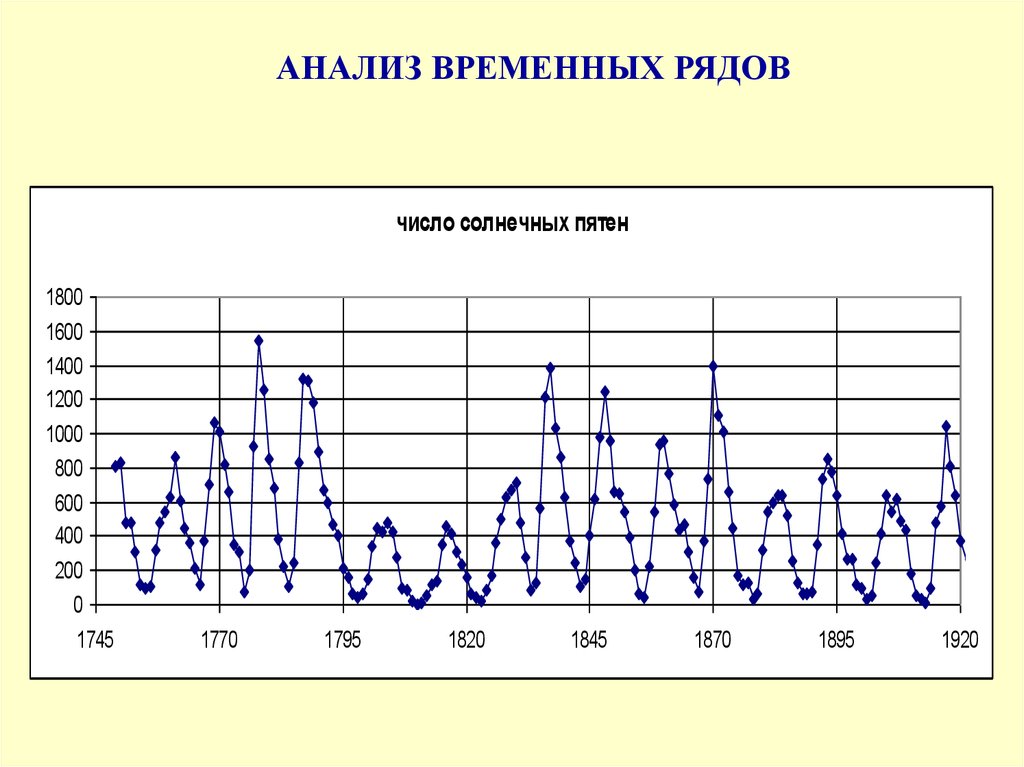
44.

АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
число солнечных пятен
1800
1600
1400
1200
1000
800
600
400
200
0
1745
1770
1795
1820
1845
1870
1895
1920

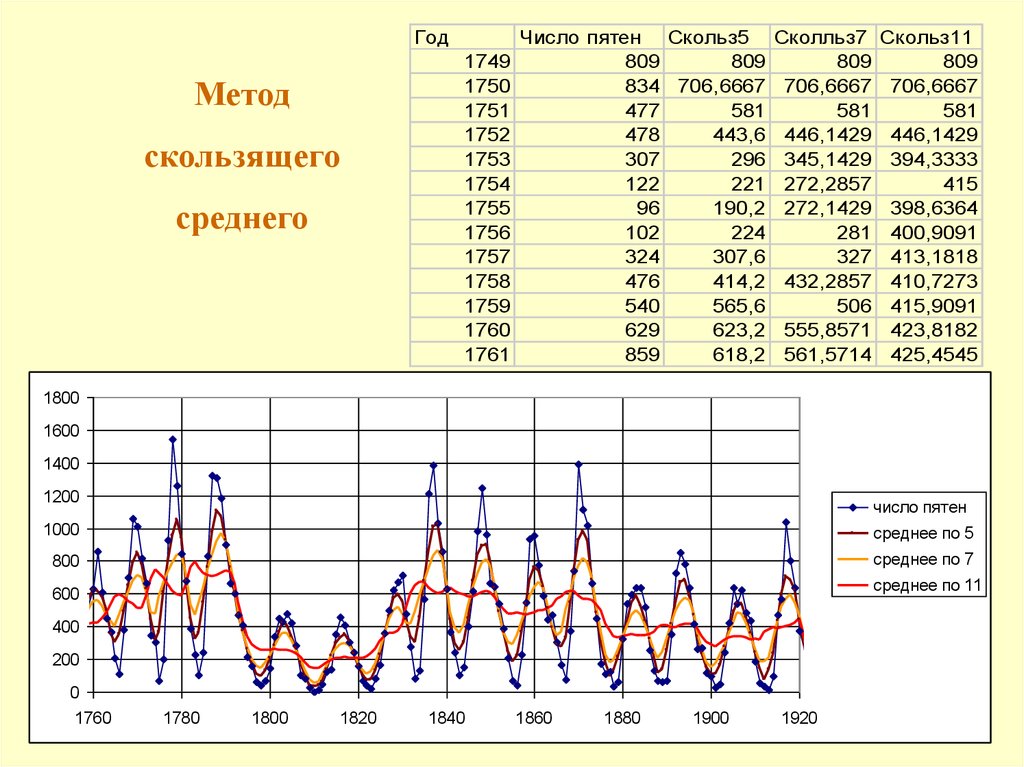
45.

Год
Метод
скользящего
среднего
1749
1750
1751
1752
1753
1754
1755
1756
1757
1758
1759
1760
1761
Число пятен Скольз5
809
809
834 706,6667
477
581
478
443,6
307
296
122
221
96
190,2
102
224
324
307,6
476
414,2
540
565,6
629
623,2
859
618,2
Сколльз7
809
706,6667
581
446,1429
345,1429
272,2857
272,1429
281
327
432,2857
506
555,8571
561,5714
Скольз11
809
706,6667
581
446,1429
394,3333
415
398,6364
400,9091
413,1818
410,7273
415,9091
423,8182
425,4545
1800
1600
1400
1200
число пятен
1000
среднее по 5
800
среднее по 7
среднее по 11
600
400
200
0
1760
1780
1800
1820
1840
1860
1880
1900
1920

46.

Метод наложения эпох
Метод наложения эпох позволяет:
1. Искать периодические процессы во временных рядах, т.е. в
мониторинговых данных, в том числе тогда, когда этот процесс не
описывается тригонометрическими функциями
2. Строить временные профили периодических процессов.
Суть метода заключается в следующем.
У нас имеется временной ряд (т.е. ряд значений, полученных в измерениях
через строго определенные промежутки времени).
Имеется возможность выбрать какой-либо период, разбить временной ряд
на части длиной в этот период и как бы наложив эти части друг на друга,
получить усредненный профиль. Если процесс не является периодическим
с выбранным нами периодом, то в качестве профиля мы увидим
исключительно флуктуации вокруг средних значений. Если такой период
действительно есть, то мы получим временной профиль процесса.

47.

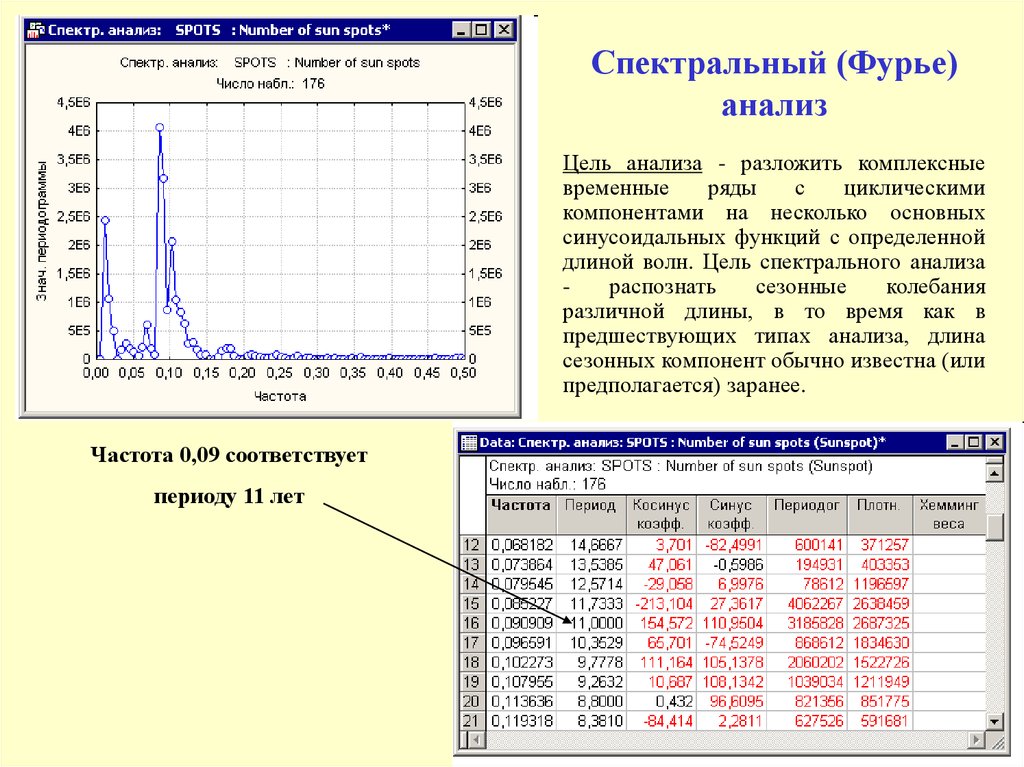
Спектральный (Фурье)
анализ
Цель анализа - разложить комплексные
временные
ряды
с
циклическими
компонентами на несколько основных
синусоидальных функций с определенной
длиной волн. Цель спектрального анализа
распознать
сезонные
колебания
различной длины, в то время как в
предшествующих типах анализа, длина
сезонных компонент обычно известна (или
предполагается) заранее.
Частота 0,09 соответствует
периоду 11 лет

48.

49.

Для оценки объёма данных предположим:
1) Спускаемый аппарат должен преодолеть расстояние 2 км.
Это максимальное расстояние. Для низших лиг может быть гораздо меньше.
2) Его скорость будет примерно 10 метров в секунду.
Быстрее нельзя, потому что аппарат разобьётся. Медленнее нельзя, потому что
аппарат может приземлиться очень далеко и его будет трудно найти
3) Измерения будут проводиться каждые 30 миллисекунд.
Ограничения, по версии присутствующих команд, связаны с электроникой и
возможностью передачи данных. В любом случае вопрос: имеет ли смысл
проводить измерения чаще?
Итак, сколько данных Вы получите?
Определите, пожалуйста, самостоятельно!

50.

Решение:
Одно измерение в 30 миллисекунд – это примерно 33
измерения в секунду.
Если в секунду аппарат пролетает 10 метров, то в 10 секунд –
100 метров, а в 100 секунд – 1000 метров, или 1 километр.
Два километра будут преодолены за 200 секунд.
Всего будет 200 сек * 33 измерений/сек = 6600 измерений.
А теперь задумаемся вот о чем:
Насколько сильно будут отличаться друг от друга соседние
измерения?
Причинами сходства или различия могут служить как
физические параметры среды (например, метеоусловия),
так и характеристики приборов.

51.

Распределения случайных величин.
Случайные величины характеризуются функцией и плотностью
распределения.
График функции распределения F(х) устроен так. По оси Х
откладывается значение случайной величины (обозначим его х). По оси Y
(значения функции) – вероятность того, что случайная величина примет
значение, меньшее или равное х.
Значение F(х) не может быть больше 1 или меньше 0. Функция –
возрастающая, притом F(-бесконечн.)=0, а F(+бесконечн.)=1.
Плотность распределения – это такая функция р(х), что вероятность
обнаружить значение в интервале от a до b выражается интегралом:
b
P (x [a ,b ]) p (x )dx
a
Для эмпирической оценки функции распределения можно провести
серию опытов , затем разбить интервал возможных значений на небольшие
отрезки и оценить вероятность попадания значения случайной величины в
каждый из отрезков как отношение числа благоприятных исходов, при
которых получено значение в пределах отрезка [a,b] к полному числу опытов

52.

Распределения случайных величин.
Нормальное распределение встречается в природе тогда, когда на
случайную величину действует большое количество независимых друг от
друга случайных факторов, действие каждого из которых на эту величину
незначительно.
Плотность нормального распределения (иначе её называют
функцией Гаусса). имеет вид симметричного колокола с максимумом,
совпадающим с истинным значением величины. Математически она
выражается как:
2
2
1
f X , ( x)
2
e ( x X )
/ 2
x
X x
Максимум соответствует среднему арифметическому значению:
n
Ширина колокола определяется стандартным отклонением,
вычисляемым по формуле:
1 n
( xi x ) 2
n 1 i 1
Вероятность получения измеренного значения в пределах Х равна 0.68.
При проведении n измерений точность результата улучшается в
число раз, равное квадратному корню из числа наблюдений.
Стандартная ошибка среднего значения равна x
x
n
i