Similar presentations:
Средства тепловой диагностики, обработка и представление результатов измерений
1.
Лекция 9. Средства тепловой диагностики, обработка ипредставление результатов измерений.
2.
Понятие об измеренииОсновные задачи измерения: 1) определение численного значения измеряемой
величины; 2) оценка допущенной при измерении погрешности.
Требования к точности измерения основных параметров двигателя
Научно-исследовательский центр им. Арнольда (США)
Погрешность
считывания, %
Число
измеряемых величин
Ширина полосы
частот, Гц
Температура газа
0,37
330
2
5
10
100
0,37
150
2
Расход топлива
0,5
20
10
Тяга
0,5
8
10
5
140
1000
(установившиеся
режимы)
Температура газа
(установившиеся
режимы)
Температура
конструкции
Давление
заторможенного потока
1
3.
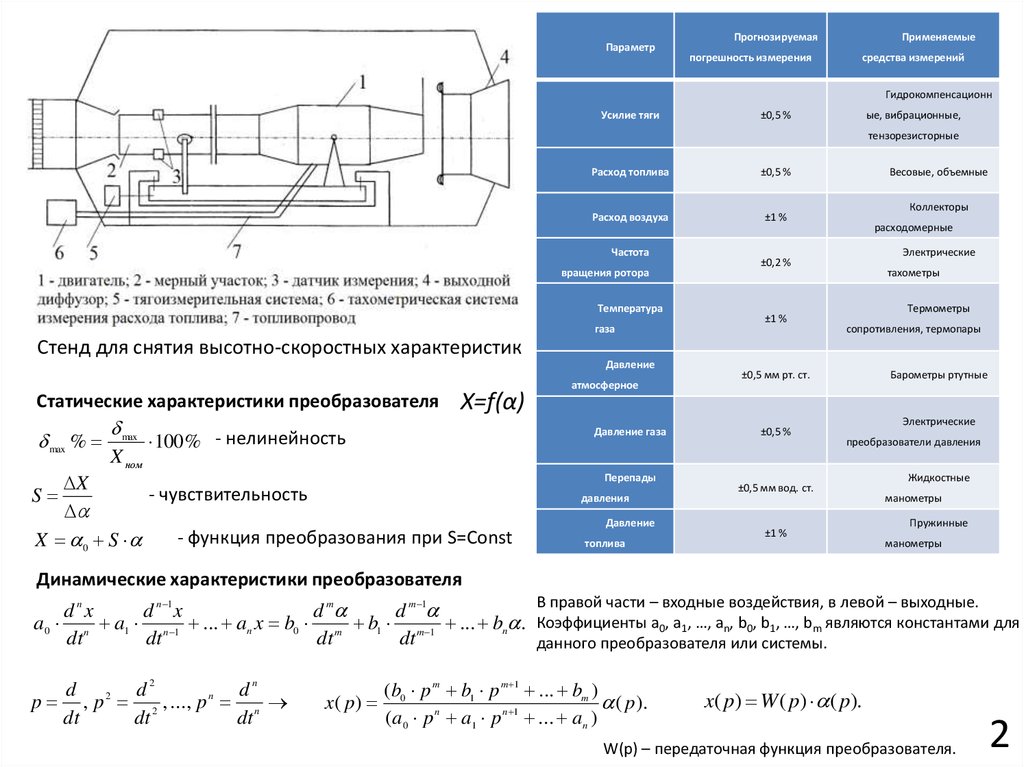
ПараметрПрогнозируемая
погрешность измерения
Применяемые
средства измерений
Гидрокомпенсационн
Усилие тяги
±0,5 %
ые, вибрационные,
тензорезисторные
Расход топлива
±0,5 %
Расход воздуха
±1 %
Частота
вращения ротора
Температура
газа
Весовые, объемные
Коллекторы
расходомерные
Электрические
±0,2 %
±1 %
тахометры
Термометры
сопротивления, термопары
Стенд для снятия высотно-скоростных характеристик
Давление
Статические характеристики преобразователя
max %
max
X ном
X=f(α)
100% - нелинейность
X
- чувствительность
S
- функция преобразования при S=Const
X 0 S
атмосферное
Давление газа
Перепады
давления
Давление
топлива
±0,5 мм рт. ст.
±0,5 %
Барометры ртутные
Электрические
преобразователи давления
±0,5 мм вод. ст.
±1 %
Жидкостные
манометры
Пружинные
манометры
Динамические характеристики преобразователя
В правой части – входные воздействия, в левой – выходные.
dnx
d n 1 x
d m
d m 1
a0 n a1 n 1 ... an x b0 m b1 m 1 ... bn . Коэффициенты a0, a1, …, an, b0, b1, …, bm являются константами для
dt
dt
dt
dt
данного преобразователя или системы.
d
d2
dn
2
n
p , p 2 , ..., p n
dt
dt
dt
(b0 p m b1 p m 1 ... bm )
x( p)
( p ).
( a0 p n a1 p n 1 ... a n )
x( p) W ( p) ( p).
W(p) – передаточная функция преобразователя.
2
4.
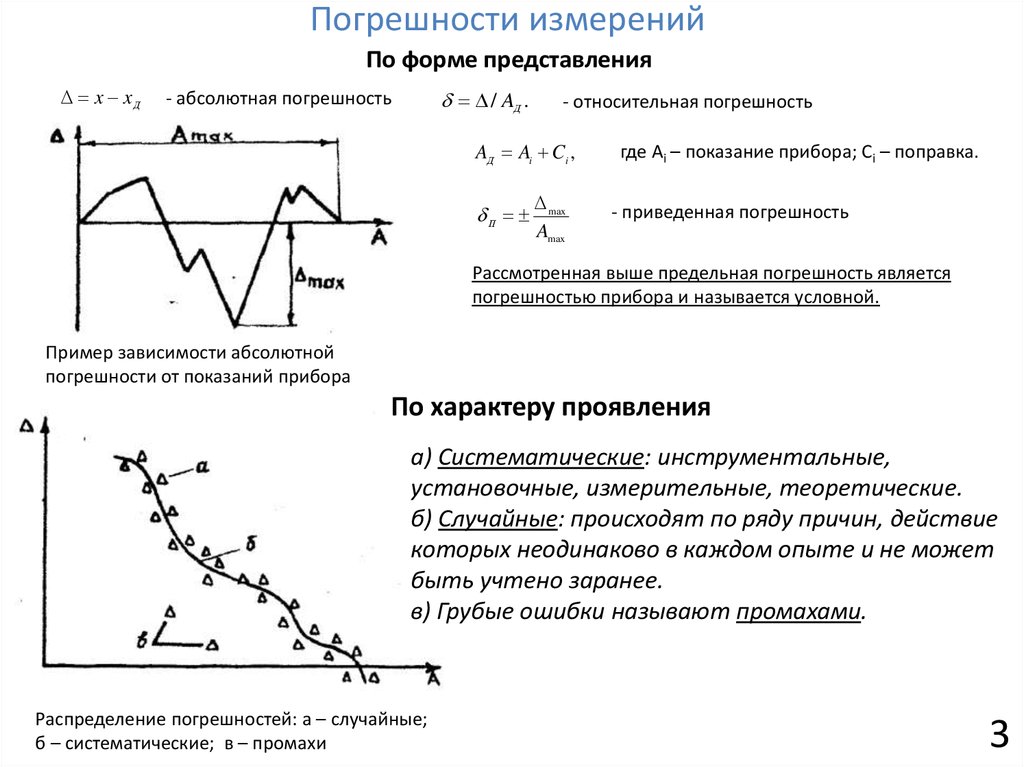
Погрешности измеренийПо форме представления
x xД
/ AД .
- абсолютная погрешность
- относительная погрешность
AД Ai Ci ,
П
max
Amax
где Ai – показание прибора; Ci – поправка.
- приведенная погрешность
Рассмотренная выше предельная погрешность является
погрешностью прибора и называется условной.
Пример зависимости абсолютной
погрешности от показаний прибора
По характеру проявления
а) Систематические: инструментальные,
установочные, измерительные, теоретические.
б) Случайные: происходят по ряду причин, действие
которых неодинаково в каждом опыте и не может
быть учтено заранее.
в) Грубые ошибки называют промахами.
Распределение погрешностей: а – случайные;
б – систематические; в – промахи
3
5.
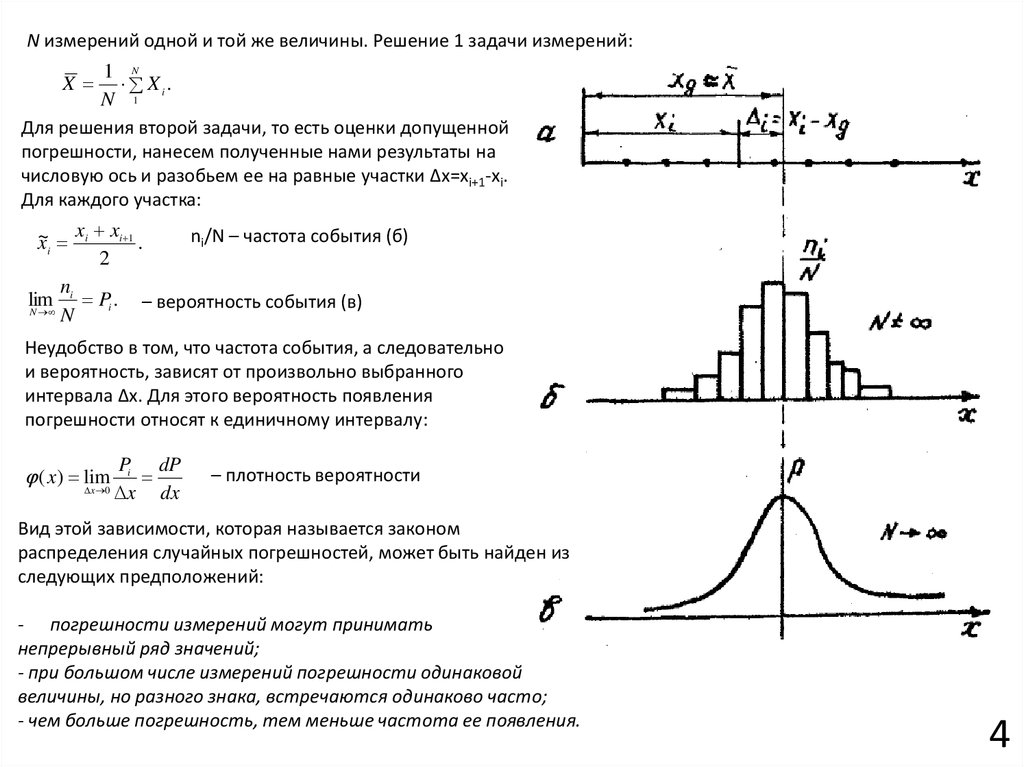
N измерений одной и той же величины. Решение 1 задачи измерений:1 N
Xi.
N 1
Для решения второй задачи, то есть оценки допущенной
погрешности, нанесем полученные нами результаты на
числовую ось и разобьем ее на равные участки ∆x=xi+1-xi.
Для каждого участка:
X
x xi 1
ni/N – частота события (б)
~
xi i
.
2
n
lim i Pi . – вероятность события (в)
N
N
Неудобство в том, что частота события, а следовательно
и вероятность, зависят от произвольно выбранного
интервала ∆x. Для этого вероятность появления
погрешности относят к единичному интервалу:
( x ) lim
x 0
Pi dP
x dx
– плотность вероятности
Вид этой зависимости, которая называется законом
распределения случайных погрешностей, может быть найден из
следующих предположений:
- погрешности измерений могут принимать
непрерывный ряд значений;
- при большом числе измерений погрешности одинаковой
величины, но разного знака, встречаются одинаково часто;
- чем больше погрешность, тем меньше частота ее появления.
4
6.
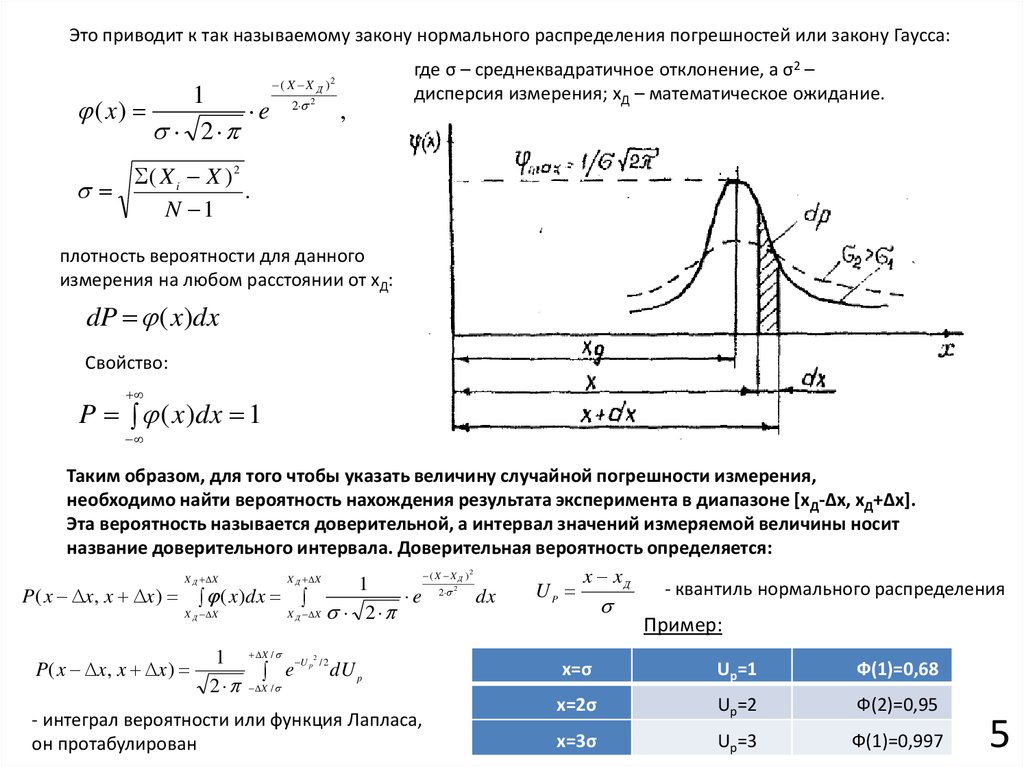
Это приводит к так называемому закону нормального распределения погрешностей или закону Гаусса:1
( x)
e
2
( X X Д )
2 2
2
,
где σ – среднеквадратичное отклонение, а σ2 –
дисперсия измерения; xД – математическое ожидание.
( X i X ) 2
.
N 1
плотность вероятности для данного
измерения на любом расстоянии от xД:
dP ( x)dx
Cвойство:
P ( x )dx 1
Таким образом, для того чтобы указать величину случайной погрешности измерения,
необходимо найти вероятность нахождения результата эксперимента в диапазоне [xД-∆x, xД+∆x].
Эта вероятность называется доверительной, а интервал значений измеряемой величины носит
название доверительного интервала. Доверительная вероятность определяется:
( X X )
X X
X X
x xД
1
- квантиль нормального распределения
UP
P( x x, x x ) ( x )dx
e 2 dx
X X
X X
2
P( x x, x x )
Д
Д
Д
Д
1
2
X /
e
X /
U p 2 / 2
Д
2
2
Пример:
dU p
- интеграл вероятности или функция Лапласа,
он протабулирован
x=σ
Up=1
Ф(1)=0,68
x=2σ
Up=2
Ф(2)=0,95
x=3σ
Up=3
Ф(1)=0,997
5
7.
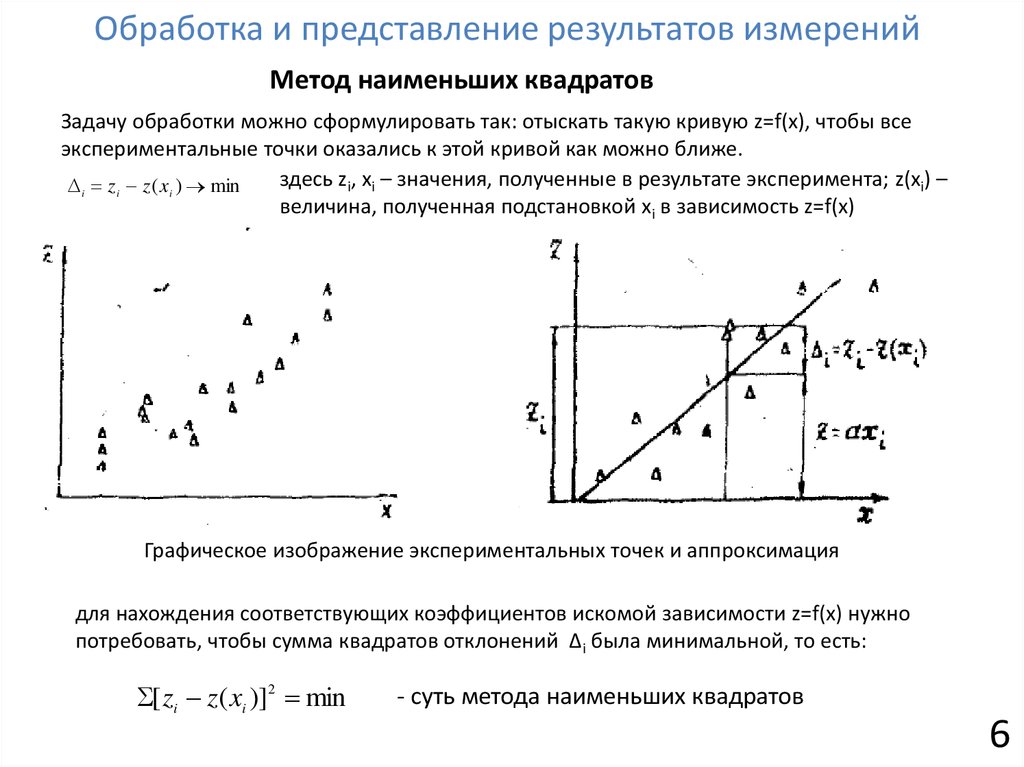
Обработка и представление результатов измеренийМетод наименьших квадратов
Задачу обработки можно сформулировать так: отыскать такую кривую z=f(x), чтобы все
экспериментальные точки оказались к этой кривой как можно ближе.
здесь zi, xi – значения, полученные в результате эксперимента; z(xi) –
i zi z ( xi ) min
величина, полученная подстановкой xi в зависимость z=f(x)
Графическое изображение экспериментальных точек и аппроксимация
для нахождения соответствующих коэффициентов искомой зависимости z=f(x) нужно
потребовать, чтобы сумма квадратов отклонений ∆i была минимальной, то есть:
[ zi z( xi )]2 min
- суть метода наименьших квадратов
6
8.
Пусть z=ax, тогда[ zi a xi ]2 0
a
a
2[ zi a xi ] xi 0
z i xi
2
xi
На практике обычно ограничиваются
многочленом четвертой степени:
z A B x C x2 D x3 E x4
2
[
]
2 [ ] 0;
A
[ ]2 2 [ ]x 0;
i
B
2
2
[
]
2
[
]
x
0;
i
C
3
2
[
]
2
[
]
x
0;
i
D
[ ]2 2 [ ]x 4 0;
i
E
[ zi A B xi C xi D xi E xi ]2 min
2
z i
x i
z i x i x i
x i
2
2
x i
3
4
x i
3
x i
4
x i
x i
4
5
z i x i x i
3
x i
4
x i
5
x i
6
z i x i x i
3
4
x i
5
x i
6
x i
7
z i x i x i
5
x i
6
x i
7
x i
8
2
4
A
3
n
x i
x i
x i
x i
x i
2
x i
3
x i
4
x i
5
2
x i
3
4
x i
2
x i
3
x i
4
x i
5
x i
6
x i
3
x i
4
x i
5
x i
6
x i
7
x i
4
x i
5
x i
6
x i
7
x i
8
7
9.
Пример:n
В случае
y ax b F (a, b) ( y i ( axi b)) 2 min
i 1
n
n
n
n x y x y
a i 1 i i i 1 i i 1 i ;
2
n
n
2
n xi xi
i 1
i 1
n
n
y
a
i
xi
i 1
i 1
;
b
n
F ( a, b)
a 0;
F ( a, b) 0;
b
i=1
i=2
i=3
i=4
i=5
cумма
xi
0
1
2
4
5
12
yi
2,1
2,4
2,6
2,8
3
12,9
xiyi
0
2,4
5,2
11,2
15
33,8
xi2
0
1
4
16
25
46
5 33,8 12 12,9
a
;
2
5 46 12
a 0,165; b 2,184; y 0,165 x 2,184
b 12,9 a 12 ;
5
8
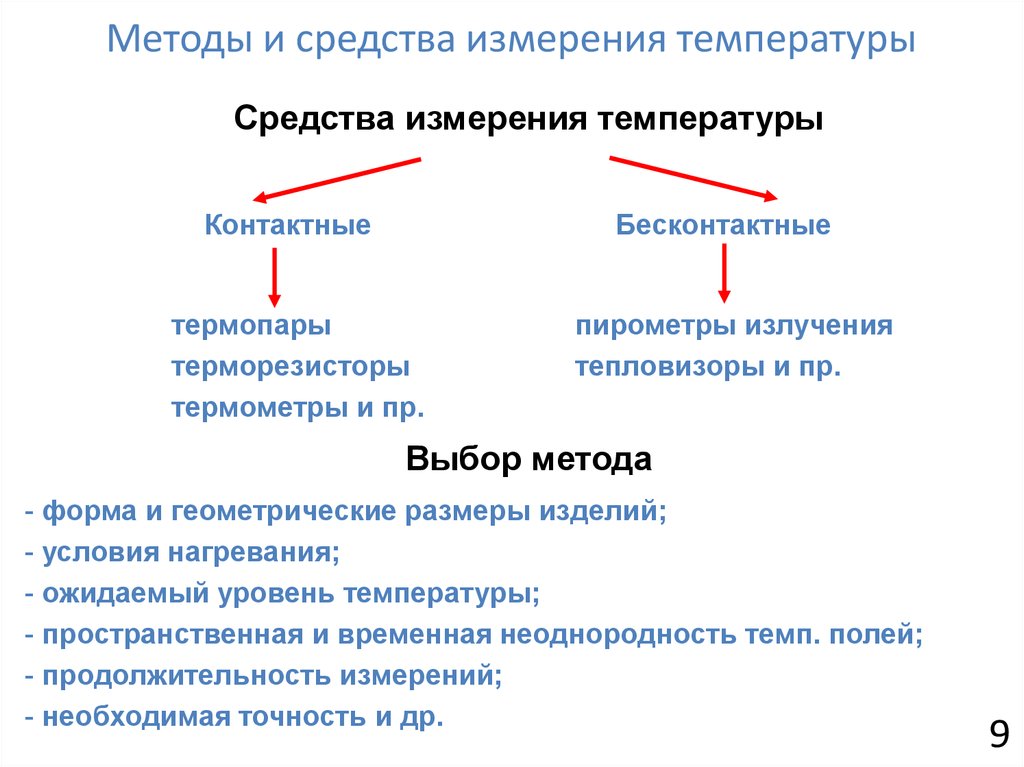
10. Методы и средства измерения температуры
Средства измерения температурыКонтактные
Бесконтактные
термопары
терморезисторы
термометры и пр.
пирометры излучения
тепловизоры и пр.
Выбор метода
- форма и геометрические размеры изделий;
- условия нагревания;
- ожидаемый уровень температуры;
- пространственная и временная неоднородность темп. полей;
- продолжительность измерений;
- необходимая точность и др.
9
11. Методическая погрешность измерения
Методическая погрешность измерения температуры (МПИТ) вызвана различиемфизических свойств материалов датчика и объекта испытаний, отводом теплоты или
теплопритоками по термоэлектродам, контактными сопротивлениями в месте установки..
T = Tt – T,
где Tt – температура спая термопары; Т – истинная температура образца.
Квадратичная погрешность измерения температуры:
e
t Tt 2 ( )d .
Методы контроля и уменьшения МПИТ
Tt Tt Tm
t m
Tw T f
1 t
t t / m 8 2 f , t t Rt / 3 m
где
t , m ,
f , t , f ,
t , m
Rt
m / m 8 f , t Rt / 3 m
– тепловые проводимости соответственно между площадью контакта и окружающей средой,
между глубинными областями образца и площадкой контакта датчика температуры, между
свободной поверхностью тела и средой в расчете на площадь контакта.
– коэффициенты теплоотдачи между боковой поверхностью датчика и окружающей средой и
между свободной поверхностью образца и окружающей средой.
– коэффициенты теплопроводности материала датчика и образца.
– радиус поперечного сечения датчика.
10
12.
Методы контроля и уменьшения МПИТ (продолжение)а) Для достижения малых погрешностей:
t m
f , t t Rt / m 1
2
б) Увеличение поверхности соприкосновения датчика с образцом.
Заключается в соединении спая с хорошо проводящим тепло металлическим диском.
Для термопар с термоэлектродами диаметром 0,1-0,3 мм используют диски из серебра
или меди с d = 0,2-1,5 мм и диаметром 1-6 мм
в) Размещение термопар в изотермических плоскостях.
11
13.
Схемы датчиков тепловых потокова) Простейший датчик. Математическая модель термически тонкого тела:
C
T
A qw T 4
где C, A, e – соответственно объемная теплоемкость, поглощательная и
излучательная способность материала чувствительного элемента; delta –
толщина элемента.
qw C b / A, b T /
12
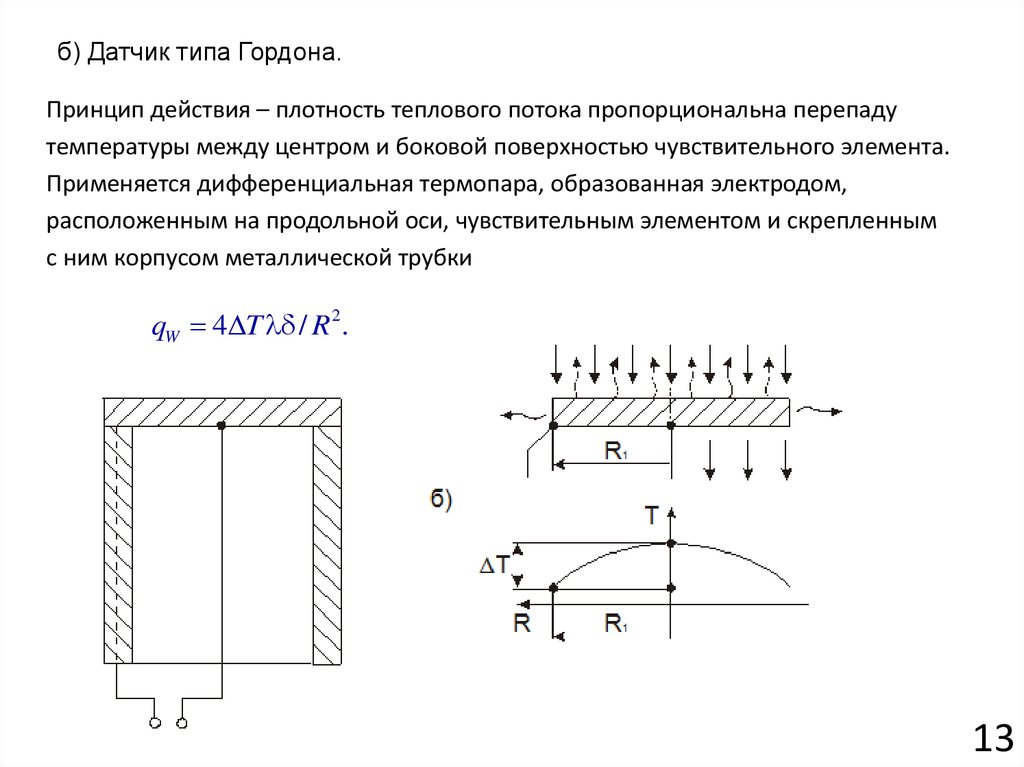
14.
б) Датчик типа Гордона.Принцип действия – плотность теплового потока пропорциональна перепаду
температуры между центром и боковой поверхностью чувствительного элемента.
Применяется дифференциальная термопара, образованная электродом,
расположенным на продольной оси, чувствительным элементом и скрепленным
с ним корпусом металлической трубки
qW 4 T / R 2 .
13
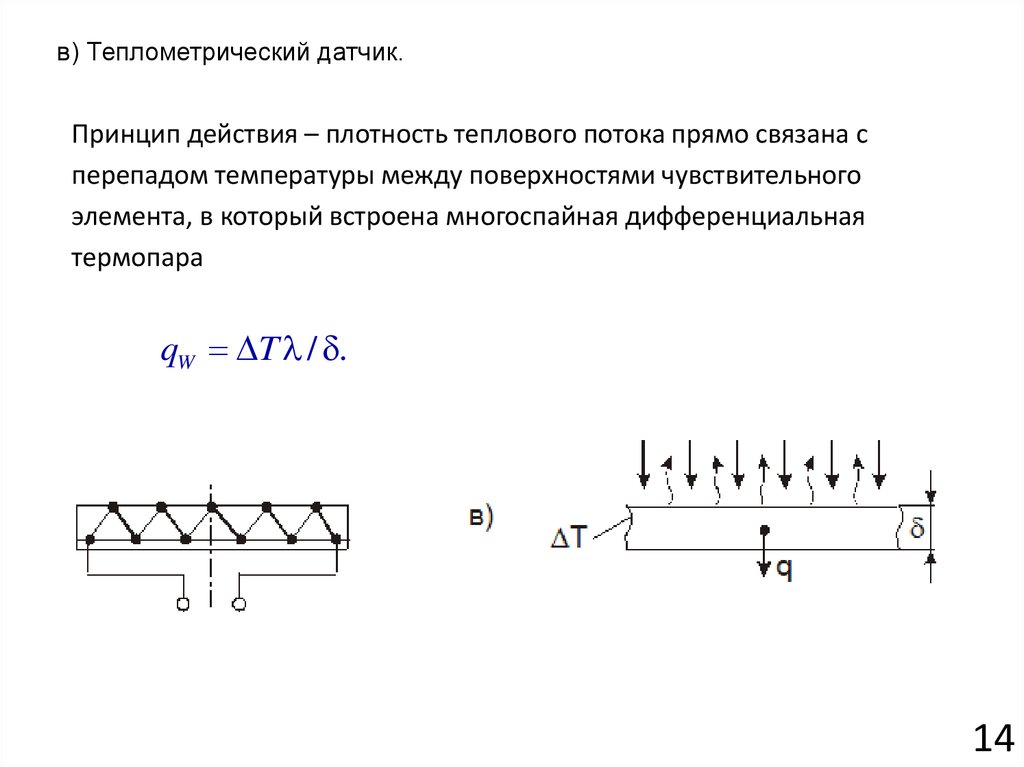
15.
в) Теплометрический датчик.Принцип действия – плотность теплового потока прямо связана с
перепадом температуры между поверхностями чувствительного
элемента, в который встроена многоспайная дифференциальная
термопара
qW T / .
14







 physics
physics








