Элементы теории полезности

1. Теория принятия решений

Лекция 2.13
Элементы теории полезности

2. СОДЕРЖАНИЕ

•Текущий контроль
•Функции полезности
•Аксиомы линейной
полезности
•Многофакторная полезность

3. Определить лузера – претендента, который не может победить

Здесь i– порядковый номер студента.
1
2
2(i+2) 4(i-1)
3
4
5
- Номер коалиции
4i
3(i+1)
2i
-
a
b
d
a
c
b
c
b
c
d
c
a
c
b
b
d
d
a
d
a
Число голосов

4. Цели и средства

Цель: дать количественную оценку
отношению предпочтения и определить
такую стратегию поведения, которая бы
гарантировала наиболее полезное
распределение имеющихся ресурсов.
Инструмент: распределение имеющихся
ресурсов.
Результат: наибольшая полезность
выигрыша.

5. Функции и аксиомы полезности

Функция
Функции и аксиомы полезности
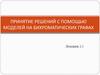
Функция полезности – это такая функция U(X), для которой
справедливо:
x2 x1 U ( x2 ) U ( x1 )
x2 x1 U ( x2 ) U ( x1 )
Отношение безразличия;
Отношение упорядочения (предпочтения)
Цель: дать количественную оценку отношению предпочтения.
Полезность
Рисунок иллюстрирует закон убывающей
предельной полезности: с увеличением
богатства рост его на единицу приводит
к меньшему возрастанию полезности,
чем в начале роста благосостояния.
Благосостояние

6. Альтернативы риска

• Совершенная функция полезности – это такая функция
U(x), для которой справедливо:
x1 x2 .
• U (x1) > U (x2) тогда и только тогда, когда
• Ожидаемая полезность.
Пусть определено множество X, элементы которого могут
представлять собой альтернативы выбора либо
последствия решений, содержащих элемент риска. Пусть
на множестве Х определены два распределения
вероятностей P и Q (их называют ставками, лотереями,
альтернативами риска, смешанными стратегиями), для
которых справедливо:
pi P, pi 0;
p 1;
i i
q j Q, q j 0;
q 1;
j j

7. Линейная комбинация альтернатив

• Линейной комбинацией альтернатив P и Q
называется распределение R для которого
справедливо:
R P (1 ) Q, где
0 1.

8. Пример. Заданы распределения P и Q:

• Исходные распределения:
P : p (0$) 0.3; p (10$) 0.2 ; p ( 20$) 0.5.
Q : q (7$) 0.7; q (10$) 0.3.
0 .5 .
• Линейная комбинация:
R P (1 ) Q ;
R : r (0$) 0.15; r (7$) 0.35 ;
r (10$) 0.25; r ( 20$) 0.25.

9. Аксиомы функции полезности

, то
на P нерефлексивно (антирефлексивно), т.е. справедливо:
Аксиомы функции полезности
Ниже полагаем: a )
p, q, r , S P;
b) 0 1.
Отношение P нерефлексивно (антирефлексивно),
т.е. справедливо: p p; q q,....
Если 0 1, p q и r S : p (1 ) r q (1 ) S

10. САМОСТОЯТЕЛЬНО

• Построить график вспомогательной функции V
применительно к личности, которая до
определенного уровня богатства склонна к
риску, а достигнув его, - избегает риска.
• Создать распределение R, являющееся
линейной комбинацией P и Q, где:
P: p(0$)=0,2; p(15$)=0,5; p(25$)=0,2; p(50$)=0,1.
Q: q(10$)=0,3; q(30$)=0,4;q(70$)=0,3.
α = 0,45.

11. Принятие наиболее полезных решений

• Содержательная постановка задачи:
Требуется на множестве альтернатив
выбрать те, которые обладают
наибольшей ожидаемой полезностью
при условии, что выбор каждой
альтернативы соответствует затратам
какого-то ресурса, запасы которого
ограничены.

12. Обозначения

R – величина ресурса;
xi – величина i-го выигрыша;
– вероятность i-го выигрыша;
p ( xi )
ri затраты ресурса на выбор i-й альтернативы;
zi
булева переменная, равная единице при
выборе i-й альтернативы и равная нулю в
противном случае;
vi полезность i-й альтернативы.

13. Формальная постановка задачи

pi vi zi max;
i
(1)
ri zi R;
i
i : zi 1,0.

14. Преобразование системы (1)

Пусть
vi pi mi
. Тогда справедлива система:
mi zi max;
i
(2)
ri zi R;
i
i : zi 1,0.
Легко убедиться, что (2) представляет собой
задачу о ранце.

15. ПРИМЕР 1

• Уложить в рюкзак наиболее полезные в
походе предметы, если его объем равен R =
10, а величины, определяющие mi и ri
приведены в таблице 1 ниже:
Табл. 1.
i
mi
ri
1
3
2
2
7
6
3
9
5
4
4
3

16. Формальная постановка задачи

3 z1 7 z 2 9 z3 4 z 4 max;
2 z1 6 z 2 5 z3 3 z 4 10; (3)
i : z 1,0.
i

17. Решение задачи перебором

№
Q
y
№
Q
y
1
0001
4
8
1000
3
2
0010
9
9
1001
7
3
0011
13
10
1010
12
4
0100
7
11
1011
16
5
0101
11
12
1100
10
6
0110
-∞
13
1101
-∞
7
0111
-∞
14
1110
-∞
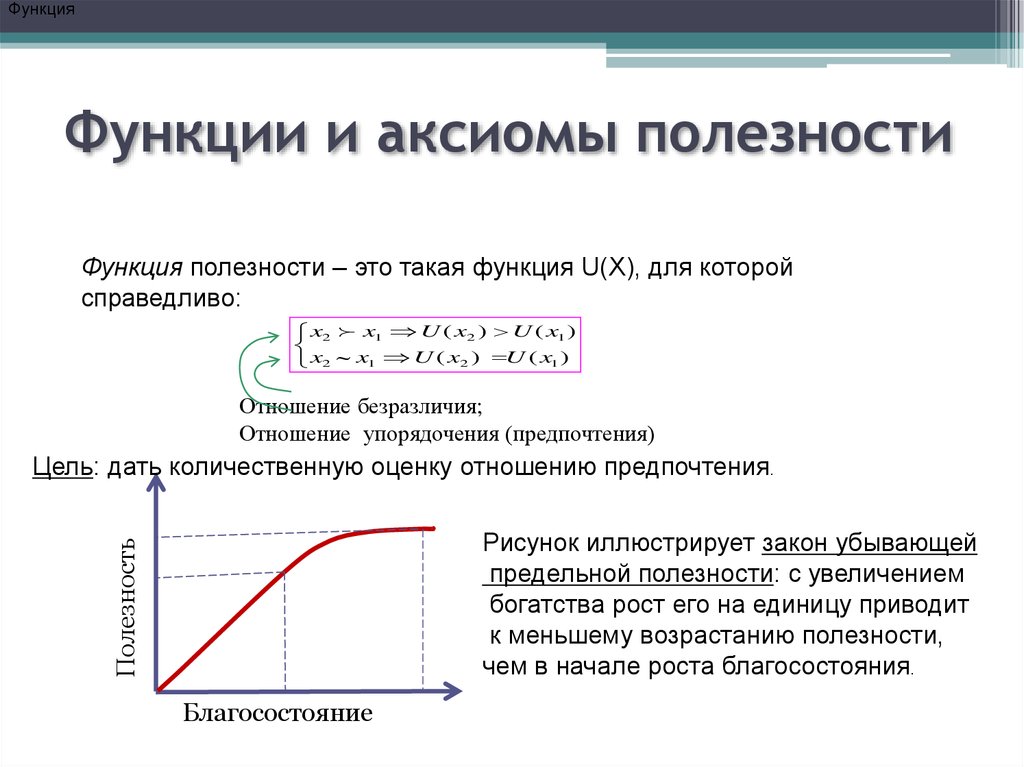
Ответ: оптимальный вектор переменных w={1011},
рекорд y =16.

18. Решить самостоятельно

• Выбрать наиболее полезные направления
развития промышленности, если объем
имеющихся для этого ресурсов равен R = 100,
а величины, определяющие mi и ri
приведены в таблице 2 ниже:
Табл. 2.
i
mi
ri
1
13
22
2
17
16
3
19
25
4
24
13

19. Многофакторная полезность

• Часто полезность является функцией не
одного, а нескольких факторов, поэтому
естественно коротко остановиться на
многофакторной полезности. Пусть Xi –
множество значений i-го фактора ( i=1,2,...,n);
X = X1 X2 ... Xn. В этом случае имеет место
условие независимости предпочтений:
i : xi , yi , ai , bi X ,
( y1 , ..., ai , ..., yn ) ( y1 , ..., bi , ..., yn ),
( x1 , ..., ai , ..., xn ) ( x1 , ..., bi , ..., xn ).

20. Аддитивная многофакторная функция полезности

Функция U является аддитивной на
множестве X, если существуют вещественные
функции полезности U1(X1), U2(X2), ..., Un(Xn)
такие, что справедливо равенство:
n
U ( X ) U i ( X i )
i 1

21. Эквивалентные векторы

• Векторы (x1, x2, ..., xm) и (y1, y2, ..., ym)
эквивалентны, т.е. (x1, x2, ..., xm) (y1, y2, ...,
ym), тогда и только тогда, когда один из них
является перестановкой элементов другого.
Если (x1, x2, ..., xm) (y1, y2, ..., ym) и U(X) –
аддитивная функция полезности на X, то
невозможно выполнение условия:
1 k m : x y .
k
k

22. Многофакторная полезность

Дать формальное описание задачи и решить ее
графически: девушке предлагают руку и сердце
три молодых человека, каждый из которых
характеризуется двумя функциями U1 ( x1,i ) и U 2,i ( x2,i ),
первая из которых определяет полезность
времени, проведенного им на работе, а вторая –
дома. Сумма времен x1,i и x2,i не превышает 18
часов. Кого следует выбрать девушке, если
функции имеют вид: U1 ( x1,i ) 4i x1,i ;
5i
U
(
x
)
x2 ,i .
2
2 ,i 2 ,i
(4 i)

23. Максимальная полезность i-го объекта

Формальная постановка задачи:
5i
U i U1 ( x1,i ) U 2,i ( x2,i ) 4ix1,i (4 i ) 2 x2,i max;
x1,i x2,i 18;
Следует решить три задачи, определив
полезность каждого претендента U и выбрать
i, j : x 0.
того, у которого этот параметр максимален.
i
,
j
i

24. Решение задачи при i=1

5
U1 4 x1,1 9 x2,1 max;
x1,1 x2,1 18;
i : x 0.
i ,1
x1,1 x2,1 18
x₂
Оптимальное решение
18
x₁

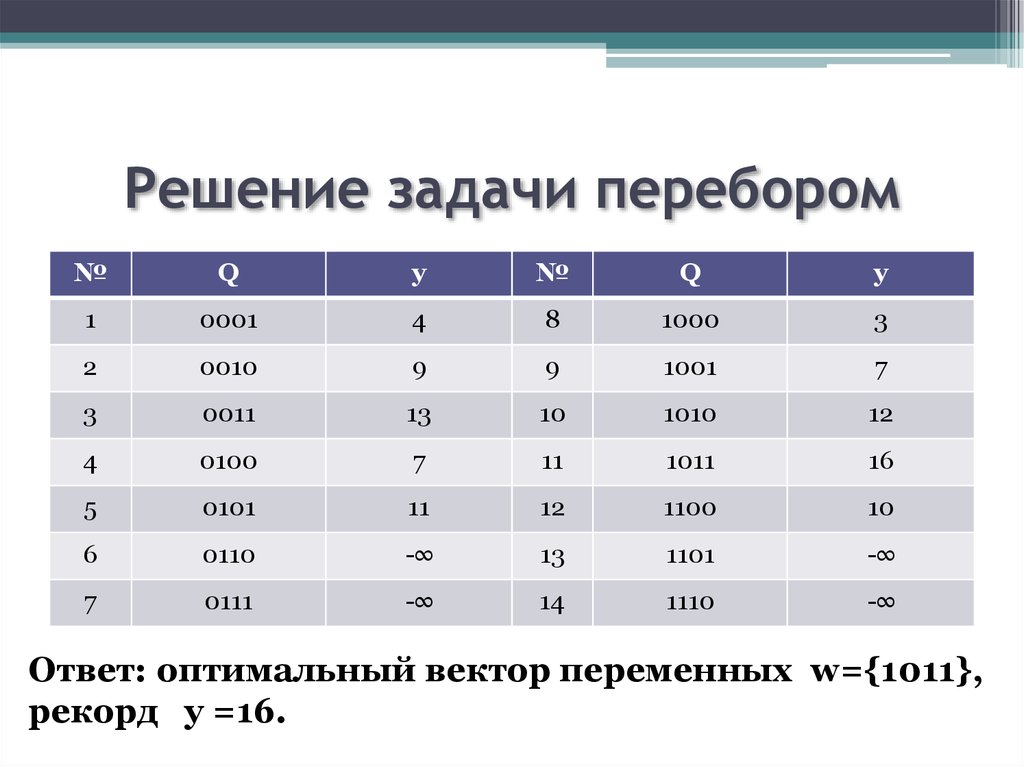
25. Решить самостоятельно

• На множестве из трех направлений развития
корпорации выбрать наиболее и наименее
перспективное при условии, что ресурс R,
выделенный на развитие, равен 100+10*i, где i–
номер студента. Ниже приняты следующие
обозначения:
• Pj – вероятность получения прибыли при
выборе j-го направления развития.
• Nj – вероятная прибыль от j-го направления
развития при условии вложения в это
направление Rj средств корпорации.
• Rj – средства корпорации, которые по мнению
экспертов следует вложить в j-е направление,
чтобы получить прибыль Nj.

26. Персональные данные 1

#i
P1
N1
R1
P2
N2
R2
P3
N3
R3
1
0.25
50
40
0.35
40
50
0.40
20
30
2
0.20
69
50
0.55
55
70
0.25
10
30
3
0.15
35
65
0.35
65
75
0.5
30
35
4
0.30
45
70
0.25
75
40
0.45
40
80
5
0.45
80
45
0.10
40
65
0.45
15
80
6
0.12
20
75
0.38
35
55
0.5
35
40
7
0.58
35
40
0.22
50
50
0.20
55
70

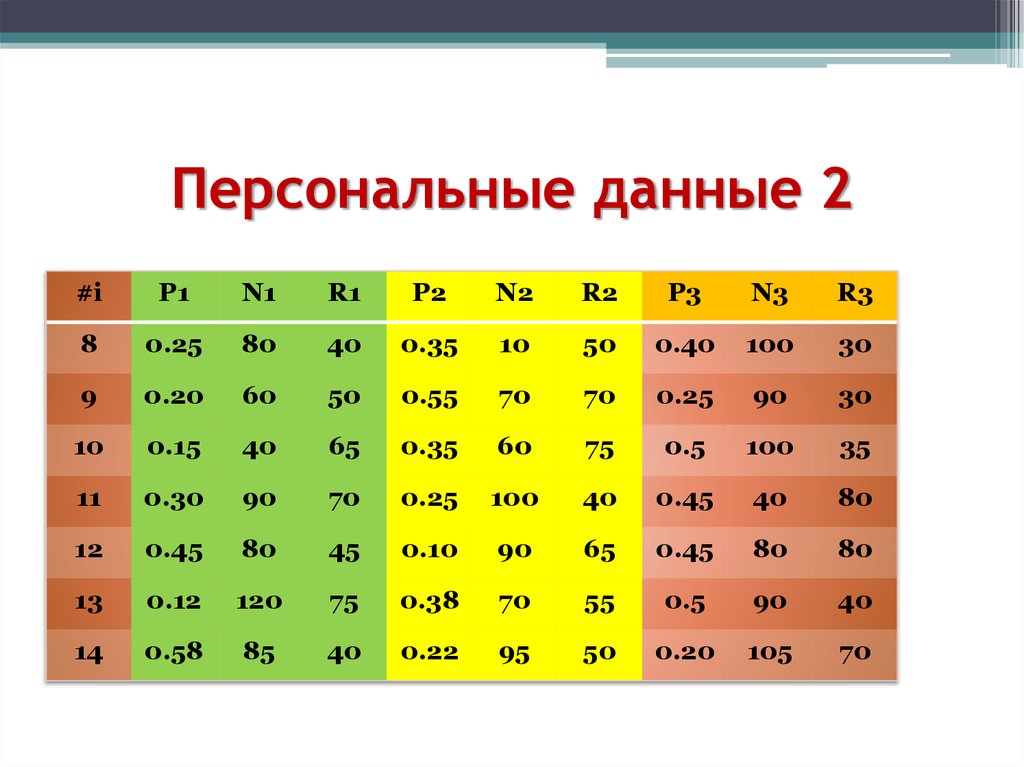
27. Персональные данные 2

#i
P1
N1
R1
P2
N2
R2
P3
N3
R3
8
0.25
80
40
0.35
10
50
0.40
100
30
9
0.20
60
50
0.55
70
70
0.25
90
30
10
0.15
40
65
0.35
60
75
0.5
100
35
11
0.30
90
70
0.25
100
40
0.45
40
80
12
0.45
80
45
0.10
90
65
0.45
80
80
13
0.12
120
75
0.38
70
55
0.5
90
40
14
0.58
85
40
0.22
95
50
0.20
105
70

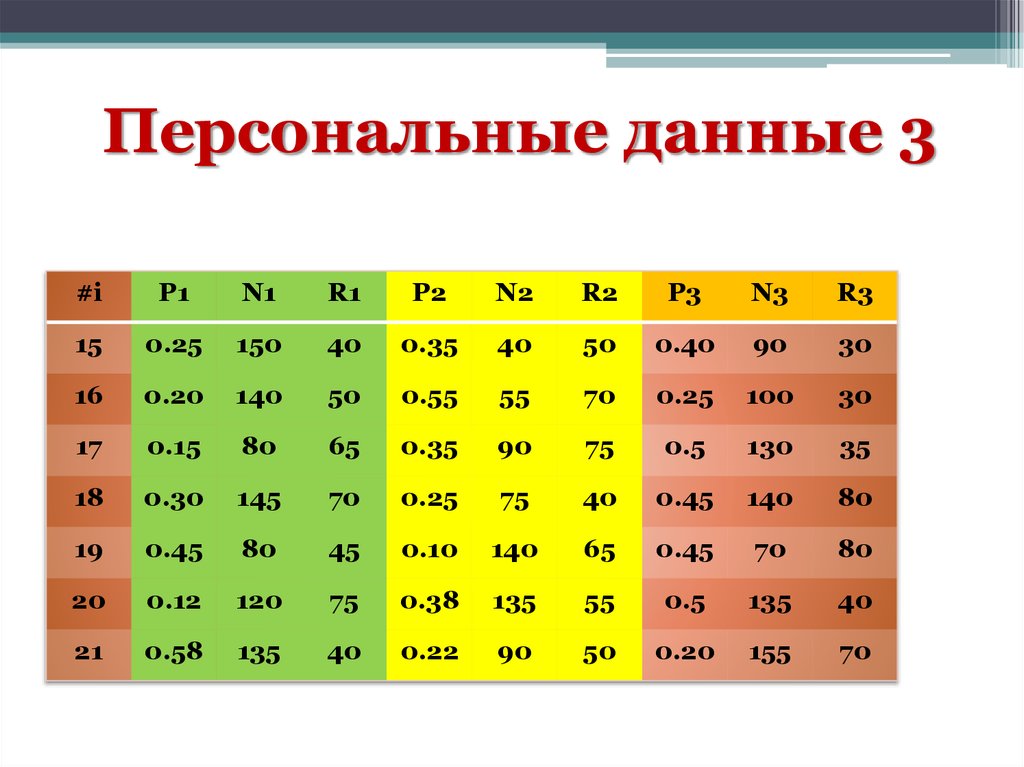
28.

Персональные данные 3
#i
P1
N1
R1
P2
N2
R2
P3
N3
R3
15
0.25
150
40
0.35
40
50
0.40
90
30
16
0.20
140
50
0.55
55
70
0.25
100
30
17
0.15
80
65
0.35
90
75
0.5
130
35
18
0.30
145
70
0.25
75
40
0.45
140
80
19
0.45
80
45
0.10
140
65
0.45
70
80
20
0.12
120
75
0.38
135
55
0.5
135
40
21
0.58
135
40
0.22
90
50
0.20
155
70