Similar presentations:
Задача о минимальном разрезе на взвешенном бисвязном графе
1. ЗАДАЧА О МИНИМАЛЬНОМ РАЗРЕЗЕ НА ВЗВЕШЕННОМ БИСВЯЗНОМ ГРАФЕ
Лекция 9ЗАДАЧА О МИНИМАЛЬНОМ РАЗРЕЗЕ
НА ВЗВЕШЕННОМ БИСВЯЗНОМ
ГРАФЕ
2. СОДЕРЖАНИЕ
1. Формальная постановка и поиск решениязадачи о минимальном разрезе между двумя
вершинами на взвешенном орграфе.
2. Текущий контроль умения решать задачи на
поиск кратчайших путей, максимальных потоков и
минимальных разрезов.
3. Формальные постановки и поиск решений
задач о минимальном разрезе и максимальной
циркуляцией на взвешенном бисвязном орграфе.
2
3. задача о минимальном разрезе между двумя вершинами на взвешенном орграфе
Часть 1ЗАДАЧА О МИНИМАЛЬНОМ РАЗРЕЗЕ
МЕЖДУ ДВУМЯ ВЕРШИНАМИ НА
ВЗВЕШЕННОМ ОРГРАФЕ
3
4. Формальная постановка задачи о минимальном разрезе между вершинами s и t
ФОРМАЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ ОМИНИМАЛЬНОМ РАЗРЕЗЕ МЕЖДУ ВЕРШИНАМИ
SИT
r (i, j ) z (i, j ) min;
i j
d : z (i, j ) 1;
d
( i , j ) L ( s ,t )
i, j i : z (i, j ) 1,0.
4
5. АЛГОРИТМ ПОИСКА РЕШЕНИЯ ЗАДАЧИ О МИНИМАЛЬНОМ РАЗРЕЗЕ МЕЖДУ ДВУМЯ ВЕРШИНАМИ ПЕРЕБОРОМ
1 Шаг. Выбор ранее не анализировавшегося сочетаниядуг. Если такового нет, то перейти к шагу 6.
2 Шаг. Выбранные на предыдущем шаге дуги удаляются
из графа G(X,U).
3 Шаг. На полученном графе ищется максимальный поток
F из “s” в “t”.
4. Если F=0, то перейти к шагу 5, нет – к шагу 1.
5. Если суммарный вес выделенных дуг Q меньше
хранящейся в памяти величины R, то R=Q, перейти к
шагу 1, в противном случае сразу перейти к шагу 1.
6. Конец алгоритма. R равно величине минимального
разреза.
5
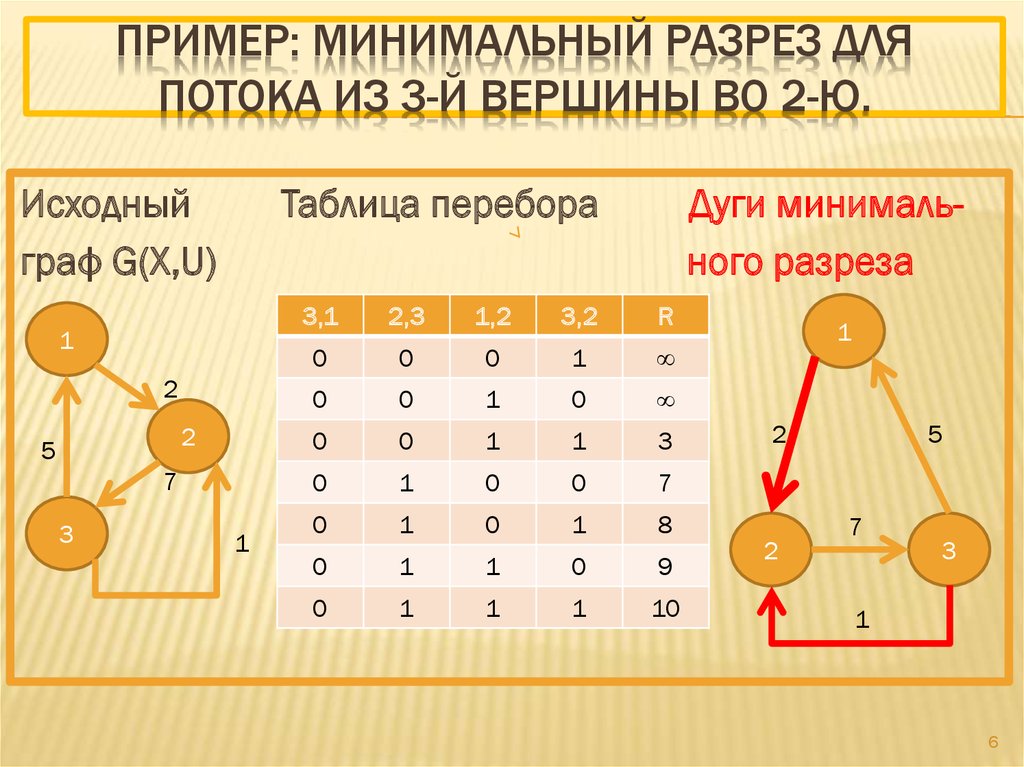
6. ПРИМЕР: минимальный разрез для потока из 3-й вершины во 2-ю.
ПРИМЕР: МИНИМАЛЬНЫЙ РАЗРЕЗ ДЛЯПОТОКА ИЗ 3-Й ВЕРШИНЫ ВО 2-Ю.
Исходный
граф G(X,U)
Таблица перебора
1
2
2
5
7
3
1
Дуги минимального разреза
3,1
2,3
1,2
3,2
R
0
0
0
1
∞
0
0
1
0
∞
0
0
1
1
3
0
1
0
0
7
0
1
0
1
8
0
1
1
0
9
0
1
1
1
10
1
2
2
5
7
3
1
6
7. Решить три задачи самостоятельно
Часть 2РЕШИТЬ ТРИ ЗАДАЧИ САМОСТОЯТЕЛЬНО
1. Определить
кратчайший
путь между
заданной
парой
вершин.
2. Определить
максимальный
поток из заданной вершины
в заданную.
3.Определить
минимальный
разрез между
заданной
парой вершин.
7
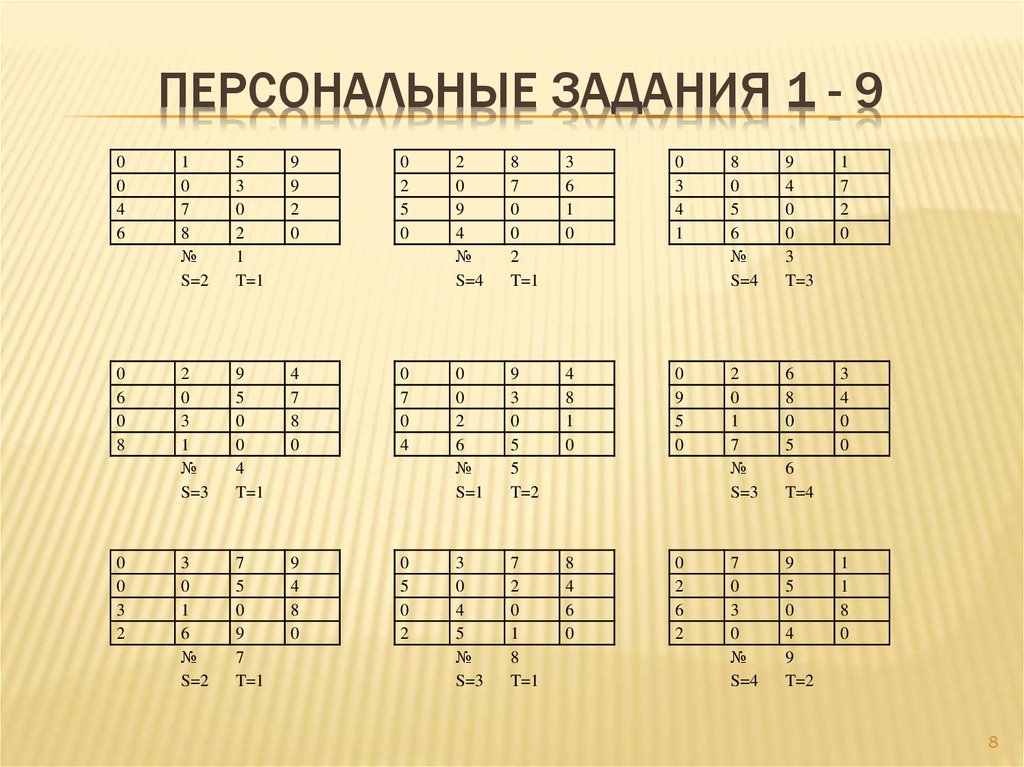
8. ПЕРСОНАЛЬНЫЕ ЗАДАНИЯ 1 - 9
00
4
6
1
0
7
8
№
S=2
5
3
0
2
1
T=1
9
9
2
0
0
2
5
0
2
0
9
4
№
S=4
8
7
0
0
2
T=1
3
6
1
0
0
3
4
1
8
0
5
6
№
S=4
9
4
0
0
3
T=3
1
7
2
0
0
6
0
8
2
0
3
1
№
S=3
9
5
0
0
4
T=1
4
7
8
0
0
7
0
4
0
0
2
6
№
S=1
9
3
0
5
5
T=2
4
8
1
0
0
9
5
0
2
0
1
7
№
S=3
6
8
0
5
6
T=4
3
4
0
0
0
0
3
2
3
0
1
6
№
S=2
7
5
0
9
7
T=1
9
4
8
0
0
5
0
2
3
0
4
5
№
S=3
7
2
0
1
8
T=1
8
4
6
0
0
2
6
2
7
0
3
0
№
S=4
9
5
0
4
9
T=2
1
1
8
0
8
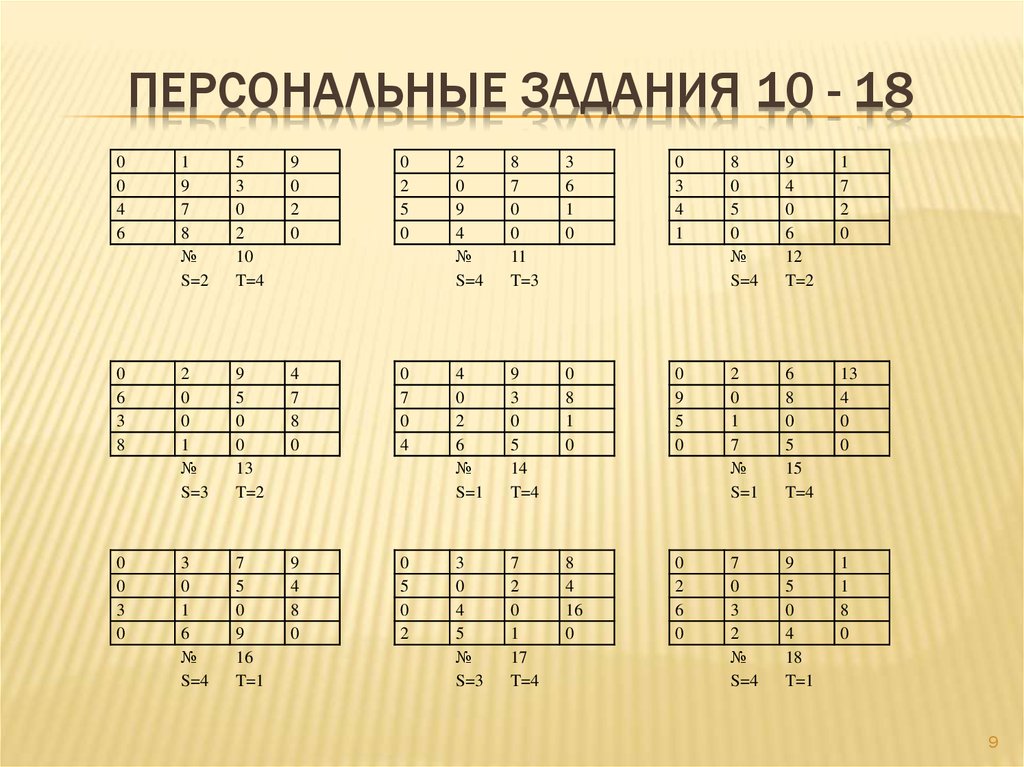
9. ПЕРСОНАЛЬНЫЕ ЗАДАНИЯ 10 - 18
00
4
6
1
9
7
8
№
S=2
5
3
0
2
10
T=4
9
0
2
0
0
2
5
0
2
0
9
4
№
S=4
8
7
0
0
11
T=3
3
6
1
0
0
3
4
1
8
0
5
0
№
S=4
9
4
0
6
12
T=2
1
7
2
0
0
6
3
8
2
0
0
1
№
S=3
9
5
0
0
13
T=2
4
7
8
0
0
7
0
4
4
0
2
6
№
S=1
9
3
0
5
14
T=4
0
8
1
0
0
9
5
0
2
0
1
7
№
S=1
6
8
0
5
15
T=4
13
4
0
0
0
0
3
0
3
0
1
6
№
S=4
7
5
0
9
16
T=1
9
4
8
0
0
5
0
2
3
0
4
5
№
S=3
7
2
0
1
17
T=4
8
4
16
0
0
2
6
0
7
0
3
2
№
S=4
9
5
0
4
18
T=1
1
1
8
0
9
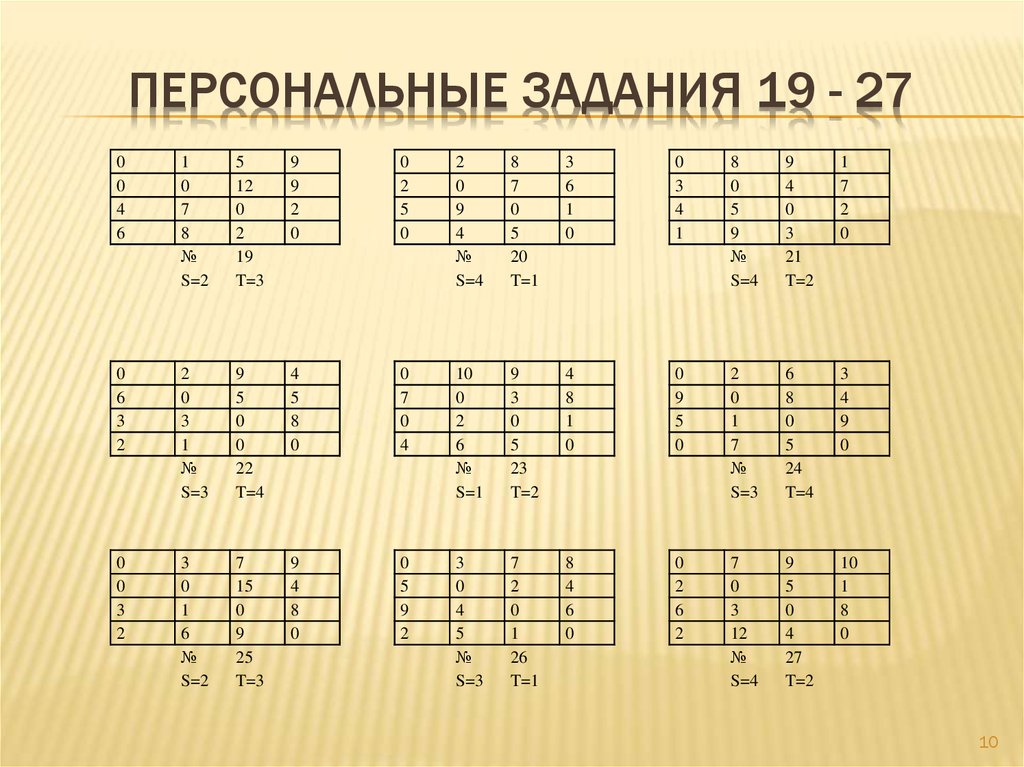
10. ПЕРСОНАЛЬНЫЕ ЗАДАНИЯ 19 - 27
00
4
6
1
0
7
8
№
S=2
5
12
0
2
19
T=3
9
9
2
0
0
2
5
0
2
0
9
4
№
S=4
8
7
0
5
20
T=1
3
6
1
0
0
3
4
1
8
0
5
9
№
S=4
9
4
0
3
21
T=2
1
7
2
0
0
6
3
2
2
0
3
1
№
S=3
9
5
0
0
22
T=4
4
5
8
0
0
7
0
4
10
0
2
6
№
S=1
9
3
0
5
23
T=2
4
8
1
0
0
9
5
0
2
0
1
7
№
S=3
6
8
0
5
24
T=4
3
4
9
0
0
0
3
2
3
0
1
6
№
S=2
7
15
0
9
25
T=3
9
4
8
0
0
5
9
2
3
0
4
5
№
S=3
7
2
0
1
26
T=1
8
4
6
0
0
2
6
2
7
0
3
12
№
S=4
9
5
0
4
27
T=2
10
1
8
0
10
11.
Часть 3.Минимальные разрезы в
сильносвязных
(бисвязных) орграфах
11
12. К ИСТОРИИ ВОЗНИКНОВЕНИЯ ПРОБЛЕМЫ
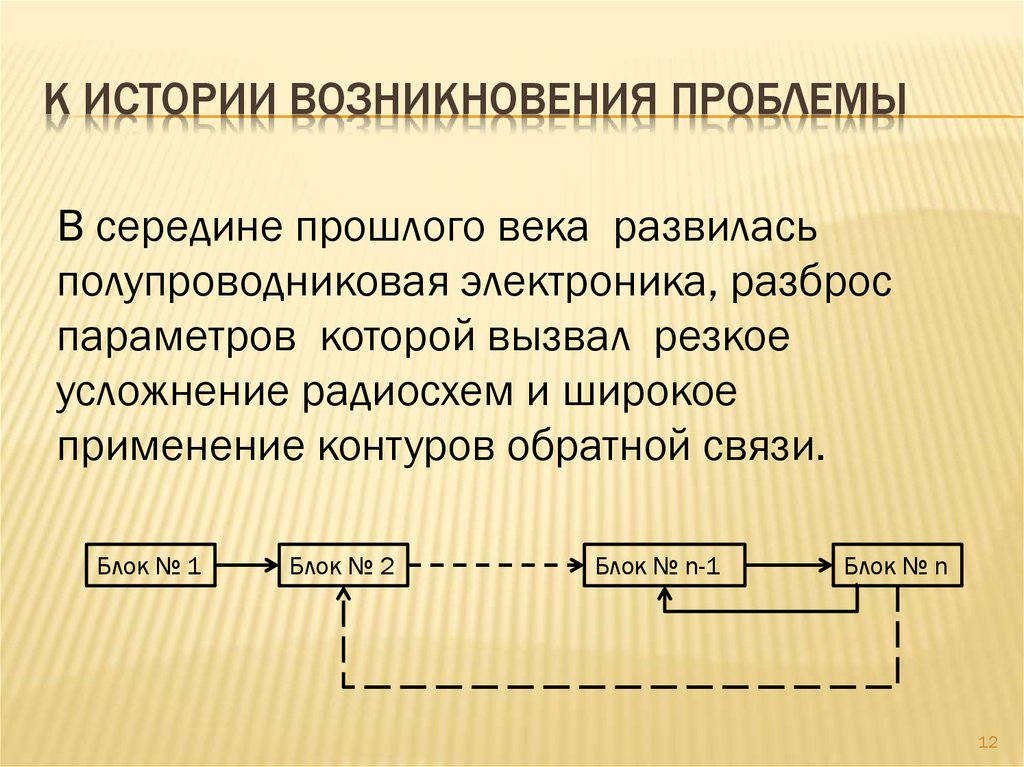
В середине прошлого века развиласьполупроводниковая электроника, разброс
параметров которой вызвал резкое
усложнение радиосхем и широкое
применение контуров обратной связи.
Блок № 1
Блок № 2
Блок № n-1
Блок № n
12
13. Экономический характер задачи
ЭКОНОМИЧЕСКИЙ ХАРАКТЕР ЗАДАЧИОтладка блоков электронных схем осуществляется в
порядке, позволяющем использовать уже
проверенные и исправные блоки при тестировании
еще непроверенных. При этом сигналы,
поступающие по контурам обратной связи от еще
непроверенных блоков, генерируются специальной
аппаратурой. Если известна стоимость
дополнительной аппаратуры, генерирующей разного
рода сигналы, то естественна постановка задачи, в
которой требуется такая организация тестирования и
отладки электронных схем, при которой затраты на
добавочную аппаратуру были бы минимальны.
13
14. Содержательная постановка задачи
СОДЕРЖАТЕЛЬНАЯ ПОСТАНОВКАЗАДАЧИ
На взвешенном бисвязном ориентированном
графе требуется выделить такое
подмножество дуг, для которого справедливо:
1. Удаление дуг выделенного подмножества
разрывает на графе все контуры.
2. Суммарный вес дуг выделенного
подмножества минимален.
14
15. Графовая интерпретация задачи о минимальном разрезе в бисвязном графе
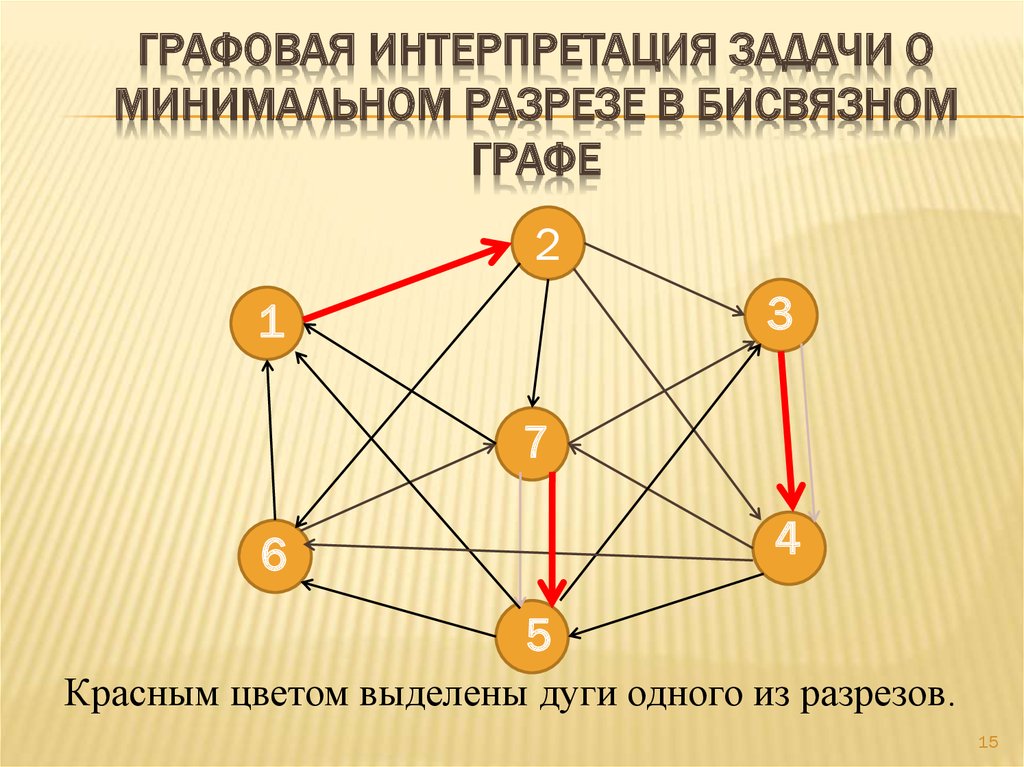
ГРАФОВАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧИ ОМИНИМАЛЬНОМ РАЗРЕЗЕ В БИСВЯЗНОМ
ГРАФЕ
2
3
1
7
4
6
5
Красным цветом выделены дуги одного из разрезов.
15
16. Обозначения и определения
ОБОЗНАЧЕНИЯ И ОПРЕДЕЛЕНИЯG ( X , U ) взвешенный орграф;
Х - множество вершин;
U - множество дуг;
A(G) - множество контуров графа;
a k k й контур множества A(G);
X(a k ) множество вершин k - го контура;
U(a k ) множество дуг k - го контура;
z(i, j) - булева переменная;
r(i, j) - вес дуги (i, j) U.
16
17. Формальная постановка задачи о минимальном разрезе в бисвязном взвешенном графе
ФОРМАЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ ОМИНИМАЛЬНОМ РАЗРЕЗЕ В БИСВЯЗНОМ
ВЗВЕШЕННОМ ГРАФЕ
r (i, j ) z (i, j ) min;
i j
a k A(G ) : z (i, j ) 1;
( i , j ) U ( a k )
(i, j ) U : z (i, j ) 1,0.
17
18. ПРИМЕР 1: постановка задачи
ПРИМЕР 1: ПОСТАНОВКА ЗАДАЧИ2
5
9
3
1
3
3
7 4
4
5 z (1,2) 9 z (2,3) 4 z (3,4) 3z (4,1) 3z (1,3) 7 z (4,2) min;
z (1,2) z (2,3) z (3,4) z (4,1) 1;
z (1,3) z (3,4) z (4,1) 1;
z (4,2) z (2,3) z (3,4) 1;
(i, j ) U : z (i, j ) 1,0.
18
19. Журнал “IEEE transactions on circuit theory”
ЖУРНАЛ “IEEE TRANSACTIONS ON CIRCUIT THEORY”60-е годы: статья Лемпела с Седербаума о
новой математике, развитой специально
для решения задачи о минимальном
разрезе в сильносвязном графе.
Начало семидесятых: статья Дивиетти и
Грассели о том, что «новая математика» мошенничество, она сводится к алгебре
логики.
Такахико Камае (Япония), Неметри
(Румыния): методы выделения всех путей
и контуров на ориентированных графах.
19
20. Пример применения Метода Лемпела и седербаума
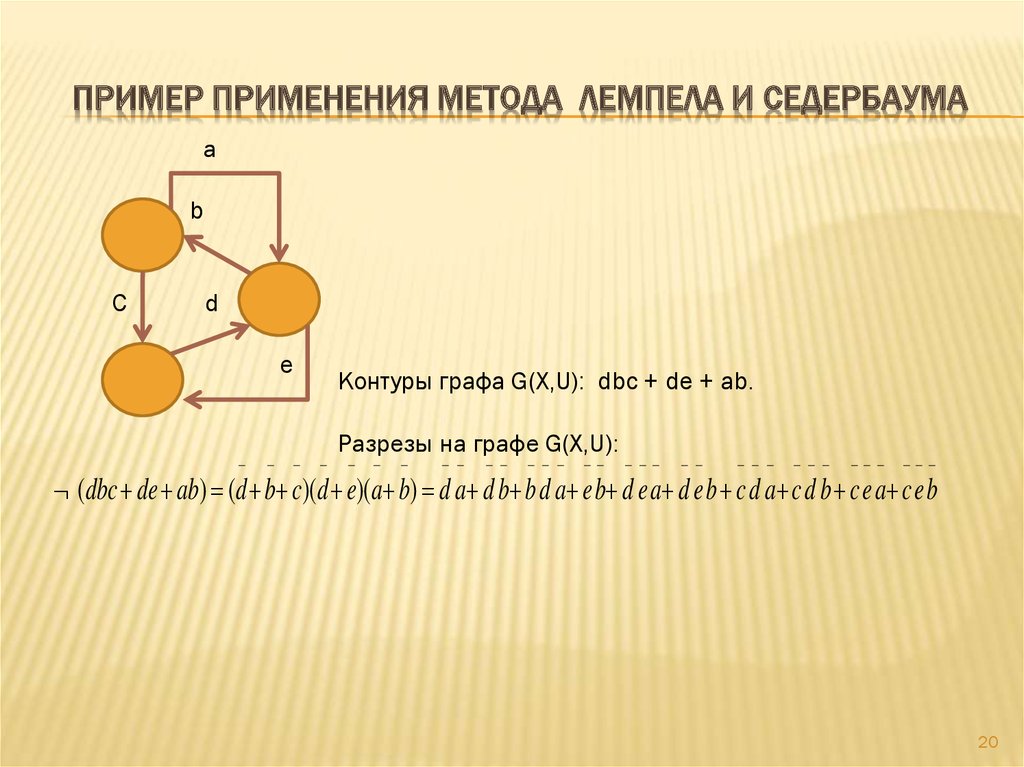
ПРИМЕР ПРИМЕНЕНИЯ МЕТОДА ЛЕМПЕЛА И СЕДЕРБАУМАa
b
C
d
e
Контуры графа G(X,U): dbc + de + ab.
Разрезы на графе G(X,U):
(dbc de ab) (d b c)(d e)(a b) d a d b b d a e b d e a d e b c d a c d b c e a c e b
20
21. Проверка графа на наличие контуров
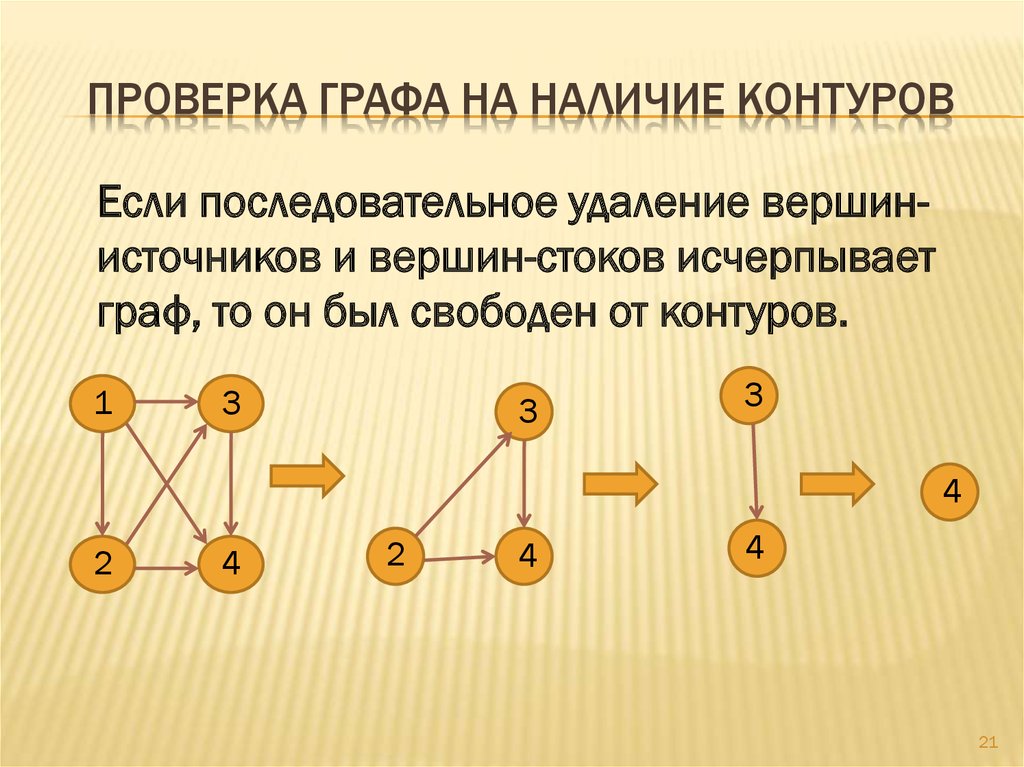
ПРОВЕРКА ГРАФА НА НАЛИЧИЕ КОНТУРОВЕсли последовательное удаление вершинисточников и вершин-стоков исчерпывает
граф, то он был свободен от контуров.
1
3
3
3
4
2
4
2
4
4
21
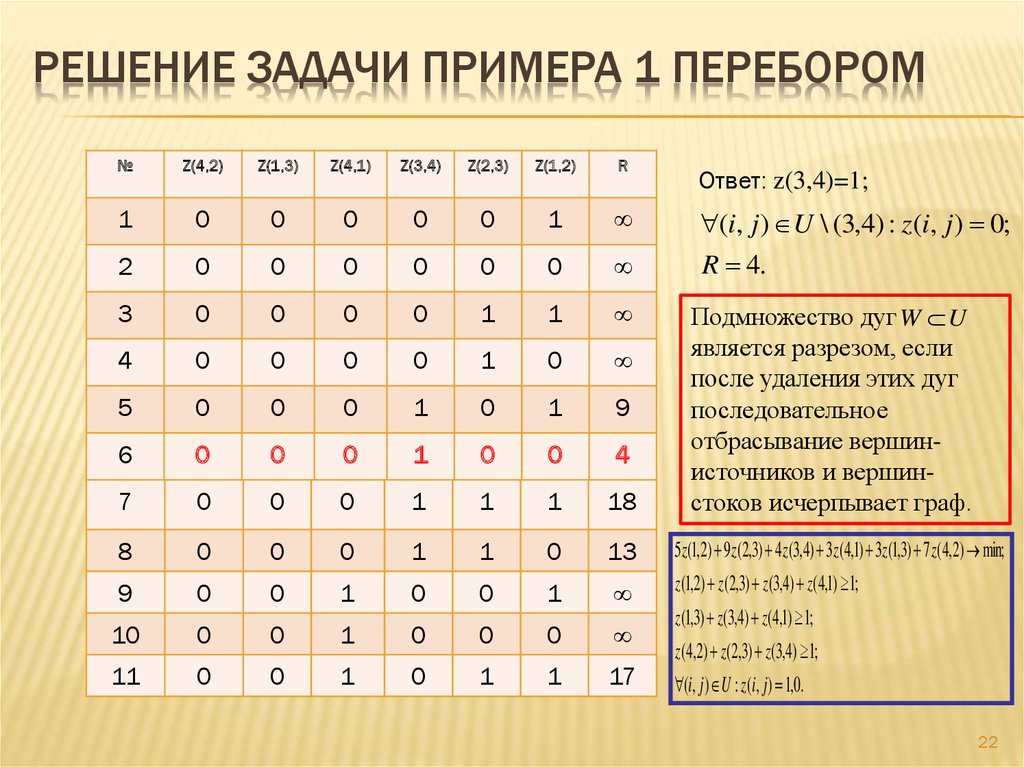
22. РЕШЕНИЕ ЗАДАЧИ ПРИМЕРА 1 ПЕРЕБОРОМ
№Z(4,2)
Z(1,3)
Z(4,1)
Z(3,4)
Z(2,3)
Z(1,2)
R
1
0
0
0
0
0
1
∞
(i, j ) U \ (3,4) : z (i, j ) 0;
2
0
0
0
0
0
0
∞
R 4.
3
0
0
0
0
1
1
∞
4
0
0
0
0
1
0
∞
5
0
0
0
1
0
1
9
6
0
0
0
1
0
0
4
7
0
0
0
1
1
1
18
8
0
0
0
1
1
0
13
5z(1,2) 9 z(2,3) 4 z(3,4) 3z(4,1) 3z(1,3) 7 z(4,2) min;
9
0
0
1
0
0
1
∞
z(1,2) z(2,3) z(3,4) z (4,1) 1;
10
0
0
1
0
0
0
∞
11
0
0
1
0
1
1
17
Ответ: z(3,4)=1;
Подмножество дуг W U
является разрезом, если
после удаления этих дуг
последовательное
отбрасывание вершинисточников и вершинстоков исчерпывает граф.
z(1,3) z(3,4) z(4,1) 1;
z(4,2) z(2,3) z(3,4) 1;
(i, j ) U : z(i, j ) 1,0.
22
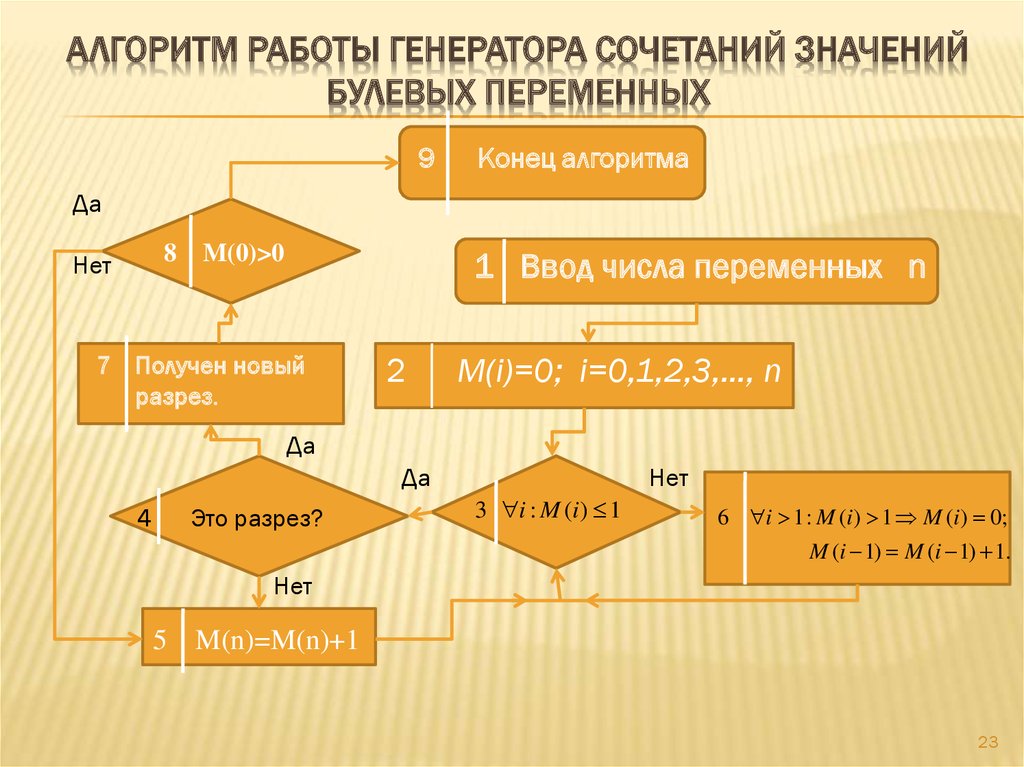
23. АЛГОРИТМ РАБОТЫ ГЕНЕРАТОРА сочетаний значений булевых переменных
АЛГОРИТМ РАБОТЫ ГЕНЕРАТОРА СОЧЕТАНИЙ ЗНАЧЕНИЙБУЛЕВЫХ ПЕРЕМЕННЫХ
9
Конец алгоритма
Да
8
Нет
M(0)>0
1 Ввод числа переменных n
7 Получен новый
разрез.
2
M(i)=0; i=0,1,2,3,…, n
Да
Да
4
Это разрез?
Нет
3 i : M (i ) 1
6 i 1 : M (i ) 1 M (i ) 0;
M (i 1) M (i 1) 1.
Нет
5 M(n)=M(n)+1
23
24. ДОСТОИНСТВА И НЕДОСТАТКИ АЛГОРИТМА ГЕНЕРАЦИИ всех сочетаний значений вектора булевых переменных
ДОСТОИНСТВА И НЕДОСТАТКИ АЛГОРИТМАГЕНЕРАЦИИ ВСЕХ СОЧЕТАНИЙ ЗНАЧЕНИЙ
ВЕКТОРА БУЛЕВЫХ ПЕРЕМЕННЫХ
Достоинства:
1. Генерация всех сочетаний значений булевых
переменных гарантирует глобальный оптимум.
2. Простота алгоритма.
3. Легкость программной реализации.
4. Низкие требования к объему памяти компьютера
5. Легкость распараллеливания алгоритма.
1.
1.
Недостатки:
В ходе работы алгоритма генерируется более 2(2 n 1)
сочетаний различных чисел:
алгоритм избыточен.
24
25. САМОСТОЯТЕЛЬНО:
1.2.
3.
4.
5.
Решить задачу о минимальном разрезе в
бисвязном взвешенном орграфе, пользуясь
графом персонального задания и приведенным
выше алгоритмом.
Составить блок-схему алгоритма поиска
минимального разреза на бисвязном графе,
включающую генератор перестановок.
Программно реализовать построенный
алгоритм.
Построить график зависимости времени счета T
от размерности задачи n.
Пользуясь методом наименьших квадратов
найти аналитические зависимости T(n).
25
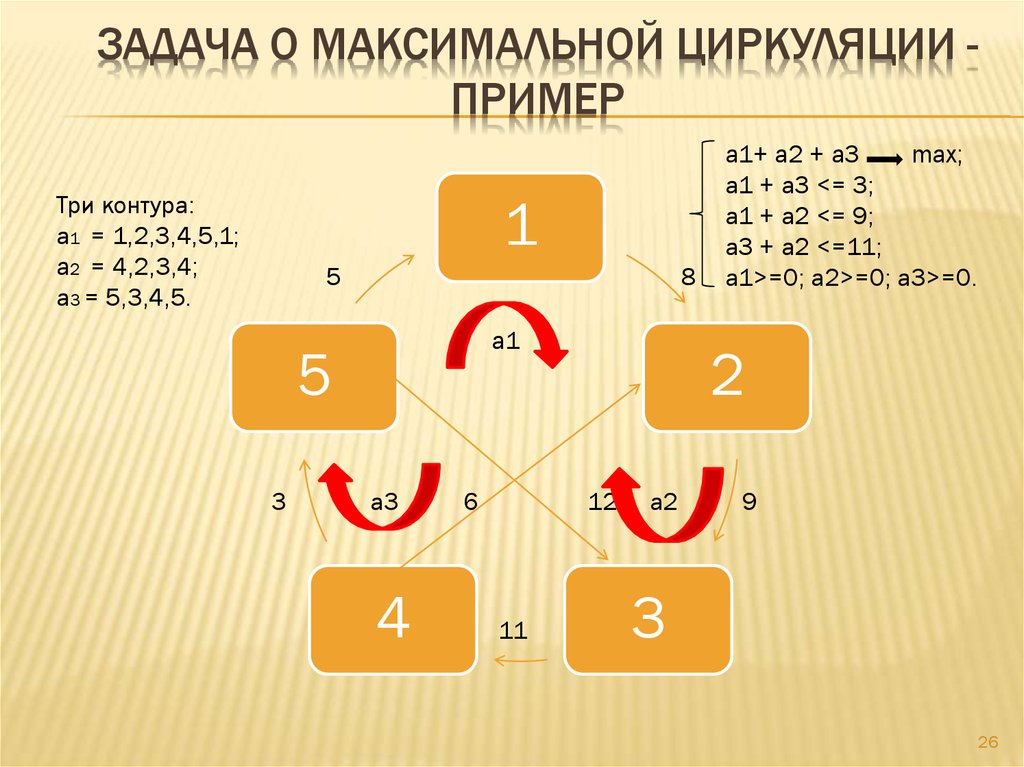
26. Задача о максимальной циркуляции - пример
ЗАДАЧА О МАКСИМАЛЬНОЙ ЦИРКУЛЯЦИИ ПРИМЕРТри контура:
a1 = 1,2,3,4,5,1;
a2 = 4,2,3,4;
a3 = 5,3,4,5.
1
5
8
а1
5
3
а3
4
6
2
12
11
а1+ а2 + а3
max;
a1 + a3 <= 3;
a1 + a2 <= 9;
a3 + a2 <=11;
a1>=0; a2>=0; a3>=0.
а2
9
3
26
27. Задача о максимальной циркуляции в бисвязном графе - обозначения
ЗАДАЧА О МАКСИМАЛЬНОЙ ЦИРКУЛЯЦИИ ВБИСВЯЗНОМ ГРАФЕ - ОБОЗНАЧЕНИЯ
S(i,j) – поток по дуге (i,j) на графе G(X,U);
r(i,j) – пропускная способность дуги (i,j);
A(G) – множество контуров графа G(X,U);
U(ak) – подмножество дуг k-го контура;
S(ak) – циркуляция в k-м контуре;
A(i,j) – подмножество контуров, в состав
которых входит дуга (i,j).
27
28. Формальная постановка задачи поиска максимальной циркуляции в бисвязном графе
ФОРМАЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ ПОИСКАМАКСИМАЛЬНОЙ ЦИРКУЛЯЦИИ В
БИСВЯЗНОМ ГРАФЕ
s (ak ) max;
k
(i, j ) U : s (ak ) r (i, j );
ak A ( i , j )
a A(G ) : min r (i, j ) s (a ) 0.
k
k
( i , j ) U ( ak )
28
29. Теорема 1 в.н. буркова
ТЕОРЕМА 1 В.Н. БУРКОВАВеличина
максимальной
циркуляции на взвешенном
бисвязном орграфе не
превышает величины
минимального разреза.
29
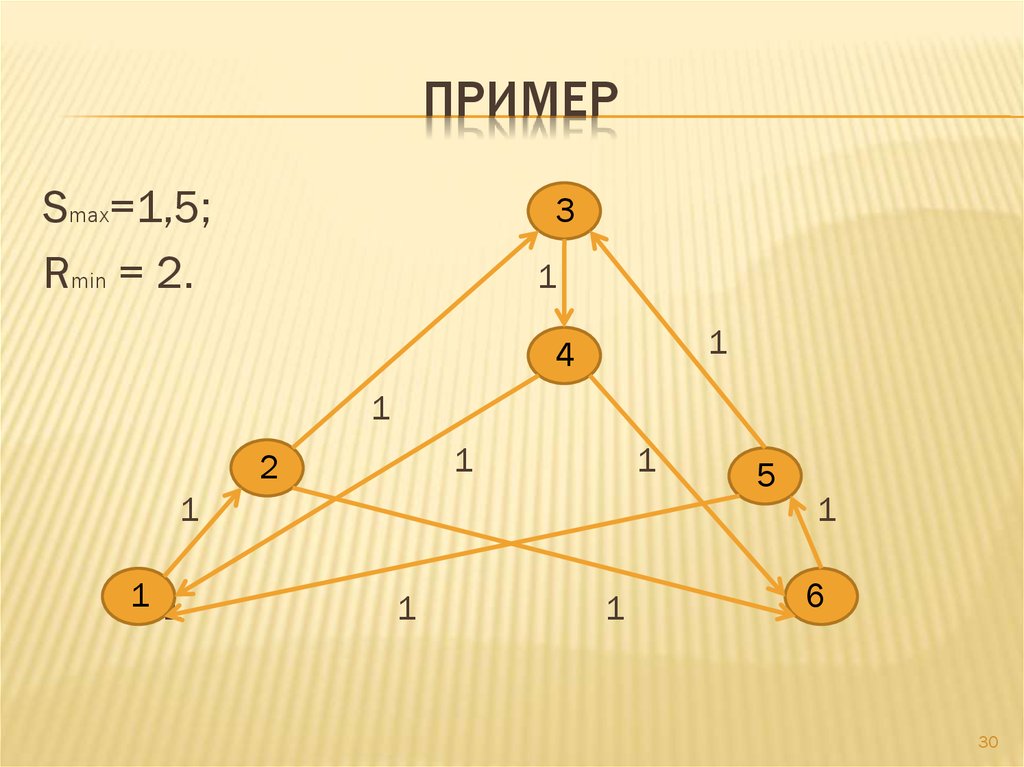
30. пример
ПРИМЕРSmax=1,5;
Rmin = 2.
3
1
1
4
1
1
2
1
1
11
1
1
5
1
61
30
31. Теорема 2 в.н. буркова
ТЕОРЕМА 2 В.Н. БУРКОВАНа
планарных ориентированных
взвешенных сильносвязных
графах величина максимальной
циркуляции всегда целочислена
и равна величине минимального
разреза.
31
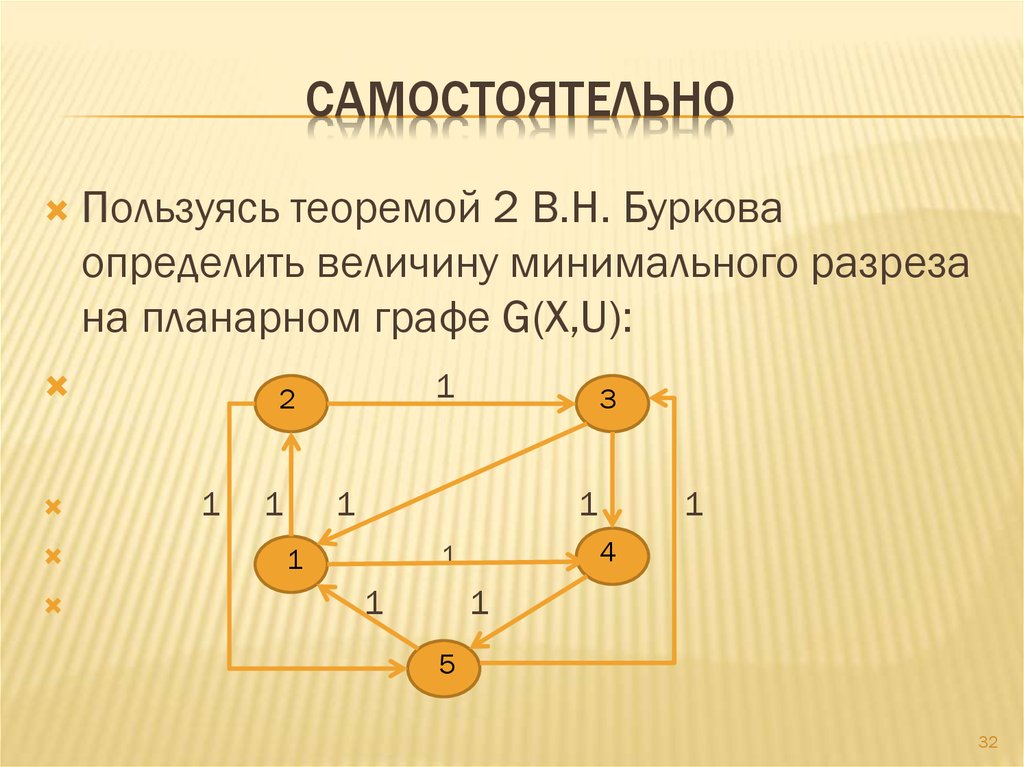
32. самостоятельно
САМОСТОЯТЕЛЬНОПользуясь теоремой 2 В.Н. Буркова
определить величину минимального разреза
на планарном графе G(X,U):
1
2
1
1
3
1
1
4
1
1
1
1
1
5
32
33. Теорема Буркова № 3
ТЕОРЕМА БУРКОВА № 3Любой
перестановке вершин
бисвязного орграфа π={i1, i2, i3, ….in}
отвечает разрез, состоящий из дуг,
идущих из вершин стоящих слева в
перестановке π, в вершины,
стоящие в ней справа.
33
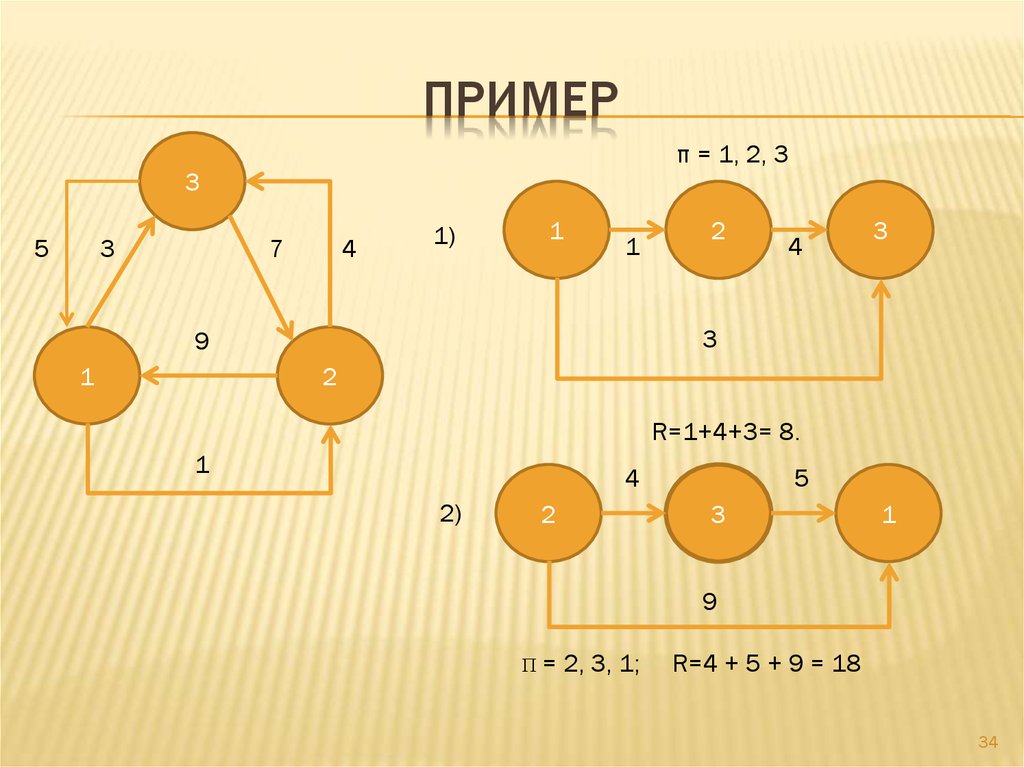
34. ПРИМЕР
π = 1, 2, 33
5
3
7
4
1)
1
1
4
3
3
9
1
2
2
R=1+4+3= 8.
1
4
2)
2
5
3
1
9
Π=
2, 3, 1;
R=4 + 5 + 9 = 18
34
35. Лемма
ЛЕММАЛюбому разрезу в
сильносвязном орграфе
G(X,U) отвечает «своя»
перестановка вершин π
множества Х.
35
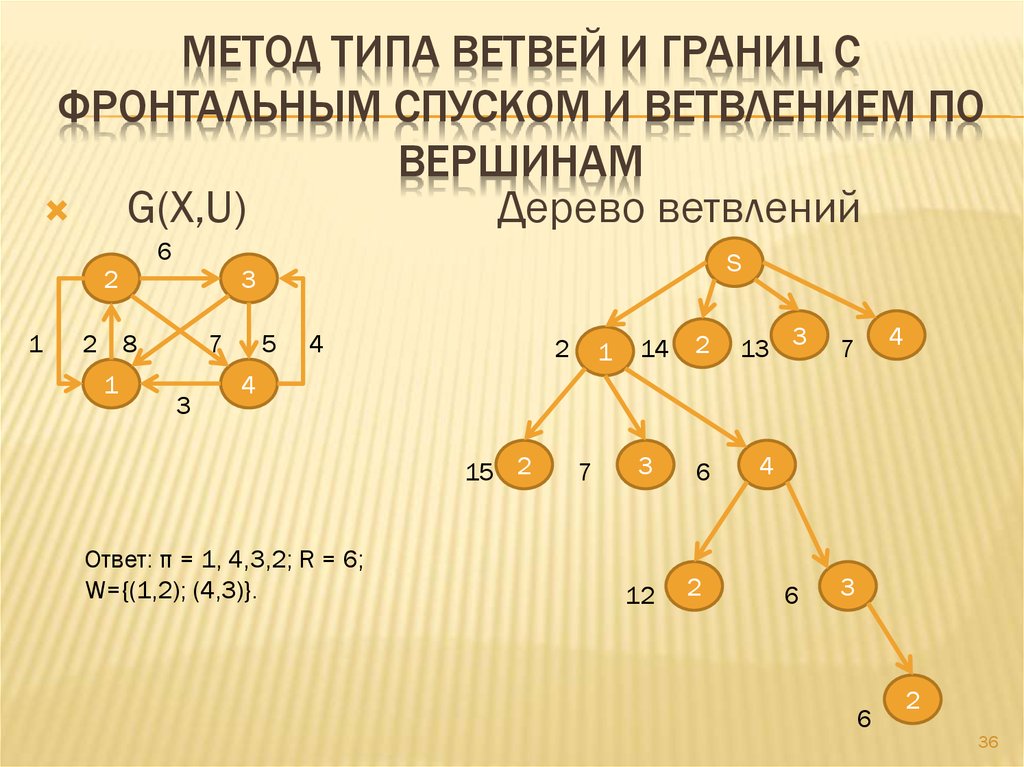
36. МЕТОД ТИПА ВЕТВЕЙ И ГРАНИЦ С ФРОНТАЛЬНЫМ СПУСКОМ И ВЕТВЛЕНИЕМ ПО ВЕРШИНАМ
G(X,U)Дерево ветвлений
2
1
6
2 8
1
S
3
7
3
5
4
2
1
14 2
13 3
4
7
4
15 2
Ответ: π = 1, 4,3,2; R = 6;
W={(1,2); (4,3)}.
7
3
12
6
2
4
6
3
6
2
36
37. САМОСТОЯТЕЛЬНО
Решить задачу о минимальном разрезе навзвешенном орграфе G(X,U), заданном
матрицей M описанным выше методом:
0
3
0
4
9
0
1
7
0
2
0
0
0
5
0
0
37
38. САМОСТОЯТЕЛЬНО
Сравнитьэффективность ветвления
по дугам с ветвлением по
вершинам при решении задачи о
минимальном разрезе методами
типа ветвей и границ.
Решить задачу о минимальном
разрезе в бисвязном взвешенном
орграфе, пользуясь графом
персонального задания и
приведенным выше алгоритмом.
38























 programming
programming








