Численные методы в астрофизике

1. Численные методы в астрофизике

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«КАЛМЫЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ Б.Б. ГОРОДОВИКОВА»
Численные методы
в астрофизике
Выполнила: Ольдеева Е.А.
Магистрант 2 года обучения
По направлению «Математика»
Магистерская программа
«Математический анализ»
Научный руководитель:
К.ф.-м. наук, доцент
Бисенгалиев Р.А.

2.

Целью работы является рассмотреть некоторые
задачи теоретической физики Солнца, которые
сводятся к численному исследованию
алгебраических уравнений и краевых задач на
собственные значения.
Актуальность работы связана с тем, что
механизм образования Солнечных магнитных
аркад и корональной петли не ясен до сих пор.

3.

Содержание работы
ВВЕДЕНИЕ
ГЛАВА ПЕРВАЯ. МЕТОД НЬЮТОНА, МЕТОД РУНГЕ-КУТТА, МЕТОД
СТРЕЛЬБ
1.1. Метод Ньютона
1.2. Метод Рунге-Кутта
1.3. Метод стрельб
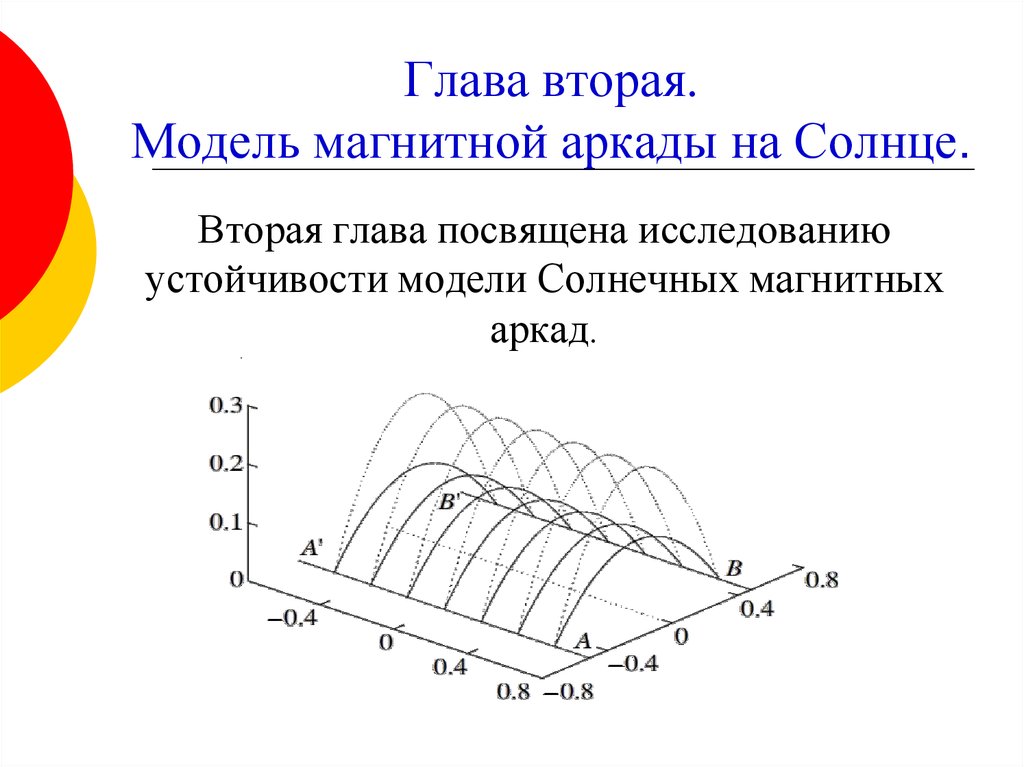
ГЛАВА ВТОРАЯ. МОДЕЛЬ МАГНИТНОЙ АРКАДЫ НА СОЛНЦЕ
2.1. Основные уравнения и равновесная модель
2.2. Постановка краевой задачи. Граничные условия
2.3. Алгоритм решения краевой задачи
2.4. Численный анализ закона дисперсии
ГЛАВА ТРЕТЬЯ. НЕУСТОИЧИВОСТЬ КОРОНАЛЬНЫХ ПЕТЕЛЬ
3.1. Модель корональной петли с продольным электрическим током
3.2. Линейные уравнения МГД в идеально проводящей среде
3.3. Обсуждение результатов.
ЗАКЛЮЧЕНИЕ
СПИСОК ЛИТЕРАТУРЫ

4. Глава первая. Метод Ньютона, метод Рунге-Кутта, метод стрельб

Использованные мною численные методы
Метод Ньютона
Метод Рунге-Кутта
Метод стрельб

5. Метод Ньютона

6. Метод Рунге-Кутта

yn 1 yn hn f ( xn , yn ), hn xn 1 xn
(1)
h
yn 1 yn k1 2k 2 2k3 k 4 ,
6
k1 f xn , yn , k 2 f x n h , y n h k1
(2)
2
2
h
h
k3 f xn , yn k 2 , k 4 f xn h, yn hk3
2
2

7. Метод стрельб.

d ˆ
A ˆ Bpˆ (1)
dx
dpˆ
C ˆ Dpˆ
(2)
dx
Здесь A,B,C и D – комплексные коэффициенты, зависящие от
стационарных (равновесных) распределение термодинамических
параметров модели, скорости и магнитного поля, от компонент
волнового вектора