Similar presentations:
Производные финансовые инструменты и их влияние на банковские риски
1.
ПРОИЗВОДНЫЕ ФИНАНСОВЫЕИНСТРУМЕНТЫ И ИХ ВЛИЯНИЕ НА
БАНКОВСКИЕ РИСКИ
ДМИТРИЙ ЮРЬЕВИЧ ГОЛЕМБИОВСКИЙ
Д.т.н., проф. каф. Исследования операций
МГУ,
заместитель
начальника
Департамента
рисков банка ЗЕНИТ, г. Москва,
FRM
d.golembiovsky@zenit.ru
1
2.
ВИДЫ ПРОИЗВОДНЫХФИНАНСОВЫХ ИНСТРУМЕНТОВ
Форварды
Фьючерсы
Опционы
Свопы
Свопционы
Кэпы
Флоры
Коллары
Фра
Структурные продукты
2
3.
РЫНКИ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ФОРВАРДЫ ПОСТАВОЧНЫЕ И РАСЧЕТНЫЕ
• Поставочный форвард – это контракт между двумя
сторонами о будущей поставке базового актива. В
качестве базовых активов могут выступать
облигации, валюта, акции, товары.
• Расчетный форвард предусматривает проведение
денежных расчетов, сумма которых зависит от
будущих
значений
некоторой
оговоренной
переменной величины. В качестве базового актива
могут выступать процентные ставки, цены на
основные и производные финансовые инструменты,
товары и услуги, индексы цен, физические и иные
расчетные величины, например, температура
воздуха,
результаты
выборов,
спортивных
состязаний и т.п.
3
4.
РЫНКИ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ПРИМЕР ФОРВАРДНОГО КОНТРАКТА
• Банки-контрагенты А и Б 30.04.09 заключили расчетный
форвардный контракт, в соответствии с которым банк Б
выступает как продавец, а банк А - как покупатель
форварда. Объем контракта - 1 млн. долларов США, дата
поставки - 30.04.10, форвардная цена - 31,75 руб.
• Если в рассмотренном примере цена доллара 30.04.10
превышает 31рубль 75 копеек, то банк А получает выигрыш
по форвардной сделке. Пусть, для примера, доллар стоит
на этот момент времени 32,05 руб. Прибыль по сделке
составит 1000000 × (32,05 − 31,75) = 300000 руб. Эту сумму банк Б
выплатит банку А 30.04.10.
• В случае поставочного форварда банк А покупая 30.04.10 у
банка Б 1 млн. долларов, имеет возможность продать
валюту на спотовом рынке по цене 32,05руб. Прибыль по
сделке
теоретически
также
составит
1000000 × (32,05 − 31,75) = 300000
руб.
Такую
же
сумму
4
составляют потери продавца контракта – банка Б.
5.
РЫНКИ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ГРАФИЧЕСКАЯ ИЛЛЮСТРАЦИЯ ФИНАНСОВОГО
РЕЗУЛЬТАТА ФОРВАРДА
Выигрыш покупателя:
Выигрыш
Выигрыш продавца:
Выигрыш
Цена поставки
Цена
базового
актива
Цена поставки
Цена
базового
актива
5
6.
РЫНКИ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ФЬЮЧЕРСНЫЕ КОНТРАКТЫ
• Поставочный
фьючерсный
контракт
–
это
соглашение между двумя сторонами о будущей
поставке базового актива, заключенное на бирже. При
заключении контракта известен момент поставки
базового актива, его количество и цена поставки.
Аналогично расчетному форварду определяется
понятие расчетного фьючерсного контракта.
Контракты на индексы акций и процентные ставки
всегда являются расчетными. Контракты на акции и
товарные контракты могут быть как поставочными, так
и расчетными.
• Значение цены поставки, на которую фьючерсный
контракт может быть заключен в текущий момент
времени, называется фьючерсной ценой
6
7.
РЫНКИ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
СРАВНЕНИЕ ФОРВАРДНЫХ И ФЬЮЧЕРСНЫХ КОНТРАКТОВ
Форвард
Все условия могут служить
предметом переговоров,
контракт составляется с
учетом потребностей каждой
стороны
Существует риск
неисполнения обязательств
Фьючерс
Стандартизированные
условия. Существует риск,
связанный с различием
между стандартным
контрактом и требуемым
Нет риска неуплаты
Вторичный рынок существует Контракт высоко ликвиден,
только по некоторым
может быть закрыт на бирже
контрактам с
в любой момент
фиксированными условиями
7
8.
РЫНКИ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
РЫНКИ ФЬЮЧЕРСНЫХ КОНТРАКТОВ
Chicago Mercantile Exchange www.cme.com
Chicago Board of Trade www.cbot.com
New York Mercantile Exchange www.nymex.com
London International Financial Futures and Options
Exchange (LIFFE), Marche a Terme International de
France (MATIF), Marche options negociables de
Paris (MONEP) www.euronext.com
London Metal Exchange www.lme.com
Eurex www.eurexchange.com
Tokyo Commodity Exchange www.tocom.or.jp
Московская биржа http://moex.com/
8
9.
РЫНКИ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ХАРАКТЕРИСТИКИ ФЬЮЧЕРСНОЙ ТОРГОВЛИ
Expiration –месяц истечения контракта
Open – первая цена, предложенная покупателем или продавцом, или цена
первой сделки
High – самая высокая цена на продажу или самая высокая цена, по которой
была заключена сделка в течение торгов
Low - самая низкая цена на покупку или самая низкая цена, по которой
была заключена сделка в течение торгов
Settlement price – расчетная цена, зафиксированная при закрытии
торговой сессии, используемая для расчетов вариационной маржи
Net change – величина, на которую изменилась расчетная цена с момента
последних торгов
Variation margin – величина прибыли или убытка по фьючерсной позиции за
истекший торговый день
Initial margin – сумма, которая должна быть депонирована на счете клиента
для открытия позиции по фьючерсу
Maintenance margin, сумма, достаточная для удержания фьючерсной
позиции на следующий торговый день после расчетов по вариационной
марже
Open interest – общее число открытых контрактов
9
Volume – количество контрактов, заключенных в течение торговой сессии
10.
РЫНКИ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ФЬЮЧЕРСЫ НА ФОНДОВЫЕ ИНДЕКСЫ
• Фондовый индекс – взвешенная сумма цен некоторого определенного
набора акций
• Фьючерс на фондовый индекс всегда является расчетным
• CME S&P 500 Futures
• Trade Unit $250 times the Standard & Poor's 500 Stock Price Index
• Contract Listing Eight months in the March quarterly cycle. Mar, Jun, Sep,
Dec.
• Ticker=SP
• Trading Venue: Floor
• Hours 8:30 a.m.-3:15 p.m.
• Minimum Fluctuation 0.10=$25.00
• Trading Venue: CME® Globex®
• Hours Mon/Thurs 5:00 p.m.-8:15 a.m. & 3:30 p.m.-4:30 p.m.; Shutdown
period from 4:30 p.m. to 5:00 p.m. nightly; Sun & Hol 5:00 p.m.-8:15 a.m.
10
• Minimum Fluctuation Regular0.10=$25.00
11.
РЫНКИ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
СПЕЦИФИКАЦИЯ ФЬЮЧЕРСА НА ИНДЕКС РТС
Базовый актив: индекс РТС
Вид контракта: расчетный
Валюта расчетов: рубли
Стоимость пункта: $2 по курсу рубль/доллар
Котировки контрактов представляются в виде «индекс РТС*100»
Минимальный шаг изменения цены: 10 единиц
Месяцами исполнения являются последние месяцы каждого квартала
Одновременно осуществляется обращение фьючерсов на три
ближайших срока исполнения
• Последним днем обращения контрактов является последний рабочий
день, предшествующий 15 числу месяца исполнения
• Расчеты по вариационной марже по фьючерсам в ФОРТС проводятся
дважды в день (в 14.00 и в 18.45 МСК путем перечисления денежных
средств со счета проигравшей стороны на счет выигравшего игрока
• Гарантийное обеспечение (начальная маржа) контракта с погашением
в марте 2013г. : 11 010,45 руб. на 09.01.13.
11
12.
РЫНКИ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ОЧЕРЕДИ НА ПОКУПКУ И ПРОДАЖУ ФЬЮЧЕРСА RTS03.13 В ТОРГОВОЙ СИСТЕМЕ «ФОРТС» 18.01.13
Объем покупки
90
88
78
36
40
Котировка
160290
160300
160310
160320
160330
160340
160350
160360
160370
160380
Объем продажи
2
39
76
48
175
12
13.
РЫНКИ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ПРИМЕР РАСЧЕТОВ ПО ФЬЮЧЕРСНЫМ КОНТРАКТАМ
НА ИНДЕКС АКЦИЙ
Открытие
позиции
Дни
1
2
3
Фьючерсная цена
7595
7745
7521
7335
Позиция покупателя:
Остаток счета перед сделкой
Остаток счета
Начальная маржа
Вариационная маржа
Суммарный выигрыш (проигрыш)
Баланс счета
Маржин колл
13000
12995
11600
0
0
1395
0
14495
11600
1500
1500
2895
0
12255
11600
-2240
-740
655
0
10395
11600
-1860
-2600
-1205
1205
Позиция продавца:
Остаток счета перед сделкой
Остаток счета
Начальная маржа
Вариационная маржа
Суммарный выигрыш (проигрыш)
Баланс счета
Маржин колл
13000
12995
11600
0
0
1395
0
11495
11600
-1500
-1500
-105
105
14735
11600
2240
740
3135
0
16595
11600
1860
2600
4995
0
13
14.
РЫНКИ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ПРОЦЕНТНЫЕ ФЬЮЧЕРСЫ
• Поставочные фьючерсы на облигации
• Расчетные фьючерсы на процентные ставки
• Поставочные фьючерсы на 30-летние
казначейские облигации США
• Биржа:
CBOT
• Размер контракта: $100000 по номиналу
• Месяцы исполнения: март, июнь, сентябрь,
декабрь
• Характеристики поставки: Последний день
торгов – за 7 рабочих дней до окончания месяца
поставки. Поставка может быть
осуществлена в любой рабочий день в течение
месяца поставки
• Минимальное изменение цены: 1/32 пункта или
$31,25 за контракт
14
15.
РЫНКИ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ЕВРОДОЛЛАРОВЫЕ ФЬЮЧЕРСЫ
Underlying
Instrument
Price Quote
Tick Size
Contract
Months
Last Trading
Day
Trading Hours
(All times listed
are Central
Time)
Ticker Symbol
Eurodollar Time Deposit having a principal value of USD $1,000,000 with a three-month maturity.
Quoted in IMM Three-Month LIBOR index points or 100 minus the rate on an annual basis over a 360 day year (e.g., a rate of 2.5% shall
be quoted as 97.50). 1 basis point = .01 = $25.
(minimum fluctuation) One-quarter of one basis point (0.0025 = $6.25 per contract) in the nearest expiring contract month;
Mar, Jun, Sep, Dec, extending out 10 years (total of 40 contracts) plus the four nearest serial expirations (months that are not in the
March quarterly cycle). The new contract month terminating 10 years in the future is listed on the Tuesday following expiration of the
front quarterly contract month.
The second London bank business day prior to the third Wednesday of the contract expiry month. Trading in the expiring contract closes
at 11:00 a.m. London Time on the last trading day.
OPEN OUTCRY
MON-FRI: 7:20 a.m. - 2:00 p.m.
CME GLOBEX
SUN - FRI: 5:00 p.m. - 4:00 p.m. CT
OPEN OUTCRY
CME GLOBEX
ED
GE
Например, если котировка рассматриваемого фьючерса возрастает с 94,79 до 94,90, то держатель длинной позиции выигрывает
11× 25 = $275 .
Отличия евродолларового фьючерса от FRA:
Ежедневные расчеты по вариационной марже; фьючерс рассчитывается в дату T1 , FRA – в дату T2 ( T2 − T1 = 3 месяца ).
15
16.
РЫНКИ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ВАЛЮТНЫЕ ФЬЮЧЕРСЫ
Поставочный валютный фьючерс – контракт на покупку одной валюты за другую
Расчетный фьючерс – контракт на курс между двумя валютами
US DOLLAR / EURO FUTURES:
Codes and classification
Unit
Unit of trading
Expiry months
Quotation
Minimum price movement
Last trading day
Settlement
Trading hours
Clearing
Mnemo
FDE
€
USD 20,000
1) Initial lifetime: 1, 2 and 3 months
Cycle: Every month
2) Initial lifetime: 6, 9 and 12 months
Cycle: March, June, September and December
3) Initial lifetime: 3 years
Cycle: September
In euros per USD 100
(EUR 0.01 represents EUR 200 per contract)
EUR 0.01
13.00 Amsterdam time on the third Friday of the delivery month,
provided this is a business day. If it is not, the previous business
day will be the last day of trading.
Cash settlement, based on the value of the euro / US dollar rate
set by EuroFX at 13.00 Amsterdam time. For FDE, the inverse
value of the EuroFX euro/Us dollar rate is used and rounded off
to four decimal places.
9.00 – 17.30 Amsterdam time
LCH.Clearnet S.A.
16
17.
РЫНКИ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ТОВАРНЫЕ ФЬЮЧЕРСЫ
• Сельскохозяйственные – www.cbot.com,
www.euronext.com (кофе, какао, пшеница, кукуруза,
сахар, соевые бобы, соевое масло, живой скот,
постная свинина)
• Энергетические – www.nymex.com (сырая нефть,
мазут, бензин, газ)
• Фьючерсы на драгоценные металлы –
www.nymex.com (золото, серебро, платина)
• Фьючерсы на промышленные металлы –
www.lme.com, www.nymex.com (алюминий, медь,
цинк, свинец, олово, никель, сталь)
17
18.
ХЕДЖИРОВАНИЕ ФЬЮЧЕРСНЫМИКОНТРАКТАМИ
СОВЕРШЕННОЕ ХЕДЖИРОВАНИЕ
Некоторое предприятие планирует осуществить закупку оборудования
за рубежом спустя полгода от текущего момента времени. Стоимость
оборудования $200тыс. В настоящий момент курс доллара составляет
30,5руб. Если за шесть месяцев курс значительно вырастет, то покупка
оборудования может не состояться из-за недостаточности средств.
Предположим, что текущая котировка фьючерсного контракта на бирже
сроком шесть месяцев составляет 30,85 руб. Предприятие
осуществляет покупку фьючерсов на сумму 200 тыс. долларов США.
Если в момент исполнения контрактов стоимость доллара спот
превысит 30,85 , то предприятие окажется в выигрыше, осуществляя
покупку валюты по курсу ниже рыночного. В противном случае доллар
будет приобретаться по курсу выше рыночного, и предприятие несет
относительные убытки. Преимущество заключения хеджирующей
сделки состоит в том, что покупка необходимого оборудования будет
осуществлена при любой динамике валютного курса в течение
последующих шести месяцев.
18
19.
ХЕДЖИРОВАНИЕ ФЬЮЧЕРСНЫМИКОНТРАКТАМИ
КОЭФФИЦИЕНТ ХЕДЖИРОВАНИЯ
МИНИМАЛЬНОЙ ДИСПЕРСИИ
σ 2 = D[∆P ] = D[∆S + ∆F ]
σ = (N S ) σ S2 + 2 N S N F kσ Sσ F ρ SF + N F2 k 2σ F2
2
2
dσ 2
= 2 N S N F σ Sσ F ρ SF + 2 N F2 kσ F2 = 0
dk
NS σ S
k = − ρ SF
⋅
NF σ F
(1)
(2)
(3)
(4)
19
20.
ХЕДЖИРОВАНИЕФЬЮЧЕРСНЫМИ
КОНТРАКТАМИ
ПРИМЕР ХЕДЖИРОВАНИЯ
Требуется
осуществить
хеджирование стоимости пакета
из 100000 акций ОАО «НЛМК» на
один день вперед. В качестве
инструмента
хеджирования
используются
фьючерсные
контракты на индекс РТС с
истечением в марте 2013 года.
Стоимость пункта индекса для
фьючерсов составляет $0,02.
Статистика котировок фьючерса и
акций ОАО «НЛМК» приведена в
табл.1. Необходимо определить
оптимальное
количество
фьючерсных контрактов.
НЛМК, акции, $
Фьючерс RTS-3.13
22.01.2013
2,2133
159040
23.01.2013
2,2065
160480
24.01.2013
2,1834
160410
25.01.2013
2,196
161890
28.01.2013
2,1961
163630
29.01.2013
2,1471
162400
30.01.2013
2,1204
161740
31.01.2013
2,1132
161960
01.02.2013
2,1307
162670
04.02.2013
2,075
161150
05.02.2013
2,1103
161160
06.02.2013
2,0818
160020
07.02.2013
2,055
159510
08.02.2013
2,0526
159000
11.02.2013
2,0351
157970
12.02.2013
2,0315
157840
13.02.2013
2,0853
161250
14.02.2013
2,0356
158310
15.02.2013
2,0378
157380
18.02.2013
2,0272
157850
19.02.2013
2,046
158890
20.02.2013
2,0123
157760
21.02.2013
1,9508
154830
Дата
Таблица 1
20
21.
ХЕДЖИРОВАНИЕФЬЮЧЕРСНЫМИ
КОНТРАКТАМИ
ПРИМЕР ХЕДЖИРОВАНИЯ
(ПРОДОЛЖЕНИЕ)
Соответствующие значения приращений цены
акций и фьючерсной цены приводятся в табл. 2.
Для расчета статистических оценок
воспользуемся возможностями электронной
таблицы Excel. Коэффициент корреляции
приращений рассчитывается при помощи
соответствующей команды надстройки «Анализ
данных». Полученное значение составляет
0,832. Расчет стандартных отклонений
временных рядов, содержащихся в табл. 2,
осуществляется функцией «СТАНДОТКЛОН».
Для приращений фьючерса соответствующая
оценка составляет 1488,06; для приращений
стоимости акции: 0,0293. Стандартное
отклонение стоимости портфеля, состоящего из
акций и фьючерсов, будет минимальным, если
будет заключено 82 коротких фьючерсных
контракта:
100000 0,0293
k = −0,832
⋅
= −81 ,91
0,02 1488 ,06
Расчет по формуле (2) дает стандартное отклонение
портфеля акций и фьючерсов: $1625, 83.
(Стандартное отклонение портфеля акций: $2930,60).
Дата
НЛМК, акции, $
Фьючерс RTS-3.13
23.01.2013
-0,0068
1440
24.01.2013
-0,0231
-70
25.01.2013
0,0126
1480
28.01.2013
1E-04
1740
29.01.2013
-0,049
-1230
30.01.2013
-0,0267
-660
31.01.2013
-0,0072
220
01.02.2013
0,0175
710
04.02.2013
-0,0557
-1520
05.02.2013
0,0353
10
06.02.2013
-0,0285
-1140
07.02.2013
-0,0268
-510
08.02.2013
-0,0024
-510
11.02.2013
-0,0175
-1030
12.02.2013
-0,0036
-130
13.02.2013
0,0538
3410
14.02.2013
-0,0497
-2940
15.02.2013
0,0022
-930
18.02.2013
-0,0106
470
19.02.2013
0,0188
1040
20.02.2013
-0,0337
-1130
21.02.2013
-0,0615
-2930
Таблица 2
21
22.
ХЕДЖИРОВАНИЕ ФЬЮЧЕРСНЫМИКОНТРАКТАМИ
ХЕДЖИРОВАНИЕ ПРОЦЕНТНОГО РИСКА
Дюрация финансового инструмента (актива или пассива) определяется по следующей
формуле:
t
n
CFt (1 + y )
D = ∑t n
t
t =1
∑ CFt (1 + y )
(5)
t =1
где CFt - платеж по инструменту в момент времени t , y - доходность данного инструмента к
погашению. Сумма
n
P = ∑ CFt (1 + y )
t
t =1
есть не что иное, как текущая стоимость финансового инструмента.
Дюрация показывает, насколько текущая стоимость финансового инструмента чувствительна к
изменению процентной ставки. Действительно,
n
d ∑ CFt (1 + y )
где
D* =
Отсюда
t
n
, P
dP
1 n
t
t +1
= t =1
= −∑ tCFt (1 + y ) = −
tCF
(
1
+
y
)
=
−
D = − PD *
∑ t
dy
dy
1 + y t =1
1+ y
t =1
D - модифицированная дюрация.
(6)
1+ y
∆P ≈ − PD * ∆y
(7)
22
23.
ХЕДЖИРОВАНИЕ ФЬЮЧЕРСНЫМИКОНТРАКТАМИ
ХЕДЖИРОВАНИЕ ПРОЦЕНТНОГО РИСКА
FC
- фьючерсная цена контракта в денежном выражении
DF
- модифицированная дюрация базового актива
фьючерсного контракта в момент его истечения
P
- текущая стоимость портфеля
DP - модифицированная дюрация портфеля на момент
истечения фьючерса
∆P = − PDP ∆y
(8)
∆FC = − FC DF ∆y
(9)
N* =
PDP
FC DF
(10)
23
24.
ЦЕНООБРАЗОВАНИЕ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ФОРВАРДНАЯ ЦЕНА НА АКЦИИ, ПО КОТОРЫМ НЕ
ВЫПЛАЧИВАЮТСЯ ДИВИДЕНДЫ
Определение. Арбитраж – это финансовая операция, не требующая вложения средств и
приносящая гарантированную положительную прибыль.
Определение.
Цена финансового инструмента, которая
исключает осуществление
арбитража с этим инструментом, называется справедливой ценой.
Пусть цена акции составляет 8,8 руб., срок до исполнения контракта 6 месяцев. Безрисковая
простая процентная ставка на срок полгода в данный момент времени составляет 15% годовых. Тогда
справедливая цена поставки форвардного контракта рассчитывается как
8,8 × (1 + 15 2 100) = 9,46руб.
Действительно, если на рынке можно заключить форвард с ценой поставки меньшей, чем 9,46руб., то
инвестор, у которого есть акция, имеет возможность совершить арбитражную операцию и получить
безрисковую прибыль. Для этого инвестор покупает форвардный контракт, продает акцию на рынке, а
полученные средства вкладывает в банк под безрисковый процент на срок 6 месяцев. Пусть,
например, инвестору удается купить форвард с ценой поставки 9,31руб. При исполнении форварда
инвестор покупает акцию по цене 9,31руб. В это же время банк возвращает инвестору
8,8 × (1 + 15 2 100) = 9,46руб.
Чистая прибыль инвестора составляет 9,46 – 9,31 = 0,15руб.
В том случае, когда предлагаемая цена поставки выше справедливой цены, возможна обратная
операция: инвестор продает форвардный контракт, занимает на рынке деньги под безрисковый
процент и покупает акцию. В рассматриваемом примере если форвард может быть заключен с ценой
поставки 9,60 руб.,
то инвестору целесообразно занять короткую позицию. Занимая 8,8 руб.,
инвестор покупает акцию. В момент исполнения форварда инвестор продает акцию контрагенту по
цене поставки и возвращает кредит. В рассматриваемом примере арбитражная прибыль инвестора
24
составит 9,60 – 9,46 = 0,14 руб. Здесь 9,46 – сумма, которую инвестор возвращает кредитору.
25.
ЦЕНООБРАЗОВАНИЕ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ТЕОРЕТИЧЕСКАЯ ФОРВАРДНАЯ ЦЕНА
Утверждение. В общем случае справедливая форвардная
цена может быть рассчитана по формуле
F = S (1 + it ) ,
(11)
где S - цена спот акции, i - простая процентная
безрисковая ставка на срок до исполнения форвардного
контракта в процентах годовых, t - время до исполнения
форварда в годах. С использованием ставки непрерывного
начисления формула (11) может быть переписана в виде:
F = Se rt ,
(12)
где r - непрерывная ставка процента для инвестиций на
rt
период времени t , 1 + it = e . Для рассматриваемого
примера i = 0,15 ,
r=
ln (1 + 0,15 × 0,5)
= 0,145
0,5
25
26.
ЦЕНООБРАЗОВАНИЕ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ПРИМЕР РАСЧЕТА ЦЕНЫ ФОРВАРДА
Цена исполнения форвардного контракта на
бездивидендную акцию, до исполнения
которого остается 4 месяца, составляет
$3,14. Текущая цена спот - $3 за акцию.
Непрерывная ставка без риска – 2% годовых.
Определить цену форвардного контракта.
Решение
f = (Se rt -F0 )e − rt = S − F0 e − rt = 3 − 3,14e −0 , 02×4 12 = −0,16 ,
(13)
т.е. за закрытие форварда его покупателю
придется уплатить 16 центов.
26
27.
ЦЕНООБРАЗОВАНИЕ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ФОРВАРДНАЯ ЦЕНА НА АКТИВЫ, ПРИНОСЯЩИЕ ДОХОД
Определение. Позиция, которая образуется путем покупки актива, называется длинной. Позиция,
которая образуется путем продажи актива, которым инвестор не обладает, называется короткой. Если
актив приносит дополнительный доход (например, купонные платежи по облигации или дивиденды по акции),
то инвестор, открывший короткую позицию, должен будет выплачивать покупателю соответствующие
суммы.
Утверждение. Если известно, что за время действия форвардного контракта по базовому активу будут
произведены выплаты дополнительного дохода dτ в моменты времени τ ∈ Τ , причем ∑ dτ e − rτ τ < S , то
τ ∈Τ
справедливая форвардная цена определяется как
F = Se t − e t
rt
rt
∑ dτ e −rττ
τ ∈Τ
,
(14)
где rτ - безрисковая ставка непрерывного начисления процентов для инвестирования на период времени τ .
Доказательство. Предположим вначале, что форвард может быть заключен по цене F0 < Se t − e t
rt
rt
dτ e − rτ τ . Тогда
∑
τ ∈Τ
арбитраж осуществляется путем покупки форварда и короткой продажи базового актива. Суммы dτ e −rττ
размещаются на безрисковых депозитах на сроки τ ∈ Τ под соответствующие процентные ставки. Остаток средств
S − ∑ dτ e − rττ размещается на безрисковом депозите под ставку rt на период t .
τ ∈Τ
В моменты времени τ ∈ Τ арбитраж осуществляет выплаты дополнительного дохода, обусловленные
короткой позицией по базовому активу, получая необходимые средства dτ e −rττ ⋅ e rτ τ = dτ , τ ∈ Τ с ранее размещенных
депозитов. При исполнении форварда осуществляется покупка базового актива по цене F0 . В этот же момент
27
28.
ЦЕНООБРАЗОВАНИЕ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ФОРВАРДНАЯ ЦЕНА НА АКТИВЫ, ПРИНОСЯЩИЕ
ДОХОД (ПРОДОЛЖЕНИЕ)
времени Арбитражер получает с депозита сумму S − ∑ dτ e −rττ
τ ∈Τ
S − ∑ dτ e −rττ
τ ∈Τ
rtt
e . Согласно предположению,
rt t
e = Se rtt − e rt t ∑ dτ e −rττ > F0 . Таким образом, арбитраж существует.
τ ∈Τ
Предположим теперь, что F0 > Se t − e t
rt
rt
∑ dτ e− rττ . Тогда арбитражер продает форвард, занимает суммы
τ ∈Τ
на сроки τ ∈ Τ под соответствующие безрисковые ставки процента, а сумму S −
∑ dτ e −rττ
τ ∈Τ
dτ e−rττ , τ ∈ Τ
на срок t под ставку rt . В
моменты времени τ ∈ Τ арбитражер получает платежи по базовому активу и погашает кредиты. При исполнении
форварда арбитражер продает акцию за F0 и возвращает кредит в размере S − ∑ dτ e − rτ τ
τ ∈Τ
rt t
e . Поскольку
F0 > S − ∑ dτ e −rττ e rtt = Se rt t − e rtt ∑ dτ e −rτ τ , то арбитражер получает безрисковую положительную прибыль.
τ ∈Τ
τ ∈Τ
Следовательно, справедливая форвардная цена определяется соотношением (14). Утверждение доказано.
С использованием номинальных процентных ставок формула (14) записывается в виде:
dτ
.
F = S (1 + it t ) − (1 + it t ) ∑
τ ∈Τ (1 + iτ τ )
(15)
28
29.
ЦЕНООБРАЗОВАНИЕ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ПРИМЕР АРБИТРАЖА
Цена акции спот составляет 14руб. Заключение форварда на акцию сроком на 135
дней может быть осуществлено по цене 14,24руб. Номинальная ставка без
риска для 135 дней составляет 5% годовых. по истечении 90 дней по акции
будет выплачен дивиденд, размер которого известен и составляет 4руб.
Требуется построить схему безрискового арбитража.
Решение. В соответствии с формулой (15), справедливая цена форварда
составляет
dτ
4
F = S (1 + it t ) − (1 + it t )
= 14(1 + 0,05 × 135 365) − (1 + 0,05 × 135 365)
(1 + iττ )
(1 + 0,05 × 90 365)
= 14,26 − 4,03 = 10,23руб.
Арбитражная схема образуется путем привлечения 14руб. под ставку 0,05%
годовых, покупки акции и продажи форвардного контракта. Спустя 90 дней
арбитражер получит дивиденд 4руб. и инвестирует его под безрисковый
процент. К моменту исполнения форварда это даст
4 × (1 + 0,05 × (135 − 90) 365) = 4,03 руб.
Кроме того, осуществив продажу акции в исполнение форвардного контракта,
инвестор выручает 14,24 руб. В этот же момент арбитражер погашает кредит,
уплачивая кредитору 14 × (1 + 0,05 × 135 365) = 14,26
29
Прибыль арбитражера в момент исполнения форварда составит
14,24 + 4,03 − 14,26 = 4,01 руб. на акцию.
30.
ЦЕНООБРАЗОВАНИЕ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
СЛУЧАЙ НЕПРЕРЫВНО НАЧИСЛЯЕМОГО ДИВИДЕНДА
Рассмотрим теперь ситуацию, при которой дополнительный доход задается процентной ставкой
q < r . При этом получаемые платежи вновь инвестируются в актив. Т.е., если купить единицу актива,
которая стоит S , то спустя время t инвестор будет обладать активом на сумму Se qt .
Утверждение. Справедливая форвардная цена на срок t составляет
r−q t
F = Se
.
(
)
Доказательство. Предположим, что форвард может быть заключен по цене
F0 < Se
(16)
r−q t
. Тогда
(
)
арбитражная схема образуется путем короткой продажи актива на сумму S , размещением средств на
безрисковом депозите и покупкой форвардного контракта. Арбитражер будет непрерывно осуществлять
выплаты по короткой позиции по ставке q . Одновременно по депозиту он будет получать ставку r . В итоге
(r − q )t . Поскольку по предположению F < Se(r − q )t ,
(r − q )t − F > 0 .
после исполнения форварда арбитражер остается с положительной прибылью Se
(r − q )t . Для осуществления арбитража следует занять сумму S , купить
Пусть теперь F > Se
к моменту t арбитражер будет обладать суммой
Se
0
0
0
qt
единицу актива и продать форвард на e
единиц актива. К моменту исполнения форварда арбитражер
qt
qt
будет обладать e единицами актива, которые при исполнении форварда принесут сумму F0 e . По
rt
кредиту необходимо вернуть сумму Se . В итоге будет получена положительная прибыль без риска в
(r −q )t qt
qt
rt
30
e > 0 . Утверждение доказано.
размере F0e − Se = F0 − Se
(
)
31.
ЦЕНООБРАЗОВАНИЕ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
СООТНОШЕНИЕ МЕЖДУ ФЬЮЧЕРСНОЙ И ФОРВАРДНОЙ ЦЕНОЙ
Расчеты по форвардному контракту производятся в момент его истечения. Расчеты
по фьючерсному контракту производятся ежедневно. Получаемая вариационная
маржа может быть инвестирована под безрисковую ставку процента. Для уплаты
вариационной маржи средства могут быть заимствованы также под безрисковую
ставку. В общем случае фьючерсная и форвардная цена одного и того же актива
могут различаться.
Теорема Кокса-Ингерсола-Росса. Если ставка безрисковых вложений на один день
δ постоянна, то форвардная и фьючерсная цены совпадают.
Доказательство. Пусть длительность форвардного и фьючерсного контракта
составляет n + 1 дней. Обозначим F i фьючерсную цену в конце дня i (0 < i < n ) .
Рассмотрим следующую стратегию.
1. Покупаем eδ фьючерсов в конце дня 0.
2. Увеличиваем позицию до e 2δ в конце дня 1.
3. И так далее.
К началу дня i размер позиции составляет eiδ . Прибыль (возможно, отрицательная)
за день i составит (Fi − Fi −1 )eiδ . К концу дня n эта прибыль вырастет до
31
32.
ЦЕНООБРАЗОВАНИЕ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
СООТНОШЕНИЕ МЕЖДУ ФЬЮЧЕРСНОЙ И
ФОРВАРДНОЙ ЦЕНОЙ. ПРОДОЛЖЕНИЕ
(Fi − Fi −1 )eiδ e(n−i )δ = (Fi − Fi −1 )e nδ . Суммарная прибыль к концу дня n составит
[(Fn − Fn−1 ) + (Fn−1 − Fn−2 ) + K + (F1 − F0 )]e nδ = (Fn − F0 )e nδ = (S n − F0 )e nδ ,
где S n - цена спот базового актива в конце дня n . Таким образом, инвестируя сумму F0 в
безрисковую облигацию сроком n дней и применяя описанную стратегию управления
фьючерсной позицией, к концу дня n можно гарантированно получить сумму
(S n − F0 )e nδ + F0e nδ = S n e nδ .
Пусть G0 - форвардная цена в конце дня 0. Покупая e nδ форвардов и инвестируя в
конце дня 0 сумму G0 в безрисковую облигацию на срок n дней, к концу дня n
гарантированно получаем (S n − G0 )e nδ + G0 e nδ = S n e nδ . В двух рассмотренных конечные
суммы одинаковы. Следовательно, должны равняться и начальные вложения (в противном
случае существуют арбитражные возможности). Поэтому F0 = G0 .
Утверждение доказано.
Если процентная безрисковая ставка изменяется случайно, то форвардные и
фьючерсные цены в общем случае не равны. Соотношение между форвардной и фьючерсной
ценами в этом случае зависит от знака корреляции между безрисковой ставкой и базовым
активов производных инструментов. Если эта корреляция положительна, то справедливая
фьючерсная цена превышает форвардную. В противном случае форвардная цены выше
32
фьючерсной.
33.
ЦЕНООБРАЗОВАНИЕ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ВАЛЮТНЫЕ И ТОВАРНЫЕ КОНТРАКТЫ
Пусть r - непрерывная процентная ставка безрисковых инвестиций в
национальной валюте, а q - аналогичная ставка для иностранной валюты.
Единица иностранной валюты в данный момент времени стоит
единиц
S
национальной валюты.
(r − q )t
(17)
F = Se
.
Все товары можно разделить на инвестиционные и потребительские.
Инвестиционные товары характеризуются тем, что на рынке существуют
игроки, готовые вкладывать в эти товары деньги с целью получения дохода от
роста цены, а также проводить с этими товарами операции арбитража. При
этом не исключается, что такие товары могут быть использованы и для
непосредственного потребления. К числу инвестиционных товаров относятся,
например, драгоценные металлы. Что касается товаров потребительской
группы, то такие товары используются только для потребления.
Обозначим
U величину приведенной стоимости издержек хранения и
страхования товара на период времени
. В случае инвестиционного товара
фьючерсная цена определяется как
F = (S + U )e rt
(18)
,
r - ставка без риска. Издержки хранения и страхования могут быть
где
представлены при помощи процентной ставки, которую будем обозначать u .
Тогда фьючерсная цена инвестиционного товара
(19)
F = Se (r +u ) t
33
34.
ЦЕНООБРАЗОВАНИЕ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ВАЛЮТНЫЕ И ТОВАРНЫЕ КОНТРАКТЫ. ПРОДОЛЖЕНИЕ
Для потребительских товаров можно только утверждать только, что
F ≤ (S +U )ert
(20)
или
(21)
F ≤ Se(r+u ) t .
Выстроить арбитражную схему в случае нарушения равенств (20) и (21) не удастся, т.е. такая схема предусматривала бы
продажу базового актива, что для товаров потребительской группы затруднительно: владельцы товара держат его для
потребления, а не для совершения арбитражных операций.
В то же время, если продажа актива и покупка форварда сулит очень большую прибыль, владельцы товара могут пойти
на это. Соответствующая ставка доходности называется ставкой полезности товара. Данная ставка (будем обозначать ее y )
определяется из уравнения
Feyt = (S +U )ert ,
откуда
F = (S +U )e(r − y )t
(22)
или
F = Se(r +u− y ) t .
(23)
Если актив приносит еще и дополнительный доход по ставке q , то формула справедливой форвардной цены принимает
вид
F = Se(r−q+u− y ) t .
Сумму r − q + u часто называют стоимостью удержания позиции (cost of carry) и обозначают c . Тогда
F = Se(c− y ) t .
(24)
34
35.
ЦЕНООБРАЗОВАНИЕ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ПРИМЕР С ТОВАРНЫМ ФОРВАРДОМ
Цена спот серебра на 10.02.04 составляет $6,777 за тройскую унцию.
Котировка форварда на 10.09.04 - $6,83 за унцию. Определить
приведенную стоимость хранения унции серебра в течение года, если
непрерывная безрисковая ставка составляет 1,25%.
Решение. Вначале рассчитаем процентную ставку, выражающую
стоимость хранения металла, используя соотношение (19). Решая это
соотношение относительно ставки , получим:
u=
ln F − ln S
ln 6,83 − ln 6,777
−r =
− 0,0125 = 0,00086
t
7 12
Для того, чтобы найти стоимость хранения в течение года, приравняем
правые части соотношений (18) и (19):
(S + U )e rt = Se(r +u )t
(
)
Выразим из полученного соотношения U :
U = S e ut − 1 . Подставив в
последнее соотношение значения u = 0,00086 и t = 1
, окончательно
получим, что стоимость хранения тройской унции серебра в течение
одного года составляет
U = 6,777 e0,00086 − 1 = 0,0058 доллара.
(
)
35
36.
ЦЕНООБРАЗОВАНИЕ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ФОРВАРДЫ НА ПРОЦЕНТНЫЕ СТАВКИ
• Базовый актив – процентная ставка или облигация
Кривая доходности бескупонных бумаг:
36
37.
ЦЕНООБРАЗОВАНИЕ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
ФОРВАРДНЫЕ ПРОЦЕНТНЫЕ СТАВКИ
e 0,1⋅1 ⋅ e rˆ⋅1 = e 0,105⋅2 = e 0, 21
e = e 0,11
rˆ = 0,11
rˆ
Утверждение: Справедливая котировка форварда на процентную ставку
составляет
r * ⋅T * −r ⋅ T
rˆ =
T * −T
(25)
Доказательство.
r ⋅T
rˆ⋅(T *−T )
r *⋅T *
e ⋅e
=e
rˆ⋅(T *−T )
r *⋅T *− r ⋅T
e
=e
37
38.
ЦЕНООБРАЗОВАНИЕ ФОРВАРДНЫХ ИФЬЮЧЕРСНЫХ КОНТРАКТОВ
FORWARD RATE AGREEMENT (FRA) –
форвардное соглашение о процентной ставке
FRA – расчетный форвард на процентную ставку
− rT
R (T *−T ) − r *T *
=e
e
r * T * −rT
R=
T * −T
e
Утверждение. Текущая стоимость FRA определяется как
V (t ) = Ne R (T *−T )e − r *(T *− t ) − Ne − r (T −t )
(26)
38
39.
РЫНКИ ОПЦИОНОВОПЦИОНЫ. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Поставочный опцион – это контракт или ценная бумага, которые дают право (но не
обязанность) купить или продать актив, лежащий в основе контракта, в течение
определенного периода времени по фиксированной цене, которая называется ценой
исполнения (strike). В качестве базового актива могут выступать основные финансовые
инструменты (акции, облигации, индексы акций) или реальные товары, например,
нефть, кофе, металлы, пшеница, а также фьючерсные контракты на перечисленные
виды активов.
Расчетный опцион – это контракт или ценная бумага, расчеты по которым зависят от
будущих значений некоторых заданных переменных величин. Контракты на индексы
акций и процентные ставки всегда являются расчетными. Контракты на акции,
фьючерсы и товарные контракты могут быть как поставочными, так и расчетными.
Чаще всего в момент заключения контракта покупатель опциона выплачивает продавцу
(которого называют также подписчиком опциона) некоторую премию. Премию называют
также ценой опциона. Опцион на покупку (опцион колл) предоставляет его владельцу
право купить, а опцион на продажу (опцион пут) – право продать актив. Опцион
американского типа может быть исполнен в любой день до момента истечения
контракта, опцион европейского типа – только в момент истечения.
Существуют опционы фьючерсного типа (future style options), по которым выплата
премии при заключении не уплачивается. Ежедневно по таким контрактам
производится начисление вариационной маржи аналогично тому, как происходит для
фьючерсных контрактов. При исполнении опциона колл на фьючерс происходит
заключение фьючерсного контракта; покупатель опциона становится покупателем
фьючерсного контракта. Если исполняется опцион пут на фьючерс, то в результате
покупатель опциона становится продавцом фьючерсного контракта. В обоих случаях
фьючерсный контракт заключается по цене, равной цене исполнения опциона.
39
40.
РЫНКИ ОПЦИОНОВВЫИГРЫШИ И ПРОИГРЫШИ ПОКУПАТЕЛЯ И
ПРОДАВЦА ЕВРОПЕЙСКИХ ОПЦИОНОВ
Прибыль продавца опциона колл
Прибыль покупателя опциона колл
Прибыль
Прибыль
Цена
исполнения
Цена акции
Прибыль покупателя опциона пут
Цена
исполнения
Цена акции
Прибыль продавца опциона пут
Прибыль
Прибыль
Цена
исполнения
Цена акции
Цена
исполнения
Цена акции
40
41.
РЫНКИ ОПЦИОНОВПРИМЕР ОПЦИОНОВ НА АКЦИИ
Contract
Contract Size Min. Price Change Contract Months
Deutsche Bank
100
Eur 0.01
60
Settlement
Physical delivery of 100 equities of the underlying
Contract
Settlement Day
Contract Months
Up to 60 months: The three nearest successive calendar months, the three following quarterly months of the March,
June, September and December cycle thereafter, and the four following semi-annual months of the June and
December cycle thereafter, and the two following annual months of the December cycle thereafter.
Last Trading Day
Last Trading Day is the third Friday, for Italian equity options the day before the third Friday, of each expiration
month, if this is an exchange trading day; otherwise, the exchange trading day immediately preceding that day.
t+3
Close of trading in the expiring option series on the Last Trading Day is at 17:30 CET, for Swiss equity options at
17:20 CET and for Spanish equity options 17:35 CET.
If for German equity options a dividend resolution is passed on the Last Trading Day, the exchange trading day
preceding that day is deemed as the Last Trading Day.
Daily Settlement Price
The last traded price of the trading day; or, if the last traded price is older than 15 minutes or does not reasonably
reflect the prevailing market conditions, Eurex will establish the official settlement price.
Exercise
American-style; an option can be exercised up to the end of the Post-Trading Full Period (20:00 CET) on any
exchange trading day during the lifetime of the option.
41
42.
РЫНКИ ОПЦИОНОВОПЦИОНЫ НА ИНДЕКС FTSE 100
FTSE 100 INDEX OPTION (EUROPEAN-STYLE)
Codes and classification
Mnemo
ESX
Exercise type
European
Unit
£
Unit of trading
Contract valued at £10 per index point (eg value
£65,000 at 6500.0).
Delivery months
Nearest eight of March, June, September, December
plus such additional months that the nearest four
calendar months are always available for trading.
Quotation
Index points (e.g. 6500.0).
Minimum price movement
0.5 (£5.00)
Exercise day
Exercise by 18:00 on the Last Trading Day only.
Last trading day
Third Friday in delivery month.
Settlement day
Settlement day is the first business day after the Last
Trading Day.
Trading hours
08:02 - 16:30
42
43.
РЫНКИ ОПЦИОНОВСИНТЕТИЧЕСКИЕ ОПЦИОНЫ
Синтетический длинный пут:
Прибыль
Цена
базового
актива
Синтетический длинный колл:
Прибыль
Цена
исполнения
Цена
базового
актива
43
44.
РЫНКИ ОПЦИОНОВОПЦИОННЫЕ СТРАТЕГИИ
Спрэд быка
Прибыль
портфеля
X1
X2
Цена
актива
Прибыль
портфеля
Спрэд медведя
Цена
актива
X1
X2
44
45.
РЫНКИ ОПЦИОНОВОПЦИОННЫЕ СТРАТЕГИИ (ПРОДОЛЖЕНИЕ)
Короткий стрэддл
Прибыль
портфеля
Цена
актива
Спот
Длинный стрэнгл
Прибыль
портфеля
Спот
Цена
актива
45
46.
РЫНКИ ОПЦИОНОВБАТТЕРФЛЯЙ СПРЭД
46
47.
РЫНКИ ОПЦИОНОВКАЛЕНДАРНЫЙ СПРЭД
Образуется путем заключения одноименных опционов различного срока,
но одинакового страйка. Например, может быть продан пут со сроком 1
год и куплен пут со сроком полгода. График прибыли календарного
спрэда:
Диагональный спрэд – календарный спрэд с различными страйками
опционов
47
48.
РЫНКИ ОПЦИОНОВSTRIP&STRAP
48
49.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВСООТНОШЕНИЯ ДЛЯ ПРЕМИЙ ОПЦИОНОВ
Утверждение 1. Премия американского и европейского опциона колл
на акции, по которым не выплачиваются дивиденды, не может
быть больше текущей цены акции:
(27)
c≤S .
Доказательство.
Если это соотношение не выполняется, то существует
возможность осуществления арбитража: достаточно продать
опцион и приобрести акцию, чтобы получить безрисковую
прибыль. Если опцион будет предъявлен к исполнению, то
акцию придется продать. В результате будет получена прибыль
без риска
c−S + X ,
где c - премия опциона, S - цена акция в момент заключения
опциона, X - цена исполнения. Если опцион не исполняется, то
выигрыш к моменту окончания срока действия контракта
составит
c−S +P ,
где P - цена акции в момент истечения опциона.
49
50.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВСООТНОШЕНИЯ ДЛЯ ПРЕМИЙ ОПЦИОНОВ
(ПРОДОЛЖЕНИЕ)
Утверждение 2. Для европейского опциона пут
(28)
pe ≤ Xe − rt ,
где pe - премия опциона, r - процентная ставка инвестиций без
риска, t - время до исполнения опциона.
Доказательство. Если последнее соотношение не выполняется, то
инвестор может продать опцион и разместить премию под ставку
без риска. В случае, если опцион не будет исполнен, его
безрисковая прибыль составит pe e rt . При исполнении опциона
инвестор, не сделав начальных вложений и ничем не рискуя, имеет
по завершении операции акцию и денежную сумму, равную
p − Xe− rt e rt > 0 .
(e
)
Утверждение 3. Поскольку американский опцион пут может быть
исполнен до окончания срока контракта, можно утверждать, что
(29)
pa ≤ X .
Доказательство. В противном случае инвестор продает опцион и
обеспечивает себе безрисковую прибыль независимо от того,
будет ли опцион предъявлен к исполнению и в какой именно
момент времени.
50
51.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВСООТНОШЕНИЯ ДЛЯ ПРЕМИЙ ОПЦИОНОВ (ПРОДОЛЖЕНИЕ)
Утверждение 4 (без доказательства).
Нижняя граница премии европейского или американского опциона колл на акции, по
которым не выплачиваются дивиденды, составляет:
ce ≥ S − Xe − rt
.
(30)
Утверждение 5 (без доказательства).
Для премии европейского опциона пут на акции, по которым не выплачиваются
дивиденды, имеет место соотношение
(31)
pe ≥ Xe − rt − S
X 2 - цены исполнения
Утверждение
6 (без доказательства). Пусть X 1 и
.
опционов колл, все другие условия которых одинаковы. Если X 1 < X 2 , то
, где c1 и c2 - премии соответствующих опционов.
c1 > c2
Утверждение 7 (без доказательства). Для опциона пут справедливо обратное: чем
выше страйк, тем выше стоимость опциона, поскольку опцион с большей ценой
исполнения позволяет продать актив по большей цене.
Утверждение 8 («Паритет опционов», без доказательства).
Европейских опционов
Американских опционов
ce + Xe− rt = pe + S
S − X ≤ ce − pe ≤ S − Xe − rt
(32)
51
52.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВГЕОМЕТРИЧЕСКОЕ БРОУНОВСКОЕ ДВИЖЕНИЕ
dS
= µdt + σdz .
(33)
S
σ - волатильность базового актива, µ - ставка ожидаемого возврата, dz - белый шум со стандартным нормальным законом
распределения; соответственно, z - винеровский процесс. В дискретном случае уравнение (33) принимает вид
∆S
∆S = µS∆t + σSε ∆t , или
(34)
= µ∆t + σε ∆t
S
∆S
где ε - случайная величина со стандартным нормальным законом распределения. D = σ 2 ∆t .
S
dS = µSdt + σSdz , или
Относительно большой интервал ∆t
∆t → 0
52
53.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВЛЕММА ИТО
Процесс Ито:
dx = a(x, t )dt + b( x, t )dz .
(35)
Лемма Ито: функция G от переменных x и t следует процессу
∂G
∂G 1 ∂ 2G 2
∂G
dG =
a+
b dt +
bdz .
+
2
∂t 2 ∂x
∂x
∂x
(36)
Если x = S - цена актива, следующая процессу (35), то
∂G
∂G 1 ∂ 2G 2 2
∂G
dG =
µS +
+
σ S dt +
σSdz .
2
∂t 2 ∂S
∂S
∂S
(37)
Используя лемму Ито, получим стохастическое дифференциальное уравнение для форвардной цены актива,
не приносящего дополнительный доход. Пусть безрисковая процентная ставка постоянна на всем периоде
действия форвардного контракта. Тогда
F = Se r (T −t ) ,
(38)
где T - момент истечения форварда, t - текущий момент времени. Тогда
∂F
∂2F
∂F
= e r (T −t ) , 2 = 0,
= − rSe r (T −t ) .
∂S
∂S
∂t
Откуда
[
]
dF = e r (T −t )µS − rSe r (T −t ) dt + e r (T −t )σSdz = (µ − r )Fdt + σFdz .
(39)
Т.о., коэффициент сноса форвардной цены есть превышение коэффициента сноса µ над безрисковой ставкой
процента.
∂G 1 ∂ 2G
1 ∂G
= , 2 =− 2,
= 0 , то из (33) и (37) следует, что
∂S S ∂S
S ∂t
σ2
dt + σdz .
dG = µ −
2
σ2
σ2
2
2
T
T
S
S
+
−
T
T
ln ST − ln S 0 ~ φ µ −
,
σ
ln
~
φ
ln
µ
,
σ
или
T
0
2
2
Пусть G = ln S . Поскольку
(40)
(41)
54.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВФОРМУЛА БЛЭКА-ШОУЛСА
а) допускается короткая продажа базового актива;
б) отсутствуют транзакционные издержки при совершении операций с банковским
счетом и базовым активом опциона;
в) базовый актив и банковский счет безгранично делимы;
г) базовый актив не приносит дополнительного дохода (например, рассматривается
акция без дивидендов);
д) на рынке отсутствуют арбитражные возможности;
е) операции на рынке осуществляются непрерывно;
ж) цена базового актива следует стохастическому дифференциальному уравнению (33).
ce = SΦ (d1 ) − he − rt Φ (d 2 )
ln (S h ) + rt 1
ln (S h ) + rt 1
d1 =
+ σ t
d2 =
− σ t
2
2
σ t
σ t
pe = he − rt Φ (− d 2 ) − SΦ (− d1 )
Если по акции выплачивается дивиденд, ставка которого равна
европейских опционов колл и пут даются следующими формулами:
ce = Se − qt Φ (d1 ) − he − rt Φ (d 2 )
ln (S h ) + rt − qt 1
d1 =
+ σ t
2
σ t
q
pe = he − rt Φ (− d 2 ) − Se − qt Φ (− d1 )
d2 =
ln (S h ) + rt − qt 1
− σ t
2
σ t
(42)
(43)
(44)
, то премии
(45)
(46)
55.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВПример 1
Текущая стоимость акции $1,595. Волатильность акции составляет 0,45. Исполнение
опциона назначено на 15.09.03, цена исполнения – $1,5 . Доходность
государственной бескупонной облигации соответствующего срока составляет 4%
годовых по ставке сложных процентов. Рассчитать премию европейского опциона
колл в день 01.07.03 при помощи формулы Блэка-Шоулса.
Решение.
d1 =
ln (1,595 1,5) + 0,039 ⋅
76
0,45
365
76
365 + 1 0,45 76
2
365
Здесь 76 – количество дней
между датами 01.07.03 и 15.09.03 . Выполняя соответствующие вычисления,
получим: d1 = 0,441 . Аналогично рассчитывается значение d 2 = 0,236 . Отсюда
Ce = 1,595Φ(0,441) − 1,5e
− 0 , 039
76
365
Φ(0,236) = 0,1867
55
56.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВДРУГИЕ ВИДЫ БАЗОВЫХ АКТИВОВ
Опционы на фьючерсы:
d1 =
ce = Fe − rt Φ (d1 ) − he − rt Φ (d 2 ) = e − rt (FΦ (d1 ) − hΦ (d 2 ))
(47)
pe =he−rtΦ(−d2) −Fe−rtΦ(−d1) =e−rt(hΦ(−d2) −F Φ(−d1))
(48)
d2 =
(49)
ln (F h ) 1
+ σ t
2
σ t
ln (F h ) 1
− σ t
2
σ t
Варранты:
Пусть N - количество акций в обращении, M - количество варрантов,
выпущенных в обращение, W - цена варранта. Каждый варрант дает право
владельцу приобрести γ акций компании в момент T по цене K за
акцию.
1. Цена акции S заменяется на
S + M N ⋅W
2. Результат формулы Блэка-Шоулса умножается на
N ⋅γ
N + M ⋅γ
56
57.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВМОДЕЛЬ КОКСА-РОССА-РУБИНШТЕЙНА
Биномиальная модель изменения цены акции:
u2S
uS
udS
S
d 2S
dS
Двухэтапная биномиальная модель цены европейского опциона колл:
max (0, uS − X )
C
max (0, dS − X )
Обозначим Cu = max(0; uS − X ) = (uS − X ) , Cd = max (0; dS − X ) = (dS − X )+ .
Утверждение. Стоимость опциона в двухэтапной модели дается соотношением
C = (C u p + C d (1 − p ))e − rτ ,
где
+
p=
e rτ − d
.
u−d
(50)
(51)
57
58.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВМОДЕЛЬ КОКСА-РОССА-РУБИНШТЕЙНА
(ПРОДОЛЖЕНИЕ)
Доказательство. Для определения стоимости опциона в начальный момент времени
рассмотрим портфель, который содержит опцион колл и некоторое количество базового
актива, которое будем обозначать ∆ . Безрисковый портфель должен иметь одинаковую
стоимость в случае роста и в случае падения цены: ∆uS − Cu = ∆dS − Cd , откуда
∆=
Cu − C d
.
S (u − d )
(52)
Доходность безрискового портфеля соответствует безрисковой ставке процента (в
противном случае существовала бы возможность арбитража). Поэтому
∆uS − Cu
= e rτ ,
∆S − C
откуда С = (∆Se − ∆uS + Сu )e . Подставляя в последнее выражение соотношение (52) и упрощая
выражение, получим:
− rτ
rt
Cu − Cd rτ Cu − Cd
− rτ Cu − Cd rτ Cu − Cd
− rτ Cu e rτ − Cd e rτ − Cu u + Cd u + Cu u − Cu d − rτ
e
С =
Se −
uS + Сu e =
e −
u + Сu e =
(u − d )
−
S (u − d )
u
d
S (u − d )
(u − d )
Cu e rτ − Cu d + − Cd e rτ + Cd u − rτ e rτ − d
− e rτ + u − rτ e rτ − d
d − e rτ + u − d − rτ
e = Cu
e = Cu
e
=
+ Cd
+ Cd
u−d
u−d
u − d
u−d
u−d
e rτ − d
(
u − d ) − e rτ − d − rt
− rτ
e = (Cu p + Cd (1 − p ))e
= Cu
+ Cd
u−d
u−d
(
) (
)
(
)
58
59.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВМОДЕЛЬ КОКСА-РОССА-РУБИНШТЕЙНА
(ПРОДОЛЖЕНИЕ)
где
C = (Cu p + Cd (1 − p ))e − rτ ,
e rτ − d
p=
u−d
u = eσ τ ,
d = e −σ
τ
(53)
(54)
Акция с дивидендом:
Su (1 − δ )
2
Su
S
Sd
Su 3 (1 − δ )
Su (1 − δ )
S (1 − δ )
Sd (1 − δ )
Sd 2 (1 − δ )
Sd 3 (1 − δ )
59
60.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВПРИМЕР 2
Требуется оценить премию европейского опциона колл из примера слайда 12 в день
01.07.03 при помощи биномиальной модели Кокса-Росса-Рубинштейна, содержащей
6 этапов.
Решение. Несложно подсчитать, что в этом случае период времени между этапами
− 0,45× 14 365
составляет 2 недели. Тогда u = e0,45× 14 365 = 1,093,
d =e
= 0,916 . Для
того, чтобы найти ставку непрерывного начисления процентов, соответствующую
заданной ставке сложных процентов 0,04 , составим следующее уравнение:
1 + 0,04 = e r . Отсюда r = ln (1,04) = 0,039
и
e 0,039 (14 / 365 ) − 0,916
p=
= 0,4856
1,093 − 0,916
, соответственно,
1 − p = 0,5144 .
60
61.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВПРИМЕР 2 (ПРОДОЛЖЕНИЕ)
2,486
0,986
2,275
0,777
2,082
0,586
1,905
0,417
1,743
0,282
1,595
0,183
1,595
0,155
1,460
0,089
2,082
0,582
1,905
0,407
1,743
0,258
1,595
0,118
1,460
0,057
1,336
0,028
1,336
0
1,743
0,243
1,460
0
1,222
0
1,222
0
1,118
0
1,023
0
61
62.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВПРИМЕР 3
Рассчитать цену американского опциона пут на акцию, по которой не выплачиваются
дивиденды. Непрерывно начисляемая ставка без риска равна 0,125 . Стандартное
отклонение цены акции за год составляет 0,41 . Расчет производится 16.12.03, текущая
цена акции составляет 8,01руб. Опцион истекает 16.06.04, цена исполнения опциона 8,6руб. Для расчета использовать биномиальную модель, содержащую 4 этапа.
Решение. Один период биномиальной модели соответствует двум месяцам.
2
= 0,167
Волатильность акции, соответствующая 2-месячному периоду, составляет 0,41
12
В случае роста цена акции увеличивается в u = e0,41× 2 12 = 1,182 раза, а в случае
падения - умножается на d = e − 0,41× 2 12 = 0,846 . Вероятность роста цены акции составляет
13,235
,
вероятность снижения цены
e 0,125 (2 / 12 ) − 0,846
p=
1,182 − 0,846
0
= 0,521
11,195
0
9,469
0,402
8,01
1,062
1 − 0,521 = 0,479
9,469
0
8,01
0,856
6,775
1,784
1,825
6,775
1,825
5,731
2,692
2,869
4,848
3,752
62
63.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВПРЕДЕЛЬНАЯ ТЕОРЕМА ДЛЯ СХЕМЫ
КОКСА-РОССА-РУБИНШТЕЙНА
Утверждение. Если u и d определяются соотношениями (54), число шагов дерева n неограниченно возрастает, и при этом величина
t = nτ остается постоянной, то цена опциона, рассчитанная по схеме Кокса-Росса-Рубинштейна, сходится к цене Блэка-Шоулса.
Доказательство. Проведем доказательство для европейского опциона колл на бездивидендную акцию. Результат расчета цены
опциона по схеме Кокса-Росса-Рубинштейна можно представить в виде одной формулы:
n
n!
n− j
C = ∑
p j (1 − p ) max 0; u j d n − j S − X e −nrτ ,
(55)
j =0 j!(n − j )!
где j - количество подъемов цены. Данная формула может быть упрощена. Пусть a - минимальное число успехов в рассматриваемой
схеме испытаний Бернулли, при котором
(
)
u ad n−a S > X .
Взяв логарифм от обеих частей неравенства и, выполняя соответствующие преобразования, получим:
(
(56)
)
ln u a d n − a S > ln ( X ) ;
a ln(u ) + (n − a ) ln(d ) + ln(S ) > ln( X ) ;
a ln(u ) + n ln(d ) − a ln(d ) + ln(S ) > ln( X ) ;
a(ln(u ) − ln(d )) > ln( X ) − n ln (d ) − ln(S ) ;
X
a > ln n
d S
(ln(u ) − ln(d )) .
(57)
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВ
X
Таким образом, a - наименьшее целое число, которое больше, чем ln
(ln (u ) − ln (d )) .
d nS
(
)
Если j < a , то u j d n − j S − X > 0 и max 0; u j d n − j S − X = 0 (опцион в момент исполнения находится вне денег). Для всех j ≥ a
(
)
(опцион в деньгах) max 0; u j d n − j S − X = u j d n − j S − X .
63
64.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВПРЕДЕЛЬНАЯ ТЕОРЕМА ДЛЯ СХЕМЫ КОКСАРОССА-РУБИНШТЕЙНА (ПРОДОЛЖЕНИЕ)
Формула (55) может быть переписана следующим образом:
n
n!
n− j
C = ∑
p j (1 − p ) (u j d n − j S − X ) e − nrτ .
j = a j!(n − j )!
Разобьем сумму в (58) на два слагаемых:
(58)
n
n
n!
n!
n− j
n− j
C = ∑
p j (1 − p ) u j d n − j S e − nrτ − Xe − nrτ ∑
p j (1 − p )
j = a j!(n − j )!
j = a j!(n − j )!
.
n
n
n!
n
!
n
−
j
n
−
j
= S∑
p j (1 − p ) u j d n − j e − nrτ −Xe − nrτ ∑
p j (1 − p )
(
)
(
)
j
!
n
−
j
!
j
!
n
−
j
!
j=a
j =a
(59)
Преобразуем первое слагаемое в (59) следующим образом:
n
S∑
j =a
(
n
n!
n!
n− j
p j (1 − p ) u j d n − j e − nrτ =S ∑
pue − rτ
j!(n − j )!
j = a j!(n − j )!
) ((1 − p )de )
j
− rτ n − j
.
Обозначим
~
p = pue− rτ .
Согласно (51)
p=
rτ
e −d
,
u−d
(60)
ЦЕНООБРАЗОВАНИЕ
ОПЦИОНОВ
e −d
u −d −e +d
u −e
поэтому
(1 − p )de−rτ
rτ
de − rτ =
= 1 −
u−d
rτ
u−d
de − rτ =
rτ
u−d
de −rτ . Вычтем и прибавим к
последнему выражению единицу и выполним следующие преобразования:
64
65.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВПРЕДЕЛЬНАЯ ТЕОРЕМА ДЛЯ СХЕМЫ КОКСАРОССА-РУБИНШТЕЙНА (ПРОДОЛЖЕНИЕ)
u − e rτ − rτ
u − e rτ
ud − de rτ − ue rτ + de rτ
ud − ue rτ
de − 1 + 1 =
d
1
1
1
+1
−
+
=
+
=
u−d
(
u − d )e rτ
(
u − d )e rτ
(
u − d )e rτ
ude − rτ − u
u − ude − rτ
u − ude − rτ
e rτ − d − rτ
=
+1 = −
+1 = 1−
= 1−
ue = 1 − ~
p
(u − d )
(u − d )
(u − d )
(u − d )
Таким образом, формула (59) может быть переписана в виде:
n
n
n!
n!
n− j
n− j
~
C = S∑
p j (1 − ~
p ) −Xe − rt ∑
p j (1 − p ) ,
j = a j!(n − j )!
j = a j!(n − j )!
где t = nτ .
Согласно теореме Муавра-Лапласа при n → ∞ сумма
n
∑ j!(n − j )! ~p j (1 − ~p )n− j стремится
n!
j =a
(61)
n~
p − a
к Φ ~
, а сумма
np (1 − ~
p )
np − a
, где Φ ( y ) - функция стандартного нормального закона распределения. При условии
- к Φ
np (1 − p )
j =a
ln(S X ) + rt 1
n~
p−a
выполнения соотношений (54) можно также показать, что если n → ∞ , то
→
+ σ t и
~
~
2
σ t
np (1 − p )
np − a
ln (S X ) + rt 1
→
− σ t . Формула Кокса-Росса-Рубинштейна переходит в формулу Блэка-Шоулса:
2
σ t
np (1 − p )
n
∑ j!(n − j )! p j (1 − p )n − j
n!
Ce = SΦ(d1 ) − Xe − rt Φ(d 2 ) ,
(62)
где
ln (S X ) + rt 1
ln (S X ) + rt 1
(63)
+ σ t , d2 =
− σ t.
2
2
σ t
σ t
Используя теорему о паритете опционов (32), можно показать, что премия европейского опциона пут дается следующей формулой:
d1 =
Pe = Xe − rt Φ(− d 2 ) − SΦ(− d1 ) .
(64)
66.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВЧУВСТВИТЕЛЬНОСТЬ ПРЕМИИ ОПЦИОНА К
ИЗМЕНЕНИЮ ЦЕНЫ БАЗОВОГО АКТИВА
Дельта опциона:
∂P
.
∂S
Утверждение. Дельта европейского опциона колл на бездивидендную акцию
∆ с = Φ (d1 ) .
∆=
Доказательство. Поскольку Φ′( x ) =
(
1
e
2π
x2
−
2
(65)
, то
)
d 22
1
1
1
Φ′(d1 ) = Φ′ d 2 + σ t =
exp −
− σd 2 t − σ 2t = Φ′(d 2 ) exp − σd 2 t − σ 2t .
2
2
2π
2
− rt
ln (S K ) + r − σ 2 2 t
1
Ke
Из выражения для d 2 =
следует, что exp − σd 2 t − σ 2t =
. Поэтому
2
S
σ t
SΦ′(d1 ) = Ke − rt Φ′(d 2 ) .
(
)
(66)
S σ
σ2
t ln S − ln K + r +
ln + r +
t
2
K
2
∂d
1
=
Далее, d1 =
. Следовательно, 1 =
.
∂S Sσ t
σ t
σ t
σ2
t
ln S − ln K + r −
2
∂d 2
1
Аналогично, d 2 =
и
=
. Т.о.,
∂S Sσ t
σ t
∂d1 ∂d 2
.
=
∂S
∂S
2
(67)
66
67.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВЧУВСТВИТЕЛЬНОСТЬ ПРЕМИИ ОПЦИОНА К ИЗМЕНЕНИЮ
ЦЕНЫ БАЗОВОГО АКТИВА (ПРОДОЛЖЕНИЕ)
Дифференцируя формулу Блэка-Шоулса для опционов колл, получим:
∂с
∂d
∂d
= Φ (d1 ) + SΦ′(d1 ) 1 − Ke − rt Φ′(d 2 ) 2 .
∂S
∂S
∂S
Отсюда, используя (66) и (67), получаем:
∂с
= Φ (d1 ) .
∂S
(68)
Дельта
1
0,5
Цена
исполнения
Цена
актива
67
68.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВЧУВСТВИТЕЛЬНОСТЬ ДЕЛЬТА К
ИЗМЕНЕНИЮ ЦЕНЫ БАЗОВОГО АКТИВА
Гамма опциона колл:
ΓC =
Φ′(d1 )
Sσ T
(69)
Гамма опциона пут:
Φ′(d1 )
ΓP =
Sσ T
(70)
Гамма
Цена
исполнения
Цена
актива
68
69.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВПОКАЗАТЕЛЬ ИЗМЕНЕНИЯ СТОИМОСТИ ОПЦИОНА
С ТЕЧЕНИЕМ ВРЕМЕНИ
Тета опциона колл:
ΘC = −
SΦ′(d1 )σ
− rXe − rT Φ(d 2 )
2 T
(71)
Тета опциона пут:
ΘP = −
SΦ′(d1 )σ
+ rXe − rT Φ (− d 2 )
2 T
Тета
опциона
колл
(72)
Время до
погашения
«у денег»
«вне денег»
«в деньгах»
69
70.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВПОКАЗАТЕЛЬ ЧУВСТВИТЕЛЬНОСТИ К
ИЗМЕНЕНИЮ ВОЛАТИЛЬНОСТИ
Вега опционов колл и пут:
Λ = S T Φ ′(d1 )
Вег
Вега
а
(73)
Вега
Вег
а
Цена
исполнения
Цена
актива
Время до истечения
опциона.
70
71.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВПОКАЗАТЕЛЬ ЧУВСТВИТЕЛЬНОСТИ ПРЕМИИ
К ИЗМЕНЕНИЮ ПРОЦЕНТНОЙ СТАВКИ
Ро европейского опциона колл:
ΡC = XTe− rT Φ (d 2 )
(74)
Ро европейского опциона пут:
ΡP = − XTe − rT Φ(− d 2 )
(75)
71
72.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВПРИМЕР 4
Волатильность акции составляет 0,45. Исполнение опциона колл
назначено на 15.09.03, цена исполнения – $1,5 . Доходность
государственной бескупонной облигации соответствующего срока
составляет 3,9% годовых по непрерывной ставке.
Оценить изменение цены опциона при снижении стоимости актива на
$0,03 в день 01.07.03 при помощи показателя дельта и путем
непосредственного вычисления по формуле Блэка-Шоулса.
Расчет по формуле (65) дает значение дельта рассматриваемого опциона
0,67. Оценка снижения цены опциона в результате снижения цены
базового актива на $0,03 составляет 0,670 × 0,03 = 0,02 доллара. Формула (42)
при снижении цены актива до 1,595 − 0,03 = 1,565
дает значение цены
опциона $0,167 . Таким образом, действительное понижение цены опциона
составляет 0,1867 – 0,167 = 0,0197 .
72
73.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВВОЛАТИЛЬНОСТЬ
1
n
2
(
)
σ =
x
−
m
∑
i
n
−
1
i
=
1
1
2
, где
xi = ln Si − ln Si −1 = ln
Si
,
Si −1
m
- среднее значение
Подразумеваемая
волатильность
Волатильность, %
120
Цена спот
Цена исполнения опциона
90
60
30
Время
историческая
подразумева
подразумеваемая
емая
73
xi
74.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВПОВЕРХНОСТЬ ВОЛАТИЛЬНОСТИ
74
75.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВДЕЛЬТА-ХЕДЖИРОВАНИЕ. ПРИМЕР
День
Цена
Стоимость
Позиция по
Покупка
Безрисковое
акции, опциона,
акциям,
Стоимость
акций,
Затраты на
заимствование/вло
руб.
руб.
Дельта
штук
акций, руб. штук
покупку, руб. жение средств, руб.
1
100,00 1309296,19
0,2843
284294 28429432,17
284294
28429432,17
27120135,98
2
102,23 1990479,54
0,3850
384980 39356046,05
100686
10293008,40
37415373,52
3
104,27 2806219,21
0,4865
486465 50721511,33
101485
10581336,68
47999785,56
4
103,69 2462770,73
0,4546
454559 47134418,40
-31906
-3308415,72
44695315,20
5
104,67 2856911,65
0,5056
505572 52919266,80
51013
5339668,21
50038657,15
6
103,27 2126166,93
0,4264
426362 44030562,77
-79210
-8180031,60
41862738,48
7
101,82 1495167,92
0,3425
342477 34871879,02
-83886
-8541474,29
33324705,11
8
100,49 1021175,90
0,2663
266268 26757266,06
-76209
-7658197,81
25669246,42
9
98,39 516641,77
0,1627
162725 16010027,05
-103543 -10187305,50
15484050,81
10
98,10 424795,11
0,1428
142845 14012585,09
-19880
-1950117,99
13535205,54
11
97,93 357492,04
0,1277
127721 12507899,70
-15124
-1481127,97
12055190,10
12
98,86 439370,47
0,1544
154351 15258417,52
26630
2632523,66
14688704,64
13
96,58 153978,56
0,0680
68018
6569415,68
-86333
-8338335,27
6351576,71
14
15
16
17
18
19
20
21
22
23
24
25
95,61
94,95
96,03
96,19
96,01
93,16
94,29
92,84
92,10
89,84
89,99
89,91
78131,48
40958,50
55019,47
42202,72
24019,82
1028,08
1109,63
32,87
0,39
0,00
0,00
0,00
0,0397
0,0236
0,0317
0,0264
0,0170
0,0010
0,0012
0,0000
0,0000
0,0000
0,0000
0,0000
39657
23564
31686
26361
16965
1043
1205
49
1
0
0
0
3791794,12
2237349,10
3042736,96
2535548,40
1628776,78
97212,32
113631,81
4569,86
74,20
0,00
0,00
0,00
-28361
-16093
8122
-5325
-9396
-15922
162
-1156
-48
-1
0
0
-2711673,40
-1528046,86
779915,41
-512143,43
-902035,36
-1483338,74
15242,41
-107308,12
-4459,45
-72,38
0,00
0,00
3640425,38
2112677,75
2892766,81
2380861,15
1479021,49
-4195,69
11046,38
-96260,83
-100728,19
-100808,85
-100817,14
-100825,42
Опцион колл
Сигма
0,3
мю
0,15
страйк
105
ставка
0,03
Объем
1000000
Премия,
руб.
1,3093
Всего,
руб.
1309296,1921
T
0,0658
75
76.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВДЕЛЬТА-ХЕДЖИРОВАНИЕ. ПРИМЕР
День
Цена
Стоимость
Позиция по
Покупка
Безрисковое
акции, опциона,
акциям,
Стоимость
акций,
Затраты на
заимствование/вло
руб.
руб.
Дельта
штук
акций, руб. штук
покупку, руб. жение средств, руб.
1
100,00 1309296,19
0,2843
284294 28429432,17
284294
28429432,17
27120135,98
2
100,93 1532840,82
0,3221
322126 32513213,51
37831
3818444,57
30940809,69
3
100,98 1484194,16
0,3195
319470 32258833,60
-2656
-268151,28
30675201,60
4
100,32 1226214,19
0,2833
283331 28425126,63
-36140
-3625699,13
27052023,82
5
100,39 1182320,67
0,2805
280472 28155388,05
-2858
-286935,03
26767312,33
6
101,79 1555370,64
0,3459
345882 35207565,69
65409
6658076,00
33427588,47
7
101,70 1454346,00
0,3360
335978 34169789,67
-9903
-1007174,78
32423161,28
8
100,30 971830,24
0,2568
256824 25759816,80
-79154
-7939257,16
24486569,14
9
99,29 681190,39
0,2012
201201 19977883,07
-55624
-5523069,18
18965512,64
10
102,04 1344495,33
0,3375
337494 34438321,54
136294
13907559,37
32874630,89
11
104,18 2116516,98
0,4664
466409 48591021,66
128915
13430514,34
46307847,36
12
106,91 3538386,45
0,6428
642758 68718260,64
176349
18853727,92
65165381,56
13
106,69 3305563,52
0,6329
632924 67529418,69
-9834
-1049208,53
64121529,31
14
15
16
17
18
19
20
21
22
23
24
25
108,05
109,36
111,33
111,40
114,80
114,49
112,08
114,16
112,70
112,83
110,14
109,47
4133707,93
5042650,34
6658598,47
6666262,92
9883949,36
9561151,54
7166819,35
9203176,07
7730688,54
7849827,14
5154152,67
4466656,52
0,7237
0,8051
0,9000
0,9145
0,9855
0,9888
0,9704
0,9964
0,9957
0,9994
0,9989
1,0000
723708
805085
899982
914515
985451
988759
970432
996435
995666
999439
998892
1000000
78199478,18
88040656,68
100192933,39
101876572,93
113128438,93
113205203,66
108764232,90
113757743,56
112212172,22
112768912,63
110022892,00
109466656,52
90784
81377
94897
14533
70936
3309
-18327
26003
-769
3773
-548
1108
9809554,08
8899010,02
10564713,17
1618933,06
8143304,64
378821,41
-2054066,67
2968643,84
-86706,30
425742,08
-60321,00
121341,94
73936353,86
82841441,10
93412963,44
95039574,59
103190691,02
103577994,21
101532441,15
104509430,46
104431314,34
104865640,17
104813938,61
104943895,75
31
эксперимент.
Средние
потери:
120250руб.
Стандартное
отклонение
результата
хеджирования
опциона:
553498руб.
76
77.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВСТОП-ЛОСС СТРАТЕГИЯ
ХЕДЖИРОВАНИЯ
112,00
110,00
108,00
106,00
104,00
Цена акции, руб.
Страйк
102,00
100,00
98,00
96,00
94,00
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
Q = max (0, S 0 − X )
77
78.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВСТОП-ЛОСС СТРАТЕГИЯ
ХЕДЖИРОВАНИЯ. ПРИМЕР
День
Цена
Стоимость
Позиция по
Покупка
Безрисковое
Стоимость
Затраты на
акции, опциона,
акциям,
акций,
заимствование/вло
руб.
руб.
Стоп-лосс штук
акций, руб. штук
покупку, руб. жение средств, руб.
1
100,00 1309296,19
0,0000
0
0,00
0
0,00
-1309296,19
2
102,39 2051739,24
0,0000
0
0,00
0
0,00
-1309403,81
3
103,61 2499790,47
0,0000
0
0,00
0
0,00
-1309511,44
4
106,24 3793675,75
1,0000
1000000 106242466,55
1000000 106242466,55
104932847,48
5
108,07 4881437,60
1,0000
1000000 108073707,62
0
0,00
104941472,45
6
109,64 5934886,85
1,0000
1000000 109639848,39
0
0,00
104950098,13
7
108,82 5259122,03
1,0000
1000000 108821568,28
0
0,00
104958724,52
8
110,68 6612350,67
1,0000
1000000 110678116,86
0
0,00
104967351,62
9
109,70 5770959,47
1,0000
1000000 109699799,71
0
0,00
104975979,43
10
111,81 7430424,71
1,0000
1000000 111805632,54
0
0,00
104984607,94
11
112,99 8419431,01
1,0000
1000000 112986762,12
0
0,00
104993237,17
12
114,25 9542976,63
1,0000
1000000 114253623,85
0
0,00
105001867,11
13
114,90 10120328,57
1,0000
1000000 114900710,86
0
0,00
105010497,75
14
116,16 11309281,78
1,0000
1000000 116159643,12
0
0,00
105019129,10
15
114,37 9547590,54
1,0000
1000000 114370740,21
0
0,00
105027761,17
16
112,35 7595414,73
1,0000
1000000 112350760,17
0
0,00
105036393,94
17
113,38 8533050,13
1,0000
1000000 113384631,43
0
0,00
105045027,43
18
114,80 9887916,91
1,0000
1000000 114802728,24
0
0,00
105053661,62
19
115,71 10770300,60
1,0000
1000000 115710991,85
0
0,00
105062296,52
20
115,18 10223413,36
1,0000
1000000 115175395,04
0
0,00
105070932,13
21
114,92 9953316,56
1,0000
1000000 114916828,72
0
0,00
105079568,45
22
114,26 9281765,89
1,0000
1000000 114255124,71
0
0,00
105088205,49
23
113,79 8803414,18
1,0000
1000000 113786069,98
0
0,00
105096843,23
24
112,67 7676215,16
1,0000
1000000 112667584,16
0
0,00
105105481,68
25
111,00 6000785,27
1,0000
1000000 111000785,27
0
0,00
105114120,84
78
79.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВСТОП-ЛОСС СТРАТЕГИЯ
ХЕДЖИРОВАНИЯ. ПРИМЕР
День
Цена
Стоимость
Позиция по
Покупка
акции, опциона,
акциям,
Стоимость
акций,
руб.
руб.
Стоп-лосс штук
акций, руб. штук
1
100,00 1309296,19
0,0000
0
0,00
2
98,58 900282,60
0,0000
0
0,00
3
99,73 1121850,63
0,0000
0
0,00
4
98,35 753519,85
0,0000
0
0,00
5
97,64 579335,90
0,0000
0
0,00
6
97,58 526513,68
0,0000
0
0,00
7
98,10 564200,52
0,0000
0
0,00
8
100,32 975365,15
0,0000
0
0,00
9
100,09 855523,78
0,0000
0
0,00
10
99,15 598266,24
0,0000
0
0,00
11
98,59 449203,39
0,0000
0
0,00
12
99,79 603172,84
0,0000
0
0,00
13
100,72 736717,95
0,0000
0
0,00
14
98,57 299702,77
0,0000
0
0,00
15
98,09 204435,36
0,0000
0
0,00
16
100,56 483755,46
0,0000
0
0,00
17
101,05 503553,30
0,0000
0
0,00
18
103,09 953522,81
0,0000
0
0,00
19
102,16 567849,12
0,0000
0
0,00
20
102,66 585839,42
0,0000
0
0,00
21
101,28 205788,50
0,0000
0
0,00
22
99,57
27418,60
0,0000
0
0,00
23
99,30
4454,43
0,0000
0
0,00
24
98,40
6,34
0,0000
0
0,00
25
99,83
0,00
0,0000
0
0,00
Безрисковое
Затраты на
заимствование/вло
покупку, руб. жение средств, руб.
0
0,00
-1309296,19
0
0,00
-1309403,81
0
0,00
-1309511,44
0
0,00
-1309619,07
0
0,00
-1309726,72
0
0,00
-1309834,37
0
0,00
-1309942,03
0
0,00
-1310049,70
0
0,00
-1310157,38
0
0,00
-1310265,07
0
0,00
-1310372,77
0
0,00
-1310480,47
0
0,00
-1310588,19
0
0,00
-1310695,91
0
0,00
-1310803,65
0
0,00
-1310911,39
0
0,00
-1311019,14
0
0,00
-1311126,90
0
0,00
-1311234,67
0
0,00
-1311342,44
0
0,00
-1311450,23
0
0,00
-1311558,02
0
0,00
-1311665,83
0
0,00
-1311773,64
0
0,00
-1311881,46
31
эксперимент.
Средняя
прибыль:
568923 руб.
Стандартное
отклонение
результата
хеджирования
опциона:
1330530 руб.
79
80.
свопыСВОПЫ
• Своп – это соглашение между двумя контрагентами
об обмене в будущем платежами в соответствии с
определенными в контракте условиями. Своп можно
рассматривать
как
портфель
форвардных
контрактов, заключенных между двумя сторонами. В
случае валютного свопа
происходит обмен
номинала и фиксированного процента в одной
валюте на номинал и фиксированный процент в
другой валюте. Осуществление валютного свопа
может быть обусловлено различными причинами,
например, ограничениями по конвертации валют,
необходимостью устранения валютных рисков,
стремлением выпустить облигации в валюте другой
страны, где эмитент мало известен.
80
81.
свопыПРИМЕР
ВАЛЮТНО-ПРОЦЕНТНОГО СВОПА
Рассмотрим две компании, одну – в Великобритании, а другую в США. Каждая компания
имеет иностранную дочернюю фирму, действующую в другой стране и нуждающуюся в
финансировании. Пусть рыночный курс одного фунта стерлингов составляет 1,9 доллара
США. Процентная ставка для стерлингов – 7%, для долларов – 4%. Дочерняя фирма
американской компании нуждается в финансировании в размере £130млн.; фирма,
имеющая учредителем компанию из Великобритании, хотела бы занять $247млн. Обе
фирмы устраивает пятилетний срок заимствования.
Обмен платежами будет
производиться один раз в год.
Год
Американская
компания
($ млн.)
Американская «дочка» английской
компании
($ млн.)
Английская
компания
(£ млн.)
Английская «дочка» американской
компании
(£ млн.)
0
-247
247
-130
130
1
9,88
-9,88
9,1
-9,1
2
9,88
-9,88
9,1
-9,1
3
9,88
-9,88
9,1
-9,1
4
9,88
-9,88
9,1
-9,1
5
256,88
-256,88
139,1
-139,1
81
82.
свопыГРАФИЧЕСКАЯ ИЛЛЮСТРАЦИЯ ВАЛЮТНОПРОЦЕНТНОГО СВОПА
£130млн.
Английская
«дочка»
американской
компании
Американская
дочка
английской
компания
Компания А
Английская
компания
£9,1млн. ежегодно,
£139,1млн. в конце срока
$247млн
.
Американская
компания
$9,88млн. ежегодно,
$256,88млн. в конце
срока
Банк
Компания Б
82
83.
свопыЧИСТЫЙ ПРОЦЕНТНЫЙ СВОП – ОБМЕН
ФИКСИРОВАННОЙ СТАВКИ НА ПЛАВАЮЩУЮ
Для компании А котировки займа на пять лет могут составить LIBOR+10 б.п. по плавающей ставке или
11% по фиксированной ставке; для компании Б ставки заимствования составляют соответственно
LIBOR+50 б.п. и 12%. Предположим, что компания А предпочитает занимать по плавающему курсу, а
компания Б – по фиксированному. Если компании действуют порознь, то А получает займ под
LIBOR+10 б.п., а Б – под фиксированные 12%. Компании могут получить займы на более выгодных
условиях. Для этого суммы займов должны совпадать. Рассмотрим схему, при которой компания А
занимает средства под фиксированные 11%, компания Б – под LIBOR+50 б.п., при этом компании
вступают в процентный своп, согласно которому А будет делать периодические выплаты Б по ставке
LIBOR, получая, в свою очередь, периодические выплаты по фиксированной ставке 11,20%. Для
компании А результат операций эквивалентен получению займа под ставку LIBOR - 20б.п. Компания Б
в итоге будет осуществлять платежи по кредиту по ставке 11,70%. Таким образом, каждый заемщик
улучшает условия финансирования на 30 б.п.
11,20%
А
Б
LIBOR
11%
Инвестор с
фиксированной
ставкой
LIBOR+0,50%
Инвестор с
плавающей
ставкой
83
84.
свопыTotal Return Swap
Своп на совокупный доход – англ. Total Return Swap, соглашение о свопе, в котором
одна сторона осуществляет платежи на базе определенной процентной ставки, либо
фиксированной или плавающей, в то время как другая сторона осуществляет платежи,
основанные на доходности от базового актива, которая включает не только производимый
активом доход, но и любой прирост капитала.
В свопах на совокупный доход базовый актив, обычно называемый «актив-ориентир»,
обычно является фондовым индексом, кредитом или облигациями. Этот актив принадлежит
стороне, получающей платежи по установленной процентной ставке.
Свопы на совокупный доход позволяют стороне, получающей платежи на основе
доходности, принять на себя риски и преимущества владения активом-ориентиром,
фактически не вступая в права собственности. Эти свопы используются хедж-фондами,
потому что они извлекают пользу из «получения» большого количества активов с
минимальными затратами.
В свопе на совокупный доход сторона, получающая доходность, получит любой доход,
произведенный активом, а так же как получит прирост его стоимости, если цена актива
будет увеличиваться в течение срока действия свопа. В свою очередь, получатель
совокупного дохода должен платить владельцу актива установленную процентную ставку в
течение срока действия свопа.
Если цена актива в течение срока действия договора упадет, то получатель совокупного
дохода будет обязан оплатить владельцу актива сумму, на которую актив-ориентир упал в
цене.Например, две стороны могут вступить в однолетний своп на совокупный доход, где
Сторона А получает ЛИБОР плюс фиксированная маржа 3,5%, а Сторона Б получают
совокупный доход по индексу S&P 500 на принципал в $3 миллиона. Если ЛИБОР составит
4,5%, а S&P 500 вырастет на 9,5%, то Сторона А оплатит Стороне Б 9,5% и получит 8%
(ЛИБОР 4,5% плюс фиксированная маржа 3,5%). Платеж будет неттингован в конце
действия соглашения о свопе, причем Сторона Б получит платеж 45000$ ($3 миллиона x
(9,5% - 8%).
84
85.
свопыДРУГИЕ ТРАДИЦИОННЫЕ СОГЛАШЕНИЯ
НА ПРОЦЕНТНЫЕ СТАВКИ
• Базовые свопы – обмен плавающих ставок (например, LIBOR на
плавающую ставку первоклассным заемщикам)
• Амортизируемые свопы – основная сумма уменьшается до окончания
срока свопа
• Увеличивающиеся свопы – основная сумма увеличивается до
окончания срока свопа
• Свопы с нулевым купоном – уплата по фиксированной ставке
осуществляется в конце срока
• Отложенный своп – купоны для поздних дат не определены
• Обратимые свопы – плательщики по плавающим и фиксированным
ставкам меняются местами
• Дифференциальный своп – платежи осуществляются в одной валюте,
купон определяется разностью ставок в той же и в некоторой другой
валюте
• Свопы с правом досрочного погашения – одна из сторон может
прервать действие свопа
• Свопы с продлеваемым сроком – могут быть пролонгированы по
85
желанию одной из сторон
86.
свопыПРИМЕР РАСЧЕТА СВОПА 1
Требуется рассчитать рублевый процентный своп на 1млрд.руб. сроком на 3 года. Процентные платежи
осуществляются спустя 1, 2 и 3 года. Плавающие платежи рассчитываются по ставке доходности государственных
облигаций со сроком 1 год, которая действовала на рынке за год до момента платежа. В момент заключения свопа ставки
инвестиций на срок 1, 2 и 3 года, соответствующие кривой доходности государственных облигаций, составляют
соответственно 3%; 4,5% и 6,2% годовых по ставке сложных процентов.
Решение. Первая выплата по плавающей ставке известна: 1000млн.0,03 = 30млн.руб. Рассчитаем ожидаемые
ставки доходности годичных государственных облигаций спустя 1 и 2 года. Из соображений отсутствия арбитража должно
выполняться следующее соотношение:
2
1 + 3 100 1 + x1 100 = 1 + 4,5 100,
где x1 - форвардная ставка (процентная ставка годичных облигаций через 1 год после заключения свопа). Решая уравнение
относительно x1 , получим:
2
(
)(
) (
)
(1 + 4,5 100)
x1 =
− 1 = 0,06
1 + 3 100
Уравнение для форвардной ставки спустя 2 года:
100) = (1 + 6,2 100 ) ,
3
(1 + 6,2 100 )3
x2 =
− 1 = 0,097
2
(1 + 4,5 100)
откуда
Ожидаемое
(1 + 4,5 100)2 (1 + x2
значение
выплаты
по
плавающей
ставке
через
2
года
после
заключения
контракта
составит
1000 × 0,06 = 60 млн.руб., а в момент погашения свопа - 1000 × 0,097 = 97 млн.руб. Рассчитаем приведенную стоимость
платежей по плавающей ставке:
Для определения
P=
30
60
97
+
+
= 165,0538
2
1 + 0,03 (1 + 0,045) (1 + 0,062 )3
млн.
ставки фиксированных платежей необходимо решить следующее уравнение:
P = 165,0538 =
1000r
1000r
1000r
+
+
2
1 + 0,03 (1 + 0,045) (1 + 0,062 )3
Фиксированная процентная ставка свопа должна составить
1000
1000
1000
= 0,061
r = 165,0538
+
+
2
3
1
+
0
,
03
(
)
(
)
1
0
,
045
1
0
,
062
+
+
86
87.
свопыПРИМЕР РАСЧЕТА СВОПА 2
Рассчитать валютный своп рубль-доллар на $100млн. на срок 3 года. Процентные платежи осуществляются
через 1, 2 и 3 года после заключения контракта. В момент погашения свопа производится обмен основными капиталами.
Платежи в обеих валютах определяются фиксированными процентными ставками. Временная структура процентных
ставок по рублям совпадает с рассмотренной в предыдущей задаче. Безрисковая ставка по долларам на период 1 год
составляет 2,3%; на период 2 года – 3,25%; на 3 года – 4,15%. Текущий обменный курс доллара составляет 28,49руб.
Решение. Вначале рассчитаем форвардные ставки по долларам на период 1 год аналогично тому, как это
делалось при решении предыдущей задачи. Форвардная ставка через год составляет
(1 + 3,25 100)2
y1 =
− 1 = 0,042
1 + 2,3 100
; через 2 года -
(1 + 4,15 100 )3
y2 =
− 1. = 0,0597
2
(1 + 3,25 100)
Приведенная стоимость ожидаемых долларовых платежей по плавающей ставке составляет
P$ =
100 × 0,023 100 × 0,042 100 × 0,0597 + 100
+
+
= 99,9885
млн. долларов.
1 + 0,023 (1 + 0,0325)2
(1 + 0,0415)3
Фиксированная ставка процентных платежей по долларам получается в результате решения уравнения
100r $
100r $
100r $ + 100 ,
$
P = 99,9885 =
+
+
1 + 0,023 (1 + 0,0325)2 (1 + 0,0415)3
100
100
100
100
= 0,041
r $ = 99,9885 −
+
+
3
2
3
(1 + 0,0415) 1 + 0,023 (1 + 0,0325) (1 + 0,0415)
откуда
.
Соответствующая величина процентного платежа: 100*0,041=$4,1млн.
В соответствии с правилами валютного свопа приведенная стоимость платежей в рублях
должна составлять 99,9885 × 28,49 = 2848,672 млн.руб. Фиксированная процентная ставка по рублям, как и в предыдущей
задаче, составляет 0,061. Остается рассчитать размер основного капитала в рублях. Для этого требуется решить
уравнение
2848,672 =
C × 0,061 C × 0,061 C × 0,061 + C
+
+
1 + 0,03 (1 + 0,045)2
(1 + 0,062)3
,
откуда размер основного капитала в рублях, выплачиваемый при погашении валютного свопа составляет
0,061
0,061
1,061
= 2846,124 млн.руб.
C = 2848,672
+
+
2
3
1
+
0
,
03
1
+
0
,
045
1
+
0
,
062
(
)
(
)
Размер процентных платежей:
2846,124 × 0,061 = 173,6136
млн.руб.
87
88.
ОПЦИОНЫ НА ПРОЦЕНТНЫЕ СТАВКИСВОПЦИОНЫ
• Свопцион - опцион на своп процентных ставок.
• Покупатель свопциона получает право заключить
соглашение о свопе процентных ставок на
определенную дату в будущем. В соглашении на
свопцион указывается, будет ли покупатель
свопциона получателем фиксированного курса
(свопцион колл) или его плательщиком (свопцион
пут).
• Продавец свопциона становится противоположной
стороной в свопе, если его покупатель принимает
решение реализовать свое право.
88
89.
ОПЦИОНЫ НА ПРОЦЕНТНЫЕ СТАВКИКЭПЫ, ФЛОРЫ, КОЛЛАРЫ
• Кэпы и флоры – многопериодные расчетные
опционы на процентные ставки. Кэп подобен
опциону
колл,
флор
–
опциону
пут.
Периодичность платежей определяется при
заключении контракта. Длинный коллар –
комбинация длинного кэпа и короткого флора
• Пример: кэп на ставку LIBOR. Цена исполнения
К=3%. Если в момент предыдущего платежа
LIBOR=2,95% , платеж не производится. В
случае значения LIBOR 3,25% продавец кэпа
должен заплатить сумму, пропорциональную 25
п.п. Если номинал кэпа 10млн. швейцарских
франков,
то
сумма
платежа
составит
0,0025*10000000 = 25000 швейцарских франков.
89
90.
ФУНДАМЕНТАЛЬНЫЕ ТЕОРЕМЫФИНАНСОВОЙ МАТЕМАТИКИ
АРБИТРАЖ И ПОЛНОТА
Стоимость опциона по Блэку-Шоулсу можно интерпретировать как стоимость непрерывного
хеджирования опциона базовым активом и безрисковым активом. Данная схема хеджирования всегда
приводит к одной и той же величине издержек вне зависимости от реализовавшейся ценовой траектории.
Однако, если не осуществлять хеджирование опциона базовым активом, а просто дождаться экспирации, то
средняя дисконтированная величина выплаты по европейскому опциону на бездивидендную акцию также
определяется формулой Блэка-Шоулса при условии, что математическое ожидание цены базового актива в
момент экспирации составляет
E [S t ] = S 0 e rt .
(76)
Данный факт является частным случаем более общего результата, который относится к основаниям
финансовой математики. Для того, чтобы сформулировать соответствующую теорему, дадим несколько
определений и приведем ряд необходимых предварительных результатов.
Вначале уточним определение арбитража, данное на слайде 24.
Пусть P - вероятностная мера, описывающая процесс изменения стоимости базового актива опциона.
Определение. Портфель, состоящий из рискового и безрискового актива, называется самофинансируемым,
если для него отсутствуют внешний приток и отток средств.
Определение. Самофинансируемый портфель называется арбитражным, если для него выполняются
следующие условия:
X 0π = 0 ,
X τπ ≥ 0 при τ ≤ t с вероятностью 1,
X tπ > 0 с положительной вероятностью.
Здесь X τπ - капитал (стоимость) портфеля в момент времени τ , t - терминальный момент времени, вероятности
выполнения условий рассчитываются на основе меры P . Содержательно данное определение означает
возможность получения прибыли без начальных инвестиций и риска. Множество самофинансируемых
арбитражных портфелей принято обозначать SFarb .
90
91.
ФУНДАМЕНТАЛЬНЫЕ ТЕОРЕМЫФИНАНСОВОЙ МАТЕМАТИКИ
АРБИТРАЖ И ПОЛНОТА (ПРОДОЛЖЕНИЕ)
Определение. Последовательность случайных переменных X 0 , X 1 ,K называется мартингалом, если
E ( X i | X i −1 , X i − 2 ,K , X 0 ) = X i −1 для всех i > 0 .
Определение. Вероятностную меру P * называют мартингальной или нейтральной к риску, если
относительно P * стохастическая последовательность (Sτ Bτ )τ ≤t является мартингалом. Множество
таких мер будем обозначать Ρ∗ .
Следующую теорему называют первой фундаментальной теоремой финансовой математики.
Теорема 1. Множество Ρ∗ непусто тогда и только тогда, когда пусто множество SFarb .
Данный результат вполне понятен с интуитивной точки зрения: если последовательность
(Sτ Bτ )τ ≤t является мартингалом, то рынок «справедливый», возможности совершения арбитража
отсутствуют и, следовательно, множество SFarb пусто.
Определение. Рынок называется полным, если для любого платежного обязательства ft существует
самофинансируемая стратегия (портфель) π , терминальный капитал которой воспроизводит ft , т.е.,
X tπ = f t .
Величина ft в общем случае зависит от траектории случайного процесса от момента времени
τ = 0 до момента τ = t . Имеет место так называемая вторая фундаментальная теорема:
Теорема 2. Полнота безарбитражного рынка имеет место тогда и только тогда, когда множество Ρ∗
состоит из единственной мартингальной меры.
Теперь можно сформулировать искомый результат для цены платежного обязательства
европейского типа:
91
92.
ФУНДАМЕНТАЛЬНЫЕ ТЕОРЕМЫФИНАНСОВОЙ МАТЕМАТИКИ
РИСК-НЕЙТРАЛЬНЫЙ МИР
Теорема 3. Если ft зависит только от St , то справедливая цена обязательства ft в момент t = 0 составляет
f
C ( f t , P *) = B0 E * t .
(77)
Bt
Здесь E ∗ - математическое ожидание по мере P * . Теорема 3 служит основанием для численных расчетов
стоимости опциона в полных рынках по методу Монте-Карло.
В модели геометрического броуновского движения (33) мера P определяется параметрами µ и σ .
Мера P * соответствует случаю µ = r . В случае биномиального рынка мера P * задается соотношением (51).
Рынок, на котором изменение цены базового актива соответствует мартингальной вероятностной
мере, называют риск-нейтральным рынком или риск-нейтральным миром. Инвесторам такого рынка
достаточно того, что актив в среднем растет в соответствии с безрисковой ставкой процента, хотя данную
доходность можно получать, ничем не рискуя. Таких инвесторов также называют риск-нейтральными
инвесторами.
Если рынок неполон, то при определенных условиях существует множество мартингальных мер и
целый интервал цен, каждая из которых гарантирует отсутствие возможности арбитража в рассмотренном
выше смысле.
92
93.
ФУНДАМЕНТАЛЬНЫЕ ТЕОРЕМЫФИНАНСОВОЙ МАТЕМАТИКИ
ЦЕНА РИСКА
Рассмотрим рынок производных инструментов на случайную переменную, которая следует процессу
Ито:
dθ
θ
= mdt + sdz .
(78)
Параметры m и s зависят только от θ и от t . Переменная θ не обязательно является ценой инвестиционного
актива.
Пусть f1 и f 2 - цены двух производных инструментов. Будем рассматривать производные инструменты
европейского типа. Согласно лемме Ито, цены рассматриваемых инструментов следуют стохастическим
дифференциальным уравнениям
df1
= µ1dt + σ 1dz
f1
(79)
df 2
= µ 2 dt + σ 2 dz ,
f2
(80)
и
где µ1 , µ 2 , σ 1 и σ 2 - функции от θ и t .
Из рассматриваемых производных инструментов можно построить портфель, стоимость которого не
подвержена действию случайного фактора на бесконечно малом промежутке времени. Для этого достаточно
открыть позицию по первому инструменты в размере σ 2 f 2 и позицию в размере − σ 1 f1 . Стоимость такого
портфеля составит
Π = (σ 2 f 2 ) f1 − (σ 1 f1 ) f 2 ,
(81)
а изменение стоимости за период времени dt с учетом (79) и (80) dΠ = (σ 2 f 2 )df1 − (σ 1 f1 )df 2 = (µ1σ 2 f1 f 2 − µ 2σ 1 f1 f 2 )dt .
(82)
93
94.
ФУНДАМЕНТАЛЬНЫЕ ТЕОРЕМЫФИНАНСОВОЙ МАТЕМАТИКИ
ЦЕНА РИСКА (ПРОДОЛЖЕНИЕ)
Поскольку на бесконечно малом промежутке времени данный портфель – безрисковый, его доходность
соответствует безрисковой ставке процента:
dΠ
= rdt .
Π
(83)
Подставляя в последнее соотношения равенства (81) и (82), получим:
или
µ1σ 2 − µ 2σ 1 = rσ 2 − rσ 1
(84)
µ1 − r µ 2 − r
=
=λ.
σ1
σ2
(85)
Параметр λ называют ценой риска. Он является функцией от θ и t , однако не зависит от вида
производных инструментов. Мы доказали следующее
Утверждение. На рассматриваемом рынке цена риска одинакова для всех производных инструментов
«европейского» типа.
Для произвольного финансового инструмента
соотношение в уравнение (78), получим:
dθ
θ
µ −r
= λ или µ = r + λσ . Подставляя последнее
σ
= (r + λσ )dt + σdz .
(86)
Пусть f и g - цены торгуемых инструментов, которые зависят от одного и того же источника
неопределенности. f и g следуют уравнению (86), волатильность цен обозначим соответственно σ f и σ g . Для
простоты будем считать, что рассматриваемые инструменты не приносят дополнительного дохода
(дивидендов, купонных платежей и т.п.). Рассмотрим процесс φ = f g .
Утверждение. Если цена риска на рынке λ = σ g , то процесс φ является мартингалом для любого финансового
инструмента f .
94
95.
ФУНДАМЕНТАЛЬНЫЕ ТЕОРЕМЫФИНАНСОВОЙ МАТЕМАТИКИ
ФОРВАРДНЫЙ РИСК-НЕЙТРАЛЬНЫЙ МИР
Доказательство. Подставляя λ = σ g в уравнение (86), для цен f и g получим:
df = (r + σ gσ f ) fdt + σ f fdz ,
dg = (r + σ g2 )gdt + σ g gdz .
Применение леммы Ито дает
(
d ln g = (r + σ
(87)
(88)
)
d ln f = r + σ gσ f − σ 2f 2 dt + σ f dz
Отсюда
или
2
g
)
2 dt + σ g dz .
(
)
d (ln f − ln g ) = σ gσ f − σ 2f 2 − σ g2 2 dt + (σ f − σ g )dz
(σ − σ g ) dt + (σ − σ )dz .
f
d ln = − f
f
g
2
g
2
Снова применяя лемму Ито, окончательно получим:
f
f
d = (σ f − σ g ) dz .
g
g
Последнее соотношение показывает, что процесс φ является мартингалом относительно выбранной
вероятностной меры. Утверждение доказано.
Говорят, что выбор λ = σ f определяет форвардный риск-нейтральный мир относительно g .
Обозначим E g математическое ожидание в форвардном риск-нейтральном мире по отношению к g .
Поскольку φ следует мартингальному процессу,
f
f0
= E g T
g0
gT
или
f
f 0 = g 0 E g T
gT
.
(89)
96.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВЕВРОПЕЙСКИЕ ОПЦИОНЫ НА БЕСКУПОННУЮ ОБЛИГАЦИЮ
Выберем gt = P(t , T ) , где P(t , T ) - стоимость бескупонной облигации с номиналом 1 и сроком погашения T в
момент времени t . Тогда из (89) следует, что
f 0 = P(0, T )E ( fT ) .
(90)
Пусть ft - стоимость опциона колл на облигацию, стоимость которой будем обозначать Bt . Тогда, на основе
(90) получаем:
c = P(0, T )E [max( BT − K ,0] .
Можно показать, что
E [max( BT − K ,0] = E [BT ]N (d1 ) − KN (d 2 ) ,
(91)
d1 =
ln(E [BT ] K ) + σ B2 T 2
ln(E[BT ] K ) − σ B2 T 2
, d1 =
= d1 − σ B T ,
σB T
σB T
где σ B - волатильность цены базовой облигации.
Утверждение. В форвардном риск-нейтральном мире относительно P(t , T )
E [BT ] = FB ,
(92)
где FB - форвардная цена облигации.
Доказательство. Цена форвардного контракта в рассматриваемом мире составляет
P(0, T )(E [BT ] − K ) ,
где K - цена поставки. Форвардная цена – это цена поставки, которая делает цену форварда нулевой. Т.о., в
форвардном риск-нейтральном мире E [BT ] = FB .
Подстановка равенства (92) в формулы (91) приводит их к виду формул Блэка цены фьючерсного контракта
(47), (48) и (49).
Аналогично можно выписать формулы цены европейского опциона пут на облигацию.
96
97.
ЦЕНООБРАЗОВАНИЕ ОПЦИОНОВЕВРОПЕЙСКИЕ ОПЦИОНЫ НА ПРОЦЕНТНЫЕ СТАВКИ
Рассмотрим однопериодный опцион колл на процентную ставку R (кэплет) со сроком истечения T .
Период действия ставки R - от момента t до момента T . Номинал кэплета равен 1. Тогда в момент времени T
он стоит (T − t ) max(R − K ,0 ) . Тогда в момент t кэплет стоит
1 + (T − t )K
(T − t )R − (T − t )K
T −t
1
1
max (R − K ,0 ) = max
,0 = max 1 −
,0 = (1 + (T − t )K ) max
−
,0 .
1 + (T − t )R
1 + (T − t )R
1 + (T − t )R
1 + (T − t )K 1 + (T − t )R
Заметим, что
1
1
1
= P(t , T ) . Следовательно, max
−
,0 - платежная функция
1 + (T − t )R
1 + (T − t )K 1 + (T − t )R
европейского опциона пут на бескупонную облигацию.
Кэпы, флоры и коллары могут быть рассмотрены как портфели опционов колл и пут европейского
типа.
Рассмотренные модели ценообразования опционов на процентные ставки основаны на допущении о
логнормальности распределения цены облигации. Они используются для оценки таких инструментов, как
кэпы, флоры , коллары, европейские свопционы. Однако, данные модели не рассматривают, как процентные
ставки изменяются во времени. Соответственно, они не могут быть использованы для оценки американских
опционов, отзывных облигаций, структурных продуктов. Для оценки стоимости таких продуктов
используются модели динамики временной структуры процентных ставок. Они описывают поведение
бескупонных ставок всех сроков. К данному классу относятся, например, модели Rendleman и Batter, Vasicek,
модели Cox, Ingersoll, Ross и другие модели.
97
98.
.МОДЕЛИ ПРОЦЕНТНЫХ СТАВОК
Краткосрочная ставка и временная структура процентных ставок
Выберем в формуле (89) в качестве процесса банковский счет. Состояние такого счета может быть
описано уравнением
.
=
,
(93)
где - в общем случае стохастическая процентная ставка. Поскольку снос в уравнении (93) теперь равен ,
то, согласно (85), цена риска нулевая, т.е. это традиционный риск-нейтральный мир. Пусть
= 1. Тогда,
решая (93), получим
.
=e
где ̅ - средняя ставка за период.
Согласно (89)
+ = ,-
̅
=
. ̅
,
(94)
+ .
(95)
Если + – цена 2 , 3 бескупонной облигации с номиналом 1 и сроком погашения 3 в момент времени , то
2 , 3 = ,-
. ̅
.9
.
(96)
С другой стороны
2 ,3 =
.< 9,
.9
.
(97)
Отсюда
@ ,3 = −
B
.9
ln 2 , 3 .
(98)
99.
.МОДЕЛИ ПРОЦЕНТНЫХ СТАВОК
Модель Васичека
Пусть ставка следует процессу
.
=E ,
+s ,
H.
B
IJ
K
M
+L
(99)
По лемме Ито
+=
IJ
+E
I9
IJ
I
+ LK
I
IJ
I
H.
(100)
Поскольку мы рассматриваем риск-нейтральный мир, цена риска λ = 0. Пусть+– бескупонная облигация с
погашением в момент времени T. Поскольку бескупонная облигация не дает дополнительного дохода, то
IJ
I9
+E
IJ
I
B
IJ
K
I M
+ LK
= +.
(101)
Модели равновесия определяют некие «разумные» траектории мгновенной ставки, не учитывая
текущую форму кривой бескупонной доходности.
Модель Васичека
=Q R−
+ S H.
(102)
Стоимость бескупонной облигации в модели Васичека дается выражением
2 ,3 = T ,3
.U 9,
9
,
(103)
100.
.МОДЕЛИ ПРОЦЕНТНЫХ СТАВОК
Модели равновесия
где
V ,3 =
B.W XY XZ
[
(104)
и
U 9,
T , 3 = \]
. ^9 [M _.`M ⁄K
[M
−
` M U 9,
b[
M
.
(105)
Модель Кокса-Ингерсолла-Росса
=Q R−
+S
H.
(106)
Стоимость бескупонной облигации:
2 ,3 = T ,3
.U 9,
9
,
где
V ,3 =
T ,3 =
K W c XZ .B
,
d^[ W c XZ .B ^Kd
KdW Yec
XZ ⁄M
d^[ W c XZ .B ^Kd
K[_⁄` M
, f = QK + 2S K .
100
101.
.МОДЕЛИ ПРОЦЕНТНЫХ СТАВОК
Безарбитражные модели
Модель Хо-Ли
где h
= i9 0,
=h
+ SK .
+ S H,
2 ,3 = T ,3
(107)
. 9
.9
,
(109)
где
jkT , 3 = jk
l ,
l ,9
+ 3−
i 0,
B
K
− SK 3 −
K
.
(110)
Модель Халла-Уайта
= h
−Q
+ S H,
(111)
или
=Q
m 9
[
−
+ S H.
(112)
101
102.
.МОДЕЛИ ПРОЦЕНТНЫХ СТАВОК
Модели Хо-Ли и Халла-Уайта
Модель Хо-Ли
где h
= i9 0,
=h
+ SK .
+ S H,
2 ,3 = T ,3
(107)
. 9
.9
,
(109)
где
jkT , 3 = jk
l ,
l ,9
+ 3−
i 0,
B
K
− SK 3 −
K
.
(110)
Модель Халла-Уайта
= h
−Q
+ S H,
(111)
или
=Q
m 9
[
−
+ S H.
(112)
102
103.
.МОДЕЛИ ПРОЦЕНТНЫХ СТАВОК
Модели Халла-Уайта и Блэка-Карасински
h
= i9 0,
+ Qi 0,
+
jk T , 3 = jk
l ,
l ,9
9
B.W XY XZ
[
B
+ V , 3 i 0, 3 − b[n S K
K[9
1−
.U 9,
2 ,3 = T ,3
V ,3 =
`M
K[
,
(113)
,
(114)
,
(115)
.[
−
.[9 K
K[9
−1 .
(116)
Модель Блэка-Карасински
jk = h
−Q
jk = h
ln
− Q ln
+S
H,
(117)
+S H.
(118)
103
104.
ЛИТЕРАТУРАОсновная:
1. Hull J.C. Options, Futures and Other Derivative Securities. 8 ed. – Englewood Cliffts, NJ, Prentice Hall. – 2011.
2. Буренин А.Н. Рынок ценных бумаг и производных финансовых инструментов. – М.: Научно-техническое общество имени академика
С.И.Вавилова, 2002.
3. Галиц Л. Финансовая инженерия / Пер. с англ. А.М.Зубкова. – М.: ТВП, 1988.
4. Мельников А.В., Волков С.Н., Нечаев М.Л. Математика финансовых обязательств. – М.: ГУ ВШЭ, 2001.
5. Мельников А.В. Финансовые рынки. Стохастический анализ и расчет производных ценных бумаг. – М.: ТВП, 1997.
6. Голембиовский Д.Ю. Оптимизация портфеля финансовых инструментов // Энциклопедия финансового риск-менеджмента / Под. ред.
А.А.Лобанова и А.В.Чугунова. – М.: Альпина Паблишер, 2003.
7. Мэрфи Дж. Технический анализ фьючерсных рынков: теория и практика. – М.: Евро, 2004. – 592с.
8. Чекулаев М.В. Риск-менеджмент: управление финансовыми рисками на основе анализа волатильности. – М.: Альпина Паблишер,
2002.
9. Чекулаев М.В. Загадки и тайны опционной торговли. – М.: ИК Аналитика, 2001. – 432с.
10. Шарп У., Александер Г., Бэйли Д. Инвестиции / Пер. с англ. А.Н.Буренина, А.А.Васина. - М.: ИНФРА-М, 1997.
11. Голембиовский Д.Ю., Барышников И. В. Стратегии управления ценовым риском (на примере экспортно-ориентированных
предприятий) // Вопросы экономики. – 2003. - №8. – С.67-80.
Дополнительная:
12. Швагер Дж. Технический анализ. Полный курс / Пер. с англ. – М.: Альпина Паблишер, 2002.
13. Доугерти К. Введение в эконометрику / Пер. с англ. О.О.Замкова, Е.Н.Лукаш, О.Ю.Шибалкина. – М.: ИНФРА-М, 2004.
14. Буренин А.Н. Рынки производных финансовых инструментов. – М.:
ИНФРА-М, 1996.
15. Вильямс Б. Торговый хаос: Экспертные методики максимизации прибыли. – М.: ИК Аналитика, 2000.
16. Вильямс Б. Новые измерения в биржевой торговле. - М.: ИК Аналитика, 2000.
17. The London Clearing House Limited (1991): Standard Portfolio Analysis of
Risk. Technical Specifications.
18. Ширяев А.Н. Основы стохастической финансовой математики. Т.1.
Факты. Модели.- М.: Фазис, 1998.
19. Ширяев А.Н. Основы стохастической финансовой математики. Т.2.
Факты. Теория.- М.: Фазис, 1998.
20. Голембиовский Д.Ю. Расчет залога по портфелю производных инструментов // Управление риском. – 2005. - №1. – С.27-48.
21. Голембиовский Д.Ю. Аппроксимация цен опционов на основе экспоненциальной модели кривой волатильности // Системы
управления и информационные технологии. – 2005. - №2 (19). – С.71-76.
22. Голембиовский Д.Ю. Прогнозирование биржевых цен опционов // Управление риском. – 2005. - №2. – С.20-27.
104




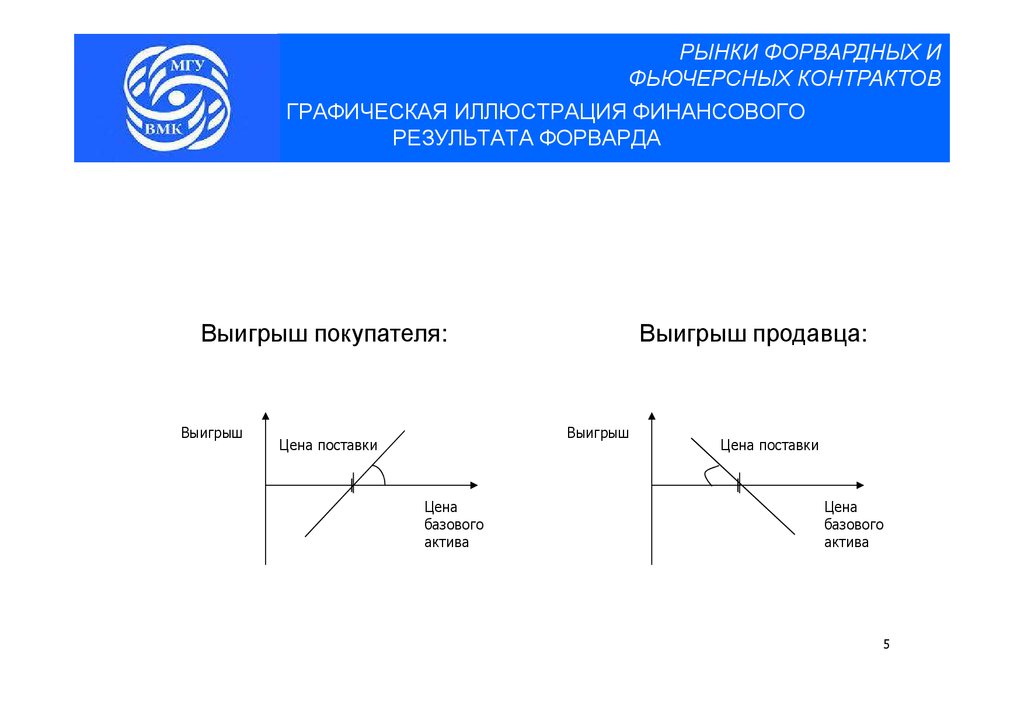






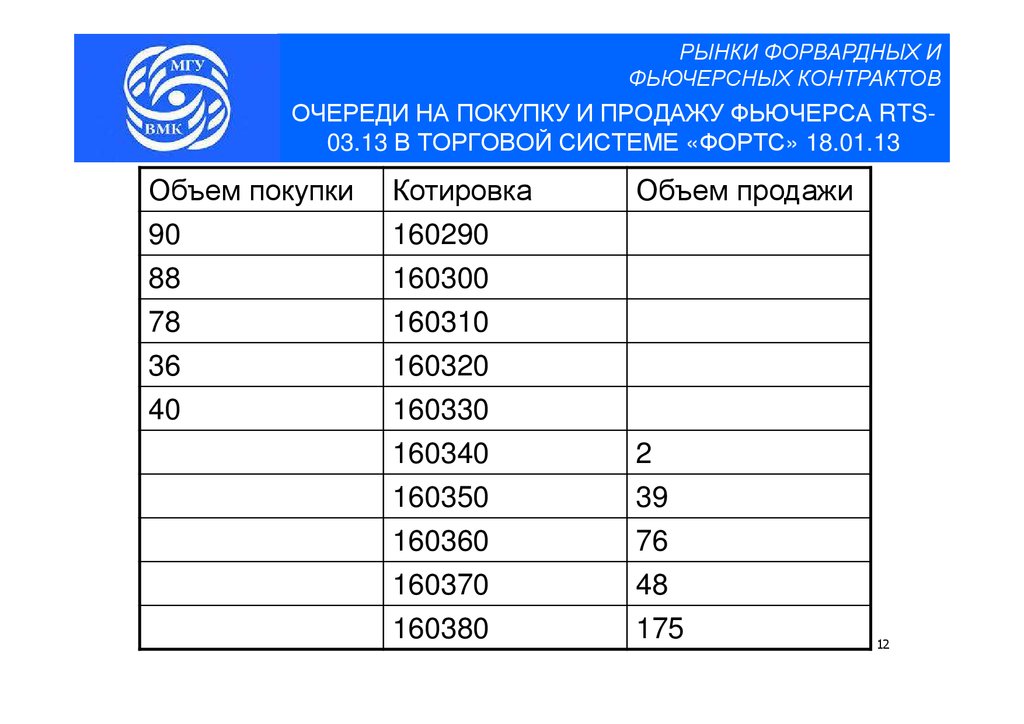





























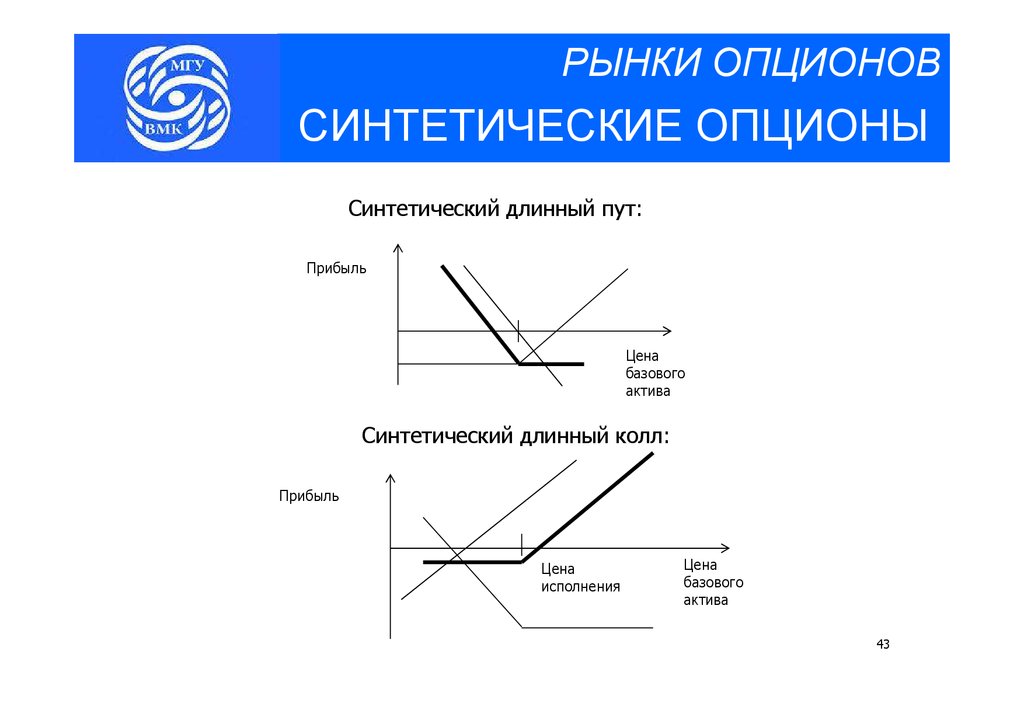
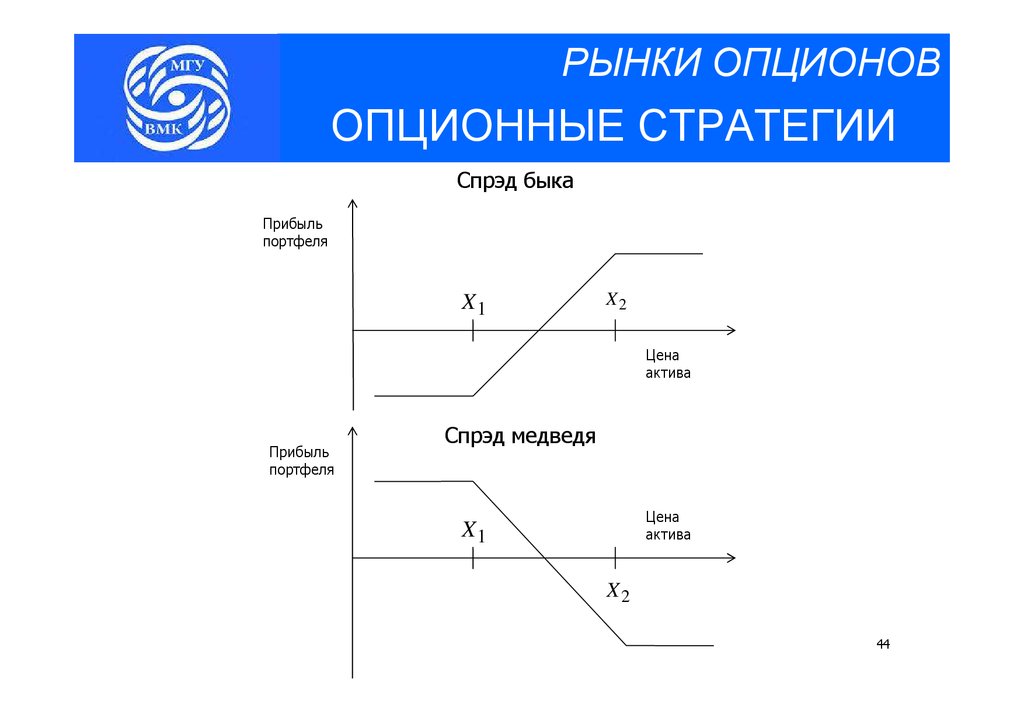
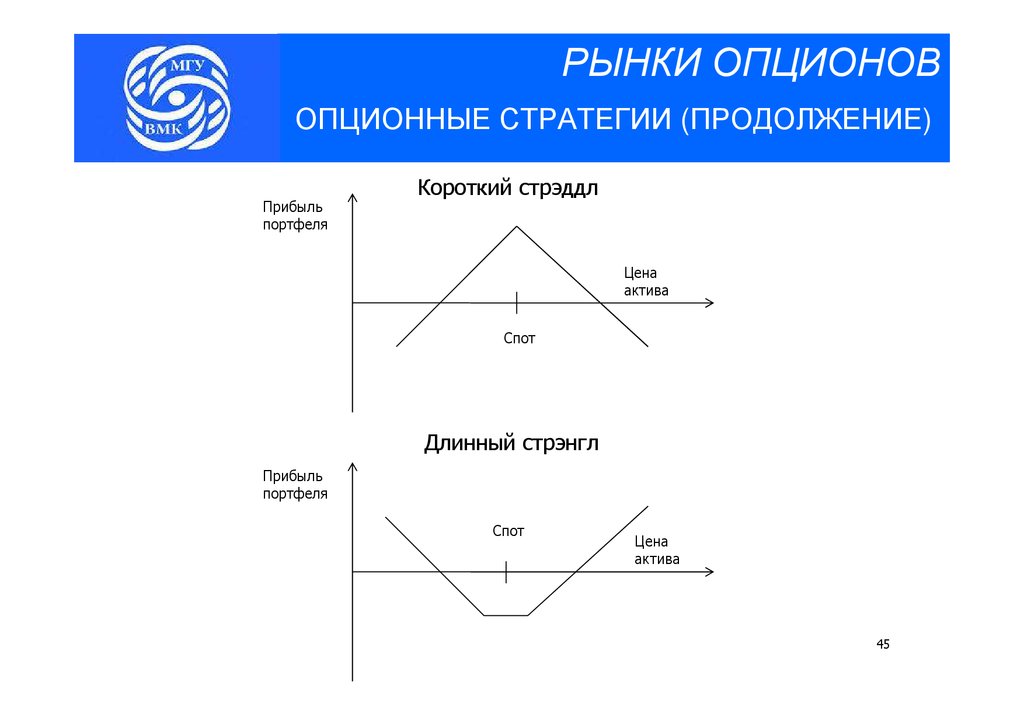
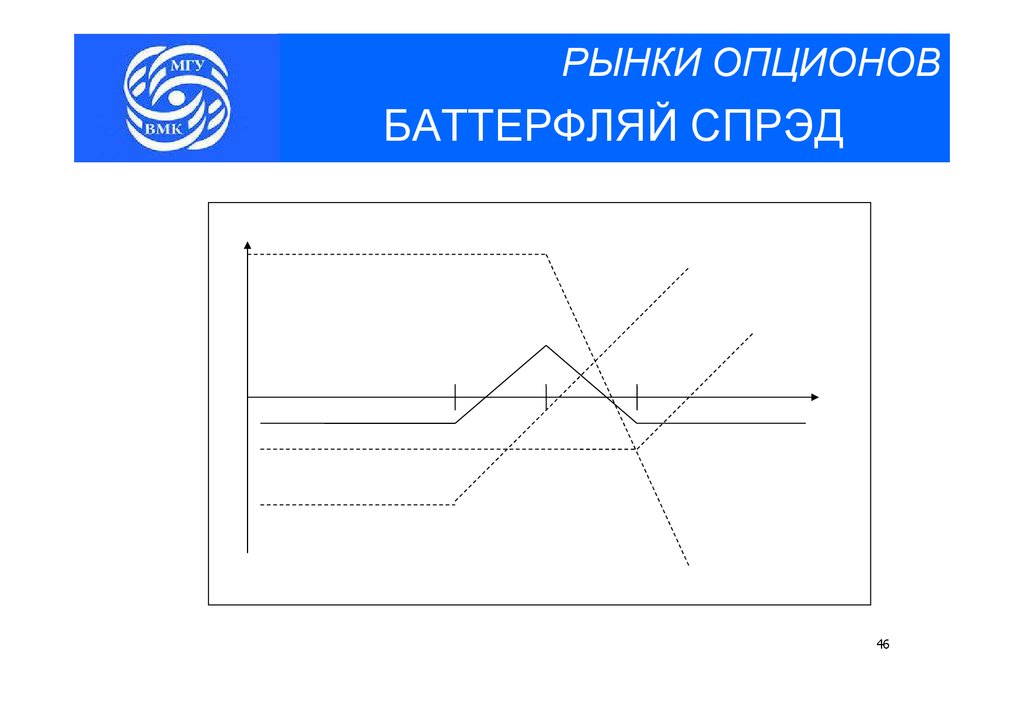
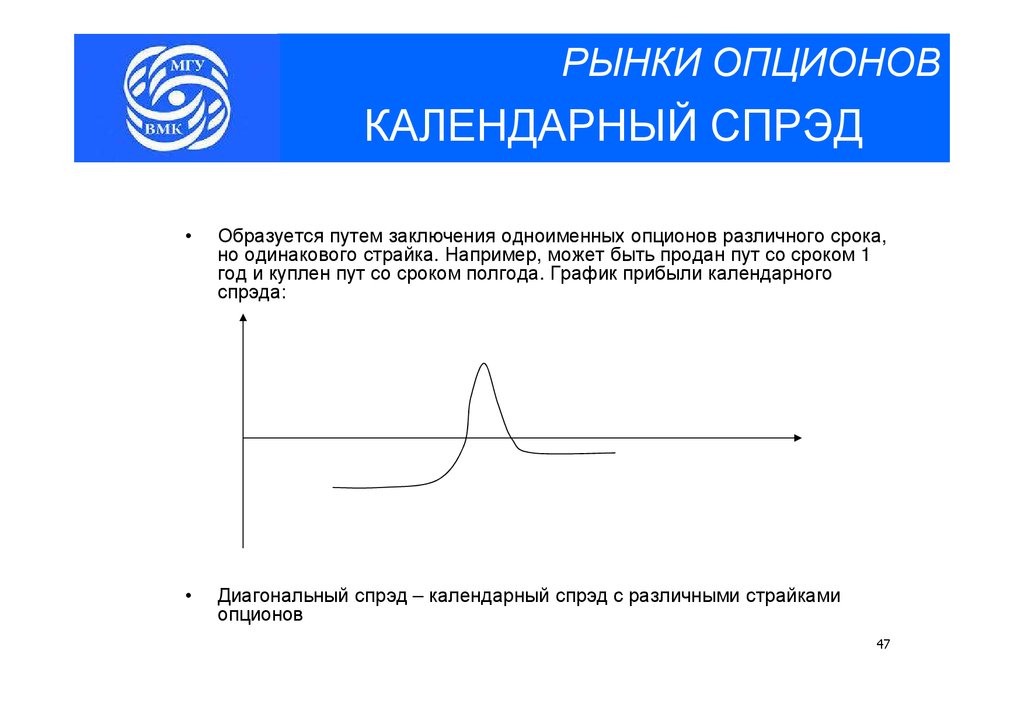




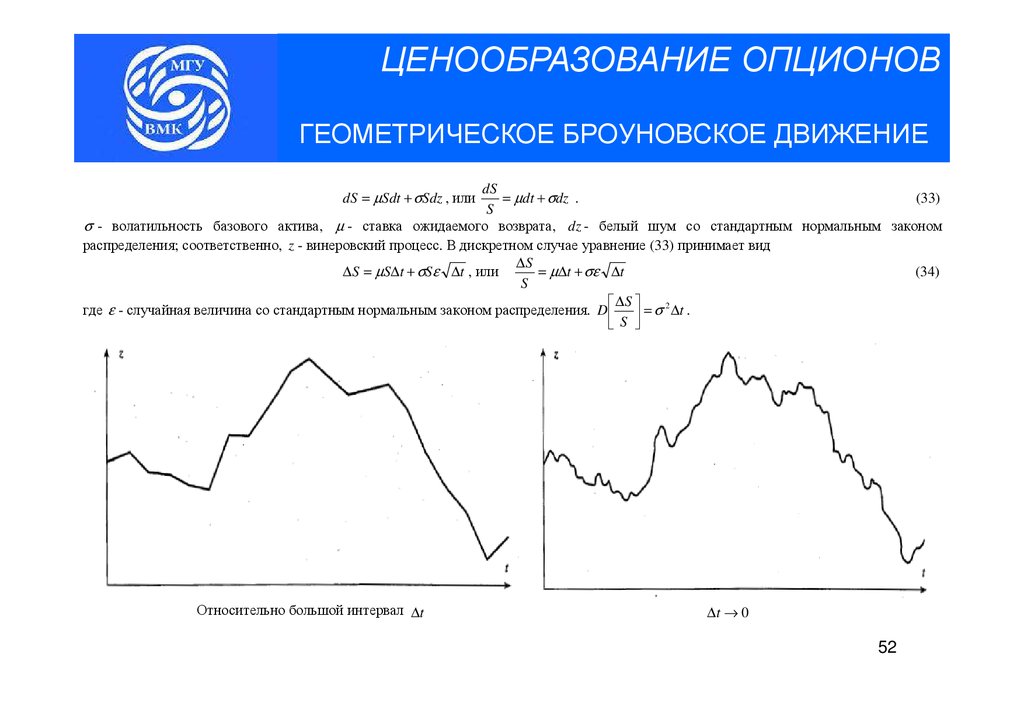




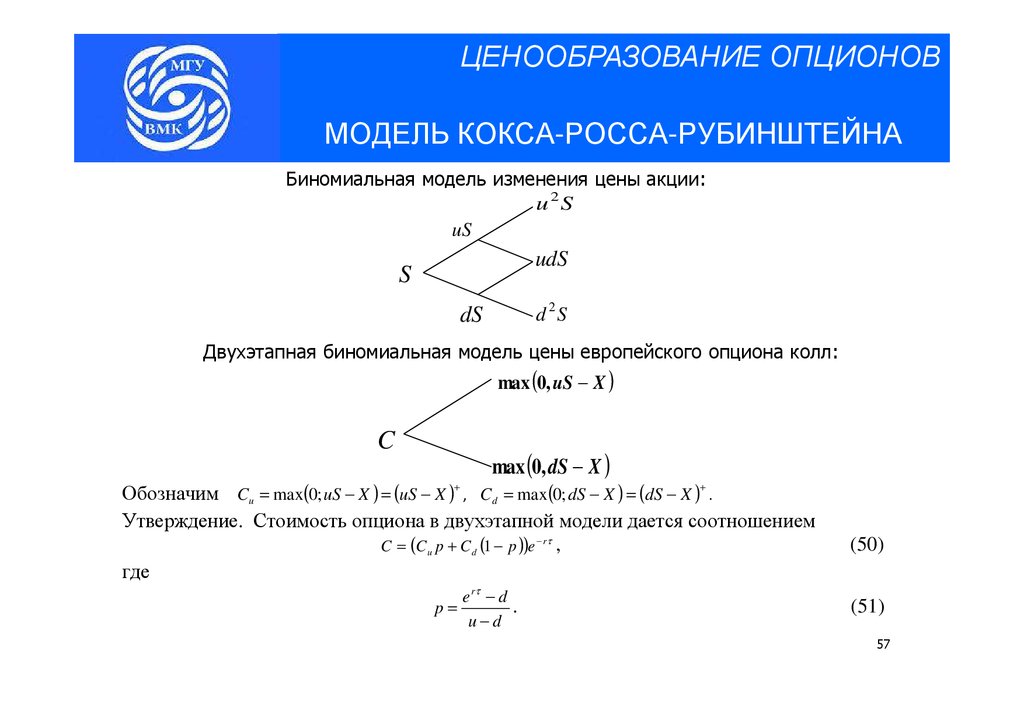



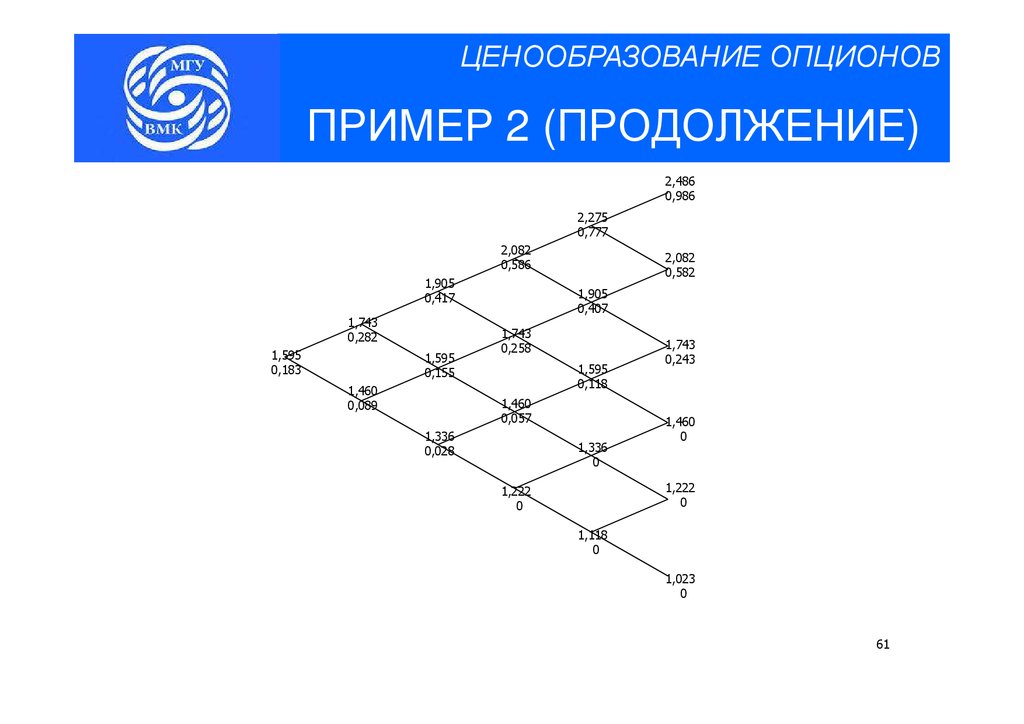





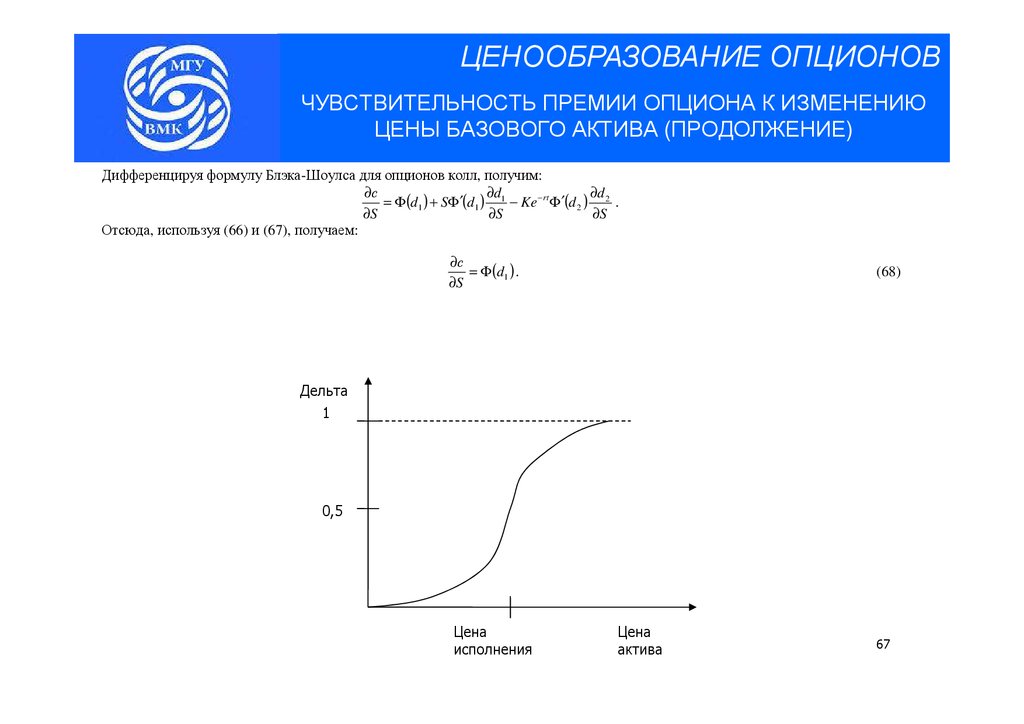
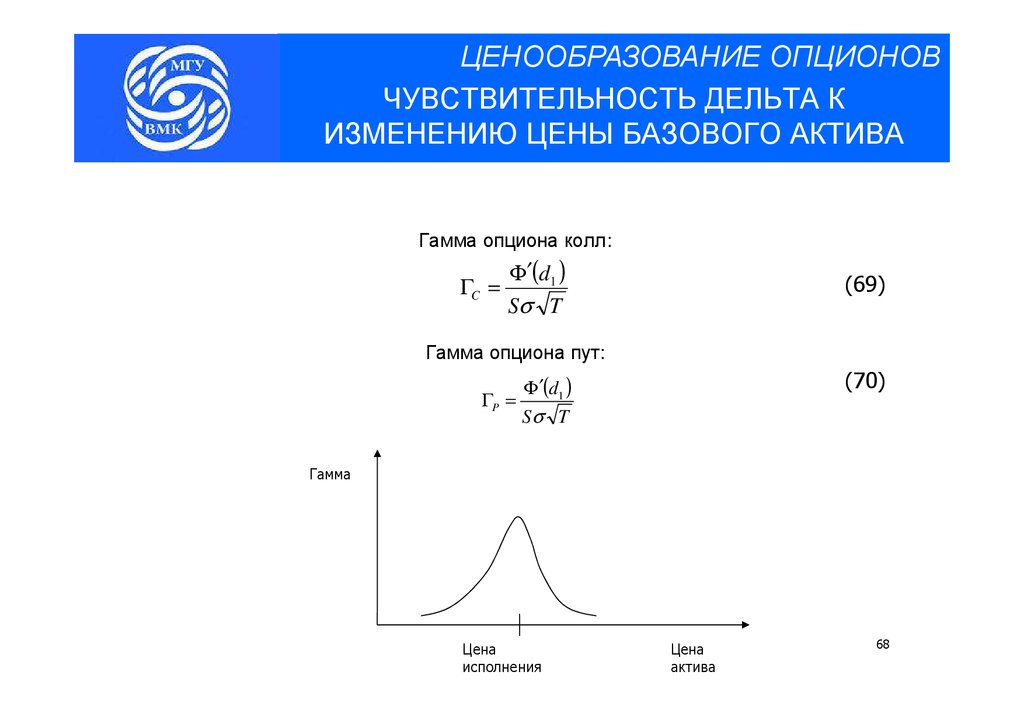

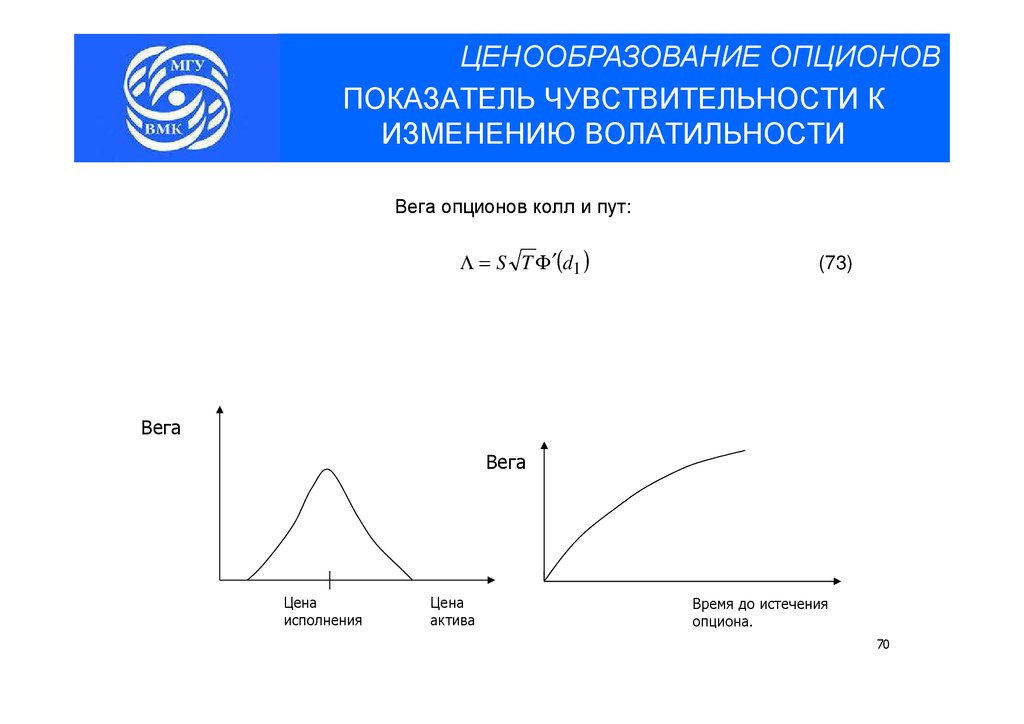


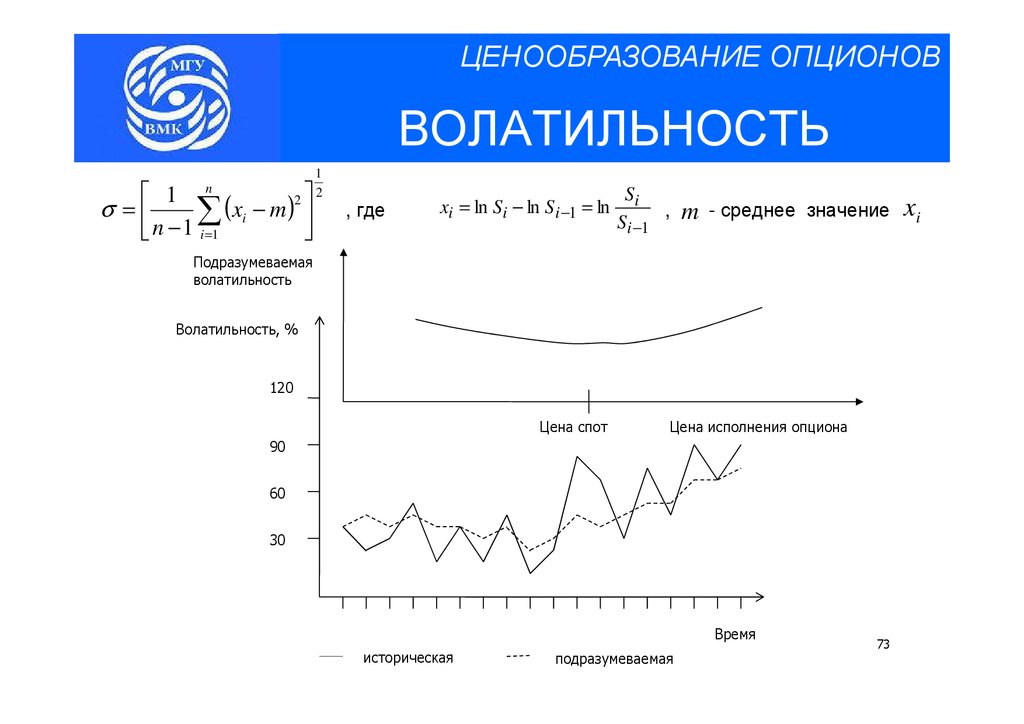
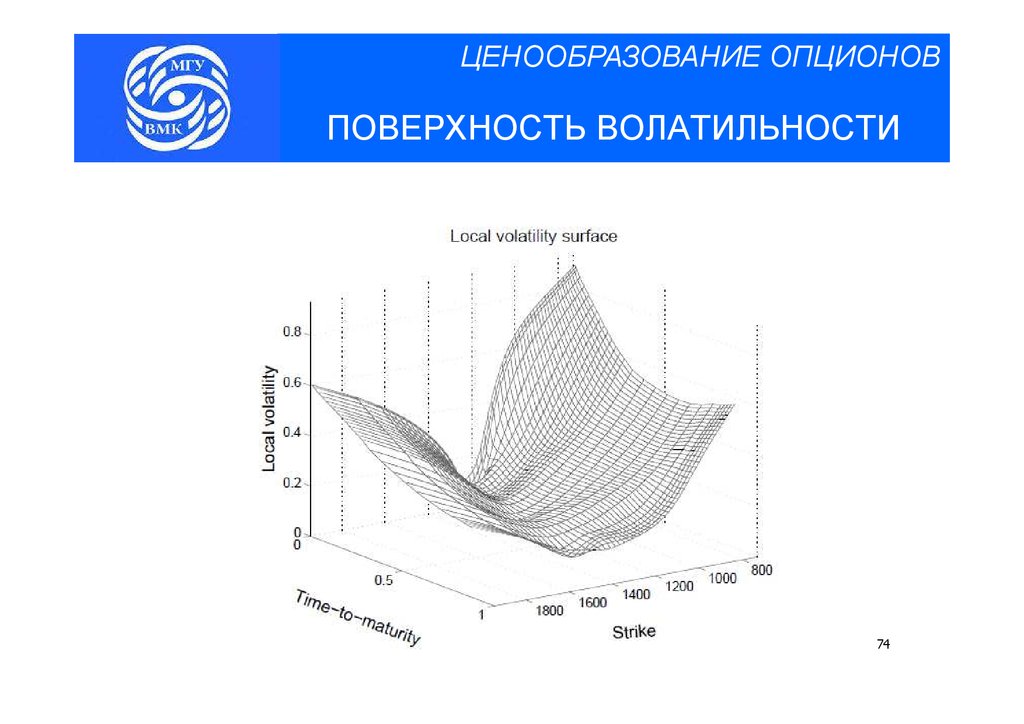
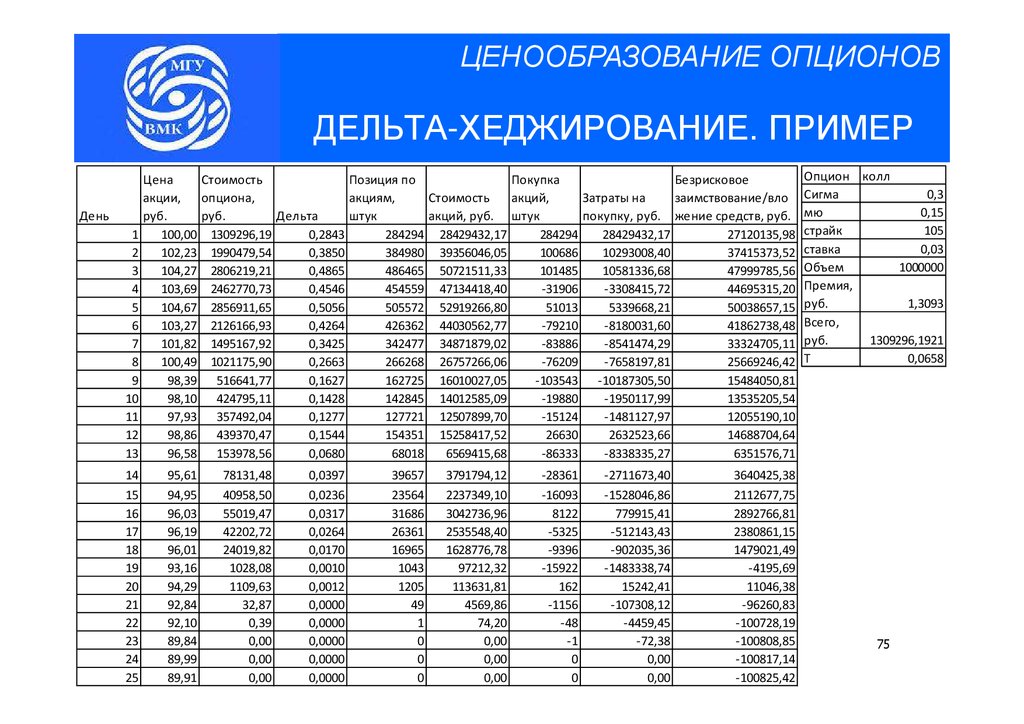

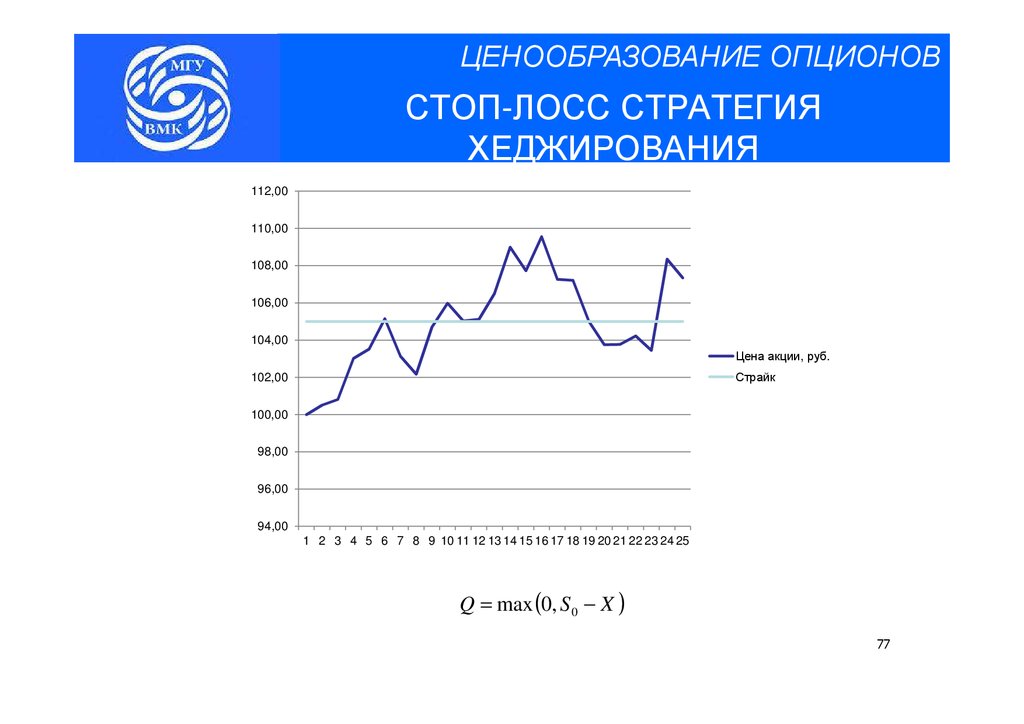
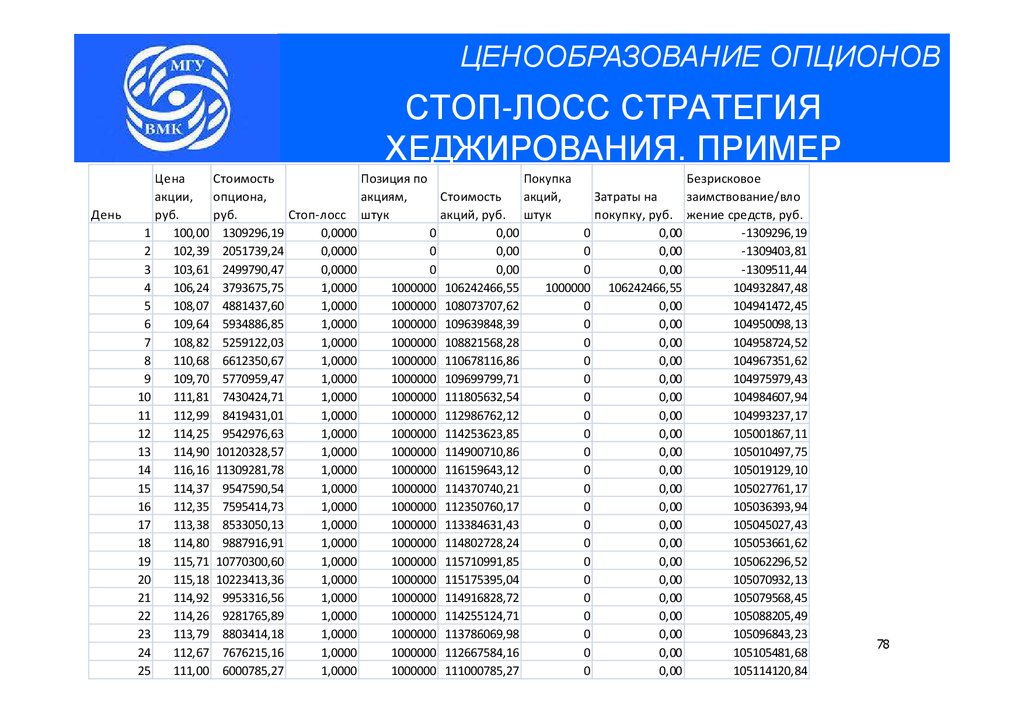
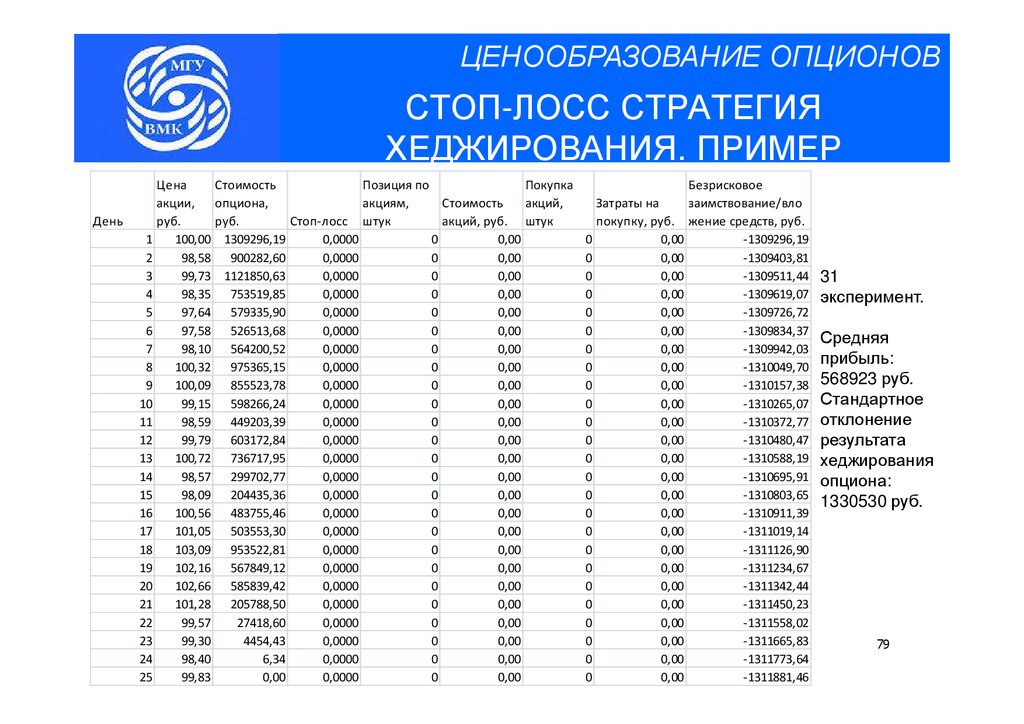


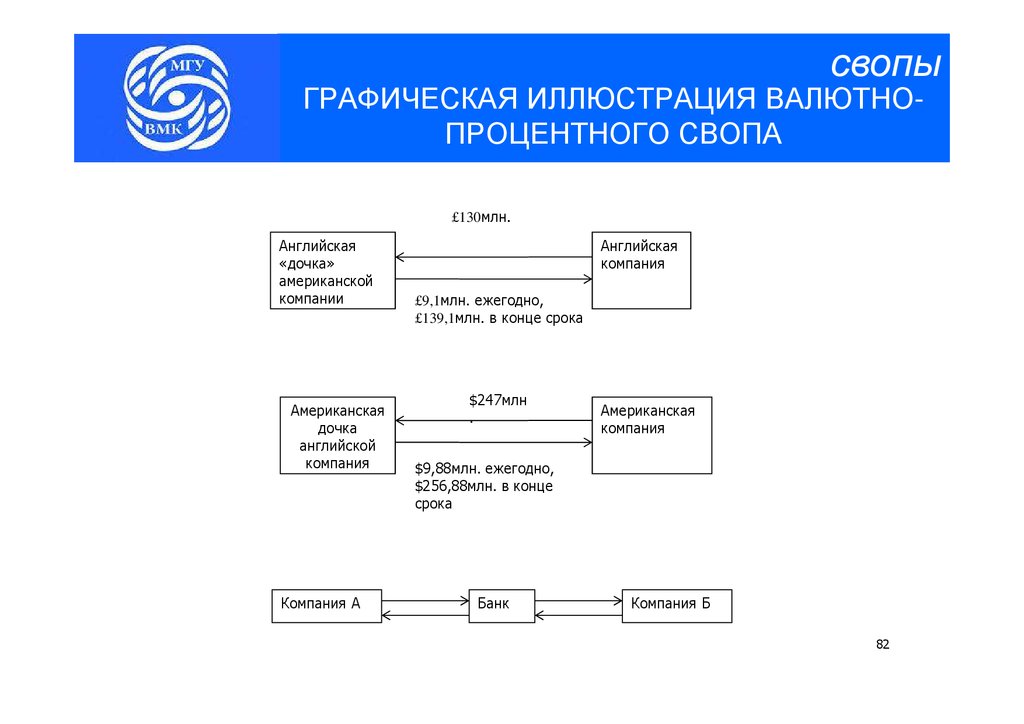






















 finance
finance








